DOI: http://doi.org/10.14483/udistrital.jour.tecnura.2014.DSE1.a12

Topological challenges in multispectral image segmentation

Retos topológicos en la segmentación de imágenes multiespectrales

José Antonio Valero Medina*, Iván Alberto Lizarazo Salcedo**, Paul Elsner***

* Systems Engineer, master in Teleinformatics, PhD student in engineering. Associate Professor of the Universidad Distrital Francisco José de Caldas. Bogotá, Colombia. Contact: jvalero@udistrital.edu.co
** Civil Engineer, PhD in Geography. Titular Professor of the Universidad Distrital Francisco José de Caldas. Bogotá, Colombia. Contact: ilizarazo@udistrital.edu.co
*** Physical Geographer. PhD in Geography. Lecturer in Geographical Information Science and Physical Geography, University of London. London, United Kingdom. Contact: p.elsner@bbk.ac.uk

Fecha de recepción: June 10th, 2014 Fecha de aceptación: November 4th, 2014

Citation / Para citar este artículo: Rodríguez, A. A., Perdomo Orjuela, L. E., Santamaría Piedrahíta, F., & Gómez Vargas, C. A. (2014). Transient surges analysis in low voltage networks. Revista Tecnura, 18 (Edición especial doctorado), 136-149. doi: 10.14483/udistrital.jour.tecnura.2014.DSE1.a12

Abstract

Land cover classification from remote sensing multispectral images has been traditionally conducted by using mainly spectral information associated with discrete spatial units (i.e. pixels). Geometric and topological characteristics of the spatial context close to every pixel have been either not fully treated or completely ignored. This article provides a review of the strategies used by a number of researchers in order to include spatial and topological properties in image segmentation. It is shown how most of researchers have proposed to perform -previous to classification- a grouping or segmentation of nearby pixels by modeling neighborhood relationships as 4-connected, 8-connected and (a, b) - connected graphs. In this object-oriented approach, however, topological concepts such as neighborhood, contiguity, connectivity and boundary suffer from ambiguity since image elements (pixels) are two-dimensional entities composing a spatially uniform grid cell (i.e. there are not uni-dimensional nor zero-dimensional elements to build boundaries). In order to solve such topological paradoxes, a number of approaches are proposed. This review discusses how the alternative of digital images representation based on Cartesian complexes suggested by Kovalevsky (2008) for image segmentation in computer vision, does not present topological flaws that are typical for conventional solutions based on grid cells. However, such approaches have not yet been applied to multispectral image segmentation in remote sensing. This review concludes suggesting the need to research on the potential of using Cartesian complexes for multispectral image segmentation.

Keywords: multispectral images, segmentation, topologic space.

Resumen

La clasificación de la cobertura de la tierra a partir de imágenes multiespectrales de sensores remotos tradicionalmente se ha llevado a cabo usando principalmente la información espectral asociada con los píxeles. Las características geométricas y topológicas del contexto espacial cercano a un píxel particular han sido usualmente ignoradas o tratadas de una manera incompleta. En este artículo se realiza una revisión de las estrategias que han sido empleadas por diversos investigadores con el propósito de incluir características topológicas y espaciales en segmentación de imágenes. La revisión muestra cómo la mayoría de ellos se han enfocado en realizar, antes de la clasificación, un agrupamiento o segmentación de los píxeles cercanos modelando las relaciones de vecindario como grafos 4-conectados, 8-conectados y (a,b)-conectados. Sin embargo, en este enfoque orientado a objetos, conceptos topológicos como vecindario, contigüidad, conectividad y límite sufren de ambigüedad ya que los elementos de la imagen (píxeles) son entidades bidimensionales que componen una retícula espacialmente uniforme. Existen algunas propuestas alternativas que buscan resolver dichas paradojas topológicas. En este artículo se analiza cómo la representación alternativa de imágenes digitales con base en complejos cartesianos sugerida por Kovalevsky (2008), para la segmentación de imágenes de visión de computador, no presenta las paradojas topológicas de las soluciones convencionales basadas en retículas. Sin embargo, dicha propuesta no se ha explorado en los procesos de segmentación y clasificación de imágenes de sensores multiespectrales. Esta revisión concluye sugiriendo la necesidad de investigar el potencial de los complejos cartesianos en la segmentación de imágenes multiespectrales.

Palabras clave: espacio topológico, imágenes multiespectrales, segmentación.

Introduction

Land cover classification from remote sensing images has been traditionally conducted by using mainly spectral information associated with discrete spatial units (i.e. pixels). However, there have been a number of attempts to include both geometric and topological characteristics of the pixel neighborhood in the image analysis process (de Jong & Van der Meer, 2004). In the last decade, a number of concepts, methods and techniques for object-oriented image analysis (OBIA) have been developed and evaluated (Blaschke, 2010). The OBIA analysis process starts by grouping spectrally similar and spatially close pixels into segments. A meaningful segmentation is essential for the subsequent analysis stages (Lizarazo & Elsner, 2009).

Most of the multispectral image segmentation algorithms assume images are a continuous space similar to the real world they depict. However, the digital representation that is finally available in any computer is performed by sampling the space and discretizing reality. In addition, multi and hyper-spectral digital images are composed of square picture elements with similar size, which is clearly inaccurate (Cracknell, 1998). This inaccuracy is present in representations of images such as 4-connected, 8-connected and -connected graphs (Rosenfeld, 1970; Kong & Rosenfeld, 1991).

Digital image processing based on representations of space that do not meet the topological axiomatic postulates causes finally geometric algorithms to be affected by paradoxes that lead to ambiguous or erroneous decisions. While it can be accepted that a raster image matches human perception to some degree, the truth is that several important concepts for image analysis, such as the connectivity of regions, their boundaries, and the adjacency between them, are ambiguously represented. This lack of topological awareness of grid-based image representation is clearly an important limitation for image analysis in computer environments (Kovalevsky, 1989). The alternative approach of digital images representation is based on complex Cartesian, suggested by Kovalevsky (2008). This concept does not present topological paradoxes that are typical of conventional solutions based on grid cells. Kovalevsky (2006) suggested such an alternative image representation using axiomatic locally finite spaces (ALFS) based on Cartesian complexes, a type of abstract cell complexes (ACC) (Listing, 1862). It has been stated that this alternative space does not arise topological paradoxes commonly found in conventional solutions (Pavlidis, 1977; Kovalevsky, 1984). Furthermore, it has been suggested that this alternative spaces could be a strong foundation for image segmentation in computer vision (Kovalevsky, 2006). However, to the best knowledge of the author, the usage of such ALFS spaces has not been yet explored for segmentation and classification of remotely sensed multispectral images.

On the other hand, it is well known that algorithms based on geometric characteristics have high complexity since the number of possible situations to be considered increases significantly as it increases objects' dimension under evaluation (Worboys & Duckham, 2004). Additionally, another problem that arises during the implementation phase of geometric algorithms is the impossibility of having an accurate arithmetic in terms of real numbers (de Berg, Cheong, Kreveld, & Overmars, 2008). A number of authors have attempted to reduce this algorithmic complexity of geometric spaces by selecting a subset of geometrical characteristics and transforming them into combinatorial structures using oriented matroids (Whitney, 1935; Oxley, 2003; Richter-Gebert & Ziegler, 2004). Examples for complex applications that have benefitted from such approaches are counter clockwise (CC) systems (Knuth, 1992), triangulation of point sets (Pfeifle & Rambau, 2002; de Loera, Rambau, & Santos, 2010), and terrain visibility analysis (Saeedi, 2012). While algorithmic complexity is part of the research reported here, it will not be further discussed due to lengths limitations.

This article begins introducing digital image segmentation basic principles. Next, it shows several attempts for involving geometric and topologic features in image segmentation. Then, it describes how Kovalevsky`s (2008) proposal unambiguously includes topologic feature through the definition of digital topological spaces. Finally, conclusions are presented.

DIGITAL IMAGES SEGMENTATION

Traditional image segmentation is the process of subdividing an image into smaller regions based on some notion of homogeneity or cohesiveness among groups of pixels (Grady, 2012). Regions are determined by two dual kind of methods (Brun, Mokhtari, & Domenger, 2003): (i) the edge-detection methods, and (ii) the region based segmentation methods. The former determine edges between regions and then close them in order to define a partition. The latter group pixels according to a homogeneity criterion aiming to obtain a partition of the image into homogeneous regions. The segmentation on an image X (the space domain) subdivides it, based on a function (the feature domain) defined on X, using a logical predicate P on subsets S of X (Equation (1) (Horowits & Pavlidis, 1976).

where e is a prescribed error tolerance. It should be noted that in general, for multispectral images, the space domain 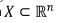and the feature domain 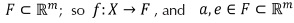. A segmentation of X is a partition of X into subsets S_j ,i = 1, ... , m for some such that: (i) 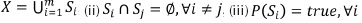, and 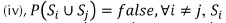and S_j are adjacent in X. The conditions (i) and (ii) ensures that the image is partitioned into a set of regions. The condition (iii) ensures that each region is homogeneous according to the homogeneity criterion P. The condition (iv) ensures that all regions are maximal, thus that any merge of two adjacent regions produces a non-homogeneous region (Brun, Mokhtari, & Domenger, 2003). Region detection methods can be addressed by two ways (Horowits & Pavlidis, 1976): The first one, also referred to as merging or bottom-up, divides the image into a large number of small regions, which are then merged to form larger regions. The other one, also referred to as splitting or top-down, successively divides the image into smaller and smaller regions until certain criteria are satisfied.

The information provided by a partition may be mainly geometric or topological. The geometrical information relate to each region considered separately from the partition. The set of pixels composing one region, the region including one pixel or the boundary of a given region, may be classified as geometrical information. The topological information describe the relationships between regions. The set of regions adjacent to a given region or the set of regions included in one region belong to the topological information field (Brun, Mokhtari, & Domenger, 2003).

Image segmentation can be seen as a labeling problem (Ishikawa, 2012), taking from the image only the neighborhood topologic relationships and putting them on an undirected region adjacency graph (RAG) (Brice & Fennema, 1970; Cheevasuvut, Maitre & Vidal-Madjar, 1986; Guigues, Ie Men & Cocquerez, 2001) along with a set of labels. The problem is then to find the best labeling according to the criteria in the problem's requirements. An energy is a translation of the criteria into a function that evaluates how good the given labeling is. A smaller energy for a labeling means a better corresponding solution to the problem. Thus, the problem becomes an energy minimization one that can be solved using general algorithms. As minimization of such energies, in general, is known to be NP-hard, graph cuts methods utilizing the s-t mincut algorithms known in operations research are used.

For segmentation quality assessment, it is common to use similarity metrics between a reference segmentation and the segmentation obtained, see, for example, Neubert, Herold, Meinel, & Blaschke (2008) (Lizarazo, 2014).

PREVIOUS WORK ON TOPOLOGY PRESERVING SEGMENTATION

Kovalevsky (1989) showed how abstract cell complexes allow for implementing topological relations needed to unambiguously perform segmentation of digital images in computer vision by developing some algorithms (Kovalevsky, 2001), (Kovalevsky, 2005). However, the authors are not aware of recent studies that rigorously evaluate the appropriateness of Kovalevsky's approach.

Felzenszwalb & Huttenlocher (2004) addressed the image segmentation problem by defining a predicate for measuring the evidence for a boundary between two regions using a graph-based representation of the image (Urquhart, 1982), (Zahn, 1971) and developing a greedy algorithm. An important characteristic of the method is its ability to preserve detail in low-variability image regions while ignoring detail in high-variability regions. The evidence for a boundary between two regions is measured by comparing intensity differences across the boundary, and intensity differences between neighboring pixels within each region.

Yu et al. (2006) assessed the capacity of Digital Airborne Imaging System (DAIS) high resolution images and topographic data for vegetation classification. Image objects were generated using the fractal network evolution (FNEA) segmentation approach by considering spectral, textural, topographic and geometric attributes. Initially for FNEA each pixel is an image object. Then, pairwise objects are subsequently merged to form bigger objects by using as merging criterion that the average image objects heterogeneity weighted by their size in pixels should be minimized (Baatz & Schape, 2000), (Benz, Hofmann, Willhauck, Lingelfelder, & Heynen, 2004). Through a hierarchical classification scheme and a set of features selected for each vegetation category, the authors carried out a detailed classification and obtained much more accurate results than those provided by the conventional pixel-based nearest neighbor and maximum likelihood methods. Furthermore, they claimed to achieve full correction of the salt-and-pepper effect present in the latter classification technique.

Kong, Xu, & Wu (2006) extracted land use information from a high spatial resolution image by using a multi-scale image segmentation approach. Urban land use was divided into different levels forming a hierarchical network structure, in which objects on the upper level are composed of objects in the lower level. Classification of image objects was performed based on attributes of color, shape, hierarchy and correlation characteristics between neighboring objects. Results showed that by including a variety of spectral and spatial features, it was possible to differentiate urban land use categories that cannot be separated through conventional per-pixel classification methods based on spectral data only.

Letscher & Fritts (2007) introduced a hybrid split-merge method for image segmentation based on computational geometry and topology by using persistent homology. The algorithm uses edge-directed topology to split the image into three types of regions based on Delaunay triangulations of points in the edge map. One type of region corresponds to objects of interests, and the remaining two types correspond to smaller regions that can be attached either to the first ones or form new objects themselves. Preliminary results showed a high quality image segmentation.

Johansen, Coops, Gergel, & Stange (2007) assessed the capacity of high spatial resolution satellite images to discriminate structural stages of vegetation in forest ecosystems. Based on semivariogram (Tso & Mather, 2009) experiments, they established that the most appropriate windows sizes for textural analysis were 3 x 3 and 11 x 11 pixels. They subsequently applied an object-oriented spectral and textural classification algorithm to produce a map of structural vegetation classes. The joint use of spectral and texture features improved thematic accuracy between 2% and 19% compared to the accuracy based only on spectral features.

Li & Sun (2010) proposed an "active image" segmentation method that distorts the image in order to match the so-called "initial" outlines and be able to segment multiple objects simultaneously. The deformation field was modeled using B-Spline free-form deformations. By penalizing the bending energy, they claimed to preserve both shape and local topology of objects of interest. Preliminary results, obtained using both synthetic and real images, showed that the proposed method allowed coping with low-contrast and occlusion issues that cannot be overcome using simple criteria for image segmentation.

Arbeláez P., Maire, Fowlkes, & Malik (2011) presented a unified approach to contour detection and image segmentation. To produce high-quality image segmentations, the contour detector is linked with a generic grouping algorithm consisting of two steps. In the first one, a new image transformation called the Oriented Watershed Transform (OWT) is introduced for building a hierarchical segmentation by exploiting the information in the contour signal (Arbeláez P., Maire, Fowlkes, & Malik, 2009). In the second one, using an agglomerative clustering procedure, an initial graph is built where the nodes are the initial regions. The links are the initial arcs separating adjacent regions, and the weights are a measure of dissimilarity between regions. The algorithm proceeds by sorting the links by similarity and iteratively merging the most similar regions. The process produces a tree of regions where leaves are the initial regions, the root is the entire image, and the inclusion relation orders the regions in a multiscale fashion.

Chen, Freedman, & Lampert (2011) proposed a new method for integrating image topological properties within a random field image segmentation model that does not pose topological restrictions in the energy minimization stage. Using such approach, they claimed to achieve an image segmentation that guarantees topological properties. It should be noted, however, that they used a graph-based image representation based on the conventional (and inaccurate) 4-connected and 8-connected neighborhood relationships.

Arbeláez P., Maire, Fowlkes, & Malik (2009) proposed a bottom-up strategy improving the agglomeration using more information besides boundary mean. Using supervised machine learning techniques they predicted whether two super pixels should be merged or not. In case of obtaining features combination lacking training data, additional training examples are generated by applying an active learning paradigm at every agglomeration hierarchy level. In active learning, the algorithm determines what example it wants to learn from at each iteration, based on the previous training data. The learning process is checked for accuracy using a coarse-scale ground truth image. They report the usage of a region adjacency graph (RAG), but do not provide a special topological representation for it.

To summarize: It is apparent that, unlike the Kovalevsky's approach, no other proposed method reports the usage of a space representation meeting the axiomatic postulates for topological spaces. Other approaches assume the correctness of either the underlying image representation using the conventional grid cell model or the graph-based image representation using 4- and 8-connected connectivity.

AXIOMATIC LOCALLY FINITE SPACES (ALFS)

The classical conception of space applied in geographic information systems (GIS) and multispectral imaging analysis is based on several concepts, including continuity. Continuity refers to the fact that a region can be always subdivided into smaller sub-regions (Stell & Webster, 2007). This concept is also known as dense sets (Worboys & Duckham, 2004). However, the digital representation is performed through space sampling that discretizes reality. As it is impossible to find a bijective function (Cantor, 1883), traditional models of digital representation of geographical phenomena (Schneider, 1977) suffer from imprecision and inaccuracy and do not include, in the particular case of the digital images, a measure of topology. These imprecisions and inaccuracies are particularly significant when geographical relationships are modeled based on concepts such as neighborhood, contiguity, connectivity and boundary. If the digital representation of those relationships is not expressed properly, GIS technology may not be able to give appropriate responses to several typical problems for remote sensing image analysis such as segmentation and classification.

Multi and hyper spectral digital images are composed of square picture elements with similar size, which is clearly inaccurate (Cantor, 1883). This inaccuracy is present in representations of images such as 4-connected, 8-connected and -connected graphs (Rosenfeld, 1970; Kong & Rosenfeld, 1991).

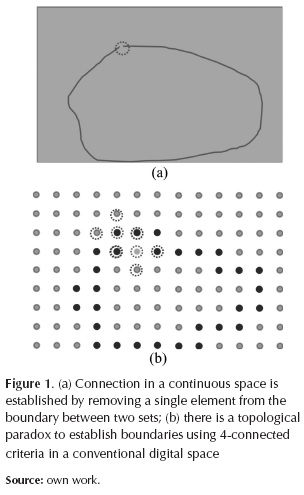
Figure 1(a) illustrates that in a continuous space, withdrawing a point from the boundary between the interior and exterior sets, previously disconnected by a Jordan curve, these become connected. Figure 1(b) shows how, in a discrete space, removing the element encircled in red from the boundary (blue points) does not connect the corresponding interior and exterior sets based on the 4-connected criterion, which is illustrated using two neighborhoods (the central element of each one is depicted as a point encircled in red). Actually, it is not possible either to establish unambiguously such a connectivity using the 8-connected criterion. In this case, for the example shown, the two sets remain always connected even without removing the element under consideration from the boundary.

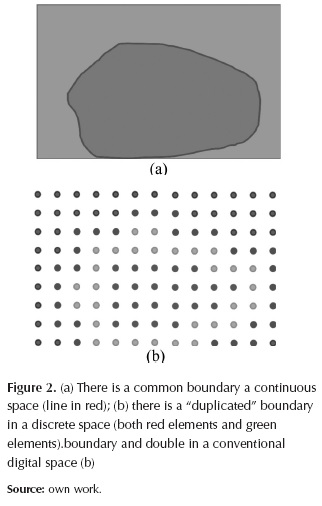
Figure 2a shows how, in a continuous space, the boundaries of the interior and exterior sets, are one-dimensional and coincide perfectly (red line). Figure 2b shows how, in the conventional digital space, each of the two sets have different boundary (exterior's boundary is red and interior's boundary is green), and that both boundaries are two-dimensional (all the elements comprising this space are two-dimensional). These paradoxes are particularly significant for image segmentation and classification when considering topological relationships such as neighborhood, contiguity, connectivity, and boundary.

Digital image processing based on representations of space that do not meet the topological axiomatic postulates (Munkres, 1999) causes finally geometric algorithms are affected by paradoxes that lead to ambiguous or erroneous decisions. Several important concepts for image analysis, such as the connectivity of regions, their boundaries, and the adjacency between them, are not explicitly represented. This lack of topological awareness of grid-based image representation is clearly an important limitation for image analysis in computer environments (Kovalevsky, 1989, 2005)

Kovalevsky (2008) performs a compendium of his proposal for the construction of a discrete geometry based on the Cartesian complex using the definition of topological spaces based on the axiomatic locally finite spaces provided by abstract cell complexes. His proposal seeks to provide an alternative representation of space based on a digital topology which is not affected by the paradoxes found on conventional representations of images such as 4-connected, 8-connected and (a, b) - connected graphs (Rosenfeld, 1970; Kong & Rosenfeld, 1991). In his work, Kovalevsky shows how Cartesian complexes allow for implementing topological relations needed to perform digital images segmentation without any ambiguity. A digital space should be a locally finite space in which each element has a neighborhood composed finitely of several elements with various topological properties. A locally finite space (LFS) is a non-empty set in which each element is assigned other elements, some being finite subsets. An LFS is called an axiomatic LFS (ALFS) when satisfies the following four axioms:

Axiom 1: For each space element there are certain subsets containing it, which are its neighborhoods. The intersection of two neighborhoods of an element is also a neighborhood of that element.

Axiom 2: There are space elements whose smallest neighborhood (SN) consists of more than one element.

Axiom 3: The frontier Fr (T, S) of any subset T ⊂ S is thin.

Axiom 4: The frontier of the frontier of a subset of an LFS is equal to the frontier of the subset.

Since the space is locally finite, there exists the smallest neighborhood (SN) for each of its elements that is the intersection of all the neighborhoods of a particular element. If one element belongs to the SN of the other, it is said that the one is incident (IN) to the other. An incidence path (IP) between a pair of elements of a subset of an LFS is a sequence of elements between the one and the other in which each pair of subsequent elements are incident. If it is possible for each pair of elements of a given subset of an LFS to find an IP entirely contained in that subset, it can be said that the subset is connected (CN). However, the classical topology of a space is defined if a set of subsets of S called the open subsets, satisfies the following axioms (Munkres, 1999):

Axiom C₁: The entire set and the empty subset θ are open.

Axiom C₂: The union of any number of open subsets is open.

Axiom C₃: The intersection of a finite number of open subsets is open.

Axiom C₄: The space has the separation property.

As for the axiom C₄, in the case of LFSs, is only needed that for any pair of elements of the space there is an open subset which contains exactly one of the elements (axiom of separation T₀). The LFS open set concept is materialized for a subset 0 when along with each element contains its SN. When it contains all the elements of its frontier it is closed. Open subsets so defined satisfy the conditions of the axioms C₁ to C₃ and, therefore, are open in the classic sense. The SN of any element of an ALFS is open in the classic sense and is called the smallest open neighborhood (SON) of a given element of the space. All elements bounded by a given element are part of its SON. The SON of an element of the space satisfies the axiom of separation (T₀).

Abstract Cells Complexes

An important special case of LFS are abstract cells complexes (Listing, 1862). In this case, the space is characterized by a relationship of partial order among its elements and a function of dimension dim (a) which maps to an element of the space a non-negative integer so that if another element b ε SON (α), then dim (α) ≤ dim (b). If dim (α) = k, then the element α is of dimension (k-dimensional).

An abstract cells complex (ACC) C= (E,B, dim) is a set E of abstract elements (cells) with a binary bounding relationship B ⊂ ExE which is antisymmetric, irreflexive and transitive among its elements and a function dim E →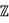⁺ provided dim (e´)< dim (e´´) for (e´, e´´) ε B. Between two elements α and k of an ACC establishes a bounding path if it is possible to find a sequence of elements between and so that each element bounds the following. The number of elements in the sequence minus one is the bounding path length. The dimension of a complex is given by the greatest dimension of all its cells. Given 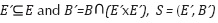is a subcomplex of C. A subcomplex will be open or closed depending on the complex from which is subcomplex.

For example, given the complex C=(E,B) where 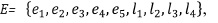the dimension function is such that dim(e_i) < dim(l_j) with 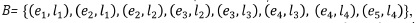the subcomplex T= (E´, B´) with is neither open nor closed in C. However, for the subcomplex E= (B´´, B´´) with 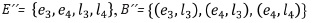and the same dimension function definition than before, T is open in S.

Given two subsets t and T of a space S such that 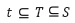, the set containing with each cell at also all cells of T bounding a is named the closure of t in T denoted by CL(t, T). The set t -Fr(t, T) is called the interior of t in T and is denoted by Int(t, T). The set t -T- Fr(t, T) is called the exterior of t in T and is denoted by Ext(t, T).

The size and shape of the SON of a cell c depends on the complex C with base in which this is defined and is denoted by SON(c, C). Two sub-complexes of a complex are mutually incidents, if any of the two contains at least one cell that is incident with any cell of the other.

CARTESIAN COMPLEXES AND COMBINATORIAL COORDINATES

A particular case of ACC are Cartesian complexes. A complex C=(E,B) where 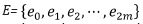with m ≥1, the bounding relationship B is such that each element e₁, with even index i, bounds the elements e_i+1, and e_i-1, with odd index, is a 1-dimensional connected ACC. Here each 0-dimensional cell is closed, while each 1-dimensional cell is open. The cells indexes are called combinatorial coordinates in the one-dimensional space.

Figure 3 shows a possible graphical representations of one-dimensional ACC of combinatorial coordinates. In the figure each complex's cell is represented as a point, only that conveniently appears the -dimensional cell with black color and the -dimensional with red.

A Cartesian ACC is obtained by performing the Cartesian product of two or more of these one-dimensional complexes. The cells set of a -dimensional Cartesian ACC Cⁿ is the Cartesian product of n one-dimensional connected ACC sets. The one-dimensional complexes are the coordinate axes of Cⁿ which become an -dimensional space. A cell of Cⁿ is an n-tuple c= (a₁, a₂, a₃, ..., a_n) of a_i cells belonging each one to a particular one-dimensional complex and becoming a component cell of c. In this case, a cell c₁= (a₁, a₂, a₃, ..., a_n) bounds another cell c₂= (b₁, b₂, b₃, ..., a_n) if for each pair of component cells a_i and b_i a_i = b_i or a_i bounds b_i. The dimension of a cell is the sum of the dimensions of its component cells.

For the one-dimensional ACCs 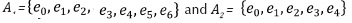, figure 4 shows a possible two-dimensional Cartesian ACC graphical representations. In the figure each complex's cell is represented as a point, but the cells have been differentiated by color.

Kovalevsky defined the combinatorial balls and spheres in order to avoid "weird" complexes (i.e. pathological cases). For example, for the 2-dimensional Cartesian complex represented in figure 4, the subcomplex 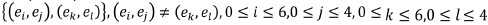is a 0-dimensional sphere and the subcomplex 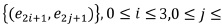is a 2-dimensional open ball.

The concept of ACC enables the definition of strange ACCs, but topological concepts such as of ball and sphere can constraint the set of valid complexes. These concepts are also necessary for increasing or reducing the granularity of Cartesian complex. To increase the granularity, the elementary subdivision is used, and to reduce it, the blocks definition. The elementary subdivision (Stilwell, 1995) of a 1-dimensional cell C¹, replaces it with two 1-dimensional cells C¹₁, C₂¹ and a 0-dimensional cell C⁰, so that the latter is a common face of the other two. In the case of 2-dimensional Cartesian complex shown in the figure 4 elementary cell subdivision must be conducted in combinatorial way on each of its two component cells, taking into account that, in general, the -dimensional cells are not subdivided.

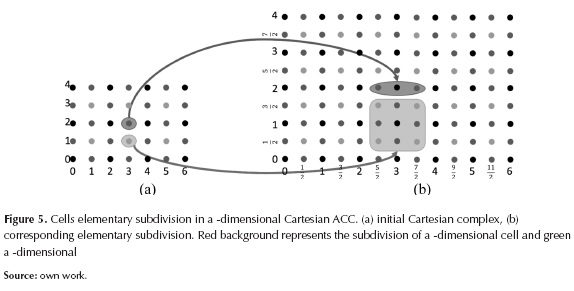
For example, in a 2-dimensional Cartesian complex, the elementary subdivision of a 2-dimensional cell (e_i, e_j) origins three Combinatorial ordered for each component cell 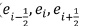and 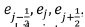, here the average indexes are closed, while integers are open). This produces nine 2-dimensional coordinates, four of them correspond to -dimensional cells, four to 1-dimensional and one is 0-dimensional as shown in figure 5. Two Cartesian complexes C₁ and C₂ are combinatorially homeomorphic if there are elementary subdivisions of C₁ and C₂ so obtained complexes are isomorphic.

Often in topological investigations and AC complexes applications to image analysis, the complexes contain thousands of cells, so it is recommended to subdivide a complex in sub-complexes that are considered uniform with respect to some criterion in particular. The result of dividing a cell complex in blocks where each one consists of a homogeneous group of cells based on a specific criterion is called blocks complex (Rinow, 1975), (Kovalevsky, 1989). Consider a partition R of an n-dimensional complex A in k-dimensional subcomplexes S_i^k (k= 0,1, ..., n,1_ 0,i, ..., m), the subsets with k = 0 are some representative 0-dimensional cells of A, while each of the subsets with k> 0 is combinatorially homeomorphic to α -dimensional ball. It is possible to define a complex B whose cells correspond to the sub-complexes S_i^k called the block complexes of A and their cells are called block cell. The subcomplexes S_i^k corresponding to the block cells are called blocks. Therefore, block cells are elements of the blocks complex, while the blocks are subcomplexes of the original cell complex. Each block cell dimension corresponds to the dimension of the respective subcomplex and the ith block with dimension m bounds jth block of dimension m,m > k, if there is in A two cell C₁ ε S_i^k and C₂ ε S^m_j such that c₁ bounds c₂. The triplet B(A) = (EB, BR, Dim) is called blocks complex of A if there is a partition of A in subcomplexes S_i^k every one homeomorphic to a k-dimensional open ball. EB is the set of block cells, each cell b_i ε EB, corresponds to a subcomplex S_i^k called the k-dimensional block or k-block of A. The ordered pair (b_i, b_j) block cells is in the bounding relationship BR if there is in A two cells C₁ ε S_i^k and C₂ ε S^m_j such that c₁ bounds c₂. Dimension function Dim assigns to each block cell b_i of B(A) the dimension of the corresponding block S^m_j.

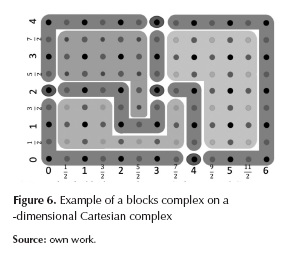
Figure 6 shows the elementary subdivision of figure 5 with a partition into 13 blocks. In figure are highlighted conveniently, with a background that surrounds the original cells, the sub-complexes corresponding to block cells of the blocks complex that would be obtained. The sub-complexes correspond to 0,1 and 2-dimensional open balls. From 35 0-cells, 58 1-cells and 24 2-cells of the original cells complex, there are four 0-block cell, six 1- block cell and three 2- block cell in the retrieved blocks complex.

DISCUSSION

It has been demonstrated that Kovalevsky´s (2006) alternative space representation does not arise topological paradoxes. Hence, it is suggested that these alternative space concepts could be a strong foundation for image segmentation in computer vision. Moreover, the usage of such ALFS spaces could be explored for remote sensing image analysis. Furthermore, it is relevant to investigate the potential of ALFS spaces for conducting a multispectral image segmentation that includes topological and geometric relationships besides spectral attributes.

It was discussed that conventional methods for remote sensing image segmentation are based on digital structures that violate well-established topological axioms and geometric algorithms that assume a continuous spatial computing model. Therefore, it is necessary to conduct a research to know how combinatorial properties of ALFS could allow the involvement of topological properties so that accuracy and efficiency of multispectral image segmentation algorithms can be improved.

In particular, it is necessary to evaluate an alternative multispectral image representation using Cartesian complexes in order to find an efficient solution to the segmentation process that takes into account topological and geometric properties. This implies to devise a conceptual model for multispectral image representation based on Cartesian complexes of abstract cells which takes into account topological and geometric properties. This can then build and evaluate a computational framework that enables the implementation of Cartesian complexes to adequately represent topological and geometric image-objects properties used in the segmentation of multispectral images.

The main hypothesis is that a spatial computational framework, based on the axiomatic locally finite spaces improves the accuracy of space algorithms for multispectral image segmentation, since using only combinatorial coordinates established by Cartesian complexes preserves topological and geometric image-objects properties.

The production of a computational framework that makes possible the representation of a digital image in a way that explicitly takes into account on topological data and uses it for digital image segmentation, would constitute a significant technological development. It would strengthen the ability of the Engineering Faculty at Universidad Distrital to produce useful solutions to technical problems and to improve geospatial knowledge.

Conclusions

Previous work attempting to produce topology preserving image segmentation in remote sensing used digital image representations that suffer from topological paradoxes. A more rigorous proposal for addressing such problems in computer vision image segmentation was suggested by Kovalevsky. It was shown that ALFS meet the classical axiomatic topological postulates and hence are able to unambiguously represent adjacency, connectedness and boundary relationships which are critical for appropriate multispectral image analysis, in particular image segmentation. It is therefore relevant and promising to conduct further in-depth research on the usage of Cartesian complexes for obtaining a topologically correct image representation in order to produce more accurate and effective image segmentation algorithms.

FINANCING

This article has been done as part of the project's research Doctoral in engineering entitled "Development of an Alternative Method for Multispectral Image Segmentation Based on Cartesian Complexes and Its Associated Oriented Matroids", which was endorsed by the doctoral program in engineering of the Universidad Distrital and funded by the University through Commission of studies granted between the period 2014I - 2016III.

References

Arbeláez, P., Maire, M., Fowlkes, C. & Malik, J. (2009). From Contours to Regions: An Empirical Evaluation. Proc. IEEE Conference Computer Vision and Pattern Recognition.         [ Links ]

Arbeláez, P., Maire, M., Fowlkes, C. & Malik, J. (2011). Contour Detection and Hierarchical Image Segmentation. IEEE Transactions on Pattern Analysis and Machine Intelligence (TPAMI), 33(5), 898-916.         [ Links ]

Baatz, M. & Schape, A. (2000). Multiresolution segmentation: An optimization approach for high quality multi-scale image segmentation. In J. Strobl, T. Blaschke & G. Griesebner (Edits.) Angewandte Geographische Informations-Verarbeitung, XII, 12-23.         [ Links ]

Benz, U. et al. Multi-resolution, object-oriented fuzzy analysis of remote sensing data for GIS-ready information. ISPRS Journal of Photogrammetry and Remote Sensing, 58(3-4), 239-258.         [ Links ]

Blaschke, T. (2010). Object based image analysis for remote sensing. International Society for Photogrammetry and Remote Sensing, Inc. (ISPRS), 65, 2-16.         [ Links ]

Brice, R. & Fennema, C. L. (1970). Scene analysis using regions. Artificial Intelligence, 1, 205-226.         [ Links ]

Brun, L., Mokhtari, M. & Domenger, J. P. (2003). Incremental modifications on segmented image defined by discrete maps. Journal of Visual Communication and Image Representation, 14(3), 251-290.         [ Links ]

Cantor, G. (1883). "Über unendliche, lineare Punktmannigfaltigkeiten V" [On infinite, linear point-manifolds (sets)]. Mathematische Annalen, 21, 545-591.         [ Links ]

Cheevasuvut, F., Maitre, H. & Vidal-Madjar, D. (1986). A robust method for picture segmentation based on a split and merge procedure. Graphical Models and Image Processing - CVGIP, 34, 268-281.         [ Links ]

Chen, C., Freedman, D. & Lampert, C. (2011). Enforcing topological constraints in random field image segmentation. IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2089-2096.         [ Links ]

Cracknell, A. P. (1998). Synergy in Remote Sensing -What's in a Pixel? International Journal of Remote Sensing, 19, 2025-2047.         [ Links ]

de Berg, M., Cheong, O., Kreveld, M. & Overmars, M. (2008). Computational Geometry: Algorithms and Applications (3rd ed.). Springer-Verlag Berlin Heidelberg.         [ Links ]

de Jong, S. M. & Van der Meer, F. D. (2004). Remote Sensing Image Analysis Including the Spatial Domain. Dordrecht, The Netherlands: Springer.         [ Links ]

de Loera, J., Rambau, J. & Santos, F. (2010). Triangulations: Structures for Algorithms and Applications. Verlag Berlin Heidelberg: Springer.         [ Links ]

Felzenszwalb, P. F. & Huttenlocher, D. P. (2004). Efficient graph-based image segmentation. International Journal of Computer Vision, 59(2), 167-181.         [ Links ]

Grady, L. (2012). Targeted Image Segmentation Using Graph Methods. In Processing and Analysis with Graphs: Theory and Practice, 111-140. CRC Press. Taylor & Francis Group.         [ Links ]

Guigues, L., Ie Men, H. & Cocquerez, J. P. (May de 2001). Graphs, cocoons and image segmentation. Third Workshop on Graph Based Representations in Pattern Recognition (GbR'2001), IAPR-TC15, CUEN. 22-31. Ischia, Italy.         [ Links ]

Horowits, S. L. & Pavlidis, T. (1976). Picture segmentation by a tree traversal algorithm. J. Association for Computing Machinery, 23(2), 368-388.         [ Links ]

Ishikawa, H. (2012). Graph Cuts-Combinatorial Optimization in Vision. In Image Processing and Analysis with Graphs: Theory and Practice, 25-64. CRC Press. Taylor & Francis Group.         [ Links ]

Johansen, K., Coops, N. C., Gergel, S. E. & Stange, J. (2007). Application of high spatial resolution satellite imagery for riparian and forest ecosystem classification. Remote Sensing of Environment, 110(1), 29-44.         [ Links ]

Knuth, D. (1992). Axioms and hulls. Berlin: Springer-Verlag.         [ Links ]

Kong, C., Xu, K. & Wu, C. (2006). Classification and extraction of urban land-use information from high-resolution image based on object multi-features. Journal of China University of Geosciences, 17(2), 151-157.         [ Links ]

Kong, T. Y. & Rosenfeld. (1991). Digital Topology, a Comparison of the graph based and Topological Approaches. In G. M. Reed, A. W. Ronscoe, & R. F. Wachter, Topology and Category Theory in Computer Science, 273-289. Oxford, U.K.: Oxford University press.         [ Links ]

Kovalevsky, V. A. (1984). Discrete topology and contour definition. Pattern Recognit, Lett. 2(5), 281-288.         [ Links ]

Kovalevsky, V. A. (1989). Finite Topology as Applied to Image Analysis. Computer Vision, Graphics, and Image Processing,45(2), 141-161.         [ Links ]

Kovalevsky, V. A. (2001). Algorithms and Data Structures for Computer Topology Digital and Image Geometry. Lecture Notes in Computer Science , 2243, 38-58.         [ Links ]

Kovalevsky, V. A. (2005). Algorithms in Digital Geometry Based on Cellular Topology Combinatorial Image Analysis. Lecture Notes in Computer Science, 3322, 366-393.         [ Links ]

Kovalevsky, V. A. (2006). Axiomatic Digital Topology. J Math Imaging, 26(41-58).         [ Links ]

Kovalevsky, V. A. (2008). Geometry of Locally Finite Spaces. Berlin, Germany: Editing House Dr Baerbel Kovalevski.         [ Links ]

Letscher, D. & Fritts, J. (2007). Image Segmentation Using Topological Persistence. Computer Analysis of Images and Patterns. Lecture Notes in Computer Science, 4673, 587-595.         [ Links ]

Li, C. & Sun, Y. (2010). Active Image: A Shape And Topology Preserving Segmentation Method Using B-Spline Free Form Deformations. Proceedings of 2010 IEEE 17th International Conference on Image Processing, 2221-2224.         [ Links ]

Listing, J. (1862). Der census räumlicher complexe. Abhandlungen der Königlichen Gesellschaft der Wissenschaften zu Göttingen, 10, 97-182.         [ Links ]

Lizarazo, I. (2014). Accuracy assessment of object-based image classification: another STEP. International Journal of Remote Sensing, 35(16), 1-22.         [ Links ]

Lizarazo, I. & Elsner, P. (2009). Fuzzy segmentation for object-based image classification. International Journal of Remote Sensing, 30(6), 1643-1649.         [ Links ]

Munkres, J. (1999). Topology (2nd ed.). Prentice Hall.         [ Links ]

Neubert, M., Herold, H., Meinel, G. & Blaschke, T. (2008). Assessing image segmentation quality concepts, methods and application. Object-Based Image Analysis. Lecture Notes in Geoinformation and Cartography, 769-784. Springer Berlin Heidelberg.         [ Links ]

Oxley, J. (2003). What is a matroid? Recuperado el 12 de abril de 2011, de Cubo 5: www.math.lsu.edu/~oxley/survey4.pdf.         [ Links ]

Pavlidis, T. (1977). Structural Pattern Recognition. New York: Springer-Verlag,         [ Links ].

Pfeifle, J. & Rambau, M. (2002). Computing Triangulations Using Oriented Matroids. ZIB-Report 02-02. Berlin: Konrad-Zuse-Zentrum für Informationstechnik.         [ Links ]

Richter-Gebert, J. & Ziegler, M. (2004). Oriented Matroids. En J. E. Goodman, & J. O'Rourke (Edits.), Handbook of Discrete and Computational Geometry, (2da ed., 29-151). Boca Raton: Chapman & Hall/CRC Press.         [ Links ]

Rinow, W. (1975). Textbook of topology. Berlin: VEB Deutscher Verlag der Wissenschaften.         [ Links ]

Rosenfeld, A. (1970). Connectivity in digital pictures. J. ACM, 17, 146-160.         [ Links ]

Saeedi, N. B. (2012). On Fully Characterizing Terrain Visibility Graphs. A thesis submitted in partial fulfillment of the requirements for the degree of Master of Science. The University of British Columbia.         [ Links ]

Schneider, M. (1977). Spatial Data Types for Database Systems: Finite Resolution Geometries for Geographic Information Systems. Lecture Notes in Computer Science, 1288.         [ Links ]

Stell, J. & Webster, J. (July de 2007). Oriented Matroids as a Foundation for Space in GIS. Computers. Environment and Urban Systems, 31(4), 379-392.         [ Links ]

Stilwell, J. (1995). Classical topology and combinatorial group theory. Springer.         [ Links ]

Tso, B. & Mather, P. (2009). Classification Methods for Remotely Sensed Data. Boca Raton, FL: CRC Press, Taylor & Francis Group.         [ Links ]

Urquhart, R. (1982). Graph theoretical clustering based on limited neighborhood sets. Pattern Recognition, 15(3), 173-187.         [ Links ]

Whitney, H. (1935). On the abstract properties of linear dependence. American Journal of Mathematics, 57, 509-533.         [ Links ]

Worboys, M. & Duckham, M. (2004). GIS: A Computing Perspective (2nd ed., 90-113). CRC Press.         [ Links ]

Yu, Q., Gong, P., Chinton, N., Biging, G., Kelly, M., & Schirokauer, D. (2006). Object based detailed vegetation classification with airborne high spatial resolution remote sensing imagery. Photogrammetric Engineering & Remote Sensing, 72(7), 799-811.         [ Links ]

Zahn, C. T. (1971). Graph-theoretic methods for detecting and describing gestalt clusters. IEEE Transactions on Computing, 20, 68-86.         [ Links ]