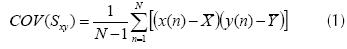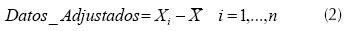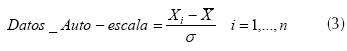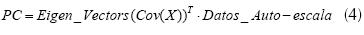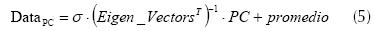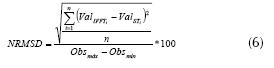Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Tecnura
versão impressa ISSN 0123-921X
Tecnura vol.19 no.44 Bogotá abr./jun. 2015
https://doi.org/10.14483/udistrital.jour.tecnura.2015.2.a03
DOI: http://dx.doi.org/10.14483/udistrital.jour.tecnura.2015.2.a03
PCA/DFT como herramienta de pronóstico para series temporales de absorbancia registradas mediante captores UV-Vis en sistemas de saneamiento urbano
PCA/DFT as forecasting tools for absorbance time series received by UV-Vis probes in urban sewer systems
Leonardo Plazas-Nossa*,
Andrés Torres**
* Ingeniero electrónico, magíster en Teleinformática, docente de la Universidad Distrital Francisco José de Caldas, Bogotá, Colombia. Contacto: lplazasn@udistrital.edu.co
** Ingeniero civil, especialista en gestión de ingeniería, magíster en Ingeniería Civil, doctor en Ingeniería, docente de la Pontificia Universidad Javeriana, Bogotá, Colombia. Contacto: andres.torres@javeriana.edu.co
Fecha de recepción: 12 de junio de 2014 Fecha de aceptación: 19 de enero de 2015
Citation / Para citar este artículo: Plazas-Nossa, L., & Torres, A. (2015). PCA/DFT como herramienta de pronóstico para series temporales de absorbancia registradas mediante captores UV-Vis en sistemas de saneamiento urbano. Revista Tecnura, 19(44), 47-57. doi: http://dx.doi.org/10.14483/udistrital.jour.tecnura.2015.2.a03
Resumen
El objetivo de este trabajo es presentar un método de pronóstico para series de tiempo de espectrometría UV-Vis, combinando el análisis de componentes principales PCA (Principal Component Analysis), la transformada discreta de Fourier, DFT (Discrete Fourier Transform) y la transformada inversa de Fourier, IFFT (Inverse Fast Fourier Transform). Se utilizaron las correspondientes series de tiempo de absorbancia para tres diferentes sitios de estudio: (i) Planta de tratamiento de aguas residuales Salitre (PTAR) en Bogotá; (ii) Estación elevadora de Gibraltar en Bogotá; y (iii) Planta de tratamiento de aguas residuales San Fernando (PTAR) en Itagüí (parte sur de Medellín). Cada una de las series de tiempo tiene igual número de muestras (5705). Al reducir la dimensionalidad de las series de tiempo de absorbancia con PCA, se utilizan para cada sitio de estudio 3, 5 y 6 componentes principales, respectivamente; explicando en conjunto más de 97% de la variabilidad. Se utiliza en el procedimiento DFT e IFFT el armónico más importante y se remueven desde uno hasta la mitad de los valores de la longitud total de las series de tiempo. Por consiguiente, los errores de pronóstico para los tres sitios de estudio y para tres rangos de longitudes de onda propuestos (UV, Vis y UV-Vis) están comprendidos entre 0,01% y 34% para 95% de los casos. Sin embargo, para 100% de los casos los errores son inferiores a 37%, independientemente de la longitud de onda y del tiempo de pronóstico.
Palabras clave: absorbancia, análisis por componentes principales, captor UV-Vis, pronóstico, transformada de Fourier.
Abstract
The purpose of this work is to introduce a forecasting method for UV-Vis spectrometry time series that combines principal component analysis (PCA), the discrete Fourier transform (DFT) and the inverse fast Fourier transform (IFFT). The corresponding absorbance time series were used for three different study sites: (i) Salitre wastewater treatment plant (WWTP) in Bogotá; (ii) Gibraltar pumping station in Bogotá; and (iii) San Fernando WWTP in Itagüí (in the southern part of Medellín). Each of these time series had an equal number of samples (5705). By reducing the absorbance time series dimensionality with PCA, 3, 5 and 6 principal components were used for each study site respectively; these altogether explain more than 97% of the variability. It was used the most important harmonic given by the DFT and the IFFT procedure, which removed from one to half values of the time series length. Therefore, forecast errors between 0,01% and 34% for 95% of the cases were obtained for the three study sites and the wavelength ranges (UV, Vis and UV-Vis). However, for 100% of the cases errors were lower than 37%, independently of the wavelength and the forecasting time.
Keywords: absorbance, forecasting, Fourier transform, principal component analysis, UV-Vis sensor.
Introducción
Los desarrollos en óptica y electrónica en los últimos años han permitido la mezcla o unión de la espectrometría UV-Vis de espectro completo con instrumentos robustos a pequeña escala, con el fin de monitorizar en línea la calidad del agua (van den Broeke, 2007). Los captores UV-Vis son sondas que registran la atenuación de la luz (absorbancia) y proporcionan resultados de la calidad del agua en relativo tiempo continuo (del orden de una señal/minuto). En el caso específico de plantas de tratamiento de aguas residuales o combinadas (PTAR), la espectrometría UV-Vis en línea (219 longitudes de onda en el rango de UV hasta Visible: 200-745 nm, con pasos de 2,5 nm) puede utilizarse para la monitorización y el control en las entradas y salidas de dichas plantas, así como para monitorizar las diferentes etapas del tratamiento, con el propósito de determinar las dinámicas de las cargas y eficiencias de remoción de materiales orgánicos (como DQO y DBO5), nitratos, nitritos y sólidos suspendidos totales (SST) (Rieger, Langergraber, Thomann, Fleischmann, & Siegrist, 2004) (Gruber, Bertrand-Krajewski, De Beneditis, Hochedlinger, & Lettl, 2006), a escalas temporales adecuadas y eventualmente utilizar esa información en tiempo real. Además de los métodos utilizados para la calibración de los captores (Torres, Lepot, & Bertrand-Krajewski, 2013) (Salgado, Pinheiro, Ferreira, Saldanha, & Louren, 2013) y el análisis de las series de tiempo de espectros de absorbancia UV-Vis, se requiere desarrollar métodos de pronóstico con el fin de utilizar la monitorización en línea para el control en tiempo real. Si bien en otros estudios se ha utilizado la FFT como complemento a la lógica difusa para el pronóstico de índices de inversión (Taiwan Stock Exchange y Dow-Jones Industrial Average) (Chen & Chen, 2014), para combinarlas con la metodología Box-Jenkins y realizar pronósticos al sistema de administración de tráfico aéreo (Di Gravio, Mancini, Patriarca, & Costantino, 2015), o modelos ARIMA combinados con el análisis de Fourier para efectuar pronósticos al consumo y producción de energía en China (Xiong, Dang, Yao, & Wang, 2014), en conocimiento de los autores del presente artículo, la FFT no se ha utilizado en pronóstico de calidad de aguas. Por otro lado, la utilización de FFT para el pronóstico de series de tiempo UV-Vis implica lidiar con un número importante de variables equivalente al número de longitudes de onda. Por consiguiente, la utilización de análisis por componentes principales podría ser una opción. En efecto, dicho análisis, que se ha empleado en numerosos estudios (ver, por ejemplo (Leonardi & Van De Ville, 2015) (He, Zhao, Zhang, Ogawa, & Haseyama, 2014)), permite reducir la dimensionalidad de un conjunto de variables.
El presente trabajo tiene como objetivo analizar los espectros de las series de tiempo de absorbancia recibidos por los captores UV-Vis instalados en sistemas de saneamiento urbano, aplicando la metodología PCA para reducir la dimensionalidad del problema y utilizar dicho análisis como base para el pronóstico por medio de DFT y la IFFT. El análisis propuesto se realizó para tres bases de datos de espectros de absorbancia UV-Vis adquiridos en los siguientes puntos: (i) afluente a la PTAR-Salitre, Bogotá, D.C.; (ii) Estación Elevadora Gibraltar, Bogotá, D.C.; (iii) afluente a la PTAR San Fernando, Itagüí (área metropolitana de Medellín).
Materiales y métodos
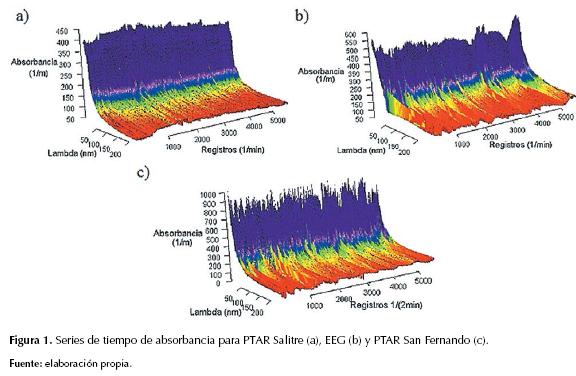
Los captores UV-Vis utilizados (spectro::lyserTM) son sondas sumergibles de aproximadamente 64,7 cm de longitud y 44 mm de diámetro, los cuales registran la atenuación de la luz (absorbancia) en relativo tiempo continuo (del orden de una señal/minuto) a partir de una fuente luminosa proporcionada por una lámpara de xenón. Los valores del espectro se encuentran entre 200 nm y 750 nm de longitud de onda, con intervalos de 2,5 nm (Langergraber, Fleischmann, Hofstaedter, & Weingartner, 2004) . El análisis que se presenta a continuación se realizó para las series de tiempo de espectros de absorbancia compuestas por 5705 registros en cada sitio de muestro (ver la figura 1): (i) para PTAR-Salitre (Bogotá, D.C.) del 29 de junio de 2011 a las 09:03 h al 3 de julio de 2011 a las 17:33 h (una muestra por minuto); (ii) para la Estación Elevadora de Gibraltar (EEG) del 18 de octubre de 2011 a las 11:08 h al 22 de octubre de 2011 a las 15:21 h (una muestra por minuto) y (iii) PTAR San Fernando de 24 de septiembre de 2011 a las 06:04 h a 2 de octubre de 2011 a las 9:16 h (una muestra cada dos minutos). En este trabajo no se hace distinción entre tiempo seco o de lluvia, dado que se propone realizar el pronóstico de los espectros de absorbancia UV-Vis incluyendo las condiciones anteriores en los hidrosistemas urbanos en análisis, además de evaluar los límites del método propuesto para incluir todas las posibles condiciones que se puedan presentar.
Análisis por componentes principales (PCA)
El PCA realiza una transformación lineal, encontrando un nuevo sistema de coordenadas a partir del conjunto original de datos. En este nuevo sistema de coordenadas la varianza de mayor valor del conjunto de datos es capturada por el primer eje, llamado primer componente principal; la segunda mayor varianza es capturada por el segundo eje, y así sucesivamente. Para construir esta transformación lineal se debe construir primero la matriz de covarianza o la matriz de coeficientes de correlación (Shlens, 2009). El objetivo es transformar un conjunto dado de datos X con dimensiones n x m, donde n es el número de observaciones y m el número de variables, a otro conjunto de datos de menor dimensión n x l, donde n sigue siendo el número de observaciones y l es el número de componentes principales, siendo menor que m y con la menor pérdida posible de cantidad de información útil. El proceso comienza calculando la matriz de covarianza, ecuación (1).
donde N es el número total de datos y n es cada uno de los valores en la matriz.
Los datos para el análisis deben tener media cero, lo que se obtiene al restar cada dato del promedio de cada columna, como se indica en la ecuación (2).
donde i hace referencia al valor de cada columna en la matriz.
Sin embargo, con el fin de estandarizar los datos, se recomienda que los datos estén en valores de auto-escala, los cuales se calculan como se indica en la ecuación (3).
donde i hace referencia al valor de cada columna en la matriz.
Es necesario calcular los autovalores (eigenvalues) y autovectores (eigenvectors), con el fin de obtener las componentes principales (PC – Principal Component), como se indica en la ecuación (4).
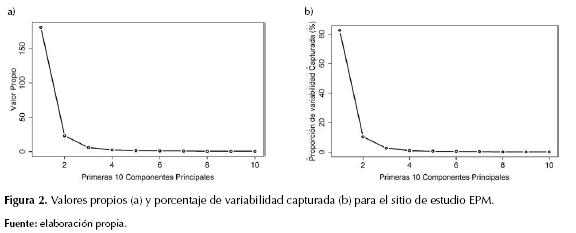
Se aplica el criterio del “codo” con el fin de seleccionar el número de componentes principales a utilizar. Este criterio indica que los valores propios asociados a cada componente principal y superiores a uno se incluirán en el número de componentes principales que capturen la mayor variabilidad de los datos con la menor pérdida de información (Peña, 2002). Como ejemplo de este criterio de selección, la figura 2(a) presenta los valores de valor propio y en la figura 2(b) se presenta el porcentaje de proporción de variabilidad capturada para el sitio de estudio PTAR San Fernando y en este, por el criterio del codo se utilizan seis componentes principales.
Se requiere reconstruir los datos (en términos de las dimensiones originales) mediante el uso de las componentes principales utilizando la ecuación (5); esta ecuación se aplicará después de haber utilizado el proceso de transformación del dominio del tiempo al dominio de la frecuencia, efectuar el pronóstico, aplicar la transformada inversa del dominio de la frecuencia al dominio del tiempo (ver Procedimiento DFT).
Procedimiento DFT
Se emplea el análisis espectral para encontrar las periodicidades presentes en las series de tiempo, utilizando la DFT (Proakis & Manolakis, 2006), con el fin de efectuar la transformación del dominio del tiempo al dominio de la frecuencia. La metodología propuesta consiste en seleccionar los armónicos (señales periódicas) con base en su importancia, evaluada según su amplitud. Después se realiza la eliminación de armónicos de menor a mayor importancia, para finalmente regresar al dominio del tiempo usando IFFT (Proakis & Manolakis, 2006). Esto se hace para todas las componentes principales obtenidas por el proceso PCA y para todos los armónicos; desde el último armónico que es igual a la mitad de longitud de la serie de tiempo hasta el armónico-cero, que es el promedio de la señal en el dominio de tiempo y es el único componente sistemáticamente tomado en cuenta para todos los análisis.
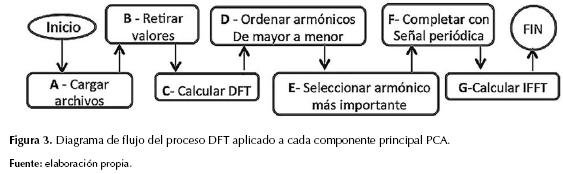
El procedimiento, siguiendo el diagrama de flujo de la figura 3, comienza retirando para cada componente principal (datos) (partes A-B), desde 1 hasta 2852 valores para obtener el pronóstico de valores calculados mediante los armónicos DFT (parte C, figura 3). De acuerdo con análisis previos efectuados, teniendo en cuenta de uno a diez armónicos importantes, se estableció que es suficiente la utilización del armónico más importante con el fin de realizar el pronóstico. Además esto tiene implicaciones con el fin de reducir tiempos computacionales, lo cual es un factor importante en sistemas de control en tiempo real y enfoque del presente método. Por tanto, se considera el armónico más importante (partes D, E y F, figura 3), retornando al dominio del tiempo utilizando la IFFT (parte G, figura 3).
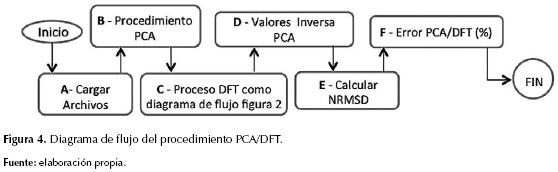
Procedimiento PCA/DFT
El procedimiento, siguiendo el diagrama de flujo de la figura 4, cargando las series de tiempo (A), se aplica el procedimiento PCA con el fin de obtener los componentes principales que corresponden a los valores propios de la matriz de covarianza (criterio de codo), PCA/DFT consiste en aplicar el procedimiento DFT antes explicado a los valores obtenidos mediante la ecuación (4) (parte B, figura 4). Se aplica el procedimiento DFT, donde el pronóstico se realiza sobre los componentes principales (PCA) en vez de las series temporales de absorbancia (pasar de series temporales de 219 longitudes de onda a series temporales de algunos componentes principales, por ejemplo 2 o 3). Se hace la extracción desde el primero hasta la mitad de los valores de las series temporales de PCA; para cada serie de tiempo se aplica la DFT, obteniendo una ecuación periódica utilizada para calcular los valores de los elementos retirados en la serie original de PCA. Se procede con el retorno al dominio del tiempo efectuado mediante la IFFT (Proakis & Manolakis, 2006) (parte C, figura 4). Se aplica la transformación inversa PCA, utilizando la ecuación (5), a los valores pronosticados (parte D, figura 4). Finalmente, se debe comparar la serie de tiempo original con la serie de tiempo pronosticada (PCA/DFT) por medio de la desviación de la raíz media cuadrática normalizada (Normalized Root-Mean-Square deviation, NRMSD) presentada en la ecuación (6)) (Liu, 2015) (O’Donncha, Hartnett, Nash, Ren, & Ragnoli, 2015).
En la ecuación (6), ValSTi es el valor de absorbancia de la serie de tiempo original para el tiempo i, ValIFFTi es el valor de absorbancia procesado para el i-ésimo tiempo y Obsmax-Obsmin es el rango de amplitud de la serie de tiempo original (partes E y F, figura 4).
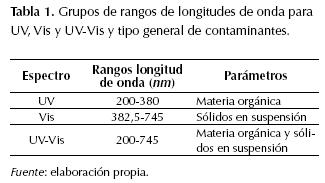
Todos los procedimientos explicados se efectúan para rangos de longitudes de onda en grupos UV (200 nm–380 nm), visible (Vis) (382,5 nm–745 nm) y UV-Vis (200 nm–745 nm) como se registra en la tabla 1 (Thomas & Burgess, 2007).
resultados y discusión
La tabla 2 muestra el número de componentes principales necesarios para capturar más de 97% de la variabilidad en las tres series de tiempo utilizadas. Esto implica una reducción en el tiempo de análisis y procesamiento de series de tiempo de absorbancia si se requiere aplicar en tiempo real.
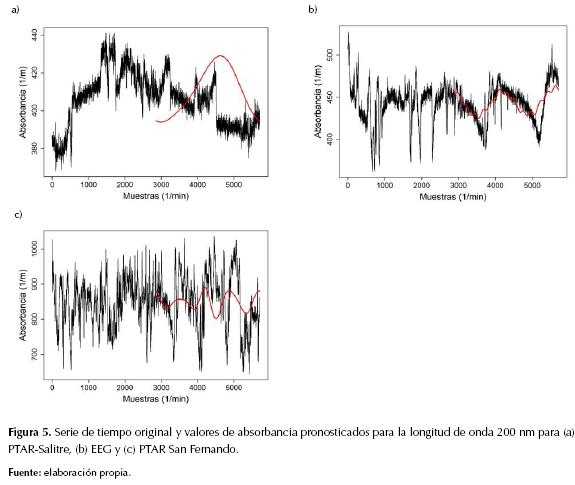
Al utilizar la metodología a cada una de las componentes principales seleccionadas según los valores de la tabla 2, se aplica el proceso DFT y se pronostican desde uno hasta 2852 valores de absorbancia para cada una de las 219 longitudes de onda y para cada uno de los sitios de estudio. En la figura 5 se ilustra la primera longitud de onda (200 nm) para cada sitio de estudio, la serie de tiempo original (línea negro) y los valores de pronóstico para el máximo rango de tiempo (línea roja) 2852 minutos PTAR-Salitre y EEG y 5704 para PTAR San Fernando, y a partir de las dos curvas (original y pronosticada) se calcula y se obtiene la desviación de la raíz media cuadrática normalizada (NRMSD ecuación (6)). Se efectúa el análisis para cada rango de longitudes de onda propuesto UV, Vis y UV-Vis.
La figura 6 muestra los tres rangos de longitudes de onda analizados, UV, Vis y UV-Vis, para PTAR-Salitre. Similares resultados se obtuvieron para los sitios de estudios EEG y PTAR San Fernando.
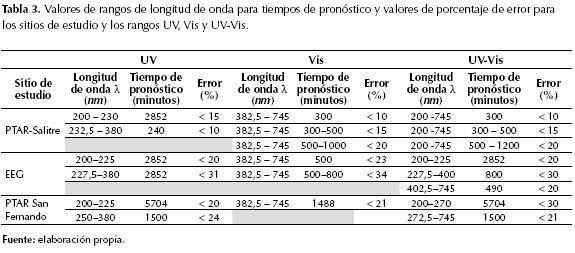
En el rango UV (figura 6(a)), se observa que para todo el rango de pronóstico 2852 minutos y para las longitudes de onda entre 200 nm y 230 nm no superan 15% y el rango desde 232,5 nm hasta 380 nm y para 240 minutos (4 h) de pronóstico los errores no superan 10%. En el rango Vis (figura 6(b)), se observa que para todo el rango de longitudes de onda y para 300 minutos (5 h) de pronóstico los errores no superan 10%, desde 300 minutos (5 h) hasta 500 minutos (8h, 20 min) de pronóstico los errores no superan 15% y desde 500 minutos hasta 1000 minutos (16h, 40 min) de pronóstico los errores no superan 20%. En el espectro completo UV-Vis (figura 6(c)), se observa que para todo el rango y para 300 minutos (5 h) de pronóstico los errores no superan 10%, desde 300 minutos (5 h) hasta 500 minutos (8h, 20 min) de pronóstico los errores no superan 15% y desde 500 minutos hasta 1200 minutos (20 h) de pronóstico los errores no superan 20%.
En el sitio de estudio EEG, los resultados obtenidos para todo el período de pronóstico, 2852 minutos, en el rango UV y específicamente desde la longitud de onda de 200 nm hasta 225 nm los errores no superan 20%, y para las longitudes de onda desde 227,5 nm hasta 380 nm los errores no superan 31%. Para todo el rango Vis y hasta el tiempo de pronóstico 500 minutos (8h, 20 min) los errores no superan 23% y desde 500 minutos hasta 800 minutos (13h, 20 min) de pronóstico, los errores no superan 37%. Para el rango UV-Vis desde la longitud de onda 200 nm hasta 225 nm y para todo el período de pronóstico 2852 minutos (47h, 30 min) los errores no superan 20%, y para el rango desde la longitud de onda 227.5 nm hasta 400 nm, hasta el tiempo de 800 minutos (13h, 30 min) de pronóstico, los errores no superan 30% y para el rango desde la longitud de onda 402.5 nm hasta 745 nm, hasta el tiempo de 490 minutos (8h, 10 min) de pronóstico, los errores no superan 20%.
En el sitio de estudio PTAR San Fernando, para todo el período de pronóstico, 5704 minutos, en el rango UV y específicamente desde la longitud de onda de 200 nm hasta 225 nm los errores no superan 20%, desde la longitud 250 nm hasta 380 nm y hasta 1500 minutos (25h) de pronóstico los errores no superan 24%. Para todo el rango Vis y hasta el tiempo de pronóstico 1488 minutos (24 h, 48 min) los errores no superan 21%. Para el rango UV-Vis y específicamente desde la longitud de onda de 200 nm hasta 270 nm y para todo el período de pronóstico 5704 minutos, los errores no superan 30%, y para la longitud de onda desde 272,5 nm hasta 745 nm y hasta 1500 minutos (25 h) de pronóstico los errores no superan 21%.
Con los resultados obtenidos para cada sitio y según (van den Broeke, 2007) y (Thomas & Burgess, 2007), para el espectro UV y específicamente para el rango de longitudes de onda desde 200 nm hasta 250 nm se puede aspirar a pronosticar, en todos los sitios de estudio, concentraciones de contaminantes como nitritos (NO2), nitratos (NO3) y detergentes (formas bencénicas a 225 nm) con el fin de monitorizar la calidad del agua presente en cada hidrosistema. Se podría hacer el análisis de los rangos de los espectros UV y Vis por separado.
En la tabla 3 se resumen los resultados para los tres sitios de estudio y los tres rangos propuestos (UV, Vis y UV-Vis).
Los resultados obtenidos en este trabajo son comparables con los obtenidos por (Plazas-Nossa & Torres, 2013). Se analizan los mismos sitios de estudio (PTAR Salitre, EEG y PTAR San Fernando), pero se utiliza menor longitud en las series de tiempo de absorbancia con 1051 muestras (17h, 30 min), utilizando solo la DFT y la IFFT e involucrando de uno a diez armónicos importantes. En ese trabajo se pronostican valores retirando valores de uno hasta la mitad de la longitud de las series de tiempo. Se presentan valores de errores mínimos para los sitios en el rango UV hasta 17% y los errores mínimos en el rango visible hasta 27%.
Conclusiones
Al aplicar el procedimiento PCA a las series de tiempo de absorbancia para reducir la dimensionalidad, se utilizan 3 componentes principales para PTAR-Salitre, 5 componentes principales para EEG y 6 componentes principales para PTAR San Fernando. Por tanto, al utilizar las componentes principales, estas explican en conjunto más de 97% de la variabilidad para todos los sitios de estudio. Esto implica una reducción en el tiempo en el análisis y procesamiento de series de tiempo de absorbancia en tiempo real.
Para el análisis del armónico más importante, al remover de uno a 2852 registros, los errores de pronóstico para los tres sitios de estudio y para los tres rangos de longitudes de onda propuestos (UV, Vis y UV-Vis) están comprendidos entre 0,01% y 34% para 95% de los casos y para 100% de los casos e independientemente de la longitud de onda y del tiempo de pronóstico, errores inferiores a 37%.
Se observa además que para los tres sitios de estudio y para el rango de longitudes de onda de 200 nm a 225 nm en el espectro UV, se obtienen errores inferiores a 20% en todo el período de pronóstico indicando que las concentraciones de nitritos (NO2), nitratos (NO3) y detergentes (formas bencénicas a 225 nm), podrían ser mejor pronosticados mediante la metodología propuesta. Para el resto del rango UV de 230 nm a 380 nm los tiempos de pronóstico se reducen debido al porcentaje de error que se incrementa, lo cual aplica para otros contaminantes orgánicos como fenoles.
Para el rango de longitudes de onda en el espectro visible (Vis) y para todos los sitios de estudio, los errores no superan 10% hasta 300 minutos (PTAR-Salitre y EEG) y 600 minutos (PTAR San Fernando). Se observa además que los errores no superan 23% hasta 500 minutos (PTAR-Salitre y EEG) y 1000 minutos (PTAR San Fernando). Esto implica que se pueden obtener errores inferiores a 10% hasta 5 horas para SST. En las plantas de tratamiento de aguas residuales, los resultados se pueden aplicar en los procesos de gestión en tiempo real, modificando el modo de operación de la planta en el afluente y según los datos de pronóstico abrir o cerrar compuertas; como también en el control de materia particulada en el espectro Vis, procesos de coagulación y floculación; aportando a una mejor eficiencia en la remoción.
De acuerdo con los resultados observados durante este estudio, se recomienda realizar el análisis de los rangos de los espectros UV y Vis por separado.
Agradecimientos
Los autores agradecen a la Empresa de Acueducto y Alcantarillado de Bogotá, EAAB (Contrato Administrativo No. 9-0725100-0763-2010) y a Empresas Públicas de Medellín, EPM) por proveer la información utilizada en esta investigación.
Referencias
Chen, M.-Y., & Chen, B.-T. (2014). Online fuzzy time series analysis based on entropy discretization anda Fast Fourier Transform. Applied Soft Computing, 156-166. [ Links ]
Di Gravio, G.; Mancini, M.; Patriarca, R., & Costantino, F. (2015). Overall safety performance of Air Traffic Management system: Forecasting and monitoring. Safety Science(72), 351-362. [ Links ]
Gruber, G.; Bertrand-Krajewski, J.-L.; De Beneditis, J.; Hochedlinger, M., & Lettl, W. (2006). Practical aspects, experiences and strategies by using UVVIS sensors for long-term sewer monitoring. Water Practice & Technology, 1-8. [ Links ]
He, Z.; Zhao, X.; Zhang, S.; Ogawa, T., & Haseyama, M. (2014). Random combination for information extraction in compressed sensing and sparse representation-based pattern recognition. Neurocomputing(145), 160-173. [ Links ]
Langergraber, G.; Fleischmann, N.; Hofstaedter, F., & Weingartner, A. (2004). Monitoring of a paper mill wastewater treatment plant using UV/VIS spectroscopy. IWA Water Science and Technology, 49(1), 9-14. [ Links ]
Leonardi, N., & Van De Ville, D. (2015). On spurious and real fluctuations of dynamic functional connectivity. (104), 430-436. [ Links ]
Liu, Z. (2015). Comparison of precipitation estimates between Version 7 3-hourly TRMM Multi-Satellite Precipitation Analysis (TMPA) near-real-time and research products. Atmospheric Research(153), 119-133. [ Links ]
O’Donncha, F.; Hartnett, M.; Nash, S.; Ren, L., & Ragnoli, E. (2015). Characterizing observed circulation patterns within a bay using HF radar and numerical model simulations. Journal of Marine Systems(142), 96-110. [ Links ]
Peña, D. (2002). Análisis de Datos Multivariantes. Madrid: McGraw-Hill/Interamericana. [ Links ]
Plazas-Nossa, L., & Torres, A. (2013). Fourier analysis as a Forecasting tool for absorbance time series received by UV-Vis probes installed on urban sewer systems. 8th International Conference on Planning & technologies for sustainable urban water management Novatech-2013 (pp. 1-8). Lyon: 8th International Conference on Planning & technologies for sustainable urban water management Novatech-2013. [ Links ]
Proakis, J., & Manolakis, D. (2006). Digital signal processing principles, algorithms, and applications (4th ed.) New Jersey, New Jersey, USA: Pearson Prentice Hall. [ Links ]
Rieger, L.; Langergraber, G.; Thomann, M.; Fleischmann, N., & Siegrist, H. (2004). Spectral in-situ analysis of NO2, NO3, COD, DOC and TSS in the effluent of a WWTP. AutMoNet - 2nd IWA Conference on Automation in Water Quality Monitoring (pp. 29-36). Vienna: IWA Conference on Automation in Water Quality Monitoring. [ Links ]
Salgado, R.; Pinheiro, H. M.; Ferreira, F.; Saldanha, J., & Louren, N. (2013). In situ UV-Vis spectroscopy to estimate COD and TSS in wastewater drainage systems. Urban Water Journal, 1-12. [ Links ]
Shlens, J. (2009, 12 10). A Tutorial on Principal Component Analysis. A Tutorial on Principal Component Analysis. La Jolla, California, USA: Salk Insitute for Biological Studies. [ Links ]
Thomas, O., & Burgess, C. (2007). UV-Visible Spectrophotometry of Water and Wastewater (1st ed.) Amsterdam: Elsevier B.V. [ Links ]
Torres, A.; Lepot, M., & Bertrand-Krajewski, J.-L. (2013). Local calibration for a UV/Vis spectrometer: PLS vs. SVM. A case study in a WWTP. 7th International Conference on Sewer Processes & Networks (pp. 1-8). Sheffield: 7th International Conference on Sewer Processes & Networks. [ Links ]
van den Broeke, J. (2007). Online and In-situ UVVis Spectroscopy Real time multi parameter measurements with a single instrument. AWE International, 55-59. [ Links ]
Xiong, P.-p.; Dang, Y.-g.; Yao, T.-x., & Wang, Z.-x. (2014). Optimal modeling and forecasting of the energy consumption and. Energy(77), 623-634. [ Links ]