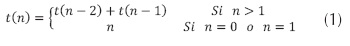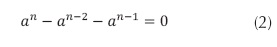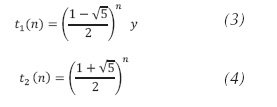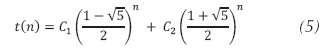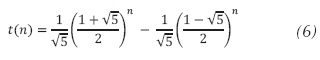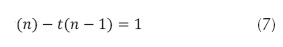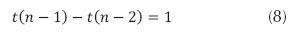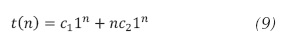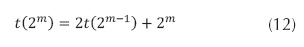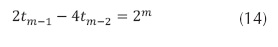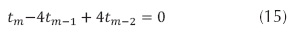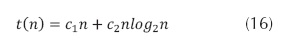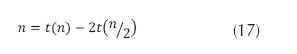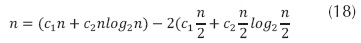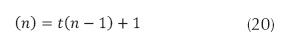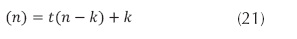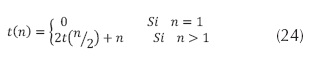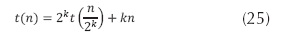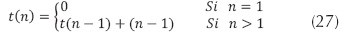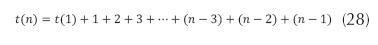Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Tecnura
Print version ISSN 0123-921X
Tecnura vol.19 no.spe Bogotá Dec. 2015
https://doi.org/10.14483/udistrital.jour.tecnura.2015.3.a07
http://dx.doi.org/10.14483/udistrital.jour.tecnura.2015.3.a07
Técnica para solución de recurrencias, usada en el análisis de la complejidad de algoritmos recursivos
Technique for recurrences solving, used in recursive algorithm complexity analysis
Luis Emilio Montenegro Salcedo1, Luz Deicy Alvarado Nieto2
1 Licenciado en educación especialidad matemáticas, magister en auditoría de Sistemas y computación, especialista en edumática. Docente de la Universidad Francisco José de Caldas. Bogotá, Colombia. Contacto: emontenegro@udistrital.edu.co
2 Ingeniera de Sistemas, magister en Ingeniería de Sistemas, Doctor en Informática, con énfasis en Ciencias de la Computación e Inteligencia Artificial. Docente de la Universidad Francisco José de Caldas. Bogotá, Colombia. Contacto: lalvarado@udistrital.edu.co
Fecha de recepción: 13 de septiembre de 2014 Fecha de aceptación: 18 de agosto de 2015
Cómo citar: Montenegro Salcedo, L. E., & Alvarado Nieto, L. D. (2015). Técnica para solución de recurrencias, usada en el análisis de la complejidad de algoritmos recursivos. Revista Tecnura, 19, 89-97. doi: 10.14483/udistrital.jour.tecnura.2015.SE1.a07
Resumen
Este artículo presenta un método alternativo, directo y poco común para solucionar recurrencias de primer orden, tanto homogéneas como no homogéneas; aplicable a ecuaciones que representan el comportamiento de algoritmos recursivos. Dicho método se asocia al funcionamiento computacional del algoritmo, facilitando su comprensión y el análisis de la complejidad. El proceso se ilustra con ejemplos de ecuaciones correspondientes a algoritmos muy conocidos y frecuentemente utilizados.
Palabras Clave: Algoritmos, análisis de algoritmos, cantidad de operaciones, complejidad algorítmica, eficiencia computacional, recurrencias, recursividad.
Abstract
This paper shows an alternative, direct and unusual method to solve both first order recurrences homogeneous and inhomogeneous; applicable to equations representing the behavior of recursive algorithms. Such method is associated with the performance of the computational algorithm, by facilitating the understanding and complexity analysis. The process is illustrated by examples of equations for well-known and frequently used algorithms.
Keywords: Algorithms, algorithmic complexity, Analysis of Algorithms, computational efficiency, operations number, recurrences, recursion.
Introducción
Desde el punto de vista computacional, cuando se busca la solución de un problema es usual utilizar algoritmos, los cuales debido a los avances tecnológicos se espera que sean correctos, sencillos, claros, eficaces, eficientes y oportunos (Baase, 1999, 2002).
El análisis algorítmico busca determinar el comportamiento de los algoritmos en términos de memoria y tiempo (Aho, 1983, Brassard, 1997). Para ello, se define una medida del tamaño del problema (la cual depende de la naturaleza de dicho problema) -llámese N- y se busca una función f(N) que refleje el comportamiento del algoritmo con base en el tamaño definido (McConnell, 2007, Sedgewick, 2013). Es importante aclarar que el análisis se hace para un N muy grande. Cuando se define en términos de tiempo, la función es comúnmente denominada t(N).
Ejemplos de funciones que representan el comportamiento de algoritmos hay muchos, entre ellos se pueden mencionar: t(N) = N + log N , t(N) = N + 5, t(N) = N2 + 3N + 3, t(N) = aN + N + 10.
Estas funciones, que evidencian de manera general el consumo de recursos por parte del algoritmo a medida que N crece, se pueden agrupar en "familias" representativas, de tal manera que es posible afirmar, por ejemplo, que un algoritmo tiene comportamiento exponencial, logarítmico, lineal, cuadrático, cúbico, etc. (Aho, Hopcroft, 1983, Baase, 1999, 2002, Brassard, 1997, Sedgewick, 2013).
Particularmente, en el caso de los algoritmos re-cursivos el comportamiento se expresa mediante relaciones lineales de recurrencia con coeficientes constantes (Baase, 1999, 2002, McConnell, 2007, Sedgewick, 2013). Una relación lineal de recurrencia implica que t(N) se expresa de la siguiente forma: 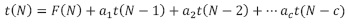 .
.
De manera particular, si en una relación lineal de recurrencia se encuentra que F(N) = 0, se dice que esta relación es homogénea. De lo contrario, dicha relación se considera no homogénea (Aho, 1983, Brassard, 1997).
En la definición de t(N) como una función de recurrencia, fácilmente se puede observar que la misma función t aparece aplicada a uno o varios valores de N, como ocurre en los siguientes casos: t(N) = t(N-1) + 1, t(N) = 2 t(N-1) + N.
Los ejemplos anteriores corresponden a relaciones lineales de recurrencia de primer orden, pues el valor actual t(N) depende solamente del valor inmediatamente anterior t(N-1). Sin embargo, algunos algoritmos también presentan comportamientos que pueden ser representados con relaciones lineales de recurrencia de segundo orden, en las cuales aparece dos veces la función t, es decir, el valor actual t(N) depende de los dos valores anteriores t(N1) y t(N-2) (Sedgewick, 2013). Un caso concreto de esto es la representación del comportamiento para el algoritmo recursivo que halla el término n-ésimo de la sucesión de Fibonacci: t(N) = t(N-1) -t(N-2).
Como se evidencia fácilmente, las relaciones de recurrencia están expresadas en términos recursivos, es decir, en términos de la misma función, pero con uno o varios tamaños menores. Sin embargo, en el análisis de algoritmos se espera que la función esté planteada únicamente en términos del tamaño del problema, es decir, hallar una expresión no recursiva de t(N). Por tal motivo se hace indispensable aquí solucionar de la manera más sencilla y clara las relaciones de recurrencia, de forma que las ecuaciones sean expresadas en términos de N.
La primera parte de este artículo muestra algunas funciones de recurrencia para algoritmos típicos, posteriormente presenta ejemplos de la aplicación de técnicas tradicionales en la solución de relaciones de recurrencia tanto homogéneas como no homogéneas y, finalmente, propone un método inductivo, directo y concreto para hallar la solución de las recurrencias antes mencionadas.
FUNCIONES QUE REPRESENTAN EL COMPORTAMIENTO DE ALGORITMOS RECURSIVOS COMUNES
En su libro Algoritmos en C++ (Sedgewick, 1995), el autor analiza el tema "recurrencias básicas" y presenta lo que él denomina "fórmulas", que describen los comportamientos más comunes de algunos algoritmos recursivos; entre ellas se encuentran las siguientes: tntn1nnt1. En este caso se describe el comportamiento de un algoritmo que efectúa una operación sobre todos los datos de entrada para descartar uno de ellos, luego hace una llamada recursiva disminuyendo dicho dato. Un claro ejemplo de esto es el algoritmo de burbuja recursivo, en donde usando un ciclo se ubica el mayor o el menor elemento del arreglo, luego se hace una llamada recursiva disminuyendo en 1 el tamaño de dicho arreglo, es decir, tomando un dato menos.
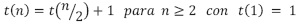 . La función de recurrencia aquí presentada describe un algoritmo que hace una operación fundamental y posteriormente hace una llamada recursiva para la mitad de los datos de entrada, es decir, se queda solamente con la mitad de los datos. Un ejemplo de algoritmos que tienen este comportamiento es el de búsqueda binaria o la búsqueda en un árbol binario ordenado y balanceado.
. La función de recurrencia aquí presentada describe un algoritmo que hace una operación fundamental y posteriormente hace una llamada recursiva para la mitad de los datos de entrada, es decir, se queda solamente con la mitad de los datos. Un ejemplo de algoritmos que tienen este comportamiento es el de búsqueda binaria o la búsqueda en un árbol binario ordenado y balanceado.
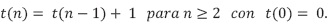 Esta función de recurrencia representa el comportamiento de un algoritmo que realiza una única operación, la cual permite descartar un dato. Posteriormente hace una llamada recursiva, descartando dicho dato. Un ejemplo de este comportamiento lo presenta el algoritmo que efectúa el cálculo del factorial de manera recursiva.
Esta función de recurrencia representa el comportamiento de un algoritmo que realiza una única operación, la cual permite descartar un dato. Posteriormente hace una llamada recursiva, descartando dicho dato. Un ejemplo de este comportamiento lo presenta el algoritmo que efectúa el cálculo del factorial de manera recursiva.
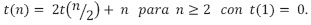 En este caso, la recurrencia describe un algoritmo que hace dos llamadas recursivas, cada una con la mitad de los datos y antes, en medio o después de dichas llamadas, hace un recorrido por todos los datos. Un claro representante de este comportamiento es el algoritmo Mergesort; también podría considerarse el Quick sort, pero solo en el mejor caso, cuando el pivote siempre se ubica en la mitad de los datos.
En este caso, la recurrencia describe un algoritmo que hace dos llamadas recursivas, cada una con la mitad de los datos y antes, en medio o después de dichas llamadas, hace un recorrido por todos los datos. Un claro representante de este comportamiento es el algoritmo Mergesort; también podría considerarse el Quick sort, pero solo en el mejor caso, cuando el pivote siempre se ubica en la mitad de los datos.
 Finalmente, esta recurrencia describe un algoritmo que realiza una operación, divide los datos en 2 y hace una llamada recursiva para cada una de las partes de la división. Los algoritmos recursivos de recorrido de un árbol binario balanceado o el conteo de sus nodos son algoritmos que ejemplifican este comportamiento. También puede considerarse dentro de este comportamiento el peor caso de búsqueda en un árbol binario no ordenado.
Finalmente, esta recurrencia describe un algoritmo que realiza una operación, divide los datos en 2 y hace una llamada recursiva para cada una de las partes de la división. Los algoritmos recursivos de recorrido de un árbol binario balanceado o el conteo de sus nodos son algoritmos que ejemplifican este comportamiento. También puede considerarse dentro de este comportamiento el peor caso de búsqueda en un árbol binario no ordenado.
TÉCNICAS TRADICIONALES DE SOLUCIÓN DE RECURRENCIAS
En general, se han establecido y generalizado dos métodos para resolver recurrencias, dependiendo de si estas clasifican como homogéneas o no (Aho, 1983, Brassard, Bratley, 1997, Cormen, 2009, Sedgewick, 2013).
Recurrencias homogéneas
Para este caso se debe aplicar el siguiente procedimiento:
- Intuir o predecir cuál es el tipo de función que puede describir el comportamiento de la recurrencia. Pasa por una sospecha acerca de la complejidad posible del algoritmo. Por ejemplo, se asume que tiene un componente de tipo exponencial en las recurrencias de segundo orden.
- Se sustituye la función predicción en la recurrencia obteniendo la ecuación característica, la cual corresponde a las raíces de un polinomio.
- La solución de la ecuación característica permite encontrar un conjunto de soluciones particulares, de las cuales se puede inferir una familia de soluciones posibles.
- Se aplican las condiciones iniciales (correspondientes a las salidas no recursivas del algoritmo), con el fin de seleccionar el ejemplar más apropiado de esa familia, obteniéndose así la solución de la recurrencia.
El ejemplo típico de recurrencias homogéneas presentado en diferentes libros (Aho, Hopcroft, 1983, Brassard, 1997, Cormen, 2009, Sedgewick, 2013), es el algoritmo recursivo que permite encontrar el término n-ésimo de la sucesión de Fibonacci, partiendo de las semillas 0 y 1, ecuación (1).
- Se intuye, especialmente al ver el comportamiento del algoritmo, que la función debe ser de orden exponencial. Por tanto, la predicción es:
 .
. - Se observa que la recurrencia de la ecuación (1) es homogénea, dado que se puede escribir como
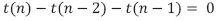 para el caso general, n > 1.
para el caso general, n > 1. - Al sustituir en la ecuación homogénea se convierte en:
- Que equivale a:
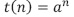 . Al aplicar la condición α > 0 se reduce a la llamada ecuación característica
. Al aplicar la condición α > 0 se reduce a la llamada ecuación característica 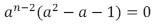 .
. - Las soluciones particulares se muestran en las ecuaciones (3) y (4).
- A partir de las cuales se expresa la familia de soluciones mediante la ecuación (5).
- Como t(n) debe satisfacer las condiciones iníciales t(0) = 0 y t(1) = 1, al sustituir n en la ecuación(5) se concluye que la solución es como se muestra en la ecuación (6).
El método anterior se puede aplicar a todas las recurrencias homogéneas y se convierte en un proceso meramente algebraico, aplicable sin mayores inconvenientes.
Recurrencias no homogéneas
Sin embargo, para el caso de recurrencias no homogéneas, que entre otras cosas son las que más se presentan en los algoritmos recursivos, es necesario convertirlas a homogéneas aplicándoles un tratamiento matemático, el cual varía dependiendo de la forma que tenga dicha recurrencia. Para este caso se consideran los siguientes ejemplos típicos:
Recurrencia del factorial
El algoritmo para calcular recursivamente el factorial de un número entero mayor o igual a cero da lugar a la recurrencia: 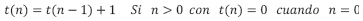 .
.
La recurrencia se escribe en la ecuación (7).
Al no ser homogénea, con el término independiente constante, la ecuación (7) se puede desarrollar de la siguiente forma:
- Se remplaza n por n-1, convirtiéndose en la ecuación (8).
La diferencia de las ecuaciones (7) y (8) se puede escribir 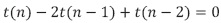
Teniendo así una recurrencia homogénea con ecuación característica 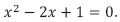 .
.
Como la solución es múltiple x = 1, la solución general se expresa en la ecuación (9).
O simplemente:
Como solo se tiene una condición inicial y se requieren dos para encontrar las constantes, se puede aplicar la recurrencia y hallar t(1) = t(0) + 1 = 1.
Por tanto,c1 = 0 y c2 = 1 y al sustituir en la ecuación (10) se encuentra la solución mostrada mediante la ecuación (11).
Recurrencia del Quick sort
Para el algoritmo Mergesort y el mejor caso del algoritmo Quick sort se deduce la recurrencia: 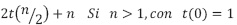
Con el fin de convertir la recurrencia 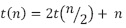 a homogénea, es necesario hacer dos cosas:
a homogénea, es necesario hacer dos cosas:
- La primera es un cambio de variable, n=2m encuyo caso se restringe el proceso a los valores de n que sean potencias de 2. Entonces la recurrencia se escribe como se muestra en la ecuación (12).
- La segunda acción es hacer que desaparezca el término 2m en la ecuación (13). De modo similar al ejemplo anterior, en este caso se remplaza m por m-1 y luego se multiplica por 2 (ecuación(14)).
- Al realizar la diferencia entre las ecuaciones (13) y (14).
La cual también se puede escribir en forma simplificada:
Haciéndose evidente que no es homogénea.
La recurrencia (15) tiene ecuación característica 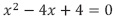 y. por tanto,
y. por tanto, 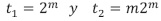 . Con solución general
. Con solución general 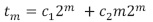
Al retornar a la variable inicial n =2m o su equivalente m = log2n
Aplicando la condición inicial en la ecuación(16), se concluye que c1 = 0
La recurrencia original 3 se puede escribir:
Como (16) es una solución de la ecuación (17) se sustituye obteniendo la ecuación (18).
Cuya simplificación es n = c2n, para concluir que c2 debe ser igual a 1. Entonces la ecuación (19) muestra la solución correspondiente a las constantes c1 y c2:
Por supuesto, con el desarrollo de este apartado no se pretende aportar nada nuevo. Solo resaltar algunos ejemplos que ilustran la gran variedad de alternativas que pueden darse al solucionar recurrencias no homogéneas y lo artificiosos que pueden ser estos métodos.
PROPUESTA
A continuación, se presenta un proceso algebraico general para solucionar recurrencias no homogéneas, el cual está íntimamente ligado al comportamiento del correspondiente algoritmo. No solo es una forma más sencilla de solución, sino que además facilita la comprensión del funcionamiento del correspondiente algoritmo recursivo.
Recurrencia del factorial
En este caso se retoma la fórmula 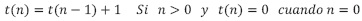
Dado que para cualquier n > 0
Mientras que el parámetro de la función sea mayor que cero, se pude aplicar la fórmula de recurrencia, obteniéndose, a partir de la ecuación(20), la siguiente secuencia de remplazos:

El anterior conjunto de ecuaciones resulta al efectuar la sencilla sustitución de cada nuevo valor en la ecuación original. Además, cada línea describe el siguiente llamado recursivo. De tal forma que la ecuación (21) permite interpretar que en el paso k-ésimo, el algoritmo ha hecho k multiplicaciones y queda pendiente el cálculo de la cantidad de multiplicaciones restantes dado por t(n-k), necesarias para calcular el factorial de n-k.
Se sabe que el algoritmo terminará los llamados y tendrá una salida no recursiva, en el paso k (caso base para algoritmos recursivos) correspondiente al llamado para hallar 0!, es decir, cuando se cumpla que:
En tal caso se tendrá el número total de multiplicaciones requeridas para calcular el factorial del número entero positivo n dado.
La ecuación (22) se logra cuando k es igual a n, y se podrá reescribir la ecuación (21) de la siguiente forma: 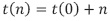 Luego la solución a la recurrencia es la que aparece en la ecuación (23).
Luego la solución a la recurrencia es la que aparece en la ecuación (23).
Recurrencia del Quick sort
Para resolver esta recurrencia se procede en la misma forma. Para cada término 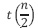 se aplica la fórmula de recurrencia con la condición de que
se aplica la fórmula de recurrencia con la condición de que 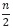 sea diferente de 1 (n > 1), obteniéndose:
sea diferente de 1 (n > 1), obteniéndose:
Llamado 1: 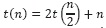
Describe las n comparaciones requeridas para clasificar el arreglo en los menores o mayores del pivote, más las comparaciones necesarias para ordenar los dos subarreglos resultantes, de tamaño 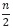 cada uno.
cada uno.
Llamado 2: 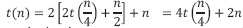 2n es el acumulado de comparaciones para clasificar el arreglo inicial y los dos subarreglos de
2n es el acumulado de comparaciones para clasificar el arreglo inicial y los dos subarreglos de 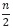 cada uno y
cada uno y 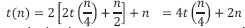 corresponderá a la cantidad de comparaciones requeridas para ordenar 4 subarreglos de tamaño
corresponderá a la cantidad de comparaciones requeridas para ordenar 4 subarreglos de tamaño 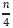 cada uno.
cada uno.
Llamado 3: 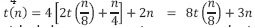 3n es la cantidad de comparaciones para clasificar el arreglo inicial de tamaño n, los dos subarreglos de tamaño
3n es la cantidad de comparaciones para clasificar el arreglo inicial de tamaño n, los dos subarreglos de tamaño 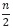 y los cuatro de
y los cuatro de 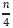 . Ahora quedan por ordenar 8 subarreglos de tamaño cada uno.
. Ahora quedan por ordenar 8 subarreglos de tamaño cada uno.
Se generaliza la fórmula para el k-ésimo llamado recursivo.
La expansión máxima de la recursividad se logra en el paso k-ésimo, para el cual el arreglo se reduce a un elemento, 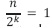 (ya no hay nada que ordenar). En ese momento la salida es no recursiva y se habrán realizado todas las comparaciones requeridas.
(ya no hay nada que ordenar). En ese momento la salida es no recursiva y se habrán realizado todas las comparaciones requeridas.
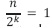 , equivale a
, equivale a 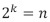 ; por tanto, se deduce que
; por tanto, se deduce que 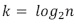 y la ecuación (25) se puede escribir de la siguiente forma:
y la ecuación (25) se puede escribir de la siguiente forma: 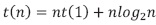 . Por último, como t(1) = 0, la recurrencia tendrá la solución presentada en la ecuación (26).
. Por último, como t(1) = 0, la recurrencia tendrá la solución presentada en la ecuación (26).
Otros ejemplos
A continuación se presentan otros ejemplos de recurrencias para ilustrar la solución por este método.
Ordenamiento por el método de burbuja recursivo
Si el tamaño del arreglo es n = 1, se requieren 0 comparaciones, t(1) = 0, ya está ordenado. Para tamaños de n mayores que 1, se realizan n-1 comparaciones para encontrar el mayor (o el menor) y mediante un llamado recursivo se ordenan los n-1 elementos restantes, realizándose t(n-1) comparaciones.
Aplicando el método propuesto a la recurrencia de la ecuación (27), se tiene:
Remplazo 1:
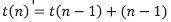
Remplazo 2:
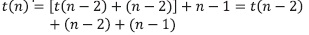
Remplazo 3:
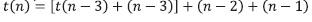
Equivale a:
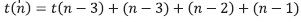
Generalizando el proceso:
Remplazo k:
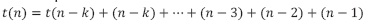
El proceso termina en el k-ésimo llamado, para el cual el tamaño del arreglo se reduce a un elemento, es decir, cuando n-k = 1, o simplemente k = n-1. En tal caso la recurrencia se reescribe:
Es decir, la ecuación (28) se resume en 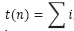 y por tanto, se tiene como solución la ecuación (29).
y por tanto, se tiene como solución la ecuación (29).
Búsqueda en un árbol binario ordenado y balanceado
Este comportamiento también puede corresponder al algoritmo de búsqueda binaria en un arreglo, siendo t(n) la cantidad máxima de comparaciones requeridas.
Si el árbol o el arreglo tienen solo un elemento, se requiere una comparación, t(1) = 1. Para una cantidad de elementos n mayor que 1, 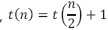 , es decir, una comparación con el elemento de la raíz (o el elemento medio) y de no coincidir, el proceso de búsqueda se reduce a la mitad de los elementos. Los menores o los mayores, pero no ambos. En este caso al aplicar a la ecuación (30) el proceso de solución planteado se obtiene:
, es decir, una comparación con el elemento de la raíz (o el elemento medio) y de no coincidir, el proceso de búsqueda se reduce a la mitad de los elementos. Los menores o los mayores, pero no ambos. En este caso al aplicar a la ecuación (30) el proceso de solución planteado se obtiene:
Remplazo 1:
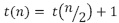 , corresponde al primer llamado recursivo.
, corresponde al primer llamado recursivo.
Remplazo 2:
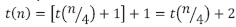 , segundo llamado recursivo.
, segundo llamado recursivo.
Remplazo 3:
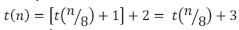 , tercer llamado recursivo.
, tercer llamado recursivo.
Remplazo k:
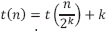 .
.
En este caso, el proceso termina cuando 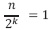 , es decir,
, es decir, 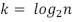 y la recurrencia se expresa
y la recurrencia se expresa 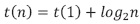 . Por tanto, la solución es la ecuación (31).
. Por tanto, la solución es la ecuación (31).
Búsqueda en un árbol binario balanceado no ordenado
Para este caso se puede plantear la recurrencia en la siguiente forma:
La diferencia con el anterior (apartado 4.3.2), consiste en que al no estar ordenado el árbol, puede implicar hacer la búsqueda sobre los dos subárboles, cada uno con aproximadamente 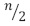 elementos y, por tanto, la recurrencia planteada corresponde al peor caso de la búsqueda, cuando el elemento no está o por casualidad corresponde al último elemento posible de revisar. El desarrollo de la ecuación (32) será:
elementos y, por tanto, la recurrencia planteada corresponde al peor caso de la búsqueda, cuando el elemento no está o por casualidad corresponde al último elemento posible de revisar. El desarrollo de la ecuación (32) será:
Remplazo 1:
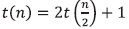
Remplazo 2:
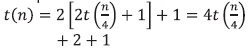
Remplazo 3:
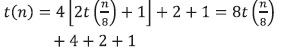
En general, para k:
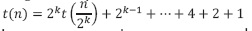
La recurrencia se puede escribir 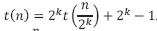 . Dado que
. Dado que 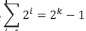 . Cuando
. Cuando 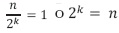 se logra
se logra 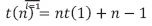
Obteniéndose la solución en la ecuación (33):
RESUMEN DEL PROCESO
El método para resolver recurrencias que se justifica y presenta en este artículo se puede resumir de la siguiente forma:
- Se escribe la fórmula de recurrencia por resolver, especialmente si es no homogénea, que es el más difícil de solucionar, como se muestra en el apartado 3.2. Para el caso de recurrencias homogéneas, la solución es más mecánica, dado que siempre se sigue el mismo proceso algebraico.
- Se remplaza paso a paso en forma reiterada, aprovechando que la función es la misma.
- Se analiza su comportamiento y se generaliza, para cualquier paso K. Este punto es el más importante y debe llevar a simplificar por alguna propiedad matemática conocida.
- Por último, se aplica la condición inicial, la cual equivale a la salida no recursiva; esto permite encontrar la solución de la recurrencia, como una función en términos únicamente de n.
Conclusiones
Los algoritmos recursivos se utilizan cada vez con mayor frecuencia al ser soluciones elegantes, simples, modulares y bien estructuradas a problemas complejos. Para analizar el comportamiento de dichos algoritmos es necesario solucionar las ecuaciones de recurrencia que lo representan.
Como puede observarse, las recurrencias son indispensables en los procesos de análisis de algo-ritmos. Los métodos tradicionalmente usados para su solución tienden a desestimular a algunos ingenieros estudiantes, debido a la gran variedad de casos y formas de solución que se pueden presentar.
El método aquí expuesto plantea seguir el mismo proceso de solución en todos los casos y generalmente no se requieren conocimientos muy avanzados de matemáticas. Dicho método promueve la observación y refuerza la exigencia de generalizar comportamientos. Siendo esta una destreza que se presume inherente a los diseñado-res de algoritmos.
En resumen, a lo largo de este documento se ha presentado y justificado un proceso cuyo desarrollo resulta más natural para los ingenieros, debido a que está especialmente ligado a la lógica del algoritmo al cual corresponde la recurrencia.
Referencias
Aho, A., Hopcroft, J., Ullman, J. (1983). Data structures and algorithms. Massachusetts, U.S.A.: Addison Wesley. [ Links ]
Baase S., Van, A. (1999). Computer Algorithms: Introduction to design and analysis. Massachusetts, U.S.A: Addison Wesley. [ Links ]
Baase, S., Van, A. (2002). Algoritmos computacionales: Introducción al análisis y diseño. México DF, México: Addison Wesley. [ Links ]
Brassard, G., Bratley, P. (1997). Fundamentos de algoritmia. Madrid, España: Prentice Hall. [ Links ]
Cormen, T., Leiserson, C., Rivest, R., Stein, C. (2009). Introduction to algorithms. Massachusetts: Massachusetts Institute of Technology. [ Links ]
McConnell, J. (2007). Analysis of Algorithms: an active learning approach. Ontario, Canada: Jones and Bartlett Publisher. [ Links ]
Sedgewick, R. (1995). Algoritmos en C++. Massachusetts, E.U.A.: Addison-Wesley/Díaz de Santos. [ Links ]
Sedgewick, R., Flajolet, P. (2013). An introduction to the analysis of Algorithms. Massachusetts: Pearson Education. [ Links ]