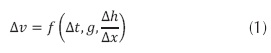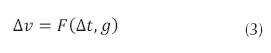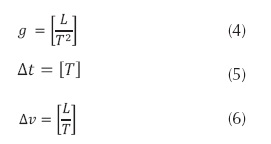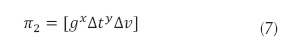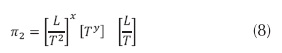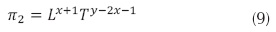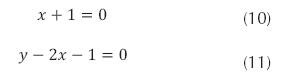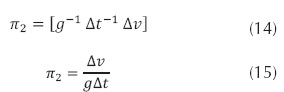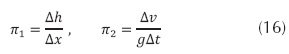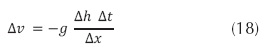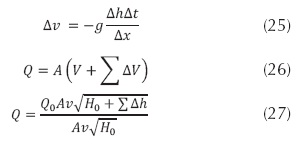http://dx.doi.org/10.14483/udistrital.jour.tecnura.2015.SE1.a12

Demostración y análisis del golpe de ariete por el método de los promedios aritméticos

Demonstration and analysis of water hammer using the arithmetic means method

Fernando González Casas¹, Eduardo Zamudio Huertas², César Augusto García Ubaque³

¹ Ingeniero civil, Universidad Nacional de Colombia; magíster en recursos hidráulicos, Universidad Nacional de Colombia; profesor asistente, Universidad Distrital Francisco José de Caldas. Bogotá, Colombia; integrante del Grupo GIICUD; director del semillero en investigación UDENS. fgonzalezc@udistrital.edu.co
² Ingeniero civil, Universidad Nacional de Colombia; especialista en estadística y magíster en recursos hidráulicos, Universidad Nacional de Colombia; profesor asistente, Universidad Distrital Francisco José de Caldas. Bogotá, Colombia; integrante del Grupo GIICUD; miembro del semillero en investigación UDENS. ezamudioh@udistrital.com
³ Ingeniero civil, Universidad Nacional de Colombia; especialista en manejo integrado del medio ambiente, magíster en ingeniería civil con énfasis en ambiental y doctor en ingeniería, Universidad de los Andes; docente, Universidad Distrital Francisco José de Caldas. Bogotá, Colombia; director del Grupo GIICUD. cagarciau@udistrital.edu.co

Fecha de recepción: 15 de septiembre de 2014 Fecha de aceptación: 18 de agosto de 2015

Cómo citar: González Casas, F., Zamudio Huertas, E., & García Ubaque, C. A. (2015). Demostración y análisis del golpe de ariete por el método de los promedios aritméticos. Revista Tecnura, 19, 143-151. doi: 10.14483/udistrital.jour.tecnura.2015.SE1.a12

Resumen

En este artículo se presenta la solución al cálculo de sobrepresiones y variación de caudal al cerrar válvulas, con la hipótesis de variación lineal en la relación entre sobrepresión y distancia recorrida por la onda de celeridad. Los problemas del golpe de ariete comenzaron a estudiarse en profundidad en el simposio realizado en 1933 [1]. El estudio de la variación lineal en la relación sobrepresión y distancia recorrida aparece desarrollado con base en la teoría del análisis matemático en el "Tratado de Hidráulica Aplicada" de Calvin Victor-George Rich, editorial Labor de Barcelona España en el año 1956 [2] y en la obra "Water-Hammer analysis by the Laplace-Mellin Transformation, Trans., ASME, 1945, de George R. Rich [3], profesor de la universidad de Columbia. En esta publicación se desarrolla la demostración de esta ecuación usando el teorema π de Vaschy-Buckingham, que utiliza los principios del análisis dimensional a la solución de problemas físicos.

Palabras clave: conducciones, golpe de ariete, presión hidráulica, tuberías.

Abstract

This article presents the calculation of overpressures and variation of discharge when closing valves, with the hypothesis of linear variation in the relation between overpressure and distance travelled by the wave of swiftness. The problem of the Water Hammer was firstly studied in the symposium realized in 1933 [1]. The demonstration of the formula with the hypothesis of linear variation in the relation between overpressure and distance travelled is developed from the theory of the mathematical analysis in the text "Treaty of Applied Hydraulics" by Calvin Victor -George Rich, published by the Labor of Barcelona Spain in 1956 [2], and also in the work "Water-Hammer analysis by the Laplace-Mellin Transformation, Trans.", ASME, year 1945 by the professor of the university of Columbia, George R. Rich [3]. In this publication we develop the demonstration of this equation using Vaschy-Buckingham's π theorem, which uses the principles of dimensional analysis for solving physical problems.

Keywords: Water Hammer, conductions, hydraulic pressure, pipelines.

Introducción

La necesidad de conducir agua a presión justifica el uso de tuberías en las instalaciones hidráulicas. Y además, se requieren válvulas bien sea para la regulación del flujo durante las operaciones o para los procedimientos de mantenimiento. Y cuando se modifica bruscamente la velocidad de un fluido en movimiento dentro de un tubo, se produce un violento cambio de presión; este fenómeno se denomina golpe de ariete. Por tanto, a lo largo de la tubería se propagan ondas de sobrepresión y de depresión a la velocidad de la onda en el fluido; las depresiones pueden crear bolsas de aire o cavitación peligrosa y las sobrepresiones pueden romper la tubería.

MECANISMO DE OCURRENCIA DEL GOLPE DE ARIETE

Las consecuencias del golpe de ariete en las tuberías a presión son una clase especial de una familia de movimientos ondulatorios mecánicos conocidos como fenómenos de transición. El golpe de ariete no está relacionado con variaciones graduales en la presión y/o la velocidad del fluido, sino con un cambio brusco. Este tipo de fenómenos se propaga aproximadamente a la velocidad del sonido: se inicia por el cierre de una válvula, y termina desvaneciéndose por el amortiguamiento o fricción en la tubería a presión.

Ahora bien, en general las depresiones del golpe de ariete solo son importantes en las operaciones de cierre rápido; sin embargo, se producen cambios de presión considerables, aunque graduales, aun si el cierre es lento.

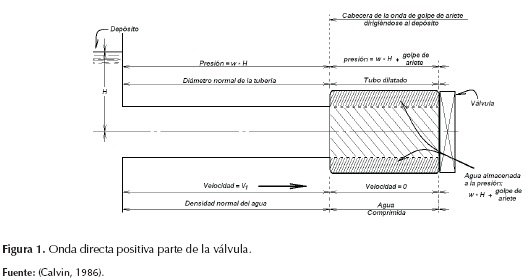
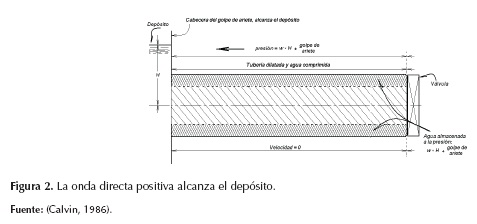
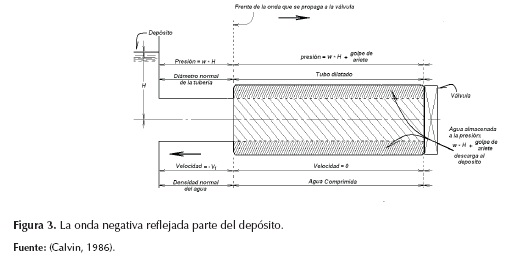
Al cerrarse una válvula, una onda de presión positiva se dirige hacia aguas arriba con la velocidad del sonido. En el extremo, la velocidad en el conducto se reduce a cero (véase la figura 1); como resultado, se comprime el agua y se dilata la pared de la tubería. Si se imagina un tanque o depósito allí, la onda de depresión cambia de signo al llegar y disminuye su magnitud a la presión en el tanque; por tanto, la presión del agua contenida en la tubería expandida desciende (véase la figura 2), y se produce una nueva onda de presión negativa hacia aguas abajo, que transforma la velocidad en el conducto de cero a -V en dirección contraria (véase la figura 3).

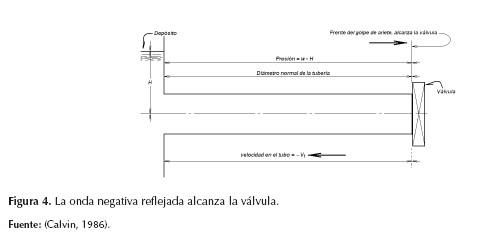
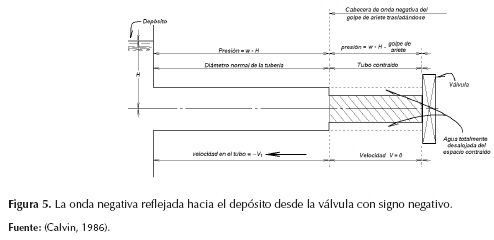
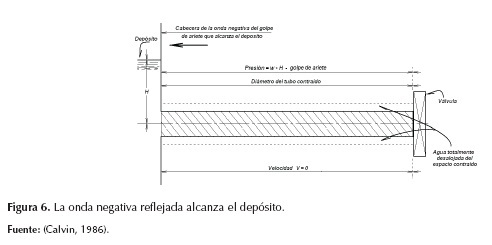
Cuando la onda negativa llega a la válvula cerrada en el extremo inferior del conducto, absolutamente toda el agua de la tubería se desplaza hacia aguas arriba a una velocidad -V (véase la figura 4); por la inercia del agua, la velocidad de esta onda disminuye y será reflejada en la válvula. Aguas debajo de la onda negativa reflejada, la velocidad en el conducto se reduce proporcionalmente respecto a su valor original (véase la figura 5), así se garantiza el volumen de agua necesario para conservar la velocidad -V en el frente de onda hasta que la onda alcanza el tanque; así, cuando esta onda negativa llega al tanque, la presión se reduce dentro de la tubería, desalojando agua del espacio contraído y disminuyendo la velocidad media del flujo a cero (véase la figura 6).

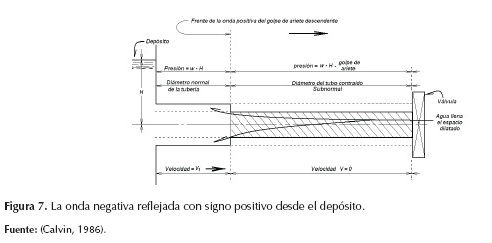
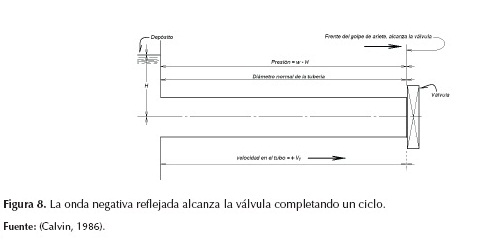
Inmediatamente después se propaga una onda de presión positiva hacia aguas abajo elevando la presión a nivel del depósito a lo largo de la tubería (véase la figura 7), la velocidad V desde y detrás del frente de onda alcanza todos los puntos de la tubería en el momento en que el frente de onda positiva llega a la válvula completando un ciclo (véase la figura 8).

DEMOSTRACIÓN DE LA FÓRMULA PARA CÁLCULO DEL GOLPE DE ARIETE, MÉTODO DEL PROMEDIO ARITMÉTICO EMPLEANDO EL TEOREMA Π DE VASCHY-BUCKINGHAM

El teorema π de Vaschy-Buckingham establece que en un problema físico en el que intervienen n magnitudes denominadas variables, con m dimensiones independientes, las n magnitudes puepueden agruparse en n-m parámetros adimensionales, conformados con las variables originales (Streeter, 2002).

Este teorema proporciona un método de construcción de parámetros adimensionales, incluso cuando la forma de la ecuación es desconocida (Acosta, y de Azevedo, 1975).

La ecuación que se va a obtener requiere el conocimiento de las variables en el problema; en el caso del golpe de ariete, la variación de velocidad del flujo en el fluido (Δv), que ocurre por el cierre de una válvula, depende de la variación en la distancia recorrida por la onda de presión (Δx), de la variación en la sobrepresión generada por el efecto del golpe de ariete (Δh), de la aceleración de la gravedad (g) y del intervalo de tiempo en que ocurre el fenómeno (Δt).

Es decir, la variable dependiente (Δv) se puede representar con la ecuación (1).

Siendo:

Sin embargo, (Δh/Δx) es adimensional porque es la relación de dos longitudes, es decir, esta relación es el primer parámetro buscado (π1) (ecuación (2)).

Los otros posibles parámetros adimensionales deben estimarse aplicando el teorema π de Buckingham y con base en las variables restantes que tienen dimensiones, resolviendo la ecuación (3).

Se tienen en la anterior ecuación tres variables (n = 3) que no son independientes porque dimensionalmente aparecen en función de la longitud (L), y el tiempo (T) (ecuaciones (4), (5) y (6)).

Por tanto (m = 2), debido a que las variables en la ecuación (3) se expresan con máximo dos dimensiones, la longitud (L) y el tiempo (T).

Según el teorema de π Buckingham, existe un parámetro adimensional como representación de la ecuación (3), porque (n-m) es igual a uno (1). Obsérvese que (n = 3) y (m = 2).

En resumen:

Número de variables 3: (Δv; g; Δt)
Número de dimensiones 2: (longitud y tiempo)
El parámetro adimensional es:

Remplazando las ecuaciones (4, 5 y 6) en la ecuación (7):

Ahora operando:

Como π₂ es adimensional:

Resolviendo las ecuaciones simultáneas (10) y (11) se obtienen las ecuaciones:

Al sustituir las ecuaciones (12), (13) en (7).

Se tienen entonces dos parámetros adimensionales:

Experimentalmente los dos parámetros anteriores se convierten de hecho en:

De donde la función Δv queda:

FASES O PERÍODOS DE LA TUBERÍA

La fase o período de la tubería (T) es el tiempo en que la onda de sobrepresión va y vuelve de una extremidad a otra, siendo (L) la longitud de la tubería y (C) la velocidad de propagación de la onda en el fluido, conocida como celeridad.

La onda al regresar cambia de sentido, efectuando el mismo recorrido que en la ida en el mismo tiempo T , bajo la forma de onda de depresión (Streeter, 2002).

Si el cierre de la válvula es muy rápido, quedará completamente cerrada antes de actuar la onda de depresión; y si la válvula se cierra lentamente, existe un tiempo para que la onda de depresión actúe previamente a la obturación completa, por lo que la operación de cierre se puede clasificar como lenta y rápida.

La maniobra es rápida si el tiempo de cierre de la válvula (ŧ) es menor que la fase o período de la tubería (T); en este caso ocurre sobrepresión máxima [4], ya que aún no ha actuado la onda de depresión (Rodríguez y Pallares, 2007).

La maniobra es lenta si el tiempo de cierre de la válvula (ŧ) es mayor que la fase o período de la tubería (T):

Si el cierre o apertura de la válvula es brusco, es decir, si el tiempo de cierre es menor que el tiempo que tarda la onda en recorrer la tubería ida y vuelta, la sobrepresión máxima se calcula como: (Streeter, 2002).

En esta expresión, (V) es la velocidad media del agua, (ha) es el aumento de la presión en metros de agua y (g) es la aceleración de la gravedad.

Si el cierre es lento, la sobrepresión se puede estimar con las fórmulas de Michaud-Vensano:

La velocidad de la onda (C) se calcula con base en la expresión de Allievi, muy útil en el cálculo de la velocidad de onda en agua, en donde (k) es un coeficiente relacionado con el módulo de estabilidad del material con que se fabrica la tubería; (e) es el espesor del tubo y (D) es el diámetro de la tubería (Vallamino Cánovas, 1999, Maganto, 2002).

APLICACIÓN A UN PROBLEMA TÍPICO

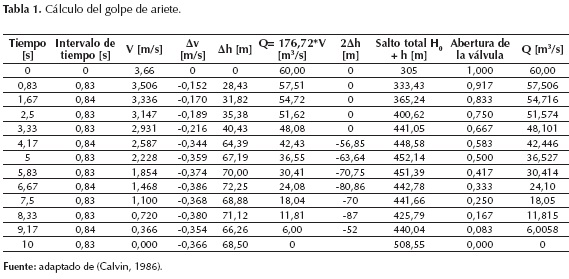
Sea una tubería de longitud 1.524 metros, diámetro de 4,57 metros que transporta un caudal de 60 m³/s y salto inicial o diferencia de nivel entre la lámina de agua en el tanque y el eje de la tubería en la descarga, de 305 m; la velocidad media con la válvula totalmente abierta es de 3,66 m/s, el tiempo de cierre de la válvula es de 10 s y la celeridad de la onda es de 915 m/s. Calcular la variación de caudales y sobrepresiones hasta que la válvula se cierre completamente (Calvin, 1986).

Solución

Los parámetros correspondientes según el enunciado son: L = 1.524 m; D = 4,57 m; Q = 60 m³/s; H₀ = 305 m; V = 3,66 m/s; ŧ = 10 s; C = 915 m/s

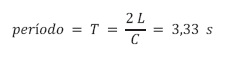
Como el tiempo de cierre de la válvula es 10 segundos, el cierre es lento; por facilidad se escoge para el valor del intervalo Δt un submúltiplo de L/C, tal como L/2C, así Δx es la longitud de tubería a presión recorrida por la onda del golpe de ariete en el tiempo Δt. (Calvin, 1986).

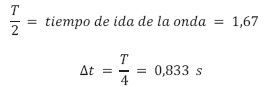
Como 2L se recorre en 3,33 segundos, se concluye que para un delta de tiempo Δt de 0,833 segundos el delta de distancia recorrido por la onda Δx es L/2, es decir, 762 metros aproximadamente.

Se aplica el principio de que el método de cálculo se basa en el concepto de integración como un proceso de adición (Calvin, 1986), en este caso por tanteo, estableciendo los valores en cada instante sucesivo de (h) y de (V) que satisfagan las ecuaciones (25), (26) y (27).

Conclusiones

Se ha presentado en este artículo el modelo lineal o de los promedios aritméticos para el cálculo de sobrepresiones en movimientos transitorios en conducciones a presión sustentado en el enfoque del análisis dimensional, facilitando la obtención de la ecuación.

Este modelo es útil para la estimación de la sobrepresión con grandes variaciones en la velocidad, presión y reducción del caudal, ocasionados por el cierre de válvulas en instalaciones hidráulicas.

Como el fenómeno del golpe de ariete aparece en maniobras como el cierre y apertura de válvulas, arranque de bombas, detención de bombas y llenado inicial de tuberías, que son operaciones necesarias para el adecuado manejo y conservación de sistemas a presión, su frecuencia es importante y no es un fenómeno eventual, por lo cual no se deben escatimar esfuerzos para la correcta comprensión de los principios o fundamentos y la aplicación de los modelos de cálculo.

Referencias

Acosta A., G. y de Azevedo N, J.M. (1975). Manual de Hidráulica. Sexta ed. México, D.F.: Editorial Harla.         [ Links ]

Calvin D., V. (1986). Tratado de Hidráulica Aplicada. Quinta ed. Barcelona: Editorial Labor S.A.         [ Links ]

Guitelman, A. y Pérez F., L. (2005). Estudio de Transitorios: Golpe de ariete. Primera ed. Buenos Aires: Universidad de Buenos Aires.         [ Links ]

Maganto, F. (2002). Límites de estabilidad de un grupo hidroeléctrico conectado a una red aislada. Revista Ingeniería Civil, No.127 (julio-septiembre).         [ Links ]

Rich R., G. (1951). Hydraulic Transients. Primera ed. New York: McGraw-Hill Book Company Inc.         [ Links ]

Rodríguez C., W., y Pallares, M.R. (2007). Modelo numérico del golpe de ariete con SCILAB. Revista Ingeniería e Investigación. Universidad Nacional de Colombia, Vol. 27, No. 3.         [ Links ]

Streeter L., V. (2002). Mecánica de Fluidos. Octava ed. México, D.F.: McGraw- Hill.         [ Links ]

Vallamino Cánovas del Castillo, E. (1999). El golpe de ariete-solución gráfica. Revista de Obras Públicas. Versión electrónica. Colegio de caminos y puertos. España, No. 2758.         [ Links ]