Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Tecnura
versão impressa ISSN 0123-921X
Tecnura vol.20 no.48 Bogotá abr./jun. 2016
https://doi.org/10.14483/udistrital.jour.tecnura.2016.2.a12
DOI: http://dx.doi.org/10.14483/udistrital.jour.tecnura.2016.2.a12
Techniques for modeling photovoltaic systems under partial shading
Técnicas para modelar sistemas fotovoltaicos bajo sombreado parcial
Luz Adriana Trejos Grisales1, Carlos Andrés Ramos-Paja2, Andrés Julián Saavedra-Montes3
1 Electric Engineer, Master in Engineering, Student at doctorate in engineering in the area of automatics Universidad Nacional de Colombia. Professor at Instituto Tecnológico Metropolitano, Medellin, Colombia. Contact: adrianatrejos@itm.edu.co
2 Electronic Engineer, Master in Engineering-Automatics, Master in Electronic Engineering, Doctor in Electronic Engineering, Automatics and Communications. Associate Professor at Universidad Nacional de Colombia, Facultad de Minas, Departamento de Energía Eléctrica y Automática. Medellín, Colombia. Contact: caramosp@unal.edu.co
3 Electric Engineer, Master in Electric Energy Generation Systems, Doctor in Electric Engineering. Associate Professor at Universidad Nacional de Colombia, Facultad de Minas, Departamento de Energía Eléctrica y Automática. Medellín, Colombia. Contact: ajsaaved@unal.edu.co
Fecha de recepción: 26 de agosto de 2015 Fecha de aceptación: 15 de febrero de 2016
Cómo citar: Trejos Grisales, L. A., Ramos Paja, C. A., & Saavedra Montes, A. J. (2016). Techniques for modeling photovoltaic systems under partial shading. Revista Tecnura, 20(48), 171-183. doi:10.14483/udistrital.jour.tecnura.2016.2.a12
Abstract
Context: The energy produced by photovoltaic (PV) systems operating under partial shading conditions depends on the connections between the modules and the shading pattern. Several mathematical models have been proposed to address this topic exhibiting different compromises between accuracy, calculation speed and PV model complexity. However, it is not evident how to choose a model for a given application to ensure reliable results.
Method: Several mathematical models of PV systems under shading conditions were analyzed to synthetize the characteristics, advantages and drawbacks of each one of them. Three main categories have been identified: analytical, simulation and experimental methods. Analytical and simulation methods require a basic PV model and mathematical analysis supported by computational tools; while experimental methods are based in data or measurements.
Results: From the analysis of the published solutions, three representative modeling techniques with different characteristics were selected to perform a practical comparison. Those techniques were implemented and contrasted in realistic scenarios to identify the effects of the compromise between accuracy, calculation speed and PV model complexity.
Conclusions: To select a mathematical model it must be taken into account the connection scheme, model of the PV unit, model of the bypass and blocking diodes, size of the system, programming complexity and simulation time. This paper provides some guidelines to choose the right model for a particular application depending on those characteristics.
Keywords: Model, blocking diode, bypass diode, mismatching, photovoltaic.
Resumen
Contexto: La energía producida por un sistema fotovoltaico (PV) operando en condiciones de sombreado parcial depende de las conexiones entre sus módulos y del perfil de sombra. En la literatura existen reportados múltiples modelos matemáticos en este tópico, los cuales presentan diferentes compromisos entre precisión, velocidad de cálculo y complejidad. No obstante, no es evidente como seleccionar uno de esos modelos para obtener resultados confiables en una aplicación particular.
Método: Se analizaron múltiples modelos matemáticos de sistemas PV operando en condiciones de sombreado para sintetizar sus características, ventajas y desventajas. De ese análisis se detectaron tres categorías principales: métodos analíticos, de simulación y experimentales. Los métodos analíticos y de simulación requieren un modelo básico PV y análisis matemáticos soportados por herramientas de cómputo; en contraste los métodos experimentales se basan en datos y mediciones.
Resultados: A partir de los análisis de los modelos reportados, se seleccionaron tres técnicas de modelado representativas para realizar una comparación práctica. Esas técnicas se implementaron y contrastaron en escenarios realistas para identificar los efectos del compromiso entre precision, velocidad de cálculo y complejidad del modelo PV.
Conclusiones: Para seleccionar un modelo matemático se deben tener en cuenta el esquema de conexión, el modelo de la unidad PV, el modelo de los diodos de bloqueo y puente, el tamaño del sistema, la complejidad de programación y el tiempo de simulación. Este artículo provee algunas guías para seleccionar el modelo adecuado para una aplicación en particular dependiendo de esas características.
Palabras clave: Modelo, diodo de bloqueo, diodo puente, irregularidad, fotovoltaico.
Introduction
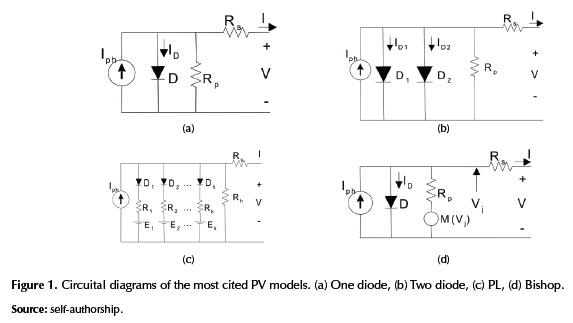
Environment issues like global warming and the constant increasing prizes of fossil fuels have drawn more attention towards the usage of renewable energy sources, particularly on photovoltaic (PV) energy. Modeling PV systems is one of the most important research areas due to the need of obtaining information about performance and energy yield prediction under different operating conditions. With the aim of represent the physical phenomenon that occurs in a PV cell, the most widely adopted approaches are the one diode model, the two diode model, the piecewise linear (PL) model, and the Bishop model (Zegaoui, Petit, & Aillerie, 2012), (Wang & Hsu, 2009a), (Bishop, 1988). Figure 1 shows the circuital diagrams of such models, which have been also extended to represent PV modules, strings and arrays, it depending on the granularity of a PV system (Ji, Kim, Park, Kim, & Won, 2009), (Wang & Lin, 2011).
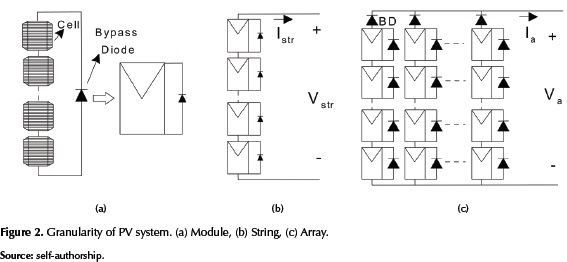
Figure 2 shows a graphical representation of the granularity concept. A PV module is defined as the series connection of several PV cells protected by an anti-parallel bypass diode; strings are defined as the connection of several modules in series and arrays are de-fined as the parallel connection of several strings, where each string is protected by a series blocking diode (BD in figure. 2(c)) (Said Samer, Ahmed, & Shehab, 2012), (Rathee, Khanna, & Das, 2013).
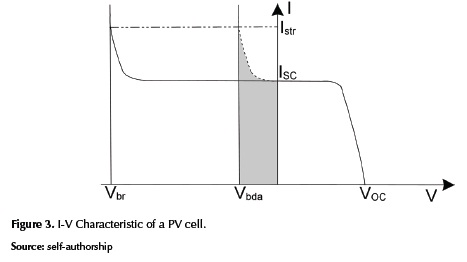
In addition to the basic photovoltaic phenomenon and the granularity of the system, the modeling of a PV array requires considering the effect of shadows on the PV system. Such a phenomenon, known as shading, is critical since the power produced by a PV system depends on the level of solar irradiance. The shadows can be produced by static objects in the neighborhood of the PV system, clouds, or inclusive by elements which fall on the PV system surface such as leaves. When series connected PV cells are under shading conditions, cells can experiment negative voltages due to the excess of current imposed by the cells with higher levels of irradiance, which forces the cell to consume power instead of produce it (Bishop, 1988), (Wang & Hsu, 2009b). Moreover, if the cell negative voltage increases due to the shading conditions, hot spots can appear causing aging effects on the cell; and if the cell negative voltage reaches the breakdown value, the cell can be damaged due to the fast increasing of the current (Zegaoui, et al., 2011). To avoid such detrimental effects, bypass diodes are connected in anti-parallel with a series-connection of PV cells. A bypass diode provides a path for the excess of cur-rent, but due to the diode operation, it imposes a small negative voltage to the cells. Such negative voltage is much lower than the breakdown voltage, but in any case it forces the cells to consume power. Figure 3 shows a typical current vs. voltage (I-V) curve of a PV cell where Vbr is the breakdown voltage, Vbda is the diode activation voltage, VOC is the open circuit voltage, ISC is the short circuit current and Ist is the string current.
In figure 3, the gray area represents the power loss caused by the bypass diode activation, which is much lower than the power loss exhibited when the cell reaches the breakdown voltage. In addition to the connection of bypass diodes, PV arrays are also protected by blocking diodes, which are connected in series with strings to block reverse current flows that may cause the PV modules behave as loads (Petrone, Spagnuolo, & Vitelli, 2007). The previous considerations increase the complexity of the modeling process. One of the most commonly adopted alternative is to use simulation packages; in such a way in (Ishaque K., Salam, Taheri, & Syafaruddin, 2011b) two ideas to evaluate the goodness of a simulation package are highlighted: (i) it should be fast but accurate in the prediction of the I-V characteristic curve, it including special conditions such as partial shading; and (ii) it should be a comprehensive tool to develop and validate the PV system design including the power converter and the maximum power point tracking control. However, simulations packages have some limitations: high cost, inaccurate, limited, bad representation of mismatching conditions, not supporting the interfacing of the PV arrays with power electronic systems, among others (Patel & Agarwal, 2008). The above considerations shows the need of appealing to different techniques, which in synergy with such simulation packages and programming languages, provide suitable analysis of PV systems (I-V curves) with a suitable balance between accuracy, computational cost and complexity. In the PV systems research area, several topics have been studied through different literature reviews: in (Woyte, Nijs, & Belmans, 2003) a review on the effects of shading in the energy production is presented, analyzing also the effect of the array position. The work presented in (Fuentes, Nofuentes, Aguilera, Talavera, & Castro, 2007) highlights the importance of the calibration of PV modules to avoid errors in the analysis. In addition, five algebraic methods to correct from STC to any operation conditions are briefly described, while in (Ishaque & Salam, 2013) an analysis of the main characteristics of the most used Maximum Power Point Tracking (MPPT) techniques for mismatched conditions is presented. Similarly, in (Olalla, Clement, Rodriguez, & Maksimovic, 2013) and (Olalla, Deline, & Maksimovic, 2014) an analysis of the power interface is presented, it making emphasis on the advantages of using submodule-integrated dc-dc converters (SubMICs), instead of bypass diodes, to avoid the effects of partial shading. Moreover, a numerical model is used to predict the power produced using a Distributed Maximum Power Point Tracking (DMPPT) down to the cell level. However, a review on techniques to model PV arrays under shading conditions is necessary. Hence, this paper analyzes the current developments in modeling techniques for PV systems under shading conditions and also provides a comparison between three modeling techniques to highlight the compromise between accuracy, calculation speed and complexity.
MODELING TECHNIQUES
This work analyses the modeling techniques grouped depending on the adopted PV model: one diode model, two diode model and other models which include Bishop model, PL model, and others.
Methods based on the one diode model
In (Karatepe, Boztepe, & Colak, 2007) the one diode model is used to design an artificial neural network (ANN) to model PV systems under different configurations as the series-parallel (SP), bridge-linked (BL) and total cross tied (TCT). Despite the use of an ANN to ensure less computational effort, the authors do not provide comparison with other methods. In (Petrone, Spagnuolo, & Vitelli, 2007) an analytical method based on an explicit relationship between the current of a string and its voltage is proposed, it using the Lambert-W function to define a set of nonlinear equations, including the bypass diodes, to simulate strings or arrays. The set of non-linear equations is solved using the Newton-Raphson method programmed in Matlab. This technique is improved in (Orozco-Gutierrez, Ramirez-Scarpetta, Spagnuolo, & Ramos-Paja, 2013), where authors propose the use of a mathematical tool known as the Schür complement, which allows to enhance the speed in the calculation of the Jacobian matrix of the system. Such an improvement is demonstrated using comparisons between the different algorithms. In (Patel & Agarwal, 2008), a Matlab-based simulator is used to analyze PV arrays taking into account temperature and irradiance variations, however, the authors do not give any detail about the algorithm. An improvement to this work is presented in (Ramabadran, 2009), which modifies the equations that define the system. Another related work is presented in (Wang & Hsu, 2009a), where a string with certain number of modules is characterized in the first and second quadrants, while the bypass diodes are modeled by piecewise resistances. Taking advantage of the C language programmable blocks in PSIM, the authors of (Ji, Kim, Park, Kim, & Won, 2009) propose a strategy to simulate the effects of partial shading conditions for developing MPPT algorithms aimed to drive power conversion systems. A work focused in the energy yield analysis of PV systems is presented in (Di Dio, La Cascia, Miceli, & Rando, 2009), in which a PV model implemented in Simulink is used to analyze different PV array connections; the model used in this work allows predicting the maximum generated power of PV generators under unequally radiation conditions. In (Villalba, Gazoli, & Filho, 2009), a widely used approach was introduced. In such a work the authors propose a method to find the parameters of the nonlinear I-V equation by adjusting the curve at three points: open circuit, maximum power and short circuit, which results useful for the analysis of the characteristic curves. This method finds the best I-V equation for the single-diode model, this including the effect of the series and parallel resistances. In (Di Piazza & Vitale, 2010), a new strategy for the analysis of PV systems is presented, which mainly consist into develop a PV field emulator. This tool provides the I-V and P-V curves of a PV array under shading conditions taking into account temperature effects. The emulator is equipped with a power interface to analyze the performance of MPPT strategies and other controllers. Another work focused in obtaining the characteristic curves is presented in (Mäki, Valkealahti, & Leppäaho, 2011), where simulation results of series-connected PV modules under different shading conditions are presented. Such simulations are used to study the shading losses, the occurrence of multiple Maximum Power Points (MPP), and the voltage behavior of the MPPs. In (Petrone & Ramos-Paja, 2011), a simplified one diode model is adopted, while the technique is based on the calculation of the voltages in which the bypass diodes become active. Such information is used to define the number of equations to be solved to obtain the I-V characteristic. In that work, the bypass diode is considered an ideal switch. An improvement to that method is presented in (Bastidas, Franco, Petrone, & Ramos-Paja, 2013), where the complete one diode model and a piecewise representation of the bypass and blocking diode are used. In (Tian, Zhao, Deng, He, & Han, 2011), a model for simulation in Matlab is presented. The influence of insolation and temperature in series-connected and parallel-connected modules is also analyzed. The authors of (Wang & Lin, 2011) present a comparison between the one diode and PL models applied to SP and TCT configurations. The solution based on the one diode model is represented through a set of equations solved by the Newton-Raphson method, while the solution based on the PL model is simulated in EMTP software. In (Wei, Ning, & Shaoyuan, 2012), a DE (Differential Evolution) algorithm is used to obtain the time-varying parameters of an array under shading conditions. The accuracy of the method is validated trough an experimental test. In contrasts, the method described in (Kadri, Andrei, Gaubert, Ivanovici, Champenois, & Andrei, 2012) is based on the classical circuit theory, it using the admittance and conductance equations to describe the connection of the system in different configurations; the method is programmed in Matlab-Simulink using a sub-circuit for each module of the array. (Alonso-Garcia & Ruiz, 2006) and (Said Samer, Ahmed, & Shehab, 2012) present simulation works; in the former the behavior of the cell in the second quadrant is analyzed, while in the latter a suitable Simulink model is used taking into account parameters related to the temperature. In (Seyedmahmoudian, Mekhilef, Rahmani, Yusof, & Taslimi, 2013) the simulation of a PV system is performed by using analytical expressions. In addition, simulations with a power interface are made to analyze the performance of the MPPT algorithm under shading conditions. A PV model based on the one diode model and the Lambert W-function, aimed to analyze PV strings down to the cell level, is presented in (Batzelis, Routsolias, & Papathanassiou, 2014); in this work the bypass diode is represented in an exponential way and the model allows representing the PV behavior in the four quadrants. As it was said, the analysis of PV systems covers several topics including the design and control of the power interface, which is mainly composed by a DC/DC converter and its controller, where MPPT algorithms take place. In this way, the work reported in (Xiao, Edwin, Spagnuolo, & Jatskevich, 2013) provides a detailed parameterization procedure for a PV model. That procedure is aimed at studying power interfaces with and without IDCL (intermediate DC link). Another research topic in PV systems is the parameterization of PV modules, which is an important issue since the accuracy in the model parameters defines in certain level the efficiency of an analysis technique. In (Orioli & Di Gangi, 2014), a tabular data procedure to evaluate the parameters of the one diode model, for a single PV module, is presented. Simulations for several commercial PV panels are made with PVSyst and t he results are compared with another procedure, named Saloux model, and with experimental measurements. Finally, interesting mathematical approaches are presented in (Lun, Du, Yang, Guo, Sang, & Li, 2013a) and (Lun, et al., 2013b); in the first one a Padé approximation method is proposed to express the exponential function of I-V characteristic equation, then an explicit analytical description of current is obtained for one cell; while in the latter one a Taylor's series expansion method is proposed with the same purpose, both works use the environment Engineering Equation Solver (EES).
Methods based on the two diode model
This model has been used by (Ishaque, Salam, & Syafaruddin, 2011a) to provide improved accuracy. The proposed method, programmed in Matlab, consists in (i) determination of shading and temperature patterns for a particular shaded group, (ii) calculation of the voltage and current for each group based on the two-diode model subjected to a known shading pattern and (iii) performing linear interpolation with extrapolation techniques to form the continuous I-V curves. In contrast, a detailed simulator for PV arrays under shading conditions based on Matlab, is presented in (Ishaque K., Salam, Taheri, & Syafaruddin, 2011b). This work is oriented to study the characteristic curves and the performance of MPPT algorithms. In (Paraskevadaki & Papathanassiou, 2011) the two diode model is used to obtain mathematical expressions to calculate the power and voltage of the MPPs for a unique shading pattern in a panel with two modules, where simulations are executed in PSpice. In (Rathee, Khanna, & Das, 2013), a combined simulation in Pspice and Matlab is presented, while in (Zegaoui, et al., 2011) a Pspice simulation is also performed but taking into account the behavior of the cell in the second quadrant.
Methods based on other models
The Bishop model was introduced in 1988. This model was used to present a new software tool (PVNet) for modeling and simulating PV systems with SP and TCT configurations under shading conditions, it considering also the behavior in the second quadrant. The PVNet software was programmed in Pascal language (Bishop, 1988). Several works have adopted this model: (Silvestre & Chouder, 2007) and (Silvestre, Boronat, & Chouder, 2009) present simulations based on Matlab and Pspice, respectively. In the former, a single module is analyzed, while in the latter an array is addressed. Both works consider the behavior in the first quadrant only. In (Liu, Nguang, & Partridge, 2011), the system is modeled through a set of nonlinear equations that are solved by a robust damped Newton method, where the convergence is guaranteed. SP, TCT, and BL configurations under shading conditions are analyzed from the point of view of the power losses and energy yield in (Ramaprabha & Mathur, 2012) by using the Bishop model. On the other hand, the PL model is used in (Wang & Hsu, 2009a) and in (Azab, 2009), both works oriented to simulate in the first quadrant. Such simulations were carried out in EMPT and in Matlab, respectively. Some works are not based in a circuital model, instead they are based in mathematical expression extracted from geometrical characteristics which is the case of the work presented in (Narvarte & Lorenzo, 2008), where an analysis of the use of tracking strategies as an option to avoid the effects of partial shading is presented. Another work based on geometrical and theoretical definitions is the one presented in (Makrides, Zinsser, Schubert, & Georghiou, 2011), which provides a comparison of the errors in annual DC energy yield prediction obtained by four different theoretical methods; results are contrasted against outdoor measurements for different grid-connected PV systems. (Hachem, Athienitis, & Fazio, 2011) analyses the impact of the geometry of a two-story single family housing in the integration of a solar generator. A particular analysis of self-shading and power losses is presented in (Brecl & Topic, 2011), where a detailed analysis of the effect of self-shading in fixed free-standing PV arrays is presented. The analysis takes into account the geometry of module and the orientation of the array, as well as the parameters of the array configuration, e.g. space between modules. Finally, in (Sánchez, Milone, & Buitrago, 2013), a neural model is used: a multilayer perceptron was adopted, where the input layer consists of two neurons whose linear entries are radiation and cell temperature. The hidden layer consists of nine neurons with sigmoid transfer functions, and the output layer has 40 nodes with linear activation functions.
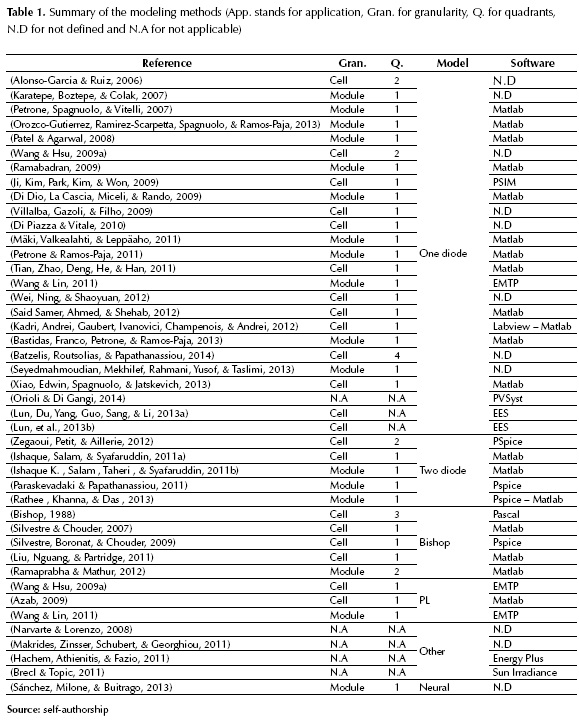
Table 1 summarizes the characteristics of the modeling methods previously analyzed. Several modeling techniques were reported, where 25 of them are based on the one diode model. Six works considered the behavior of the system in the second quadrant; however 3 of the works based on the Bishop model did not present any analysis about this matter. Other approaches were based on the two diode model, the PL model, a neural model and models based on theoretical concepts (no-circuital models). A preference to use Matlab and PSpice was identified; however in 11 references the software used is not described explicitly.
Results
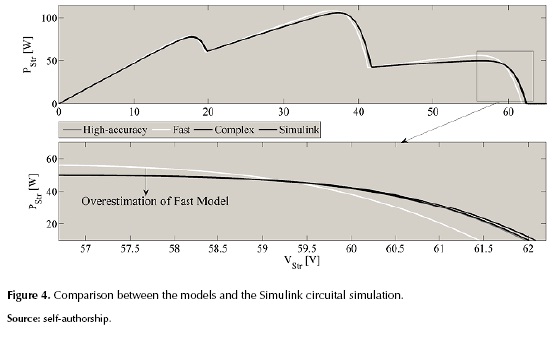
A comparison between three of the reported methods was performed with the aim of illustrate the compromise between accuracy, complexity and calculation speed. The methods selected for the comparison were reported in (Petrone, Spagnuolo, & Vitelli, 2007), which is named High-accuracy model; in (Petrone & Ramos-Paja, 2011), which is named Fast model; and in (Bastidas, Franco, Petrone, & Ramos-Paja, 2013), which is named Complex model. Such models were selected because they provide different characteristics as is described by the authors: High-accuracy model is very accurate but takes long calculation times; Fast model is less accurate but provides short calculation times, while the Complex model provides a balance between the previous. The methods were implemented in Matlab and contrasted with a Simulink circuital simulation. The PV system used for the simulation consists of a single string of three modules with 36 cells each. The parameters of the PV modules used in the simulation are: VOC = 21.78 V, ISC = 5.13 A, Iph1 = 0.94*ISC A, Iph2 = 0.6*ISC A, Iph3 = 0.2*ISC A. Figure 4 shows the P-V curve comparison between the models and the Simulink circuital simulation. The results show the good approach obtained with the High-accuracy model, however its simulation time was 83.860 s. The Fast model requires a short simulation time equal to 1.369 s, but it introduces some overestimation in power compared to the circuital simulation. Finally, the Complex model provides a similar behavior to the High-accuracy approach with a simulation time equal to 51.42 s, but its equations change dynamically, which increases the implementation complexity.
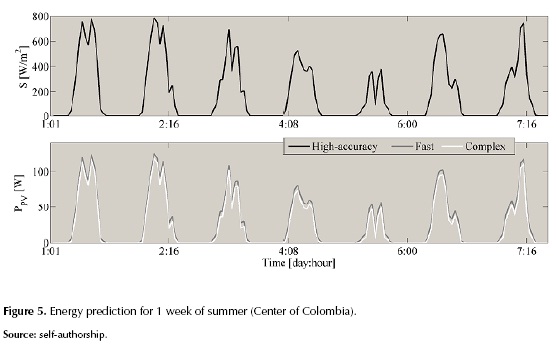
It is evident that the Fast method predicts higher power values that can lead to errors in planning of PV systems, however it could be useful to carry on simulations aimed at contrasting different PV fields, e.g. SP, TCT, BL. The relative mean errors of the three studied methods for the power prediction, with respect to the Simulink circuital simulation, are: 2.93% for the High-accuracy, 13.04% for the Fast and 8.39% for the Complex. The upper part of figure 5 shows an irradiance profile of the center of Colombia for 7 days with samples taken hour by hour, while the lower part shows the predicted power provided by the three methods for a 3x2 PV field (2 strings with 3 modules each) with a shading pattern of 95%, 50% and 20% for the first string and 70%, 40% and 10% for the second one.
It is observed that the prediction provided by the Fast method is higher than the prediction provided by the other two methods, which put in evidence an overestimation effect. In any case, the Fast method requires only 2.02 % of the simulation time, hence it is useful for comparing different PV systems under similar conditions.
ACKNOWLEDGEMENTS
This work was supported by the Universidad Nacional de Colombia, the Instituto Tecnológico Metropolitano and Colciencias (Fondo nacional de financiamiento para ciencia, la tecnología y la innovación Francisco José de Caldas) under the projects MicroRENIZ-25439 (Code 1118-669-46197) and MICRO-RED-26861 and the doctoral scholarships 34065242 and 095-2005.
FINANCING
This work was supported by the Universidad Nacional de Colombia, the Instituto Tecnológico Metropolitano and Colciencias (Fondo nacional de financiamiento para ciencia, la tecnología y la innovación Francisco José de Caldas) under the projects MicroRENIZ-25439 (Code 1118-669-46197) and MICRO-RED-26861 and the doctoral scholarships 34065242 and 095-2005.
Conclusions
The modeling techniques for PV systems under partial shading conditions have been analyzed. The key concepts concerning the modeling of PV systems were highlighted to contextualize the problem of the analysis of PV systems by means of analytical and simulation methods. The works reported in (Petrone, Spagnuolo, & Vitelli, 2007), (Petrone & Ramos-Paja, 2011) and (Bastidas, Franco, Petrone, & Ramos-Paja, 2013) were compared through simulation. The results show that accurate results can be obtained with relatively simple implementations but requiring long simulation times, while other approaches provide very short simulation times but introducing errors. In contrasts, it is possible to obtain a balance between accuracy and calculation speed by increasing significantly the model complexity, which in turns increases the implementation time. Hence, the selection of a method for analyzing a PV system must to consider the size of the system, the required hardware to execute the simulation, the programming complexity and the tolerance error to obtain a suitable solution for each particular case.
Agradecimientos
Este trabajo fue soportado por la Universidad Nacional de Colombia, el Instituto Tecnológico Metropolitano y Colciencias (Fondo nacional de financiamiento para ciencia, la tecnología y la innovación Francisco José de Caldas) bajo los proyectos MicroRENIZ-25439 (Code 1118-669-46197) y MICRO-RED-26861 y las becas doctorales 34065242 y 095-2005.
References
Alonso-Garcia, M., & Ruiz, J. (2006). Analysis and modelling the reverse characteristic of photovotaic cells. Solar Energy Materials & Solar Cells, 90, 1105-1120. [ Links ]
Alonso-Garcia, M., Ruiz, J., & Herrmann, W. (2006). Computer simulation of shading effects in photovoltaic arrays. Renewable Energy, 31, 1986-1993. [ Links ]
Azab, M. (2009). Improved Circuit Model of Photovoltaic Array. International J. of Power and Energy Systems and Engineering, 2(3), 185-188. [ Links ]
Bastidas, J., Franco, E., Petrone, G., & Ramos-Paja, C. (2013). A model of photovoltaic fields in mismatching conditions featuring an improved calculation speed. Electric Power Systems Research, 96, 81-90. [ Links ]
Batzelis, E., Routsolias, I., & Papathanassiou, S. (2014). An explicit PV string model based on the Lambert W function and simplified MPP expressions for operation under partial shading. IEEE Transactions on Sustainable Energy, 5(1), 301-312. [ Links ]
Bishop, J. (1988). Computer Simulation Of The Effects Of Electrical Mismatches In Photovoltaic Cell Interconnection Circuits. Solar Cells, 25, 73-89. [ Links ]
Brecl, K., & Topic, M. (2011). Self-shading losses of fixed free-standing PV arrays. Renewable Energy, 36(11), 3211-3216. [ Links ]
Di Dio, V., La Cascia, D., Miceli, R., & Rando, C. (2009). A mathematical model to determine the electrical energy production in photovoltaic fields under. Clean Electrical Power International Conference (pp. 46-51). Capri: IEEE. [ Links ]
Di Piazza, M., & Vitale, G. (2010). Photovoltaic field emulation including dynamic and partial shadow conditions. Applied Energy, 87(3), 814-823. [ Links ]
Fuentes, M., Nofuentes, G., Aguilera, J., Talavera, D., & Castro, M. (2007). Application and validation of algebraic methods to predict the behaviour of crystalline silicon PV modules in Mediterranean climates. Solar Energy, 81(11), 1396-1408. [ Links ]
Hachem, C., Athienitis, A., & Fazio, P. (2011). Parametric investigation of geometric form effects on solar potential of housing units. Solar Energy, 85(9), 1864-1877. [ Links ]
Ishaque, K., & Salam, Z. (2013). A review of maximum power point tracking techniques of PV system for uniform insolation and partial shading condition. Renewable and Sustainable Energy Reviews, 19, 475-488. [ Links ]
Ishaque, K., Salam, Z., Taheri, H., & Syafaruddin. (2011b). Modeling and simulation of photovoltaic (PV) system during partial shading based on a two-diode model. (Elsevier, Ed.) Simulation Modelling Practice and Theory, 19(7), 1613-1626. [ Links ]
Ishaque, K., Salam, Z., & Syafaruddin. (2011a). A comprehensive MATLAB Simulink PV system simulator with partial shading capability based on two-diode model. Solar Energy, 85, 2217-2227. [ Links ]
Ji, Y.-H., Kim, J.-G., Park, S.-H., Kim, J.-H., & Won, C.-Y. (2009). C-language based pv array simulation technique considering effects of partial shading. Industrial Technology, 2009. ICIT 2009. IEEE International Conference on (pp. 1-6). IEEE. [ Links ]
Kadri, R., Andrei, H., Gaubert, J., Ivanovici, T., Champenois, G., & Andrei, P. (2012). Modeling of the photovoltaic cell circuit parameters for optimum connection model and real-time emulator. Energy, 42(1), 57-67. [ Links ]
Karatepe, E., Boztepe, M., & Colak, M. (2007). Development of a suitable model for characterizing photovoltaic arrays with shaded solar cells. Solar Energy, 81(8), 977-992. [ Links ]
Liu, G., Nguang, S., & Partridge, A. (2011). A general modeling method for I-V characteristics of geometrically and electrically configured photovoltaic arrays. Energy Conversion and Management, 52, 3439-3445. [ Links ]
Lun, S., Du, C., Yang, G., Guo, T., Sang, J., & Li, J. (2013a). A new explicit I-V model of a solar cell based on Taylor's series expansion. Solar Energy, 94, 221-232. [ Links ]
Lun, S., Du, C., Yang, G., Wang, S., Guo, T., Sang, J., et al. (2013b). An explicit approximate I-V characteristic model of a solar cell based on padé approximants. Solar Energy, 92, 147-159. [ Links ]
Mäki, A., Valkealahti, S., & Leppäaho, J. (2011). Operation of series-connected silicon-based photovoltaic modules under partial shading conditions. Progress in photovoltaics: research and applications, 20(3), 298-309. [ Links ]
Makrides, G., Zinsser, B., Schubert, M., & Georghiou, G. (2011). Energy yield prediction errors and uncertainties of different photovoltaic models. Progress in photovoltaics: research and applications, 21(4), 500-516. [ Links ]
Martinez-Moreno, F., Muñoz, J., & Lorenzo, E. (2011). Experimental model to estimate shading losses on PV arrays. Solar Energy Materials & Solar Cells, 94(12), 2298-2303. [ Links ]
Narvarte, L., & Lorenzo, E. (2008). Tracking and Ground Cover Ratio. Progress in photovoltaics: research and applications, 16, 703-714. [ Links ]
Olalla, C., Clement, D., Rodriguez, M., & Maksimovic, D. (2013). Architec-tures and Control of Submodule Integrated DC-DC Converters for Photovoltaic Applications. IEEE Transactions On Power Electronics, 28(6), 2980-2997. [ Links ]
Olalla, C., Deline, C., & Maksimovic, D. (2014). Performance of Mis-matched PV Systems With Submodule Integrated Converters. IEEE Journal of Photovoltaics, 4(1), 396-404. [ Links ]
Orioli, A., & Di Gangi, A. (2014). Review of the energy and economic parameters involved in the effectiveness of grid-connected PV systems installed in multi-storey buildings. Applied Energy, 113, 955-969. [ Links ]
Orozco-Gutierrez, M. L., Ramirez-Scarpetta, J. M., Spagnuolo, G., & Ramos-Paja, C. A. (2013). A technique for mismatched PV array simulation. Renewable Energy, 55, 417-427. [ Links ]
Paraskevadaki, V., & Papathanassiou, A. (2011). Evaluation of MPP Voltage and Power of mc-Si PV Modules in Partial Shading Conditions. IEEE Transactions On Energy Conversion, 26(3), 923-932. [ Links ]
Patel, H., & Agarwal, V. (2008). MATLAB-Based Modeling to Study the Effects of Partial Shading on PV Array Characteristics. IEEE Transactions On Energy Conversion, 23(1), 302-310. [ Links ]
Petrone, G., & Ramos-Paja, C. (2011). Modeling of photovoltaic fields in mismatched conditions for energy yield evaluations. Electric Power Systems Research, 81, 1003-1013. [ Links ]
Petrone, G., Spagnuolo, G., & Vitelli, M. (2007). Analytical model of mismatched photovoltaic fields by means of Lambert W function. Solar Energy Materials & Solar Cells, 91, 1652-1657. [ Links ]
Ramabadran, R. (2009). MATLAB Based Modelling and Performance Study of Series Connected SPVA under Partial Shaded Conditions. J. of Sustainable Development, 2(3), 85-94. [ Links ]
Ramaprabha, R., & Mathur, B. (2012). A Comprehensive Review and Analysis of Solar Photovoltaic Array Configurations under Partial Shaded Conditions. International Journal of Photoenergy, 2012, 1-16. [ Links ]
Rathee, R., Khanna, V., & Das, B. (2013). Comparative Analysis To Study The Effects Of Partial Shading On PV Array Withlt-Spice And Matlab/Simulink Environment. International Journal of Engineering Research & Technology (IJERT), 2(5), 1501-1508. [ Links ]
Said Samer, B. M., Ahmed, M., & Shehab, A. (2012). A matlab/simulink-based photovoltaic array model employing simpowersystems toolbox. Journal of Energy and Power Engineering, 6(12), 1965-1975. [ Links ]
Sánchez, C., Milone, D., & Buitrago, R. (2013). Simulation of photovoltaic centrals with dynamic shading. Applied Energy, 103, 278-289. [ Links ]
Seyedmahmoudian, S., Mekhilef, S., Rahmani, R., Yusof, R., & Taslimi, E. (2013). Analytical Modeling of Partially Shaded Photovoltaic Systems. Energies, 6(1), 128-144. [ Links ]
Silvestre, S., & Chouder, A. (2007). Effects of Shadowing on Photovoltaic Module Performance. Progress in Photovoltaics: Research and Applications, 16, 141-149. [ Links ]
Silvestre, S., Boronat, A., & Chouder, A. (2009). Study of bypass diodes configuration on PV modules. Applied Energy, 86, 1632-1640. [ Links ]
Tian, Q., Zhao, Z., Deng, Y., He, F., & Han, X. (2011). Modeling and analysing to the forward PV cells for large-scale PV array. International Conference on Electrical Machines and Systems (pp. 1-7). Beijing: IEEE. [ Links ]
Villalba, M., Gazoli, J., & Filho, E. (2009). Comprehensive Approach to Modeling and Simulation of Photovoltaic Arrays. IEEE Transactions on Power Electronics, 24(5), 1198-1208. [ Links ]
Wang, Y.-J., & Lin, S.-S. (2011). Analysis of a partially shaded PV array considering different module connection schemes and effects of bypass diodes. Utility Exhibition on Power and Energy Systems: Issues & Prospects for Asia (ICUE), 2011 International Conference and (pp. 1-7). IEEE. [ Links ]
Wang, Y., & Hsu, P. (2009a). Analysis of Partially Shaded PV Modules Using Piecewise Linear Parallel Branches Model. World Academy of Science, Engineering and Technology, 60(2), 783-789. [ Links ]
Wang, Y., & Hsu, P. (2009b). Analytical modelling of partial shading and different orientation of photovoltaic modules. IET Renewable Power Generation, 4(3), 272-282. [ Links ]
Wei, W., Ning, L., & Shaoyuan, L. (2012). A Real-time Modeling of Photovoltaic Array. Chinese Journal of Chemical Engineering, 20(6), 1154-1160. [ Links ]
Woyte, A., Nijs, J., & Belmans, R. (2003). Partial shadowing of photovoltaic arrays with different system configurations: literature review and field test results. Solar Energy, 74(3), 217-233. [ Links ]
Xiao, W., Edwin, F., Spagnuolo, G., & Jatskevich, J. (2013). Efficient Approaches for Modeling and Simulating Photovoltaic Power Systems. IEEE Journal of Photovoltaics, 3(1), 500-508. [ Links ]
Zegaoui, A., Petit, P., & Aillerie, M. (2012). Experimental Validation of Photovoltaic Direct and Reverse Mode Model: Influence of Partial Shading. Energy Procedia, 8, 1247-1253. [ Links ]
Zegaoui, A., Petit, P., Aillerie, M., Sawicki, J., Belarbi, A., Krachai, M., et al. (2011). Photovoltaic Cell/Panel/Array Characterizations and Modeling Considering Both Reverse and Direct Modes. Energy Procedia, 6, 695-703. [ Links ]