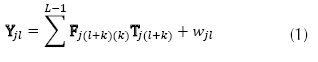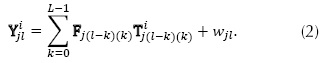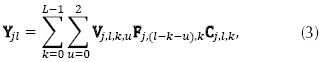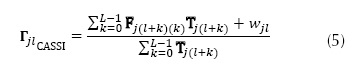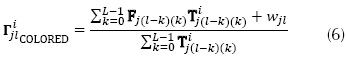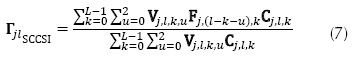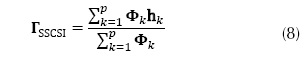Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Tecnura
versão impressa ISSN 0123-921X
Tecnura vol.21 no.52 Bogotá jan./abr. 2017
https://doi.org/10.14483/udistrital.jour.tecnura.2017.2.a03
DOI: http://dx.doi.org/10.14483/udistrital.jour.tecnura.2017.2.a03
Further compression of focal plane array in compressive spectral imaging architectures
Compresión adicional de los datos del plano focal en arquitecturas de sensado comprimido en imágenes espectrales
Jeison Marín Alfonso1, Leonardo Betancur Agudelo2, Henry Arguello Fuentes3
1 Electronic Engineer, master in Electronic, student at doctorate in Telecommunications at Universidad Pontificia Bolivariana. Medellín, Colombia. Contact: jeison.marin@upb.edu.co
2 Electronic Engineer, master in Telecommunications Engineering, doctor in Telecommunications Engineering. Associated Professor at Universidad Pontificia Bolivariana. Medellín, Colombia, Contact: leonardo.betancur@upb.edu.co
3 Electrical Engineer, master in Electrical power, doctor in Electrical and Computer Engineering. Titular professor at Universidad Industrial de Santander. Bucaramanga, Colombia, Contact: henarfu@uis.edu.co
Fecha de recepción: 23 de agosto de 2016 Fecha de aceptación: 15 de febrero de 2017
Cómo citar: Marín A., J.; Betancur A., L. y Arguello F., H. (2017). Further compression of focal plane array in compressive spectral imaging architectures. Revista Tecnura, 21(52), 45-52. doi: 10.14483/udistrital.jour.tecnura.2017.2.a03
Abstract
Context: It is possible to capture High-resolution 3D hyper-spectral images in a single 2D image through techniques based on compressed sensing. A variety of architectures have proposed Compressive Spectral Imaging (CSI) technique during the last years. An optical camera designed to capture spatio-spectral information of the scene prints projections towards a Focal Plane Array (FPA) giving the capability of storing or transmitting them. Afterwards, the original image can be reconstructed via an 11 -norm-based optimization algorithm. The size in bytes of the FPA measurement is less than the original image; for that reason, this FPA is considered a 2D compressed version of the original 3D image.
Objective: To perform a further compression of the FPA measurement for four CSI architectures, in order to increase transfer rates or to decrease storing sizes.
Method: In this work, the design of the further compression using arithmetic coding is presented for four CSI architectures, and an inverse transformation is proposed. This transformation is applied to the FPA based on the structure of the optical filters and the coded apertures of the cameras used in the CSI, allowing an increasing in the compression rate.
Results: Results show that the compression rate rises between 1 and 2 points in three of the architectures.
Conclusions: Despite data loss in the process of transformation-quantification-compression-decompression of the FPA, the quality of the reconstructed data cube (expressed in terms of the PSNR between the reconstructed image and the original one) remains close to the original version with no further compression.
Keywords: Compression Techniques, Compressive Sensing, Compressive Spectral Imaging, Focal Plane Array, Hyperspectral Images.
Resumen
Contexto: Las imágenes híper-espectrales 3D de alta resolución pueden ser capturadas en una imagen 2D mediante técnicas basadas en "sensado compresivo" (compressive sensing, en inglés). Entre estas técnicas, hay una denominada Compressive Spectral Imaging (CSI), de la cual se han propuesto diversas arquitecturas en los últimos ocho años. Una cámara óptica especialmente diseñada captura la información espacio-espectral de la escena e imprime proyecciones en un plano focal 2D (Focal Plane Array, FPA). Estas muestras se pueden transmitir o almacenar; luego la imagen original puede ser reconstruida usando comúnmente un algoritmo de optimización de la norma l1. El tamaño en bytes del FPA es menor que la imagen original, y éste por lo tanto puede ser considerado una versión comprimida en 2D de la imagen original en 3D.
Objetivo: Realizar una compresión adicional del FPA para cuatro arquitecturas CSI, para incrementar las velocidades de transmisión o disminuir tamaños de almacenamiento.
Método: En este trabajo se presentan los resultados de esta compresión adicional usando la codificación aritmética y se propone una transformación inversa que se aplica al FPA con base en la estructura de los filtros ópticos y los códigos de apertura de las cámaras usadas en CSI, lo cual permite aumentar su factor de compresión.
Resultados: Los resultados muestran que el factor de compresión aumenta entre 1 y 2 puntos en tres de las arquitecturas.
Conclusiones: A pesar de que hay pérdidas de datos en el proceso de transformación-cuantificación-compresión-descompresión del FPA, para cada arquitectura CSI usada, la calidad del cubo de datos posteriormente reconstruido expresada en el PSNR entre la imagen original y la reconstruida, no difiere significativamente de la versión original.
Palabras clave: algoritmos de compresión, imagen híper-espectral, plano focal, sensado compresivo.
INTRODUCTION
Compressive Spectral Imaging (CSI) is a technique that represents the spectral and spatial information of a multispectral image through a 2D set of code projections where the image is modeled by a 3D cube 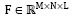 where M X N corresponds to the spatial dimensions and L is the number of spectral bands.
where M X N corresponds to the spatial dimensions and L is the number of spectral bands.
In the past few years, several CSI architectures have been proposed such as the spatio-spectral encoded compressive HS imager (SSCSI) (Lin, Liu, Wu, & Dai, 2014); the coded aperture snapshot spectral imagers (CASSI) (Arce, Brady, Carin, Arguello, & Kittle, 2014); the CASSI with colored coded apertures (Arguello & Arce, 2014); and the snapshot colored compressive spectral imagers (SCCSI) (Correa, Arguello, & Arce, 2015). CSI architectures are used in different fields as computer tomography (Espitia, Mejía, & Arguello, 2016), or agricultural crops (Camacho, Velasco, Vargas, & Arguello, 2016), among others applications in science and industry. In most CSI architectures this 2D set is a representation of a 3D cube in one Focal Plane Array (FPA) with fewer measurements than the original data cube. From this 2D set is possible to recover the spectral image through the compressed sensing techniques (Figueiredo, Nowak, & Wright, 2007). If the imaging platform is far from the central station, it is usually better to transmit the FPA data to the station and then recover the data cube, so that the receiver handles the computational load.
In CSI, the FPA measurements can be seen as a compressed version of the spectral data cube; however, a further compression to the compressed measurements can be useful and desirable for taking full advantage of the communication channel, reducing both transmission time and cost. This further compression can be performed with different coding schemes, such as Huffman and Arithmetic coding (Rissanen & Langdon, 1979).
According to compressive sensing theory, a low correlation in the FPA is desirable to guarantee low coherence between the sensing basis and the representation basis (Candes & Wakin, 2008). Additionally, it states that it is much better to have a high correlation among data (high redundancy) because it would mean that the entropy is lower and, according to the Shannon theorem, a higher compression rate can be achieved. In CSI, the FPA measurements have lower correlation than the original data cube (Li, Xiong, Arguello, & Arce, 2014), due to the effects of the dispersive element depending on the CSI architecture. In the cases of CASSI (Arce, Brady, Carin, Arguello, & Kittle, 2014), CASSI with colored coded aperture (Arguello & Arce, 2014), and SCCSI (Correa, Arguello, & Arce, 2015) this dispersive element is usually a prism.
Also, depending on the CSI architecture, lower correlation occurs for many reasons. First, due to the effects of the block-unblock lithographic masks or spatial light modulators in the CASSI and the CASSI with colored coded aperture cases (Arce, Brady, Carin, Arguello, & Kittle, 2014) (Arguello & Arce, 2014). Second, due to the diffraction grating in conjunction with a static coding mask in the SSCSI case (Lin, Liu, Wu, & Dai, 2014). Third, the SCCSI case is produced by the color filter array (Correa, Arguello, & Arce, 2015). In all these cases, the effects of the different elements can be modeled by arrays, and the FPA measurements can be accurately represented as a linear combination of the vectors of these arrays and the data cube voxels.
This paper presents a methodology to achieve a higher compression ratio for the FPA compressive measurements. This is possible through a transformation using the structure of the different arrays that modeled the coded aperture or the color filters in the CSI architectures and considering the dispersive process occurred. In this methodology (depending on the CSI architecture) a transformation matrix is generated to modify the FPA compressive measurements. The modified FPA compressive measurements possesses a higher compression rate than the original FPA, but in some cases it is better to perform a loss-tendency compression to reduce computational complexity due to the nature of the data. However, the system performance in the CSI architectures is not significantly affected by this, as simulations show.
This process is proved in the following CSI architectures: CASSI, CASSI with colored coded aperture (SSCSI), and SCCSI. For each one, a transformation matrix is generated.
METHODOLOGY
Compressive FPA measurements in CSI architectures
The essential information of spectral images can be captured using Compressive Spectral Imaging (CSI) techniques. This makes it possible to use a sensing strategy that allows representing the image by a small number of compressed measurements. This capability is obtained thanks to two characteristics of signals under a basis of representation: sparsity and incoherence (Candes & Wakin, 2008). The data capturing is possible because of the development of systems that allow to sense with a few measurements and condense the information contained in a data cube, that corresponds to one focal plane array measurement (FPA) of the scene (Arce, Brady, Carin, Arguello, & Kittle, 2014).
One of the first CSI architectures is the coded aperture snapshot spectral imagers (Arce, Brady, Carin, Arguello, & Kittle, 2014). In this architecture, a block-unblock lithographic mask named coded aperture encodes the spectral image; then, a dispersive element acts on the image, and finally it is projected to the FPA. This projection can be modeled as shown in equation (1).
Where F is the data cube with L spectral bands and N X N pixels of spatial information; Yjl is the intensity measurement of the detector at the j,l position. The detector dimension is N x (N + L-1); Tjl is the binary coded aperture, and wjl is the noise of the system (Arce, Brady, Carin, Arguello, & Kittle, 2014).
Note that each point of FPA intensity is the result of a linear combination of data cube spectral voxels in all spectrum bands and points of the coded aperture, so the structure of this code determined the distribution of intensities in the FPA. In other CSI architectures, a similar pattern is observed for the FPA construction. Arguello and Arce in (Arguello & Arce, 2014) replaced the traditional block-unblock coded apertures by multi-patterned arrays of selectable optical filters or colored arrays. In that work, the discretized coded aperture T is a three-dimensional structure, and the ith discretized FPA measurement can be expressed as equation (2).
In the case of the SCCSI architecture, the FPA in its discreet form can be modeled as shown in equation (3).
Where Cj,l,k corresponds to a colored filter array, Vj,l corresponds to the weights that index the corresponding proportion of energy from each region and (j,l) are the indexes of the spatial coordinates. In this architecture, unlike in CASSI, the dispersive element is located at the entrance of the optical camera and the signal is filtered before forming the FPA (Correa, Arguello, & Arce, 2015).
Finally, in the SSCSI architecture, a light dispersive element is located after the lens. This diffraction grating is followed by yet another lens, and then by a mask that modulates the target image in both spatial and spectral dimensions (center) before projecting it into a sensor image. The coded projection operator is expressed as a sparse modulation matrix f. The FPA, as referred to in that work as spatial-spectral encoded HS projection, is modeled as equation (4).
Where Y is the vectorized sensor image; h is the vectorized target hyperspectral image; and f is the modulation matrix (Lin, Liu, Wu, & Dai, 2014).
Matrix transformation for further compression
FPA projections can be additionally compressed using transformation techniques. The more similar the statistical distribution and the correlation between the FPA data with the hyperspectral data cube, the higher the compression ratio (Li, Xiong, Arguello, & Arce, 2014). In all the presented CSI architectures, sampling aperture that filters the input image has a known structure.
It can be noted in equations (1) to (4) that the lineal combinations between elements of the hyperspectral data cube and the used aperture (or filter) compose the array Y. For this reason, the matrix Y can be filtered again by an inverse process that eliminates (in average) the effect of the aperture.
This aperture is represented by matrices T of equations (1) and (2), C of equation (3) and f of equation (4). If the values of these apertures are taken as weights that multiply the data cube voxels, each pixel of Y can be divided by those weights, conforming a mean filter. A transformed version of matrix Y can generally be obtained for each architecture, dividing it by another matrix of the same size formed only by the sum of the weights of each pixel, as shown in equations (5) to (8) for CASSI, CASSI with colored coded apertures, SCCSI and SSCSI, respectively.
Compression process
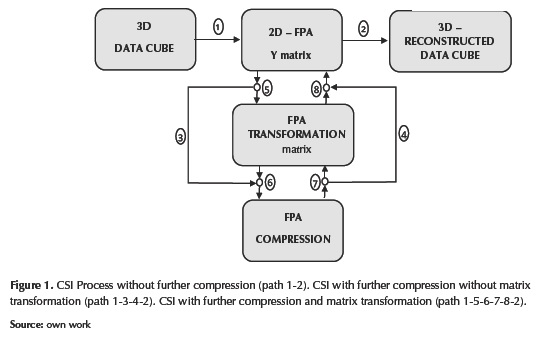
Figure 1 shows the CSI process with further compression in the FPA. Conventional CSI process is described by following the path 1-2. However, further compression is included using quantification and coding of matrix Y, following the path 1-3-4-2. This case includes the further compression by performing a traditional arithmetic-coding algorithm, with quantification applied to the cases where the elements of Y are decimals. For modifying the data the least possible during the quantification process, each value of Y was rounded to the closest integer possible, so the quantification was not uniformly performed. The FPA measurements are compressed and later uncompressed for reconstructing purposes. In the compression process, the compression ratio (CR) is defined as the ratio between the size of the uncompressed data and the size of the compressed data.
Path 1-5-6-7-8-2 indicates the CSI process with FPA transformation before further compressing. In order to compress the transformed version of the matrix Y shown in equations (5) to (8), it has to be taken into account that due to the Hadamard division of the original matrices their elements are decimal numbers. Hence, for the arithmetic coding compression process a stage of quantification is mandatory, and we have a loss-tendency compression. The paths 7 and 8 indicate a decompression process and an inverse transform, respectively, in order to recover the original matrix Y.
RESULTS
Compression ratio results
Each of the mentioned architectures were tested with a data cube of 256 X 256 X 8 voxels. This data cube corresponds to a hyperspectral image with 8 spectral bands. The SCI algorithms have random coded apertures of filters depending on the architecture. However, in order to compare results between the process with and without further compression, a fixed coded aperture was used in all the simulations. For the calculations, the size of the matrix Y was obtained by taking into account that each FPA pixel was represented with 64 bits in MATLAB.
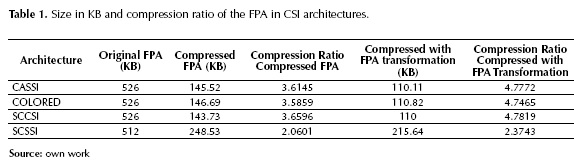
Table 1 shows the sizes of FPA measurements with and without compression. Note that the original FPA size is 526 KB, except in SSCSI case where the size is 512 KB. First, FPA data is compressed without matrix transformation. The results of FPA compressed size and its CR (Compression Ratio) are shown in columns two to three. After that, the compression was made with the FPA matrix transformation. Results are shown in columns four and five. Note that the CR increases, thereby decreasing the size of the data for each of the CSI architectures.
The matrix was quantified in the compression process, yielding to it being conformed only by integer numbers that can be represented with at least 10 bits.
Data cube reconstruction results
To determine the effect of data loss during the processes of compression and decompression, the inverse problem of reconstructing the data cube from the compressed data was solved for each architecture using the compressed sensing reconstruction techniques. Figure 2 shows the average PSNR in dB between the original data cube and the reconstructed data cube.
The first column shows the results without further compression of the FPA. The second column shows the results under the described quantification and encoding processes. The third column shows the results of applying the transformation to the FPA before compressing. It is to note how the variations in the PSNR are minimal for each case and the differences between the reconstructed images using and not using further compression are imperceptible to the naked eye.
The PSNR shown in figure 2 is calculated with the minimum loss possible in the quantification process. It is of interest to know how the PSNR is affected when the quantification levels decrease. This translates into an increasing of the losses during the compression and decompression processes. It has to be taken into account that increasing the losses allows a higher compression ratio of the data and yields to a faster transmission of it or lesser storage space needed for it.
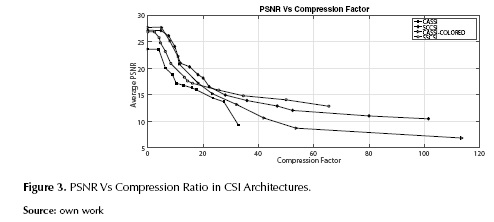
Figure 3 shows the behavior of the PSNR as the compression ratio rises. An algorithm was developed to decrease the number of values in the FPA during the quantification in order to increase the compression ratio. The algorithm has the maximal number of allowed different integer elements as input, and chooses n values among the existing ones to round all data values to the closest integer. This algorithm allows to minimize the number of modified data despite the decrease of the non-uniform quantification levels during the process. The results were obtained using the transform of the FPA as described above.
CONCLUSIONS
In this paper we presented an alternative to increase the compression ratio of the FPA in CSI architectures when further compression is desirable. Given that the coded apertures in optical cameras of these architectures are known, an inverse transformation matrix can be formed based on its structure and makes the FPA further compressed. The compression ratio increased in more than one point in some cases when the transformation was applied. Although in most cases the compression was loss-tended, this does not significantly affects the performance of the system, given that the PSNR between the original image and the reconstructed image is kept steady even when further compression is included in the processing.
REFERENCES
Arce, G.; Brady, D.; Carin, L.; Arguello, H. & Kittle, D. (Jan 2014). Compressive Coded Aperture Spectral Imaging: An Introduction. Signal Processing Magazine, IEEE, 31(1), 105-115. [ Links ]
Arguello, H. & Arce, G. (April 2014). Colored Coded Aperture Design by Concentration of Measure in Compressive Spectral Imaging. Transactions on Image Processing, IEEE, 23(4), 1896-1908. [ Links ]
Camacho, A.; Velasco, A.; Vargas, C, & Arguello, H. (2016) A comparative study of target detection algorithms in hyperspectral imagery applied to agricultural crops in Colombia. Revista Tecnura,20(49), 86-99. [ Links ]
Candes, E. y Wakin, M. (March 2008). An Introduction To Compressive Sampling. Signal Processing Magazine, IEEE, 25(2), 21-30. [ Links ]
Correa, C.V.; Arguello, H. & Arce, G.R. (Oct 2015). Snapshot colored compressive spectral imager. J. Opt. Soc. Am. A, 32(10), 1754-1763. http://josaa.osa.org/abstract.cfm?URI=josaa-32-10-1754 [ Links ]
Espitia, M.; Óscar, J.; Mejía, M.; Yuri, H. & Arguello, H. (2016). Tomografía computarizada: proceso de adquisición, tecnología y estado actual. Revista Tecnura, 20(47), 119-135. [ Links ]
Figueiredo, M.; Nowak, R. & Wright, S. (Dec 2007). Gradient Projection for Sparse Reconstruction: Application to Compressed Sensing and Other Inverse Problems. Journal of Selected Topics in Signal Processing, IEEE, 1(4), 586-597. [ Links ]
Li, P.; Xiong, H.; Arguello, H. & Arce, G. (March 2014). Embedded Transform Coding Based Lossless Compression in Compressive Spectral Imaging with Coded Aperture. Data Compression Conference (DCC), 2014, (pp. 414-414). [ Links ]
Lin, X.; Liu, Y.; Wu, J. & Dai, Q. (#nov# de 2014). Spatial-spectral Encoded Compressive Hyperspectral Imaging. ACM Trans. Graph., 33(6), 233:1-233:11. http://doi.acm.org/10.1145/2661229.2661262 [ Links ]
Rissanen, J. & Langdon, G.J. (March 1979). Arithmetic Coding. IBM Journal of Research and Development, 23(2), 149-162. [ Links ]