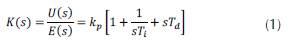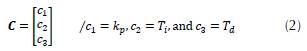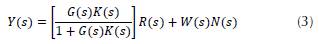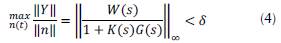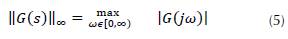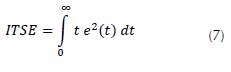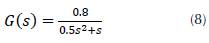INTRODUCTION

Control theory has come a long way in schemes such a Model Predictive Control (MPC), Internal Model Control (IMC), and Sliding Mode Control (SMC). Many of the specialized control design works use any of these schemes, or combinations of them (^{Chen, Zeng, and Xie, 2018}; ^{Wang, Mihalec, Gong, Pompili, and Yi, 2018}). Still, in many everyday industrial applications, it is normal to find PID (Proportional, Integral, Derivative) control schemes (^{Armin, Roy, Sarkar, and Das, 2018}; ^{Wang, Wang, Yun, and Wang, 2018}). This is because these controllers have a very straightforward and intuitive structure, besides working well for systems with second-order behavior, with a relatively simple principle of adjustment (^{Arbulú, Martínez and Montiel, 2015}).

While their structure replicates second-order linear compensation, PID controllers are also used in higher-order, non-linear, industrial systems (^{Jayaraman, Vijayakumar, Nandagopal, and Rameshkumar, 2018}; ^{Patil, Waghmare, and Uplane, 2019}). With good tuning, these schemes can provide robust and stable behavior, and these are systems that can be implemented both analogically and digitally (^{Sanghavi, Tejaswini, and Venkateshappa, 2019}). They can even be tuned on-line without stopping the process if the control criteria over the plant changes. Tuning corresponds to a search problem matching a performance function. Conventional tuning strategies are based on the frequency response of the plant, but they are rarely used in real applications. For example, this is the case of the Ziegler-Nichols method, whose tuning rule can produce an oscillating response system if the plant is non-linear (^{Tasoren, Orenbas, and Sahin, 2018}).

Many strategies for tuning PID controller parameters for open-loop systems have been documented (^{Vanavil, Krishna, and Seshagiri, 2015}). Several strategies are based on direct synthesis (DS), taking advantage of the knowledge of the plant model and its desired behavior (^{Chanti, Santosh, and Padma, 2017}; ^{Ravi and Padma, 2018}). In general, these strategies raise the characteristic equation of the process, including the PID control block, and compare it to the desired characteristic equation in the closed-loop. Then, it is possible to mathematically define the parameters of the PID block.

Therefore, since tuning is a search problem, many tuning strategies based on uninformed search algorithms such as Genetic Algorithms (GA) (^{Febina, Sunil, and Jacob, 2018}), Particle Swarm Optimization (PSO) (^{Ramirez, López, and noz, 2018}), and Ant Colony Optimization (ACO) (^{Jagatheesan, Anand, Dey, and Ashour, 2018}) have also been proposed. Other randomized search strategies inspired by collective behaviors observed in nature have also been considered (^{Ali, Afandi, Parwati, Hidayat, and Hasyim, 2019}; ^{Ataslar-Ayyildiz and Karahan, 2018}). These strategies are based on evaluating the performance of possible solutions to the problem (e.g. a set of parameters that can be PID gain values) and several values according to the behavior of some performance function (^{Abhishek, 2015}). This being applied to a set of solutions uniformly distributed in the search space guarantees to find a pseudo-optimal solution faster than the traditional gradient-based algorithm.

The search problem becomes more complex when the plant has a changing dynamic; for example, when there are disturbances in the system (^{Habibi, Rahimi, and Howard, 2018}; ^{Hettrick and Todd, 2019}). In these cases, the tuning strategies include automatic tuning schemes, adaptive PIDs, and intelligent systems. In such cases the tuning is dynamic, and they consider some kind of information about the changes in the process as part of the adjustment.

This research proposes an intelligent tuning strategy of a PID controller for a system with disturbances based on the idealized behavior of bacteria, including their QS to reduce the convergence time (^{Martínez, Rendón, and Arbulú, 2018}; ^{Jacinto, Giral, and Martinez, 2016}). The strategy is implemented and evaluated by simulation.

The article is organized as follows. Section 2 formulates the problem and presents some preliminary concepts, the functional profile, and other design considerations. Section 3 details the design of the system, including the selection criteria and the final specifications that were adopted. Section 4 presents the performance evaluation observed through simulation, and Section 5 concludes the article.

PROBLEM STATEMENT

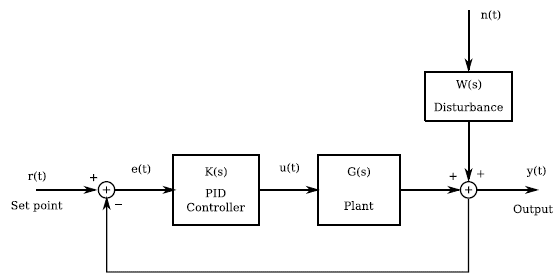
The model of the system under study with the proposed control scheme is shown in Figure 1.

Fuente: Own production

Figure 1 Control system with PID Controller and disturbance 

In Figure 1 K(s) is the transfer function of the PID controller, G(s) is the transfer function of the plant, r(t) is the reference signal for controlling the plant, e(t) is the system error, u(t) is the controlled input, n(t) is the disturbance, W(s) is the disturbance dynamics, and y(t) is the output signal. According to Figure 1 (Equation 1):

Where the new constants correspond to the tuning of the PID controller. These can be rewritten vectorially as (Equation 2):

Also, from Figure 1 (Equation 3):

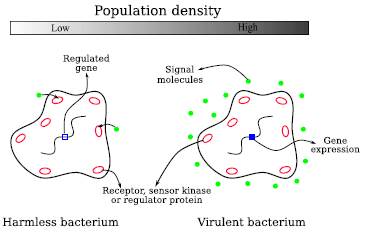
The tuning process consists of finding the vector C so that the performance function (a function that evaluates the steady-state error) is minimal. As a search scheme, we propose a simplified bacterial interaction model that includes QS. Our model of bacterial interaction is based on the cellto-cell communication. We have technically called this process local communication between artificial agents that emulate biological bacteria. Biological bacteria read local information from the identification of chemical elements in the environment and their concentration densities (^{Martínez, Hernández, and Acero, 2017}). The QS follows the principles of this local communication scheme, with the particular characteristic that it allows coordinating the collective behavior of the bacterial population from certain specific readings. For instance, one of these readings can determine that the bacterial population is high and can activate a collective attack mechanism on the host environment (Figure 2). Bacteria deposit chemical information in the environment, and when the concentration is elevated they decode an attack action written in their genetic code. It is possible to imitate this behavior in artificial agents, making bacteria move to steady-state zones (possible solutions to the problem) that they find attractive (as if they were looking for food) guided by the performance function of the problem. When the number of agents in a state-space zone exceeds a quorum threshold T, the QS is activated making this zone more attractive. The point in the state space where the greatest number of individuals are grouped corresponds to the optimal solution of the problem.

Fuente: Own production

Figure 2 Bacterial QS. 

METHODOLOGY

The design restriction for the model in Figure 1 is (Equation 4):

Where ||∙||∞ is H∞-norm and δ < 1 is a constant that defines the desired rejection rate. Since (Equation 5):

Then the restriction for resistance to disturbance is given by (Equation 6):

As the performance function we select the Integral Time Squared Error (ITSE) (Equation 7):

This error function was selected because it includes time in its structure, which increases the effect on long-lasting errors, thus ensuring a small settling time. The structure of e(t) implicitly contains the parameters of both the controller and the plant; therefore, the performance function must be minimized by tun ing vector C. The proposed search algorithm based on bacterial behavior has the structure shown in Figure 3. A population of n bacteria is randomly established in the state space of possible values of vector C, whose spatial position is defined by three coordinates. For example, for bacteria i we have V_i (c_1i, c _2i c _3i ) Each bacterium evaluates the performance of its current position through the performance function and the signal deposited in the medium by other bacteria and places a signal in the environment according to the result. Consistent with the performance value, the bacterium makes the decision to either continue exploring the environment or maintaining its position.

Fuente: Own production

Figure 3 Pseudo code of bacterial algorithm for optimization of the PID controller. 

Depending on the signal concentration in the local environment, a bacterium evaluates the number of neighboring bacteria in the same position (within a radius of neighborhood), and if the concentration exceeds the threshold of quorum T, the QS is activated. When the QS is activated, the bacteria place a second signal in the environment that increases the performance value of its position, attracting other bacteria more quickly. The coordinates of the meeting point of the bacteria correspond to the value of vector C.

In the Explorer behavior, the agent moves in the state space to find other areas of interest. In general, Virulent behavior is only activated by population density, which only happens if the area is attractive for many bacteria. The movement involves changing the value of the constants of the PID controller (tuning) and is done by trying to minimize the error (increasing the performance value). The region with the highest concentration of bacteria will be the optimal solution.

RESULTS

We used the second-order linear shape shown in Eq. 8 as a model of the plant:

We tested different types of disturbances with 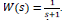. For example, for a sinusoidal perturbation the bacterial scheme with QS determined the following values:

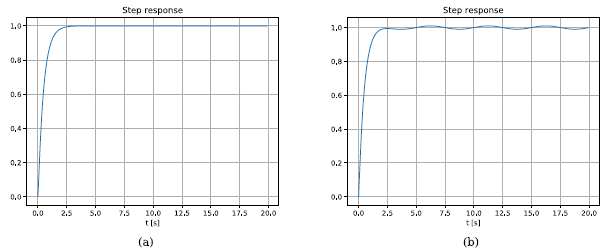
Figure 4. shows the behavior of this design. Image 4(a) shows the step response of the system without applying disturbances, while Image 4(b) shows the same behavior with disturbance applied. In both cases, there is a short rise time and scanty steady-state error. Image 4(b) also shows how the control responds positively to the disturbance.

Fuente: Own production

Figure 4 Step response of the PID controller tuned with the bacterial scheme. (a) No disturbance. (b) With sinusoidal perturbations. 

CONCLUSIONS

In this paper, we propose a PID controller tuning scheme for plants with disturbances using a parameter-search method based on bacterial interaction with QS. The scheme poses the constraints of PID control design and a performance function based on ITSE. Through basic rules of interaction on a community of agents designed on the state space of the solution, we make interact the bacteria until they gather at the points of greater performance. QS is activated at these points, which accelerates the convergence of the algorithm. The intelligent tuning scheme converged quickly at a very low computational cost. In addition, the tuning parameters found proved to satisfy the design conditions.