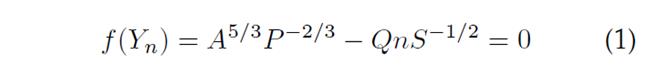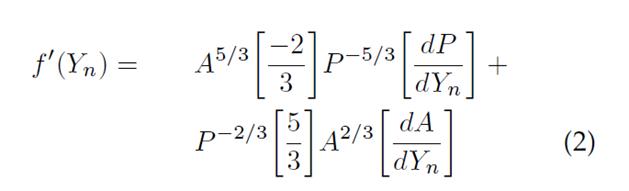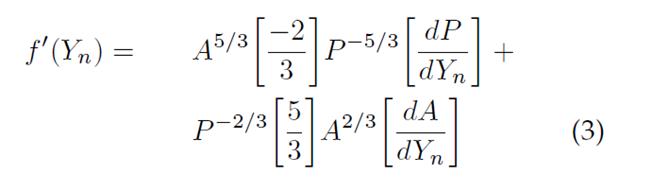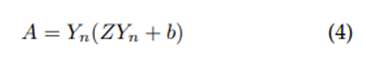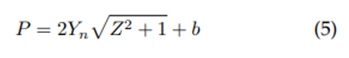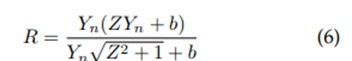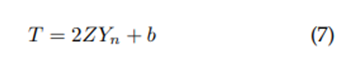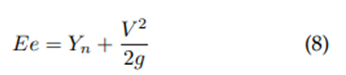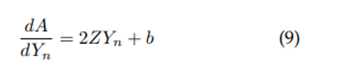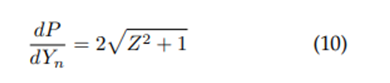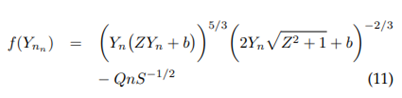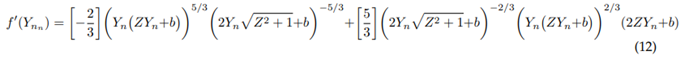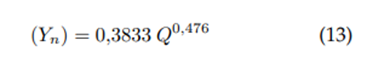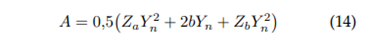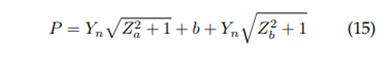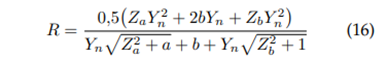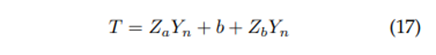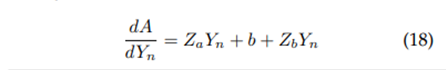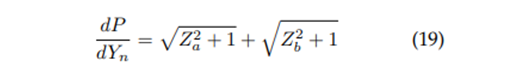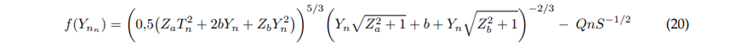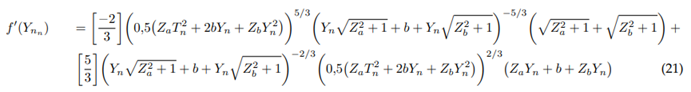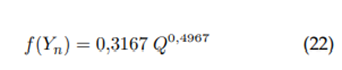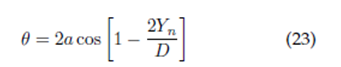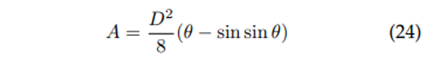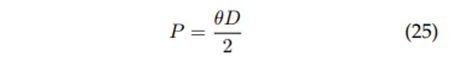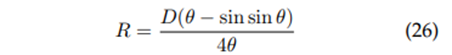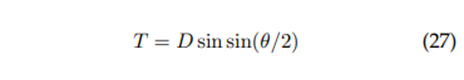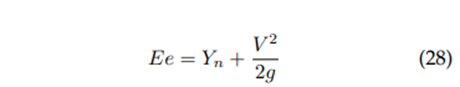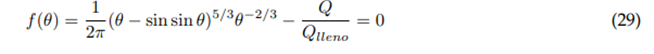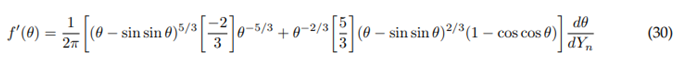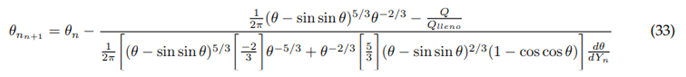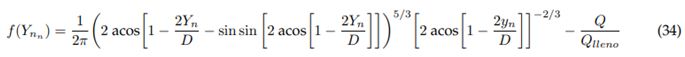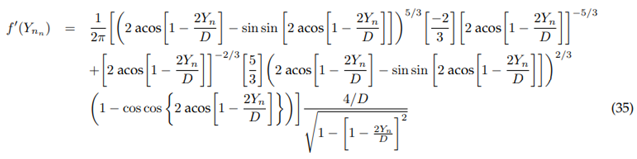INTRODUCTION
The study of water flow in open channels is a critical issue for multiple projects related to Civil Engineering about the evacuation of water under controlled speed and flow. Several engineering projects use surface drainage systems for the evacuation of free-flowing water at different scales, from small channels in road works and slopes (measured in centimeters) to channeling currents through channels with large hydraulic sections of several meters wide (Chaudry, 2008) (Marusic & Hutchins, 2008) (Monty, Hutchins, Ng, Marusic, & Chong, 2009) (Roy, Buffin-Belánger, Lamarre, & Kirkbride, 2004) (Cameron, Nikora, & Stewart, 2017). The optimization of the hydraulic design of these structures through numerical methods is a key component in the training of civil engineers and comes second to conducting laboratory tests on models to explain the concepts associated to the design of the hydraulic channel. (Chaudry, 2008) (Monty, Hutchins, Ng, Marusic, & Chong, 2009) (Cameron, Nikora, & Stewart, 2017). Despite the conventional presentation of the design of open channels in the training curricula of civil engineering, concerns persist in the background of students because some concepts in this topic are abstract, and in some cases they can only be understood from laboratory tests (Monty, Hutchins, Ng, Marusic, & Chong, 2009) (Cameron, Nikora, & Stewart, 2017). Particularly, students in developing countries do not always have easy access to physical laboratory models for the appropriation of concepts associated with flow in open channels. Therefore, concepts such as the hydraulic total energy line, the specific energy, the wetted perimeter, and the hydraulic radius are often confused or not sufficiently understood when referring to a real-world situation (Woods, 1994) (Mirauda, Capece, & Erra, 2020).
Considering that the hydraulic section of an open channel depends fundamentally on the relationships between roughness, flow type, fluid velocity, and flow rates through iterative processes, the preparation of a numerical solution in conventional spreadsheets is often not sufficient for long-term concept appropriation. Thus, conventional pedagogy results in restrictions on students’ imaginations and inadequate training for the development of practical skills; also, it tend to work within the boundaries of computers instead of taking advantage of more modern learning environments (Khan & Chiang, 2014) (Buck, McInnis, & Randollph, 2013) (Jou, Lin, & Tsai, 2016) (Drumea, 2012).
For hydraulic engineering education, problem-based learning (PBL) is considered an ideal learning strategy as it encourages students to take a multidisciplinary approach to the basic sciences by applying numerical methods and strengthening their skills and confidence in handling new problems (Kai, Lam, Zou, & Quiang, 2018). Consequently, the PBL methodology began to be considered a crucial key for modern engineering practice and became a central theme of development for engineering education since the end of the XX century (Woods, 1994) (Mirauda, Capece, & Erra, 2020). In this context, the implementation of numerical methods in cloud web applications have become relevant as innovative elements in the education of civil engineering students in developing countries (Woods, 1994) (Mirauda, Capece, & Erra, 2020) (Drumea, 2012).
Since 1990, the advance of wireless technologies has experienced a significant expansion in both developed and developing countries. This increase took place from the first generation of mobile telephony (analogous) to the fourth generation (digital). Currently, 5th generation mobile telephony is in its implementation stage. This advance has allowed the development of cellphones, tablets, and other smart devices of higher performance in terms of memory and processing capacity (Buck, McInnis, & Randollph, 2013) (Jou, Lin, & Tsai, 2016). In the same way, this technology has contributed to the elaboration of mobile apps in commercial, environmental, industrial, medical, and educational fields (Chaudry, 2008) (Mirauda, Capece, & Erra, 2020) (Buck, McInnis, & Randollph, 2013) (Drumea, 2012).
The increasing popularity of smart mobile devices means that many students are already familiar with their use and features (Mirauda, Capece, & Erra, 2020) (Hsu, Rice, & Dawley, 2012). Hence, there is an expected positive impact that the use of mobile devices for teaching hydraulics and other areas in civil engineering have on the motivation and effectiveness of learning within developing countries.
It is worth highlighting that there are some key aspects in educational software development to be considered, such as accessibility, simplicity, the building of high-quality documents where key concepts are synthesized, and lower cost for licensing (Marusic & Hutchins, 2008); and commercial educational software is expensive and of limited access to part of the population. Hence, free or open-source software is a better option for educational purposes in open channels since they allow users to implement their own needed software and generate new possibilities for content, mobility, and understanding (Monty, Hutchins, Ng, Marusic, & Chong, 2009) (Roy, Buffin-Belánger, Lamarre, & Kirkbride, 2004) (Mirauda, Capece, & Erra, 2020).
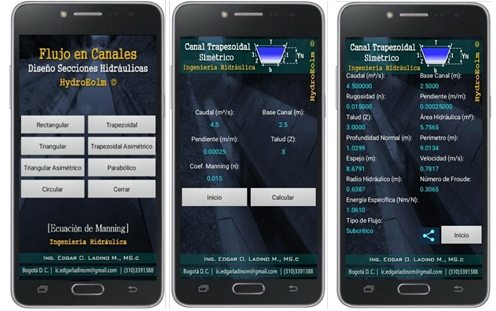
This work shows the development of a mobile application in Android for the analysis and design of open channels with the incorporation of a Newton-Raphson numerical solution for different geometries. Unlike the examples presented in a conventional channel hydraulics class, the application presents a wide range of examples that promote interest in the subject and act as a complementary resource to conventional education through texts, graphic aids, and friendly graphic environments (Mirauda, Capece, & Erra, 2020) (Jou, Lin, & Tsai, 2016) (Hsu, Rice, & Dawley, 2012). The mobile app has been downloaded by engineering students in Latin-American countries, which suggests the positive acceptance of this tool as a complement to university education on this topic.
App Development
PBM learning approach seeks that students understand the application of concepts in real-problem civil-engineering situations. Open channels of trapezoidal or circular sections are widely used in geotechnical work (e.g. surface drainage works slope stabilization), highway projects, and hydraulic projects for flood mitigation and flow control. Then, Newton-Raphson formulation of the problem for hydraulic design optimization is applicable to any of the scenarios described.
Basic Problem
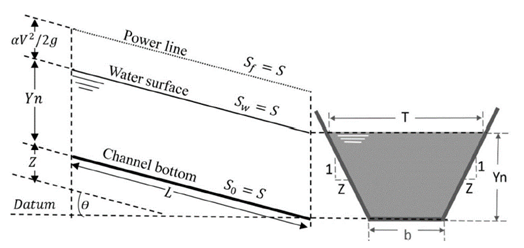
In a prismatic channel subjected to atmospheric pressure, uniform flow conditions can be established if the depth, wet area, and flow speed remain constant. That is, the slope of the bottom channel, the slope of the water surface, and the energy line are parallel; and the component of the gravitational force parallel to the flow in any laminar layer is balanced by the frictional force for a uniform laminar flow (Chaudry, 2008) (Cameron, Nikora, & Stewart, 2017). The equation that governs the flow behavior in open channels is represented by Chézy's equation, developed by Irish engineer Robert Manning (Chaudry, 2008) (Woods, 1994) (Mirauda, Capece, & Erra, 2020). This empirical development is based on the channel roughness, flow speed, water depth, and bottom slope.
Equation (1) shows Chezy's equation using SI units (Chaudry, 2008):
Where, Q: Flow (m3/s); n: Manning roughness coefficient; A: Hydraulic area (m2); P: wet perimeter (m); R: Hydraulic ratio (m); and S: Slope (m/m).
In derivative form, equation 1 can be expressed as:
And the Newton-Raphson formulation would be (equation 3):
Development of Numerical Solution
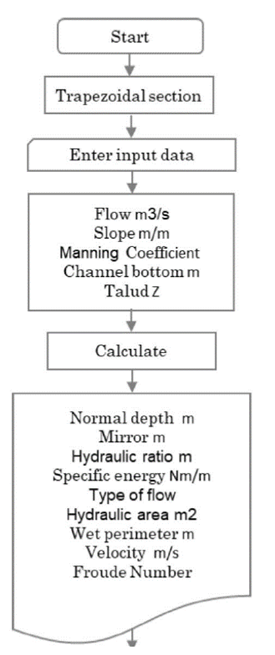
Based on iterative and incremental processes, three stages of the solution were developed for the numerical formulation within the app. In the first stage, a flow diagram was developed for each of the hydraulic sections by using an iterative process. In the second stage, the source code was developed for Android platforms using JavaScript as it is open source and Android is based on object-oriented programming language. Finally, the third stage consisted of validating the app code by comparing its results against those calculated by other programs and exercises proposed in Hydraulics books (Chaudry, 2008). The flow chart for the user interface is presented in Figure 2. The flow of activities varies depending on the selected hydraulic section.
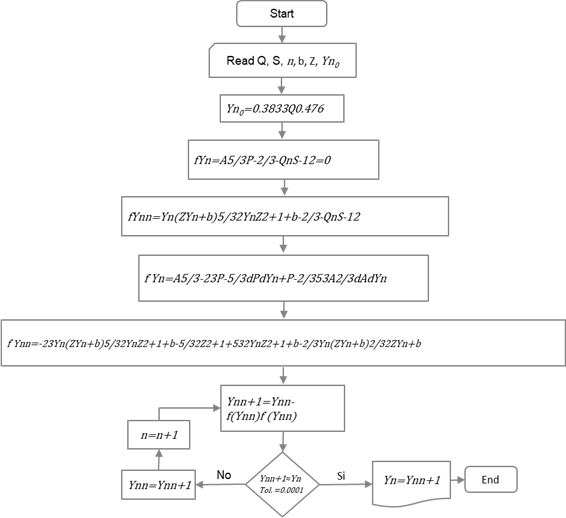
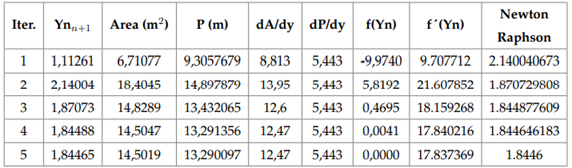
According to the Newton-Raphson method, the probability of divergence increases significantly if the initial value is zero or presents different inflection points. To overcome this anomaly, a method is suggested to obtain a regression of dependent and independent variables for the initial value (seed value). In the case of trapezoidal channels, a potential expression was obtained for the normal depth as a function of the flow rate, which guarantees that the method will reach convergence, regardless of the initial value moving away or being close to zero. The relative error between successive approximations in this scenario is 0.000001 meters. Figure 3 shows the algorithm used to program the solution for the trapezoidal channel. A similar formulation was implemented for the circular section.
App Formulation and Validation
The development of the mobile application is presented below in detail for trapezoidal and circular channels, along with the Newton-Raphson type solution. The graphic aspects of data input, analysis, and output of the application in the Android environment are also presented.
Trapezoidal Channel
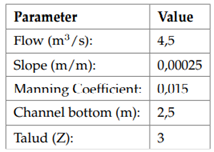
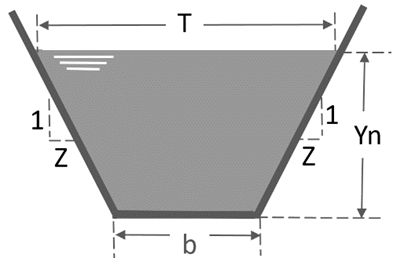
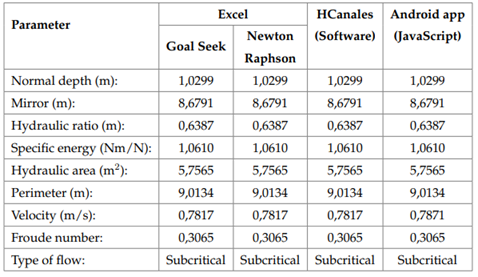
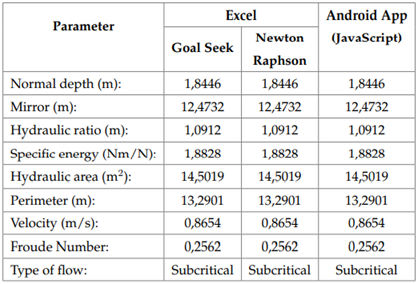
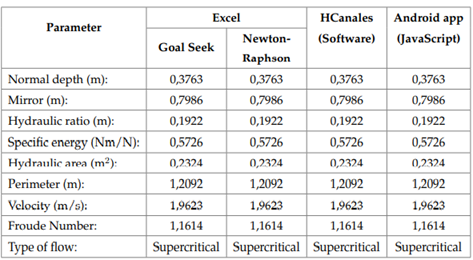
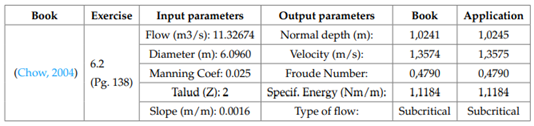
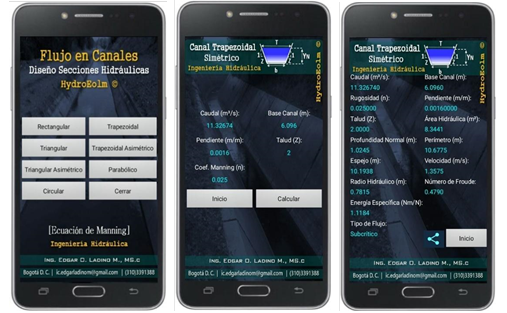
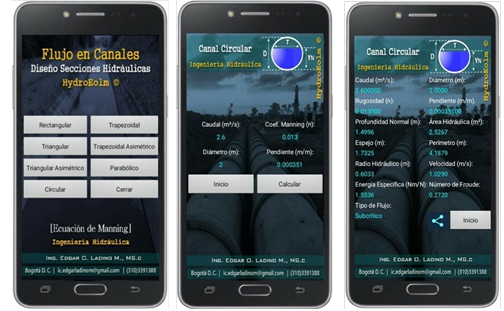
The first screen presents a menu showing different variables. The algorithm calculates the normal depth, hydraulic radius, specific energy, flow type, hydraulic area, wet perimeter, flow velocity, and Froude number for each of the hydraulic sections. In order to validate the app calculations, determining the normal depth for a symmetric trapezoidal channel is suggested (Figure 4), which will be done through three different methodologies (Newton-Raphson app, Goal Seek tool in Excel®, and the software Hcanales®).
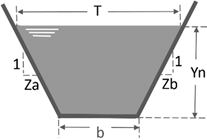
The channel presents the following hydraulic conditions:
Hydraulic area:
Wet perimeter:
Hydraulic ratio:
Mirror:
Specific energy:
Applying Manning equation under the uniform flow assumption (equations 1, 2 and 3), we have the variables expressed in derivative form as follows:
Hydraulic area:
Wet perimeter:
Newton-Raphson approximation:
Normal depth:
In the symmetric trapezoidal channel case, a potential model for the normal depth as a function of the flow rate for the initial value (seed value) was obtained, so it is guaranteed that the method will reach convergence, regardless of whether the initial value moves away or stays close to zero (equation 13).
Where, Q: Flow (m3/s); Y: Normal depth (meters).

Source: Authors
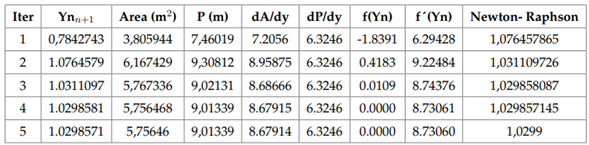
Figure 5 Visual Code (Excel). Calculation iteration for Yn (symmetric trapezoidal channel).
The comparison of the results obtained by three different methodologies are shown in Table 3. It is possible to see that the calculations from the Android app have a high degree of precision for normal depth calculation in prismatic channels.
Asymmetric trapezoidal channel
To estimate the capacity that the Android app has for calculating the normal depth from the paradigm proposed by Manning, a symmetric trapezoidal channel that presents the following hydraulic conditions is proposed:
Hydraulic area:
Wet perimeter:
Hydraulic ratio:
Mirror:
A potential model for the normal depth in an asymmetric trapezoidal channel as a function of the flow rate for the initial value (seed value) was obtained. This guarantees the convergence of the method, regardless of whether the initial value moves away or approaches zero.
Hydraulic area derivative:
Wet perimeter derivative:
Newton-Raphson Approximation:
Table 5 Normal depth calculation (Excel, Newton-Raphson), (asymmetric trapezoidal channel).
Source: Authors.

Source: Authors
Figure 8 Visual Code (Excel). Iteration for Yn calculation. (asymmetric trapezoidal channel).
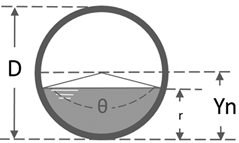
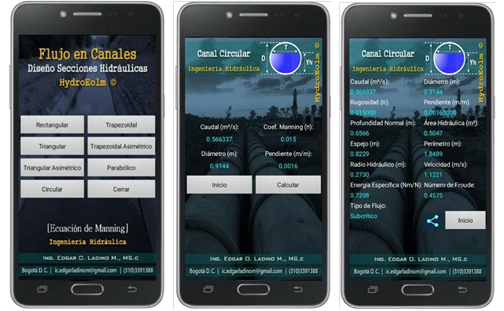
Circular channel
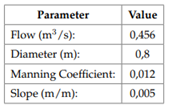
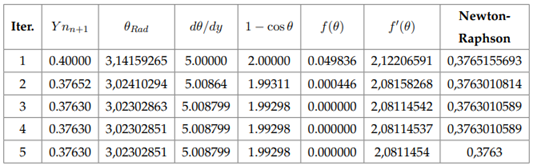
The solution for a circular channel was obtained from the ratio of the flow through the pipe and the flow to full pipe, which guarantees that the algorithm developed calculates the independent normal depth whether it is below or above the radius. To evaluate the implementation, the following hydraulic problem is proposed:
Central angle:
Hydraulic area:
Wet perimeter:
Hydraulic ratio:
Mirror:
Specific energy:
Newton-Raphson approximation depending on the angle:
Function:
Derivative:
Where:
Newton-Raphson approximation according to normal depth:
Function:
Derivative:
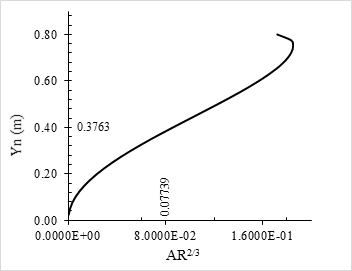
The graph in Figure 12 was constructed from the section factor for uniform flow.
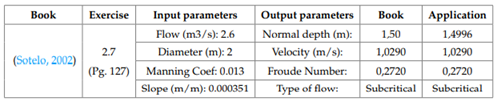
Finally, the calculations made by the app were evaluated using exercises proposed in different Hydraulics books (Chaudry, 2008) and their respective solutions to confirm the accuracy of the app. The results are presented in Tables 10, 11, and 12. Likewise, the results calculated by the app are shown in Figures 14, 15, and 16.
Source: Authors
Figure 14 Exercise 2.7, Hidráulica de canales, Gilberto Sotelo (app’s normal depth calculation).
(app’s normal depth calculation).
App Impact from Google Play Store
App Hydroelm has had over 7000 downloads over a period of 10 months since it was released in the Google Play Store. A follow up shows that the downloads have occurred mainly in Central and South American countries (Peru 40%, Colombia 20%, Guatemala 20%, and Honduras 20%). Within the percentage of downloads in each country, more than 80% correspond to college students (Peru 86%, Colombia 92%, Guatemala 81%, and Honduras 88%). The rating of the app exceeds 4.5 points; this value constitutes an indirect indication of the positive impact the tool has had in strengthening the learning of this subject in engineering students from developing countries. Although the motivation of the assessment is not clear, it is possible to infer that the app constitutes a useful tool in the educational environment, either to corroborate results of manual calculation exercises or electronic sheets by students. It is also a reflection of the impact of using digital media on smartphones for the appropriation of knowledge in a modern education practice on topics in civil engineering.
CONCLUSIONS
The algorithm implemented for the app “HydroEolm Hydraulic Channel Design” avoids the use of nomograms and optimizes the calculation process for the normal depth and other hydraulic parameters in open channels. The assessment of the results shows the accuracy of the calculations for various hydraulic sections and confirms the reliability of the tool for process designing.
The app indicates an accuracy of 10-6 meters for the calculations. This is a good result compared to other methods like electronic sheets. Thus, the app’s effectiveness for solving hydraulics problems for prismatic channels is demonstrated. This was validated by comparing the results in the app against the results obtained from three different methodologies (Goal Seek, Newton-Raphson, and Hcanales®). For future developments it will be possible to include an integration with web and mobile interfaces for a massive diffusion.
From the number of downloads of the app within developing countries, it is possible to infer the wide acceptance specialized public has towards this tool, probably due to its contribution to explaining concepts and its usability in the educational field.