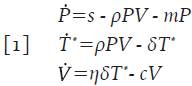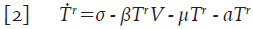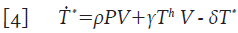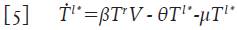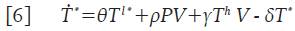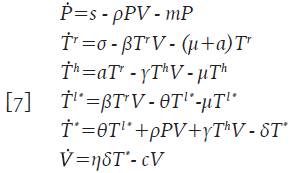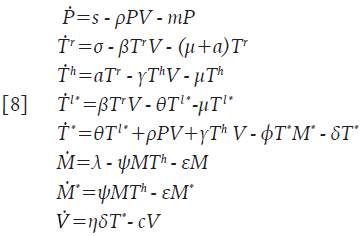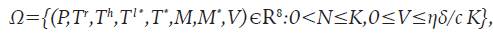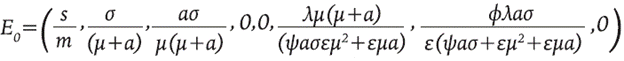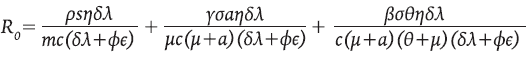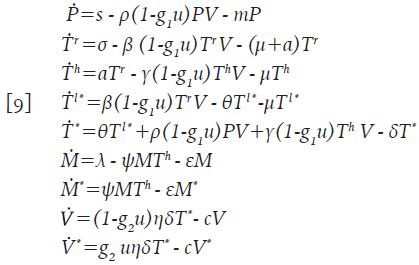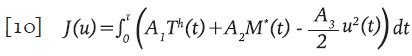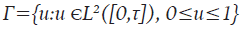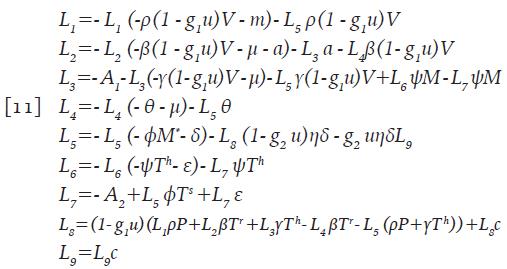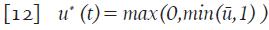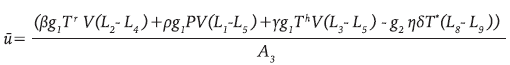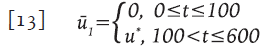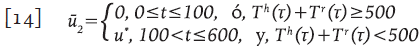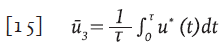La infección por el Virus de Inmunodeficiencia Humana (VIH) y el Síndrome de Inmunodeficiencia Adquirida (SIDA) son un problema de salud a escala mundial, con impactos a todo nivel. Las principales vías de transmisión son el contagio por relaciones sexuales con una persona infectada, por transfusión de sangre contaminada, por compartir objetos corto-punzantes o de la madre al feto. El virus logra desgastar el sistema inmune hasta que produce una deficiencia que incrementa el riesgo de sufrir infecciones oportunistas. Una vez la persona es diagnosticada como portadora del VIH, deberá iniciar tratamiento antirretroviral (TAR), que generalmente consiste en una politerapia constituida por tres o más antirretrovirales, los cuales actúan inhibiendo la replicación del virus, bloqueando las enzimas del VIH o creando nuevas barreras para la enfermedad 1. Precisamente, con respecto a la terapia antirretroviral, el reporte global de ONUSIDA indica que para el año 2013, 12,9 millones (equivalente al 37%) de todas las personas que vivían con el VIH tenían acceso a dicha terapia. Además, un 38% de los adultos que vivieron con el VIH recibieron la terapia que necesitaban, mientras que tan solo un 24% de los niños que vivieron con el VIH accedieron a la misma 2.
Una vez el VIH ingresa en el cuerpo es fagocitado por las células dendríticas y los macrófagos, también conocidos como células presentadoras de antígenos. Ellas procesan el virus y lo presentan en su superficie para que sea reconocido por las células T, las cuales se activan y pasan a ser células T colaboradoras, cuyo rol es decidir el tipo de respuesta inmune que debe ser desplegada: respuesta inmune humoral o respuesta inmune celular. Simultáneamente, las mismas células T son infectadas por el virus e inician su proceso de replicación; en particular, cuando una célula T colaboradora es infectada por el virus, ésta pierde la capacidad de desplegar la respuesta inmune adecuada para enfrentar la infección 3,4.
La relación entre el virus, las células T colaboradoras y la respuesta inmune, es determinante en la evolución futura de la infección, debido a que si la concentración de células T colaboradoras es baja, la respuesta inmune no será desplegada efectivamente y el cuerpo no contará con las herramientas necesarias para controlar la infección. La terapia con antirretrovirales es una estrategia reactiva frente a la enfermedad, que aunque busca mejorar la calidad de vida de los pacientes portadores del VIH, no se ocupa de evitar que la enfermedad prospere en la población. En efecto, la rápida expansión del acceso a terapia ha ayudado a reducir el número de muertes relacionadas con el SIDA pero también contribuye al aumento en la prevalencia del VIH. Dadas las condiciones actuales de la enfermedad a escala global, es necesario realizar estudios teóricos que brinden fundamento científico a la toma de decisiones en cuanto al terapia de la infección por VIH y del SIDA con antirretrovirales 5.
En este trabajo se estudian teóricamente estrategias óptimas y sub-óptimas de terapia antirretroviral en la infección por VIH. Inicialmente se presenta un modelo matemático para describir la interacción entre el VIH y el sistema inmune y luego se utiliza la teoría de control óptimo, para determinar una función óptima de control de la infección mediante antirretrovirales y a partir de ella se definen estrategias alternativas de terapia (sub-óptimas), que en un contexto clínico serían más aplicables.
Formulación del modelo básico
Uno de los sistemas más simples que pueden encontrarse en la literatura para describir la etapa inicial de la infección por VIH es:
Donde la variable V=V(t) denota la concentración promedio de partículas virales en un tiempo t, la subpoblación de células que recoge las clases de células presentadoras de antígenos se denota con la variable promedio P=P(t) y las células T infectadas y activadas por el virus para iniciar la replicación viral, se denotan con la variable promedio T * =T * (t) las cuales producen grandes cantidades de partículas virales 4. La interpretación de los parámetros involucrados puede encontrarse en la Tabla 1. Este modelo tiene en cuenta que las células presentadoras de antígenos buscan, engullen y analizan el antígeno para luego presentarlo a los linfocitos T circundantes en un proceso denominado sinapsis inmunitaria o simplemente presentación de antígenos 3,4. También se asume que las células T infectadas están activadas y que inmediatamente se infectan, dando inicio a la replicación viral; los supuestos que recoge el modelo 1 se pueden estudiar con detalle en 6,7.
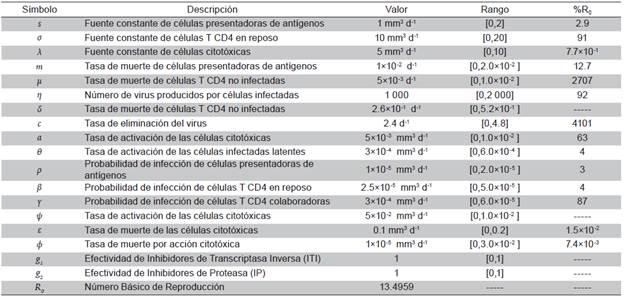
Tabla 1 Definición de parámetros y valores usados en simulaciones. El rango de variación del parámetro corresponde a ±100% del valor. La última columna muestra el máximo porcentaje de variación de R0 obtenido con cada parámetro variado sobre el rango dado
El modelo 1 corresponde a la estructura más simple y más popular de la dinámica de infección y ha sido estudiado por diferentes autores 8-13; sin embargo, solo considera la intervención de las células presentadoras de antígenos y la parte de ellas que resulta productivamente infectada por el virus. Asuma que la población de células T está dividida en dos categorías que corresponden a células T en reposo, que aún no han sido activadas inmunológicamente frente a ningún antígeno en particular, denotada por la variable promedio T r =T r (t), y a las células T que ya han sido activadas y se denominan usualmente células T colaboradoras, que se denotan aquí con la variable promedio T h =T h (t). La importancia de considerar estas dos subpoblaciones, es que el VIH se detecta infectando células en reposo, pero sólo en un 1% de ellos se replica activamente; lo que indica que el 99% se alberga en el genoma proviral de manera latente 4,12,14.
Asuma que la población de células T en reposo T r , es liberada en el organismo a una tasa constante σ y que mueren por causas no relacionadas con la infección a una tasa de proporcionalidad μ. Adicionalmente, en presencia de infección, éstas células se infectan con una probabilidad β; por lo tanto, el número promedio de células T en reposo que se infectan en un tiempo t está dado por βT r V y la ecuación que describe su variación es,
Donde aT r es el número promedio de células que son activadas frente a algún patógeno y salen del reposo en un tiempo t; es decir, αT r define el incremento de las células T colaboradoras T h . Asuma que las células T h mueren por causas ajenas al virus a tasa μ y que las células colaboradoras se infectan con una probabilidad γ, se tiene entonces la ecuación:
Donde γT h V representa el número promedio de células colaboradoras T h que se infectan y μΤ h es el número promedio de células T h que mueren por causas no relacionadas con la infección. Las células T h infectadas, se vuelven productoras de partículas virales de manera inmediata; por lo tanto, constituyen un flujo de entrada en la dinámica de las células T * , con lo que la segunda ecuación de 1 queda de la forma:
Las células T en reposo que se infectan (la cantidad βT r V en la ecuación 2) dan origen a células infectadas en estado de latencia, ya que la producción viral dará inicio tras la activación inmunológica de la célula 4,12-14. Denote con la variable promedio T l* =T l* (t) a las células T infectadas en estado de latencia; asumiendo que su tasa de muerte es también μ, se puede formular su variación mediante la ecuación:
Donde θT l * representa el número promedio de células T infectadas en estado de latencia que se activan y que por lo tanto, inician la replicación masiva de partículas virales. Este último término ahora modifica la ecuación 4 para las células infectadas T * y adopta la forma:
De este modo, el sistema 1 se transforma en uno más completo, que se muestra a continuación:
Se asume que las células citotóxicas están circulando en el cuerpo hasta que son activadas para reaccionar contra cualquier infección y que no son infectadas por el virus; adicionalmente, su acción citotóxica se considera específicamente dirigida a eliminar células infectadas, y no afectan a las células no infectadas 7,13-16. Considere la nueva variable M=M(t) como la concentración promedio de células citotóxicas inactivas. Esta población se incrementa a una tasa constante λ y muere a una tasa ε. Una vez la infección está presente, estas células empiezan a activarse a un promedio de ψΜΤ h células, el cual refleja la acción de las células colaboradoras en el proceso, es decir, ψ representa la tasa de activación de las células citotóxicas. Las nuevas células citotóxicas activadas M * =M * (t), inducen apoptosis de las células infectadas a un promedio de φΤ * Μ * células, donde φ es la tasa de muerte de las células infectadas por acción citotóxica. Finalmente, se asume que ambos tipos de células, mueren en promedios εΜy εΜ", respectivamente. El sistema queda de la forma:
En la Proposición 1 se determina la Región de Invarianza, cuya importancia radica en que garantiza que las soluciones están acotadas y no es posible que se hagan negativas o que «exploten» hacia el infinito. Además, la región aporta sentido biológico al sistema 8.
Proposición 1
El sistema 8 está definido en la región positivamente invariante
Donde N=P+T r + T h +T ι* +Τ * +Μ+Μ * , Κ=(s+σ+λ)/ξ y ξ=min(μ,δ,m,ε).
La demostración de esta proposición se realizó siguiendo la metodología de autores reconocidos como Perelson AS y Patrick WN6.
Análisis del modelo
El sistema 8 tiene dos puntos de equilibrio denotados por E 0 (trivial) y E 1 (no trivial). El equilibrio trivial representa el estado alcanzado en ausencia de la enfermedad, es decir, muestra los valores hacia los cuales tienden las poblaciones cuando no hay infección y está dado por:
Se puede observar que M y M * están presentes en el sistema todo el tiempo debido a la suposición de que la activación de inmunidad puede ocurrir en contra de cualquier patógeno. El equilibrio no trivial no se muestra porque su expresión es muy larga, pero se observa de manera numérica en la Figura 1, en el valor final de cada población.
El Número Básico de Reproducción R 0 es determinado usando el método de la Matriz de la Siguiente Generación, como se hace por ejemplo en 12,14,17.
Proposición 2
R 0* . El Número Básico de Reproducción para el sistema 8 está dado por
El R 0 describe «el número secundario de células infectadas que se obtienen a partir de una sola célula infectada en una población enteramente susceptible». Cada uno de los sumandos que componen a R 0 representa el aporte que hacen las poblaciones celulares susceptibles a la infección, al tener contacto con el virus: células presentadoras de antígenos, células colaboradoras y células en reposo. La importancia de R 0 radica en que desempeña el papel de un umbral, el cual determina condiciones de estabilidad, tal y como se muestra en la proposición 3, en cuya demostración se empleó la teoría clásica de los signos de los valores propios 18 y el criterio de Routh-Hurwitz.
Proposición 3
El equilibrio E 0 del sistema 8 es local y asintóticamente estable si y sólo si R0<1.
Este resultado indica que si una persona se encuentra en una situación de riesgo de adquirir el VIH, pero satisface R 0<1, entonces la infección no se establece en su organismo. Vale la pena recordar que este es un resultado además de teórico, puntual para el modelo planteado y no es conveniente hacer generalizaciones.
Resultados numéricos
Se muestran tres simulaciones del modelo 8, teniendo en cuenta los valores de los parámetros de la Tabla 1, la mayoría de ellos fueron tomados de 15,19. Como el modelo presenta 16 parámetros, se hicieron 16 simulaciones variando uno de ellos mientras los otros 15 permanecían fijos. Se eligieron 20 valores para el parámetro en un conjunto de valores admisibles, denominado rango en la Tabla 1 y construido a partir de un valor central tomado de la literatura, y luego aumentado o disminuido en un 100%.
De las 16 simulaciones, se ha decidido mostrar en la Figura 1 la correspondiente a η, debido a que en ella se apreciaron comportamientos interesantes, como por ejemplo la marcada variación de máximos (picos) en seis de las ocho poblaciones o la diferencia tan significativa de los valores finales de las poblaciones, exceptuando T * y V. El hecho de que las poblaciones no se extingan, fue un comportamiento esperado debido al elevado porcentaje de variación de R 0 que se observa en la columna 5 de la Tabla 1; es decir, que se presentó un cambio del 92% con respecto al valor original de R 0 calculado con los valores de la columna 3. A partir de las simulaciones, se tiene que el aumento del parámetro η disminuye las poblaciones susceptibles (P, T r , T h ), mientras que incrementa las poblaciones infectadas (T * , T l* ), por lo tanto, conviene reducir η. Es relevante mencionar que en cada cuadro de la Figura 1 se muestran solo cuatro curvas, correspondientes únicamente a cuatro de los 20 valores del parámetro considerados.
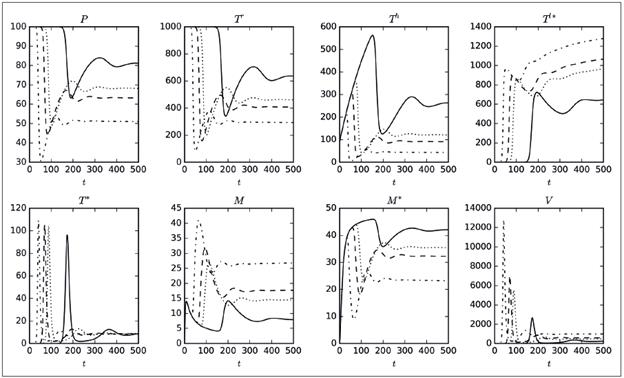
Figura 1 Tamaño de las poblaciones del modelo 8 variando el parámetro η. El eje horizontal corresponde a los días de simulación, mientras que el eje vertical corresponde al número máximo de cada variable. Los valores usados para el parámetro son: 175,552 (línea continua), 446,721 (puntos), 789,497 (guiones) y 1 155,907 (guiones y puntos).
El parámetro ρ es el que genera los mayores máximos (picos), aunque no influye mucho en el tamaño de las poblaciones finales, como sí ocurría con η. Otro aspecto que vale la pena destacar es que el parámetro ρ solo está presente en las ecuaciones para P y T * , pero su influencia se reflejaba en todas las poblaciones. Por lo tanto, se muestra la Figura 2, en la cual se ha capturado la variación de los máximos alcanzados por las poblaciones del modelo 8 al variar el parámetro ρ (eje horizontal). Se observa que a medida que ρ crece de cero a 2.0xl0 -5 , el número máximo promedio de las poblaciones P, T h , T * y M * disminuye, situación interesante, ya que una disminución en P, T h y M * , implica un mayor nivel de infección en el organismo. Por otro lado, el aumento de T l* implica que hay muchas células infectadas en estado de latencia. Como otra observación preliminar, puede decirse que disminuir ρ es conveniente para controlar la infección. Comportamientos análogos se obtuvieron al realizar simulaciones para β y γ; es decir, que según este modelo, es recomendable reducir las probabilidades de infección con el virus de todas las poblaciones celulares susceptibles.
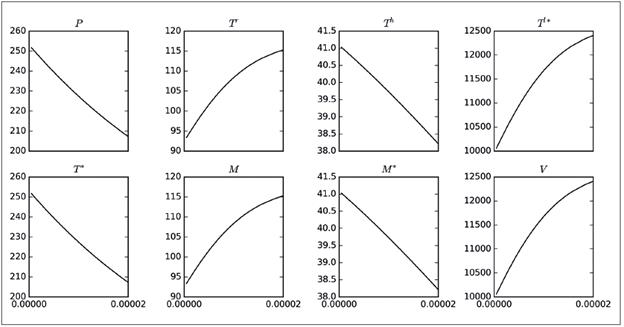
Figura 2 Variación de los valores máximos ocasionados por el brote viral de las soluciones del modelo 8 con respecto a los valores asumidos por el parámetro ρ en el intervalo [0,2.0x105]
Por último, en la Figura 3 se observa cómo varía el equilibrio no trivial de las poblaciones del modelo 8 cuando se modifica el parámetro γ. Nótese que cuando γ se incrementa de cero a 6.0xl0 -5 , también se incrementan las células infectadas en latencia T l " y las partículas virales V que habrá en «equilibrio» al cabo de los 500 días. La situación lleva a confirmar que una forma adecuada de controlar la infección es reduciendo γ.
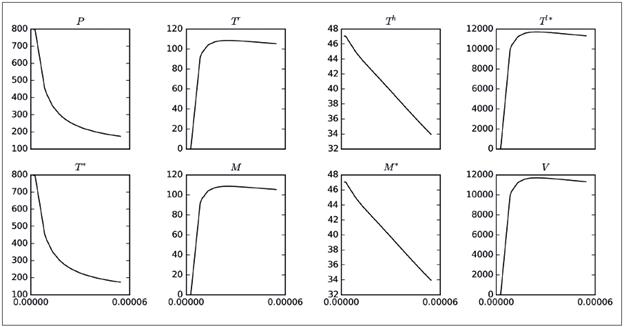
Figura 3 Variación del equilibrio no trivial de las poblaciones del modelo 8 con respecto a los valores asumidos por el parámetro γ en el intervalo [0,6.0x105]
Problema de control óptimo mediante terapia antirretroviral
Durante los últimos 20 años, el Panel on Antiretroviral Guidelines for Adults and Adolescents ha hecho cambios en las recomendaciones acerca de cuándo empezar la terapia basada en terapia clínica, datos de cohortes y opciones terapéuticas disponibles en el momento de cada revisión.
De acuerdo al Panel, los ensayos controlados aportan evidencia de que la aplicación de terapia en pacientes cuyo conteo de células T es menor a 350 células/mm3 resulta benéfico. El panel recomienda terapia para pacientes con conteo celular entre 350 y 500 células/mm3, mientras que para pacientes con un conteo sobre las 500 células/mm3, los miembros del Panel están divididos, así que el 50% favorece el inicio de la terapia en las primeras etapas, mientras que el otro 50% la considera opcional 20.
Defina u=u(t), con 0≤u(t) ≤1, como un esquema de control basado en la combinación de terapias de Inhibidores de Transcriptasa Inversa (ITI) e Inhibidores de Proteasa (IP) con efectividades manipuladas mediante dosificaciones, g 1 y g 2 , respectivamente. El caso u=0 indica que la terapia no es aplicada y u=1 indica terapia completa. Teniendo en cuenta las conclusiones preliminares obtenidas a partir de las Figuras 1, 2 y 3, con respecto a la disminución de los parámetros η, ρ, β y γ, se propone el siguiente sistema, donde los controles han sido incorporados precisamente en los parámetros mencionados.
Sujeto a las condiciones iniciales necesarias para las simulaciones. Adicionalmente, V * =V * (t) es la concentración promedio de partículas virales defectuosas producidas por el efecto de los IP. Se propuso una funcional de réditos que tiene en cuenta la población de células T colaboradoras T h y las células activas citotóxicas inmunes M * para maximizarias al tiempo que se minimiza el costo de la aplicación del control. El funcional J está definido por la expresión;
Sujeto al sistema 9 y A, A 2 y A 3 son valores de ponderación. El objetivo consiste en encontrar una función óptima u * ϵF tal que J(u * )≥J(u), para todo uϵΓ, donde Γ es el conjunto de todas las posibles funciones de control, denominado conjunto de accesibilidad y está dada por:
El uso del Principio del Máximo de Pontryagin permite obtener el siguiente resultado:
Proposición 4
Existe un control óptimo u*ϵΓ y las correspondientes soluciones del sistema 9 que maximizan J sobre Γ. Para que la aseveración anterior sea cierta, es necesario que existan funciones continuas L i . tales que:
Con las condiciones de transversalidad L ¡ (t)=0, para i=1,...,9 y además
Donde
Los detalles de la metodología empleada pueden consultarse en 21,22. Con los parámetros de la Tabla 1 se realizó la simulación del sistema 9 y la terapia óptima u * dada en 12, con lo que se obtienen las gráficas en línea continua gruesa de la Figura 4.
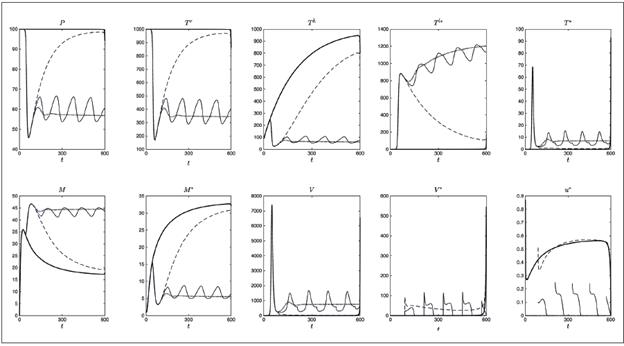
Figura 4 Simulación de diferentes estrategias de control. No se aplica terapia (puntos), terapia óptima (línea continua gruesa), terapia tardía cuyo inicio está sujeto al periodo de ventana definida en 13 (guiones), interrupciones controladas de la terapia dependiendo del conteo de células T definida en 17 (línea continua delgada) y Analmente control constante definido como el promedio de la función de control óptima u^* sobre el intervalo [0,600] definida en 15 (guiones y puntos)
Estrategias sub-óptimas de terapia antirretroviral
La estrategia de control óptimo discutida previamente, correspondiente al perfil de control en línea continua gruesa mostrado en el último recuadro de la Figura 4, no puede ser aplicada en situaciones realistas. De hecho, la función u determina la terapia que debería ser administrada cada día para obtener la efectividad requerida. De otro lado, tampoco es realista considerar que la terapia empieza en el tiempo t=0, correspondiendo al tiempo en el cual la infección inicia; se acepta que dependiendo de la condición inmunológica del paciente, se requieren aproximadamente unos 100 días como mínimo, para que el diagnóstico sea posible con alguna prueba clínica. Aunque este diagnóstico podría hacerse mucho más tarde en la mayoría de los portadores, debido a que la infección es inicialmente asintomática. Por otro lado, la simulación del modelo 8 permitió observar que 100 días fueron suficientes para que se presente infección (Figura 1). Este tiempo considerado previo al diagnóstico, conocido como periodo de ventana, es muy variable y depende de muchos factores. Para efectos de simulación se asumen 100 días como periodo de ventana.
En la Figura 4 se muestran conjuntamente cinco diferentes estrategias de control, simuladas para 600 días con los valores de la Tabla 1. Tales estrategias son: no aplicar terapia (puntos), terapia óptima (línea continua gruesa), terapia tardía cuyo inicio está sujeto al periodo de ventana (guiones), interrupciones controladas de la terapia dependiendo del conteo de las células T (línea continua delgada) y finalmente, control constante definido como el promedio de la función u * sobre [0,τ], para τ=600 días (guiones y puntos). Las últimas tres estrategias, denominadas sub-óptimas, serán descritas a continuación.
Terapia tardía
Fueron considerados 100 días como el periodo de ventana, después del cual, el virus puede ser detectado por algún ensayo clínico. Se asume que el control óptimo u" es usado justo después del diagnóstico, dando origen a la siguiente función de control sub-óptimo:
En la Figura 4 la terapia tardía corresponde a las líneas trazadas con guiones.
Interrupciones controladas de la terapia
La estrategia se basa en una de las recomendaciones de 19. Se considera que la terapia es obligatoria cuando el conteo de células T está por debajo de 500 células/mm3, y no se aplica terapia por arriba de este valor. Esto corresponde a la función de control sub-óptimo:
donde τ varía cada dos meses desde el día 100 (periodo de ventana) hasta el día 600. Se asume que cada 60 días el paciente asiste a los servicios de salud para el conteo de células T y si la cantidad T h +Τ r es menor que 500, entonces la terapia es aplicada 19. En la Figura 4 se observa que después del diagnóstico, la terapia fue usada durante los días 100 a 160, lo que da lugar a la primera parte de la línea continua delgada (creciente). Este proceso continúa hasta que se alcanzan los 600 días, teniendo presente que el decrecimiento de la curva representa la ausencia de terapia y el crecimiento corresponde a su aplicación.
Control constante
Se considera la función de control sub-óptimo descrita por la función:
que corresponde al valor medio de la función u * sobre el intervalo [0,τ], de este modo, el control sub-óptimo ū 3 es un control constante. Con los parámetros de la Tabla 1, se obtuvo la función de control óptima (línea continua gruesa) y calculado su valor medio en un intervalo de 600 días, se obtuvo ū 3 =0.5342 (guiones y puntos)( Figura 4).
Del modelo 8 se aprende que, teóricamente, la infección no se establece en el organismo, si el sistema inmune del individuo al momento de contacto con el virus está en un estado específico que satisface R 0 <1, y este hecho podría reflejar los casos donde las personas no han sido infectadas incluso después de varias exposiciones al virus. Si ese no es el caso, la infección prospera y entonces, la respuesta inmune celular es muy importante para determinar la evolución de la infección.
Del análisis de las estrategias de control se aprende que una vez el VIH infecta el cuerpo, la terapia óptima u * es la más efectiva estrategia para reducir la infección, ya que inhibe completamente la replicación viral durante el tiempo simulado, con un ligero aumento al final del periodo debido al cese de la terapia. En el caso del inicio tardío de la terapia se obtienen beneficios para el paciente, porque después del pico de infección se adquieren altos niveles de células T en reposo, células T colaboradoras, células presentadoras de antígenos y células activas citotóxicas. De la misma manera, la carga viral y las células infectadas (latentes y activas) son reducidas a bajos niveles.
De las interrupciones controladas de la terapia, se observa un comportamiento oscilatorio no amortiguado alrededor de la curva sin terapia, indicando que la condición del paciente será mejor o peor (en comparación con la ausencia de terapia) dependiendo del régimen seguido en los últimos dos meses. Las interrupciones de la terapia parecen ser no recomendables, pero se deben hacer más estudios.
La estrategia sub-óptima dada por el valor medio de la función de control óptimo, ha demostrado ser una estrategia de control adecuada a través de la simulación del sistema 9 como un problema de control constante; a pesar de no ser óptima, es tan buena como la terapia óptima y como el inicio tardío de la terapia, durante los primeros 600 días.
La mejor estrategia que puede ser alcanzada a nivel inmunológico es aplicar control óptimo lo antes posible después de la infección (desde el momento del diagnóstico) para obtener el máximo beneficio. Sin embargo, resulta evidente que con la estrategia del control óptimo promedio se obtienen resultados muy semejantes; por lo tanto, resulta más «práctico» mantener un esquema de terapia constante, que ajustarse al perfil propuesto por el control óptimo. Como es evidente, los médicos tienen que hacer las evaluaciones y consideraciones necesarias para diseñar esquemas de terapia de acuerdo a las condiciones particulares del paciente