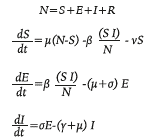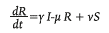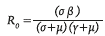La enfermedad por el nuevo coronavirus (co-VID-19) se ha convertido en una gran amenaza a la salud de las personas en todo el mundo. Hasta el 9 de abril de 2020 se habían reportado 1 601 018 casos, 95 699 muertes (5,5%) y 354 464 recuperados (21,7%) en 184 países afectados. Los países hasta esa fecha con mayor número de infectados eran Estados Unidos (465 750), España (153 222), Italia (143 626), Francia (118 783), Alemania (118 235) y China (82 919). El mayor número de muertes se había presentado en Italia (18 279), Estados Unidos (16 684) y España (15 447) 1.
Para Colombia, las cifras reportadas hasta ese día iban en 2 223 casos, 69 muertes (2,9%) y 174 recuperados (5,6%). En Cali, la tercera ciudad con mayor población en el país, se habían reportado 243 casos, 5 muertes y 11 recuperados 2.
Ante el progreso de esta pandemia, los países alrededor del mundo han implementado diferentes medidas sin precedentes, como el cierre de fronteras, escuelas, universidades, iglesias, todo tipo de eventos sociales y aislamiento de la población en sus casas. Todas estas estrategias han sido influidas por la limitación en el número de pruebas realizadas, la falta de recursos médicos y la baja capacidad para la atención ante un brote de esta magnitud, además de la dificultad para tener otras herramientas de prevención inmediatas 3.
Desde el inicio de la epidemia, se han estimado varios modelos de predicción utilizando diferentes metodologías, como los modelos determinísticos, estocásticos o una combinación de ambos 4-6. Todos tienen un mismo objetivo: la predicción del número de personas infectadas en las próximas semanas, la fecha probable del pico y la estimación del número de casos críticos que requieren manejo en UCI. Esta información permite no solo preparar medidas de contingencia en los servicios de salud y de construcción de planes para atender otros sectores afectados, sino además evaluar las intervenciones realizadas por las autoridades.
Para Colombia, el Instituto Nacional de Salud (INS) realizó proyecciones utilizando un modelo determinista SIR; además, Manrique et ál. también muestran los resultados del mismo modelo para el país 7. Sin embargo, en la literatura aún no se reportan modelos epidemiológicos para la ciudad de Cali que ayuden en la toma de decisiones; por ello, el objetivo de este estudio es mostrar las predicciones realizadas a través de un modelo epidemiológico determinista en la ciudad.
MÉTODOS
Se ajustó un modelo compartimental determinista SEIR basado en el estado epidemiológico de los individuos. La ventana de tiempo fue de 400 días a partir del 15 de marzo, fecha en la que se reportó el primer caso en la ciudad. Las proyecciones del modelo se realizaron en el software R; para los gráficos se usó la librería ggplot 8.
Datos
Se utilizaron datos del reporte de casos diario de la Secretaría de Salud Municipal de Cali para el cálculo de la tasa de letalidad, teniendo en cuenta la fecha de inicio de síntomas la cuál se ajusta más a la dinámica de transmisión. La población de la ciudad en el año 2020 se obtuvo a través de la proyección poblacional del Departamento Administrativo Nacional de Estadística (DANE).
Modelo SEIR
Los procesos de transmisión de agentes infecciosos en poblaciones hospederas representan uno de los principales objetivos de estudio de los modelos epidemiológicos compartimentales, los cuales se basan en sistemas de ecuaciones diferenciales para el movimiento de la población a través de estados discretos. De esta forma, cuando un patógeno aparece en una comunidad hospedera, estos modelos dividen los individuos en categorías que dependen del tipo de infección 9. Estas categorías o también llamados compartimientos son representadas teniendo en cuenta una notación estándar desarrollada por Kermack y Mckendrik 10. En el caso del modelo SEIR, su sigla significa que tienen en cuenta: fracción de la población hospedera que es susceptible a la infección (S), fracción de infectados pero que aún no transmiten la infección a otros durante el periodo de latencia (E), fracción de infectados que pueden transmitir la infección (Γ) y la fracción de recuperados que adquieren inmunidad temporal o permanente (R).
El sistema de ecuaciones diferenciales ordinarias del modelo SEIR para una población fija es el siguiente:
donde μ es la tasa de mortalidad en la población (no relacionada con la enfermedad), β es la tasa efectiva de contacto (parámetro que controla qué tan frecuente un contacto susceptible-infectado resulta en una nueva exposición), ν es la tasa de vacunación si una vacuna existiera (en este caso se asume cero), o es la tasa a la cual una persona expuesta se convierte en infecciosa, y γ es la tasa a la cual un infectado se recupera y pasa a ser resistente.
Este modelo asume que la población es constante, que la tasa de letalidad es baja comparada con otras enfermedades, y que, además, todos los hospederos infectados adquieren inmunidad.
Así mismo, el número reproductivo R 0 que representa el número esperado de individuos secundarios resultantes de una infección inicial se obtiene a través de la siguiente fórmula:
El cálculo de este parámetro se realiza sin tener en cuenta la existencia de una vacuna, además asumiendo que es constante en toda la población. Si este es mayor a 1, cada persona infectada produce más de un nuevo caso y la enfermedad es capaz de propagarse e infectar la población susceptible. En la práctica, este parámetro puede ser difícil de medir, debido a que depende de datos de seguimiento muy específicos en la población, como la frecuencia en que una persona infectada-susceptible resulta en una nueva exposición y la tasa en la cual una persona se vuelve infectiva. Para el modelo de este estudio, se utilizaron diferentes escenarios del valor de R 0 , de acuerdo a lo reportado en la literatura, teniendo en cuenta que las posibles medidas de intervención realizadas o a realizar afectarán principalmente este parámetro. Las proyecciones del número de infectados se realizaron para R 0 igual a 1,5, 2,0, 2,4 y 2,6, valores que fueron reportados por el equipo de respuesta del coViD-19 del Imperial College. Además, otros parámetros reportados en otros estudios como se indica en la Tabla 1.
Las proyecciones de los diferentes escenarios del modelo se compararon con la serie observada de casos confirmados desde el 15 de marzo hasta el 9 de abril. Por otro lado, usando la distribución de casos según severidad, se realizó el cálculo de casos leves, severos y críticos en los puntos más altos por cada escenario 11.
Por último, se realizó la estimación de un modelo exponencial para determinar la tasa de crecimiento de los casos confirmados antes y después de la medida de cuarentena impuesta por el Gobierno nacional, esto con el objetivo de medir el posible efecto de la intervención, además de aportar información complementaria a la proyección de casos reportada por el modelo SEIR.
RESULTADOS
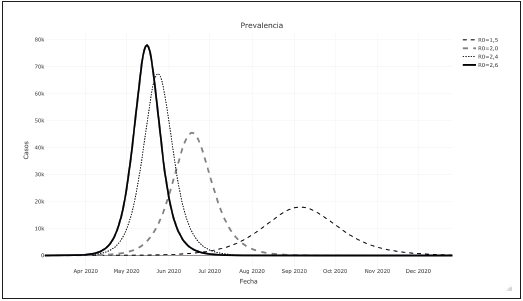
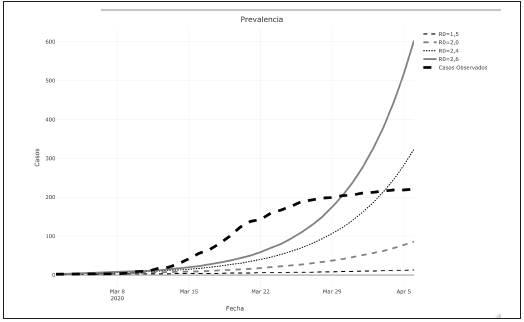
Hasta el 9 de abril, en Cali se habían reportado 243 casos y 5 muertes para una tasa de letalidad de 2,0%. Teniendo en cuenta una población de 2 200 000 de habitantes para Cali, la estimación de prevalencia de infectados bajo el escenario menos optimista (R 0 =2,6) mostró una curva con un punto máximo de 195 666 casos para el primero de junio, mientras que para un número de reproducción igual a 2,4 el pico se presentaría el 10 de junio con 172 991; para un R 0 de 2 el pico sería el 5 de julio con 122 364; y finalmente el escenario más optimista muestra un curva disminuida en su frecuencia de casos, con un punto alto el 22 de septiembre (50 713 casos) (Figura 1). Además, las proyecciones muestran que el porcentaje de contagiados en la ciudad respecto a la población total serían: 59% (R 0 =1,5), 80% (R 0 =2,0), 88% (R 0 =2,4) y 91% (R 0 =2,6).
Al comparar la serie de casos confirmados con la predicción realizada para los diferentes números de reproducción (R 0 ), se encuentra que la serie observada al inicio presenta una ocurrencia de casos mayor a la proyectada con un número de 2,6; sin embargo, a partir del 26 de marzo, la tendencia cambia y muestra que, posiblemente, si se analizan los datos en semanas posteriores, su comportamiento pueda ser similar al presentado teniendo en cuenta un R0 igual a 2 o menor (Figura 2).
Debido a la necesidad de determinar no sólo el número de personas infectadas en el tiempo, sino además cuántos de estos van a requerir de los servicios de salud, se encontró que el número de casos críticos para un número básico de reproducción de 1,5 en el punto más alto de la epidemia es 2 119, para R 0 =2,0 es de 5 113, con R 0 =2,4 son 7 228 y finalmente para un R0 de 2,6 se esperarían 8 176 casos críticos (Tabla 2).
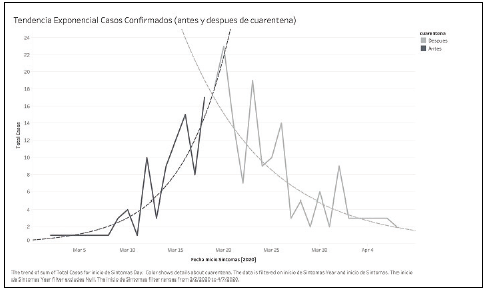
Por otro lado, los resultados del modelo exponencial muestran que la tasa de crecimiento de casos confirmados antes de la medida de cuarentena fue de 1,2 IC95% [1,11,3]. Esto quiere decir que, si -por ejemplo- un día se inicia con un reporte de unos 100 casos, cada día aumentaría en un 21% y al cabo de dos semanas se podrían tener 1 744 casos diarios; y de estos más o menos unos 73 casos necesitarían uci diariamente; sin embargo, la tendencia después de la medida presentó un descenso de 11% en los casos nuevos presentados a diario (Tasa=0,9 IC95%[0,8-0,9]) (Figura 3).
A través del modelo SEIR se encontró que, para el número básico de reproducción más alto de 2,6 y utilizando la letalidad calculada para la ciudad de 2%, el número máximo de casos se alcanzaría el primero de junio con 195 666 (prevalencia). Sin embargo, al comparar los casos observados con la proyección se observa que al inicio la ocurrencia estaba por encima de las predicciones pero luego cambia la tendencia disminuyendo el grado de inclinación. Con unas semanas más de información (posteriores al 9 de abril) se podrá determinar si los casos observados siguen el comportamiento de un número básico de reproducción de 2 o 1,5. Por otro lado, a través del modelo exponencial se pudo medir el efecto generado por la cuarentena sobre la ocurrencia de casos confirmados; este hecho evidencia que, antes de la medida, el crecimiento diario de casos era de 21%, mientras que después de la misma se presentó una disminución en el reporte en 11%.
La construcción de este tipo de modelos durante la ocurrencia de una pandemia de esta magnitud se hace necesario, dado que ayuda a los Gobiernos en la planeación y construcción de intervenciones de forma anticipada. Los modelos epidemiológicos SEIR son una opción tradicional y sencilla que a través de un sistema de ecuaciones y la suposición o generación de valores iniciales predice la ocurrencia de casos de una enfermedad infecciosa, proporcionando datos a largo plazo sobre el comportamiento de la prevalencia e incidencia. Permiten, además, considerar la dinámica de la epidemia a través de los diferentes estados en los que se pueden mover los hospederos del virus y valorar los efectos de posibles intervenciones, como las vacunas, si existieran 12.
Sin embargo, estos modelos, aunque son muy utilizados, presentan varias limitaciones. Una de estas es la suposición en el comportamiento de parámetros, aunque podría ser una ventaja inicialmente, dado que la ausencia de estos valores permite incluir estimaciones de otros estudios (como sucede en este artículo). También podría resultar en proyecciones imprecisas, debido a que no se está considerando la distribución local de valores como el número básico de reproducción, que puede estar muy influida por dinámicas culturales o sociales del país o de la ciudad, además de cambiar a medida que evoluciona el brote 13. Así mismo, no considera factores socioeconómicos como las condiciones de vivienda de la población, lo cual podría ser crucial en la propagación del virus, o las condiciones climáticas que ya se ha demostrado tiene un efecto en la ocurrencia de casos 14.
Aunque este tipo de modelos pueden presentar incertidumbre en sus resultados, se debe mencionar que, en general, los datos epidemiológicos también pueden afectarse por varios inconvenientes, como es el retraso en la entrega de resultados de las pruebas, en la notificación y limitaciones en la cobertura, inconvenientes que generan posibles imprecisiones en la información. Sumado a esto, en ninguna región se conoce con certeza absoluta la cantidad de infectados reales (considerando los posibles asintomáticos), lo que finalmente puede resultar en modelos epidemiológicos con proyecciones imprecisas o con un alto grado de incertidumbre, aun si se ajustan por los factores mencionados anteriormente.
En el futuro inmediato, se deben considerar modelos que incorporen las características dinámicas locales de la transmisibilidad, por ejemplo, estimando el número efectivo de reproducción (R t ), el cual varía en el tiempo y puede emplearse para hacer seguimiento y evaluación de las medidas de contención del brote en tiempo real 15. Variaciones de estos modelos podrían incorporar la incertidumbre en un marco de modelación bayesiana, así como el concepto de epicentros, que surge de modelar adicionalmente la transmisibilidad en función de la proximidad geográfica de los casos ·