Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en
SciELO
Similares en
SciELO -
 Similares en Google
Similares en Google
Compartir
Revista de Economía Institucional
versión impresa ISSN 0124-5996
Rev.econ.inst. v.4 n.6 Bogotá ene./jun. 2002
LA NUEVA ECONOMÍA INSTITUCIONAL Y LA TEORÍA DE LA IMPLEMENTACIÓN
NEW INSTITUTIONAL ECONOMICS AND IMPLEMENTATION THEORY
Ernesto Cárdenas*
Jaír Ojeda**
* Profesor de la Facultad de Economía de la Universidad Externado de Colombia, calle 12 n.o 1-17 este, Bogotá, ernycardenas@hotmail.com.
** Investigador de la Facultad de Economía de la Universidad Externado de Colombia, calle 12 n.o 1-17 este, jnojeda2000@yahoo.com. Agradecemos la evaluación y los comentarios del comité de árbitros de la Revista de Economía Institucional a versiones anteriores del texto. Fecha de recepción: 17 de julio de 2001; fecha de aceptación: 6 de diciembre de 2001.
RESUMEN
[Palabras clave: Nueva Economía Institucional, Teoría de la Implementación, costos de transacción, derechos de propiedad, individualismo metodológico, JEL: B52, D23, D78]
Este artículo muestra que algunos de los más importantes conceptos de la Nueva Economía Institucional (NEI) se pueden expresar en términos de la Teoría de la Implementación (TI). Primero revisa algunos conceptos de la NEI: instituciones, costos de transacción, derechos de propiedad e individualismo metodológico. Luego presenta una definición amplia de la TI y por último señala algunas correspondencias entre ambas teorías.
ABSTRACT
[Key words: New Institutional Economics, Implementation Theory, transaction costs, property rights, methodological individualism, JEL: B52, D23, D78]
This paper shows how some of the most important concepts of the New Institutional Economics (NIE) can be expressed in terms of Implementation Theory (IT). First, it explains some of the expressions used by the NIE, such as institutions, transaction costs, property rights and methodological individualism. Afterwards, it gives a wide definition of the IT in order to establish correspondences between both theories.
El presente ensayo intenta mostrar que las discrepancias metodológicas entre la teoría económica walrasiana y la Nueva Economía Institucional se pueden entender mejor a la luz de la teoría de la implementación. Por teoría económica walrasiana entendemos la teoría derivada del modelo Arrow-Debreu (1954, 1959) y de sus versiones dinámicas, como el modelo de generaciones traslapadas de Samuelson (1958) y el de Ramsey-Cass-Koopmans (1965)1. Y por Nueva Economía Institucional, la corriente económica basada en los trabajos de Coase (1937, 1960), North (1993) y Furubotn y Richter (1997).
El ensayo consta de tres secciones. La primera expone los principales conceptos de la Nueva Economía Institucional; entre ellos el concepto de institución y su relación con los costos de transacción y los derechos de propiedad. La segunda presenta una síntesis de los principales conceptos de la teoría de la implementación y un ejemplo ilustrativo. La tercera, a modo de conclusión, muestra que los principales conceptos de la Nueva Economía Institucional encuentran pares en la teoría de la implementación y que las discrepancias con la teoría económica walrasiana se pueden conciliar hasta cierto punto.
LA NUEVA ECONOMÍA INSTITUCIONAL
En esta sección se presentan algunos conceptos e inquietudes de la Nueva Economía Institucional (en adelante NEI). Debemos destacar desde ahora que la NEI no surge necesariamente como una contraposición de la teoría neoclásica o walrasiana sino como una ampliación de sus postulados, puesto que intenta incorporar elementos que el modelo walrasiano no tuvo en cuenta explícitamente y que son de gran importancia para entender mejor el comportamiento de los agentes económicos. Por esa razón, en este artículo es a veces ineludible tratar los conceptos e inquietudes de la NEI como un ejercicio de debilitamiento de algunos supuestos básicos de la teoría walrasiana, en particular, los del modelo Arrow-Debreu. North (1993) dice claramente:
El marco analítico es una modificación de la teoría neoclásica. Lo que conserva es el supuesto básico de la escasez y por lo tanto de la competencia, así como los instrumentos analíticos de la teoría microeconómica. Lo que (se) modifica es el supuesto de la racionalidad, lo que (se) añade es la dimensión del tiempo.
North reconoce que en primera instancia puede ser bastante difícil incorporar la dimensión temporal y, de hecho, este es un tema de investigación en la reciente literatura sobre juegos evolutivos2. Aquí no se intenta introducir el tiempo de manera explícita sino exponer algunos de los conceptos de la NEI referentes a la racionalidad de los agentes en marcos institucionales alternativos.
Quizás la idea de institución sea el concepto básico en este tipo de pensamiento. Su definición, en el sentido más amplio, incluye todas las creencias y modos de conducta instituidos por la colectividad (Durkheim, 1938 [1895])3, es decir, creencias y conductas que no dependen solamente de un juicio o hábito de individuos aislados. No obstante, esta definición plantea dos interrogantes: a) ¿por qué, en ambientes de racionalidad individual, una institución dada puede ser exitosa en unas circunstancias y no en otras, con respecto a conflictos entre motivaciones individuales y prescripciones sociales acerca de la efectividad de las instituciones?, y b) ¿existe algún límite de las combinaciones de creencias y conductas que pueden persistir como instituciones, con respecto a conflictos entre motivaciones individuales y prescripciones sociales acerca de la perdurabilidad de las instituciones?
El enfoque de la elección racional acerca del comportamiento social e institucional es un intento de responder estos interrogantes. En la literatura reciente se pueden identificar tres métodos generales en este enfoque: a) concebir las instituciones como características de las preferencias de los individuos; la función de utilidad del individuo puede incluir argumentos para el altruismo, la cooperación, las normas sociales, etc., b) tratarlas como restricciones de comportamiento o como reglas del juego’ y examinar el comportamiento racional dentro de las restricciones impuestas por las reglas o instituciones y c) considerar una institución como equilibrio del comportamiento en un juego. Cualquiera que sea el método, el objetivo es describir las instituciones de tal manera que expliquen el comportamiento observado e identifiquen las condiciones en que puede ser efectiva una institución.
En el presente artículo se adopta el concepto de institución como reglas del juego. En palabras de North (1993), como el conjunto de reglas formales e informales a través de las cuales se rige el proceso de interacción humano. En este sentido, las instituciones son los límites concebidos por el hombre para estructurar su propia interacción. Las reglas formales o intencionales son creadas con un objetivo específico y en forma deliberada por una autoridad. Las limitaciones formales incluyen reglas políticas, judiciales, económicas y contratos. Las reglas informales o espontáneas surgen de los propios individuos sobre la base de su propio interés. En general, son informaciones heredadas de generación en generación y forman parte de la cultura de un grupo dado de individuos4. Por cultura se entiende la transmisión de una generación a la siguiente por la enseñanza y la limitación de conocimientos, valores y otros factores que influyen en la conducta (Boyd y Richerson, 1985)5. Las normas informales, a diferencia de las formales, no se pueden cambiar rápidamente y el proceso de transformación o adecuación a nuevas circunstancias requiere largos períodos de tiempo.
Las instituciones cumplen la función de conducir los comportamientos individuales al logro de objetivos específicos, mediante una estructura de incentivos que, además de reducir la incertidumbre de los procesos de interacción humana, facilite los intercambios políticos y económicos, entre otros. Es importante señalar que la existencia de instituciones no implica que su carácter sea socialmente eficiente; en la mayoría de los casos son creadas para satisfacer los intereses de quienes ostentan poder de negociación y, en general, para satisfacer intereses privados. Aquí aparece el problema de la manipulación institucional, ocasionado por el surgimiento de organizaciones formales con un poder de negociación que les permite influir en el orden institucional6. Se entiende por organización formal un grupo de individuos que busca lograr metas comunes o, en otras palabras, maximizar una función objetivo (Arrow, 1970)7.
Dentro de las organizaciones formales pueden aparecer intereses privados de sus miembros, que aprovechando los problemas de información buscan optimizar sus propias funciones de utilidad, diferentes de las de la organización. El caso típico es el de un sindicato que puede ver afectado el logro de sus objetivos como organización formal por el conflicto de intereses entre sindicados y dirigentes del sindicato.
Dentro de los costos de transacción8, los trabajos de la NEI identifican los costos de transacción de mercado, objeto de este artículo, como problemas de información. Corresponden a los costos en que incurren los diferentes agentes económicos debido a problemas de información, bien sea acerca de una mercancía, el derecho de propiedad de otro agente sobre un recurso o las reglas establecidas en un marco institucional9. Ante la dificultad de los agentes para adquirir toda la información necesaria, las partes establecen contratos para g arantizar comportamientos determinados y estipular las sanciones respectivas por su incumplimiento. Los contratos son un medio institucional que induce un compromiso creíble entre dos o más partes y requiere el soporte de normas formales e informales de obligatorio cumplimiento, con el fin de facilitar la realización de las actividades políticas y económicas y reducir su costo.
Por último es necesario aclarar el concepto de derechos de propiedad utilizado en la definición de costos de transacción. El derecho de propiedad especifica lo que un agente puede o no hacer con un recurso tangible o intangible, bien sea transferirlo o usufructuarlo. La mala especificación de los derechos de propiedad ha sido utilizada por algunos autores de la NEI para explicar el surgimiento de costos de transacción no nulos. Los costos de transacción y los derechos de propiedad son conceptos utilizados en la literatura de la NEI que provienen del derecho económico. Más adelante veremos que estos conceptos pueden tener equivalentes en el lenguaje de la teoría de juegos.
COSTOS DE TRANSACCIÓN, DERECHOS DE PROPIEDAD Y TEOREMA DE COASE
Son bien conocidos los dos teoremas del bienestar económico de las economías competitivas tipo Arrow-Debreu10. El primero dice que, en ciertas condiciones, un equilibrio walrasiano11 o competitivo es un óptimo en el sentido de Pareto12. El segundo, que en condiciones aún más fuertes, un óptimo en el sentido de Pareto es un equilibrio walrasiano o competitivo para alguna distribución de riqueza y precios no negativos. Cabe señalar que en presencia de externalidades13 (positivas o negativas) puede ocurrir que no se cumplan los dos teoremas del bienestar. En términos del primer teorema del bienestar, en presencia de externalidades, es bien conocido que el mecanismo pigouviano14, a través de impuestos (o subsidios respectivamente), puede corregir una asignación de equilibrio de tal forma que sea necesariamente una asignación eficiente en el sentido de Pareto. En otras palabras, el mecanismo de Pigou es un mecanismo de intervención gubernamental que permite mantener el primer teorema del bienestar en presencia de externalidades. No obstante, en su artículo The Problem of Social Cost de 1960, Coase muestra que el mecanismo pigouviano puede ser innecesario con costos de transacción nulos:
Lo que mostré en ese artículo [el problema del costo social], como yo lo pienso, es que en un régimen de costos de transacción nulos –un supuesto estándar en la teoría económica–, negociaciones entre los agentes conllevarían eventualmente a arreglos que maximizan la riqueza agregada de forma independiente de los derechos de propiedad inicialmente asignados (Coase, 1991, 11).
Este argumento se denomina popularmente Teorema de Coase’. Debemos señalar que aunque Coase utiliza el criterio de maximizar la riqueza agregada, ésta se ha interpretado como maximización del bienestar agregado. Se puede demostrar que, en ciertas condiciones, una asignación que maximiza el bienestar agregado (llamado a veces óptimo social) es una asignación eficiente en el sentido de Pareto15. En otras palabras, el Teorema de Coase dice que cuando los costos de transacción son nulos es posible que los agentes negocien de tal forma que se logre una asignación eficiente en el sentido de Pareto, independientemente de quien posea los derechos de propiedad sobre los recursos.
En este punto es útil presentar un ejemplo sencillo que ilustra el Teorema de Coase.
Ejemplo 1: preferencias por el ambiente
Consideremos una economía competitiva de propiedad privada de intercambio puro con dos bienes, X y Y, y dos consumidores, A y B. Cada consumidor tiene una función de utilidad de buen comportamiento16 sobre su conjunto de consumo, uA, uB, y unas dotaciones iniciales, wA y wB. Para esta economía es posible encontrar la curva de contrato que representa el conjunto de asignaciones eficientes en el sentido de Pareto. Esto se ilustra en la caja de Edgeworth de la figura 1.
Figura 1
Preferencias por el medio ambiente

La mercancía X es el ingreso nominal y la mercancía Y, el ambiente contaminado (por tanto, 1 – Y es el ambiente limpio). En este contexto es importante hacer énfasis en la interpretación de las mercancías X y Y como mercancías Arrow-Debreu. Por esta razón suponemos que la contaminación y el ingreso se pueden medir en unidades físicas bien especificadas (metros cúbicos y unidades monetarias) en un espacio determinado (una habitación o salón) y en un tiempo determinado (una hora, un día o unos minutos). Además suponemos que estas mercancías hacen parte del conjunto de consumo de A y de B. Supondremos que el ingreso nominal es un bien para cada consumidor, en el sentido de que a mayor ingreso mayor utilidad. Mientras que la contaminación es un bien únicamente para el consumidor A (un fumador compulsivo, por ejemplo), para el consumidor B mayores niveles de contaminación producen menores niveles de utilidad. Es claro que la contaminación (o el aire limpio) es una externalidad negativa para el consumidor B (o el consumidor A). Medimos la contaminación desde el origen del consumidor A, mientras que el aire puro (el que no está contaminado) se mide desde el origen del consumidor B, como se representa en la figura 1.
Cada consumidor posee una cantidad de ingreso nominal dado por D > 0 (la base de la caja de Edgeworth es entonces 2D) y el derecho a contaminar pertenece únicamente a un consumidor. Consideremos dos casos:
1. El consumidor B tiene el derecho de propiedad sobre el ambiente en el espacio considerado. Esto se representa en la caja sobre el punto w, que no es una asignación óptima en el sentido de Pareto (no pertenece a la curva de contrato). Siguiendo a Coase, el consumidor A podría ofrecer parte de su ingreso nominal para que, sin empeorar el bienestar del consumidor B (de hecho B alcanza un mayor nivel de utilidad), pueda aumentar su bienestar; situación que se ilustra en el punto E. Los precios relativos en donde el intercambio es favorable para ambos consumidores corresponden a la recta que pasa por los puntos w y E.
2. El consumidor A tiene el derecho de propiedad sobre el ambiente en el espacio considerado. Esto se representa en la caja sobre el punto w’. Igual que en el caso anterior, B podría ofrecer parte de su ingreso nominal para que, sin empeorar el bienestar de A (de hecho, éste alcanza un mayor nivel de utilidad) pueda aumentar su bienestar, punto E’. Los precios relativos en donde el intercambio es favorable para ambos consumidores corresponden a la recta que pasa por w’ y E’.
¿Dónde aparecen los costos de transacción nulos? Para responder esta pregunta usamos el mecanismo pigouviano, que supone la existencia de un tercero, quizá el Estado (planificador), con información completa, es decir, que puede visualizar la caja de Edgeworth con toda su información y advertir que a través de un mecanismo de impuestos (o subsidios) puede incentivar a los consumidores a no mantenerse en un punto como w (o w’) que no es óptimo en el sentido de Pareto. Con estos impuestos puede lograr que los consumidores se desplacen hasta E (o E’), que sí es óptimo en el sentido de Pareto. Aquí los costos de transacción nulos se refieren a la capacidad del tercero para obtener toda la información, sin ningún costo, que le permite saber que E y E’ proporcionan mayor utilidad a un consumidor sin empeorar al otro. Pero, a la luz del Teorema de Coase, es claro que la existencia de un tercero con la infraestructura necesaria para cumplir sus funciones, en un contexto de costos de transacción nulos y derechos de propiedad bien definidos, es casi innecesaria pues basta suministrar la información contenida en la caja a uno de los consumidores para lograr que interactúen directamente hasta lograr las asignaciones eficientes en el sentido de Pareto.
De aquí se puede concluir que los costos de transacción nulos significan que un tercero o alguno de los consumidores posee la información necesaria y suficiente para alcanzar una asignación eficiente en el sentido de Pareto. Debe notarse que, con costos de transacción positivos, el mecanismo pigouviano recobra importancia en cuanto puede incentivar a unos agentes tal vez desinformados a alcanzar ciertas asignaciones eficientes.
RACIONALIDAD ACOTADA E INFORMACIÓN INCOMPLETA
¿Qué pasa cuando los agentes tienen dificultades para conseguir y procesar la información? Son precisamente este tipo de interrogantes los que plantea la NEI con el ánimo de ampliar los postulados del modelo walrasiano Arrow-Debreu, es decir, caracterizar de mejor manera el comportamiento de los agentes económicos cuando tienen problemas de información.
Existen dos posibles interpretaciones de racionalidad acotada:
1. La primera se refiere a la dificultad de los agentes para tener información completa, bien sea por sus elevados costos o simplemente porque no se puede conocer cierto tipo de información. En otras palabras, no siempre se puede allegar toda la información deseada para caracterizar adecuadamente el comportamiento de los agentes. Por esto, la NEI subraya la necesidad de trabajar con información incompleta (como veremos más adelante, esta interpretación da lugar a la teoría de la implementación), es decir, tener presente la existencia e importancia de costos de transacción positivos en la actividad económica. Los agentes económicos siguen siendo racionales: optimizan una función que representa sus preferencias. Es decir, tienen racionalidad sustantiva (Simon, 1976), pero la información es acotada. A diferencia de la racionalidad sustantiva (completa) que adoptan los modelos tipo Arrow-Debreu, la NEI supone racionalidad sustantiva y acotada. Este tipo de racionalidad, con incertidumbre o información incompleta, se suele representar con funciones de tipo von Neumann-Morgenstern, como se hace en teoría de contratos17.
2. La segunda se refiere a la posibilidad de modelar la racionalidad sin que los agentes maximicen una función objetivo. Esto implica dejar de modelar las preferencias con preórdenes18 u ordenamientos, como es normal en microeconomía. Además se reconoce que los preórdenes no son constantes a través del tiempo. La opción de modelar la racionalidad en forma alternativa a la sustantiva se conoce como racionalidad procesal (Simon, 1976). Este tipo de racionalidad intenta modelar los procesos de aprendizaje de los agentes. Los procesos de aprendizaje denotan el desarrollo de una estructura para interpretar las diversas señales recibidas por medio de los sentidos (North 1993). Siguiendo a Simon (1976), podemos decir que en economías tipo Arrow-Debreu los agentes son sustantivamente racionales pero no procesalmente. Si queremos modelar la racionalidad procesal, debemos modelar explícitamente la manera como los agentes procesan la información para luego tomar una decisión. Esto sugiere que las instituciones evolucionan transformándose como consecuencia del proceso de aprendizaje de los agentes.
Pese a la necesidad de modelar la racionalidad procesal, las dificultades y los pocos resultados obtenidos hasta hoy son obstáculos para incluir este tipo de racionalidad, en forma explícita y operativa, en los modelos teóricos19. Por esa razón suponemos una racionalidad sustantiva acotada (Furubotn y Richter, 1997).
INDIVIDUALISMO METODOLÓGICO Y MODELO PRINCIPAL-AGENTE
La NEI recalca que, a diferencia de los modelos de economía walrasiana20, los colectivos u organizaciones no se deben analizar como si fueran un individuo, es decir, como si todos los individuos que los conforman buscaran maximizar la función objetivo de la organización, pues dentro de ella puede haber individuos que buscan maximizar sus propias funciones objetivo antes que la función objetivo de esa organización.
El reconocimiento de los incentivos individuales de los miembros de las organizaciones permite reinterpretar el individualismo metodológico. Éste parte de que los individuos son diferentes y que poseen gustos, metas y propósitos diferentes, e implica por tanto que “la sociedad’, el estado’, la firma’, los partidos políticos’... no se deben entender como entidades colectivas que se comportan como si fueran agentes individuales (Furubotn y Richter, 1997).
Esta reinterpretación del individualismo metodológico en la cual, debido a problemas de información, un principal está interesado en diseñar un mecanismo que incentive a los agentes a realizar la acción que le conviene, y que a su vez sea la mejor acción para cada agente (que maximice su función objetivo), se ha usado en la teoría de la implementación recurriendo a modelos de principal-agente.
TEORÍA DE LA IMPLEMENTACIÓN O DISEÑO DE MECANISMOS
La teoría de la implementación se basa en la existencia de un planificador y de unos agentes en un ambiente determinado. El ambiente determina las preferencias de los agentes y el planificador escoge el resultado deseado a priori mediante una función o regla de elección social. Dado el conjunto de resultados deseados, el planificador debe diseñar un mecanismo o juego cuyos equilibrios coincidan con los resultados que desea. El planificador debe tener en cuenta que el comportamiento de los agentes depende de la cantidad de información que poseen y de sus expectativas de interacción con los demás agentes. La teoría de juegos ha desarrollado diversos conceptos de equilibrio21 (con información completa e incompleta), dependiendo de las expectativas de interacción y de la cantidad de información que los agentes poseen al tomar sus decisiones. Esto permite hablar de diversos tipos de implementación, uno para cada concepto de equilibrio. Y la teoría de la implementación es entonces el dual de la teoría de juegos, pues en la primera, el problema es diseñar un mecanismo o juego cuya solución es un resultado específico mientras que en la segunda, dado un juego, el fin es encontrar su solución.
La teoría de la implementación ha enfrentado dos problemas asociados a los requerimientos de información: la recolección de información por el planificador y la posible manipulación estratégica por algunos agentes. En cuanto al primero, la información deseada por el planificador puede resultar demasiado costosa de recolectar y de procesar o imposible de obtener. El segundo problema surge porque algunos agentes pueden tener incentivos para no decir la verdad acerca de la información que se les pide, puesto que pueden obtener mayor utilidad suministrando información falsa.
Otra dificultad, no relacionada con problemas de información, es la incapacidad del planificador para incidir directamente en las preferencias o acciones de los agentes, es decir que no puede forzarlos a que se ubiquen en la solución que desea. Aquí también intervienen las expectativas de los agentes acerca de la forma como el planificador usará la información obtenida. Si el planificador no se compromete a usarla de manera adecuada, podría incentivar a los agentes a incurrir en una manipulación estratégica. Estos problemas se ilustran en la siguiente sección mediante un ejemplo.
Una vez que el planificador, usando el concepto de equilibrio de la teoría de juegos más conveniente, se da a la tarea de diseñar el mecanismo, debe resolver tres inconvenientes:
1. El primero es el de asegurar la participación de los agentes en el mecanismo, pues estos tienen un nivel mínimo de utilidad o utilidad de reserva si deciden no intervenir en el mecanismo. Si este nivel de utilidad de reserva es mayor que la utilidad esperada por participar en el juego, los agentes no tienen incentivos para participar en el mecanismo. Denominamos este problema restricción de participación. En algunos casos se supone por hipótesis que los agentes no pueden dejar de participar en el mecanismo y así se satisface trivialmente este requerimiento.
2. El segundo es el de compatibilidad de incentivos. Es decir, una vez el planificador ha escogido el estado deseado y puesto que no puede incidir directamente en las decisiones de los agentes, debe existir en el mecanismo una estructura de incentivos tal que la mejor opción para los jugadores sea la que el planificador desea.
3. El último es el de equilibrios no deseados, puesto que un mecanismo puede resolver los inconvenientes anteriores pero generar otras situaciones de equilibrio no deseadas por el planificador.
Para los propósitos de este artículo no es necesario presentar formalmente los conceptos anteriores. Los lectores interesados pueden consultar el trabajo de Cárdenas (1999), que además muestra cómo se pueden formalizar en términos de implementación los dos teoremas del bienestar característicos de una economía walrasiana. No obstante, a continuación presentamos una aplicación que aclara los conceptos presentados en esta sección.
EJEMPLO 2: IMPLEMENTACIÓN DE UNA NORMA
El siguiente ejemplo22 permite comparar los resultados que se obtienen cuando una misma situación de conflicto entre dos agentes se resuelve mediante tres esquemas diferentes: a) el principal conoce y procesa toda la información necesaria, b) el principal, denominado funcionario público, no tiene acceso a toda la información y c) existen derechos de propiedad claramente definidos que permiten la negociación directa entre agentes sin la existencia de un principal.
Supongamos que dos agentes, A, B deben elegir una hora, x, entre 9:30 p.m. y 10:00 p.m., a partir de la cual no se debe hacer ruido. Cada agente escogería x (si pudiera), según sus preferencias individuales. El agente A, a quien no le gusta el ruido, escogería x = a. Esa hora es información privada para A, pero es conocimiento común uniformemente distribuido entre [a-, a+]. Suponemos también que el agente B, que prefiere escuchar música hasta tarde, escogería x = b. Otros agentes no conocen b, sólo saben que está uniformemente distribuida entre [b-, b+]. Asumimos que a+< b-; por tanto, a< b.
La función de pago del agente A es U(x, a) = -a(x - a)2, en donde a representa la importancia de la elección de A. La función de pago del agente B es V(x, b) = -b(x - b)2, en donde b representa la importancia de la elección de B.
Suponemos que las funciones de pago se expresan en términos monetarios, de modo que cualquier pago o multa adicional a los agentes debe ser sumada o restada a u y v. Además, los agentes son neutrales al riesgo, la forma de las funciones de utilidad es de conocimiento común y a + b = 1.
El valor esperado de a es E(a) = [a- + a+]/2 y el de b, E(b) = [b- + b+]/2 por lo que el valor esperado del conflicto es E(a) - E(b). Y se puede demostrar que la varianza de a, denotada por r, es r = [a- - a+]2/12 y la varianza de b, denotada por s, es s = [b- - b+]2/12.
El principal conoce y procesa toda la información necesaria
Si a y b fueran de conocimiento común, es decir, que se conociera la hora a la que cada agente quiere que se deje de hacer ruido, se podría obtener un resultado óptimo en el sentido de Pareto encontrando la solución de x* que maximiza la función de bienestar social u + v, es decir:
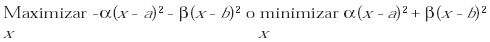
El óptimo sería entonces: x* = aa + bb.
El principal que conoce la información necesaria no tendría mayores dificultades para implementar x = x*, aun si a y b fueran información privada, pues es posible diseñar el mecanismo adecuado.
Este mecanismo consiste en preguntar a A, B cuál es su información privada. Puesto que cada agente tiene incentivos para mentir23, se establece el siguiente sistema de multas: si A reporta a = a’, A debe pagar a B el valor esperado b(aa’ + bb - b)2, el efecto neto sobre el pago de B si reporta a = a’. De igual manera, si B reporta b = b’, B debe pagar a A el valor esperado a(bb’ + aa - a)2, el efecto neto sobre el pago de A si reporta b = b’. Este mecanismo hace que cada agente internalice la función de bienestar social y que existan incentivos para reportar adecuadamente la información privada.
Más concretamente, de acuerdo con la teoría de la implementación24, el mecanismo está compuesto por:
– Jugadores: A, B.
– Conjunto de estrategias: cada jugador puede escoger un elemento de su intervalo correspondiente [a-, a+] o [b-, b+].
– Conjunto de resultados: Dado que A reporta a = a’ y B reporta b = b’, el planificador implementa x = aa’ + bb’ y cada jugador paga la multa correspondiente.
Así, la función de pago para el jugador A es - a(x - a)2 + Eb[b(aa´ + bb - b)2]; reemplazando x por su valor tenemos -a(aa’ + bb’ - a)2 + Eb[b(aa’ + bb - b)2], en donde Eb es el valor esperado de la expresión en el término b.
Y la función de pago para el jugador B es -b(x - b)2 + Ea[a(bb’ + aa - a)2]; reemplazando x por su valor tenemos -b(aa’ + bb’ - b)2 + Ea[a(bb’ + aa - a)2], en donde Ea es el valor esperado de la expresión en el término a.
Para resolver el mecanismo, cada jugador escoge el resultado que maximiza su función de pago. Por ejemplo, A escoge a’ que maximiza la función de pago descrita, la cual, desarrollando el cuadrado, equivale a
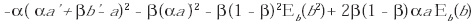
Derivando la expresión anterior con respecto a a’ se obtiene la condición de primer orden aa’ = aa - abb’ + b(1 - b) Eb(b). Puesto que el jugador A no conoce la elección de B sobre b’, espera que elija b’ = Eb(b); y como a = (1 - b), para el agente es óptimo revelar la verdad, es decir, a’ = a.
En forma análoga, b’ = b cuando el jugador B maximiza su pago.
El principal no tiene acceso a toda la información necesaria
Para un burócrata común es difícil allegar la información privada, por lo que debe implementar un mecanismo basado únicamente en la información pública y, por tanto, su mejor elección se basa en los valores esperados: xF = aE(a) + bE(b). Cabe señalar que x* difiere de xF excepto si a = E(a) y b = E(b), es decir, si los valores esperados coinciden con los valores verdaderos. En general, cuando el funcionario implementa xF causa una pérdida de bienestar con respecto al resultado del caso anterior.
Esa pérdida de bienestar está dada por a2r + b2s, la cual está asociada a la amplitud de los rangos en que se distribuyen a y b (a mayor rango mayor varianza).
Derechos de propiedad claramente definidos que permiten la negociación directa entre agentes sin la existencia de un principal
Puesto que los derechos de propiedad están bien definidos, podemos suponer que uno de los agentes (por ejemplo, A) tiene derecho a elegir x. Por su parte, B puede ofrecer una serie de sobornos a A para afectar su elección de x en forma indirecta. En concreto existe un contrato entre las partes por el cual A escoge x y, dependiendo del valor escogido, recibe de B un pago monetario (soborno).
Existe un contrato que siempre lleva a que A escoja el valor más eficiente de x. E ste contrato especifica que B le paga p(x) = b[(a - b)2 - (x - b))2] si A escoge x. Así, A internaliza toda la ganancia social y hace una elección responsable de x. Cabe anotar que este contrato maximiza el excedente conjunto, pero B estaría mejor si no participa en el contrato pues si lo hace su utilidad es -b(a - b)2, peor que el resultado que obtendría si no participa, -b(a - b)2. B no tiene incentivos para participar en este contrato.
Puesto que a B no le interesa maximizar el excedente conjunto sino su participación en el excedente, preferiría ofrecer un soborno menos generoso a A, que garantice su participación, reduzca sus pagos adicionales pero no elimine totalmente los beneficios obtenidos en un contrato socialmente superior (uno que genere menor excedente conjunto pero mayor excedente individual).
Para determinar cuál es el contrato que resulta debemos establecer una negociación entre A y B. Supongamos que B tiene todo el poder de negociación y hace a A una oferta de tómalo o déjalo. Como B no conoce a’ , no puede preguntar simplemente el valor eficiente de x y ofrecer a A el dinero suficiente para que coincidan (es decir, que x = a), B ofrece entonces un esquema completo de pares posibles (x, p) que A puede escoger.
En sí mismo, este es también un problema de implementación con información incompleta porque se puede analizar mediante la teoría del principal-agente. El individuo B sería el principal que trata de maximizar su pago ofreciendo un contrato al agente A, que tiene información privada.
NUEVA ECONOMÍA INSTITUCIONAL Y TEORÍA DE LA IMPLEMENTACIÓN
En esta sección mostramos que los principales conceptos de la NEI tienen conceptos equivalentes en la teoría de la implementación; lo que permite hasta cierto punto reconciliar las discrepancias e inquietudes planteadas por la NEI con respecto a la teoría económica walrasiana. Esta afirmación presume que el equilibrio general Arrow-Debreu se puede interpretar como el resultado de un mecanismo diseñado de acuerdo con los parámetros conceptuales mencionados. A continuación mencionamos dichas equivalencias, aunque sabemos que aun falta mucha discusión sobre la validez de cada una de estas afirmaciones.
Primero debemos señalar que el concepto de institución, tal como lo define North (1993), hace referencia al conjunto de reglas formales e informales que rigen el proceso de interacción humana. En la teoría de la implementación, este concepto se asemeja a un juego o mecanismo, diseñado por el planeador, a través del cual interactúan los agentes. En el ejemplo sobre la implementación de una norma se supuso que la regla que rige la interacción entre los dos individuos es el sistema de multas implementado por el planeador. La existencia y permanencia de esta institución se justifica en cuanto permite lograr un resultado socialmente eficiente.
Por otra parte en la teoría de la implementación, los costos de transacción se modelan como requerimientos de información, que determinan el concepto de equilibrio escogido por el planeador. En dicho ejemplo, el costo de transacción que impide que los dos individuos se pongan de acuerdo y firmen un contrato es la información privada que posee cada uno de su hora preferida, puesto que tienen incentivos a mentir cuando se les pregunta por sus gustos.
En la teoría de la implementación, los derechos de propiedad pueden estar contenidos en el conjunto de acciones posibles de los jugadores o ser un resultado de la regla que el planeador desea implementar, como sucede en el ejemplo canónico del Rey Salomón25, en donde la distribución final de pagos monetarios es el resultado del mecanismo señalado. Pero si los derechos de propiedad son definidos claramente desde el principio, es más razonable que los agentes entablen una negociación directa sin que intervenga un planeador.
Por último, el mecanismo o forma de juego que implemente una determinada regla de elección tiene que cumplir tanto con la restricción de incentivos como con la de participación. En este contexto, un análisis basado en la teoría de la implementación tiene en cuenta la racionalidad de cada uno de los agentes, igual que la teoría económica walrasiana.
NOTAS AL PIE
1. Ver Barro y Sala-I-Martin (1995).
2. Remitimos el lector interesado a la abundante literatura sobre juegos evolutivos, por ejemplo, Weibull (1995) y Samuelson (1997).
3. Ver Calvert (1995).
4. Ver North (1993) y Furubotn y Richter (1997).
5. Ver North (1993, 55).
6. Este problema de manipulación institucional se retoma más adelante en la exposición de la teoría de la implementación.
7. Ver Furubotn, E. y Richter, R. (1997, 7). Las organizaciones se valen de las oportunidades que brinda una determinada estructura institucional para maximizar su función de utilidad y buscarán incidir en la creación, la eliminación o la modificación de las normas que no promuevan sus intereses (North, 1993).
8. Existen costos de transacción de mercado, administración y políticos. Para información más detallada, ver Furubotn y Richter (1997).
9. En el lenguaje de la teoría de juegos se trata de problemas de información incompleta y de la hipótesis de conocimiento común invocada en dicha teoría.
10. Una economía competitiva tipo Arrow-Debreu es una economía de propiedad privada definida por a) los conjuntos de consumo completamente preordenados de los n consumidores, b) los conjuntos de producción de los m productores, c) la distribución de riqueza o dotaciones iniciales y d) las participaciones de los consumidores en los beneficios de los productores. Donde n, m son números enteros positivos. Ver Monsalve (1999, cap. 1).
11. Un equilibrio walrasiano se presenta cuando existe un sistema de precios para el que a) cada consumidor maximiza su utilidad sujeto a su restricción presupuestal, b) cada productor maximiza sus beneficios sujeto a sus posibilidades tecnológicas y c) la demanda y la oferta agregadas de cada bien son iguales. Ver Monsalve (1999, cap. 1) y Varian (1992, cap. 17).
12. En economías walrasianas, una asignación factible es un óptimo en el sentido de Pareto si no existe otra asignación factible que mejore el bienestar de un consumidor sin empeorar el bienestar de otro. Ver Monsalve (1999, cap. 1) y Varian (1992, cap. 17).
13. Una externalidad es el efecto indirecto de una actividad de consumo o una actividad de producción sobre el conjunto de consumo de un consumidor, la función de utilidad de un consumidor o la función de producción de un productor. Ver Varian (1992, cap. 24).
14. Ver Pigou (1920).
15. Ver Varian (1992, cap. 17).
16. Una función de utilidad de buen comportamiento es monótona creciente estrictamente, cuasicóncava estricta y doblemente diferenciable con continuidad. Ver Monsalve (1999, cap. 1).
17. Ver Macho Stadler y Pérez Castrillo (1997).
18. Un preorden o cuasiorden es una relación binaria R, que a veces se interpreta como al menos tan bueno como’, tal que para dos estados cualesquiera x, y de un conjunto de estados posibles, se tenga reflexividad (xRx) y transitividad (para todo x, y, z si xRz y zRy entonces xRy). Un preorden total o completo impone además la condición de que los agentes siempre puedan comparar dos estados (para todo x, y ocurre xRy o yRx o ambas). Ver Varian (1992, cap. 7).
19. Se recomienda consultar a Rubinstein (1998).
20. Aquí entendemos por teoría económica walrasiana aquella que proviene del modelo Arrow-Debreu (1954,1959) y de sus versiones dinámicas, como el modelo de generaciones traslapadas de Samuelson (1958) y el de Ramsey-Cass-Koopmans (1965).
21. Ver Gibbons, R. (1992).
22. Esta aplicación se basa en Farrel (1987).
23. El agente que prefiere escuchar música hasta tarde tiene incentivos para exagerar su gusto; análogamente, el otro tiene incentivos para reportar una hora menor a su preferida.
24. Para una explicación formal de los conceptos de la teoría de la implementación, ver Cárdenas (1999), Osborne y Rubinstein (1994).
25. Ver Cárdenas (1999).
REFERENCIAS BIBLIOGRÁFICAS
1. Arrow, K. y Debreu. G. “Existence of an Equilibrium for a Competitive Economy”, Econometrica 22, 1954.
2. Barro, R. y Sala-I-Martin, X. Economic Growth, McGraw Hill, 1995, pp. 59-95. [ Links ]
3. Calvert, R. Rational actors, Equilibrium, and Social Institutions, Knigth, J. y Sened, I., Explaining Social Institutions, 1995. [ Links ]
4. Cárdenas, E. La teoría de la implementación y su relación con la Nueva Economía Institucional, tesis de pregrado en economía, Universidad Externado de Colombia, 1999. [ Links ]
5. Cass, D. “Optimum Growth in an Aggregative Model of Capital Accumulation, Review of Economic Studies 32, 1965.
6. Coase, R. “The Nature of the Firm, Economica4, 1937.
7. Coase, R. “The Problem of Social Cost”, Journal of Law and Economics 3, 1960.
8. Coase, R. “The Institutional Structure of Production, The 1991 Alfred Nobel Memorial Prize in Economic Science, Essays on Economics and Economists, The University of Chicago Press, 1991.
9. Debreu, G. Theory of Value, Cowles Foundation, Yale University, 1959. [ Links ]
10. Farrell, J. “Information and the Coase Theorem, Journal of Economic Perspectives 1, 2, 1987.
11. Furubotn, E y Richter, R. Institutions and Economic Theory, The Contribution of the New Institutional Economics, The University of Michigan Press, 1997. [ Links ]
12. Gibbons, R. Game Theory for Applied Economists, Princeton University Press, 1992. [ Links ]
13. Koopmans, T. “On the Concept of Optimal Economic Growth, The Econometric Approach to Development Planning, North Holland, 1965.
14. Macho Stadler, I. y Pérez Castillo, D. An Introduction to the Economics of Information: Incentives and Contracts, Oxford University Press, 1997. [ Links ]
15. Monsalve, S. Introducción a los conceptos de equilibrio en economía, Unibiblos, Universidad Nacional de Colombia, 1999. [ Links ]
16. North, D. Desarrollo económico a través del tiempo, Trimestre Económico 61, 244, octubre-diciembre, 1994. [ Links ]
17. North, D. Instituciones, cambio institucional y desempeño económico, Fondo de Cultura Económica, 1993. [ Links ]
18. Osborne, M. y Rubinstein, A. A Course in Game Theory, MIT Press, 1994. [ Links ]
19. Pigou, A. C. The Economics of Welfare, Macmillan & Co., 1920. [ Links ]
20. Rubinstein, A. Modeling Bounded Rationality, The MIT Press, 1998. [ Links ]
21. Samuelson, P. “An Exact Consumption – Loan Model of Interest with or without the Social Contrivance of Money”, Journal of Political Economy 66, 1958.
22. Samuelson, L. Evolutionary Games and Equilibrium Selection, MIT Press, 1997. [ Links ]
23. Simon, H. “From Substantive to Procedural Rationality”, Latis, J., editor, Methods and Appraisal in Economics, Cambridge University Press, 1976.
24. Varian, H. Microeconomic Analysis, W. W. Norton & Company, 1992. [ Links ]
25. Weibull, J. Evolutionary Game Theory, MIT Press, 1995. [ Links ]














