Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
 Citado por Google
Citado por Google -
 Similares en
SciELO
Similares en
SciELO  Similares en Google
Similares en Google
Compartir
Revista de Economía Institucional
versión impresa ISSN 0124-5996
Rev.econ.inst. v.6 n.10 Bogotá jun. 2004
RIESGO MORAL Y CONTRATOS: CIERTA EVIDENCIA EXPERIMENTAL
MORAL RISK AND CONTRACTS: CERTAIN EXPERIMENTAL EVIDENCE
Julián Arévalo B.* y Jair Ojeda J.**
* Docente e investigador de la Facultad de Economía, Universidad Externado de Colombia. Docente, Universidad Nacional de Colombia; jarevalo@uexternado.edu.co
** Docente de la Facultad de Economía, Universidad Externado de Colombia. Investigador, Subgerencia de Estudios Económicos, Banco de la República; jojedajo@banrep.gov.co
Los autores agradecen a la Asociación Externadista de Estudios Económicos por la financiación del proyecto, así como a Jasson Cruz, Jorge Gallego, Francisco Lozano, Olga Manrique, Sergio Monsalve, Mauricio Pérez, César Velásquez y un jurado anónimo por sus comentarios a una versión preliminar.
RESUMEN
[Palabras clave: riesgo moral, contratos, evidencia experimental, información asimétrica; JEL: B41, C90, D89]
Este artículo presenta una clase de problemas de información asimétrica, las consecuencias teóricas de esos problemas, el diseño de contratos para mitigarlos y alguna evidencia experimental. Además, ilustra algunas implicaciones macroeconómicas a partir de extrapolaciones de los resultados que se obtienen en ambientes controlados.
ABSTRACT
[Key Words: moral risk, contracts, experimental evidence, asymmetric information; JEL: B41, C90, D89]
This paper shows one type of asymmetric information problems, their theoretical implications, the design of contracts that mitigate them, as well as some experimental evidence. Furthermore, by extrapolating the results, the paper tries to illustrate certain macroeconomic implications obtained under a controlled environment.
INTRODUCCIÓN
Aunque las recientes crisis financieras de los países asiáticos, el comportamiento despreocupado de algunos empleados en el desempeño de su labor o la falta de precaución de quienes conducen automóvil parezcan disímiles, pueden tener una explicación común. Esta consiste en un fenómeno que se observó inicialmente en los mercados de seguros y se extendió a otros ámbitos: el riesgo moral. Un caso extremo es el de los individuos que adquirían edificaciones en mal estado, las aseguraban por un alto valor y luego provocaban un incendio, de modo que obtenían ganancias extraordinarias a costa de las pérdidas de las compañías aseguradoras. Si bien no es necesario llegar a ese límite en el estudio de problemas de asimetrías de información, el punto que se debe destacar es la falta de interés de una de las partes en prestar debido “cuidado” a los intereses de la otra, por la posición favorable que genera la distorsión de la información. En los mercados financieros ocurre algo similar: algunos agentes (por ejemplo, los bancos) reciben dinero de sus ahorradores, por lo general prometiendo altos intereses, y lo invierten en proyectos de alto riesgo; si los resultados son favorables, ambas partes se ven beneficiadas. En el caso contrario, que ocurre con alta probabilidad, la quiebra del banco lleva a la de los ahorradores, que seguramente no habrían asumido riesgos tan altos con su dinero.
En general, una situación de riesgo moral es una clase especial de problemas de información asimétrica en la que ésta surge después de celebrarse el contrato entre un principal y un agente. La literatura distingue dos tipos de problemas de riesgo moral: acción oculta e información oculta. El primero se refiere a los casos en los que la acción del agente no es una variable verificable. Por ejemplo, el de un vendedor puerta a puerta (agente): su jefe (principal) difícilmente puede constatar si éste se esfuerza mucho o poco en su labor. La información oculta se refiere a los casos en los que la acción del agente es verificable, pero éste tiene información privada que finalmente permite determinar cuál es la acción adecuada. Un ejemplo usual es el de un representante de ventas en el exterior: el gerente local, que desconoce las condiciones del mercado externo, puede observar la política de ventas de su representante, pero dadas sus restricciones de información no puede saber si esa política es o no adecuada.
Las implicaciones cualitativas de los modelos que incluyen asimetrías de información que influyen en el comportamiento de los individuos y los mecanismos para controlarlo son muy conocidos, pero su comprobación empírica es aún insuficiente. Chiappori y Salanié (2000) explican esta insuficiencia por la escasez de bases de datos sobre contratos en las que se registre el desempeño de los agentes. Examinan el mercado de seguros de automóviles, donde los contratos son estandarizados y los clientes “suministran” la información necesaria para analizar las decisiones de las partes. Emplean métodos paramétricos y no paramétricos y no encuentran evidencia de información asimétrica en este mercado o, en caso de que existiera, concluyen que no determina el comportamiento de las partes. Laffont, Ossard y Voung (1995) también reconocen la escasez de estudios empíricos sobre los modelos teóricos de subastas. Usan el método de mínimos cuadrados no lineales para simular una función objetivo y concluyen que este enfoque tiene importantes limitaciones.
Este artículo presenta evidencia experimental sobre el problema de información asimétrica de acción oculta, para indicar otra manera de hacer pruebas empíricas de este tipo de modelos, y señala algunas implicaciones prácticas1. El artículo consta de cuatro secciones incluida esta introducción. En la segunda se presenta un modelo convencional de riesgo moral y el diseño óptimo de un contrato que mitigue los efectos de la asimetría de información, así como un par de ejemplos que ilustran su funcionamiento. En la tercera se presenta el experimento que se realizó para obtener evidencia empírica, y en la cuarta se hacen algunos comentarios.
RIESGO MORAL: UNA CLASE PARTICULAR DE PROBLEMAS DE INFORMACIÓN ASIMÉTRICA
Una situación de riesgo moral se presenta cuando, una vez establecido un contrato entre un principal y un agente, el primero no puede controlar las acciones del segundo ni ciertos aspectos del entorno. Y lo que es esencial, las acciones del agente no se pueden especificar en los términos del contrato2.
La secuencia de las etapas de un problema de riesgo moral de acción oculta se representa en la siguiente gráfica:
Gráfica 1
Acción oculta
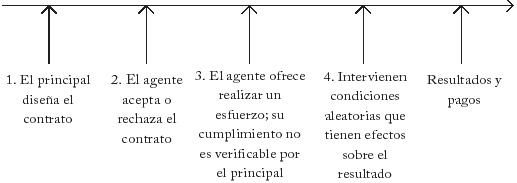
En la primera, el principal diseña el contrato, que sólo puede incluir variables verificables para que, en caso de que sea violado, pueda reclamar ante un tercero. Luego, el agente acepta o rechaza el contrato; en este modelo no hay espacio para la negociación. Si el agente acepta, se compromete a hacer un esfuerzo, que el principal no puede verificar. Luego se producen los resultados, en parte determinados en forma aleatoria y, en parte, por el esfuerzo del agente. El principal observa los resultados pero no puede determinar el nivel de esfuerzo del agente. Por ejemplo, si el principal ofrece un salario fijo, el agente no estaría interesado en hacer el mayor esfuerzo, la elección que maximiza sus beneficios es hacer el menor esfuerzo posible.
El problema de riesgo moral surge del conflicto de intereses entre principal y agente: para el principal, el pago es un costo, para el agente un ingreso. De forma análoga, al principal le interesa que el agente haga un gran esfuerzo mientras que a éste le interesa minimizar su esfuerzo. A menos que el principal logre diseñar un esquema de incentivos que induzca al agente a hacer su mejor esfuerzo, éste elegirá siempre esforzarse lo menos posible.
El riesgo moral se ha analizado ampliamente en los últimos 30 años, pero su reconocimiento se remonta a los comienzos de la ciencia económica. Adam Smith (1994, [1776], 695-696) se refiere así a los socios de sociedades por acciones:
[...] la mayor parte de estos accionistas [...] no se interesan en sus asuntos y están satisfechos con recibir el dividendo semestral o anual que los directivos consideran conveniente pagarles. Esta ausencia total de inconvenientes y riesgos, más allá de una suma muy limitada, anima a muchas personas a volverse empresarios en una sociedad por acciones, personas que en ningún caso arriesgarían su fortuna en una sociedad particular [...] Ahora bien, no es razonable esperar que los directivos de estas compañías, al manejar mucho más dinero de otras personas que de ellos mismos, lo vigilen con el mismo ansioso cuidado con el que frecuentemente vigilan el suyo los socios de una empresa particular [...] En consecuencia, el manejo de los negocios de esas compañías siempre está caracterizado en alguna medida por la negligencia y la prodigalidad.
A continuación se presenta en detalle el problema de acción oculta; se siguen los lineamientos de Macho-Stadler y Pérez-Castrillo (1992), y Mas-Colell et al. (1995).
ESTRUCTURA BÁSICA
Una vez el agente conoce el contrato ofrecido por el principal, decide aceptarlo si su utilidad esperada es mayor o igual a su utilidad de reserva (U), determinada por la mejor opción alternativa que le ofrezca el mercado; en caso contrario, no lo acepta. Si lo acepta, debe elegir un nivel de esfuerzo e que, para facilitar la exposición, se limita a alto (ea) o bajo (eb). El esfuerzo que dedique a su labor, junto con alguna distribución de probabilidad a priori determinan un resultado 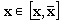 . El agente recibe un pago w. Se supone que su utilidad sólo depende de este pago y del esfuerzo que hace; en particular, se supone que sus preferencias pueden representarse mediante una función de utilidad cuasicóncava, aditivamente separable de la forma:
. El agente recibe un pago w. Se supone que su utilidad sólo depende de este pago y del esfuerzo que hace; en particular, se supone que sus preferencias pueden representarse mediante una función de utilidad cuasicóncava, aditivamente separable de la forma:
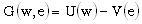
con
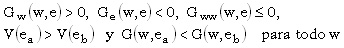
Las dos últimas desigualdades significan que la desutilidad del esfuerzo alto es mayor que la del esfuerzo bajo, y que para cualquier pago dado w, la utilidad de hacer un esfuerzo alto es menor que la de hacer el esfuerzo bajo. Como se incluyen elementos probabilísticos, la probabilidad de alcanzar el resultado x cuando el esfuerzo del agente es e se representa como 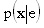 .
.
Se asume que
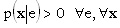
es decir, que cualquier resultado se puede alcanzar con cualquier nivel de esfuerzo. También se supone que
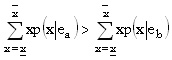
o sea que el valor esperado del resultado del esfuerzo alto es mayor que el del esfuerzo bajo, es decir, los resultados de mayor valor tienen mayor probabilidad de ocurrir cuando el esfuerzo es alto que cuando es bajo3.
En cuanto al principal, su utilidad sólo depende del resultado obtenido por el agente y del pago que debe hacerle. En general, al principal no le interesa el esfuerzo del agente; le interesan sus resultados. Su utilidad se representa entonces como B(x – w).
El punto de referencia es el caso en el que la acción del agente es verificable. Luego, se examina el caso de información asimétrica.
Información simétrica
En este escenario, el problema del principal se puede expresar como:
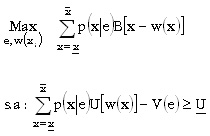
Suponiendo sólo dos resultados posibles
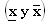
las condiciones de primer orden de este problema implican que
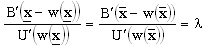
Con una pequeña transformación algebraica esto indica la igualdad entre las tasas marginales de sustitución del principal y del agente a una misma constante. Por ejemplo, si el principal es neutro al riesgo y el agente es averso al riesgo, el numerador de ambas fracciones de la expresión anterior es una constante, y para que se mantenga la igualdad, la utilidad marginal del agente debe ser igual en ambas. Como la función de utilidad es cuasicóncava, la única manera de que la utilidad marginal en dos puntos sea igual es que éstos sean el mismo punto, es decir, el salario debe ser constante. Por tanto, cuando el agente es averso al riesgo y el esfuerzo es verificable, el esquema de compensación óptimo es de salario fijo; es decir, el principal asume totalmente el riesgo. Sea w0 el salario del agente. Sustituyendo en la restricción del principal, con igualdad4:
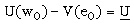
y se obtiene
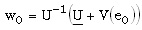
Puesto que
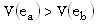
y el esfuerzo es verificable, el agente recibirá un salario mayor si se le pide que realice un esfuerzo alto que si se le pide un esfuerzo bajo5.
Siguiendo con el caso de dos resultados posibles 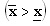 , esta situación puede representarse en una caja de Edgeworth, en la que las dimensiones corresponden a cada uno de los resultados posibles. La aversión al riesgo del agente se aprecia en la forma de sus curvas de indiferencia: un ingreso bajo seguro (en ambos estados) es preferido a un ingreso alto en uno solo de los posibles estados. De forma análoga, la neutralidad al riesgo del principal se refleja en curvas de indiferencia lineales que indican que le son indiferentes ingresos bajos seguros frente a ingresos altos en sólo uno de los estados.
, esta situación puede representarse en una caja de Edgeworth, en la que las dimensiones corresponden a cada uno de los resultados posibles. La aversión al riesgo del agente se aprecia en la forma de sus curvas de indiferencia: un ingreso bajo seguro (en ambos estados) es preferido a un ingreso alto en uno solo de los posibles estados. De forma análoga, la neutralidad al riesgo del principal se refleja en curvas de indiferencia lineales que indican que le son indiferentes ingresos bajos seguros frente a ingresos altos en sólo uno de los estados.
La gráfica 2 muestra que el agente está completamente asegurado: su pago es el mismo independientemente del resultado. Para el principal ocurre lo contrario: su pago depende del resultado alcanzado, pues en cualquier caso debe hacer el mismo desembolso por el salario del agente.
En caso de que el agente fuera neutro al riesgo y el principal averso, el principal se aseguraría totalmente mientras que el agente asumiría el riesgo, es decir, el contrato sería de tipo franquicia. Si ambas partes fueran neutrales al riesgo, su repartición dependería exclusivamente de las pendientes de las curvas de indiferencia, permitiendo infinitas soluciones o soluciones de esquina.
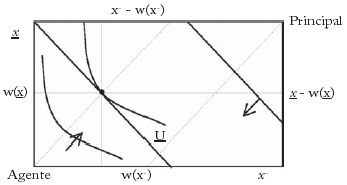
Para determinar el esfuerzo óptimo, se incluye el salario óptimo en el problema del principal. La solución de este problema en términos del esfuerzo, depende de los valores de las variables y de la forma específica de las funciones de utilidad6.
Información asimétrica
En esta situación, el esfuerzo del agente no es verificable. Es preciso aclarar que las asimetrías de información se refieren únicamente al comportamiento del agente, es decir, ambas partes conocen las funciones de pago, las distribuciones de probabilidad y los pagos de cada resultado.
La solución que se busca es un equilibrio bayesiano perfecto en subjuegos. Resolviendo por inducción hacia atrás, y teniendo en cuenta que el esfuerzo del agente no es observable y que éste decide en la última etapa cuánto esfuerzo realiza, si el principal desea cierto nivel de esfuerzo del agente debe darle incentivos, es decir, pagar al agente considerando los resultados obtenidos. Si el nivel de esfuerzo que desea es e, se debe satisfacer
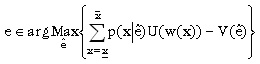
A esta condición se le conoce como restricción de compatibilidad de incentivos. Después de conocer el contrato, el agente decide si lo acepta o no; al igual que en el caso de información simétrica, esto se presenta por la restricción de participación:
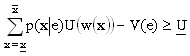
Teniendo en cuenta este par de restricciones, el problema del principal en el caso de información simétrica es de la forma:
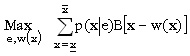
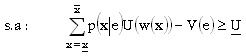
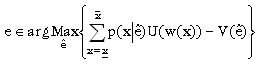 |
Como el agente sólo puede elegir entre dos niveles de esfuerzo {ea, eb}, es razonable pensar que implementar un nivel de esfuerzo bajo no presente inconvenientes. Puesto que con un salario fijo, el agente siempre elige el nivel de esfuerzo menor, el principal debe prever este comportamiento y ofrecerle el salario correspondiente al nivel de esfuerzo bajo, para que el agente acepte el contrato y ofrezca un esfuerzo bajo.
Los problemas aparecen cuando se desea que el agente ofrezca un esfuerzo alto. En este caso, la restricción de compatibilidad es de la forma:
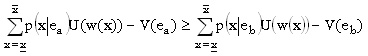
que también se puede expresar como:
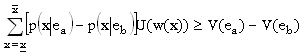
Por tanto, el problema del principal (neutro al riesgo) se puede representar mediante la siguiente expresión:
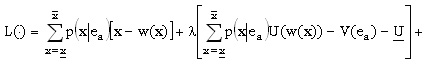
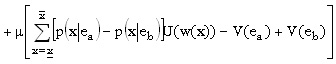
Las condiciones de Kuhn-Tucker establecen que
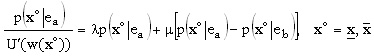
Para determinar la condición de igualdad o no de las restricciones es necesario analizar el comportamiento de los multiplicadores de Lagrange. Al sumar sobre los términos xo se obtiene:
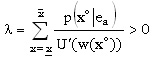
Siendo l > 0, la restricción de participación se satisface con igualdad. Escribiendo la condición de primer orden de la forma:
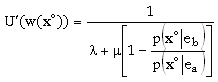
o, lo que es igual,
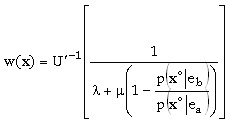
es claro que si m es igual a cero el salario del agente es fijo, pero como en ese caso elige el esfuerzo más bajo, m es mayor que cero y la restricción de compatibilidad de incentivos también se satisface con igualdad. Así, el salario depende de la relación entre las probabilidades de obtener cierto resultado condicionadas por el esfuerzo incorporado. A esta expresión
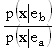
se le conoce como el cociente de verosimilitud. Para ver su importancia, fijemos un salario w0 constante, tal que
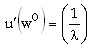
De acuerdo con la expresión anterior, resulta que
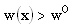 | si | 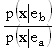 | < 1 |
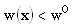 | si | 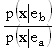 | > 1 |
Y la solución para el problema de diseño del contrato corresponde a lo que se esperaba intuitivamente; el principal debe involucrar el resultado en el pago del agente, de modo que le pague una mayor cantidad de dinero por aquellos resultados cuya ocurrencia es más probable con un esfuerzo alto que con uno bajo.
A continuación se presentan dos ejemplos que ilustran el funcionamiento de este modelo y que luego se utilizan en el análisis del experimento7.
Ejemplo 1
Un individuo (principal) contrata a un inversionista (agente) para que emplee su dinero ($10) en la actividad que juzgue conveniente a cambio de una remuneración. El inversionista debe elegir entre dos proyectos: el proyecto A tiene un costo de $10 y produce $30 con una probabilidad del 90% y $15 con una probabilidad del 10%. El proyecto B tiene un costo de $5 y produce $30 con una probabilidad del 40% y $15 con una probabilidad del 60%. El principal observa el resultado pero no sabe qué proyecto escogió el agente, y obtiene los beneficios del proyecto menos el pago que debe hacerle. Por su parte, el agente recibe la diferencia entre los $10 que le dio el principal y el costo del proyecto, más el pago que recibe del principal.
Supongamos, además, que si el principal decide no contratar al agente, el pago de cada uno es $2, igual que si el agente decide no aceptar el contrato que ofrece el principal. Por simplicidad, sólo se emplean enteros.
El objetivo es encontrar el esquema de compensación óptimo para el principal y la elección del agente en caso de que ambos sean neutros al riesgo. Esto significa que sus utilidades son lineales en la riqueza. Podemos empezar calculando la utilidad esperada del agente para cada una de sus dos posibles elecciones
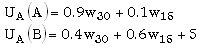
donde w30 y w15 son los salarios del agente por obtener los resultados 30 y 15, respectivamente. El número 5 que aparece a la derecha en la segunda ecuación corresponde al “ahorro” del agente por elegir la opción menos costosa. La restricción de compatibilidad de incentivos (RCI), cuando el principal desea implementar la opción A, requiere que la utilidad del agente por elegir A sea mayor que la de elegir B, es decir,
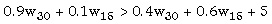 |
| o | 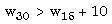 | (RCI) |
Por otro lado, la restricción de participación (RP) requiere que la utilidad esperada del agente por elegir A sea mayor que la utilidad de reserva; es decir,
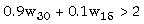 | (RP) |
Los dos enteros no negativos más pequeños que satisfacen este par de restricciones son w30 = 11 y w15 = 0. A esta solución se le conoce como “esquema de compensación óptimo”. Lo más notable es que cuando el principal ofrece este esquema de compensación, el agente acepta el contrato y elige A.
La ganancia esperada del principal es 18,6 y la del agente 9,9. La ganancia esperada total es de 28,5 igual a la que se obtendría si se eligiera A en forma centralizada.
Ejemplo 2
Consideremos ahora el ejemplo 1 modificando las probabilidades del proyecto A; ahora produce un resultado de $30 con una probabilidad del 70% y $15 con una probabilidad del 30%. La restricción de compatibilidad de incentivos es
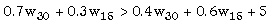 |
| o | 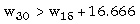 | (RCI) |
y la restricción de participación es
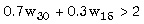 |
| o | 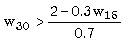 | (RP) |
Los dos enteros no negativos más pequeños que satisfacen estas restricciones son
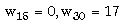
Al disminuir la probabilidad de éxito en el proyecto A, respecto del caso anterior, es necesario que el principal ofrezca un incentivo mayor ($17) para que el agente decida elegirlo. Sin embargo, es necesario calcular las utilidades esperadas del principal en ambos casos:
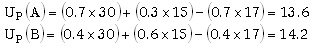
Es claro que con el esquema de compensación que incentiva al agente a elegir el proyecto A, la utilidad esperada es menor que la del proyecto B. Por esta razón, el principal no estará interesado en que se elija A, y sólo necesitará ofrecer un esquema de compensación que satisfaga únicamente la restricción de participación, pues la de compatibilidad de incentivos se tendría en sentido contrario. Un salario fijo de $3, independientemente del resultado, cumple estas condiciones y maximiza la utilidad esperada del principal.
Las conclusiones del modelo de riesgo moral, así como los ejemplos que presentamos, ilustran en forma coherente los resultados cualitativos que se esperarían “intuitivamente”. Sin embargo, uno de los logros de la teoría de contratos es que permite estimar no sólo las relaciones de orden entre diferentes esquemas de compensación sino también sus magnitudes. La comprobación empírica de estas predicciones requiere información que es difícil recoger y manipular; por ello ha quedado relegada y los principales resultados siguen derivándose de modelos teóricos. La economía experimental permite, en principio, superar esa limitación y abre nuevas áreas de investigación. Para comprobar empíricamente las predicciones del modelo de riesgo moral que acabamos de exponer, hicimos un experimento controlado que permitiera hacer extrapolaciones a fenómenos de riesgo moral fuera del laboratorio. En la siguiente sección se expone la metodología que empleamos para diseñar el experimento e ilustramos algunos conceptos básicos de la economía experimental.
DISEÑO EXPERIMENTAL Y RESULTADOS
Tradicionalmente se ha subrayado que la economía no es una ciencia experimental, que sus datos no provienen de muestreos y que no se puede pretender sacar conclusiones de acciones individuales en ambientes diferentes al de la realidad. No obstante, los desarrollos de la economía experimental en los últimos 35 años han permitido que los investigadores exploren temas que no era posible estudiar con las técnicas tradicionales8. Esto ha llevado a entender mejor las teorías existentes y a desarrollar otras nuevas, y a obtener resultados importantes, sobre todo con ayuda de la teoría de la elección, la teoría de juegos y sus aplicaciones a otros contextos.
Para algunos autores, son dos las principales ventajas de la economía experimental: la replicabilidad y el control (Davis y Holt, 1993; Hey, 1991). La primera se refiere a la posibilidad de reproducir el experimento y, así verificar los hallazgos en forma independiente. El control, a la capacidad para manejar las condiciones de laboratorio con el fin de evaluar teorías y políticas alternativas.
Dada una hipótesis que se desee contrastar, uno de los pasos más importantes es el diseño del experimento, en el que se usa el concepto de paralelismo: los individuos no necesariamente deben conocer el fenómeno económico que se estudia, sólo el experimento (conjunto de situaciones) en que se involucran, lo que puede “disfrazar” el objetivo del experimento aunque mantenga una estrecha relación con éste9.
En nuestro caso era necesario formar parejas en las que uno de los miembros actuara como principal y el otro como agente, sin que el principal pudiera controlar la acción del agente, y los resultados dependieran de una elección de este último y de factores aleatorios. El diseño del experimento y su paralelismo se describen a continuación:
1. Después de invitarlos con una semana de anticipación, algunos estudiantes universitarios se reunieron en dos grupos de quince personas en cada ronda, en salones separados10. Allí recibieron información escrita sobre el experimento y luego se “mezclaron” con los del otro grupo (para efectos prácticos, grupos 1 y A). Se les pidió que formaran parejas, con la única restricción de que un miembro del grupo 1 hiciera pareja con uno del grupo A. Llenaron un formato que recopilaba información personal para saber si se conocían (y en qué términos) antes del experimento. Después se pidió a los miembros del grupo 1 que volvieran al salón inicial. Allí, cada uno recibió instrucciones (de acuerdo con el grupo en el que estuviera) para participar en el juego principal-agente del ejemplo 1 (con pagos en miles de pesos colombianos)11.
2. Los miembros del grupo 1 serían los “principales” y los del grupo A, los “agentes”. A cada principal se le informaban las dos opciones de su compañero y luego debía enviar en un sobre un bono por valor de $10.000 (asignado por la organización del experimento) junto con un contrato que especificaba una remuneración para cada uno de los dos posibles resultados que obtendría su compañero ($15.000 o $30.000). En caso de que un principal decidiera no participar, el pago de cada miembro de la pareja sería de $2.000.
3. Después de llenados todos los sobres, se entregaban a sus parejas respectivas (reunidas en otra sala). Entonces, cada miembro del grupo A debía decidir si aceptaba o no el contrato; en caso de aceptarlo debía elegir una de dos urnas, de la que debía sacar una balota12. En la primera, tenía un costo de $10.000 y recibía $30.000 con una probabilidad del 90% o $15.000 con una probabilidad del 10% (nueve balotas ganadoras y una perdedora). En la segunda, el costo era de $5.000 y producía $30.000 con una probabilidad del 40% y $15.000 con una probabilidad del 60%13. El agente hacía su elección y los organizadores entregaban los premios. A cada principal se le entregaba lo que había exigido del agente sin informarle qué opción había elegido su compañero.
4. Cada experimento terminaba en ese punto. Pero, para analizar el impacto de la “experiencia” en la elaboración del contrato, cada principal tuvo la oportunidad de jugar nuevamente. Para esto se formó otro grupo de agentes con el que debían formar parejas e iniciar de nuevo el juego. Ningún principal sabía, antes de entregar su primer pago, que tendría la posibilidad de jugar nuevamente; así el comportamiento de la primera ronda no se veía influido por algún “plan de contingencia” para la segunda.
5. En un segundo experimento (con grupos diferentes) se siguió el mismo procedimiento, pero las probabilidades de la primera urna se cambiaron de 90%-10% a 70%-30%; es decir, el resultado favorable era más difícil de alcanzar.
Vale la pena señalar que, para permitir la replicabilidad, las instrucciones fueron leídas por los organizadores del experimento y entregadas por escrito a los participantes. Para dar una motivación suficiente a los sujetos experimentales todos los pagos fueron reales y, para hacer ajustes finales, se hicieron dos sesiones previas con personas que no participarían en el experimento.
RESULTADOS DEL EXPERIMENTO
Control
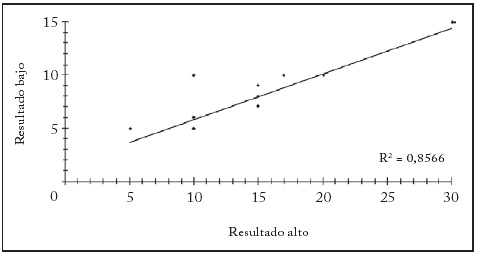
Es necesario evaluar el control que los investigadores ejercieron sobre el experimento. Para esto se tomó como variable de referencia el coeficiente de correlación entre las elecciones de los principales ante los dos resultados posibles. Si el experimento era claro para los jugadores, era de esperar que se ofreciera una mayor suma para el resultado de 30 que para el de 15. Es decir, que hubiese relación con la solución teórica del problema en la que interviene el coeficiente de verosimilitud antes mencionado. En la primera ronda de ambas sesiones, este coeficiente de correlación fue de alrededor 0,88, es decir, satisfactorio en cuanto a la comprensión del experimento por los principales y a su motivación para participar. Este resultado se observa en las gráficas 3a y 3b, en las que después de ordenar a los jugadores de menor a mayor según su oferta para el resultado B, se aprecia una estrecha relación entre las dos ofertas de cada jugador. Como era de esperar, la experiencia de los jugadores en la primera etapa modifica el diseño de su contrato en la segunda. En el primer experimento (con bajas probabilidades de fracaso) el coeficiente de correlación asciende hasta 0,96, mientras que en el segundo cae hasta 0,65.
Gráfica 3a
Correlación de pagos exigidos por los resultados alto y bajo.
Primer experimento
Gráfica 3b
Correlación de pagos exigidos por los resultados alto y bajo.
Segundo experimento
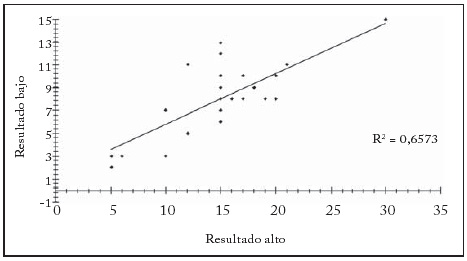
Esto último merece un análisis especial pues cuando las probabilidades de fracaso eran menores (experimento 1), los pagos ofrecidos para ambos resultados se redujeron respecto a los de la primera etapa, mientras que cuando las probabilidades de fracaso eran altas (experimento 2), los pagos ofrecidos se mantuvieron estables y redujeron su variabilidad frente a la primera ronda14. La reducción de la varianza de ambos pagos haría esperar un mayor coeficiente de correlación. Al no ser así, se evidencia una reducción notable de la covarianza entre ambos pagos, es decir, que mayores probabilidades de fracaso reducen la coherencia en el diseño de los contratos. Esto podría indicar diferentes actitudes frente al riesgo en el grupo de los principales.
En lo referente al control del comportamiento de los agentes, se estimó un modelo logit con la siguiente ecuación:
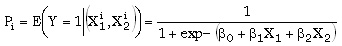
La variable dependiente (dicótoma) era 1 si el agente elegía la opción menos riesgosa (A) y cero en caso contrario (B); las dos variables independientes fueron los pagos que ofrecían los principales por el resultado alto y bajo, respectivamente. Los resultados, para un nivel de significancia de más del 98%, indican que si bien pagos ofrecidos más altos incrementan la probabilidad de que los agentes elijan la opción con baja probabilidad de fracaso, ese incremento no es demasiado alto, y que son más importantes los pagos por resultados bajos que por resultados altos15. Más adelante se presentan mayores detalles.
Resultados
Después de verificar el control que ejercieron los experimentadores, se puede extraer una primera conclusión a partir de los datos: la oportunidad de repetir el juego tiene mayor efecto sobre la reducción de la compensación que se ofrece en los contratos cuando la probabilidad de obtener un resultado desfavorable es baja que cuando es alta. En el cuadro 1 se observa que en el experimento 1 el salario que se ofrece por el resultado alto disminuye de la primera a la segunda etapa, mientras que en el experimento 2 aumenta. Es decir, en un entorno favorable, los principales advierten su posición dominante y, quizá a causa de los resultados satisfactorios de la primera etapa, exigen más de sus agentes (ofrecen un menor pago). Ocurre lo contrario cuando el entorno es menos favorable; los principales, “conscientes” de la dificultad, ofrecen contratos similares a los de la primera ronda. En resumen: bajas probabilidades de fracaso inducen a elegir la opción riesgosa, mientras que altas probabilidades de fracaso inducen a elegir la opción “segura”.
Al extrapolarlo, el resultado anterior puede tener consecuencias interesantes. Por ejemplo, en épocas de prosperidad, los ahorradores exigirán mayores retornos a las entidades financieras y éstas a los proyectos de inversión. La aversión al riesgo de los agentes, que se observa en el experimento cuando en la elección importa más la remuneración ante un mal resultado que ante uno favorable, lleva a que éstos empiecen a elegir opciones más riesgosas para asegurarse parte del retorno, poniendo en riesgo el capital de sus principales. En el contexto “fuera de laboratorio”, esto significa que a quienes se contrata para realizar ciertas labores elegirán acciones cada vez más riesgosas, lo cual por ley de los grandes números genera sucesivos resultados indeseables. Es decir, ocurre un fenómeno similar a las burbujas especulativas; condiciones iniciales favorables generan unas expectativas tales que su retroalimentación termina generando resultados esperados demasiado altos. En tales condiciones las partes que deben realizar una labor en pos de esos objetivos preferirán opciones poco costosas con altas probabilidades de fracaso que, como vimos, desatan crisis sucesivas. A causa del riesgo que asumen los agentes ante las “exigencias” de sus principales, las pérdidas generalizadas en la economía llevan a una contracción económica.
Resultados experimentales como los que obtuvimos no sólo evidencian el fenómeno de riesgo moral, sino que pueden ser cruciales para explicar su potencial para generar ciclos económicos a partir de comportamientos individuales en presencia de asimetrías de información, a diferencia de lo que postulan algunos economistas como Caballero, Engel y Haltiwanger (1997).
Examinemos ahora el comportamiento de los principales desde el punto de vista del diseño del contrato. Los esquemas de compensación óptimos (tomados de los ejemplos 1 y 2), y los promedios calculados en la primera y segunda ronda de cada experimento aparecen en el siguiente cuadro.
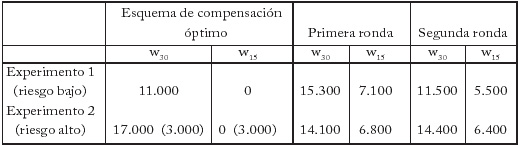
De la primera a la segunda ronda de ambos experimentos w30 se “mueve” en la dirección que prevé la teoría, es decir, hay evidencia de que los principales aprenden del primer resultado y en su segundo intento se acercan a la solución teórica. En cuanto al pago que se ofrece por el resultado bajo, los datos muestran una gran similitud con los que se obtienen en experimentos de juegos de negociación, en particular el juego del ultimátum, aunque en nuestro experimento no hubo negociación explícita entre las partes.
En un juego de negociación, dos agentes deben decidir cómo repartirse una suma teniendo en cuenta que si no llegan a un acuerdo cada uno recibe una cantidad predeterminada (por lo general cero). Estos juegos se pueden clasificar según si se permite o no la comunicación. En los experimentos sin barreras a la comunicación, los resultados son eficientes y, casi en su totalidad, simétricos (Hoffman y Spitzer, 1982 y 1985). Pero cuando la comunicación es restringida y el juego se estructura de modo que en una primera etapa uno de los jugadores debe hacer una oferta al otro, que a su vez decide si la acepta (y se efectúa la repartición) o no (y el pago de cada uno es cero), los resultados varían con respecto al caso anterior y van en dirección diferente a la que indica la teoría. Según esta, el jugador 1 podría reclamar el 99% del dinero, y el otro debería aceptar, pues el 1% es preferible a nada. Sin embargo, la evidencia experimental muestra que las ofertas del jugador 1 oscilan alrededor de una repartición 70%-30% y que aún así, solo en el 20% de los casos no hay acuerdo (Guth, Schmittberger y Schwarz, 1982). Son diversas las explicaciones: desde el cuestionamiento de la teoría de juegos como herramienta con capacidad de predicción (en particular el concepto de equilibrio de Nash perfecto en subjuegos) hasta las propuestas de una “teoría del comportamiento de justicia distributiva”.
Volviendo al experimento, cabe señalar que la diferencia entre el pago observado por el resultado bajo y el que indica la teoría (cero) lleva a conjeturas similares a las del juego del ultimátum. Una explicación (bastante intuitiva) sería que los jugadores “tratan de ser justos”. Pero los resultados de otra serie de experimentos (Ochs y Roth, 1989) muestran que cuando el juego del ultimátum se transforma en uno de dictador (donde un jugador decide cómo debe ser la repartición y el otro no puede decidir nada), los resultados son reparticiones menos “altruistas”. Como en la función de utilidad de cada jugador se incluyen criterios distributivos, se puede entender que en el juego del ultimátum los jugadores del grupo 1 obran con este criterio cuando eligen su estrategia. En nuestro experimento, los principales posiblemente tienen una creencia similar y por ello ofrecen una cantidad positiva a su compañero aun en caso de que se produzca el resultado indeseable. Hay que profundizar más: la evidencia experimental no indica que los principales jueguen en forma altruista ofreciendo cerca de $6.000 por el resultado bajo y no cero como indica la teoría, sino que, partiendo de que la función de utilidad de su pareja consta por lo menos de dos parámetros, riqueza y participación en los beneficios, tratan de incentivar su buen comportamiento (no rechazar el contrato) haciéndole esa oferta.
Antes dijimos que en el juego del ultimátum las ofertas para el segundo jugador oscilaban alrededor del 30%. En el nuestro, esto equivaldría a $4.500, una diferencia de 10 puntos porcentuales mayor que podría ser explicada por la comunicación entre las parejas en el momento de depositar su información personal16, y a que algunos se conocían previamente. El porcentaje de casos que terminó en desacuerdo fue despreciable.
Las principales conclusiones del experimento son las siguientes:
1. Los principales ajustan su comportamiento a medida que ganan experiencia. Los hallazgos de este experimento son conformes con los de la generalidad de los experimentos reseñados en la literatura17.
2. El “ajuste” del comportamiento de los principales va en la dirección que indica la teoría para el resultado alto.
3. El pago que se ofrece por el resultado bajo evidencia que en las funciones de utilidad subjetivas de los agentes intervienen aspectos diferentes del pago monetario; uno de ellos puede ser la participación de los beneficios propios en el total. Parece ser que la hipótesis de altruismo se podría descartar, no así la de aversión al riesgo.
4. Al decidir qué opción deben tomar, los agentes dan mayor importancia al pago por el resultado bajo que por el resultado alto. Pero el impacto de tales pagos sobre la decisión es pequeño.
5. No se encuentra evidencia en favor del contrato óptimo cuando se quiere inducir un esfuerzo bajo. El papel de los pagos altos, que ocurren con mayor probabilidad cuando el esfuerzo es alto, produce equilibrios focales.
6. Escenarios favorables (con menores probabilidades de fracaso) son más propensos a problemas de riesgo moral que los de mayores dificultades.
7. Las soluciones numéricas que ofrece la teoría seguirán siendo aproximaciones parciales a fenómenos reales hasta tanto las funciones objetivo no se especifiquen adecuadamente18.
COMENTARIOS FINALES
La influencia del riesgo moral sobre los resultados económicos se puede extrapolar a diversos contextos para explorar sus implicaciones.
El modelo de financiamiento del crédito de Stiglitz y Weiss (1981), pionero en esa área, incluye inversionistas que compiten por recursos. El banco es el principal y el inversionista el agente; éste puede invertir como desee los recursos que le presta el banco con el único compromiso de pagar la tasa de interés pactada. La principal conclusión es que cuando la tasa de interés sobrepasa cierto nivel, el inversionista elige siempre la opción de mayor riesgo. Conclusiones como esta explican la asignación de recursos a actividades ilícitas, donde si bien las ganancias en caso de éxito son muy altas, también lo es el riesgo.
Haciendo una analogía con el trabajo de Gutiérrez et al. (2001) se puede reinterpretar el modelo de financiamiento del crédito equiparando la necesidad de conseguir votos para un cargo público a la de un empresario para conseguir la financiación de un proyecto. El banco que busca proyectos para financiar se comporta de manera similar al elector que busca un candidato por quien votar. Limitando el análisis a la forma de financiación del programa de gobierno, la información asimétrica consiste en que los electores no saben cómo se llevará a cabo. Partiendo de que ambas partes conocen los riesgos y beneficios (presentes y futuros) de cada forma de financiación, el mayor nivel de exigencia de la sociedad al gobierno lleva a que éste se financie en forma ineficiente desde el punto de vista social.
Como se dijo en la introducción, la crisis asiática se podría explicar de la misma manera19. En períodos de auge, las condiciones de la economía inducen a buscar mayores rendimientos de las inversiones, hasta que estos sólo se alcanzan en proyectos de alto riesgo. Hay un aspecto que relaciona las crisis financieras con los resultados del experimento. Establecimos que el hecho de que el principal exija retribuciones demasiado altas es el factor que genera riesgo moral; en entornos favorables y con competencia entre principales, los agentes (para el efecto, entidades financieras) se podrían ver incentivados a ofrecer tales retribuciones. Los principales (los ahorradores, en este caso) atraídos por sus ofrecimientos firman el contrato, y los agentes se ven obligados a elegir opciones riesgosas de colocación de cartera. Así, la oferta de rendimientos excepcionales en el sistema financiero u otro tipo de “premios” que atraigan ahorradores en entornos macroeconómicos favorables indica la posibilidad de que los recursos se destinarán a proyectos riesgosos.
En cuanto al análisis del experimento, cabe señalar la necesidad de elaborar otros similares para estudiar cuidadosamente aspectos como el altruismo y la aversión al riesgo. El experimento se hizo con una muestra relativamente pequeña (alrededor de 120 jugadores); con muestras más grandes y en diferentes contextos se pueden obtener resultados más robustos. También es necesario analizar comportamientos en juegos repetidos y en donde se alterne el anonimato de los jugadores con la posibilidad de ser reconocidos, pues esto20 suele modificar los resultados. Por último, es necesario ser prudente en la interpretación de los resultados hasta tanto no se obtengan otros en entornos diferentes y con variaciones en condiciones controladas.
NOTAS AL PIE
1. Esta investigación fue motivada por el artículo de Gutiérrez et al. (2001) sobre economía política y finanzas públicas, cuyo objetivo es “destacar los factores político-institucionales que influyen en los niveles de deuda pública y de déficit fiscal en países y entidades subnacionales con economías similares [...]”. Allí se argumenta que las diferencias en los niveles de deuda pública entre países se deben principalmente a factores institucionales. Emplean un modelo de principal-agente en el que los electores son el principal y los gobernantes el agente, y éste debe actuar de manera óptima desde el punto de vista de sus electores. Sostienen que las diferencias en los niveles de deuda pública obedecen a la asimetría de información, y para contrastar las predicciones con la evidencia recurren a la recolección directa de datos debido a la dificultad para usar información que revele el comportamiento de los agentes y principales. Pensamos que su empleo de las herramientas de teoría de contratos, teoría de juegos y lo que llaman economía experimental no fue adecuado y, por ello, llegaron a resultados ambiguos. Ver, para más detalles, Arévalo y Ojeda (2001).
2. Hay otra clase de problemas de información asimétrica que se conoce como selección adversa: situaciones en las que, antes de firmar el contrato, el agente tiene información privada que el principal estaría interesado en conocer. Los modelos de señalización buscan mitigar las asimetrías de información mediante la “comunicación” de señales del agente al principal.
3. El uso de sumatorias supone un conjunto finito de posibles resultados.
4. Si no hubiese igualdad el agente estaría interesado en pagar por firmar el contrato y el principal podría cobrarle en cualquier resultado, lo que equivaldría a reducir el salario.
5. Si el agente es también neutro al riesgo, las condiciones de primer orden se cumplen en cualquier esquema de compensación: todo w (p) es óptimo.
6. Para un análisis detallado, ver Macho-Stadler et al. (1992).
7. Para otros ejemplos con diferentes actitudes de los jugadores frente al riesgo, ver Gardner (1995).
8. Un reconocimiento a la importancia de la economía experimental fue el premio Nobel que se concedió a Vernon Smith en 2002, por sus aportes a esta área, y a Daniel Kahneman por su esfuerzo para integrar elementos de la sicología al análisis económico.
9. Ilustremos esta idea con un conocido ejemplo sobre la hipótesis del free rider en la provisión de bienes públicos (Roth, 1995a). Se reúne a cuatro individuos (sujetos experimentales) que deben aportar una suma de 0 a 20 unidades monetarias (asignadas por los organizadores del experimento). Al dar las instrucciones no es necesario explicar a los sujetos el problema del bien público; basta decirles que la suma de los aportes de todos ellos será multiplicada, por ejemplo, por 2 (cuyo resultado cumple el papel del bien público), y repartida entre todos. Es decir, se crea un paralelismo entre el producto final de los aportes y el bien público. Seguramente los sujetos nunca supieron que el experimento estaba relacionado con la provisión de bienes públicos, pero es probable que actúen de forma similar al caso de tal fenómeno.
10. Los participantes eran estudiantes de los primeros semestres de Economía y de Finanzas, Gobierno y Relaciones Internacionales de la Universidad Externado de Colombia.
11. En la fecha del experimento, la tasa de cambio era de $2.800 pesos por dólar.
12. Si el agente no aceptaba el contrato, cada miembro de la pareja recibiría $2.000.
13. Para que no hubiera sesgos debidos a la numeración de las urnas, se les presentaron a los sujetos como urna R y urna B.
14. La desviación estándar de los contratos ofrecidos en el experimento con mayores probabilidades de fracaso se redujo casi un 50% entre la primera y la segunda ronda.
15. La ecuación se estimó incluyendo a todos los participantes; es decir, más de 60 observaciones.
16. Aunque en ese momento los sujetos no sabían en qué consistía el experimento.
17. Ver, también, Roth (1995b).
18. Para una revisión de los trabajos en esta dirección, ver Gintis (2000, cap. 11).
19. Para un análisis informal de esta afirmación, ver Krugman (1999).
20. Tampoco cabe descartar la posibilidad de que particularidades culturales de los sujetos del experimento (estudiantes universitarios colombianos de clase media) hayan influido en los resultados.
REFERENCIAS BIBLIOGRÁFICAS
1. Arévalo J. y J. Ojeda. “Economía política y finanzas públicas: una revisión metodológica”, Universidad Externado de Colombia, policopiado, 2001.
2. Caballero, R.; E. Engel y J. Haltiwanger. “Aggregate Employment Dynamics: Building from Microeconomic Evidence”, American Economic Review 87, 1, marzo, 1997, pp. 115-137.
3. Chiappori, P. A. y B. Salanié. “Testing for Asymmetric Information in Insurance Markets”, Journal of Political Economy 108, 1, 2000, pp. 56-78.
4. Davis, D. y C. Holt. Experimental Economics, Princeton, Princeton University Press, 1993. [ Links ]
5. Gardner, R. Juegos para empresarios y economistas, Barcelona, Antoni Bosch Editor, 1995. [ Links ]
6. Gintis, H. Game Theory Evolving, Princeton, NJ, Princeton University Press, 2000. [ Links ]
7. Guth, W.; R. Schmittberger y B. Schwarz. “An experimental Analysis of Ultimatum Bargaining”, Journal of Economic Behavior and Organization 3, 1982, pp. 367-388.
8. Gutiérrez, J.; C. Guzmán y U. Jiménez. “Economía política y finanzas públicas: teoría, evidencia y resultados de laboratorio”, Revista de Economía Institucional 3, 2000, Universidad Externado de Colombia.
9. Hey, J. Experiments in Economics, 1991, Oxford, Basil Blackwell. Traducción al español del Fondo de Cultura Económica, 1996.
10. Hillier, B. The Economics of Asymmetric Information, Londres, Mc Millan Press, 1997. [ Links ]
11. Hoffman, E. y M. L. Spitzer. “The Coase Theorem Some Experimental Tests”, Journal of Law and Economics 25, 1982, pp. 73-98.
12. Hoffman, E. y M. L. Spitzer. “Entitlements, Rights and Fairness: An Experimental Examination of Subjects Concepts of Distributive Justice”, Journal of Legal Studies 14, 2, 1985, pp. 259-297.
13. Kagel, J. y A. Roth, eds. The Handbook of Experimental Economics, Princeton University Press, 1995. [ Links ]
14. Krugman, P. De vuelta a la economía de la Gran Depresión, Bogotá, Grupo Editorial Norma, 1999. [ Links ]
15. Laffont, J. J.; H. Ossard y Q. Voung. “Econometrics of First-Price Auctions”, Econometrica 63, 4, julio, 1995, pp. 953-980.
16. Macho-Stadler, I. y D. Pérez-Castrillo. Introducción a la economía de la información, Barcelona, Editorial Ariel, 1994. [ Links ]
17. Mas-Colell, A.; M. Whinston y J. Green. Microeconomic Theory, Nueva York, Oxford University Press, 1995. [ Links ]
18. Ochs, J. y A. Roth. “An Experimental Study of Sequential Bargaining”, American Economic Review 79, 1989, pp. 355-384.
19. Roth, A. “Introduction to Experimental Economics”, J. Kagel y A. Roth, eds., The Handbook of Experimental Economics, Princeton, Princeton University Press, 1995a.
20. Roth, A. “Bargaining Experiments”, J. Kagel y A. Roth, eds., The Handbook of Experimental Economics, Princeton, Princeton University Press, 1995b.
21. Stiglitz J. y A. Weiss. “Credit Rationing in Markets with Imperfect Information”, American Economic Review 71, 1981, p. 393.
22. Smith, A. La Riqueza de las Naciones, [1776], Madrid, Alianza Editorial,1994. [ Links ]














