Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en
SciELO
Similares en
SciELO -
 Similares en Google
Similares en Google
Compartir
Revista de Economía Institucional
versión impresa ISSN 0124-5996
Rev.econ.inst. vol.15 no.29 Bogotá jul./dic. 2013
LA POBREZA EN COLOMBIA,2001-2005. CURVAS GLOBALES, DOMINANCIA Y ASPECTOS INFERENCIALES
INFERENTIALS ASPECTS OF THE DOMINANCE IN POVERTY THROUGH GLOBAL CURVES AND THEIR EVOLUTION IN COLOMBIA (2001-2005)
María Margarita Bahamón*
Juana Domínguez**
José Javier Núñez***
*Doctora en Economía, consultor independiente, Bogotá, Colombia, [ Margarita.bahamon@gmail.com].
**Doctora en Economía, profesor titular, Universidad de Alcalá de Henares, España, [josej.nunez@uah.es].
***Doctor en Economía, profesor titular, Escuela Universitaria Universidad de Alcalá de Henares, España, [juana.dominguez@uah.es].
Fecha de recepción: 17 de febrero de 2012, fecha de modificación: 13 de septiembre de 2012, fecha de aceptación: 22 de octubre de 2013.
RESUMEN
Este artículo propone un método para analizar la pobreza mediante curvas TIP/IID. Analiza la dominancia estocástica de primero y segundo órdenes entre las curvas, incluyendo sus aspectos inferenciales, y propone un contraste de hipótesis adecuado. Empleando datos de la Encuesta Continua de Hogares de 2001 a 2005 demuestra que la pobreza en Colombia no depende de errores de las muestras sino que corresponde a las variaciones registradas en esos años.
[Palabras clave: pobreza, curvas TIPs/IID, dominancia, inferencia estocástica, encuesta continua de hogares; JEL: I32, C10, O54]
ABSTRACT
In this article, the methodology to analyze the poverty in Colombia using the TIPs/IID curves is explored. In addition, the stochastic dominance of first and second order in curve studies is analyzed, including its inferencial aspects, and a suitable contrast of hypothesis is proposed. For this we used the data of the Colombian survey Encuesta Continua de Hogares for the period 2001-2005. The results show that poverty in Colombia does not depend on the errors in the samples; it corresponds to variations in poverty experienced in those years.
[Key words: poverty, TIPs/IID curves, dominance, stochastic inference; JEL: I32, C10, O54]
La pobreza se puede medir según su dimensión: pobreza estática y pobreza dinámica. En el primer caso se mide su incidencia, su intensidad y las desigualdades. En el segundo se incluye el tiempo como elemento adicional. Este trabajo intenta hacer ordenaciones de pobreza, bien sea mediante un rango de líneas de pobreza o un tipo de medidas o curvas globales que incluyen toda la información sobre la posición de un grupo o sector de la población en la distribución del ingreso.
Igual que en el estudio de las desigualdades en la distribución del ingreso, para describir las diferencias entre distribuciones de ingreso y la posible relación de dominancia entre ellas se usan métodos gráficos, como las funciones de distribución o las curvas de Lorenz, sencillas o generalizadas. Para examinar las relaciones de pobreza entre dos distribuciones de ingresos, Jenkins y Lambert (1997 y 1998) proponen un instrumento gráfico de fácil aplicación y de suma utilidad: las curvas TIP, que representan en forma concisa y simultánea las tres dimensiones de la pobreza: incidencia, intensidad y desigualdad1. En este artículo se estudia la pobreza estática en Colombia empleando curvas TIP/IID; para lo cual se analizan las relaciones de dominancia entre ellas y se adapta y aplica un estadístico que evalúa las relaciones de dominancia entre curvas de Lorenz.
En general, los trabajos que estudian la pobreza en el país se centran en su incidencia, como los de May (1996), Millán (2004) y el CID (2006). Otros exploran sus causas, como los de Núñez y Ramírez (2002), Guevara (2005), López y Núñez (2007) y Núñez et al. (2007). En este artículo proponemos usar curvas TIP/IID para valorar la pobreza en forma global (en sus tres dimensiones) y adaptar contrastes de hipótesis apropiados para tener en cuenta los aspectos inferenciales inherentes al uso de muestras.
La primera sección presenta el marco teórico; en la segunda se expone la manera de construir las curvas TIP/IID. La tercera sección detalla la inferencia estadística de la dominancia de la pobreza. En las dos siguientes se describen los datos utilizados, se analizan los resultados y se sintetizan las conclusiones.
MARCO TEÓRICO
Para comparar el grado de pobreza de dos poblaciones se debe hacer una clara distinción entre los dos aspectos fundamentales de su medición: la identificación de los pobres y las medidas de agregación. En general, hay mucha incertidumbre sobre el nivel apropiado del umbral de pobreza (z). Por ello conviene trabajar con un rango Z de líneas de pobreza que aumenta las posibilidades de comparación. Aquí se usan los postulados de la teoría de la dominancia estocástica, de primero y segundo órdenes2.
Ahamdanech y García (2007) ofrecen una descripción de la dominancia. Sean x = (x(1), x(2),..., x(I),..., x(N))' la distribución de ingresos que reciben N hogares o personas, I = {1,2,..., N}l el conjunto de hogares y T el conjunto de distribuciones alternativas de ingresos que podrían conseguir los N hogares dados los recursos de la sociedad, T ⊂ Rn . Sin perder generalidad se supone que el vector de ingresos ordenados es X = (x1, x2,..., x)'X, donde x ≤ x... ≤ xN.
La función de bienestar social w se define como w: T → R. Se usan funciones de bienestar W simétricas que cumplen el principio de anonimato, es decir que lo importante es el orden dentro del vector de ingresos y no qué hogar recibe y qué tanto, de modo que w(x) = W(X), ∀ w ∈ W. Los principios de anonimato y de Pareto (este implica que la función de bienestar social es creciente en los ingresos) llevan al criterio de dominancia por rangos:
![]()
el cual, de acuerdo con Saposnik (1981 y 1983), equivale a:
![]()
y lleva al siguiente resultado:
Teorema 1 (Saposnik): Si Wp es el conjunto de las funciones de bienestar social crecientes y simétricas, entonces:
![]()
En consecuencia:
![]()
Foster y Shorrocks (1988a, 1988b) obtienen la relación de dominancia de primer orden en pobreza, que corresponde al criterio de eficiencia, mediante el siguiente resultado:
Corolario 2 (Foster y Shorrocks): Si la proporción de pobres se define como H = q/N, donde q es el número de individuos u hogares pobres y N la población, entonces:
![]()
Por tanto, al considerar una línea de pobreza z ∈ Z, la distribución de ingresos x domina en primer orden a la distribución y, para esa línea de pobreza, y cualquier otra debajo de ella, si H es mayor o igual en la distribución y que en la distribución x.
Pero el criterio de dominancia por rangos no tiene en cuenta la desigualdad de ingresos entre hogares. Si se transfieren ingresos de un individuo más rico a uno más pobre debe aumentar la igualdad. Esto equivale a decir que la distribución cumple el principio de transferencia Pigou-Dalton, según el cual la desigualdad disminuye cuando hay una transferencia progresiva, manteniendo la ordenación original (Ruiz, 2007), o a suponer que la función de bienestar social es S-cóncava (Dasgupta et al., 1973)3.
Por otro lado, las ordenadas de la curva de Lorenz para un vector de ingresos x son:
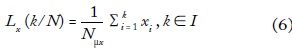
y la relación de dominancia está dada por la siguiente definición: el vector de ingresos x domina al vector de ingresos y (x ≥L y) si:
![]()
Atkinson (1970) desarrolla el concepto de dominancia de segundo orden introduciendo el criterio de igualdad, y demuestra que si µ = µy y las curvas de Lorenz no se cruzan, la dominancia de segundo orden es equivalente a la dominancia de Lorenz, y esto equivale al uso de funciones de bienestar S-cóncavas y simétricas.
Shorrocks (1983) extiende el teorema de Atkinson al caso donde µx ≠ µy, introduciendo la curva de Lorenz generalizada para tener en cuenta las diferencias de ingresos y la desigualdad del ingreso:
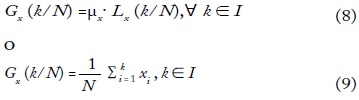
Esta curva es continua, convexa y no decreciente en el intervalo. Además, Gx (0) = 0 y Gx (1) = µx. La altura de la curva de Lorenz generalizada refleja los niveles de ingresos mientras que su curvatura indica el grado de desigualdad de los ingresos.
El criterio de dominancia generalizada con esta curva de Lorenz (x ≥GL y) es:
![]()
La dominancia equivale a un mayor bienestar para todas las funciones de bienestar S-cóncavas y crecientes. Shorrocks (1983) demostró que:
Teorema 2 (Shorrocks): Si Wpe es el de las funciones de bienestar S-cóncavas y crecientes, entonces:
![]()
Foster y Shorrocks (1988a) establecieron la relación de dominancia de segundo orden a partir de la familia de medidas de pobreza pα definida como:
![]()
y demostraron que:
![]()
Además la ordenación de pobreza de P está relacionada con la curva
![]()
El caso de µx = µy requiere especial atención pues en estas circunstancias las ordenaciones mediante la curva de Lorenz generalizada (GL)coinciden con la ordenación mediante la curva de Lorenz (L) realizada por Atkinson (1970).
Siguiendo a Atkinson y adoptando las funciones de bienestar Wpe se tiene que la ordenación de bienestar no solo implica la ordenación en desigualdad sino también las ordenaciones en pobreza basadas en P2.
Por su parte, Bishop et al. (1989) demuestran que:
![]()
Bishop et al. (1991) establecen la relación entre dominancia de primery segundo orden de la siguiente manera:
![]()
Una vez establecidas las relaciones de los órdenes de dominancia entre las curvas podemos establecer dicha relación para nuestro caso de estudio.
LAS CURVAS TIP/IID
Las curvas se construyen con base en la distribución de los déficits de pobreza en la población. Con la ventaja de que se pueden usar para hacer comparaciones en el tiempo, entre regiones, países y hogares o subgrupos con características diferentes, además de que generan ordenaciones de pobreza consistentes con las que se obtendrían con una amplia gama de índices y umbrales de pobreza, como señalan Gradin y del Río (2001).
Sea X = (x1, x2,..., xN) la distribución de los ingresos que reciben N hogares o personas ordenados en forma ascendente -de modo que 0 < x1 ≤ x2 ≤... ≤ xN la línea de pobreza. Además, sea gx el vector de brechas o déficits de pobreza asociado a los ingresos X y a la línea de pobreza z, donde el déficit de cada hogar i es:
![]()
Y sea bx el vector asociado a los ingresos básicos o censurados4:
![]()
De modo que, dado el valor de z, se pueden definir muchos índices de pobreza en función de gi o de bi. También se pueden definir las brechas normalizadas:
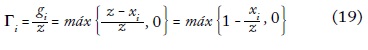
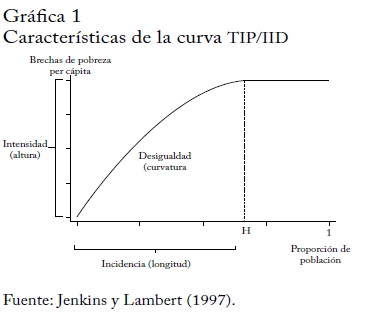
La representación de las brechas de pobreza acumuladas per cápita contra el porcentaje de hogares correspondiente, ordenados de menor a mayor ingreso, da lugar a la curva TIP/IID (gráfica 1).
La curva de brechas de pobreza, TIP(g; p), representa la suma acumulada de los primeros 100 • p valores de la brecha dividida por el total de individuos, donde p = k / N, ∀ k ∈ I y 0 ≤ p ≤ 1. Esta curva es una función cóncava, no decreciente, que aumenta en función de p, de modo que:
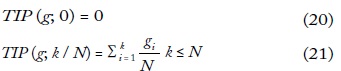
En la gráfica 1 se observa que la curva es constante a partir de H = q/N,de modo que solo se hace referencia a los pobres y no tiene en cuenta a quienes están por encima de la línea de pobreza. La curva muestra la incidencia a través de la longitud, en el punto donde es paralela al eje x, y la abscisa coincide con el porcentaje de pobres. La altura (eje y) mide la intensidad de las brechas de pobreza. La desigualdad corresponde a la curvatura porque la pendiente corresponde a la brecha de pobreza asociada a cada percentil.
Los déficits de pobreza también se pueden expresar en forma normalizada, con lo que se obtienen curvas TIP/IID normalizadas, TIP (Γ;p), con características similares a las de las curvas sin normalizar.
Como ya se dijo, la representación mediante curvas permite comparar distintas distribuciones de ingreso, aunque para entender los resultados es necesario definir la relación de pobreza en términos de dominancia. En este caso, la curva dominante (superior) que no corte a la dominada (inferior) revela que su distribución incluye más pobreza que la dominada. Según Jenkins y Lambert (1998), se pueden presentar dos situaciones: que las dos curvas tengan una línea de pobreza común y que cada distribución de ingresos tenga una línea de pobreza distinta.
LÍNEA DE POBREZA COMÚN
Dada una línea de pobreza z, sea P el tipo de índices de pobreza, definido sobre los déficits de pobreza agregados, gx, tales que, dada la línea de pobreza z, son funciones crecientes, invariantes ante réplicas y S-convexas. Un índice de pobreza de este tipo se denota por P (X|z). Sea Q el tipo de índice de pobreza, definido sobre los déficits de pobreza normalizados, γx, tales que, dada la línea de pobreza z, son funciones crecientes, invariantes ante réplicas y S-convexas. Un índice de pobreza de este tipo se representa como Q (X|z). Es evidente que Q ⊆ P. Así, se
encuentran criterios compatibles con los órdenes de pobreza unánimes inducidos por la clase P, aplicables a un conjunto de líneas de pobreza asociadas a las distribuciones objeto de estudio. De esta forma dan un salto cualitativo en las técnicas de medición de la pobreza existentes, resumiendo en una sola estimación lo que hasta ahora se traducía en múltiples cálculos utilizando diversos índices y líneas de pobreza alternativas (del Río y Ruiz, 1998, 5).
Teorema 4 ( Jenkins y Lambert, 1998). Dadas dos distribuciones de ingresos X e Y con una línea común de pobreza z, el que gy domine a gx según el criterio de las curvas TIP/IID es una condición necesaria y suficiente para garantizar que p(X|z') ≤ p(Y|z') para todas las líneas de pobreza z ≤ z' y para todos las medidas de pobreza.
Si tenemos una línea de pobreza z y dos distribuciones de ingresos X, Y, la no intercepción de las curvas TIP/IID resultantes equivale a una ordenación unánime de pobreza para todos los índices P y todas las líneas menores e iguales a z. Esto significa que una vez se encuentra una relación de dominancia a partir de una línea absoluta común, no se necesita comparar ambas distribuciones con líneas de pobreza menores (del Río y Ruiz, 1999).
Jenkins y Lambert encuentran, además, que hay una relación estrecha entre las ordenaciones de dominancia según el criterio de las curvas TIP/IID y las ordenaciones derivadas de la relación de dominancia entre curvas de Lorenz generalizadas que expresan mediante el teorema 5.
Teorema 5 ( Jenkins y Lambert, 1998). X domina a Y según el criterio de las curvas de Lorenz generalizadas si y solo si para todas las líneas de pobreza comunes posibles z, gy domina a gx según el criterio de las curvas TIP/IID. Por otra parte, esta dominación en el sentido de Lorenz ocurre cuando los ingresos son censurados sobre z+ si y solo si gy domina a gx según el criterio de las curvas TIP/IID para todas las líneas de pobreza z ≤ z+.
Para comparar distribuciones de ingresos, el enfoque de la dominancia según el criterio de las curvas TIP/IID se puede extender al caso en que las líneas de pobreza son distintas, con umbrales de pobreza diferentes.
LÍNEAS DE POBREZA DISTINTAS
Incluir diferentes líneas de pobreza permite ganar robustez en los test de dominancia, ya que se flexibiliza la relatividad que pueden tolerar las líneas de pobreza ( Jenkins y Lambert 1998). En este caso, los resultados obtenidos proceden de aplicar el enfoque de la dominancia a las distribuciones de las brechas normalizadas en lugar de las distribuciones de las brechas de pobreza absolutas.
Teorema 6 ( Jenkins y Lambert, 1998). Sean X e Y dos distribuciones de ingresos con líneas de pobreza zx, zy. La dominancia de la distribución de la brecha de pobreza normalizada (Yy) sobre la distribución de la brecha de pobreza normalizada (Yx ) es una condición necesaria y suficiente para garantizar que Q(X|k • z) ≤ Q(Y|k • zy) para todos los k ∈ [0,1] y todas las medidas de pobreza Q ∈ Q.
Si las curvas TIP/IID normalizadas no se interceptan la situación equivale a ordenar unánimemente las ordenaciones de pobreza para todos los índices generalizados Q y sus subclases, así como para las líneas de pobreza zx, zy e incluso menores, pero a condición de que se mantenga la misma relación entre ellas.
Aunque las curvas TIP/IID son un instrumento útil y de fácil uso, su aplicación empírica no es muy extendida5.
INFERENCIA ESTADÍSTICA DE LA DOMINANCIA EN POBREZA
Hasta ahora se ha hecho referencia a las relaciones de dominancia, existentes entre las curvas de Lorenz, de primer y segundo orden, que pueden existir entre dos distribuciones de ingresos. Tales relaciones son válidas cuando las curvas no se cruzan. Si se cruzan no se pueden aplicar los conceptos de dominancia estocástica mencionados y es necesario definir si son significativos o no.
Beach y Davidson (1983) definen las pruebas necesarias para comparar distribuciones mediante las curvas de Lorenz. Se pueden hacer dos tipos de comparaciones: el primero consiste en comparar las distribuciones con respecto a un valor determinado; el segundo, en comparar muestras independientes, con su propio tamaño de muestra, para determinar la relación entre esas distribuciones. Para comparar y contrastar la igualdad de las medias de dos muestras independientes, Bishop et al. (1989) sugieren comparar pares de ordenadas de las curvas de Lorenz y de Lorenz generalizadas.
En general, cuando se trata de comparar dos distribuciones independientes, de periodos, regiones o grupos demográficos cuyos tamaños son Ny N, se supone que cada distribución se caracteriza por un conjunto de K cuantiles tales que ψ^1 = (ψ^11, ψ^12... ψ^1K)' y ψ^2 = (ψ^21, ψ^22... ψ2k^)'. Las hipótesis a contrastar serían:
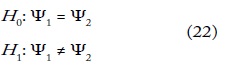
donde el estadístico apropiado para probar las hipótesis es:
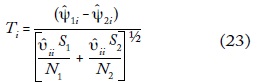
donde υ^ii S1 y υ^ii S2 son las varianzas estimadas correspondientes.
En términos de las curvas de Lorenz:
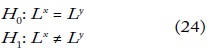
Para esta prueba se emplea el estadístico:
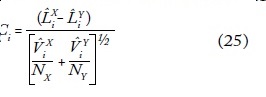
donde Li representa la i-ésima ordenada de las curvas de Lorenz, V^ es el vector estimado de los elementos de la matriz de varianzas y covarianzas, Nx y Ny son los tamaños muestrales de X e Y. Este estadístico se distribuye asintóticamente, como una distribución normal. El valor crítico se obtiene de la distribución del módulo máximo estudentizado (SMM). El contraste de curvas de Lorenz generalizadas sigue un procedimiento análogo.
Hasta aquí se ha expuesto la dominancia de las curvas de Lorenz para evaluar ordenaciones entre dos distribuciones de ingresos. Pero, para el caso de la pobreza y, en particular de las curvas TIP/IID, no se ha extendido esta aplicación.
Teniendo en cuenta los teoremas de Jenkins y Lambert (1998), que encuentran una relación entre la dominancia de las curvas de Lorenz generalizadas y las curvas TIP/IID, y dado que en la literatura existente no se ha aplicado este método; aquí se propone adaptar y aplicar el contraste de las curvas de Lorenz generalizadas a las curvas TIP/IID.
Proposición: Sean X e Y dos vectores de ingresos de tamaño Nx y Ny; y ΓX y ΓY las curvas TIP/IID normalizadas respectivas. La hipótesis a contrastar es la siguiente:

Para un nivel de significación α, el estadístico de contraste es:
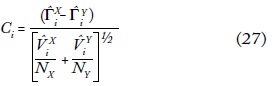
donde Γ representa la i-ésima ordenada de la curva TIP/IID correspondiente y V^ es el vector estimado de los elementos de la matriz de varianzas y covarianzas.
Este estadístico se distribuye asintóticamente, como una distribución normal, y los valores críticos se obtienen a partir de la distribución del módulo estudentizado (SMM). La demostración es análoga a la de Beach y Davidson (1983) para muestras independientes, cada cual con su tamaño muestral.
LA POBREZA ESTÁTICA EN COLOMBIA
El DANE es la entidad encargada de proporcionar los datos oficiales colombianos. Desde mediados de los años setenta elabora la Encuesta Nacional de Hogares (ENH), concebida como:
Un sistema de muestras de propósitos múltiples por el cual se observarían los hogares y se obtendrían datos y estimaciones intercensales, capaces de cubrir las necesidades estadísticas básicas en lo que respecta a la información sobre las personas que integran el hogar (DANE, 2009a) [...] que observarían los hogares para obtener datos y estimaciones intercensales, capaces de producir estadísticas básicas relacionadas con la situación demográfica, social y económica de la población colombiana (DANE, 2009c).
La encuesta ha experimentado transformaciones desde sus inicios hasta 2001, cuando empezó a aplicarse con mayor continuidad y se denominó Encuesta Continua de Hogares (ECH). Desde entonces se empezó realizar en las 13 principales ciudades del país, hasta 2006, cuando se modificó la cobertura y la recolección de información, transformándose en la Gran Encuesta Integrada de Hogares (GEIH).
Debido al método que se emplea en este trabajo, solo se tienen datos de 2001-2005 y se toma la información proporcionada por la ECH. El procedimiento de muestreo es probabilístico, estratificado, multietápico, por conglomerados y autoponderado (DANE, 2009b y 2009c). Por otro lado, la muestra utilizada incluye toda la población, aunque el objetivo de la encuesta es estudiar el mercado laboral y, por tanto, la población en edad de trabajar.
El DANE calcula la línea de pobreza en las 13 principales ciudades teniendo en cuenta la Encuesta de Ingresos y Gastos (Contraloría General de la República, 2004), empleando una canasta normativa (que satisface las necesidades nutricionales a un costo mínimo y respeta los hábitos de los hogares). Así, la línea de pobreza puede obtenerse mediante estándares de consumo, según el gasto en alimentos, o multiplicando la línea de indigencia por la relación entre consumo total y consumo de alimentos observado en la población de referencia (López y Núñez, 2007), que no es más que el inverso del coeficiente de Engel.
Las líneas se calculan de manera exógena. El cuadro 1 muestra las líneas de pobreza e indigencia del mes de septiembre con base en marzo de 2005.
Conociendo los valores de las líneas de pobreza y dada la heterogeneidad entre familias es necesario elegir una escala de equivalencia. Millán (2004) analiza la sensibilidad de los índices de pobreza y desigualdad del ingreso ante ajustes por escalas de equivalencia que tengan en cuenta las economías de escala. Para ello utiliza una comparación entre la escala de equivalencia de la OCDE y una aplicación específica a Colombia realizada por Lasso (2002), en la que encuentra que el tamaño promedio, las unidades de consumo y la edad promedio de los hogares pobres y no pobres en 7 ciudades fueron similares en el año 2002. Por razones metodológicas, aquí se utiliza la escala de la OCDE para analizar la medición de la pobreza.
RESULTADOS
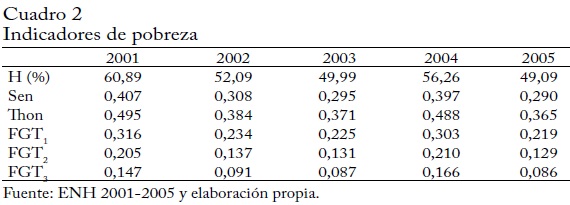
Lo primero que se hizo fue elaborar y revisar un conjunto de indicadores para ver cómo se comportó la pobreza en el periodo de estudio. Los resultados se presentan en el cuadro 2. En general, los indicadores muestran oscilaciones con una tendencia decreciente. En la familia de índices Foster, Greer y Thorbecke (FGT) el valor de α corresponde al parámetro de aversión a la pobreza: a medida que aumenta es mayor la importancia que se da a los más pobres.
Los valores de los índices FGT presentan las mayores variaciones, lo que indica que la mejoría de los hogares más pobres es significativa; así mismo se evidencia una mejoría en el número de pobres (FGT1), en la intensidad (FGT2) y la gravedad de la pobreza (FGT3). El número de pobres H mostró oscilaciones, aunque entre 2001 y 2005 tendió a disminuir. El índice de Sen, que tiene en cuenta la desigualdad, la brecha de ingresos y la intensidad, también tendió a disminuir, lo cual confirma los resultados de los índices FGT, es decir que los hogares estaba mucho mejor en 2005 que en 2001. Igual ocurre con el índice de Thon.
Aunque los indicadores presentan oscilaciones, la tendencia es decreciente. En el periodo de estudio se observa una disminución de la gravedad y la incidencia de la pobreza, y mejoras en la distribución, de modo que es un poco más igualitaria.
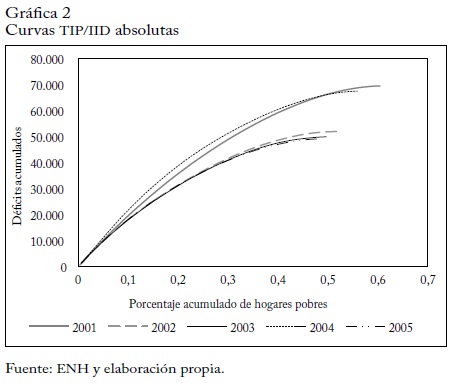
En cuanto a las curvas TIP/IID absolutas y relativas (gráficas 2 y 3), 2001 es el año que presenta mayor incidencia de la pobreza, como lo confirma el valor H del cuadro 2, mientras que 2005 es el año que presenta menores niveles. Con respecto a la desigualdad, se observa que 2004 es el que presenta mayor curvatura y 2005 el de menor curvatura, lo que indica una distribución más igualitaria. En 2004 se observa una mejoría en la incidencia y la intensidad de la pobreza con respecto a 2001. En 2002, 2003 y 2005 el comportamiento es similar y las curvas están casi superpuestas. No obstante, en 2002 la pobreza es más severa.
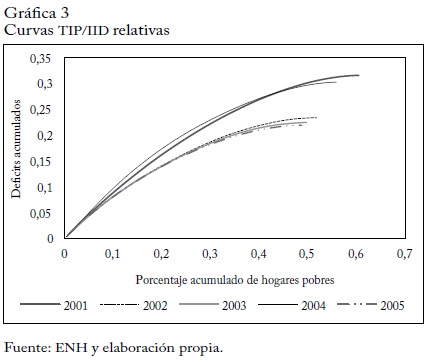
En cuanto a las curvas relativas, todos los indicadores de 2002 muestran un nivel mucho menor que en 2001, de modo que la curva de este año está más alejada del origen que la de 2002. La curva de 2004 está por encima de las curvas de 2002, 2003 y 2005, lo que indica que en 2004 el número de hogares pobres, la desigualdad entre ellos y la intensidad de la pobreza son mayores que en esos otros.
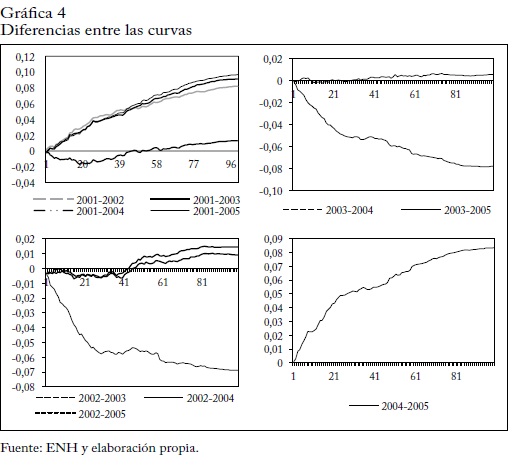
Como las curvas se cortan, una primera idea fue hacer una diferencia entre ellas para ver cómo se comportaba. El resultado se presenta en la gráfica 4. Como se comparan dos años, hay cuatro cuadrantes; en el primero (superior izquierdo) se compara el año 2001 con 2002,2003, 2004 y 2005. En el segundo (superior derecho) el año 2002 con2003, 2004 y 2005. En el tercero (inferior izquierdo) se compara 2003con 2004 y 2005, y en el último (inferior derecho), 2004 con 2005.
Para 2001, los valores tienen el mismo signo, positivo, con respecto a 2002, 2003 y 2005, lo que indica que siempre está por encima de esos años, es decir, que domina fuertemente. Pero con respecto a 2004 hay cruces, pues tiene valores positivos y negativos. En 2002 presenta cruces con los años 2003 y 2005 y estuvo fuertemente dominada por 2004; en 2003 se cruza con 2005 y tiene una fuerte dominancia con respecto a 2004; en 2004 domina fuertemente a 2005.
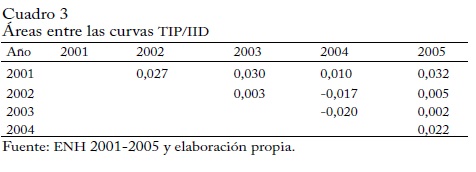
En los ejercicios empíricos, las curvas TIP/IID suelen presentar cortes; Sordo et al. (2007) proponen un enfoque teórico para estudiar los cruces mediante las áreas bajo las curvas. Así se puede determinar la relación entre las curvas comparando sus áreas antes y después del corte. El cuadro 3 muestra las áreas comunes entre las curvas TIP/IID. Las gráficas mostraban que la curva de 2001 siempre estaba por arriba de las curvas de 2002, 2003 y 2005, y se cruzaba con la de 2004. Este resultado se confirma considerando que los valores de las áreas son positivos, de modo que 2001 domina a 2002, 2003 y 2005.
Para 2004, el valor del área común es positivo, de modo que cuando la curva de 2001 está por encima de la de 2004 el área es mayor que cuando la de 2004 está por encima de la de 2001. En 2002, las gráficas mostraban un cruce con 2003 y 2005, y que estaba por debajo de la curva de 2005. Los resultados del cuadro 3 muestran que, en efecto, la curva de 2002 está por debajo de la curva de 2004 ya que el valor de su área común es negativo. En cuanto a los cruces, los resultados muestran que para 2003 y 2005 el área común es positiva, de modo que el área es mayor cuando 2002 está por arriba que cuando está por debajo.
La curva de 2003 está dominada por la de 2004; por ello el valor del área común de las curvas es negativo. Gráficamente, para 2005 se evidencia un cruce al comparar las áreas bajo la curva; el área es mayor cuando la curva de 2003 está por encima de la curva de 2005 que cuando está por debajo. Finalmente, el área común entre las curvas de 2004 y 2005 es positiva, lo que indica que 2004 dominó fuertemente a 2005.
En suma, la curva de 2001 está más alejada del origen que las curvas de 2002, 2003, 2004 y 2005. La curva de 2002, domina las curvas de 2003 y 2005, y es dominada por la de 2004. La de 2003 domina a la de 2005 pero es dominada por la de 2004, y finalmente, la de 2004 domina a la de 2005.
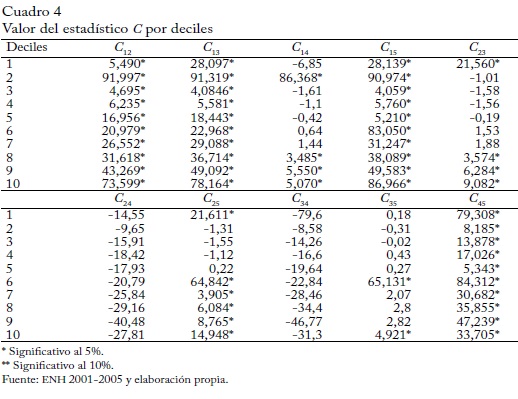
Hasta aquí se ha presentado el análisis gráfico, pero en esta sección se busca usar el estadístico adaptado y propuesto en la anterior para contrastar, mediante un planteamiento formal, las relación entre las curvas. Los resultados del estadístico C se presentan en el cuadro 4. Se discriminan por deciles y el subíndice de C corresponde a los años analizados; Ces el estadístico cuando se comparan 2001 y 2002. El valor de C se compara con el valor del máximo módulo estudentizado; el valor crítico para un grado de significancia del 10% es de 3,086 y para uno del 5% es de 3,5526.
En todos los deciles, los valores de C12, C13, C15 y C45 son mayores que el valor crítico, lo que indica que 2001 tiene niveles de pobreza mucho mayores que los de 2002, 2003 y 2005; y que los de 2004 son mayores que los de 2005. En todos los deciles, los valores de C24 y C34 son negativos y mayores que el valor crítico; de modo que los niveles de pobreza de 2002 y 2003 son inferiores a los de 2004. Los demás valores, como C25 y C35, indican cortes entre las curvas. En todos los casos hay dos cruces significativos. Para los niveles más bajos, el corte se presenta como máximo en el segundo decil, mientras que en los segmentos altos puede presentarse desde el sexto decil. Los cruces son significativos y, por tanto, no se deben a errores de las muestras sino que corresponden a variaciones de la pobreza registradas en esos años.
CONCLUSIONES
Este artículo analiza la pobreza mediante curvas TIP/IID empleando datos de la ECH, un método empírico que hasta ahora no se utilizado en la medición de la pobreza en el país. Los índices que construimos muestran oscilaciones entre 2001 y 2005, con una tendencia claramente decreciente, lo que indica que el número de pobres, la intensidad de la pobreza y su desigualdad se han reducido.
Las curvas TIP/IID relativas y absolutas indican que, en todos los tramos de población, la pobreza fue más pronunciada en 2001 y 2005, que hubo una mejora en 2002 y 2003, una mejora en 2004,y que empeora de nuevo en 2005. Puesto que las curvas se cortan, tomando como referente el análisis de dominancia TIP/IID de Sordo et al. (2007), se estimaron la áreas bajo las curvas siguiendo el método gráfico y luego se calculó el valor de su área común, lo cual confirmó los resultados de las curvas iniciales.
Utilizando el teorema de Jenkins y Lambert sobre la existencia de una relación entre curvas de Lorenz y curvas TIP/IID, dada la inexistencia de trabajos que expliquen la dominancia de la curvas TIP/IID, el hecho de relacionarlas es un avance. Primero se caracterizaron las relaciones de dominancia de primer y de segundo orden, y luego se presentaron los estadísticos empleados para hacer inferencias estadísticas acerca de dicha dominancia.
Estas técnicas inferenciales se aplicaron a las curvas de Lorenz ordinarias y generalizadas, y se adaptaron a las curvas TIP/IID, donde los estadísticos propuestos confirmaron los resultados obtenidos de manera puntual.
Las curvas TIP/IID permiten ver de manera simultánea las tres características de la pobreza estática, de modo que los diseñadores de política pueden focalizar los recursos y aunar esfuerzos para reducir las diferencias de pobreza cada año.
Pie de página
1Domínguez y Núñez (2007a) proponen utilizar la nomenclatura "curvas IID" en su traducción al castellano y de aquí en adelante las llamamos curvas TIP/IID.
2Tomando como referencia los trabajos de Atkinson (1970), Dasgupta et al.(1973), Saposnik (1981 y 1983) y Shorrocks (1983).
3Una función de bienestar social w(.) es S-cóncava si, para cualquier matriz bioestocástica B, se cumple que w(Bx) ≥ w(y). En una matriz bioestocástica todos sus elementos son no negativos y la suma de cada fila es igual a 1.
4En este caso son censurados porque solo se consideran los ingresos de los pobres, y los ingresos censurados quedan iguales al umbral de pobreza en los hogares no pobres.
5No obstante, cabe mencionar los trabajos de del Río y Rossi (2001) sobre Uruguay y los de Gradin y del Río (2001), Domínguez y Núñez (2007a), del Ríoy Ruiz (1996, 1999 y 2001), Casas et al. (2003) y Domínguez y Núñez (2007a, 2007b) sobre España y algunas de sus comunidades autónomas.
6Para la metodología de este estadístico, ver Miller (1981); los cuadros se encuentran en Stoline y Ury (1979).
REFERENCIAS BIBLIOGRÁFICAS
1. Atkinson, A. "On the measurement of inequality", Journal of Economic Theory 2, 1970, pp. 244-263. [ Links ]
2. Beach, C. y R. Davidson. "Distribution-free statistical inference with Lorenz curves and income shares", Review of Economic Studies, 1983 L,pp. 723-735. [ Links ]
3. Bishop, J.; J. Formby y J. Smith. "International comparisons of income inequality: Tests for Lorenz dominance across nine countries", Economica 58, 232, 1991, pp. 461-477. [ Links ]
4. Bishop, J.; J. Formby y P. Thistle. "Statistical inference, income distributions, and social welfare research", Research on Economic Inequality 1, 1989, pp. 49-82. [ Links ]
5. Casas, J. M.; J. Domínguez y J. J. Núñez. "La pobreza en España: estudio a partir de curvas IID y su sensibilidad frente a escalas de equivalencia", J. M. Casas y A. Pulido S. R. Información económica y técnica de análisis en el siglo XXI, Madrid, INE, 2003, pp. 161-173. [ Links ]
6. CID. "Bien-estar III. Informe técnico", Bogotá, CID, Universidad Nacional de Colombia, 2006. [ Links ]
7. Contraloría General de la República. "Coincidencias y diferencias en la estimación de la pobreza", Informe técnico, Bogotá, Contraloría General de la República, 2004. [ Links ]
8. DANE. Gran Encuesta Integrada de Hogares, 2009a, [http://www.dane.gov.co/files/investigaciones/fichas/Gran_encuesta_integrada_hogares.pdf ] [ Links ].
9. DANE. Metodología de la Encuesta Continua de Hogares, 2009b, página web, documentos 1 a 12. [ Links ]
10. DANE. Metodología de la Encuesta Nacional de Hogares, 2009c, página web, documentos 1 a 14. [ Links ]
11. Dasgupta, P.; A. Sen y D. Starret. "Notes on the measurement of inequality", Journal of Economic Theory 6, 1973, pp. 180-187. [ Links ]
12. Del Río, C. y M. Rossi. "El enfoque de la dominancia en el análisis dela pobreza. Una aplicación al caso de Uruguay", documento de trabajon.º 20/2001, Departamento de Economía, Universidad de la República, Uruguay, 2001. [ Links ]
13. Del Río, C. y J. Ruiz-C. "Ordenaciones de bienestar e inferencia estadística. El caso de las EPF de 1980-81 y 1990-91", La desigualdad de recursos, II Simposio sobre igualdad y distribución del ingreso y la riqueza, v. 6, Madrid, Fundación Argentaria, 1996, pp. 9-44. [ Links ]
14. Del Río, C. y J. Ruiz-C. "El enfoque de dominancia en el análisis de la pobreza", Documento de trabajo 1998-01-01, Departamento de Economía, Universidad Carlos III, 1998. [ Links ]
15. Del Río, C. y J. Ruiz-C. "El enfoque de la dominancia en el análisis de la pobreza", Dimensiones de la desigualdad, v. 1, Madrid, Fundación Argentaria, 1999, pp. 429-460. [ Links ]
16. Domínguez, J. y J. J. Núñez. "Análisis de la pobreza en Andalucía a partir de curvas IID, durante el periodo 1997-2000, utilizando diversas escalasde equivalencia", Revista de Estudios Regionales 79, 2007a, pp. 15-42. [ Links ]
17. Domínguez, J. y J. J. Núñez. "Globalización, convergencia regional y pobreza. El caso de la Comunidad Autónoma de Castilla-La Mancha al final del milenio", CLM. Economía 10, 2007b, pp. 335-374. [ Links ]
18. Foster, J. y A. Shorrocks. "Inequality and poverty orderings", European Economic Review 32, 1988a, pp. 654-662. [ Links ]
19. Foster, J. y A. Shorrocks. "Poverty orderings and welfare dominance", Social Choice and Welfare 5, 1988b, pp. 179-198. [ Links ]
20. Gradin, C. y C. del Río. "Desigualdad, pobreza y polarización en la distribución del ingreso en Galicia", La Coruña, Instituto de Estudios Económicos de Galicia Pedro Barrié de la Maza, 2001. [ Links ]
21. Guevara, D. "Dinámica de la pobreza en Colombia; análisis de los ingresos de los jefes de hogar urbano 1984-2003", Economía y Desarrollo 4, 2, 2005, pp. 77-104. [ Links ]
22. Jenkins, S. y P. Lambert. "Three 'I's of poverty curves, with an analysis of UK poverty trends", Oxford Economic Papers 49, 1997, pp. 317-327. [ Links ]
23. Jenkins, S. y P. Lambert. "Three 'I's of poverty" curves and poverty dominance: Tips for poverty analysis", Research on Economic Inequality 8, 1998, pp. 39-56. [ Links ]
24. Lasso, F. "Economías de escala en los hogares y pobreza", Archivos de Economía 212, 2002, pp. 1-59. [ Links ]
25. López, H. y J. Núñez. "Pobreza y desigualdad en Colombia. Diagnóstico y estrategia", Bogotá, DNP, 2007. [ Links ]
26. May, E. La pobreza en Colombia. Un estudio del Banco Mundial, Bogotá, Tercer Mundo Editores, 1991. [ Links ]
27. Miller, R. Simultaneous statistical inference, 2a ed., Nueva York, Springer-Verlag, 1981. [ Links ]
28. Millán, N. "La pobreza en Colombia: medidas de equivalencia de escala y la dinámica del ingreso per cápita del hogar", Cuadernos PNUD-MPS: Investigaciones sobre desarrollo social en Colombia, 2004, pp. 63-97. [ Links ]
29. Núñez, J. y J. C. Ramírez. "Determinantes de la pobreza en Colombia. Años recientes", Documento CEDE 2002-19, Universidad de los Andes, 2002. [ Links ]
30. Núñez, J.; J. C. Ramírez y L. Cuesta. "Determinantes de la pobreza en Colombia 1996-2004", Bogotá, DNP, Cepal, 2007. [ Links ]
31. Ruiz-C., J. "La medición de la desigualdad del ingreso: una revisión dela literatura", Documentos de trabajo 07-02, Universidad Carlos III, 2007. [ Links ]
32. Saposnik, R. "Rank dominance in income distribution", Public Choice 36,1981, pp. 147-151. [ Links ]
33. Saposnik, R. "On evaluating income distributions: Rank dominance, the Suppes-Sen Graging principle of justice and Pareto optimality", Public Choice 40, 1983, pp. 326-336. [ Links ]
34. Shorrocks, A. "Ranking income distributions", Economica 50, 1983, pp. 3-17. [ Links ]
35. Sordo, M.; H. Ramos y C. Ramos. "Poverty measures and poverty orderings", SORT 31, 2, 2007, pp. 169-180. [ Links ]
36. Stoline, M. y H. Ury. "Tables of the Studentized maximun modulus distribution and application in multiple comparisons among means", Technometrics 21, 1, 1979, pp. 87-93. [ Links ]