Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en
SciELO
Similares en
SciELO -
 Similares en Google
Similares en Google
Compartir
Revista de Economía Institucional
versión impresa ISSN 0124-5996
Rev.econ.inst. vol.16 no.31 Bogotá jul./dic. 2014
CAMALEONES: EL MAL USO DE MODELOS TEÓRICOS EN FINANZAS Y ECONOMÍA
Chameleons: The misuse of theoretical models in finance and economics
Paul Pfleiderer*
*Doctor en Economía, profesor de la Universidad de Stanford, Stanford, CA, Estados Unidos, [pfleider@stanford.edu].
Agradezco a Anat Admati, Jonathan Bendor, Jules van Binsbergen, Steve Ross, Mark Wolfson y Jeff Zwiebel por las útiles discusiones y los atinados comentarios. Traducción de Alberto Supelano. Se publica con las autorizaciones correspondientes.
Fecha de recepción: 13 de agosto de 2014, fecha de aceptación:1 de octubre de 2014.
Sugerencia de citación: Pfleiderer, P. “Camaleones: el mal uso de modelos teóricos en finanzas y economía”, Revista de Economía Institucional 16, 31, 2014, pp. 23-60.
Un ingeniero, un físico y un economista naufragan en una isla desierta sin nada que comer. En cuentran una caja de madera que contiene latas de sopa y los tres proponen cómo abrirlas.
Ingeniero: Subamos a ese árbol y lancemos las latas contralas rocas.
Físico: Calentemos en el fuego cada lata hasta que el aumento de la presión interna la abra. Economista: Supongamos que tenemos un abrelatas.
RESÚMEN
En este ensayo muestro que los modelos teóricos en finanzas y economía se usan de un modo que los vuelven “camaleones”, y que los camaleones devalúan la moneda intelectual y enturbian los debates de política. Un modelo se convierte en camaleón cuando se basa en supuestos con conexiones dudosas con el mundo real pero sus conclusiones se aplican acríticamente (o sin suficiente crítica) para entender la economía. Muestro que los camaleones son creados y alimentados por la idea errónea de que un modelo no se debe juzgar por sus supuestos, por el argumento infundado de que los modelos deben estar en pie de igualdad hasta que se hagan pruebas empíricas definitivas, por apelaciones improcedentes a argumentos “como si”, a la elegancia matemática, a la sutileza, por referencias a supuestos “estándar en la literatura”, y por la necesidad de manejabilidad.
[Palabras clave: modelos teóricos, finanzas, economía; JEL: A20, B41, C18].
ABSTRACT
In this essay I discuss how theoretical models in finance and economics are used in ways that make them “chameleons” and that chameleons devalue intellectual currency and obscure policy debates. A model becomes a chameleon when it is based on assumptions with dubious connections with the real world but draws conclusions that are uncritically (or not critically enough) applied to understand our economy. I discuss how chameleons are created and nurtured by the mistaken notion that a model should not be judged by its assumptions, by the unfounded argument that models should have equal standing until definitive empirical tests are conducted; and by misplaced appeals to “as-if ” arguments, by mathematical elegance, by subtlety, by references to assumptions that are “standard in the literature,” and by the need for manageability.
[Keywords: theoretical models, finance, economics; JEL: A20, B41, C18].
Por necesidad los modelos teóricos en economía y finanzas se basan en supuestos simplificadores, que en algunos sentidos son "irrealistas". Esto no significa que las conexiones entre los supuestos de un modelo y lo que sabemos del mundo real no importen y se puedan ignorar. (Un abrelatas supuesto pero inexistente no abrirá una lata de sopa real.) En este ensayo muestro que los modelos se usan de modos que los vuelven "camaleones". Un modelo se convierte en un camaleón cuando se construye a partir de supuestos que tienen conexiones dudosas con el mundo real pero que no obstante obtiene conclusiones que se aplican en forma acrítica (o no suficientemente crítica) para entender nuestra economía. Los camaleones no solo son traviesos sino que pueden ser perjudiciales -en especial cuando se usan para informar la política y otras decisiones- y devalúan la moneda intelectual.
Dada mi historia personal, no niego la importancia de los modelos en economía y finanzas. Los fenómenos económicos ocurren en sistemas dinámicos sumamente complejos, donde los resultados suelen ser determinados por decisiones que toman millones de agentes económicos que interactúan en entornos no estacionarios. Nuestra principal esperanza de entender lo que ocurre es construir modelos simplificados que capten lo que es importante y, cuando sea apropiado y posible, someterlos a pruebas empíricas rigurosas. No hay alternativas reales. Para decirlo simplemente, este es un artículo sobre la importancia de usar apropiadamente los modelos y no un artículo contra el uso de modelos.
Decir que los modelos teóricos son necesarios para entender nuestro sistema económico no implica que tener un modelo teórico particular signifique automáticamente que entendemos algo útil. Si se es razonablemente hábil y se elige el conjunto de supuestos "correcto", se puede producir todo tipo de resultados. Quizá iría muy lejos si dijera que se puede producir cualquier resultado con modelos teóricos, pero sin duda es posible producir una amplia gama de resultados. Esto crea un problema que se podría llamar "selección teórica". Es bien sabido que en el trabajo empírico se obtienen resultados sesgados y erróneos si se seleccionan los datos, es decir, si se seleccionan datos que apoyan un resultado deseado y se excluyen los datos que no lo apoyan. Es comprensible que los empiristas cuidadosos consideran que este es un pecado mortal.
En forma análoga, en el trabajo teórico a menudo es posible seleccionar supuestos para producir un resultado dado. Se trata en esencia de un problema de ingeniería inversa: ¿qué debo suponer para obtener que la configuración X es óptima o que incrementar Y aumentará Z? El hecho de que "la selección teórica" sea posible no significa necesariamente que sea un problema. Quizá sea obvio cuando un modelo es el resultado de escoger que el modelo sea rechazado rápidamente o al menos sometido a intenso escrutinio. ¿No se verá inmediatamente que los supuestos seleccionados con poco fundamento en el mundo real no son razonables? ¿No será claro que el argumento teórico es un artificio ideado para producir el resultado? En algunos casos será claro, por supuesto. Si los supuestos críticos para el resultado son claramente falsos, el modelo no se tomará en serio. Pero en muchos otros casos los problemas de un modelo (como algo que se puede aplicar al mundo real) no serán tan evidentes. Como se ha observado a menudo, un modelo puede ser útil para entender el mundo real aunque sus supuestos no sean "perfectamente verdaderos". De hecho, todo modelo simplificador -lo que por supuesto son todos los modelos- se basa en supuestos que no se deben considerar descripciones perfectas de la realidad1. En vista de ello, los supuestos seleccionados no necesariamente se consideran artificiosos, y a menudo se pueden defender como supuestos simplificadores para que el modelo sea manejable2. Puesto que un modelo no puede incluir todos los factores económicos (p. ej., toda posible "fricción" del mercado y todo posible problema de incentivos), el modelador debe escoger los factores importantes. Los resultados no solo están determinados por lo que se incluye sino también por lo que se excluye.
Introduje la noción de selección teórica no porque quiera afirmar que los teóricos son intelectualmente deshonestos y seleccionan supuestos descaradamente. Aquí considero cómo se usan los modelos y no los incentivos de quienes los construyen. De hecho, no hay nada absolutamente erróneo en la ingeniería inversa per se, porque identificar el conjunto de supuestos necesarios o suficientes (o necesarios y suficientes) para obtener un resultado dado puede ser de gran ayuda para guiar las intuiciones. Los resultados de Modigliani y Miller (1958) son importantes en este sentido, porque identifican lo que debemos suponer para que la estructura de capital sea irrelevante y lo que podría hacerla relevante. Lo que cuenta es que la naturaleza de este tipo de argumento se reconozca por lo que es.
Mi razón para introducir la noción de selección teórica es subrayar que puesto que un resultado dado casi siempre puede ser respaldado por un modelo teórico, la existencia de un modelo teórico que lleve a un resultado dado, en sí y por sí misma, no nos dice nada definitivo acerca del mundo real. Aunque esto es obvio cuando se enuncia sin rodeos, en la práctica se suele dar crédito a algunas afirmaciones -por cierto más del que merecen- solo porque en la literatura hay modelos teóricos que las respaldan. En otras palabras, a los resultados de los modelos teóricos se les da un estatus ontológico que no merecen. En mi opinión esto ocurre porque los modelos, y específicamente sus supuestos, no siempre se someten a la evaluación crítica necesaria para ver si y cómo se aplican al mundo real.
En lo que sigue haré una clara distinción entre lo que llamo modelos de cajón y modelos destinados a ser aplicados al mundo real. La modelación teórica a menudo se emprende simplemente para entender las implicaciones de un conjunto dado de supuestos. Por ejemplo, se puede usar para identificar el contrato óptimo que se debe utilizar cuando se supone que existe un problema particular de incentivos entre un principal y un agente y los únicos contratos que se pueden redactar pertenecen a cierto conjunto. Los resultados obtenidos al analizar este modelo "de cajón" nos pueden dar o no algunas ideas aplicables al mundo real. Este problema de incentivos puede o no surgir en la práctica o, si surge, tener consecuencias insignificantes. Quizá los formatos de contrato supuestos no estén disponibles y no puedan estarlo en la práctica. Quizá estén disponibles otros formatos de contrato mucho más efectivos. Cuando sacamos un modelo "del cajón" y pensamos aplicarlo al mundo real, es razonable preguntar si se basa en supuestos que en general concuerdan con lo que sabemos del mundo y captan los factores que son de importancia de primer orden. En otras palabras, usamos el conocimiento previo que tenemos del mundo en que vivimos (conocimiento basado en últimas en evidencia empírica) para filtrar los modelos que no son útiles para entender lo que ocurre en la economía o para tomar decisiones de política.
En la sección 1 discuto en detalle cómo se deberían usar los modelos teóricos para entender el mundo y cómo surgen los camaleones: modelos que se fundamentan en supuestos dudosos a los que se da acríticamente más crédito del que merecen. Las secciones 2 y 3 presentan algunos ejemplos de modelos que se han convertido en camaleones. Mis ejemplos de estas secciones se toman de las finanzas, porque es mi campo, y específicamente de la literatura bancaria, porque esta literatura me hizo más consciente de los camaleones. En cada uno de los casos examino intentos de aplicar los resultados del modelo al mundo real sin aplicar antes el filtro del mundo real. En las secciones 4 a 8 examino diversos argumentos y opiniones que llevan a la idea de que se debe permitir que los modelos eviten el filtro del mundo real y, por ello, que se conviertan en camaleones. Muestro que esos argumentos y opiniones son defectuosos y a menudo basados en buenos deseos. La afirmación de Milton Friedman de que los modelos solo se deben juzgar por sus predicciones y no por el realismo de sus supuestos se comenta en la sección 4. En la sección 5 considero el argumento de que los modelos deben estar en pie de igualdad hasta que se hagan pruebas empíricas definitivas. En la sección 6 discuto argumentos defectuosos basados en la idea de que si se observa debe ser óptimo, mientras que en la sección 7 considero las limitaciones de los argumentos "como si". En la sección 8 argumento que aunque haya necesidad de manejabilidad, aunque la sutileza y la elegancia sean atractivas y aunque la complejidad pueda ser una cortina de humo que oculta supuestos dudosos, nada de esto debería permitir que los camaleones eludan los filtros del mundo real. En la sección 9 pregunto si mi posición de que los modelos económicos deben pasar a través de filtros del mundo real antes de aplicarlos al mundo real se contradice con el éxito de los modelos en las ciencias duras, como los que se usan en mecánica cuántica. Los modelos en mecánica cuántica parecen basarse en supuestos irrazonables -que violan burdamente el "sentido común"- pero son aceptados porque sus predicciones son confirmadas hasta muchos decimales. Como explico en esa sección, hay enormes e instructivas diferencias entre los contextos en que se aplican los modelos de finanzas y economía y aquellos en que se aplica la mecánica cuántica, haciendo una analogía entre la economía y la física inadecuadas. En la última sección hago algunas observaciones finales.
1. CAMALEONES
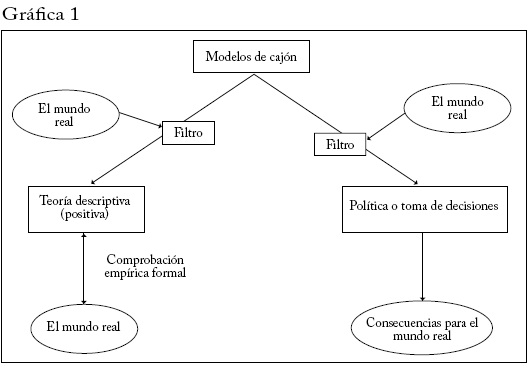
El esquema de la gráfica 1 muestra con más detalle el papel que pueden jugar los modelos teóricos para ayudarnos a entender fenómenos económicos. En la parte superior sitúo los modelos de cajón. Aclaro que no uso este término en sentido peyorativo. En este nivel, un modelo teórico simplemente argumenta que cierto conjunto de resultados se deduce de un conjunto dado de supuestos. Si el argumento es válido (el modelo no contiene defectos lógicos o matemáticos), puede ser útil al darnos intuiciones o al ser un bloque de construcción que se puede usar para construir modelos que podemos aplicar a fenómenos del mundo real3. Los modelos de cajón pueden responder preguntas tales como qué diseño de seguridad minimiza los costos de selección adversa en un contexto particular, cuál será el equilibrio bayesiano-de Nash en un juego dado de forma extensiva, o qué precio fijar a diversos riesgos si los inversionistas tienen ciertas preferencias. Pueden ser modelos de juguete diseñados únicamente para suscitar intuiciones o pueden ser intentos ambiciosos de captar muchos elementos de nuestra economía.
Como ya se mencionó, no todos los modelos de cajón son igualmente aplicables al mundo real, y algunos no lo son en absoluto. Para dar un ejemplo extremo, imaginemos un modelo de fijación de precios de activos basado en el supuesto de que no hay incertidumbre sobre los rendimientos de ningún activo. Aparte de ser un modelo nada interesante, es claro que tiene poca o ninguna relevancia para el mundo real, porque el supuesto es claramente falso. Ninguna persona seria sugeriría que sus predicciones se deberían someter a una prueba empírica rigurosa antes de rechazarlo. El modelo puede ser rechazado simplemente con base en que un supuesto crítico se contradice con lo que ya sabemos que es verdadero.
Como se señaló más atrás, se pueden elaborar modelos teóricos que apoyen toda clase de resultados, pero muchos de ellos se basarán en supuestos dudosos. Esto significa que cuando sacamos un modelo del cajón y consideramos aplicarlo al mundo real, necesitamos que pase por un filtro, por ejemplo, preguntar en forma directa si los supuestos son razonables o el modelo ignora o no capta fuerzas que sabemos o tenemos buena razón para pensar que son importantes.
Sospecho que algunas personas se sentirán incómodas con la idea de que se necesita aplicar un filtro de este modo en esta etapa del proceso. Quizá algunas opinen, como Friedman, que los modelos no se deben juzgar por sus supuestos sino solo por sus predicciones. Una opinión relacionada es que todo modelo válido (lógicamente coherente) es potencialmente aplicable al mundo real y que solo debemos rechazar tal modelo cuando tenemos evidencia empírica decisiva en su contra. Más adelante (sección 4) argumento que una interpretación sensata de la opinión de Friedman no excluye la necesidad de filtros. También argumento (sección 5) que la pretensión de que todos los modelos están en pie de igualdad hasta que son sometidos a pruebas empíricas se basa en una visión demasiado optimista de nuestra capacidad para probar y discriminar modelos usando el tipo de datos que podemos recoger y usar en estudios empíricos formales, y en una visión demasiado pesimista del papel que pueden y deben jugar los filtros del mundo real. Puesto que los modelos suelen ser argumentos causales, es bien sabido que una prueba empírica debe ser una prueba directa del mecanismo causal identificado por el modelo. En general esto significa que debemos encontrar fuentes de variación que sean realmente exógenas antes de que podamos aprender algo definitivo de los datos que nos permita rechazar un modelo u optar por un modelo sobre otro. En un mundo ideal (o al menos en uno mucho mejor que el nuestro) estaríamos inundados de experimentos naturales de todo tipo, donde cada cual produciría datos que se pueden recoger y analizar a bajo costo. En ese mundo ideal podríamos comprobar rápidamente "todo" modelo teórico posible y no se necesitarían filtros. Ese no es nuestro mundo.
La gráfica 1 muestra dos circuitos en los que se deberían usar filtros para evaluar modelos que sacamos del cajón e intentamos aplicar al mundo real. En el lado izquierdo, los filtros se emplean cuando intentamos construir modelos diseñados para describir cómo funciona realmente el mundo (teoría positiva). Como se muestra, los filtros basados en nuestro conocimiento del mundo real se aplican a los modelos de cajón en la selección de aquellos modelos (junto con sus intuiciones y sus resultados) que se van a usar para construir una teoría positiva del mundo. Estas teorías luego se someten (cuando es posible) a pruebas empíricas formales.
En el lado derecho tenemos lo qué llamaré teoría de política4. Preguntemos, por ejemplo, cómo estructurar una subasta de espectro de banda. Los insumos no solo incluyen modelos de cajón (p. ej., resultados teóricos de la eficiencia de diversos formatos de subasta) sino también insumos de teoría positiva que han sido sometidos a pruebas empíricas, pues estos ayudan a entender el ambiente en el que se realizarán las subastas y quizá el comportamiento de los postores. Un modelo teórico de cajón que supusiese que todos los postores son idénticos y que no hay asimetrías de información sin duda sería "filtrado" y considerado inaplicable a una subasta de espectro de banda. El resultado de este proceso es una recomendación de política, que tiene consecuencias potenciales para el mundo real (cuánto recaudará el gobierno y si las licencias se asignan eficientemente).
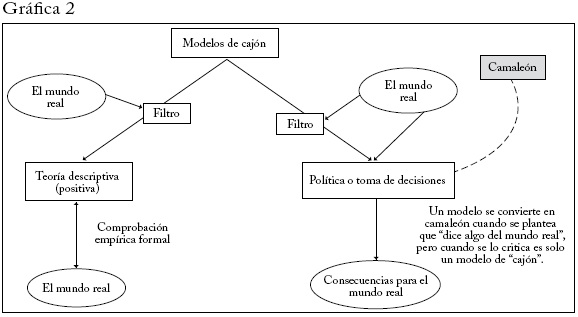
En la gráfica 2 muestro cómo se convierte un modelo en un camaleón. En este caso un "modelo camaleón" afirma que tiene implicaciones de política, pero cuando se pregunta si sus supuestos son razonables y se cuestiona su conexión con el mundo real, se bate en retirada y pasa a ser un simple modelo teórico (de cajón) que tiene inmunidad diplomática cuando se cuestionan sus supuestos. En suma, un modelo se convierte en camaleón cuando intenta eludir los filtros relevantes. Por supuesto, aquí uso un lenguaje pintoresco que antropomorfiza los modelos. Los modelos no tienen incentivos. Se convierten en camaleones por la forma en que los usan quienes los elaboran o quienes apelan a ellos.
Los camaleones aparecen y a menudo son alimentados por la siguiente dinámica. Primero se construye un modelo de cajón que involucra términos y elementos que parecen tener alguna relación con el mundo real y supuestos que no son tan irreales que podrían ser descartados de inmediato. La intención del autor, llamémoslo Q, al elaborar el modelo puede ser decir algo del mundo real o simplemente explorar las implicaciones de cierto conjunto de supuestos. Una vez se conocen el modelo de Q y los resultados, se hacen referencias a él, con afirmaciones tales como "Qmuestra que X". Esto se debería tomar como una forma abreviada de "Q muestra que bajo cierto conjunto de supuestos se sigue (deductivamente) que X", pero algunas personas empiezan a tomar X como una afirmación creíble acerca del mundo real. Si alguien escéptico acerca de X cuestiona los supuestos adoptados por Q, algunos dirán que un modelo no se debe juzgar por el realismo de sus supuestos, pues todos los modelos tienen supuestos irrealistas. Otra réplica de quienes respaldan X como algo que se aplica plausiblemente al mundo real podría ser que la verdad o falsedad de X es un asunto empírico y que X se debe tomar en serio hasta que se hayan hecho pruebas empíricas o análisis apropiados y se haya rechazado X. En otras palabras, X es inocente hasta probar que es culpable. Quizá estas afirmaciones no se expresen en forma tan tajante como lo hago aquí, pero la idea subyacente es que debido a que hay un modelo para X, debido a que no es apropiado cuestionar los supuestos que llevan a X, y debido a que las implicaciones comprobables del modelo que respalda a X no han sido rechazadas empíricamente, debemos tomar en serio a X. El modelo de Q (y X como resultado) se convierte en un camaleón que evita los filtros del mundo real.
2. CONVERSIÓN DE MODELOS EN CAMALEONES: EJEMPLO 1
En abril de 2012 Harry DeAngelo y René Stulz circularon un artículo titulado "Por qué el alto nivel de apalancamiento es óptimo para los bancos". El título del artículo es importante aquí: sugiere fuertemente que los autores afirman algo de los bancos reales en el mundo real. En su introducción los autores explican que su modelo es diseñado para:
Establecer que el alto apalancamiento bancario es el resultado natural (libre de distorsiones) de la intermediación centrada en la producción de depósitos líquidos; el modelo excluye problemas de agencia, seguros de depósito, impuestos y demás factores distorsionantes. Postulando estas condiciones idealizadas, el modelo obviamente ignora algunos determinantes importantes de las estructura del capital bancario en el mundo real. Sin embargo, en contraste con el marco MM -y las generalizaciones que solo incluyen distorsiones relacionadas con el apalancamiento- permite que los bancos jueguen un papel significativo como productores de liquidez y muestra claramente que, si se extiende el modelo MM para tener en cuenta ese papel, para los bancos es óptimo tener alto apalancamiento (cursivas añadidas).
Es decir, su modelo está diseñado para mostrar que si excluimos muchas cosas importantes y nos centramos en un solo factor, obtenemos el resultado particular de que los bancos deben ser altamente apalancados. Este argumento es a todos los efectos análogo al de otro artículo titulado "Por qué el alto consumo de alcohol es óptimo para los humanos", de Bacardi y Mondavi5, quienes en su introducción explican qué hace su modelo:
Establecer que la alta ingesta de alcohol es el resultado natural (libre de distorsiones) del consumo humano de bebidas líquidas; el modelo excluye enfermedades del hígado, conducción en estado de embriaguez, beneficios para la salud, abuso del cónyuge, pérdidas de trabajo y demás factores distorsionantes. Postulando estas condiciones idealizadas, el modelo obviamente ignora algunos determinantes importantes del consumo humano de alcohol en el mundo real. Sin embargo, en contraste con el marco del alcohol neutral -y las generalizaciones que solo incluyen distorsiones relacionadas con el consumo excesivo- permite que los humanos jueguen un papel significativo como productores de ese placentero "zumbido" que se obtiene con el consumo de alcohol, y muestra claramente que si se extiende el modelo del alcohol neutral para tener en cuenta ese papel, para los humanos es óptimo beber todas sus horas de vigilia (cursivas añadidas).
El modelo de DeAngelo y Stulz es claramente un modelo teórico de cajón que no pasaría ningún filtro razonable si deseáramos tomar sus resultados y aplicarlos directamente al mundo real. Además de ignorar mucho de lo que es importante (problemas de agencia, impuestos, riesgo sistémico, garantías del gobierno y demás factores distorsionantes), los resultados de su modelo principal se refieren a activos bancarios libres de riesgo y a una función objetivo postulada que es lineal con respecto al porcentaje de activos financiados con depósitos.
Dado esto, los autores obtienen naturalmente una solución de esquina con activos 100% financiados por depósitos. (No tienen un modelo explícito que aborde lo que ocurre cuando los activos bancarios son riesgosos, pero aun así sostienen que el apalancamiento bancario debería ser "alto" cuando hay riesgo.) Dado todo esto, un título más preciso del artículo sería:
Por qué el "alto" apalancamiento es óptimo para los bancos en un modelo ideal que omite muchas cosas de importancia de primer orden
El artículo de DeAngelo y Stulz es un buen ejemplo de mi afirmación de que en general se puede elaborar un modelo teórico para producir cualquier resultado dentro de un amplio rango. ¿Se quiere un modelo que produzca el resultado de que los bancos se deben financiar 100% con depósitos? Aquí hay un conjunto de supuestos y un argumento que da ese resultado. Que ese modelo exista nos dice muy poco. Pretender relevancia sin pasarlo por el filtro lo convierte en un camaleón.
Se podría preguntar "¿Y qué si el modelo de DeAngelo y Stulz se presenta de un modo que lo hace un camaleón? ¿Qué tiene de malo?". ¿Los lectores del artículo no verán sus limitaciones? Algunos las verán, no todos. Por ejemplo, en un artículo titulado "Castigo al capital: obligar a los bancos a mantener más capital no siempre es prudente", publicado en The Economist el 14 de septiembre de 2013, se decía:
En un nuevo artículo, Harry DeAngelo de la Universidad del Sur de California y René Stulz de la Universidad Estatal de Ohio muestran que esta prima significa que los bancos, a diferencia de otras firmas, no son indiferentes al apalancamiento, como sugiere el teorema de Modigliani-Merton. DeAngelo y Stulz muestran que para los bancos es mejor estar altamente apalancados aun sin fricciones como el seguro de depósitos y las garantías implícitas.
Como mínimo los camaleones añaden ruido y contribuyen a la incomprensión y a la confusión pública sobre temas importantes6.
3. CONVERSIÓN DE MODELOS EN CAMALEONES: EJEMPLOS 2 Y 3
Mis siguientes ejemplos también se toman de la literatura bancaria y se relacionan con la idea de que la deuda exigible que emiten los bancos (p. ej., los depósitos) evita la mala conducta administrativa o disciplina a los gerentes bancarios7. En "El papel de la deuda exigible en la estructuración de arreglos bancarios óptimos", Calomiris y Kahn suponen que un gerente bancario puede fugarse con los fondos del banco sin ser atrapado. En su modelo "toda promesa de pagar al depositante una cantidad P es una opción de que el banquero pague P o deje la ciudad con sus activos disminuidos en la proporción A". En su modelo el incentivo para que el gerente se fugue con el dinero es mayor cuando los activos del banco tienen menor valor, y muestran que en el contexto de su modelo esto puede crear un incentivo para que los depositantes supervisen el valor de los activos del banco y retiren su dinero antes de que el gerente pueda tomar el dinero y abordar un avión a Suramérica.
Un argumento más complejo sobre el papel de la deuda exigible en disciplinar a los gerentes se encuentra en un artículo de Diamond y Rajan titulado apropiadamente "Una teoría del capital bancario". (El título del artículo es apropiado porque sugiere claramente que lo que sigue es una teoría de cajón: un conjunto de supuestos que lleva a algunos resultados, de modo admirable y quizá inusual en la literatura, no pretende la aplicación directa al mundo real de la banca.) Conforme a la teoría de Diamond y Rajan, "los bancos pueden crear liquidez debido precisamente a que los depósitos son frágiles y propensos a corridas". La teoría que plantean se basa en el supuesto de que existen significativos problemas de hurto entre un banco y acreedores del banco y entre gerentes bancarios y quienes financian el banco. Detrás del primer problema de hurto está la idea de que un empresario que ha recibido un préstamo del banco puede amenazar con dejar de trabajar a menos que el banco haga más favorables los términos del préstamo. Detrás del segundo está el supuesto de que un gerente bancario puede amenazar con dejar de usar su habilidad para recaudar los préstamos que el banco ha hecho a menos que los financiadores del banco acuerden concederle una mayor remuneración por sus habilidades especiales. Diamond y Rajan dicen:
El prestamista es un intermediario que ha tomado prestado de otros inversionistas. Así como el empresario puede negociar sus obligaciones de reembolso amenazando con no aportar su capital humano, el intermediario puede amenazar con no aportar sus habilidades de recaudo específicas y, por tanto, capturar una renta a los inversionistas.
Diamond y Rajan sostienen que la manera de resolver estos problemas de hurto en su modelo es que el banco se asegure de que su estructura de financiación es muy frágil. Por ejemplo, si el banco es financiado por depositantes que pueden retirar su dinero cuando deseen siguiendo el orden de llegada, la amenaza de una corrida bancaria reduce la habilidad del empresario y del gerente bancario para cumplir sus amenazas. El gerente no puede renegociar con los depositantes porque cada depositante retirará su dinero si teme que pueda haber una transferencia de los depositantes al gerente.
Esta idea de que la deuda de corto plazo y la fragilidad disciplinan a los gerentes bancarios ha sido citada como una razón para que los bancos no tengan "demasiado capital". Por ejemplo, en el Squam Lake Report encontramos la siguiente afirmación:
El efecto disciplinante de la deuda de corto plazo, por ejemplo, hace más productiva a la gerencia. Los requerimientos de capital que van contra la deuda de corto plazo impulsan a los bancos hacia otras formas de financiación que pueden llevar a que los gerentes sean más laxos.
No es claro en qué se basan los autores del Squam Lake Report para hacer esta fuerte afirmación (no hacen referencia a ningún trabajo teórico o empírico), pero en todas las conversaciones que he tenido con personas que dicen que la deuda de corto plazo disciplina a los gerentes, los artículos de Calomiris y Kahn y de Diamond y Rajan se citan como principales argumentos de su posición.
No obstante, si estos modelos teóricos se sacaran del cajón y se aplicaran a la banca moderna del mundo real, ¿pasarían un filtro de preguntas razonables acerca de sus supuestos? A continuación enumero algunas preguntas que pienso que se deberían hacer para evaluar su aplicabilidad a la banca moderna, y que son ejemplos de filtros empíricos razonables:
- ¿Con cuánto dinero se podrían fugar los gerentes bancarios, y es de tal magnitud que vale la pena que los depositantes supervisen estrechamente el banco?
- ¿Exactamente cuáles acreedores de corto plazo son vulnerables a que el gerente se fugue con dinero (como en el modelo Calomiris-Kahn) y cuáles se empeñarían en una corrida de depósitos en respuesta a la amenaza del gerente (como en el modelo Diamond y Rajan)? Es de presumir que no son los depositantes asegurados. El seguro existe para proteger a los depositantes y evitar corridas. ¿Podrían ser los prestamistas de repos? El problema es que estos prestamistas tienen garantías en su poder y no están sujetos a la restricción de servicio secuencial (primero en llegar, primero en ser atendido).
- ¿Qué empleado de un banco importante como JP Morgan o Barclays puede amenazar con no usar sus habilidades si los inversionistas no le dan un mejor trato como se plantea en el modelo de Diamond y Rajan? ¿El gerente general? ¿O un funcionario de crédito que ha hecho algunos préstamos comerciales de finca raíz? ¿Qué préstamo o activo en un balance de un billón de dólares es tan grande que esta amenaza tiene consecuencias que ocasionan una corrida de acreedores?
- ¿El problema de hurto de Diamond y Rajan no es un problema potencial en otras firmas y por qué no vemos estructuras de financiación muy frágiles en esas firmas? ¿No pueden los Socios Generales (SG) de un fondo de capital privado amenazar con no hacer su trabajo en la realización del valor del portafolio de sus firmas a menos que los Socios Limitados (SL) les den un mejor trato? ¿No pueden los empleados de Microsoft amenazar con no terminar el sistema operativo a menos que les den un mejor trato? ¿Por qué la fragilidad no es usada en otras firmas? ¿Cómo resuelven el problema?
Aún más importante, en ambos modelos también podemos hacer preguntas sobre la magnitud de la "fragilidad" que sería necesaria para lograr los resultados saludables postulados. Por ejemplo, para evaluar el modelo de Diamond y Rajan consideremos lo que sucedió a JP Morgan en el escándalo "London Whale" de 2012. Se informó que las pérdidas comerciales debidas a posiciones poco aconsejables de Bruno Iksil ascendieron a 6.200 millones de dólares. Es importante reconocer que estas enormes pérdidas no provocaron una corrida en JP Morgan. Una razón para no haberla provocado es que así estas pérdidas hayan sido enormes en términos absolutos, no eran suficientes para generar pánico entre los acreedores dada la posición financiera global de JP Morgan en ese momento. Por supuesto, los acreedores quizá tampoco entraron en pánico por su creencia bien fundada de que el gobierno probablemente respaldaría a JP Morgan si el banco entraba verdaderamente en problemas. ¿Qué significa todo esto? Que Jamie Dimon podría hacer el siguiente discurso ante los inversionistas de JP Morgan (accionistas y acreedores):
Como saben, mi equipo directivo y yo somos absolutamente críticos sobre el éxito futuro de JP Morgan. Si no nos pagan 6.200 millones adicionales en bonificaciones este trimestre, nos negaremos a ejecutar todas las posiciones complicadas que hemos tomado en el banco,
y no sufriría ninguna de las consecuencias del tipo postulado en el modelo de Diamond y Rajan debido a la fragilidad de corto plazo. Esto sugiere que para impedir que Jamie Dimon hurtara al banco 6.200 millones usando el mecanismo concebido en el artículo de Diamond y Rajan, JP Morgan necesitaría ser mucho más frágil de lo que es. Se necesitaría un colchón de capital sumamente delgado y que los depositantes y acreedores de corto plazo estuviesen en posiciones vulnerables, y preparados para una corrida. Es claro que algo evitó y sigue evitando que Jamie Dimon haga el discurso anterior, pero es igualmente claro que no es el mecanismo discutido en Diamond y Rajan. Si hay un problema de hurto en JP Morgan y otros bancos similares, no se resuelve con la fragilidad9.
La idea de que la deuda de corto plazo cumple un papel crítico para disciplinar a los gerentes bancarios en el mundo real parece estar basada en camaleones: los resultados teóricos se sacan del cajón y se aplican al mundo real sin pasarlos por un filtro razonable. Si el resultado de un modelo depende críticamente de un mecanismo de funcionamiento particular y queremos aplicar este modelo al mundo real, deberíamos poder ver que los fundamentos de ese mecanismo existen y funcionan realmente en el mundo real. Debe ser más que una historia que se puede contar.
Algunas personas me han dicho que el "jurado aún está deliberando" para determinar si la deuda de corto plazo disciplina a los gerentes bancarios. Ellas afirman que es un "asunto empírico", lo que significa que el jurado solo decidirá cuando tengamos una prueba empírica definitiva de la proposición. Pregunté a estas personas en qué consistiría esta prueba y les pedí que describieran cómo se llevaría a cabo. En la mayoría de los casos pusieron los ojos en blanco. En algunos casos me dijeron que podíamos buscar un experimento natural donde hubiese un choque exógeno sobre el volumen de financiación con deuda de corto plazo y pudiésemos medir el "desempeño" del banco después del choque, suponiendo que toda variación en el desempeño revela los efectos de un cambio en la disciplina o en la prevención de la mala conducta. Los problemas involucrados en tal prueba son obvios. Aunque pudiéramos encontrar un choque exógeno que afecte cómo se financia el banco, no es claro que toda variación posterior en el desempeño se pueda asociar sin ambigüedades con el canal disciplinario postulado, pues el choque puede afectar diversos factores, muchos de los cuales son difíciles de tener en cuenta. Ahora bien, es posible que un empirista hábil pueda identificar alguna manera de hacer avances significativos en esta senda, pero dados los obstáculos involucrados, no parece probable. ¿Esto significa que debemos ser totalmente agnósticos? El agnosticismo total exige que ignoremos todo el conocimiento anterior que poseemos (p. ej., Jamie Dimon no hurtó cientos de millones de dólares a los accionistas de JP Morgan, aunque esto claramente no causaría una corrida bancaria; las firmas de capital privado no dependen de una estructura de financiación frágil aunque se podría pensar que los SG pueden estar en posición de robar a los SL; etc.) Ignorar totalmente este conocimiento anterior es una extraña manera de razonar acerca del mundo.
4. SE DEBEN JUZGAR LOS SUPUESTOS DEL MODELO
En su famoso artículo de 1953, "La metodología de la economía positiva", Milton Friedman argumentó que no debemos juzgar un modelo con base en el realismo de sus supuestos sino solo por la exactitud de sus predicciones. Esta afirmación ha suscitado gran controversia a través de los años y muchos han rechazado los argumentos de Friedman, aunque algunos los han defendido10. No pretendo hacer una crítica completa de la posición de Friedman, pero argumentaré que no se puede usar para cobijar a los camaleones permitiéndoles evitar el filtro del mundo real.
Si Friedman solo dijera que un modelo no se debe rechazar automáticamente porque sus supuestos no llegan al "realismo completo", tendría razón en este nivel simple. Puesto que todos los modelos son simplificaciones del mundo real, sus supuestos no son y no pueden ser completamente realistas. Si tuviésemos que rechazar todo modelo que tenga supuestos irrealistas en este sentido, tendríamos que rechazar todos los modelos. Friedman argumenta, sin duda, a favor de algo que va más allá de este punto trivial, pero no es claro cuál es exactamente su argumento y hasta dónde está dispuesto a llevarlo.
Una interpretación literal de la afirmación de Friedman de que los modelos solo se deben juzgar por sus predicciones lleva al absurdo. Como muestro más adelante, la única manera de respaldar la visión extrema de Friedman requiere que lleguemos a todo problema de predicción con antecedentes bayesianos totalmente agnósticos acerca del mundo. Por ejemplo, supongamos que estamos interesados en los modelos económicos diseñados para predecir la tasa de inflación de Estados Unidos en el año t con base en información conocida en el año t-1. Tomemos literalmente la noción de que debemos juzgar estos modelos únicamente por el éxito de sus predicciones y que debemos ignorar totalmente el realismo de los supuestos de estos modelos. En este contexto simplemente estaríamos buscando el modelo que tenga el mejor récord de predicción de la inflación. Si dejamos hacer cualquier supuesto sin importar cuán fantasioso sea, podemos usar cualquier dato que esté disponible en t-1 para predecir la tasa de inflación en el periodo t.
El número de modelos que hagan predicciones sumamente precisas (dentro de una muestra) que podríamos construir es muy grande, si no infinito. Friedman reconoce, por supuesto, que el ajuste dentro de la muestra carece de sentido en este contexto y dice que el objetivo es obtener "predicciones válidas y significativas (es decir, no triviales) acerca de fenómenos aún no observados" (1953, 7). Pero si esperamos algunos años y usamos los nuevos datos fuera de muestra para "probar" todo los modelos rivales de predicción de la inflación, no es el caso que surja victorioso el único modelo "verdadero" y se derrumben todos los modelos "falsos". Podemos, por supuesto, encontrar que el desempeño de la mayoría de los modelos que consideramos intérpretes estelares dentro de la muestra se degrada notablemente en el periodo fuera de muestra, pero aún sobrevivirá un gran número de ellos. Muchos supervivientes se basarán sin duda en supuestos fantasiosos e irrealistas. Por ejemplo, podemos encontrar que en alguno la tasa de inflación en t está determinada por una función simple de la estatura promedio de los ganadores masculinos del Oscar en t-1. Por supuesto, soy consciente de que este es un argumentum ad absurdum, pero estoy tomando literalmente la afirmación de Friedman de que debemos ignorar el realismo de los supuestos. De hecho, a partir de lo que dice Friedman es difícil saber cómo separa lo absurdo de lo meramente irrealista. Él dice:
se encontrará que las hipótesis verdaderamente importantes y significativas tienen "supuestos" que son representaciones descriptivas sumamente inexactas de la realidad, y, en general, cuanto más significativa es la teoría, más irrealistas son los supuestos (en este sentido)11.
También dice:
El realismo "completo" es claramente inalcanzable, y la pregunta de si una teoría es "suficientemente" realista solo se puede responder viendo si sus predicciones son suficientemente buenas para el propósito en cuestión o si son mejores que las predicciones de teorías alternativas.
Casi siempre será el caso que los modelos aparentemente "mejores" para predecir (basados en los datos disponibles) serán modelos "fantasiosos" como el modelo del "premio Oscar". Estos "ganadores" parecerán mejores para predecir la inflación (de nuevo, dados los datos disponibles) que modelos alternativos basados en supuestos claramente más razonables que involucren, por ejemplo, políticas del banco central, tasas de inflación anteriores y expectativas de los consumidores sobre la inflación futura. En otras palabras, si consideramos todos los modelos posibles, está prácticamente garantizado que los de mejor desempeño son sumamente irrealistas, como el modelo del premio Oscar. La simple identificación de los que arrojan predicciones "suficientemente buenas para el propósito en cuestión" no elimina estos modelos absurdos. Pues siempre se puede inventar una historia inverosímil (un modelo internamente coherente con supuestos muy irrealistas) que "explica" el éxito de predicción de un modelo. Por ejemplo, con suficiente imaginación se pueden idear supuestos disparatados y usarlos para construir un modelo que "explica" que en las personas que fijan los precios de la economía influye la estatura de los actores masculinos en películas bien hechas. Pero la total inverosimilitud de esta historia y de historias como esta llevará a que ninguna persona reflexiva las tome en serio. Sin importar cuál sea el éxito de sus predicciones, estos modelos serán y deben ser juzgados por el realismo de sus supuestos.
Rechazamos el modelo del premio Oscar porque poco o nada concuerda con nuestro conocimiento anterior del mundo. No pasa ningún filtro razonable del mundo real. Debido a que nuestro precedente bayesiano sobre el modelo del premio Oscar es igual a cero, un registro de éxitos de predicción no cambia este precedente. Este precedente bayesiano se basa en nuestro conocimiento del mundo, y la única manera de dar algún valor a este modelo sería ignorar ese conocimiento y tener un precedente bayesiano "totalmente uniforme" o "agnóstico", suponiendo que este se pudiese definir.
También podemos pensar que el modelo del premio Oscar hace otras predicciones además de la tasa de inflación. Si hay una cadena causal entre estatura de los actores y tasas de inflación, esperaríamos ver más evidencia de esta cadena que las meras tasas de inflación resultantes. ¿Por ejemplo, vemos que los agentes económicos que toman decisiones de compra y fijación de precios realmente comprueban la estatura de los principales aspirantes masculinos al Oscar? Para alguien que tome literalmente la afirmación de Friedman, esta es quizá una pregunta ilegítima porque parece dirigida al realismo de los supuestos del modelo y no a la exactitud de sus predicciones, lo cual es tabú. Para el resto de nosotros, es una pregunta bastante razonable, porque hace pasar el modelo por el filtro del mundo real.
La pregunta no es si debemos juzgar la utilidad y aplicabilidad práctica de los modelos por el realismo de sus supuestos. Eso debemos hacer (y así lo hacemos rutinariamente). La pregunta es qué tipos de irrealismo son relativamente innocuos -simplificaciones que hacen manejable y útil el modelo pero que no crean una grave desconexión con el mundo real y nos llevan a una tierra fantástica- y qué tipos nos deben llevar a rechazar el modelo. Esta es una pregunta que no es fácil responder y, sin duda, una pregunta que implica buen criterio. La afirmación de Friedman se puede ver como un intento valiente de evitar totalmente tener que enfrentar esta difícil pregunta, porque parece sugerir que el realismo de los supuestos de un modelo no tiene importancia, y que solo la tiene la exactitud de sus predicciones. Pero esa afirmación no se puede usar para evitar estas preguntas, pues da vida al modelo del premio Oscar y a innumerables modelos como este. No podemos evitar la necesidad de hacer pasar los modelos por el filtro del mundo real. La interpretación literal de las afirmaciones de Friedman no es un argumento para dejar que los camaleones eludan estos filtros.
5. UNA DEFENSA DÉBIL: "EL JURADO AÚN ESTÁ DELIBERANDO"
Una afirmación relacionada con el argumento de Friedman dice que no se debe rechazar un modelo hasta que se hayan hecho las pruebas empíricas definitivas (aquellas que examinan las predicciones del modelo). Esto equivale a decir que mientras "el jurado de la prueba empírica aún esté deliberando" debemos tomar el modelo tan seriamente como a cualquier otro. En otras palabras, que un modelo no se debe juzgar por el realismo de sus supuestos sino por el éxito del trabajo empírico que aún está por realizar.
Este "corolario" del argumento de Friedman lleva a la visión estrechamente asociada de que el papel de un teórico es simplemente producir modelos internamente coherentes que serán probados empíricamente en el futuro. Estos modelos se deberían desarrollar sin prestar mucha atención a que los supuestos en que se basan sean en algún sentido "verdaderos" o aplicables al mundo real, porque esto será resuelto en últimas por los empiristas que prueben las predicciones de los modelos. Quienes así opinan parecen creer que cuantos más modelos tengamos en el cajón, mejor equipados estaremos para entender el mundo. Llevada a su extremo, esta visión de "cuantos más modelos mejor" nos llevaría a crear una "Biblioteca de Babel"12. Hay un número infinito de modelos que se pueden construir y analizar en forma lógica y matemáticamente correcta, pero la mayoría se construye con supuestos irrealistas e inútiles. Construir modelos sin prestar seria atención al realismo de sus supuestos y simplemente suponer que la comprobación empírica resolverá en últimas las cosas, es una absurda manera de hacer investigación.
El problema de estos puntos de vista es que no reconocen las dificultades que se suelen enfrentar en la comprobación de teorías. Es fácil idear teorías falsables (en el sentido de Popper) y, por tanto, no vacuas ni tautológicas, pero que al mismo tiempo sean difíciles de comprobar. Esto significa que la afirmación de que todas las teorías son igualmente buenas hasta que pruebas empíricas definitivas separen a las "ganadoras" de las "perdedoras" nos pone de hecho en el camino de una Biblioteca de Babel13.
Para ilustrar esto, a continuación presento el esquema de un modelo de disciplina gerencial en la banca que "explica" por qué los bancos son tan complejos. Estos son los supuestos:
- Debido a la gran complejidad y la opacidad de las entidades financieras modernas, los gerentes bancarios tienen amplio margen para tomar acciones que los benefician y perjudican a los accionistas y a otros. Llamemos "estafas" a estas oportunidades.
- Las oportunidades de que los gerentes cometan estafas llegan al azar conforme a un proceso de Poisson con intensidad l.
- El gerente tiene una capacidad de procesamiento limitada ("ancho de banda" limitado), y esto significa que la probabilidad de que reconozca una oportunidad de estafa y pueda aprovecharla depende de la magnitud del ancho de banda a su disposición en el momento en que se le presenta la oportunidad de estafa.
- La manera más eficiente de evitar que el gerente cometa estafas es asegurar que el ancho de banda disponible sea limitado.
- La magnitud del ancho de banda a disposición del gerente depende de la complejidad de la estructura de capital del banco. Una estructura de capital más complicada requiere más atención del gerente y le deja menos ancho de banda para identificar estafas.
- El capital es simple (solo acciones ordinarias) pero la deuda puede ser muy complicada (varía en madurez, prioridad y muchas otras características). En otras palabras, es más complicada que el capital.
Esto da lugar a la siguiente conclusión:
Para los bancos es eficiente tener una estructura de capital compleja, y esto se logra usando una deuda elevada y haciendo muy complicada la estructura de obligaciones. Esto ocupará más ancho de banda del gerente y reducirá su capacidad para reconocer y aprovechar las oportunidades de estafa.
Este modelo proporciona claros fundamentos teóricos para reflexionar sobre cuestiones importantes relacionadas con las normas bancarias y los requerimientos de capital. ¿Qué tan seriamente lo debemos tomar? ¿Lo debemos tomar tan seriamente como a cualquier otro modelo hasta que sea rechazado por una prueba empírica? El modelo propuesto no es vacuo: es falsable en el sentido popperiano. Por ejemplo, predice nítidamente que a medida que las oportunidades de estafa aumentan, las estructuras de capital bancario deberían ser cada vez más complejas. Se podría imaginar un experimento natural donde haya un aumento exógeno de las oportunidades de estafa que permita probar esto. Si viésemos que las estructuras de capital bancario se vuelven sistemáticamente más simples después de aumentos exógenos de las estafas, tendríamos razones para rechazar el modelo.
Por supuesto, no es probable que surjan las condiciones para una prueba decisiva y que esa prueba se pueda llevar a cabo. Se pueden imaginar muchos problemas prácticos. Esto no solo se aplica a la "teoría del ancho de banda del gerente" que acabamos de presentar, infortunadamente también se aplica a muchas teorías de la literatura sobre economía y finanzas. Esto no significa que debamos dejar de desarrollar teorías e intentar probarlas. Solo significa que dado que nuestra capacidad para probar directamente las teorías es limitada, debemos usar otros medios para juzgar la aplicabilidad y la utilidad de una teoría o modelo dados. El modelo de ancho de banda simplemente no pasa ningún filtro de cómo funciona el mundo real. Es cierto que algunos de sus supuestos son plausibles14, pero ninguna persona reflexiva que sea consciente del mundo tomaría en serio la historia. Primero, el supuesto de que la manera más eficiente de evitar estafas es ocupar el ancho de banda gerencial es muy dudoso. Segundo, si los gerentes son los que determinan la complejidad de las obligaciones bancarias, ¿por qué elegirían algo que les impida beneficiarse mediante estafas o, más en general, por qué deberían elegir algo que los discipline? Tercero, si la junta directiva impone la estructura de capital compleja al gerente para evitar estafas, ¿por qué nunca hemos oído que los miembros de una junta expliquen así sus acciones?; etc. Cuando empecé a escribir este artículo estaba resuelto a no usar la expresión "sentido común", pero es inevitable: el simple sentido común (basado en el conocimiento del mundo en que vivimos) nos dice que el modelo de ancho de banda no se debe tomar en serio. No sería una asignación eficiente del tiempo de los teóricos desarrollar el modelo de ancho de banda o modelos como ese, ni sería eficiente que los empiristas dediquen tiempo y esfuerzo a probar ese modelo.
El modelo de ancho de banda es deliberadamente absurdo a propósito. Es claro que no pasa el filtro del mundo real. Pero si se insiste en que no debemos rechazar modelos porque sus supuestos no son razonables y, además, en que salvo que las hipótesis comprobables de un modelo teórico sean rechazadas en una prueba empírica formal, ese modelo está en pie de igualdad con cualquier otro, no hay razón para tratar el modelo de ancho de banda como un modelo absurdo. Para alguien que adopte este punto de vista, este modelo se debe tomar en "serio". El hecho de que la mayoría de las personas -espero que todas- no lo tomaría en serio significa que al menos en casos extremos como este aplicamos el filtro del mundo real. El problema, y mi motivación para escribir este ensayo, es que hay camaleones: modelos teóricos que, así no sean tan absurdos como el modelo de ancho de banda, no obstante tienen conexiones dudosas con el mundo real y, sin embargo, parecen dar pasos a través del filtro del mundo real y son tomados como descripciones serias de la realidad, al menos por algunas personas.
6. EL HECHO DE VERLO NO LO HACE ÓPTIMO
Como economistas tenemos la fuerte y en general bien fundada creencia de que no se dejarán grandes sumas de dinero sobre la mesa. En muchas situaciones los agentes económicos encontrarán maneras de cambiar las estructuras o prácticas organizativas ineficientes o de superar los obstáculos que reducen el tamaño del pastel. Esto significa que cuando vemos contratos escritos de un modo particular o transacciones realizadas de cierta manera, es razonable pensar que no son resultados aleatorios sino que solucionan problemas potenciales importantes. Aunque la hipótesis de que el dinero no se deja sobre la mesa tenga un sólido registro de predicción, no se deduce que todo lo que vemos es óptimo15.
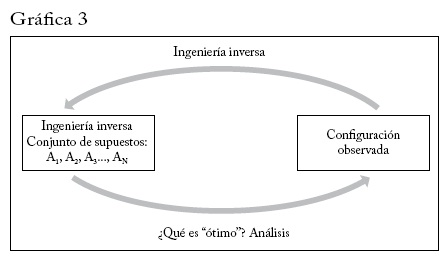
Supongamos que observamos algo en el mundo real -un contrato o una estructura organizativa- y llamémoslo "configuración observada". Como muestra la gráfica 3, a menudo es bastante posible que alguien haga "ingeniería inversa" con un conjunto de supuestos (A1, A2, A3..., AN) bajo los cuales la configuración observada será óptima.
Ahora bien, si empezamos suponiendo que los supuestos de ingeniería inversa son válidos y preguntamos qué es óptimo, el análisis mostrará necesariamente que la configuración observada es óptima.
Esto puede dar lugar al siguiente argumento defectuoso. A partir de la configuración observada, laxamente "inferimos" que los supuestos (Aj, A2, A3..., AN) deben cumplirse conforme a la idea de que lo que vemos debe ser óptimo, lo cual significa que (Aj, A2, A3..., AN) "deben" ser válidos, porque si no lo fuesen no veríamos la configuración observada. Habiendo aceptado los supuestos, tenemos respaldo adicional para la idea de que los agentes económicos encuentran soluciones óptimas, porque la configuración observada es un buen ejemplo de que los agentes optimizan. Cuando todo esto se dice en el mismo párrafo, como lo he dicho aquí, es fácil de ver el carácter "circular" del argumento, lo que lo hace falaz16. El problema es que el argumento nunca se expone en un solo párrafo. No se expone en forma rigurosa y sus componentes no se presentan necesariamente en el mismo escrito o en el mismo contexto. Por ejemplo, como se comentó más atrás, Diamond y Rajan desarrollan un modelo en el que en esencia se preguntan qué conjunto de supuestos hará que la deuda de corto plazo y la fragilidad sean una solución óptima (o al menos de segundo o tercer óptimo). Una vez desarrollado y publicado su modelo teórico, las personas asumen en otros contextos que estos supuestos deben ser válidos en forma aproximada (porque vemos que se está usando deuda de corto plazo) y laxamente argumentan que si los bancos fueran obligados a depender menos de financiación de corto plazo esto los alejará de lo que es una configuración óptima e impondrá potencialmente un costo. La circularidad sigue allí, pero no expuesta en el mismo lugar.
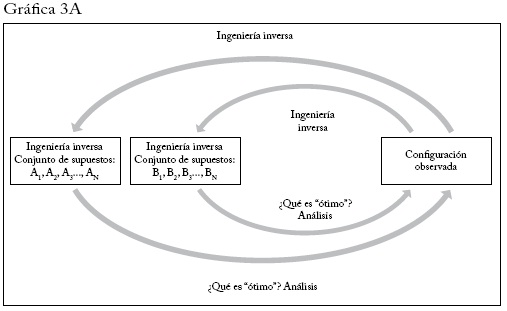
Aunque podamos suponer legítimamente que la configuración observada es óptima, en general no podremos inferir qué conjunto de supuestos se "debe mantener", ya que en la mayoría de los casos habrá varios conjuntos bajo los cuales la configuración observada sería óptima, como ilustra la gráfica 3A, en la que se identifican dos conjuntos como posibles candidatos. Los supuestos son suficientes pero no necesarios.
En vista de todo esto, debería ser claro que alguien que idee un conjunto de supuestos bajo los cuales una configuración observada es óptima no puede argüir legítimamente que ha explicado esa configuración. En la gráfica 3A tenemos dos explicaciones rivales y hay muchas otras posibles. Es claro que no podemos "probar" el modelo que incorpora los supuestos (Kv A2, A3..., AN) preguntando si se observa la configuración óptima; el modelo se construyó para "explicar" por qué una configuración ya observada es "óptima". Lo que podemos hacer, por supuesto, es preguntar si los supuestos (Aj, A2, A3..., AN) son razonables. Cuando los mantenemos, ¿pasan el filtro de todo el conocimiento anterior que tenemos del mundo real?
7. LAS LIMITACIONES DEL "COMO SI"
En el ensayo sobre economía positiva de Friedman se nos dijo que podemos entender las acciones de un billarista experto suponiendo
que hizo sus tacadas como si conociese las complicadas fórmulas matemáticas que dan la dirección óptima y pudiese estimar exactamente los ángulos a ojo, etc., y viendo la localización de las bolas pudiese calcular instantáneamente las fórmulas, para luego hacer que las bolas vayan en la dirección indicada por las fórmulas.
La fuerza del argumento "como si" de Friedman aplicado al jugador de billar se basa en dos características muy importantes de su ejemplo:
- Cuando aprende a jugar, un billarista experto hace muchas tacadas y para cada una recibe retroalimentación casi inmediata sobre si la tacada tuvo éxito o no. Esto le permite experimentar y afinar los ángulos, el efecto que aplica, etc. Si, como a veces se dice, se tardan 10.000 horas para volverse experto y si un billarista hace unas 100 tacadas en una hora, un billarista experto ha hecho casi un millón de experimentos, viendo casi inmediatamente cada resultado.
- Conocemos todos los detalles importantes del juego de billar pool. Conocemos el peso de las bolas, el tamaño de la mesa y, muy importante, el objetivo del billarista (ganar el partido según las reglas). Esto significa que si le presentamos toda esta información a un físico y le pedimos que prediga, por ejemplo, el ángulo con el que el billarista experto golpearía la bola blanca para meter una bola particular en la tronera lateral, el físico podría deducir y usar con éxito las fórmulas apropiadas para hacer la predicción.
Ahora consideremos el argumento "como si" tal como se usa en algunos modelos de finanzas y economía. Como ejemplo consideremos los modelos dinámicos de la estructura de capital de una firma. En un artículo sobre este tema (Titman y Tsyplakov, 2007) encontramos la siguiente fórmula para el capital de la firma en un nodo particular de una grilla usada para resolver numéricamente los problemas de control estocástico que surgen en el modelo:
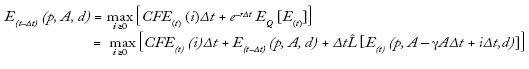
donde
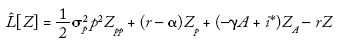
y donde i* es la estrategia de inversión que resuelve el problema de maximización anterior.
El modelo es bastante complicado y las "fórmulas" que se supone que los agentes económicos deben resolver son muy complejas. Los agentes no solo deben ser capaces (en algún sentido) de resolver el problema de programación dinámica, también deben ser capaces de estimar el valor de los parámetros (p. ej., α, σ2P y γ). Se podría considerar que es un modelo normativo o de política (es decir, este es el problema que los gerentes corporativos deberían resolver). Pero en ese artículo y en artículos como ese, el modelo se presenta como un aporte a la teoría positiva (el modelo ayuda a explicar lo que vemos en la práctica). De hecho, los autores del artículo intentan calibrar su modelo y comparar los resultados con regularidades empíricas. Afirman que "las regresiones estimadas con los datos simulados generados por nuestro modelo son relativamente consistentes con regresiones reales estimadas en la literatura empírica".
Si este modelo se considera un aporte a la teoría positiva, es claro que el argumento debe ser un argumento "como si". El supuesto es que los gerentes financieros (GF) y las juntas directivas toman decisiones sobre la estructura de capital "como si" estuviesen calculando, entre otras cosas:
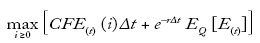
Aunque pocos GF, si existe alguno, están bien versados en los principios de la programación dinámica, quizá podamos suponer que, como los billaristas expertos, los GF juegan el "juego" de la estructura de capital como si resolviesen numéricamente problemas de control estocástico. Pero en este punto debemos ser conscientes de las enormes diferencias entre los contextos en que actúan los GF y el contexto en que los billaristas se convierten en expertos. A diferencia de un billarista experto, el GF solo hace algunas "tacadas" de estructura de capital significativas en un año y, a diferencia del billarista, no recibe retroalimentación inmediata sobre si ha tomado la decisión correcta (ningún equivalente de una bola entra a la tronera lateral dos segundos después de que el GF aumenta la deuda y recompra capital). De hecho, se puede argumentar que el GF en esencia no recibe ninguna retroalimentación o, en el mejor de los casos, que la retroalimentación tiene mucho ruido. ¿Cómo aprende el GF a resolver, de una manera "como si", estas complejas ecuaciones cuando solo puede hacer tan pocos experimentos y recibe tan poca retroalimentación?17.
Otra diferencia crítica entre GF y billaristas se relaciona con el hecho de que conocemos con detalles muy precisos el juego que juega el billarista experto, pero no conocemos todos los detalles del "juego" que juega el GF. Un grupo de físicos en el que todos trabajen de manera independiente dará básicamente la misma explicación (conjunto de fórmulas) de cómo tacará un billarista experto en una circunstancia dada. Esto se debe a que las dimensiones de la mesa se dan con exactitud junto con los demás detalles del entorno físico y lo que se considera éxito es también conocido porque es dado por las reglas explícitas del juego. Un grupo de economistas financieros en el que todos trabajen independientemente para predecir qué hace un GF "experto" dará muchas descripciones y fórmulas conflictivas diferentes. Esto se debe a que el "juego" al que juega un GF (aun si suponemos que es un súper humano "experto" capaz de resolver los problemas de programación más complicados) se juega en un entorno que no se define con precisión (por cierto, no de la misma manera que la mesa de billar) y no sabemos de manera confiable cuáles son los objetivos (¿se busca maximizar el valor del accionista, o las preferencias conflictivas de los directivos juegan algún papel?).
Quienes plantean modelos dinámicos de estructura del capital primero deben conjeturar la naturaleza del juego que se está jugando y las dimensiones de la mesa en que se juega. Luego deben suponer -si el modelo se ha de considerar como un modelo positivo- que los GF y otros tomadores de decisiones que juegan el juego postulado toman decisiones "como si" pudiesen resolver los complicados problemas de programación dinámica.
La pregunta que se debería hacer es si estos supuestos son razonables. ¿Qué base tenemos para creer que los GF toman decisiones "como si" tuviesen que resolver complicados problemas de control estocástico? He oído decir que deberíamos confiar en algún fenómeno de "sabiduría popular" o efecto similar que haría "como si" fuese cierto "en promedio" que los GF resuelven problemas de control estocástico. Es cierto que si se pidiera a cien personas que adivinen cuántos caramelos hay en un frasco, es probable que el promedio de sus conjeturas sea cercano al número verdadero y que sea mejor que la mayoría de las conjeturas individuales. Pero si preguntamos a cien o un millón de personas que adivinen el dígito 10100 de la expansión decimal de p, la conjetura promedio no será mejor que cualquier conjetura individual. Tenemos buenas razones (y evidencia) para creer que un individuo (incluso de 10 años de edad) puede hacer una conjetura razonable del número de caramelos que hay en un frasco y que al promediar esas conjeturas los errores tienden a "compensarse". Podríamos suponer que las personas pueden estimar de algún modo el dígito 10100 de p "como si" fuesen supercomputadores mucho más poderosos que los que hoy tenemos, pero este argumento "como si" no nos debería dar confianza en la conjetura promedio de tal dígito. Simplemente no tenemos fundamento para suponer que los individuos tienen capacidad para adivinar la identidad del dígito 10100 de p. ¿Qué fundamento tenemos para creer que los GF y otros gerentes pueden resolver problemas de programación sumamente complicados que en últimas se deben resolver numéricamente en un computador usando programas que un investigador tarda semanas o meses para escribir? Al menos sería razonable preguntar a algunos GF si esos son los problemas que están resolviendo y cómo los resuelven18. Resolver estos problemas es menos difícil que determinar el dígito 10100 de p, pero está lejos de ser obvio que sea razonable suponer que los GF los están resolviendo, así sea heurísticamente.
Todos los argumentos que he escuchado respecto de por qué podemos suponer que los GF actúan "como si" tuviesen habilidades extraordinarias parecen débiles, muy débiles, mucho más débiles que cuando el argumento "como si" se aplica al jugador de billar cuyas habilidades "como si" se basan en miles de horas de juego y retroa-limentación inmediata. No digo que el argumento "como si" nunca se aplique para entender lo que hacen los agentes económicos, solo digo que requiere más apoyo que encoger los hombros o pensar con el deseo. Los supuestos "como si" deben ser respaldados por lo que sabemos del mundo real. Deben pasar por el filtro19.
8. SUTILEZA, ELEGANCIA MATEMÁTICA, COMPLEJIDAD Y MANEJABILIDAD
Muchos resultados importantes en economía y finanzas no son obvios. Para un economista educado, la teoría de la ventaja comparativa en el comercio es muy simple; para muchas personas es desconcertante, intrigante y difícil de aceptar. Los resultados de irrelevancia de Modigliani y Miller son difíciles de explicar incluso a los mejores estudiantes y solo son plenamente internalizados por unos cuantos. Muchos resultados en finanzas y economía son contraintuitivos y dependen de interacciones y tradeoffs muy complicados.
Las teorías "profundas" que producen resultados sorprendentes son intrínsecamente interesantes y, sin duda, es entretenido desarrollarlas y exponerlas. Las explicaciones que involucran un razonamiento sutil y complejo parecen tener, al menos en la mente de algunas personas, un estatus más alto que el de las que son más simples y directas. Por supuesto, la sutileza en sí y por sí misma no se debe considerar una virtud cuando se trata de juzgar la contribución de un modelo o una teoría a nuestra comprensión del mundo. No hay ninguna razón para suponer que la explicación de algo debe ser sutil ni para suponer que un modelo más sutil y más profundo es mejor que un modelo rival menos profundo y menos sutil.
Dado que no se atribuye mucho prestigio y honor a quienes plantean modelos simples y obvios para explicar o entender fenómenos económicos, hay un sesgo hacia los modelos profundos y sutiles. Ligada a esto hay una preferencia por la "elegancia" o "sofisticación" matemática20. Las matemáticas han proporcionado herramientas útiles para analizar problemas difíciles que surgen en finanzas y economía, y no estoy sugiriendo que nos deberíamos limitar al razonamiento "verbal" y tampoco que la sutileza y la elegancia matemáticas sean cosas que se deben evitar: una explicación correcta puede ser de hecho muy sutil e incluso matemáticamente elegante21. Mi punto es simple: el uso habilidoso de herramientas matemáticas y el logro de sutileza no deberían ser las fuerzas que impulsan la elaboración de modelos. Aún más importante, cuando sacamos un modelo del cajón con la intención de aplicarlo al mundo real, la sutileza y la elegancia matemática nada tienen que ver con cuán bien capta el modelo lo que es importante en la realidad. Se suele atribuir a Albert Einstein la frase "Hacer las cosas tan simples como sea posible, pero no más simples" (aunque no hay evidencia convincente de que la haya pronunciado)22. En mi opinión, un corolario importante es: "Hacer las cosas tan sutiles como sea necesario, pero no más sutiles".
Así como la sutileza y la sofisticación matemática -en y por sí mismas- no hacen mejor un modelo para explicar nuestro mundo real, tampoco lo hace la complejidad. Mientras que un modelo puede tener que involucrar algunas "partes móviles" para captar los factores económicos importantes en juego, los modelos que se construyen con un enorme número de supuestos dudosos no son más útiles que los que se construyen con pocos supuestos. Aunque el mundo real es complejo, eso no significa que todo paso hacia la complejidad en la modelación nos lleve necesariamente más cerca de entender los fenómenos económicos que estamos considerando. No sé de nadie que argumente expresamente que la complejidad es una virtud en sí misma, pero veo que a veces la complejidad sirve como cortina de humo para que surjan camaleones. Es probable que un modelo simple con un supuesto dudoso que orienta los resultados sea reconocido como lo que es. Es más difícil evaluar un modelo más complicado con muchos supuestos, incluido el supuesto dudoso mencionado. El supuesto dudoso no solo no se destaca tanto como en el modelo simple, sino que suele ser más difícil determinar cuán importante es para orientar los resultados. Esto es cierto en particular en modelos complejos que se calibran numéricamente para aproximar lo que observamos. La importancia del supuesto dudoso para el éxito del ejercicio de calibración no siempre es clara y el éxito de ese ejercicio puede ser aprovechado en forma ligera para ocultar el carácter dudoso del supuesto. Estos problemas solo se magnifican cuando el modelo está conformado por muchos supuestos dudosos.
Por último, a menudo se sostiene que los supuestos son necesarios para que los modelos sean manejables. Todo el mundo entiende que es muy posible que un supuesto que se haga con este fin sea un supuesto que nos aleja de lo que puede ser importante en el mundo real y reduce potencialmente la posibilidad de aplicar el modelo y sus resultados. Todos sabemos que no tiene sentido buscar las llaves perdidas debajo del farol cuando sabemos que se perdieron donde hay oscuridad. A pesar de ello y quizá por simpatía con el teórico y por saber cuán difícil es elaborar modelos manejables, se tiende a restar importancia a la brecha entre supuestos manejables y lo que sabemos del mundo real. Si el objetivo es construir un modelo de cajón que mediante su argumento lógico nos proporcione intuiciones, estos supuestos manejables (o "estilizados") pueden ser una virtud y no un problema. Pero si el modelo se va a aplicar al mundo real, la manejabilidad, así como la sutileza, la elegancia matemática y la complejidad, no debería ser un pase gratuito que permita eludir el filtro.
9. POR QUÉ LOS MODELOS EN FINANZAS Y ECONOMÍA NO SON COMO LOS MODELOS EN MECÁNICA CUÁNTICA
Más atrás argumenté que antes de aplicar modelos económicos teóricos al mundo real debemos evaluarlos críticamente para ver qué tan bien pasan los filtros del mundo real. Se podría pensar que esto no es habitual en las ciencias duras. En particular podría parecer que el éxito de los modelos en campos tales como la mecánica cuántica muestra que no debemos juzgar los modelos considerando si sus supuestos son razonables o si los modelos son plausibles. Después de todo, en mecánica cuántica casi todo parece desafiar el sentido común. A Richard Feynman se le atribuye la frase: "Si piensa que entiende la mecánica cuántica, no entiende la mecánica cuántica". Los modelos de mecánica cuántica son bien aceptados debido a la solidez de sus predicciones, no a la "sensatez" de sus supuestos.
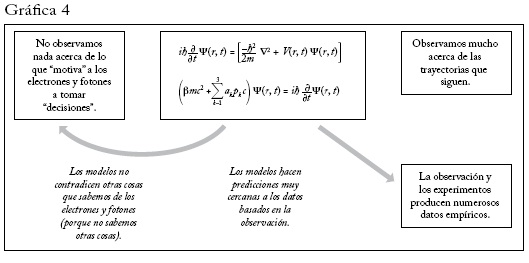
Hay, sin embargo, grandes diferencias entre el contexto en que se aplican los modelos de mecánica cuántica y aquellos en que intentamos aplicar modelos económicos. La gráfica 4 describe cómo se usan los modelos en mecánica cuántica. No recibimos información acerca de lo que "motiva" a los electrones y fotones a tomar "decisiones", pero vemos los resultados de esas "decisiones" en las trayectorias que siguen y en otras evidencias basadas en la observación. Por supuesto, es absurdo antropomorfizar a los electrones y fotones y pensar que toman decisiones. El punto clave es que toda nuestra evidencia observacional se basa en las interacciones que estas partículas tienen con otras partículas, y que podemos producir numerosos datos mediante observaciones y experimentos. En mecánica cuántica los modelos han tenido extraordinario éxito para hacer predicciones, y estas predicciones son coherentes con lo que se mide en los experimentos hasta muchos lugares decimales.
Aún más importante, los modelos de mecánica cuántica no contradicen abiertamente nada que sepamos de los electrones y fotones. Son básicamente coherentes con todo lo que se observa. Si surgiese una incoherencia sistemática entre lo que suponen los modelos y lo que se observa, los modelos se considerarían incompletos o defectuosos y se harían esfuerzos para corregirlos23.
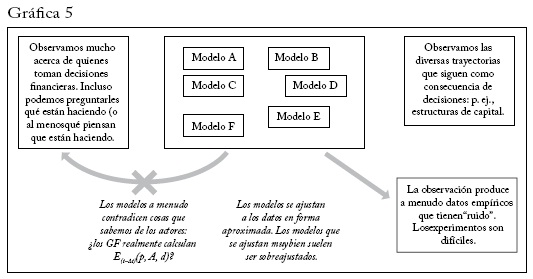
Examinemos ahora modelos que se usan a menudo en finanzas o economía. Creo que la gráfica 5 es una buena descripción de lo que enfrentamos en muchos casos. Es frecuente tener modelos rivales (p. ej., los modelos A a F) que son más o menos coherentes con algunos aspectos de lo que observamos (p. ej., ciertos patrones de decisiones de estructura de capital). La cantidad de datos que tenemos suele ser muy limitada (pero no siempre) y los problemas de endogeneidad en general hacen difícil probar los modelos y discriminar entre ellos. (Tenemos justificación para sospechar de los modelos que se ajustan sumamente bien a los datos porque pueden ser sobreajustados.) Un grave problema es que los modelos a menudo se basan en supuestos o tienen implicaciones que contradicen cosas que sabemos de quienes toman decisiones económicas o de otros fenómenos económicos que observamos. Como argumenté más atrás, no es justificado ignorar o desestimar estas contradicciones y no es una buena costumbre para elaborar modelos y teorías que sean útiles para mejorar la comprensión de nuestra economía.
Los agentes económicos (es decir, los seres humanos) son mucho más complicados que los electrones y fotones e interactúan en contextos que son mucho más complejos y cambian continuamente. Incluso es posible que el desarrollo de una teoría económica o la publicación de un artículo académico sobre economía puedan alterar el comportamiento de estos agentes. No se puede decir que los electrones o fotones alteren su comportamiento con base en lo que pueda escribir un físico. Esto significa que el desarrollo de modelos útiles en economía y finanzas involucra retos que no se encuentran en mecánica cuántica y otros campos de investigación en física y ciencias duras, donde en general se dispone de muchos más datos y, al menos en muchos casos, son posibles los experimentos controlados.
Debido a estos mayores desafíos, los modelos en economía y finanzas son por necesidad simplificaciones y abstraen mucha de la complejidad del campo que pretenden explicar. Esto significa que habrá tensiones entre lo que suponen estos modelos y las cosas que sabemos que son ciertas. El hecho de que este sea el caso no quiere decir que debamos ignorar estas tensiones. Cuando los principales impulsores de los resultados de un modelo no se pueden conectar con lo que vemos en el mundo real, tenemos justificación para cuestionar la utilidad del modelo como explicación de lo que vemos. Esto es cierto incluso cuando las predicciones del modelo son respaldadas por pruebas empíricas. Cuando el modelo ignora factores que tenemos buena razón para creer que son de importancia de primer orden, también tenemos justificación para cuestionar la utilidad del modelo. Enfrentar estas tensiones es una mejor manera de avanzar que ocultarlas.
CONCLUSIÓN
Los argumentos que expongo en este ensayo se basan en una afirmación simple y -según creo- incontrovertible: cuando se usan modelos económicos para entender la economía no debemos ignorar o descartar el conocimiento previo que tenemos del mundo real. Aunque algunos modelos teóricos pueden ser muy útiles para generar intuiciones, un modelo teórico en esencia solo argumenta que un conjunto de conclusiones se deduce de un conjunto dado de supuestos. El que sea lógicamente correcto le puede ganar un lugar dentro del cajón de modelos teóricos, pero cuando se saca del cajón y se aplica al mundo real es necesario preguntar si sus supuestos concuerdan con lo que sabemos del mundo. ¿La historia que está detrás del modelo capta lo que es importante o es una ficción que tiene poca conexión con lo que vemos en la práctica? ¿Se han omitido factores importantes? ¿Se supone que los agentes económicos hacen cosas de las que tenemos serias dudas que puedan hacer? Estas preguntas y otras semejantes nos permiten filtrar los modelos inadecuados para darnos intuiciones auténticas. Para que se tomen en serio los modelos deben pasar por el filtro del mundo real.
Los camaleones son modelos que se presentan como si dijesen algo significativo del mundo real aunque no pasen el filtro. Cuando se cuestionan los supuestos de un camaleón, se recurre a diversas defensas (p. ej., que no se debe juzgar un modelo por sus supuestos, que un modelo está en pie de igualdad con los demás modelos hasta que se hayan hecho pruebas empíricas apropiadas, etc.). En muchos casos el camaleón cambiará de colores según sea necesario, adoptando los colores de un modelo de cajón cuando es cuestionado, pero volviendo a los colores de un modelo que se pretende aplicar al mundo real cuando no es cuestionado.
Aunque más atrás di ejemplos de camaleones y de casos donde pienso que es bastante claro que los supuestos no son sometidos al filtro del mundo real tanto como se debería (p. ej., algunos supuestos "como si"), no afirmo que en la práctica nunca se empleen filtros. Mi experiencia ha sido que cuando se presentan escritos en seminarios y conferencias, los supuestos de los modelos y teorías de esos escritos en general son cotejados con el mundo real y cuestionados, a menudo agresivamente, por una audiencia escéptica. Aunque esto es cierto, veo muchos casos donde se da un pase a los camaleones. Por ejemplo, a menudo he oído defender un supuesto con la afirmación "es el supuesto estándar en la literatura". De hecho, el expositor a veces intenta evitar la necesidad de defender el supuesto presentándolo con la frase "como es estándar en la literatura". Si el modelo solo se presentara como un modelo de cajón, decir que es estándar en la literatura no sería un grave problema. Si el modelo solo se va a usar como un modelo cajón, se puede considerar que facilita la exploración del terreno "lógicamente posible" en la vecindad de lo que otros autores han explorado cuando hacen los mismos supuestos "estándar en la literatura". Pero si se nos pide que tomemos el modelo como algo que se puede aplicar al mundo real, un supuesto no se puede defender diciendo simplemente que otros lo han supuesto.
En una conferencia a la que asistí no hace mucho, el comentarista de un artículo dijo que su autor había hecho un mal trabajo intentando defender uno de los supuestos de su modelo. Y luego dijo que el autor debería "simplemente hacer el supuesto y seguir adelante". La implicación parecía ser que como el supuesto en cuestión era difícil de defender, era mejor no llamar la atención del lector armando una defensa muy débil. Quizá este fuera un "buen" consejo para construir un modelo de cajón y eludir a un árbitro editorial, pero lo caracterizaría como una estrategia para convertir el modelo del artículo en camaleón, un modelo dirigido a eludir el filtro.
Como ya señalé, aunque un modelo sea internamente coherente, aunque sea sutil y el análisis sea matemáticamente elegante, nada de eso garantiza que sea aplicable al mundo real. Se podría pensar que la aplicabilidad o "verdad" de un modelo teórico siempre puede ser establecida por un análisis empírico formal que pruebe las hipótesis comprobables del modelo, pero esto es un tanto fantástico. La comprobación empírica formal, por supuesto, se debe buscar enérgicamente, pero la falta de datos y de experimentos naturales limita en muchos casos nuestra capacidad para elegir entre modelos rivales. Además, aunque podamos comprobar formalmente algunas hipótesis de esos modelos rivales, los resultados de estas pruebas solo permiten rechazar algunos de ellos, dejando varios sobrevivientes que tienen implicaciones diferentes sobre asuntos que no podemos comprobar. Los filtros del mundo real son esenciales en todos estos casos.
Sospecho que algunas personas se sentirán incómodas con la idea de aplicar filtros del mundo real a los modelos, sobre todo porque no hay criterios formales disponibles para determinar cuáles deberían ser esos filtros ni una manera inequívoca de establecer el umbral que determine lo que se debería permitir que pase por ellos. Para algunas, esto parecerá muy subjetivo y por tanto inadmisible en lo que nos gusta ver como un campo de investigación que usa métodos "objetivos". Esta no es una objeción defendible. Como ya mencioné, los filtros que discuto se pueden interpretar como precedentes bayesianos. Toda persona razonable pone un precedente muy bajo (esencialmente cero) a la estatura de los actores masculinos en el año t-1 para determinar la tasa de inflación de Estados Unidos en el año t. Se necesitaría una cantidad extraordinaria de datos en contra para alterar esos precedentes en forma visible. Descartar el uso de filtros porque son demasiado subjetivos significa decir que debemos evaluar todos los modelos con base en un precedente bayesiano agnóstico (uniforme), cualquier cosa que esto signifique. (Es "igualmente probable" que la inflación de Estados Unidos esté determinada por la estatura de los actores masculinos o por las acciones de los bancos centrales.) Es obvio que en la práctica no realizamos nuestra investigación como si tuviésemos estos precedentes agnósticos o uniformes. Rutinariamente tenemos en cuenta estos precedentes. Ahora bien, es cierto que las personas no tienen exactamente los mismos precedentes y que "las personas razonables pueden no estar de acuerdo", pero esto no abre la puerta para tomar en serio modelos cuyos supuestos contradicen gravemente lo que vemos en el mundo real e ignoran factores que sabemos son de importancia de primer orden. Un modelo que afirma que el "alto" apalancamiento es óptimo para los bancos mientras que ignora casi todo lo que sabemos que es importante es un modelo de cajón. No es un modelo que pueda pasar un filtro razonable del mundo real porque es contrario a toda la información previa que tenemos del mundo, información que usamos para formar precedentes razonables.
Pie de página
1Al examinar las diversas maneras en que un modelo es irrealista a veces se puede hacer una distinción útil entre idealización aristotélica y galileana. La primera ignora ciertos aspectos de un contexto que, al menos para el problema en cuestión, no se consideran de primer orden de importancia. Por ejemplo, en ciertos contextos se pueden ignorar o "abstraer" los costos de transacción. La idealización galileana involucra distorsiones deliberadas diseñadas para que el modelo sea más simple y más fácil de resolver. Por ejemplo, para hacer más manejable un modelo se podría suponer que los agentes viven infinitamente, aunque sabemos que esta es una distorsión. Este tipo de distinción se hace en Gibbard y Varian (1978), donde los modelos se dividen en "aproximaciones" (idealización aristotélica) y "caricaturas" (idealización galileana). Ellos explican que las caricaturas "buscan "dar una impresión" de algún aspecto de la realidad económica no describiéndola directamente, sino subrayando -aun hasta el punto de distorsionarla- ciertos aspectos de la situación económica".
2La selección no es necesariamente el resultado de un diseño consciente. Para evitar esto puede ser necesario que el investigador dé un paso atrás y se pregunte si los supuestos son involuntariamente artificiosos y sirven más para producir el resultado particular que para simplificar el análisis.
3Gilboa et al. (2013) hacen varias observaciones interesantes que explican el valor potencial de muchos modelos de cajón. Ellos sugieren que los modelos teóricos a menudo son útiles porque crean casos que se pueden usar analógicamente para analizar problemas del mundo real. Los modelos teóricos elaborados con este propósito se pueden considerar como experimentos mentales que enriquecen el conjunto de resultados que los economistas tienen a disposición para hacer predicciones y abordar problemas de política. El modelo de los limones de Akerlof y el modelo de señalamiento de Spence son buenos ejemplos. Al aplicar estos modelos de experimento mental a asuntos específicos del mundo real, la preocupación clave es la fuerza de la analogía. Esta depende de cuán bien pasa el modelo los filtros del mundo real que discuto más adelante.
4En general, las preguntas de política involucran dos consideraciones. Primero se debe determinar qué resultados se pueden lograr y cómo lograrlos (qué acciones se deben emprender para lograrlos). En segundo lugar se debe determinar qué resultado, entre los que se pueden lograr, es el más deseable. Esta última consideración, en especial cuando se trata de política social, suele involucrar juicios de valor (p. ej., justicia) y cae de lleno en el campo de la economía normativa. Lo que intento captar en el lado derecho es la primera consideración, la cual es independiente de los juicios de valor. En otras palabras, supongo que los juicios de valor están dados, y me centro en la decisión de política que lleve al resultado más deseable tal como lo definen estos supuestos normativos.
5Como sin duda ha sospechado el lector, este es un artículo ficticio.
6Para una discusión adicional del uso indebido del artículo de DeAngelo y Stulz, ver Admati (2013).
7Para un análisis mucho más extenso de los diversos problemas que se encuentran al aplicar la noción de que la deuda tiene un efecto disciplinante para la banca moderna en el mundo real, ver Admati (2013), Admati et al. (2013) y Admati y Hellwig (2013).
8El lector podría objetar que si Jamie Diamond intentara hurtar 6.200 millones al banco, los accionistas (a través de la Junta Directiva) simplemente contratarían a otro equipo administrativo. La suma que Jamie Diamond podría hurtar al banco está limitada por la pérdida en que el banco incurriría al contratar un equipo externo, y esta podría ser menor de 6.200 millones. Todo esto es cierto y simplemente refuerza el argumento que planteo. Si el valor máximo que Jamie Diamond podría hurtar al banco son 400 millones, podría sustraer este valor sin generar una corrida puesto que 400 millones es mucho menos que 6.200 millones. Para evitar este hurto de 400 millones el banco debe ser aún más frágil.
9Este argumento también se aplica al modelo de Calomiris y Kahn, porque podemos suponer que los depositantes en JP Morgan tendrían poco o ningún incentivo para supervisar el banco a fin de asegurar que los altos ejecutivos no se fuguen con 6.200 millones.
10Ver Bear y Orr (1967), Boland (1979), Caldwell (1982 y 1984), Hausman (1989), Machlup (1955), Máki (2009), Melitz (1965) y Samuelson (1963). Las controversias suscitadas por el artículo de Friedman están relacionadas con el debate entre una visión "realista" y una visión "instrumentalista" de la ciencia. Para la primera, el objetivo de la investigación científica es descubrir la realidad subyacente del mundo tal como es, mientras que para la segunda el objetivo es menos ambicioso: producir un conjunto de herramientas que hagan posible hacer predicciones útiles. Reiss (2012), por ejemplo, argumenta a favor del enfoque ins-trumentalista en economía. No es mi intención abordar en forma sistemática los muchos asuntos que se plantean en el debate realista/instrumentalista. Aquí solo argumento que esa interpretación literal de la visión instrumentalista planteada por Friedman no es defendible, y que sus argumentos no dan cobijo para que los modelos se conviertan en camaleones. Si bien es cierto que muchos de quienes han escrito sobre asuntos metodológicos en economía en las últimas décadas no defienden el punto de vista de Friedman (Hausman dice que "se dará un paso adelante cuando los economistas lleguen a ver el artículo de Friedman únicamente como un documento históricamente interesante"), la idea de que el realismo de los supuestos de un modelo no es importante, que solo lo es su poder de predicción, aún parece ser aceptada y creo necesario abordarla aquí.
11Para ser justos, en una nota de pie Friedman dice: "la proposición inversa no es válida: los supuestos que son irrealistas (en este sentido) no garantizan una teoría significativa". Pero a pesar de esta cualificación, Friedman sigue sugiriendo que un conjunto de supuestos muy irrealistas puede ser la base de una teoría "significativa" y parece sostener que el irrealismo es una virtud. Nada de esto nos da una guía para determinar cuál (si hay alguno) del enorme número de modelos que hacen predicciones "exactas" con supuestos muy irrealistas se debería tomar en serio. En otras partes de su artículo sugiere que deberíamos valorar más los modelos simples que los más complejos, pero esto no nos lleva muy lejos porque algunos de los mejores modelos de predicción pueden ser muy "simples", y quizá depender de una sola variable, como la altura de los actores masculinos.
12En su cuento "La biblioteca de Babel", Jorge Luis Borges habla de una biblioteca inútil que contiene todos los KN libros que se pueden escribir con K caracteres (letras y signos de puntuación) y que tienen una longitud dada de N caracteres.
13Otro problema de basarse en pruebas empíricas para separar los buenos modelos de los malos modelos en una larga lista de modelos rivales se relaciona con la tesis de la indeterminación de las teorías científicas de Quine-Duhem. Puesto que normalmente se deben hacer numerosos supuestos adicionales a los que hace una teoría cuando esta se somete a comprobación, los resultados negativos no necesariamente refutan la teoría porque se pueden atribuir a uno de estos supuestos auxiliares. Una buena ilustración en finanzas es la de los intentos de comprobar la hipótesis del mercado eficiente. Como bien se sabe, las pruebas de esta hipótesis son en general pruebas de las hipótesis conjuntas de eficiencia del mercado y de un modelo particular de fijación de precios de activos. Cualquier resultado negativo siempre se puede interpretar como un rechazo del modelo de fijación de precios de activos y no de la hipótesis de eficiencia del mercado.
14Por ejemplo, los gerentes, por ser humanos, tienen "ancho de banda limitado". El supuesto de que las oportunidades de estafa son posibles no se puede descartar, aunque se pueda cuestionar su importancia. Cabe señalar que así la mala conducta gerencial sea o no importante en la práctica real, en muchos escritos sobre banca se hace este supuesto en diversas formas, como en Calomiris y Kahn (1991), artículo que ya comenté. El supuesto de que estructuras de obligaciones más complejas requieren más atención administrativa es plausible.
15Es necesario distinguir entre lo que es privadamente óptimo (es decir, lo que maximiza el tamaño del pastel disponible para las partes involucradas en la contratación) y lo que es socialmente óptimo (donde se tiene en cuenta a todas las partes, no solo a las involucradas en la contratación). Aunque es indiscutible que la contratación privada no siempre lleva a un óptimo social, la distinción entre privado y social a veces se pasa por alto, y a veces parece suponerse implícitamente que lo que surja será socialmente óptimo. Mi punto aquí es que en muchos contextos es dudoso incluso el supuesto de que el resultado será privadamente óptimo.
16El argumento involucra la falacia de afirmar el consecuente. De las dos afirmaciones "si P entonces Q" y "Q", no se puede concluir "P". Por ello, aun si (A1, A2, A3..., AN) implica la configuración observada, el hecho de que la configuración observada se mantenga no permite concluir que (A1, A2, A3..., AN) se cumple.
17Puede existir la tentación de argumentar que mientras que un GF individual solo hace pocos experimentos con retroalimentación limitada, hay más información potencialmente disponible si consideramos todos los experimentos realizados por los GF. Quizá con el tiempo esta información se agregue de algún modo en "reglas empíricas" que lleguen a formar parte del saber que se transmite a los GF. Los teóricos que formulan, calibran y resuelven complicados problemas de programación dinámica darían entonces luz sobre los fenómenos que surgen entre los GF que siguen estas reglas empíricas. Hay dos problemas en usar esto como justificación para adoptar un enfoque "como si". Primero y más importante, las complicadas soluciones a problemas de programación dinámica que se basan en numerosos parámetros en general no se pueden condensar en reglas empíricas simples. Segundo, si estamos interesados en predecir cómo se toman (y no cómo se deberían tomar) las decisiones de estructura de capital, y creemos que las toman GF que siguen reglas empíricas, ¿no sería más fácil (y más confiable) entrevistar GF y preguntarles qué reglas empíricas siguen?
18Cuando sugiero que podría ser razonable preguntar a los GF qué problema de control estocástico creen que están resolviendo, la respuesta que suelo recibir invoca la afirmación de que no se debe juzgar un modelo por el realismo de los supuestos o una frase que hace eco al argumento de Friedman, "como si" los GF se comportasen (en promedio) como si pudieran resolver estos complicados problemas.
19Aunque me he centrado en las decisiones de estructura del capital para dar ejemplos donde la aplicación del argumento "como si" es dudosa, hay muchos otros casos donde suponemos que los agentes económicos resuelven problemas muy complejos con retroalimentación limitada. En muchos de ellos la suposición "como si" en que se fundan esos supuestos merece más escrutinio del que suele recibir. Por ejemplo, en modelos teóricos de fijación de precios de activos a menudo se supone que los inversionistas resuelven complicados problemas de optimización dinámica que incluyen preferencias complejas sobre corrientes de consumo a lo largo del ciclo de vida y riesgos difíciles de medir. Si bien es cierto que muchos inversionistas delegan estos problemas a administradores de inversión profesionales, que quizá tengan algo más de capacidad para resolver estos problemas que los inversionistas "ingenuos", sigue siendo dudoso que los asesores financieros y administradores profesionales de valores estén resolviendo los problemas de inversión que postulan muchos modelos de fijación de precios de activos, aunque tengan la capacidad para resolverlos. En primer lugar, estos administradores tienen incentivos propios y no es claro que concuerden con los de los inversionistas principales. En segundo lugar, deben promover la venta de sus servicios de un modo que los inversionistas puedan entender y en general miden su desempeño en formas más simples de las que serían consistentes con los modelos postulados. Para más discusión, ver Cornell y Hsu (2014).
20Esto guarda relación con la observación de Caballero (2010) de que se da una prima potencialmente inmerecida a la precisión, al menos entre los ma-croeconomistas que usan modelos de equilibrio general dinámico estocástico. Señala que se tiende a confundir la precisión que estos modelos han alcanzado con respecto a su propio mundo con la precisión que se puede aplicar al mundo real. La interpreto como una afirmación de que esos modelos se han convertido en cierto sentido en camaleones, donde la precisión de sus resultados se aplica falsamente porque no se ha tenido en mente una apreciación completa de los límites de los modelos derivada de hacerlos pasar por filtros del mundo real.
21Algunos físicos parecen creer (o tener la esperanza) que las explicaciones últimas de nuestro mundo físico serán matemáticamente elegantes y simples. Las explicaciones que carecen de esta cualidad suelen ser vistas con sospecha. No sé de alguien que afirme que las explicaciones últimas en ciencias sociales serán necesariamente elegantes y simples matemáticamente, y parece haber pocas razones para creer que lo serán. En ciencias sociales parece claro que la elegancia matemática no es necesaria ni suficiente, y no puede ser un criterio guía.
22La idea de que la simplicidad es deseable se remonta a la navaja de Occam y al dictum de que "las entidades no se deben multiplicar más allá de lo necesario".
23Es bien sabido, sin embargo, que en su estado actual la teoría cuántica no se puede unificar con la teoría de la relatividad general, y esto ha llevado a buscar una teoría cuántica de la gravedad que describa la gravedad en términos de mecánica cuántica.
REFERENCIAS BIBLIOGRÁFICAS
1. Admati, A. R. "The compelling case for stronger and more effective leverage regulation in banking", Stanford working paper, 2013. [ Links ]
2. Admati, A. R.; P. M. DeMarzo et al. "Fallacies, irrelevant facts, and myths in the discussion of capital regulation: Why bank equity is not socially expensive", Stanford working paper, 2013. [ Links ]
3. Admati, A. R. y M. F. Hellwig. "Does debt discipline bankers? An academic myth about bank indebtedness", Stanford University, 2013. [ Links ]
4. Bear, D. V. T. y D. Orr. "Logic and expediency in economic theorizing", Journal of Political Economy 75, 1967, pp. 188-196. [ Links ]
5. Boland, L. A. "A critique of Friedman's critics", Journal of Economic Literature 17, 2, 1979, pp. 503-522. [ Links ]
6. Caballero, R. J. "Macroeconomics after the crisis: Time to deal with the pretense-of-knowledge syndrome", Journal of Economic Perspectives 24, 4, 2010, pp. 85-102. [ Links ]
7. Caldwell, B. Beyond positivism: Economic methodology in the Twentieth Century, Nueva York, Allen and Unwin, 1982. [ Links ]
8. Caldwell, B. ed. Appraisal and criticism in economics, Londres, Allen and Unwin, 1984. [ Links ]
9. Calomiris, C. WW. y C. M. Kahn. "The role of demandable debt in structuring optimal banking arrangements", American Economic Review 81, 3, 1991, pp. 497-513. [ Links ]
10. Cornell, B. y J. Hsu. "The 'machinery' of asset pricing and its implications", working paper, 2014, [http://papers.ssrn.com/sol3/papers.cfm?abstract_id=2374441] [ Links ].
11. DeAngelo, H. y R. M. Stulz. "Why high leverage is optimal for banks", Fisher College of Business working paper, agosto de 2013. [ Links ]
12. Diamond, D. W y R. G. Rajan. "A theory of bank capital", Journal of Finance 55, 6, 2000, pp. 2431-2465. [ Links ]
13. French, K. R. et al. The Squam Lake Report: Fixing the financial system, Princeton, NJ, Princeton University Press, 2010. [ Links ]
14. Friedman, M. "The methodology of positive economics", The methodology of positive economics, Chicago, University of Chicago Press, 1953, pp. 3-43. [ Links ]
15. Gilboa, I.; A. Postlewaite et al. "Economic models as analogies", PIER working paper, 2013. [ Links ]
16. Hausman, D. M. "Economic methodology in a nutshell", Journal of Economic Perspectives 3, 2, 1989, pp. 115-127. [ Links ]
17. Machlup, F. "The problem of verification in economics", Southern Economic Journal 22, 1, 1955, pp. 1-21. [ Links ]
18. Máki, U. "Unrealistic assumptions and unnecessary confusions: Rereading and rewriting F53 as a realist statement", The methodology of positive economics: Reflections on the Milton Friedman legacy, Cambridge, Cambridge University Press, 2009, pp. 90-116. [ Links ]
19. Melitz, J. "Friedman and Machlup on the significance of testing economic assumptions", Journal of Political Economy 73, 1965, pp. 37-60. [ Links ]
20. Reiss, J. "Idealization and the aims of economics: Three cheers for instrumentalism", Economics and Philosophy 28, 3, 2012, pp. 363-383. [ Links ]
21. Samuelson, P. "Problems of methodology - Discussion", American Economic Review 53, 2, 1963, pp. 231-236. [ Links ]
22. Titman, S. y S. Tsyplakov, "A dynamic model of optimal capital structure", Review of Finance 11, 3, 2007, pp. 401-451. [ Links ]