El objetivo es iluminar la verdad acerca de la toma de decisiones a modo de dar luces sobre la relación de las decisiones. La estrategia no es preguntar lo qué es una decisión; con la esperanza de una teoría metafísica sobre lo que la naturaleza es. Es, más bien, observar primero el lenguaje de las decisiones. La metáfora detrás de la toma de decisiones se remite a la agencia. No es absurdo, sin embargo, proponer que el concepto de toma de decisiones de alguna manera se desprende de una característica que tiene que ver con la agencia. Esta es la afirmación que explora este trabajo. La manera de hacerlo es a través del expresivismo. La verdad en la toma de decisiones hace que las reclamaciones, en general, sean reclamaciones en las que expresamos estados mentales vinculados a nuestra manipulación de conceptos, como la verdad. En particular, estos expresan la disposición para llevar a cabo derivaciones utilizando reglas de inferencia, en las cuales la introducción de reglas tiene un papel específico. A continuación, se muestra cómo esta teoría explica nuestras intuiciones sobre la dependencia asimétrica de la verdad sobre el ser.

Agencia, prescripciones causales, expresivismo, manipulación, toma, verdad, la verdad en la toma de decisiones, introducción de reglas del conocimiento.

My goal is to illuminate truth-making by way of illuminating the relation of making. My strategy is not to ask what making is; in the hope of a metaphysical theory about is nature. It's rather to look first to the language of making. The metaphor behind making refers to agency. It would be absurd to suggest that claims about making are claims about agency. It is not absurd, however, to propose that the concept of making somehow emerges from some feature to do with agency. That's the contention to be explored in this paper. The way to do this is through expressivism. Truth-making claims, and making-claims generally, are claims in which we express mental states linked to our manipulation of concepts, like truth. In particular, they express disposition to undertake derivations using inference rules, in which introduction rules have a specific role. I then show how this theory explains our intuitions about truth's asymmetric dependence on being.

Agency, causal recipes, expressivism, manipulation, making, truth, truth-making, introduction rules grounding.

The facts of truth are not primitive facts. Unless we accept the identity theory of truth –and equate truth and fact– the fact that a proposition is true must obtains in virtue of something: how things are with its subject matter¹. We might express this thought as the idea that truth supervenes on, is asymmetrically determined by, being (Cf. Bigelow). But that would be misleading, since it suggests that truth is not part of being. The facts of truth, those certain propositions are true or false, are part of how things are, and so, and are aspects of being. We should say rather that the facts of truth, the alethic facts, are made the case by non-alethic facts. (Still, as we shall see, that claim will need qualification.) Viewed in this way, the problem of truth-making reduces to the problem of making. What's making?

We are very familiar with causal making, that is, causation. It occurs through time linking events. Non-causal making is atemporal and operates through levels of reality. For just about any predicate F, we can discern F-making, that is, what makes something F. We might say that making-the case is the most basic kind of non-causal making – all kinds of non-causal making can be reduced to it. Fred's being unmarried and male makes it the case that he is a bachelor. Logically simpler facts frequently make various logically more complex facts the case. Certain facts make it the case that some propositions are true or false. And so on. Truth-making then reduces to non-causal making-the-case of facts by facts.

How do we understand making? (I leave out non-causal unless required.) My strategy is not to ask what making is with the hope of providing a metaphysical theory about its nature. It's rather to look to the language of making. The metaphor behind making refers to agency. It would be absurd to suggest that claims about making, be they non-causal or causal, are claims about agency. It is not absurd, however, to propose that the concept of making somehow emerges from features to do with agency². Agency resides in capacities to manipulate things. Agency theorists of causation invoke causal recipes, procedures for an agent to get what she wants by manipulating the world. In the case of non-causal making, the recipes are not procedures for manipulating things in the world. They are, rather, analytic recipes: capacities to manipulate concepts.

An analytic recipe finds its paradigm form in an introduction rule for a logical constant. Introduction rules are linked to construction in the sense that they reveal the canonical grounds for use of a logical constant. I liberalise the idea of introduction-rule to that of any inference whose premises are canonical grounds for the application of a concept, be that concept a logical constant or non-logical concept. Roughly, my proposal is that non-causal making-claims express commitments to derivations, as in M – here 'F' appended to sentences, p, q, etc. forms a term denoting a fact:

M: In asserting <Fp₁, Fp₂, …Fp_n, makes-the case Fq>, U expresses a commitment to a derivation of q using only introduction rules employing all of {p₁, p₂, ...p_n}.

(M needs some qualification in the case of negation, as we shall see.) I am not claiming that making-claims are claims about inference, that is, kinds of metalinguistic claims. I am not offering reductive truth-conditions for making-claims in terms of inferential commitments. Instead, I am offering an explication of making-talk in terms of the activities and cognitive structures underpinning its production. The form of theoretical orientation naturally sees itself allied with expressivism. So, I am offering an expressivist treatment of making-and making-true-claims. None of this implies non-cognitivism about making-statements. They are, on this approach, truth-apt and about the world.³

In what follows I assume that truth-bears are propositions. Let '<p>' denote the proposition that p. For any true proposition <p>, I submit, the TM-sentences below are true, and their converses are false:

TM: (i) <p> is true because p;
(ii) <p> is true in virtue of the fact that p;
(iii) the fact that p makes <p> true.

TM-sentences all convey the same basic fact about the dependency of a proposition's truth on how things are with its subject matter. But since truth-making is just one kind of making, they express the dependence of one kind of fact on another. If so, the facts that true TM-sentences express, facts like that below – here again 'Fp' means the fact that p, etc,

are reduced to facts of making-the-case as in:

In what follows I use both locutions makes-the-case, and makes-true, depending on whether the reduction of making-true to making-the-case is being emphasized.

Many philosophers don't like facts. So they won't like my reduction of truth-making to fact-making. They may want truth-making without truth-makers. Such theorists might be happy with TM-sentences like TM (i), which, on the surface, don't seem to refer to facts (Cf. Hornsby). It strikes me the denial of facts is utterly implausible. If there are objects and properties, and objects instantiate properties, then there are facts. Even set-theoretic nominalists cannot deny that. To avoid facts one has to embrace a serious nominalism about properties, which is difficult to do⁴. I argue in §5 below, that ontological concerns about facts are exaggerated, and we can make perfect sense them.

Amongst philosophers who don't mind facts, there are those who don't like negative facts. Negative facts are standardly viewed as ontologically dubious entities (Cf. Molnar, Cf. Simons). These philosophers won't like my espousal of all true TM-statements, in particular TM-sentences like:

Foes of negative facts, who want, as I think they should, negative truths to have truth-makers have to provide alternative truth-makers for such truths. Take Armstrong's approach. For him, truth-making is about a relation of necessitation between facts and propositions, as in NEC:

Armstrong's fact-ontology comprises positive atomic facts and one totality fact TOT. TOT is the fact that the atomic facts are all the atomic facts there are. For Armstrong, TOT makes negative propositions true: they are all made true by the same totality fact. It works this way. Given that Fp is not amongst the atomic facts, TOT necessitates <¬p>. Thus, TOT is the truth-maker of <¬p>.

The problem with Armstrong's proposal is that NEC is false. Armstrong is forgetting that alethic facts are part of being. Where <¬p> is true, then the alethic fact, that <¬p> is true, exists. The existence of this fact necessitates <¬p>. So, the fact that <¬p> is true makes-true <p>. But the fact that a proposition is true does not make that proposition true. Here's another aspect of the problem. Suppose <snow is white> is true. It's true in virtue of snow's being white. Suppose proposition 1 says that <snow is white> is true. Suppose proposition 2 says that 1 is true. Suppose proposition 3 says 2 is true. And so on, up to proposition N. Clearly, N is true in virtue of <snow is white>'s being true. But given the alethic fact, that N is true, necessitates <snow is white>, then by NEC, we can conclude that <snow is white> is true in virtue of N's being true. But that reverses the order of dependency of alethic facts on other alethic facts. The order of making is inverted.

We cannot solve the problem by denying that alethic facts exist, since, surely, if there are propositions possessing the property of truth, and we accept the general category of fact, then we must accept alethic facts. We cannot deny that alethic facts can be truth-makers, since if alethic facts are facts; they must be truth-makers for the propositions that describe them.

You might think other kinds of modification of NEC will solve the problems. I don't think so⁵. Other approaches to removing negative facts are just as problematic for very much the same reason. Bringing in the world as a truth-maker of negatives (Cf. Cameron) won't help, since, the world must include alethic reality, and we will get the same problem we have just articulated. I suggest that invoking totality, or the world, to explain negative truth is not going to work. So, we have some reason to believe negativity is unavoidable. I don't think this is a problem in itself. The arguments against negative facts are overrated (Cf. Barker and Jago). And as I suggested above, a general treatment of fact-talk awaits us in §5, which I think renders talk of fact, logically simple and complex, unproblematic.

The TM (i)-(iii) are not the only kinds of TM-sentences. There are also those that express the dependency of logically complex truths on logically simpler facts, such as:

Fp makes-true <p v q>.
Fp and Fq together make-true <p & q>.

On the other hand, the logically complex does not make logically simpler truth. Witness:

It's false that <p> is true in virtue of the fact that (p & q), (even assuming that q). The reason CON isn't acceptable, I think, is that q has nothing to do with the securing of the fact that <p> is true. Philosophers who think otherwise confuse necessitation with making. Making may involve necessitation, but it's not identical to it. If I ask you what makes something the case, I am asking how it came to be. The truth of <p> necessitates the fact that p, the fact that p necessitates the truth of p. There's necessitation in both directions. So the question, how did <p>'s being true come to be? Is not answered by a claim about necessitation. Those impressed by NEC, will naturally gravitate to CON, since the existence of F(p & q) necessitates <p>. But F(p & q) has nothing to do with how <p> comes to be true, any more than that Fp comes to be through <p>'s being true. And as we have seen, NEC is false.

The issue concerning relevance is sharpened when we consider the fact that more than one fact can contribute to the making of another fact: there is collective making, just as there is collective causal making. The following are cases thereof:

(1) Fp, Fq (together) make-the case F[p & q];
(2) Fp, Fq (together) make-true <p & q>.

Togetherness requires explanatory relevance. All the facts entering into the making relation have to do their bit: they must contribute to the bringing about. So in the cases above, Fp and Fq make essential contributions to the making. They are essential parts of the explanation for the obtaining of the fact F[p & q] and the truth of <p & q>. Hence intuitively these statements (1) and (2) of collective making seem correct. In contrast those below look wrong:

(3) Fp, Fq, and Fr (together) make-the case F[p & q].
(4) Fp, Fq (together) make-true <p>.

In (3), Fr makes no contribution. The Fr has nothing to do with the explanation of the obtaining of F(p & q). Similarly, in (4), Fq makes no contribution to <p>'s truth. It's not part of how <p>'s truth comes about. This shows again that a necessitation approach is off the mark.

A friend of necessitation an analysis of making might point out that a disjunctive truth, <p v q> could be made by Fp and Fq, since both obtain, even though just one would be sufficient for the disjunctive truth. The right thing to answer here is that the making of the disjunctive truth is over-determined. Where both Fp and Fq obtain, both independently, and not collectively, make-true <p v q>. I see no fundamental problem with that idea.

My claim that all truths have truth-makers might be challenged by the case of logically necessary truths. The claim that necessary truths don't require truth-makers is odd. How can a class of facts about truths suddenly be primitive facts? One might object that they are true in virtue of meaning. That might apply to sentences, sentences have meanings, but not to propositions, they are meanings. If it is logically necessary that p v ¬p for some p, then, that's because it's logically necessary that there is some truth-maker of some contingent kind or another. The proposition <p v ¬p> is guaranteed to have a truth-maker no matter what. The truth-makers are either Fp or, allowing negative facts, F¬p. In turn, the truth, <It's necessary that p or ¬p> has as its truth-maker a fact of necessity. This is a modal fact. This fact could be the fact that in every possible world, either Fp holds or F¬p holds. What provides the guarantee that one of these facts will always obtain? That is a matter about the making of facts, and not the making of truths, and does not undermine the claim that truths of logical necessity are true in virtue of fact.

I have been urging that facts make propositions true. But a challenge to that idea is that objects such as people, electrons, or numbers, can make propositions true. What makes existential propositions true, like <2 exists> if not 2? If one has the necessitation conception of truth-making distilled in NEC, this conclusion follows. But NEC is false. If we return to explanatory making, and the locutions through which it is expressed, we have to assert:

This may not make sense. Just as objects don't cause, objects don't make. Makers are conditions, states of affairs, and facts. Even necessitation-theorists tacitly accept this. It's X's existing that necessitates, not X itself.

We have perhaps said enough about the phenomenal features of making. The question now is how can we illuminate the nature of this relation? I don't think there is going to be any analysis to be had drawn from the usual bag of tools: supervenience, counterfactual dependence, necessitation. For example, one might think that an analysis of making in terms of necessitation with an added condition about logical complexity might work, such as:

Fp₁, Fp₂, …Fp_n makes-the case Fq iff (p₁, p₂, p₃, …) necessitate q, and q is more logically complex than any of (p₁, p₂, p₃, …).

The problem with this proposal is that it will validate sentences like:

This is not in accord with the real explanatory dependence, which is as follows: Fp is the common maker of F¬¬p and F[p v (¬¬q & r)]. The path of making does not go through Fp to F¬¬p, then F[p v (¬¬q & r)].

Instead of seeking an analysis of making, I am going to recommend an alternative strategy, as I enounced in §0. I won't look for an analysis of making, but of making-language. The strategy is to take the metaphor of making seriously, and see where it leads. This will come through a theory of what's expressed in making-claims. I have already put forward the basic proposal, with M (§0). The metaphor in making is that of agency. In making we construct something. In logical proofs, introduction rules are linked to construction in the sense that they reveal the canonical grounds for use of a logical constant. So, I suggest, in a non-causal making-claim, a speaker expresses a commitment to a certain kind of proof construction. The proof is one linking propositions, which describe the making-facts, to the proposition describing the made-fact. The proof will only use introduction rules. (Though, as we shall see in §4, proofs that underpin claims about the making of negative facts, and indeed, negative truths, involve a qualification. These proofs are reductio proofs, and reductio proofs require use of elimination rules, rather than introduction rules, in that part of the proof that unpacks consequences of accepting the hypothesis.) We liberalise the idea of introduction-rule to that of any inference whose premises are canonical grounds for the application of a concept, be that concept a logical constant or non-logical concept. I call these analytic recipes. So, non-causal making-statements express commitments to constructions using analytic recipes.

TM: In asserting Fp₁, Fp₂ , …Fp_n make-true <q>, U expresses a commitment to a derivation of <q> is true using only introduction rules using all of {p₁, p₂...p_n}.

In this account, we require that all the premises in the derivations are involved at some stage in the application of introduction rules.

What logic governs the derivations? Is it classical or relevant, or some other kind of logic? In fact, the analytic-recipe approach is fairly neutral on questions of the logic used. The logic is not the central constraint on making-statements, it's in the restriction on introduction-rule that does the work. For simplicity, I shall assume classical logic.

The theses, M and TM, are not truth-condition accounts of making and truth-making claims. We are not offering truth-conditional analysis. On the other hand, we are not denying that making-statements have truth-conditions. They are truth-apt claims, and the T-schema applies to them. It's just that no illumination about making comes through looking at truth-conditions.

The required idea of expressing that I invoke in M and TM is one drawn from the literature on expressivism. I am not going to explore this here (Cf. Barker, Global Expressivism, "Faultless Disagreement"). Clearly, we need a kind of cognitivist expressivism, since truth-making claims are truth-apt.

There is some question about the psychological reality of the proposal. We do not require that speakers have an explicit grasp of introduction and elimination rules, or the concept thereof. It may be that the psychological reality for speakers involves cognitive representations of such rules, but possessing those states does not require being in possession of the concept of a derivation. It is rather, that the speaker could, relatively easily, acquire such concepts.

Let's get down to the details of the account. Let us suppose, as seems right, that the elimination and introduction rules for the truth-predicate are those below:

In terms of TM, we now explain the basic asymmetry between being and truth and our assertion of TM-statements, Fp makes-true <p>, and our rejection of anti-TM-statements, like F[<p> is true] makes-the case Fp.

It would be wrong to say that, on this theory, the asymmetric fixing of truth by being is constituted by facts about introduction-rules. Rather, it is that our assertion of this asymmetry involves our defending commitments to derivations involving introduction rules. Yet this assertion of a worldly asymmetry, has its correlate in a cognitive/logical asymmetry: that between introduction rules and elimination rules. But what is the latter distinction?

I argue that what characterises an inference-rule as an introduction rule are certain cognitive and epistemic asymmetries that are linked to the idea of a canonical ground. Basically in an introduction rule, A₁, A₂, … A_n.⌉ B, there is a concept on the right hand side, in B–expressed by a predicate, operator, or connective–not present in A₁, A₂, … A_n. New right-hand concept characterises the general form of the conclusion.⁶

The analytic recipe theory is meant to explain our assertion of making-statements like (8):

(8) F[Fred is an unmarried man] makes-true <Fred is a bachelor>
The introduction rule for bachelor is the following:

Fred is an unmarried man ⌉ Fred is a bachelor

Fred is a male sibling ⌉ Fred is a brother.

Fred is a brother ⌉ Fred is a sibling.

You will accept the first truth-making claim, I will not. Who is right? The answer is that there is no objective fact about who is right. There does not have to be. Perhaps what we have there is a case of faultless disagreement about which facts ground which facts. That does not imply any relativity of fact or subjectivity (Cf. Barker, "Faultless Disagreement").

The analytic-recipe theory drags truth-making away from entailment and towards causation. That means some familiar principles, beloved of certain theorists, have to go. One is the entailment principle – see Armstrong:

EP: If f makes-true <p>, p → q, then f makes-true <q>.

EP^AR: If U asserts f makes-true <p>, and accepts, p ⌉ q (only with introduction rules) then U ought to accept f makes-true <q>.

EP^AR is not particularly informative, since it is just a trivial consequence of the analytic- recipe view.

Transitivity of making is also validated in the recipe view. If there is a proof construction underpinning assertion of Fp₁, Fp₂, …Fp_n makes-the case Fq. And one underpinning assertion of Fq makes-the case Fr. Then there will be one underpinning assertion of Fp₁, Fp₂, …Fp_n makes-the case Fr.

It might be objected that the analytic recipe approach to truth-making cannot work generally. Armstrong (2004) takes the claim,

X's being H₂0 makes it true that X is water,

to refute a reduction of truth-making to entailment. My recipe approach doesn't reduce making-true to entailment, nevertheless, you could wonder how it treats this case. The explanation is fairly straightforward. What underlies assertion of this TM-claim are the following introduction rules:

(9) X is water ⌉ <X is water> is true.
(10) X is the underlying stuff causing watery appearances. ⌉ X is water.
(11) X is H₂0. H₂0 causes watery appearances. Nothing else does. ⌉ X is the underlying stuff causing watery appearances.

Let's explain these in turn (9) is just the basic truth-introduction rule for the instance at hand (10) corresponds to a canonical rule of introduction for the concept water. We can think of the concept of water as being captured in the phrase: the underlying stuff that is causing watery appearances. Finally, (11) is an instance of a canonical ground for use of a definite description. More schematically:

Since definite descriptions carry uniqueness implications, it's unsurprising that the canonical ground for use of a definite description should be information that a given object, N, uniquely satisfies a certain condition. Putting together (9) to (11), we can construct a proof, using only introduction rules, from the propositions,

X is H₂0. H₂0 causes watery appearances. Nothing else does.
<X is water> is true.

Of course, the facts corresponding to the initial propositions, jointly make the proposition <X is water> true. But we can treat the second two facts as background conditions for the making-true of <X is water> by the fact that X is H₂0.

So much for the basics about TM-statements and their expression of proof constructions, that link making facts with facts made. We have some evidence that this theory captures the basic sense of the asymmetric determination of facts of truth by the facts pertaining to the subject matter of those truths. We now move on to a refinement of these ideas: making and truth-making for logically complex propositions and facts. First, let us consider, conjunction, disjunction, existential quantification, and universals.⁷ I treat negation in §4, which, as we already noted, brings with it some refinements of the conception of derivations underpinning making-statements. Part of the goal is to explain our sense that logically complex truths and facts depend for their truth or their obtaining on logically simpler facts. Isn't the introduction rule-account a rather shallow explanation of that intuition? Maybe it is, but it isn't merely a stipulation of the condition that the logically complex depends on the logically simpler.

The treatment of conjunction is straightforward. Our acceptance of the introduction rule, p, q ⌉ (p & q), means our acceptance of:

(12) Fp, Fq (together) make-true <p & q>

(13) F[p & q] makes-true <p>

The conjunctive thesis is argued against explicitly by Rodriguez-Peyera (2006), who sees truth-making as explanatory. Of course, those philosophers like Armstrong (2004) who do not see truth-making as explanatory do not necessarily deny (13). But my suggestion is that the latter have missed the point about truth-making in failing to see the explanatory connection.⁸

In the case of disjunction we accept the introduction rule: p ⌉ p v q. So we have the following intuitively correct making-statements:

(14) Fp makes-the case F[p v q]
(15) Fp makes-true <p v q>

(16) Fp, Fq (together) make-true <p v q>

According to our agency proposal, this cannot be right, it involves explanatory irrelevance. We use an introduction rule to derive (p v q) from either the p or from q. Either way, one premises, either p or q, is left doing no work.

There is no reason to accept the validity of the disjunctive principle – see Read (2000) and Rodriguez-Pereyra (2006):

DP: If Fr makes-true <p v q>, then Fr makes-true either <p> or <q>.

This principle fails if we allow disjunctive facts. And that's what we are doing. Thus, F[p v q] makes-true <p v q> but does not make-true any of its disjuncts. If we confine ourselves to atomic facts, then DP is acceptable.

The rule of disjunctive elimination, (p v q), (p v r), (q v r) + r, does not furnish us with intuitively correct making-statements:

(17) F[p v q], F[p v r], F[q v r] (together) make-true <r>.

(17) does not seem right. It has the same kind of counter-intuitiveness as (6). It may be that our belief that r is brought about by a deduction using disjunction elimination. But that does not mean that the factual reality Fr is brought about by a disjunctive fact, along with certain facts of entailment.

The case of existential quantification is unproblematic, given the obvious introduction rule. So we accept:

(18) F[T is a G], F[T is H] (together) make-true <At least one G is H>.

Intuitively, these seem right if we consult our sense of explanatory order. Likewise the elimination rule does not furnish us with any intuitively correct making-statements.

Existential quantifications confront us with the potential over-determination of analytic making. There may be many things that are G and H. So there are many pairs of facts of the form F[T is a G], F[T is H] that in themselves (together) make-true <At least one G is H>. Again, that's ok with the recipe view.

Existential quantifications are related to another matter of interest. We are taking it that facts make propositions true. But propositions about existence are often cited as cases in which objects make propositions true. Is <At least one bird exists> made true by individual birds, Tweety, for example? I have resisted the idea that things, like material objects, make propositions true. Since we are being unconstrained about facts, there is no problem with our saying that it is facts of individual existence that make true, each independently, <At least one bird exists>.

Universal truths, it might seem, present us with a special problem. In terms of a Fitch-style natural deduction system, the introduction rule for universals is:

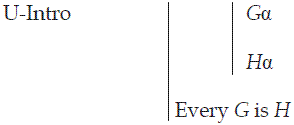
In this rule, a is an eigen variable or arbitrary object term. U-Intro involves a sub-proof in which we suppose that an arbitrary object a is G and derive a conclusion that it is H. How are we to understand truth-making of universals in terms of this rule? The answer is that it is not the proof that is the truth-maker. It is the premises for the proof that correspond to the truth-makers. What the speaker expresses in asserting a truth-making claim is a derivation from premises, that is, assertions, using introduction rules, to the truth of a claim. U-intro, unlike, say, disjunction introduction, does not specify premises, in the sense of propositions. It specifies a kind of proof. Obviously, what we want are the premises that could support application of the U-Intro, and not the derivation itself. The question now is what these premises are.

There are two cases that we have to consider in answering this question. There is the case of non-accidental universals, true by virtue of necessitation of some kind, and accidental generalities, true by virtue of brute facts.

Where Every F is G is an accidental truth. One might wonder in this case, how U-Intro will be applied? What is the minimal information about contingent facts required to apply U-Intro? We answer this by considering what premises we need in order to carry out a suppositional proof that begins with suppose Fa and ends with Ga. The supposition is that some arbitrary a has F. The answer is simple. The premises we require are the following:

{T₁, T₂, T₃….T_n} are all the Gs
T₁ is H, T₂ is H, T₃ is H, ….T_n is H.

(19) F[T₁ is H], F[T₁ is H], F[T₂ is H], F[T₂ is H], …F[Every G is in the class
{T₁, T₂, T₃….T_n}] (together) make-true <Every G is H>

This result entails that universals need facts of totality as part of their truth-makers, facts like F[Every G is in the class {T₁, T₂, T₃….T_n}]. This is more or less what Armstrong (2004) argues, and indeed, it seems intuitively correct. We have derived a conservative result in (19), but at least we get a principled reason for explaining an intuition shared by many people.

That's our account of intuition about positive making and truth-making. Now for negations. Let us begin that investigation with the introduction and elimination rules for negation. Take the standard introduction rule:

There is a concern about this being an introduction rule given my analysis of what an introduction rule is – see §2. This was that the right-hand side of the rule contains a concept not present on the left. One might object: here we find ⊥, which is, it could be claimed presupposes negation. But I suggest that goes not itself presuppose negation ⊥ is absurdity. One form of absurdity is explicit contradiction, which will require negation. But absurdity is not constituted by explicit contradiction.

(20) Fp makes-true <¬¬p>

We now address the promised modification of the basic proposal about introduction rules outlined in §2. Here is the issue. The analysis as we have developed it so far does not quite work. It generates the result that we should assert (21), below, but not (22):

(21) F[¬(p v q)] makes-the case F¬p,
(22) F¬p, F¬q (together) make-the case F¬(p v q).

The proof underpinning (21) is P1 below, and that underpinning (22) is P2. P1 only used introduction rules, but P2 uses elimination rules in the reductio sub-proof with (p v q) as its premise:

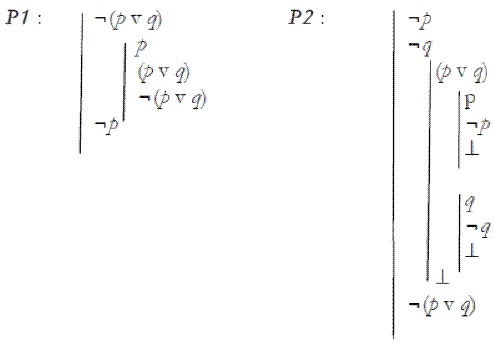
So by the lights of the hypotheses offered, (21) ought to be accepted, and (22) rejected. But surely it should be the other way around (21) looks wrong: an atomic negative fact F¬p is not explained by the compound negative F[¬(p v q)]. Rather, F¬p is part of the explanation of the compound fact. Accepting (21) is akin to accepting (5) that a positive atomic fact is made the case by a conjunctive fact, which we reject. In contrast, (22) looks right. We explain why F¬(p v q) is the case through the negative facts corresponding to its negated disjuncts. (That's just as we explain the falsity of a disjunction by appeal to the falsity of disjuncts.)

The way out is to block proof P1, and allow P2. How can we do that given that it looks P1 involves only introduction rules, and P2 has elimination rules at the second sub-proof level? The answer, which I shall justify below, is that the proofs supporting making statements can included elimination rules, under certain circumstances. Those circumstances are met in P2. Furthermore, elimination rules cannot be deployed under certain circumstances, and those are met in P1.

To motivate these ideas, we look to causation again. Consider the structure of causation of negative events or absences. (I assume these things exist.) Say that the placing of a hand in a certain position caused a shadow in the grass. The shadow is an absence, the absence of light. How is the placing of the hand able to cause the absence of light on the grass? The causing of an absence is intimately connected to the prevention of a positive event. The hand prevented light from being on the grass. How does the placing of the hand prevent the light from being on the grass? The hand excluded a condition that would have caused light on the grass. Generally speaking we can say:

Fact/Event C causes fact ¬E (C prevents E) iff C is identical to, or causes, a condition D that excludes a causally sufficient condition for E.

Exclusion here means that given the physical laws, it follows from C, and other facts, that D will not obtain.

The suggestion I want to pursue is that analytic making of negative facts works in a structurally identical way to prevention. If some facts, Fp₁, Fp₂… Fp_n bring about a negative fact F¬q, that is,

(23) Fp₁, Fp₂… Fp_n (together) make-the case F¬q,

Then the facts Fp₁, Fp₂… Fp_n do so by preventing a positive fact Fq. That means that they together exclude a condition that brings about Fq. To determine what would bring about Fq we need to apply the converse of introduction rules to q – we need to apply elimination rules to specify a condition that is explicitly incompatible with p₁, p₂… p_n. In other words, in the proof that supports the making judgement (23), elimination rules have to come in a specific point. That point is the following. The proof the underpins the judgement for assertion of (23) will be a reductio proof with supposition q, with premises p₁, p₂… p_n, with the structure below:

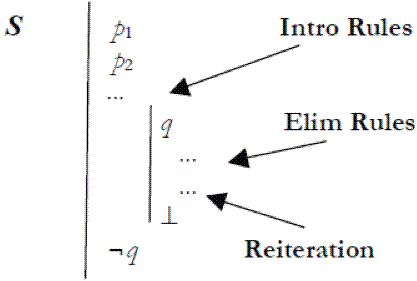
In this proof, we may use introduction rules in the main line, on the premises p₁, p₂… p_n, but in the main line of the reductio sub-proof, beginning with hypothesis q, all the inference rules we apply to q are elimination rules.

The proof structure S is exhibited by P2, but not by P1. In P1 introduction rules are deployed in the reduction sub-proof, whereas they should be elimination rules for the hypothesis p. On the other hand, P2 uses only elimination rules in the main line of the reduction sub-proof for hypothesis (p v q). That is the solution to our problem. We have modified the basic picture of the analytic recipe theory presented in §2, but not drastically, and in line with the intuitive idea that analytic making parallels the structure of causation. So, in sum, in making a making statement, the speaker expresses a commitment to a derivation that used introduction rules at all places, except for the rules applied to suppositions of reductio proofs.

We have not yet finished with analytic making and negation. We need to consider elimination rules for negation. We have assumed classical logic, and so the elimination rule is: ¬¬p ⌉ p. The corresponding making statement is predicted to be unintuitive:

(24) F¬¬p makes-true <p>.

And that seems right, for already familiar reasons. The proposition <p> is made true by Fp, and Fp makes-the case F¬¬p, but not vice versa.

Assertions about making express commitments to derivations involving introduction rules – but with elimination rules applied in the manner specified in §4 in the case of negatives. I emphasize that it is not being proposed that statements about making are statements about commitments to derivations. Derivations are semantic/cognitive entities. We are not giving the truth-conditions for statements of making. Rather we must say that statements of making are expressions of commitment to such derivations, where expressing is not a semantic relation, like representing.

Isn't the fact that we have offered an analysis of making-claims in expressivist terms an indication that there is no making after all? Compare the case of value. Expressivists propose that in asserting that x is good, the speaker expresses a motivational state. Values have no role in the account at all in the analysis of how value-language works. So values have been dispensed with in the explanation of our talk about value. So isn't that a good reason to conclude that values don't exist. So our talk about value needs to be understood in quasi-realist or fictionalist terms.⁹ There are not values, but we talk as if there are. So, you might think the same holds for making. Making does not exist, but we talk as if it does.

Now maybe we can live with fictionalism or quasi-realism about making. But I don't think we have to accept the argument that leads to that conclusion. The argument was this: if a referent has no role in the account of talk about it, then we should conclude that the referent does not exist. But why accept this premise? Why can't we hold that value terms really do pick out values, it's just that values have no explanatory role in the account of talk about values. We are not proposing that values have no explanatory roles whatsoever. Perhaps they can have a role in explaining why people behave in certain ways. We are just denying that they have a role in the account of what goes on in the language activity of value-talk (In the account of the causal structure of speech-acts, and the causal-account of their production.)

In taking this line, however, we really have to insist that in using value language, we are really referring to values. They are really there to be referred to. But to take this line we have to deny the following thesis, which, to some, will appear quite natural:

(ER) Explanatory Representationalism: Any assignment to sentences or phrases of reference to real things F requires that Fs, or things in terms of which they can be defined, be part of the account of how the talk using those sentences and phrases function.

We must deny this thesis. So, in other words, we must be able to assert O is referring to Fs with her terms T, but Fs have no role in the account of O's use of T. Value-expressivism's non-representational stance to value-vocabulary cannot help but have implications for the kind of stance we take to certain other vocabularies, in particular the semantic vocabularies. So, O may say things like The term 'goodness' is being used to refer to goodness. If the language activity underpinning term refers requires an explanatory representationalist stance –explaining use of O is referring to Fs requires appeal to Fs or things in terms of which they can be defined– then that conflicts with the expressivism in relation to goodness. What we must do here is bite the bullet, and extend our expressivism to the semantic vocabulary. So, in explaining what goes on when a speaker U asserts, O is referring to goodness, the referent of the term goodness cannot have an explanatory role. Generally: an expressivist about a vocabulary D who wants to be a realist about D, will have to extend their expressivism to the semantic vocabulary for talk about the semantic features of D.

Just what expressivism about the semantic vocabulary looks like is another matter. But let us bypass that question, which I deal with elsewhere,¹⁰ and ask how the resulting theory will differ from straight realism. It is thought that expressivism about value is attractive because it allows us to escape questions to which a commitment to values gives rise. The feared questions are metaphysical: what are these queer beings that we call values that somehow have a compelling power on our motivational systems. I submit, however, that if our expressivism extends to the semantic vocabulary, to talk of reference and truth, then we do not have to dump realism. We can keep realism, but still escape metaphysical quandaries about value. Concerning values, we can say: values exist, but there is no theoretical requirement to give a theory of what value is. This is not to say that values are metaphysically primitives, but to say that they are without metaphysical nature. The empire of metaphysical concern cannot extend to them. In short, we have realism without an attendant obligation to uncover the metaphysical nature of things we take to exist.

If we apply this orientation to the language of making, and its subject matter, the relation of making, the result we get is this. There is making, the making that goes on when how things are with the world make propositions true, it's just that there is nothing to say about what it is. We have evacuated the question of its nature of any positive content. In other words, making is real but without any positive metaphysical nature. That conclusion seems very paradoxical. In metaphysics, we are very used to asking questions about the nature of Fs for any F. We always ask: what does being F consist in? It seems our answer in the case of values, or making, if we follow the present line, is that there is nothing these things consist in. We have realism but without any metaphysical essence to the beings concerned.

We can now turn this attitude and orientation to fact-talk itself. My strategy in relation to making-statements embraces ecumenicalism about facts. So the facts are all out there. But of course, the commitment to a plenitude of facts will offend those committed to ontological austerity problems. How can you allow all these beings? But what lies behind this fear of ontological hypertrophy about facts is an assumption that facts, if they exist, have some metaphysical nature, and the metaphysical nature of negative or universal facts will be odd indeed. So, goes the familiar line of thought, we need to deny their existence. But here's the alternative approach I want to pursue. We extend our expressivism to talk of facts, and the result will be that we can say that facts of all kinds exist, it's just that they have no inherent metaphysical nature to speak of, and so, positing them comes with no ontological cost about what they are, with the attendant fear of the supposed queerness of negative facts or universals facts. What would this expressivism about fact-talk be?

The core idea is that fact-talk involves nominalization. Basically, in using the fact that p as a referring term to refer to a fact, the speaker U asserts p but, through the grammatical modifier the fact that attached to p, U enables the asserted sentence to combine with a predicate to form a sentence. So in assertion of a sentence like:

Fp makes-the case Fq.

The speaker U performs three intimately connected assertions: (i) U asserts that p and that q; (ii) U attaches 'F' to each sentence enabling the resulting expressions to combine with the predicate make-the case; and (iii) U makes an assertion with the whole sentence, which means U expresses a commitment to a proof-construction involving p and q.¹¹ Any assertion, of no matter what logical complexity, can be nominalized.

This analysis of fact-talk does not give facts themselves any explanatory role in the account of what goes on in the production of sentences about facts. Yet, I submit, it is consistent with realism about facts. Facts exist. Of course, some people may balk at the idea that in the speech acts we perform in using Fp and Fq –nominalized assertions– we are performing referring acts. How can these terms, used in this way, really be referring terms?¹² The reason they balk at this is that they are implicitly accepting explanatory representationalism or ER. ER implies that in order for something to be a referring term, it must be part of the explanation of what a speaker does in using the term that an object is assigned to the term. But in characterising the function of Fp and Fq, on the nominalization model, no such function is assigned.

The expressivism we offer, however, is all for denying ER, and so will challenge this object. If that response works, then I think we can move towards possibly saying the following. Facts of all kinds exist, but facts as such have no metaphysical nature to speak of, and so, worries about the inherent nature of negative or even positive facts assume falsely that there is something to worry about–the metaphysical nature of facts. If this response works, then we are fully on our way to embracing a fully articulated conception of truth-making, but without the distortions that come with metaphysical austerity programs. But they way to do this is to embrace expressivism about truth-making.

¹ Rodriguez-Pereyra (2005) presents this kind of argument for truth-making.
² That's the path taken by agency theorists of causation, such as Gasking (1955), Von Wright (1971), Price (1992), and Woodward (2003).
³ See Barker (Global Expressivism) and ("Faultless Disagreement"), for sketches of the expressivist framework I work with.
⁴ If you're a fact-foe, you can treat this paper as an explication of sentences like TM (i), interpreted as carrying no commitment to facts.
⁵ See Barker ("Alethic Reality") for development of these issues.
⁶ One may be concerned about the introduction-rule for the predicate fact: p. ⌉ it is a fact that p. If this is accepted as an introduction rule we should ideally be disposed to assert: the fact that p makes-the case the fact that it is a fact that p. But that looks perfectly acceptable. Note: we are committed to an infinite hierarchy of facts, Fp, FFp, etc. If find this no more problematic than an heirarch of facts of truth.
⁷ I will not consider indicative conditionals here. That's because it is not clear at all that they have truth-conditions, and so, that they are truth-apt.
⁸ However, an issue of some subtlety arises in relation to the schema: (*) F[p & p] makes-true <p>. It might seem that we should accept (*). Here's an argument from Jago (2009). He accepts: M: Whatever truth-makes <p> ought to truth-make <p & p>, and vice versa.
If F[p & p] makes-true <p & p> it ought to truth-make <p>, but that means accepting (*). However, the current analytic recipe hypothesis won't allow us to accept (*). To assert (*) we need a derivation from (p & p) to p, to <p> is true, but that means using an elimination rule. Is the recipe theory's denial of (*) objectionable? Jago's argument is open to dispute. M is a theoretical principle, without independent intuitive power. This is particularly so, since it asks us to have intuitions about weird sentences that we do not normally use. I mean here conjunctions of the form: P and P. In standard formal treatments, these are acceptable, but for natural language in which semantics and pragmatics interpenetrate they are not obviously. A conjunction (p & q) is only well-formed if p and q don't contain each other informationally. This fact about the intuitive weirdness of (p & p) is enough to undermine appeals to the supposed intuitiveness of M.
⁹ This seems to be Blackburn's (1984) view. It's also taken on by Kalderon (2007).
¹⁰ See Barker (Global Expressivism) for a theory about what such expressivism looks like.
¹¹ This approach needs further development to deal with embedding of fact-locutions, as in: If Hitler had invaded England, then the fact that he invaded England would have meant all subsequent history was different. In this case, the use of the fact locution carries no commitment to a fact.
¹² We are not saying that some asserted sentences are referring terms. It is rather that some terms of the form that S is derived from sentences, but addition of that. The resulting term has the syntax of a referring term. One might say that primary referring terms, terms that are not nominalizations, fix the syntax, which nominalizations, then borrow, enabling them to function as referring terms.

Armstrong, David M. Truth and Truthmakers. Cambridge: Cambridge University Press, 2004. Print.         [ Links ]

Barker, Stephen. Global Expressivism. Nottingham: The University Nottingham, 2007. Print.         [ Links ]

---. "Faultless Disagreement, Cognitive Expressivism, and Absolute, but Non-Objective Truth". Proceedings of the Aristotelian Society. 2011: 183-199. Print.         [ Links ]

---. "Truth-Making and the Alethic Undecidability of the liar". Discusiones Filosóficas. Jul-Dic. 2012: 13-31. Print.         [ Links ]

Barker, Stephen and Mark Jago. "Being Positive about Negative Facts". Philosophy and Phenomenological Research. Jul. 2012: 117-138. Print.         [ Links ]

Bigelow, John. The Reality of Numbers: A Physicalist's Philosophy of Mathematics. Oxford: Oxford University Press, 1988. Print.         [ Links ]

Blackburn, Simon. Essays in quasi-realism. New York: Oxford University Press, 1993. Print.         [ Links ]

Cameron, Ross. "How to be a Truthmaker maximalist". Nous. Sep. 2008: 410-421. Print.         [ Links ]

Gasking, Douglas. "Causation and Recipes". Mind. Oct. 1955: 479-487. Print.         [ Links ]

Hornsby, Jennifer. "Truth without Truth-making Entities". Eds. Beebee, Helen and Julian Dodd. Truthmakers. Oxford: Oxford University Press, 2005. Print.         [ Links ]

Jago, Mark. "The Conjunction and Disjunction Theses". Mind. Apr. 2009: 411-415. Print.         [ Links ]

Kalderon, Mark. Moral Fictionalism. Oxford: Oxford University Press, 2007. Print.         [ Links ]

Molnar, George. "Truthmakers for Negative Truths". Australasian Journal of Philosophy. Jul. 2000: 72-86. Print.         [ Links ]

Lewis, David. "Things qua Truthmakers". Ed. Lillehammer, Hallvard and Gonzalo, Rodriguez-Pereyra. Real Metaphysics. Essay in honour of D. H. Mellor. London: Routledge, 2003. Print.         [ Links ]

Price, Huw. "Agency and Causal Asymmetry". Mind. Jul. 1992: 501-520. Print.         [ Links ]

Read, Stephen. "Truthmakers and the Disjunction Thesis". Mind. 2000: 67-79. Print.         [ Links ]

Rodriguez-Pereyra, Gonzalo. "Why Truthmakers". Eds. Beebee, Helen and Julian Dodd. Truthmakers. Oxford: Oxford University Press, 2005. Print.         [ Links ]

---. "Truthmaking, Entailment, and the Conjunction Thesis". Mind. Oct. 2006: 957-982. Print.         [ Links ]

Simons, Peter. "Negatives, Numbers and Necessity: Some Worries about Armstrong's Version of Truthmaking". Australasian Journal of Philosophy. Feb. 2007: 253-261. Print.         [ Links ]

Woodward, James. Making Things Happen: A Theory of Causal Explanation. Oxford: Oxford University Press, 2005. Print.         [ Links ]

Como citar:
Barker, Stephen. "Expressivism about Making and Truth-Making". Discusiones Filosóficas. ene.-jun. 2014: 41-66.