Caracterización matemática de la unión de la proteína PfNBP-1 al eritrocito mediante la aplicación de la probabilidad y entropía

Mathematical characterization of binding between PfNBP-1 protein and erythrocyite by applying probability and entropy

Javier Rodríguez-Velásquez¹, Catalina Correa-Herrera², Germán Forero-Bulla³, Jessica Mora-Villarraga⁴, Sarith Vitery-Erazo⁵, Fredy López-García⁶, Viviana Torres-Ballesteros⁷, Diana Pineda-Bayona⁸, Nichole Rojas-Chaverra⁹, Simha Ramírez¹⁰

¹ MD. Director Grupo Insight. Investigador y docente de la Facultad de Medicina*. Universidad Militar Nueva Granada, Centro de Investigaciones Clínica del Country. Bogotá, Colombia. e-mail: grupoinsight2025@yahoo.es
² Ps. Investigadora Grupo Insight. Docente de la Facultad de Medicina*. Universidad Militar Nueva Granada, Centro de Investigaciones Clínica del Country. Bogotá, Colombia. e-mail: scatalinacorreah@hotmail.com
³ MD. Especialista en Neurocirugía y Docencia Universitaria. Docente Facultad de Medicina, Universidad Militar Nueva Granada. Bogotá, Colombia. e-mail: german.forero@unimilitar.edu.co
⁴ Interna Especial.* Universidad Militar Nueva Granada, Centro de Investigaciones Clínica del Country. Bogotá, Colombia. e-mail: jessicatatiana.mora@gmail.com
⁵ MD. Universidad Militar Nueva Granada. Bogotá, Colombia. e-mail: samari1478@hotmail.com
⁶ Ing. Investigador Grupo Insight, Universidad Militar Nueva Granada, Centro de Investigaciones Clínica del Country. Bogotá, Colombia. e-mail: flogarcdos@gmail.com
⁷ Estudiante.* Universidad Militar Nueva Granada, Centro de Investigaciones Clínica del Country. Bogotá, Colombia. e-mail: vivitob_91@hotmail.com
⁸ Estudiante.* Universidad Militar Nueva Granada, Centro de Investigaciones Clínica del Country. Bogotá, Colombia. e-mail: dianayamile.pineda@gmail.com
⁹ Estudiante.* Universidad Militar Nueva Granada, Centro de Investigaciones Clínica del Country. Bogotá, Colombia. e-mail: nicholemarcela1468@hotmail.com
¹⁰ Investigador Grupo Insight. Universidad Militar Nueva Granada. Bogotá, Colombia. e-mail: semramirez@yahoo.com

Grupo Insight - Universidad Militar Nueva Granada, Centro de Investigaciones Clínica del Country. *Línea de profundización e internado especial: Física y Matemáticas Aplicadas a la Medicina

Fecha de recepción: Febrero 13 - 2014 / Fecha de aceptación: Octubre 15 - 2014

Resumen

Objetivo: Estudiar la proteína Plasmodium falciparum Normocyte Binding Protein-1 (PfNBP-1), partiendo de un método de caracterización físico-matemática desarrollado previamente para péptidos de alta unión del merozoito de malaria al eritrocito, siendo esta un posible ligando asociado a una vía de invasión alternativa. Materiales y métodos: Se tomaron 21 péptidos con tamaño de 20 aminoácidos no sobrelapados de los cuales dos son de alta unión, se cuantificó la frecuencia de aparición de los 20 aminoácidos esenciales en cada posición y se calculó la probabilidad, sumatoria de probabilidad y la entropía con el objetivo de diferenciar matemáticamente los péptidos de alta y baja unión. Posteriormente se calcularon los mismos valores para péptidos teóricos análogos, en los que fueron cambiados por glicinas los aminoácidos críticos confirmados experimentalmente. Resultados: Los péptidos de PfNBP-1 comprobados experimentalmente de alta unión, presentaron valores de probabilidad, sumatoria de probabilidad y entropía ubicados dentro del macroestado de unión y sus péptidos teóricos análogos presentaron resultados que se diferenciaban cada vez más del macroestado de unión a medida que se reemplazaban aminoácidos críticos por glicinas. En cuanto a las secuencias de no unión de PfNBP-1, se encontró que los valores calculados son diferentes a los asociados al macroestado de unión, comprobando que en el 100 % de casos estudiados es posible diferenciar los péptidos de no unión y alta unión matemáticamente. Conclusiones: La probabilidad y la entropía permiten caracterizar adecuadamente los péptidos de alta unión de PfNBP-1, y evidenciar el orden matemático subyacente al proceso de unión de proteínas de malaria.

Palabras clave: Eritrocito, sitios de unión, péptidos, probabilidad. (Fuente: DeCS, Bireme).

Abstract

Objective: Study the Plasmodium falciparum Normocyte Binding Protein-1 (PfNBP-1), based on a method of physical-mathematical characterization previously developed for high binding peptides of malaria merozoite to erythrocyte, it was a possible ligand associated to an alternative invasion pathway. Materials and methods: 21 non overlapped peptides with size of 20 amino acids, including two of high binding were taken; the frequency of occurrence of the 20 essential amino acids in each position was quantified and probability, summation of probability and entropy were calculated, in order to mathematically differentiate high and low binding peptides. Later the same values were calculated for theoretical analogs peptides, where the critical amino acids confirmed experimentally were changed by glycine. Results: The experimentally validated high binding peptides of PfNBP-1, showed values of probability summation of probability and entropy located within the binding macrostate peptides and their theoretical analogues presented results that differed increasingly of the binding macrostate as critical amino acids were replaced by glycine. For the PfNBP-1 sequences of non-binding, it was found that the calculated values are different from those associated with the macrostate of binding, verifying that in 100% of cases studied is possible to mathematically differentiate binding and non-binding peptides. Conclusions: The probability and entropy allow adequately characterize the high-binding peptides of PfNBP-1, and show the mathematical order underlying the process of protein binding of malaria to the erythrocyte.

Key words: Erythrocyte, binding sites, peptides, probability. (Source: DeCS, Bireme).

Introducción

La malaria es una enfermedad producida por el parásito Plasmodium y afecta principalmente las poblaciones de regiones tropicales y subtropicales._1,2 En esta enfermedad el merozoíto del Plasmodium falciparum ataca a los glóbulos rojos dentro de un ciclo denominado eritrocítico, en un proceso de invasión mediado por interacciones específicas receptor-ligando que intervienen y hacen posible que el merozoíto reconozca, se una y se oriente hacia el interior del glóbulo rojo._3-6

Plasmodium falciparum Normocyte Binding Protein-1 (PfNBP-1) es una proteína del P. falciparum, homologa de la proteína PvRBPs de Plasmodium vivax. PfNBP-1 se expresa en la zona apical de los merozoítos y se une a la membrana del eritrocito, a un receptor aun no caracterizado. Por lo tanto, PfNBP-1 parece ser un ligando de una vía de invasión alternativa. Dos cepas de P. falciparum con mutaciones específicas en PfNBP-1 no son capaces de invadir al eritrocito por esta vía; esto tiene implicaciones para la comprensión del proceso de invasión y el desarrollo de vacunas dirigidas al bloqueo de la invasión a eritrocitos._7,8

La teoría de la probabilidad es un sistema que permite cuantificar la posibilidad de ocurrencia de un evento en el futuro. Esta teoría matemática tiene muchas aplicaciones ya que muchos sucesos de la naturaleza son altamente variables y sólo con el lenguaje de las probabilidades pueden ser cuantificados. La probabilidad varía en el rango real de cero a uno, donde cero indica la imposibilidad de la ocurrencia de un evento y uno señala la total seguridad de que éste suceda._9-11

Por otra parte la definición de entropía ha evolucionado, desde el contexto de la termodinámica y la teoría cinética de los gases hasta el desarrollo de la mecánica estadística. Boltzmann la define como una medida proporcional al logaritmo del número de microestados. Los conceptos de macroestados y microestados fueron formulados para caracterizar el estado de sistemas como el gaseoso, constituidos por un número de cuerpos de orden del número de Avogadro, (10²³).₁₂

El macroestado determina una distribución general del sistema y el microestado hace referencia a las diferentes configuraciones particulares que posee un sistema en estado de equilibrio para conservarse sin cambios macroscópicamente. Así mismo en los sistemas en equilibrio, la entropía aumenta de manera proporcional a su número de microestados._12,13

En la mecánica estadística, de la que hace parte la termodinámica, se redefinió la entropía y se generalizó para los sistemas que no están en equilibrio a partir de medir las probabilidades de distribución microscópica, lo que es proporcional a sumar los productos de la probabilidad de cada microestado por su logaritmo natural, siendo la constante de Boltzmann la constante de proporcionalidad.₁₃

En este mismo sentido, en el contexto de la teoría de la información, Shannon reformuló la ecuación de la entropía para determinar la cantidad de información contenida en un mensaje, de tal modo que la entropía equivale a la medida objetiva de la información de un sistema._14,15

Dada la utilidad de la teoría de la probabilidad y la ley de la entropía, han sido aplicadas a una amplia gama de tópicos, entre ellos en la determinación de los macroestados de unión y no unión de péptidos pertenecientes a proteínas de Plasmodium falciparum con papeles claves en la invasión al eritrocito humano. En efecto, se aplicaron en el desarrollo de una metodología de caracterización de los 79 péptidos no sobrelapados de MSP-1, la cual fue posteriormente aplicada a las 61 secuencias de EBA-140, 25 de MSA-2 y 31 de AMA-1._16-19

Para cada uno de los trabajos con estas proteínas se partió de la construcción de un espacio de probabilidad no equiprobable con base en los péptidos de alta unión, en el que se cuantifica para secuencias peptídicas de 20 aminoácidos, la probabilidad de aparición de cada aminoácido en cada una de las 20 posiciones, calculando valores de sumatoria de probabilidad, probabilidad y entropía para todas las secuencias y encontrando que para las secuencias comprobadas experimentalmente de alta unión, estos valores varían entre los rangos asociados al macroestado unión, mientras que para todos los péptidos comprobados de no unión se encuentran fuera de los rangos asociados al macroestado de unión. La diferenciación de los péptidos de unión y no unión, según estudios experimentales ha sido 100% acertada en todas las proteínas estudiadas.

Adicionalmente, en el caso de EBA-140, se realizaron los mismos cálculos para péptidos teóricos análogos, donde se cambiaron por glicinas aminoácidos comprobados experimentalmente como críticos, con el fin de evaluar desde estas leyes, la modificación de los valores de sumatoria de probabilidad, probabilidad y entropía respecto a los valores del péptido original, determinando las implicaciones del remplazo de uno o más aminoácidos críticos.₁₇

Teniendo en cuenta que PfNBP-1 es clave en la invasión del parásito al eritrocito, se han realizado estudios experimentales para determinar las secuencias que podrían incluirse en una vacuna que bloquee la invasión de Plasmodium al eritrocito, en efecto se ha encontrado que la cepa 7G8 de PfNBP-1, consta de 21 aminoácidos, de los cuales 2 son de alta unión al eritrocito._7,8 El objetivo de este trabajo es caracterizar matemáticamente los péptidos de la proteína PfNBP-1, diferenciando péptidos de unión y no unión al eritrocito con base en las metodologías previamente desarrolladas a partir de la teoría de la probabilidad y la ley de la entropía, así como caracterizar matemáticamente péptidos teóricos análogos en los cuales se remplazarán aminoácidos críticos por glicinas._16,17

Definiciones
Macroestado unión: conjunto de secuencias reconocidas como de alta unión.₁₆
Macroestado no unión: conjunto de secuencias reconocidas por no presentar alta unión.₁₆
Microestados: cualquier secuencia de veinte aminoácidos.
Probabilidad laplaciana [P(Ai)]: la probabilidad de un aminoácido A en una posición especifica i es definida como la frecuencia de aparición de este aminoácido en dicha posición dividido entre el total de aminoácidos._9,10

Sumatoria de probabilidad (SumP): para cada secuencia específica, resulta de la suma de la probabilidad de los aminoácidos componentes de la secuencia por posición específica.

Probabilidad de una secuencia [P(S)]: multiplicación de la probabilidad de los aminoácidos componentes de la secuencia por posición específica i._9,10

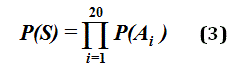
Entropía (S): dado un sistema de microestados no equiprobables, la entropía de un péptido se define como:

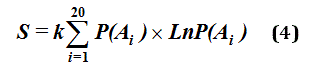
Donde k es la constante de Boltzmann [1,38 × 10^-23 (J/K)], S el valor de la entropía y P(Ai) el valor de la probabilidad del aminoácido A en la posición i._12,13

Materiales y métodos

La metodología empleada en el presente estudio se basa en dos estudios previos, en los cuales se caracterizaron los péptidos de alta unión de las proteínas MSP-1 y EBA-140, mediante las leyes de la probabilidad y la entropía, además en el segundo se realizaron cálculos de péptidos teóricos análogos._16,17

Se tomaron las secuencias de 20 aminoácidos de los 21 péptidos no sobrelapados de la proteína PfNBP-1, de los cuales dos son de alta unión, según se ha confirmado experimentalmente.8 Mediante la construcción de un espacio de probabilidad no equiprobable, se calculó la frecuencia de aparición de cada uno de los 20 aminoácidos en cada una de las 20 posiciones para los péptidos de alta unión; posteriormente se evaluó la probabilidad de cada aminoácido en cada posición, a través del cálculo de la probabilidad laplaciana, ecuación (1). De forma simultánea, en otro espacio muestral se realizó la cuantificación de la probabilidad de aparición de cada aminoácido en cada posición para los péptidos experimentalmente hallados de no unión.

Se realizaron los cálculos de sumatoria de probabilidad ecuación (2), probabilidad de secuencia ecuación (3) y Entropía ecuación (4) para cada uno de los 21 péptidos de la proteína PfNBP-1, a partir de los valores obtenidos del espacio de probabilidad construido; de esta forma se evaluó la probabilidad de pertenencia al macroestado de unión para cada secuencia específica.

Por último se construyeron péptidos teóricos reemplazando consecutivamente por glicinas los aminoácidos conocidos como críticos según estudios experimentales, en las secuencias de alta unión, de forma que por cada reemplazo se obtuvo un péptido análogo al péptido original. Sobre estos péptidos análogos teóricos se realizaron los mismos cálculos de sumatoria de probabilidad, probabilidad de secuencia y entropía planteados y los valores obtenidos se estudiaron con respecto a los límites matemáticos del macroestado de unión, determinando si hay un aumento, disminución o no hay cambios en los valores evaluados al remplazar uno, luego dos, luego tres, etc., aminoácidos críticos en los péptidos.

Resultados y discusión

Respecto a las secuencias del macroestado de unión se evidenció que las frecuencias de aparición para los veinte aminoácidos en todas las posiciones se encontraron entre cero, para los aminoácidos Arginina (R), Histidina (H), Prolina (P) y Glicina (G), y siete para la Lisina (K) (ver tabla 1), mientras que para las secuencias asociadas al macroestado de no unión variaron entre cero y 67, valores correspondientes a los aminoácidos Triptófano (W) y Asparagina (N), respectivamente (Tabla 1).

En el macroestado de unión, el número de repeticiones de un mismo aminoácido nunca fue mayor a uno (ver tabla 1), en cambio, para el macroestado de no unión se presentaron hasta siete repeticiones de un mismo aminoácido en una posición, número que correspondió a la Asparagina (N) en las posiciones 17, 18 y 20 (no se muestran datos).

Para las secuencias asociadas al macroestado de unión, los valores de la probabilidad Laplaciana variaron en un rango de cero a 0,025, encontrando 360 posiciones con un valor de cero de las 400 totales y 0,025 en las 40 restantes (Tabla 1).

El valor de la probabilidad fue de 9,09E-33, la sumatoria de probabilidad de 0,5 y la entropía de 2,55E-23 para las dos secuencias especificas del macroestado unión y para las secuencias del macroestado de no unión la probabilidad se encontró entre cero y uno, sumatoria de probabilidad entre cero y 0,15 y entropía entre cero y 7,64E-24 (Tabla 2).

Esto significa que las secuencias que previamente de manera experimental habían sido definidas como secuencias de alta unión, presentaron resultados de Probabilidad, sumatoria de probabilidad y entropía dentro del macroestado unión mientras que los valores para los péptidos que no son de alta unión se encuentran fuera de los rangos asociados al macroestado de unión. En otras palabras, se determinaron características físico-matemáticas que diferencian el estado de unión del estado de no unión, a partir de la metodología aplicada.

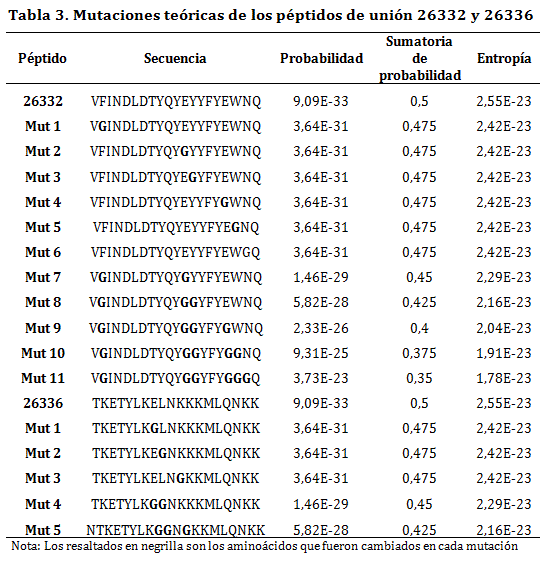
Para las 11 secuencias teóricas del péptido 26332, los valores de probabilidad variaron entre 3,64E-31 y 3,73E-23, los de sumatoria de probabilidad entre 0,35 y 0,475 y los de entropía entre 1,78E-23 y 2,42E-23. Las 11 secuencias teóricas presentaron valores menores al péptido original, los cuales fueron disminuyendo progresivamente y alejándose de los valores del macroestado de unión, a medida que se remplazaban más aminoácidos críticos por Glicinas (Tabla 3).

Para las cinco secuencias teóricas del péptido 26336, los valores de probabilidad variaron entre 5,82E-28 y 3,64E-31, los de sumatoria de probabilidad entre 0,425 y 0,475 y los de entropía entre 2,16E-23 y 2,42E-23. Todas presentaron valores menores al péptido original; a medida que se cambio uno, dos y tres aminoácidos críticos por Glicinas, los valores de probabilidad, sumatoria de probabilidad y entropía eran más lejanos de los valores del macroestado de unión (Tabla 3).

Este es el primer trabajo en el que se caracteriza matemáticamente la especificidad de unión de secuencias no sobrelapadas de 20 aminoácidos de la proteína PfNBP-1 del merozoíto del P. falciparum, mediante la aplicación de la teoría de la probabilidad y la ley de la entropía, al establecer un espacio de probabilidad no equiprobable que permitió cuantificar la aparición de cualquier aminoácido en cualquier posición de las secuencias estudiadas, determinando dos macroestados, uno conformado por secuencias de alta unión al eritrocito y otro con secuencias que no lo son, con valores de probabilidad, sumatoria de probabilidad y entropía que claramente diferencian los dos macroestados.

Este trabajo, junto con los estudios realizados previamente a las proteínas MSP-1, EBA-140, MSA-2 y AMA-1 evidencian que esta metodología permite una caracterización objetiva del fenómeno de unión, revelando una auto-organización matemática no equiprobable de las secuencias peptídicas._16-19

Del mismo modo las mutaciones teóricas realizadas en los péptidos conocidos experimentalmente como de alta unión, al sustituir aminoácidos críticos por glicinas revelaron a través de cambios en los valores calculados, que hay un orden matemático subyacente al fenómeno de unión del merozoíto al eritrocito, evidenciando que los cambios consecutivos de estos aminoácidos presentan valores que se alejan progresivamente de los valores asociados al macroestado de unión.

Esto confirma una vez más, la importancia de realizar experimentos teóricos basados en leyes, dado que no solo economizan recursos sino que permiten hacer generalizaciones. Los trabajos empíricos que se han venido realizando acerca de este tipo de procesos son de gran utilidad, sin embargo requieren numerosas pruebas de ensayo y error.₈ Existen también, metodologías de simulación computacional que con base a la información experimental, buscan relaciones entre las secuencias de unión y de éstas con las proteínas presentadoras y a partir de ello, cuantifican la capacidad de unión de un péptido dado, cuyas medidas dependen de la muestra de estudio y el análisis empleado._20,21

El enfoque de este estudio, así como en la física teórica donde lo que importa es el orden acausal del fenómeno y no las causas, permitió caracterizar y diferenciar matemáticamente secuencias de unión y de no unión, al observarlas como secuencias numéricas de probabilidades y no como secuencias de aminoácidos, simplificando con ello, detalles como las características bioquímicas y motivos de los péptidos, contribuyendo a una comprensión objetiva y reproducible del fenómeno de unión de péptidos.₂₂ Metodologías como la planteada en esta investigación, constituyen una base esencial para el estudio de la malaria de forma teórica y eficiente, sin necesidad de análisis estadísticos.

Otros trabajos desde esta perspectiva físico-matemática han permitido el desarrollo de teorías predictivas de la unión de péptidos al HLA clase II y al eritrocito, la primera con un porcentaje de acierto del 100% de los péptidos evaluados y la segunda con una sensibilidad del 95% y una especificidad del 90%, comparada con resultados experimentales, resultados que facilitarían la escogencia de péptidos claves en el desarrollo de vacunas._23,24

En otros ámbitos de la investigación médica, como la predicción de epidemias, la morfometría celular o la dinámica cardiaca, el uso de teorías de la física o la matemática, también ha facilitado el desarrollo de metodologías objetivas de evaluación y predicción diagnostica; tal es el caso de una nueva metodología predictiva de linfocitos T CD4 con base en el conteo de leucocitos y linfocitos disponibles en el cuadro hemático, útil para el seguimiento y la planeación de los tratamientos de los pacientes con VIH/SIDA.₂₅

En morfometría celular se desarrolló una generalización diagnóstica cuantitativa de aplicación clínica que diferencia células normales, pre neoplásicas y neoplásicas, solucionando la indeterminación diagnostica de las células ASCUS.₂₆ Los conceptos de AMI y geometría fractal sirvieron para obtener el conjunto de posibles prototipos arteriales sanos y enfermos en el proceso de restenosis.₂₇ En el campo de la cardiología, mediante el cálculo de las proporciones de la entropía de atractores cardiacos se logró diferenciar dinámicas cardiacas normales, con enfermedad crónica o aguda, así como la evolución entre cada uno de estos estados; metodología que fue aplicada posteriormente al estudio de la evolución de la dinámica cardiaca de pacientes en la unidad de cuidados coronarios, mostrando que su uso permitiría evaluar objetivamente el impacto de intervenciones quirúrgicas y/o farmacológicas, constituyendo una medida de carácter preventivo._25,19

Desde la teoría de sistemas dinámicos se estableció una ley matemática exponencial de la dinámica caótica cardiaca de aplicación clínica que logra diferenciar normalidad de enfermedad y la evolución entre las dos.₂₈ Recientemente en este campo se desarrolló una metodología de ayuda diagnóstica del ventriculograma cardiaco izquierdo que permite evaluar de forma precisa y objetiva la evolución de un ventriculograma hacia la normalidad o la enfermedad.₂₉ En salud pública, el cálculo de los valores de probabilidad, entropía y restas de la relación S/k de grupos de tres semanas epidemiológicas, permitieron predecir brotes de malaria en 820 municipios de Colombia.₂₆ Estos trabajos evidencian la importancia y utilidad del uso de aproximaciones estrictamente físicas y matemáticas a los fenómenos médicos, para ampliar su comprensión y desarrollar metodologías de medición de aplicación práctica.

Agradecimientos
Este producto es derivado del proyecto PIC MED-851, financiado por la Vicerrectoría de Investigaciones de la Universidad Militar Nueva Granada. Agradecemos especialmente a la Dra. Martha Bahamón, vicerrectora académica, al Dr. Juan Miguel Estrada, decano de la Facultad de Medicina, al Ing. Alejandro Castro, Jefe de la división de Investigación Científica y a la Dra. Esperanza Fajardo, Directora del Centro de Investigaciones de la Facultad de Medicina, por su colaboración en la realización de nuestras investigaciones. Agradecemos también al Centro de Investigaciones de la Clínica del Country, especialmente al Dr. Jorge Ospina, Director Médico de la Clínica del Country, al Dr. Tito Tulio Roa, Director de Educación Médica, a Adriana Lizbeth Ortiz, epidemióloga del Centro de Investigaciones, a las enfermeras Silvia Ortiz y Sandra Rodríguez, y al Dr. Alfonso Correa, director del Centro de Investigaciones, por su apoyo a las investigaciones del Grupo Insight.

Referencias

1. World Health Organization. 10 facts on malaria. Disponible en: http://www.who.int/features/factfiles/malaria/en/index.html; 2010.         [ Links ]

2. Shuman EK. Global climate change and infectious diseases. New England Journal of Medicine. 2010;362(12):1061-1063.         [ Links ]

3. Chitnis CE, Blackman MJ. Host cell invasion by malaria parasites. Parasitology Today. 2000;16(10):411-415.         [ Links ]

4. Botero D, Restrepo M. Parasitosis humanas. 4ª ed. Corporación para Investigaciones Biológicas, Medellín, 2003: 156,164-168.         [ Links ]

5. Aikawa M, Miller LH, Johnson J, Rabbege J. Erythrocyte entry by malarial parasites. A moving junction between erythrocyte and parasite. The Journal Cell Biology. 1978;77:72-82.         [ Links ]

6. Hadley TJ, Klotz FW, Miller LH. Invasion of erythrocytes by malaria parasites: a cellular and molecular overview. Annual Review of Microbiology. 1986; 40:451-477.         [ Links ]

7. Rayner CJ, Vargas E, Huber S, Galinski MR, Barnell JW. Plasmodium falciparum homologue of Plasmodium vivax reticulocyte binding protein (PvRBP1) defines a trypsin-resistant erythrocyte invasion pathway. The Journal Experimental Medicine. 2001;194:1571–81.         [ Links ]

8. Valbuena J, Vera R, García J, Puentes A, Curtidor H, Ocampo M, et al. Plasmodium falciparum normocyte binding protein (PfNBP-1) peptides bind specifically to human erythrocytes. Peptides. 2003;24(7):1007-1014.         [ Links ]

9. Feynman RP, Leighton RB, Sands M. Probabilidad. En: Feynman RP, Leighton RB, Sands M. Física. Vol. 1. Wilmington: Addison-Wesley Iberoamerican S.A. 1964; p. 6-1, 6-16.         [ Links ]

10. Laplace P. Ensayo filosófico sobre las probabilidades. Barcelona: Altaya; 1995.         [ Links ]

11. Obregón I. La magia y belleza de las probabilidades. En: Obregón I. Magia y belleza de las matemáticas y algo de su historia. Intermedio Editores, Colombia, 2007:369. p. 113-128.         [ Links ]

12. Matvéev A. Física molecular. Mir, Moscú. 1987.         [ Links ]

13. Tolman RC. Principles of statistical mechanics. 1st ed., New York: Dover Publications; 1979.         [ Links ]

14. Shannon CE. The mathematical theory of communication. The Bell System Technical Journal. 1948;27:379–423, 623-656.         [ Links ]

15. Frodden E, Royo J. Entropía e Información, Seminario final del curso de termodinámica, Depto. de Física, Facultad de Ciencias, Universidad de Chile, 2004.         [ Links ]

16. Rodríguez J. Caracterización física y matemática de péptidos de alta unión de MSP-1 mediante la aplicación de la teoría de la probabilidad y la entropía. Archivos Alergia Inmunología Clínica. 2008a:39(2):74-82.         [ Links ]

17. Rodríguez J, Correa C, Prieto S, Puerta G, Vitery S, Bernal P, et al. Aplicación de la probabilidad y la entropía a la proteína EBA-140. Caracterización matemática de péptidos de alta unión. Inmunología. 2009a:28(2):65-73.         [ Links ]

18. Rodríguez J, Correa C, Prieto S, Cardona D, Vitery S, Puerta G, et al. Caracterización física y matemática de péptidos de alta unión de MSA-2. Aplicación de la teoría de la probabilidad y la entropía. Revista de la Academia Colombiana de Ciencias Exactas, Físicas y Naturales. 2009b;33(129):549-557.         [ Links ]

19. Rodríguez J. Proportional Entropy of the cardiac dynamics in CCU patients. 7th International Meeting Intensive Cardiac Care. Tel Aviv, Israel. 2011a.         [ Links ]

20. Zhao B, Sakharkar KR, Lim CS, Kangueane P, Sakharkar MK. MHC-Peptide binding prediction for epitope based vaccine design. International Journal of Integrative Biology. 2007;1(2):127.         [ Links ]

21. Lundegaard C, Lund O, Kes C, Brunak S, Nielsen M. Modeling the adaptive immune system: predictions and simulations. Bioinformatic. 2007;23(24):3265–3275.         [ Links ]

22. Fernández A. Introducción. En: Rañada A. Orden y Caos. Prensa científica S.A, Barcelona. 1990.         [ Links ]

23. Rodríguez J. Teoría de unión al HLA clase II teorías de probabilidad combinatoria y entropía aplicadas a secuencias peptídicas. Inmunología. 2008b;27(4):151-166.         [ Links ]

24. Rodríguez J. Entropía proporcional de los sistemas dinámicos cardiacos: Predicciones físicas y matemáticas de la dinámica cardiaca de aplicación clínica. Revista Colombiana de Cardiología. 2010a;17:115-129.         [ Links ]

25. Rodríguez J, Prieto S, Bernal P, Pérez C, Álvarez L, Bravo J, et al. Predicción de la concentración de linfocitos T CD4 en sangre periférica con base en la teoría de la probabilidad. Aplicación clínica en poblaciones de leucocitos, linfocitos y CD4 de pacientes con VIH. Infectio. 2012a;16(1):15-22.         [ Links ]

26. Rodríguez J, Prieto S, Correa C, Posso H, Bernal P, Puerta G, et al. Generalización fractal de células preneoplásicas y cancerígenas del epitelio escamoso cervical. Una nueva metodología de aplicación clínica. Revista Facultad de Medicina. 2010b;18(2):173-181.         [ Links ]

27. Rodríguez J, Prieto S, Correa C, Bernal P, Puerta G, Vitery S, et al. Theoretical generalization of normal and sick coronary arteries with fractal dimensions and the arterial intrinsic mathematical harmony. BMC Medical Physics. 2010c:10(1):1-6.         [ Links ]

28. Rodríguez J. Mathematical law of chaotic cardiac dynamic: Predictions of clinic application. Journal of Medical and Medical Science. 2011b:2(8):1050-1059.         [ Links ]

29. Rodríguez J, Prieto S, Correa C, Bernal P, Forero G, Vitery S, et al. Diagnóstico fractal del ventriculograma cardiaco izquierdo: Geometría fractal del ventriculograma durante la dinámica cardiaca. Revista Colombiana de Cardiología. 2012b:19(1):18-24.         [ Links ]