Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Ciencia e Ingeniería Neogranadina
versão impressa ISSN 0124-8170versão On-line ISSN 1909-7735
Cienc. Ing. Neogranad. v.20 n.2 Bogotá jul./dez. 2010
Helbert Espitia Cuchango2
José Soriano Méndez3
1Ing. Electrónico, Facultad de Ingeniería, Investigador grupo LAMIC. Universidad Distrital Francisco José de Caldas, Bogotá, Colombia, linam_26@hotmail.com
2Ing. Electrónico Mg., Profesor asistente, Facultad de Ingeniería, Investigador grupo LAMIC. Universidad Distrital Francisco José de Caldas, Bogotá, Colombia, heespitiac@unal.edu.co
3Ing. Electrónico Mg., Profesor asistente, Facultad de Ingeniería, Investigador grupo LAMIC. Universidad Distrital Francisco José de Caldas, Bogotá, Colombia, josoriano@gmail.com
Fecha de recepción: 16 de junio de 2010 Fecha de aprobación: 15 de octubre de 2010
RESUMEN
Este artículo propone la predicción de la serie de tiempo Lorenz usando un nuevo método conocido como sistema Neuro-DBR y su comparación, con un diseño neurodifuso convencional. La técnica Neuro-DBR es el resultado de la unión de las redes neuronales y la metodología de Defuzificación basada en relaciones booleanas (DBR). La teoría DBR pretende facilitar la implementación de una inferencia difusa y mejorar el tiempo de procesamiento de los sistemas difusos, para obtener a su vez, un buen desempeño. Los sistemas Neuro-DBR tratan de explotar la complementariedad que existe entre ambas técnicas, aprovechando las ventajas y eludiendo las desventajas de cada una de ellas. En una primera parte, se presenta el algoritmo de entrenamiento Neuro-DBR propuesto para identificar sistemas no lineales. Después, se presenta el diseño del identificador para las ecuaciones de Lorenz, usando un sistema Neuro-DBR y comparándolo con un diseño Neurodifuso convencional mediante la raíz del error cuadrático medio (RMSE), y el coeficiente de correlación (IC), como índices de desempeño. Los resultados obtenidos con el sistema propuesto, muestran la reducción del tiempo de entrenamiento y cálculo computacional. La teoría relacionada con lógica y conjuntos booleanos es una buena herramienta para diseñar de automatismos y sistemas digitales; una variación con la cual se busca mejorar los sistemas basados en automatismos consiste en emplear conjuntos difusos en lugar de booleanos. Lo anterior se realiza con el objetivo de tener una acción continua en el actuador del automatismo. Al realizar esta variación y aplicar la metodología de diseño de los sistemas de automatismos, aparecen los sistemas de inferencia difusa basados en relaciones booleanas.
Palabras claves: ecuaciones de Lorenz, DBR, back-propagation, sistemas Neuro-DBR, sistemas no lineales.
ABSTRACT
This paper proposes the Lorenz time series prediction using a new method known as neural-DBR system and comparing this with a typical fuzzy-neural design. the neural-DBR technique is a union of neural networks and the defuzzification methodology based on Boolean relations (DBR). The DBR theory aims to facilitate the implementation of a fuzzy inference and improve processing time of fuzzy systems, getting also a good performance. Neural-DBR systems try to take advantage of the complementarity between both techniques, using their benefits and avoid the unfavorable ones of each. Firstly, the paper presents the neural-DBR training algorithm proposed for identification of nonlinear systems. Later, the identifier for Lorenz equations, using a neural-DBR system and comparing it with a typical fuzzy-neural design through the root mean square error (RMSE) and the correlation coefficient (IC) as performance indices. The results of the system proposed show the reduction in training time and computation calculation. Boolean logic is accepted as a useful tool for automata and digital systems design. An alternative to improve automation systems is using fuzzy sets instead of Boolean logic. This is to obtain a continuous description for the actuator. By such a change and implementing the methodology of design automation systems, the fuzzy inference systems based on Boolean relations may appear.
Key words: Lorenz equations, DBR, back-propagation algorithm, Neuro-DBR systems, nonlinear systems.
INTRODUCCIÓN
La lógica booleana es una herramienta útil en el diseño de sistemas automáticos [4], [14], sin embargo, estos sistemas de control presentan un desempeño limitado debido a sus cambios abruptos en las acciones de control. Una forma de mejorar el desempeño de estos sistemas consiste en reemplazar los conjuntos booleanos por difusos. Un trabajo donde se busca aprovechar las características del diseño de automatismos basados en álgebra booleana se presenta en [16], donde se propone un método de optimización para los sistemas de inferencia difusa, empleando lógica booleana.
Desde el punto de vista de la lógica difusa, los sistemas basados en relaciones booleanas se consideraron como un posible mecanismo para implementar el proceso asociado con la defuzificación [2], [18]; sin embargo, con las últimas investigaciones realizadas, esta orientación se puede interpretar como un sistema de inferencia difusa.
El concresor basado en relaciones booleanas (CBR), o como se denominó originalmente en inglés Defuzification Based on Boolean Relations (DBR), busca plantear un mecanismo de implementación para los sistemas de lógica difusa, tomando como referencia el diseño de automatismos, ya que estos sistemas son muy empleados en el control de procesos por su facilidad para implementarlas. Esta técnica de diseño considera los sensores, actuadores y las relaciones booleanas que se emplean en las estrategias de control [17]. Las características que se esperan lograr con este nuevo enfoque son:
- Facilitar la implementación computacional del sistema de inferencia difusa.
- Debido a la anterior característica, se espera tener un mejor desempeño en cuanto al tiempo de procesamiento del sistema de inferencia difusa.
- Proporcionar una metodología de diseño para sistemas de lógica difusa.
Los sistemas de lógica difusa tienen un buen comportamiento al trabajar con sistemas físicos y aunque su diseño no es complicado, la implementación del defuzifcador sí lo es, debido a los cálculos complejos que debe realizar para encontrar el valor de la salida, demorándose un tiempo considerable y haciendo que el diseño del algoritmo no sea tan sencillo [17]. Lo anterior genera la necesidad de utilizar plataformas o dispositivos más robustos según el desempeño que se desee del sistema, haciéndolo más costoso y menos práctico. El DBR constituye entonces, un método sencillo y simplificado de diseñar e implementar la defuzifcación, y además, presenta un buen desempeño [17], [19] y las ventajas de los sistemas difusos. La anterior característica lo convierte en una alternativa viable en relación con los modelos convencionales de inferencia difusa.
Los sistemas Neuro-DBR además de los rasgos que son comunes a ambas técnicas, facilitan la representación del conocimiento estructurado que es propio de los sistemas DBR. Esto permite mejorar la comprensión de la red neuronal y la capacidad de aprender y adaptarse de las redes neuronales, aportando un mecanismo de sintonización automática y adaptabilidad al sistema DBR [13]. Por otra parte, tanto las redes neuronales como los sistemas DBR, son sistemas que pueden ser considerados como aproximadores de funciones sin modelo, entendiéndose como sistemas que tienen la capacidad de estimar el valor de la función que caracteriza su relación entrada-salida, sin necesidad de disponer de un modelo o descripción analítica de la misma [3], [6], [10], [11], [13].
El algoritmo de entrenamiento para la red Neuro-DBR propuesto en este artículo es utilizado para realizar la predicción de la serie de tiempo Lorenz. Las ecuaciones de Lorenz son un conjunto de tres ecuaciones diferenciales no lineales acopladas, para las variables x , y , z que describen el estado del sistema y que pueden presentar un comportamiento caótico para ciertos rangos de valores de sus parámetros [20].
1. MARCO CONCEPTUAL
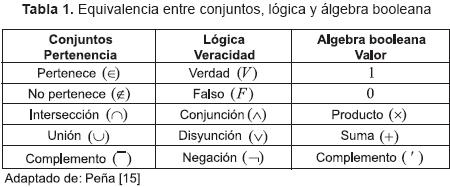
Una de las características importantes por considerar en esta propuesta, es la relación (isomorfismo), [15], observada entre: teoría de conjuntos, lógica y sistemas matemáticos (retículos y álgebra booleana), [5], [8]. Algunas de las equivalencias más importantes de estos isomorfismos se pueden observar en la tabla 1.
Otro aspecto de importancia para considerar en la propuesta desarrollada consiste en las operaciones entre conjuntos difusos.
1.1. INTERSECCIÓN DE CONJUNTOS DIFUSOS
En el contexto de la lógica difusa, se denomina T-norma a esta operación. Una forma general para representar la operación difusa de intersección es:
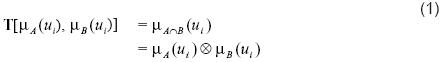
Una T-norma es una función de la forma: T: [0,1] x [0,1] →[0,1] que cumple con las siguientes propiedades:
Conmutativa: µA 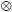 µB = µB
µB = µB 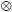 µA, ∀µA,µB ∈[0,1].
µA, ∀µA,µB ∈[0,1].
Asociativa: µA 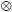 (µB
(µB 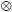 µC) = (µA
µC) = (µA 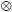 µB)
µB) 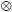 µC, ∀µA, µB, µC ∈[0,1].
µC, ∀µA, µB, µC ∈[0,1].
Si µA, ≤ µB Y µC ≤ µD entonces µA 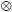 µC ≤ µB
µC ≤ µB 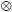 µD
µD
Condiciones de frontera:
- µA 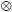 0 = 0, µA ∈[0,1].
0 = 0, µA ∈[0,1].
- µA 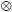 1 = µA, µA ∈[0,1].
1 = µA, µA ∈[0,1].
Existen varios métodos para calcular esta operación, siendo de los más empleados, el mínimo (estándar), y el producto.
1.2. UNIÓN DE CONJUNTOS DIFUSOS
Se conoce en lógica difusa, como S-norma una forma general para representar la operación difusa de unión es [9]:
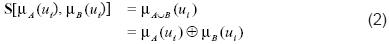
Una S-norma es una función de la forma: S: [0,1] x [0,1] → [0,1] que cumple con las siguientes propiedades [9]:
Conmutativa: µA  µB = µB
µB = µB  µA, ∀µA,µB ∈[0,1].
µA, ∀µA,µB ∈[0,1].
Asociativa: µA 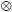 (µB
(µB  µC) = (µA
µC) = (µA  µB)
µB) 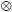 µC, ∀µA, µB, µC ∈[0,1].
µC, ∀µA, µB, µC ∈[0,1].
Si µA, ≤ µB Y µC ≤ µD entonces µA  µC ≤ µB
µC ≤ µB  µD
µD
Condiciones de frontera:
- µA  0 = 0, µA ∈[0,1].
0 = 0, µA ∈[0,1].
- µA  1 = µA, µA ∈[0,1].
1 = µA, µA ∈[0,1].
Al igual que el caso anterior, la S-norma presenta varios métodos de cálculo, siendo de los más empleados el máximo (estándar), y la suma probabilística.
1.3. COMPLEMENTO DIFUSO
En lógica difusa, existen diferentes formas para calcular el complemento de un conjunto difuso Ai, con base en su función de pertenencia µA(ui) [9]. Una forma general para representar el complemento de un conjunto difuso es:

La forma más empleada (estándar), del complemento difuso consiste en definir el conjunto difuso complemento con la función de pertenencia (4).

2. SISTEMAS DE INFERENCIA BASADOS EN RELACIONES BOOLEANAS
Los sistemas de inferencia difusa basados en relaciones booleanas son concebidos como una alternativa para mejorar el desempeño de los sistemas de control basados en automatismos.
Desde el punto de vista de automatismos, se tiene una acción sobre uno o varios actuadores, esta acción suele ser todo o nada y genera transiciones bruscas en el proceso. Con el DBR, se pretende lograr que estas transiciones no sean bruscas al convertir conjuntos booleanos en difusos y al mismo tiempo, aprovechar la metodología de diseño de automatismos desde el dominio booleano. En Rovatti et al [16], se presenta un concepto similar, pero sólo se considera como un proceso de optimización y no como una posible forma para implementar sistemas de lógica difusa.
El concepto de los sistemas de inferencia basados en relaciones booleanas, se encuentra fundamentado en las siguientes premisas:
- Segmentación de los universos con conjuntos booleanas.
- Transiciones monótonas entre regiones booleanas.
Los bloques estructurales de un sistema de inferencia difusa basado en relaciones booleanas son en esencia: la fuzificación y la concreción de la información difusa, ya que el proceso de defuzificación es una tarea intrínseca a la manera como se realiza la concreción. Un esquema de dicho proceso se observa en la figura 1.
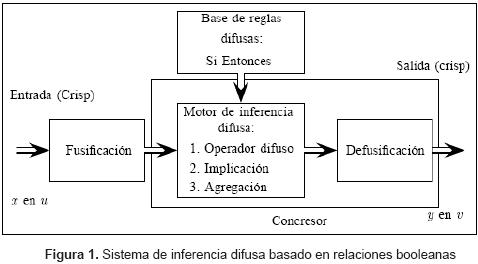
2.1. MODELO DE LOS SISTEMAS DE INFERENCIA DIFUSA BASADOS EN RELACIONES BOOLEANAS
Para un sistema de w funciones de activación, p conjuntos, q posibles implicaciones, siendo Ym la m -ésima salida de activación y 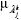 la j -ésima función de pertenencia de la k -ésima implicación. El proceso de inferencia de la m -ésima salida de activación, considerando conjuntos difusos, se puede expresar como:
la j -ésima función de pertenencia de la k -ésima implicación. El proceso de inferencia de la m -ésima salida de activación, considerando conjuntos difusos, se puede expresar como:

En el caso de considerar funciones de pertenencia, se tiene la siguiente expresión:

La salida puntual del sistema se puede calcular como:

Donde vm corresponde al m -ésimo actuador virtual, entonces la m -ésima salida virtual es:

La T-norma se aplica sobre las filas que corresponden a las entradas en la tabla 2. Estas representan las reglas que aportan a una salida de activación. La S-norma se aplica sobre las columnas de las salidas de activación de la tabla 2. La S-norma se puede considerar como un operador de agregación de las reglas que aportan para cada una de las salidas de activación.
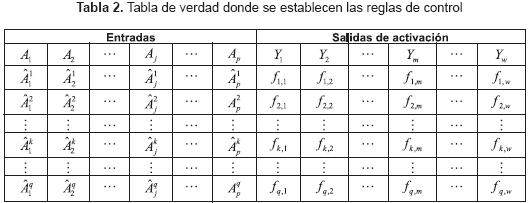
En este esquema, se distinguen dos partes, una que corresponde a la codificación booleana de las funciones de pertenencia de cada universo de discurso de entrada y otra, que corresponde a las salidas de activación asociadas a las salidas virtuales del sistema. En la parte de las entradas, cada fila representa una regla de inferencia; en la sección de las salidas, cada columna representa una salida de activación.
Para el cálculo de la salida (sin simplificar), como primer paso se aplica por separado la T-norma entre los conjuntos a lo largo de las filas, cuya salida de activación en la tabla de verdad es activa (reglas de inferencia). El siguiente paso consiste en aplicar la S-norma entre todos los resultados obtenidos del paso anterior para cada columna, los cuales corresponden a las salidas de activación (proceso de agregación). La tabla 2 muestra un esquema general de la respectiva colección de reglas en la tabla de verdad.
Finalmente, dadas las funciones difusas que determinan las salidas de activación, se procede a realizar la ponderación de cada una de ellas por el respectivo valor del actuador virtual. Este producto se llama salida virtual, y sumando los anteriores productos, se obtiene una salida concreta de acción.
Salida virtual. En el diseño de automatismos, la salida se puede considerar como el consecuente de una función booleana de las entradas que corresponden a los antecedentes. El sistema de inferencia difusa basado en relaciones booleanas toma este esquema, que es el mismo en lógica difusa. Sin embargo, la salida desde el punto de vista de automatismos, se considera como la acción total que se tiene por parte de los actuadores que están afectando el sistema. En el caso cuando sólo se dispone de un elemento de acción, este se puede considerar como la suma de varios actuadores que se denominan virtuales y que a su vez, tienen asociada una salida virtual.
Dependiendo de los conjuntos empleados y de las acciones por realizar en las regiones de operación, es posible tener un solapamiento de las acciones, por lo cual, la salida total puede ser mayor que las acciones virtuales parciales.
Para el sistema de inferencia, la salida corresponde a la suma de las respectivas salidas virtuales, siendo de la forma:
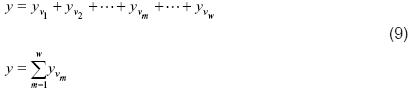
Donde yvm = Ymvm siendo Ym la salida de activación y vm el respectivo valor del actuador virtual. El término de salida virtual fue concebido bajo una correspondencia física real en aplicaciones de control, para la salida total del sistema de inferencia.
Con el fin de ilustrar el concepto de salida virtual, se puede observar la acción que tiene una válvula de 3" para el llenado de un tanque. Para el caso, esta válvula se puede considerar como el aporte que tienen tres válvulas (virtuales), de diferente diámetro que dan lugar a los actuadores virtuales:
- Flujo pequeño: v1 = 0.5"
- Flujo mediano: v2 = 1.0"
- Flujo grande: v3 = 1.5"
3. DESCRIPCIÓN DEL SISTEMA NEURO-DBR
Los sistemas Neuro-DBR pueden considerarse como una modificación de los sistemas DBR, al incorporar algoritmos de aprendizaje que se emplean en redes neuronales. Los sistemas Neuro-DBR presentan características de ambas técnicas, tienen la capacidad de aprender como una red neuronal y pueden realizar inferencia como un sistema difuso. El sistema Neuro-DBR utiliza algoritmos de entrenamiento empleados en redes neuronales, y uno de los algoritmos más conocidos es el Back-Propagation [3], [13], [10], que es usado en este trabajo.
En las redes neuronales ordinarias, los nodos tienen la misma funcionalidad y son plenamente conectados a los nodos de las capas vecinas, pero en un sistema Neuro-DBR, los nodos tienen diferentes funcionalidades y no son completamente conectados a los nodos de las capas vecinas. Estas diferencias vienen dadas por la arquitectura del DBR, donde cada nodo y enlace corresponden a un componente específico del sistema.
Para el algoritmo de aprendizaje del sistema Neuro-DBR, se consideran sistemas multivariables en antecedente, univariable en consecuente, y una extensión de conjuntos booleanos adyacentes disjuntos a conjuntos gaussianos (figura 2) [17]. Las funciones de pertenencia gaussianas son derivables, condición necesaria para poder usar el algoritmo de entrenamiento por gradiente descendiente [6], [11], [13].
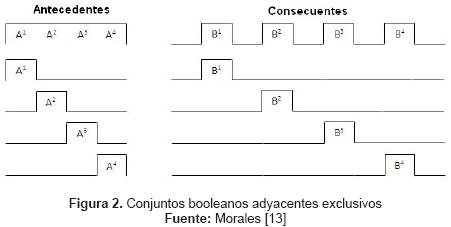
Considerando la arquitectura del DBR [17], usando como T-norma el producto y empleando conjuntos difusos gaussianos, se obtiene:
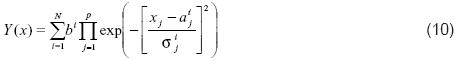
Donde N es el número de reglas difusas, p es el número de entradas al sistema, bi es el centro del conjunto Bi (constante para el modelo Singleton), xj es el elemento evaluado (dato de entrada al sistema), aij y σ ij son el centro y la desviación estándar del conjunto gaussiano respectivo en el antecedente. Entonces, la estructura del sistema DBR es (11).
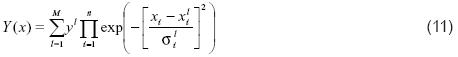
Donde M = N , yl = bi , n= p , xi =xj , xil = aij y σil =σij . El valor de M es fijado, y yl, xil , σil son parámetros libres. Una vez se especifiquen los parámetros yl , xil y σil , se obtiene el sistema DBR diseñado, esto es, el diseño del sistema DBR es ahora equivalente a determinar los parámetros yl , xil y σil . Por lo tanto, el mapeo de la entrada a la salida se mantiene con las siguientes operaciones:
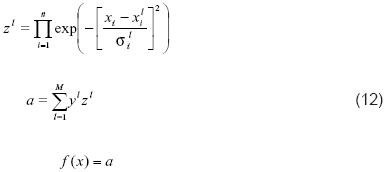
Por lo tanto, la representación del sistema DBR en forma de red neuronal, se muestra en la figura 3.
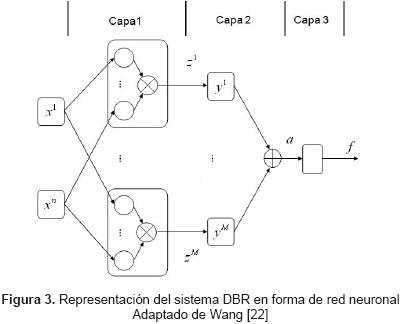
Teniendo en cuenta el algoritmo Back-Propagation para un sistema Neurodifuso convencional [11], [12], [22], [23], la estructura del sistema DBR (11), y usando el algoritmo de gradiente descendiente, entonces para actualizar los parámetros, se calculan las derivadas del error tal como se muestra en la ecuación (13).
Donde el error por cada dato de entrada p , es dado por (14) y las ecuaciones definitivas para actualizar los parámetros se presentan en el sistema (15) [13].

Siendo yp la salida deseada del sistema.
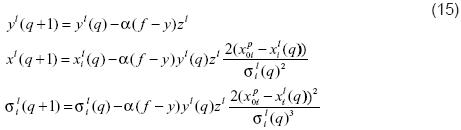
El algoritmo para la identificación Neuro-DBR se presenta a continuación [13]:
-
Determinar la estructura y establecer los parámetros iniciales. se debe escoger el sistema DBR de la forma (11), y determinar M y n. Entre mayor sea M resultarán más parámetros y mayor complejidad, pero se logra una mejor aproximación. Adicionalmente, se debe especificar los parámetros yl(0), x1i(0) y σ1i(0). Estos parámetros iniciales pueden ser determinados de acuerdo con el experto o ser escogidos de tal manera, que las correspondientes funciones de pertenencia cubran uniformemente el espacio de entrada y salida [22].
-
Calcular la salida del sistema Neuro-DBR. Para un par de entrada-salida (Xp0-Xp0) p = 1,2,..., en la q-ésima etapa de entrenamiento, q = 0,1,2,..., y con xp0 en la entrada del sistema Neuro-DBR, se calculan las salidas de cada capa. Esto es, computar (12).
-
Actualizar los parámetros. Ectualizar los parámetros yl(q + 1), x1i(q + 1) y σ1i(q + 1), según (15), donde y = ypo y ƒ(x) = ƒ. El parámetro a es conocido como ritmo de aprendizaje. Si α es escogido muy grande, puede hacer que el algoritmo no converja, mientras escoger un valor muy pequeño puede causar que el algoritmo tome mucho tiempo para converger. En la práctica, este valor es escogido entre 0 y 1 [12], [22], [23].
-
Retomar el paso 2 con q = q + 1, hasta que el error |ƒ-yp0 | sea menor que un número ε definido o hasta que q sea igual a un número definido.
-
Retomar el paso 2 con p = p + 1; esto es, actualizar los parámetros, usando la siguiente pareja de entrada-salida (x0p+1,Y0p+1).
El anterior algoritmo es definido para una época cuando cada elemento del conjunto de entrenamiento es usado sólo una vez, y los parámetros son actualizados, usando una función de error (14) que depende solamente de un dato en el tiempo.
4. PREDICCIÓN DE LA SERIE DE TIEMPO LORENZ
Las ecuaciones de Lorenz que describen la serie de tiempo por trabajar, son propuestas en Strogatz [20], y se presentan a continuación:

Donde σ,r,b > 0 son parámetros, σ es el número de Prandtl, r es el número de Rayleigh y b no tiene nombre (en problemas convencionales está relacionado con la proporción de las capas). Estas ecuaciones han sido usadas en estudios de láseres, dínamos, e incluso, puede construirse simples ruedas de molino cuyo comportamiento está descrito por estas ecuaciones. El objetivo del experimento es usar cuatro valores pasados, x(k), y(k-1), y(k), z(k), para encontrar el valor futuro y(k + 1).
Los parámetros de las Ecuaciones de Lorenz se fijaron, considerando Strogatz [20], el valor de σ es 10, de b es 8/3 y de r es 28. Este valor de r es mayor que el valor de bifurcación de Hopf rH ≈ 24.74, estableciendo un comportamiento caótico (figura 4).
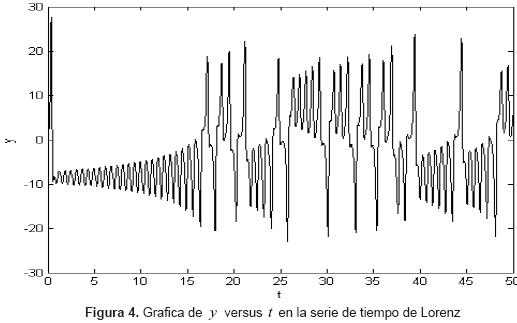
Se evalúa la serie de tiempo Lorenz con 1.212 datos, y(0), y(0.1) ,...,y(50) y un período de muestreo de 0.041 aproximadamente. Esto fue determinado según el mejor comportamiento obtenido con diferentes cantidades de datos y muestreo. Utilizando el principio de Pareto 80/20 [7], se define el 80% de los datos totales (970), como datos de entrenamiento y 20% de los datos totales (242), como datos de validación. Basándose en el diseño neurodifuso realizado en [12] para la serie de tiempo mackey-glass, se tiene en cuenta sólo dos conjuntos difusos para cada uno de los cuatro antecedentes; por lo tanto, el número de reglas difusas es igual a (M=16).
Los parámetros iniciales de cada función de pertenencia gaussiana se escogieron de manera que cubran todo el dominio de los universos de discurso de entrada y salida. Las desviaciones estándar de las gaussianas se fijan en 20. Se eligen 16 consecuentes correspondientes a las 16 reglas difusas definidas, de forma aleatoria dentro de un intervalo de -30 a 30. Este intervalo se establece de manera que incluya todos los valores de salida en el rango de y(0) a y(50) (figura 4).
Se toman 40 épocas de entrenamiento, que se determinaron según la disminución del RMSE en cada época, cuando se observa que a partir de cerca de la época 40 el RMSE se nivela; es decir, el RMSE disminuye pero en menor cantidad (aproximadamente 0.001). Así mismo, teniendo en cuenta [12], el ritmo de aprendizaje en el entrenamiento, se define como α = 0.2 y q =1 como número mínimo de iteraciones en el paso 4 del algoritmo. El comportamiento del modelo es medido de acuerdo con la raíz del error cuadrático medio (RMSE), y el coeficiente de correlación (IC), índices utilizados en la literatura (ver [1], [21]) para series de tiempo.
Se utiliza la herramienta computacional Simulink® de MatLab® para obtener los valores de entrada y salida de la serie de tiempo Lorenz. Las condiciones iniciales de los inte-gradores son establecidas como 0, 1, 0 para x , y , z , respectivamente, considerados [20]. El editor para comandos de código de MatLab®, se emplea para desarrollar en software, el algoritmo de entrenamiento y poder realizar la predicción del sistema no lineal considerado.
5. RESULTADOS OBTENIDOS
Los parámetros del sistema son sintonizados y el RMSE se calcula en cada época; para tal fin se utiliza la salida del sistema original y los datos de validación en cada época. En la figura 5, se aprecia una reducción sustancial del RMSE desde la primera época con un valor de 1.8239 hasta la época 40 con un valor de 0.4694.
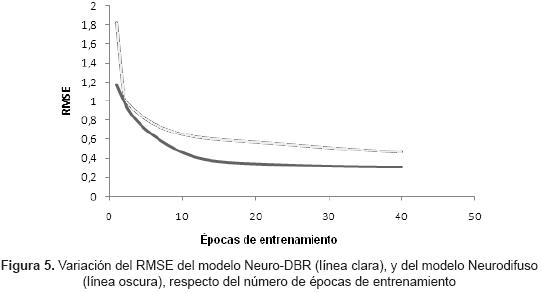
El índice de correlación entre los datos de salida de validación del sistema original y los datos de salida de validación del modelo diseñado es de 0.9987. Esto significa que el modelo estima bien las fuctuaciones de los datos con respecto de la media. El tiempo de entrenamiento total correspondiente a las 40 épocas de entrenamiento es de 1.9819 segundos. La figura 6 presenta la salida del modelo diseñado y la salida del sistema original, usando los datos de validación.
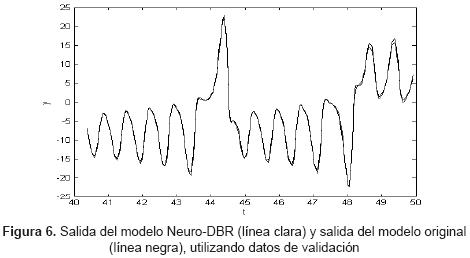
Para observar el desempeño del sistema Neuro-DBR, se hace la identificación Neurodifusa convencional, cuya estructura difusa es caracterizada por el producto como motor de inferencia difusa, fuzificador singleton, defuzificador centro promedio, y funciones de pertenencia gaussianas [12], [22]. Adicionalmente, el algoritmo de entrenamiento empleado para este propósito, es el Back-Propagation y los parámetros iniciales de la red neurodifusa, son los mismos establecidos en la red Neuro-DBR.
De la misma manera que en la identificación Neuro-DBR, existe una reducción en el RMSE desde la primera época con un valor de 1.1674 hasta la época 40 con un valor de 0.3088. El índice de correlación entre los datos de salida originales de validación y los datos de salida del modelo es de 0.9994; esto quiere decir, que el modelo estima bien las fuctuaciones de los datos con respecto de la media. La figura 7 muestra la salida del modelo obtenido en la identificación Neurodifiusa. El tiempo de entrenamiento total correspondiente a las 40 épocas de entrenamiento es de 2.1773 segundos.
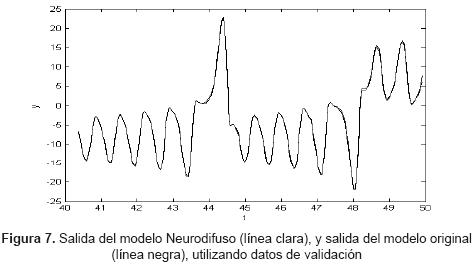
En la tabla 3 se presenta un resumen de los resultados obtenidos, donde se puede observar que el modelo neurodifuso convencional muestra un menor RMSE, en comparación con el Neuro-DBR. sin embargo, existe una reducción desde la primera a la época 40 de 0.8586 para el sistema Neurodifuso, mientras que para el sistema neuro-DBR se tiene una reducción mucho mayor de 1.3545.

A pesar de ser mayor el índice de correlación para el sistema Neurodifuso, el sistema Neuro-DBR presenta un IC muy similar (con una diferencia de 0.0007). Estos valores de IC tan cercanos a 1 significan que el modelo estima muy bien las fuctuaciones de los datos con respecto de la media. El tiempo de entrenamiento cuando se utilizan 40 épocas es mucho menor en el sistema Neuro-DBR, y demuestra que la implementación de la metodología DBR en algoritmos de entrenamiento como el Back-Propagation, reduce el esfuerzo y el tiempo computacional.
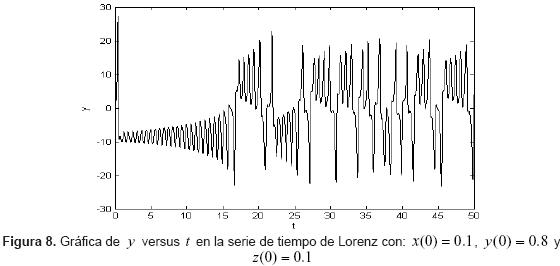
Dado que las ecuaciones de Lorenz son sensibles a las condiciones iniciales, para observar el comportamiento del sistema Neuro-DBR que ha sido entrenado, se toman como nuevas condiciones iniciales: x(0) = 0.1, y(0) = 0.8 y z(0) = 0.1. En la figura 8, se observa el comportamiento de la variable y(t) para las condiciones iniciales anteriores, siendo apreciable la diferencia con el comportamiento mostrado por el sistema de la figura 4.
El resultado de la predicción del sistema Neuro-DBR para las nuevas condiciones iniciales se puede apreciar en la figura 9.
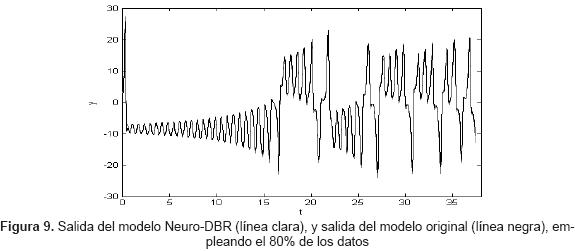
Aunque en este caso no se realizó entrenamiento, se empleó el 20% de los datos para evaluar el sistema Neuro-DBR, con el fin de poder comparar el resultado obtenido con los casos con entrenamiento (figura 10).
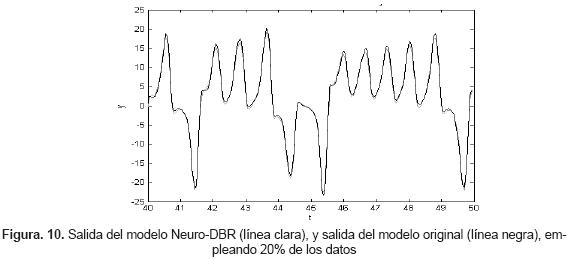
Para las nuevas condiciones iniciales, el RMSE obtenido fue de 0.4719 y el índice de correlación igual a 0.9978. Con estos datos, se observa que el desempeño del sistema Neuro-DBR disminuye para las nuevas condiciones iniciales. Sin embargo, se logra una adecuada predicción del sistema caótico.
6. CONCLUSIONES
Se evidencia la capacidad de los sistemas Neuro-DBR para identificar sistemas no lineales.
Utilizar sistemas Neuro-DBR para la predicción de la serie de tiempo Lorenz, reduce el tiempo total de entrenamiento y muestra un RMSE tolerable.
Considerando el coeficiente de correlación IC como índice para evaluar el desempeño de los modelos, puede observarse que se obtiene un resultado favorable puesto que el modelo Neuro-DBR presenta un IC muy cercano a 1, es decir, el modelo estima muy bien las fuctuaciones de los datos de salida con respecto de la media.
La reducción del RMSE a medida que aumentan las épocas de entrenamiento es mucho mayor en el modelo Neuro-DBR que en el modelo Neurodifuso, y con el modelo Neuro-DBR se obtiene un menor RMSE, trabajando con más épocas de entrenamiento.
Se observó que el sistema Neuro-DBR logra predecir el comportamiento del sistema para condiciones iniciales diferentes a las empleadas para los datos de entrenamiento.
Este artículo genera propuestas para otros trabajos en el futuro. Por ejemplo: aplicar el modelo Neuro-DBR a otros tipos de sistemas no lineales, así como explorar los diferentes métodos de DBR aplicados a otros algoritmos de entrenamiento como la regla de Widrow-Hoff asociado a la Adaline.
REFERENCIAS BIBLIOGRÁFICAS
[1] Badjate S., Dudul S. (2008). Prediction of Mackey-Glass chaotic time series with effect of superimposed noise using FTLRNN model, En: Proceedings on Advances in Computer Science and Technology, pp 384-389. [ Links ]
[2] Ballén Alexander, Rodriguez Cesar (2003). Diseño e implementación de un controlador difuso autosintonizado sobre microcontroladores, aplicado al control del péndulo invertido, Tesis de pregrado, Bogotá, Universidad Distrital Francisco José de Caldas. [ Links ]
[3] De Jesús R. (2000) Diseño y aplicación de Controladores Neurodifusos integrados en modo mixto de alta complejidad., Málaga, España, 301p, Tesis de doctorado. Universidad de Málaga. [ Links ]
[4] Dougherty Edward, Giardina Charles (1998). Mathematical methods for artificial intelligence and autonomous systems. Upper Saddle River. Prentice-Hall. 446 p. [ Links ]
[5] Dubisch Roy (1964). Lattices to Logic. New York: Blaisdell Publishing Company, 88 p. [ Links ]
[6] Figueiredo M., Gomide F. (1999). Design of Fuzzy Systems using Neurofuzzy Networks. En: IEEE transactions on Neural Networks, Vol. 10, No. 4, pp. 815-827. [ Links ]
[7] Goldfeld S., Quandt R. (1972). Nonlinear Methods in Econometrics. Amsterdam North Holland, 292 p. [ Links ]
[8] Irazo Pascual J. (2005). Lógica Simbólica para informáticos Madrid: Alfaomega Ra-Ma, 328 p. [ Links ]
[9] Klir George, Yuan Bo (1995). Fuzzy Sets and Fuzzy Logic, Upper Saddle River. Prentice Hall, 592 p. [ Links ]
[10] Martín J. (2000). Implementación de Redes Neurodifusas para ser aplicadas en problemas de clasificación y modelización. Universidad de Valencia, España. Dissertation.com, 112 p. [ Links ]
[11] Meesand D., Yen, G. (2001). A Neurofuzzy Networks and its application to machine health monitoring, En: IEEE Neural Networks IJCNN'01, Vol. 3, pp. 2298-2303. [ Links ]
[12] Mendel J. (2001). Rule Based Fuzzy Logic Systems, Upper Saddley River N.J. Prentice Hall, 576 p. [ Links ]
[13] Morales L. (2009). Estudio y evaluación del método de defuzificación basado en Relaciones Booleanas (DBR) aplicado a las redes Neurodifusas, para la identificación de sistemas no lineales; Bogotá, Colombia. Tesis de pregrado, universidad distrital Francisco José de Caldas. [ Links ]
[14] Ogata Katsuhiko (1987). Dinámica de Sistemas. México: Prentice-Hall Hisp, 631p. [ Links ]
[15] Peña Carlos A. (2004). Coevolutionary Fuzzy Modeling. Germany: Springer Verlag, 129 p. [ Links ]
[16] Rovatti Riccardo, Guerrieri Roberto e Baccarani Giorgio (1995). An Enhanced Two-Level Boolean Synthesis Methodology for Fuzzy Rules Minimization, En: IEEE Transactions On Fuzzy Systems, Vol. 3, No. 3, pp. 288-299. [ Links ]
[17] Soriano, J. J. (2001). Propuesta de concresor basado en relaciones booleanas, En: Revista de Ingeniería. Vol. 6, No. 1, pp. 44-50, Universidad Distrital Francisco José de Caldas. [ Links ]
[18] Soriano, José J., Gálvez Camilo A., Vargas David E., (2004). Identificación de personas por medio de diometria en la planta de la mano usando técnicas digitales de procesamiento de imágenes y concresor difuso basado en relaciones booleanas, Bogotá, 47 p. Tesis de grado, Ingeniería Electrónica, Universidad Distrital Francisco José de Caldas. [ Links ]
[19] Soriano J., Figueroa, J. (2007). A Comparison of ANFIS, ANN and DBR systems on volatile Time Series Identification, En: Proceeding on NAFIPS, pp. 319-324. [ Links ]
[20] Strogatz, S. (1994). Nonlinear dynamics and chaos with applications to physics, biology, chemistry and engineering, Cambridge, Perseus Books, 512 p. [ Links ]
[21] Velásquez, J. (2004). Pronóstico de la serie de tiempo Mackey-Glass usando modelos de regresión no lineal, En: Revista de la Facultad de Minas, Vol. 71, No. 142, p. 85-95. Medellín: Universidad Nacional de Colombia. [ Links ]
[22] Wang L. X. (1996). A course on Fuzzy Systems and Control, New Jersey: Prentice Hall, 448 p. [ Links ]
[23] Zak S. (2003). Systems and Control. New York: Oxford University Press, 720 p. [ Links ]















