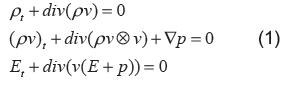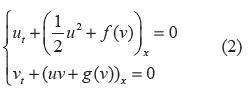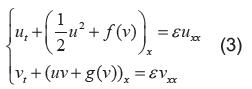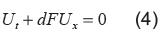Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Ciencia e Ingeniería Neogranadina
versão impressa ISSN 0124-8170versão On-line ISSN 1909-7735
Cienc. Ing. Neogranad. v.21 n.1 Bogotá jan./jun. 2011
Docente en el Departamento de Matemáticas, Universidad Militar Nueva Granada
adrian.gomez@unimilitar.edu.co
Fecha de recepción: 24 de enero de 2011 Fecha de aprobación: 11 de mayo de 2011
RESUMEN
En este artículo se presenta la existencia de soluciones viscosas al sistema general de Euler sin fuente para un fluido comprensible. El método que se usó para solucionar el sistema, no es el de las regiones invariantes que se encuentra en la literatura. En paralelo, encontraremos las soluciones viscosas globales suaves del sistema, usando el principio del máximo.
Palabras clave: leyes de conservación hiperbólica, principio del máximo, estimaciones a priori, ecuaciones diferenciales parabólicas, problema de Cauchy.
ABSTRACT
This paper reveals the existence of solutions to a general Euler system without source for a compressible fluid. The method used to solve the system is not the common invariant regions found in literature. In parallel, we will find the smooth global viscous solutions of the system using the maximum principle.
Key words: hyperbolic conservations laws, maximum principle, a priori estimate, Cauchy problems.
INTRODUCCIÓN
Un fluido compresible es aquel en donde existen variaciones de densidad significativas producidas por cambios de temperatura, presión o por grandes velocidades.
La ecuación de Euler para un fluido compresible en coordenadas eulehanas, se puede escribir en la siguiente forma conservativa como:
Donde la energía total está dada por:
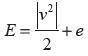
p(x,t) es la densidad, v es el campo de velocidades, e es la energía interna, p es la presión termodinámica y  representa el producto de Kronecker entre pv y v.
representa el producto de Kronecker entre pv y v.
Las ecuaciones representan en su lectura de arriba hacia abajo, la ley de conservación de masa, la ley de conservación de momento lineal y la ley de conservación de energía total. Este sistema complementa una ecuación de estado para el fluido de la forma:
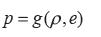
que determina la presión en términos de las densidades de masa y de energía interna. La forma de la función g se establece mediante observaciones experimentales y debe ser consistente con las leyes de la termodinámica según [1].
Es posible estudiar el sistema de ecuaciones de Euler en una dimensión espacial, como caso particular del sistema (1) y que modela por ejemplo: la dinámica de un gas que fluye a través de un tubo y donde la densidad, la velocidad y la energía son constantes a lo largo de secciones transversales del tubo; este fenómeno es claramente unidimensional.
Es importante decir que hay suficientes estudios desde el análisis numérico para este tipo de sistemas, ya que la demostración de soluciones explícitas es casi imposible por métodos clásicos. Por ejemplo: para el sistema de Ecuaciones de Euler unidimensional véase [2], para las ecuaciones de Euler en 2D véase [3] o para ecuaciones de Euler de forma general, véase [4], o una aplicación a la economía con métodos numéricos, se puede ver en [5].
En este artículo, se presenta la existencia de soluciones viscosas al sistema de flujo de fluido comprensible en forma general y que mantiene las leyes de conservación de masa y de momento lineal del sistema (1). Para tal fin, se estudia el sistema de ecuaciones diferenciales parciales dado por:
Con condiciones acotadas medióles en la norma r dadas por
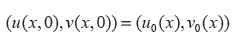
Físicamente, se puede entender este sistema como el modelo para la dinámica de un fluido compresible no viscoso que no conduce calor y cuyas ecuaciones se pueden interpretar como la conservación de la masa:
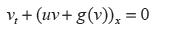
Donde la densidad por unidad de hipervolumen de la masa del fluido se puede representar por v y la velocidad del fluido es representada por u. La conservación del momento lineal total, se puede entender como:
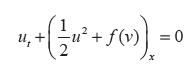
Un caso particular del sistema dos es el conocido sistema de ecuaciones dinámico para un gas politrópico como se puede encontrar en [6] y [7].
La metodología que se usa en este artículo, se fundamenta en un método que existe en la teoría de leyes de conservación hiperbólica, consistente en que para encontrar aproximaciones de soluciones viscosas de un sistema hiperbólico, se perturba en cierta forma dicho sistema y se convierte en parabólico para aplicar el método de las regiones invariantes o el principio del máximo. Una ley de conservación hiperbólica es un sistema de ecuaciones quasilineal de la forma
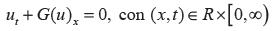
Donde: 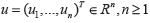 , es una función vectorial desconocida que modela una cantidad física y
, es una función vectorial desconocida que modela una cantidad física y 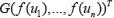 es un vector dado que denota un término de conservación asociado generalmente a dicha cantidad física.
es un vector dado que denota un término de conservación asociado generalmente a dicha cantidad física.
Se sabe que una perturbación al anterior sistema para convertirlo en un sistema hiperbólico según [7], se puede realizar de la siguiente forma:
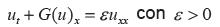
Que es un sistema de ecuaciones parabólicas semilineales y donde las soluciones al sistema de Cauchy a este sistema, es lo que comúnmente se llaman soluciones viscosas.
A finales del siglo pasado, se descubrieron los métodos de compacidad compensada y de entropía que permiten establecer la existencia de soluciones débiles a este tipo de sistemas de leyes de conservación hiperbólica como se puede ver [8] [9] [10] y [11]. Gran parte de los más recientes desarrollos de nuevos métodos los han aportado investigadores en matemáticas de China, y son ellos quien en el momento se han adelantado para establecer técnicas que permiten generalizar sistemas de leyes de conservación ya existentes.
1. PRINCIPIO DEL MÁXIMO-LEYES DE CONSERVACIÓN HIPERBÓLICA
Evans en [6], hace una clara introducción a las ecuaciones parabólicas, operadores parabólicos y al principio del máximo débil y fuerte, en particular Murray y otro en [12] estudia el principio del máximo para ecuaciones diferenciales ordinarias y pasa al principio del máximo para ecuaciones diferenciales parciales parabólicas. En especial Landis [13] hace una profunda y elegante presentación de este tipo de ecuaciones.
Lu [7], hace una breve y precisa introducción a los sistemas de leyes de conservación y define los invariantes de Riemann.
2. CALCULO DE ESTIMACIONES A PRIORI
Se puede garantizar la existencia de soluciones viscosas locales suaves en L∞ , y para tal fin, ver el teorema 1.0.2 en Lu [7] y en el capítulo 10, usa el método de las regiones invariantes para garantizar la existencia de soluciones del sistema con las condiciones acotadas medibles enunciadas en (2).
Estimaciones a priori, usando el principio de máximo. Se estima cotas para las soluciones de (2), por lo tanto, convertiremos el problema de encontrar la solución de (2), en el problema de encontrar la solución de una ecuación parabólica asociado al problema hiperbólico planteado para (2). Esta forma de atacar el problema es lo que se conoce como encontrar soluciones viscosas a un sistema de ecuaciones diferenciales, que para este caso en especial, usará el principio del máximo para ecuaciones parabólicas. Considerando el sistema (3), con las condiciones acotadas medibles enunciadas en (2) y suponiendo, para f , g que:
A. 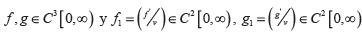
Satisface f1 ≥ d, con d ε R, y:
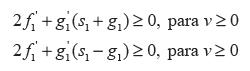
Donde: 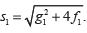
B. u0 y v0acotadas y medibles
Existen funciones que cumplen las condiciones en A, por ejemplo: si se toma 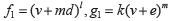 donde k,d,l,e,m son constantes positivas y e>d y l>m se puede verificar que fl , gl satisfacen dichas condiciones.
donde k,d,l,e,m son constantes positivas y e>d y l>m se puede verificar que fl , gl satisfacen dichas condiciones.
El siguiente teorema establece la existencia de soluciones globales suaves para el sistema (2).
Teorema 1. Para un ε > 0, el problema de Cauchy (3), con las condiciones de (2) y suponiendo que cumple las condiciones de A y B, tiene solución única global suave 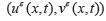 que satisface:
que satisface:
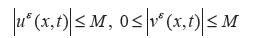
Donde M es una constante positiva independiente de ε.
Demostración: El sistema (1) se puede escribir como
Donde 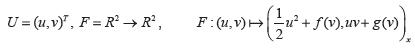 y
y
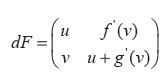
Para calcular los valores propios de esta matriz dF, se hace det(dF - λ) = 0, de donde al resolver
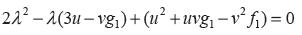
Se tiene
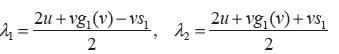
Resolviendo los siguientes sistemas de ecuaciones respectivamente, 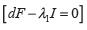 y
y 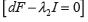 se obtiene que los vectores propios a derecha de
se obtiene que los vectores propios a derecha de 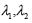 que son:
que son:
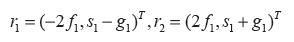
Al calcular los invariantes de Riemann, es decir, al resolver 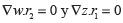 Se obtiene:
Se obtiene:
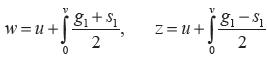
Calculando 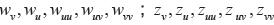 tenemos
tenemos
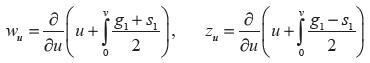
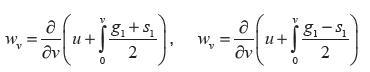
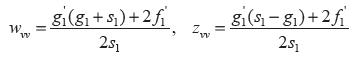
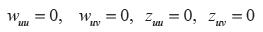
Multiplicando el sistema (3) por 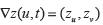 , tenemos
, tenemos 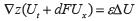 , si
, si 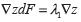 encontramos:
encontramos:
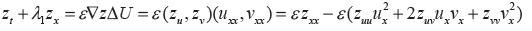
Remplazando 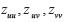 encontramos:
encontramos:
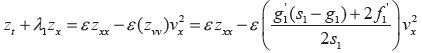
Si v ≥ 0, 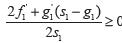 , entonces
, entonces
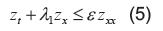
Multiplicando el sistema (3) por 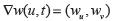 , tenemos
, tenemos 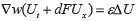 , si
, si 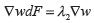 encontramos:
encontramos:
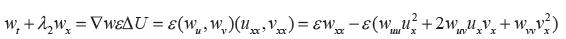
Remplazando 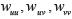 encontramos:
encontramos:
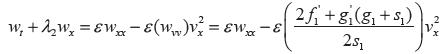
Si 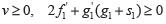 , entonces
, entonces
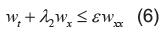
Tomando (5) y (6) así:
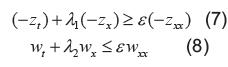
Al considerar las desigualdades (7) y (8) con variables en w y z, por el principio del máximo se puede conseguir estimaciones
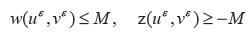
y por lo tanto
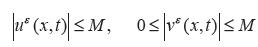
para una constante positiva M que depende de la norma L∞ en los datos iniciales.
3. CONCLUSIONES
Los sistemas de asociados a fluidos comprensibles como en (2), se dicen sin fuente, que se puede tratar de generalizar este tipo de sistemas, colocando un término adicional así:
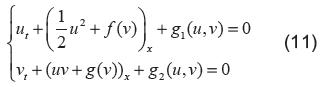
La idea en este caso, es encontrar soluciones globales de (11), guiados en el trabajo que Yan y otros realizan en [10] [11] y [14], usando la información suministrada en dichos artículos, se puede buscar soluciones débiles al sistema (11); de hecho, Lu en [7], encuentra soluciones débiles al sistema (2), basados en métodos de compacidad compensada.
Por otra parte, es importante decir que son diversas las aplicaciones de este sistema. Por ejemplo: la física e ingeniería resuelven diversas manifestaciones del sistema para resolver problemas aplicados particulares; pero lo cierto es que cada aplicación es un reto diferente porque, aunque se puede garantizar la existencia de soluciones en la mayoría de aplicaciones, no se puede decir con certeza que se puede establecer soluciones explícitas o implícitas por los métodos clásicos y es por esto, que es posible encontrar muchos artículos numéricos que resuelven casos muy concretos relacionados a este tipo de sistemas.
REFERENCIAS BIBLIOGRÁFICAS
[1] Plaza C. R., (2011). Sistemas hiperbólicos de leyes de conservación. En preparación. http://www.fenomec.unam.mx/ramon/publications.html [ Links ]
[2] Ávila C.A., Hortúa H.J., and Castañeda L., (2010). Ecuación de Euler unidimensional. En: Revista colombiana de física, 42, N.3 pp. 252-256. [ Links ]
[3] Bassi. F., and Rebay. S., (1997). High-order accurate discontinuous finite element solution of the 2D Euler equations. In: Journal of computational physics, 138, pp. 251-285. [ Links ]
[4] Chung Chang S., (1995). The method of space-time conservation element and solution element-A new approach for solving the navier-stokes and Euler equations. In: Journal of computational physics, 119, pp. 295-324. [ Links ]
[5] Maldonado W., y Moreira H., 2006. Solving Euler equations: classical methods and the C1 contraction mapping method revisited. En: Revista Brasileira de Economía, 60, N.2, pp. 167-178. [ Links ]
[6] Evans Lawrence, (1998). Partial differential equation. Vol 19, American Mathematical Society. [ Links ]
[7] Lu Yuguang, (2002). Hyperbolic conservations laws and the compensated compactos method. 128, Chapman and Hall, New York. [ Links ]
[8] Tsuge N., (2008). Global solutions to the compressible Euler equations with gravitational source. In: Journal of hiperbolic differential equations, Vol 5, N.2, pp. 317-346. [ Links ]
[9] Gui-Qiang G. Chen and Perepelitsa M., (2010). Vanishing viscosity limit of the Navier-Stokes equations for compressible fluid flow. Communications on Pure and Applied Mathematics, 63, N.11 pp. 1469-1504. [ Links ]
[10] Yan, J. Zhixin, C. Ming, T. (2007). Conservations Laws II: Weak Solutions, En: Revista Colombiana de Matemáticas, Vol. 41, pp. 91-106. [ Links ]
[11] Yan, J. Zhixin, C. Ming, T. 2007. Conservations Laws III: Relaxation limit, En: Revista Colombiana de Matemáticas, Vol. 41, N° 1, pp. 107-115. [ Links ]
[12] Protter M. H., Weinberger H. F., (1999). Maximum principles in differential equations. Ed. Springer. [ Links ]
[13] Landis E. M., (1997). Second order equations of elliptic and parabolic type. American Mathematical Society. Vol. 171. [ Links ]
[14] Yan J., Zhixin C, and Ming T., (2007). Conservations Laws I: Viscosity Solutions, En: Revista Colombiana de Matemáticas, Vol. 41, pp. 81-90. [ Links ]