Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ciencia e Ingeniería Neogranadina
Print version ISSN 0124-8170On-line version ISSN 1909-7735
Cienc. Ing. Neogranad. vol.21 no.2 Bogotá July/Dec. 2011
Ricardo Alberto Hincapié Isaza2
Ramón Alfonso Gallego Rendón3
1Estudiante Ingeniería Eléctrica, Investigador Grupo de Planeamiento. Universidad Tecnológica de Pereira, Pereira, Colombia. juposso@gmail.com
2Ing. Electricista, M.Sc., Profesor Auxiliar, Facultad de Ingeniería, Investigador Grupo de Planeamiento. Universidad Tecnológica de Pereira, Pereira, Colombia. ricardohincapie@utp.edu.co
3Ing. Electricista, Ph.D., Profesor Titular, Facultad de Ingeniería, Investigador Grupo de Planeamiento. Universidad Tecnológica de Pereira, Pereira, Colombia. ragr@utp.edu.co
Fecha de recepción: 8 de abril de 2011, Fecha de aprobación: 13 de septiembre de 2011.
RESUMEN
En este artículo, se presenta una metodología para resolver el problema de la expansión del sistema de distribución de baja tensión. Para solucionar este problema, se elabora un modelo trifásico con los diferentes costos operativos y de diseño que incluyen el efecto del desequilibrio, reubicación y repotenciación de elementos existentes, y localización y dimensionamiento de elementos nuevos. Como costos operativos, se consideran las pérdidas de energía en fases y neutros de conductores. Para resolver el modelo, se usa el algoritmo genético de Chu-Beasley. La metodología fue probada, usando un sistema de 54 nodos y 57 líneas propuestas y analizado bajo condiciones de equilibrio y desequilibrio. Los resultados obtenidos son de buena calidad porque presentan un bajo nivel de pérdidas como resultado de una efectiva localización de transformadores, una adecuada selección del calibre de conductores y un buen equilibrio de fases.
Palabras clave: algoritmo genético de Chu-Beasley, equilibrio de carga, planeamiento de redes secundarias de distribución de energía eléctrica.
ABSTRACT
This paper presents a methodology to solve the distribution system planning problem. In its solution a three-phase model is taking into account with different design and operational costs, including relocation and upgrading of existing elements and location and dimensioning of the new ones. The operational costs consider energy losses in conductors. To solve this model the genetic algorithm of Chu-Beasley is used. The methodology is tested using a system with 54 points to link new users, and analyzed under different operative conditions. Results obtained present good quality, due to low losses as a result to adequate transformers location, appropriate selection of conductors and a good load balancing.
Keywords: Chu-Beasley genetic algorithm, load balancing, secondary distribution system planning.
INTRODUCCIÓN
Los sistemas de distribución reciben la energía eléctrica que proviene de la red de subtransmisión y la conducen hasta el punto de conexión de los consumidores. Estos sistemas están compuestos por subestaciones de distribución, circuitos primarios, transformadores de distribución y circuitos secundarios.
Planear los sistemas de distribución, es encontrar para un horizonte de tiempo, la configuración que garantice la atención de la demanda al menor costo posible, teniendo en cuenta criterios de calidad, continuidad y confiabilidad. Para lograr una adecuada planeación, se considera la ubicación de nuevos elementos y la reubicación y repotenciación de elementos existentes.
La inadecuada planeación de estos sistemas conlleva a la instalación de elementos sobredimensionados que presentan elevados costos de inversión y/o subdimensionados que pueden ocasionar problemas operativos como bajos voltajes, altos niveles de pérdidas, y congestionamiento de líneas y transformadores, entre otros.
Por su naturaleza operativa, los sistemas de distribución presentan un grado de desequilibrio de las corrientes que circulan por el sistema, debido a la asimetría en el diseño y/o operación de las cargas, lo cual se traduce en aumento de la corriente en la fase más cargada y en la aparición de corriente por el neutro [1]. Este desequilibrio de corrientes ocasiona un incremento en las pérdidas técnicas que se ve reflejado directamente en un incremento de los costos operativos. La operación se ve aún más deteriorada, cuando no se ha llevado a cabo un eficiente esquema de planeación.
Lo anterior refleja la importancia de contar con adecuadas metodologías de planeamiento de redes de distribución que minimicen costos de inversión y optimicen el modo de operación. Una adecuada metodología para planear sistemas secundarios de distribución, debe considerar las siguientes estrategias:
- Equilibrio de fases
- Ubicación y dimensionamiento de nuevos tramos de red secundaria
- Ubicación y dimensionamiento de nuevos transformadores de distribución
- Reubicación de transformadores de distribución existentes
- Cambio del calibre de conductores existentes
Este problema se ha resuelto de diferentes maneras.
En Galeano Ossa et al [2], el problema se representa usando un modelo lineal entero mixto y se soluciona, empleando un algoritmo Branch and Bound. El sistema se considerado equilibrado por que se trabaja solamente con el equivalente monofásico.
Costa A.M. et al [3], plantea una metodología basada en técnicas heurísticas y su solución se lleva a cabo en varias etapas. El modelo matemático propuesto incluye costos fijos de instalación de transformadores de distribución y tramos de red primarios y secundarios. La función objetivo es linealizada, y la red se representa como un sistema equilibrado.
García V.C. et al [4], propone el método GRASP (Greedy Randomized Adaptive Search Procedures), para resolver el problema que se formula como un problema de programación no lineal entero. La red es modelada por su equivalente monofásico. El problema se soluciona en tres etapas. Inicialmente, son ubicados los transformadores de distribución, empleando una formulación del problema de la p-medianas. Una vez determinada la capacidad y ubicación de los transformadores, en la segunda etapa se selecciona la red secundaria mediante la técnica de caminos mínimos. Finalmente, se determina el costo fijo de la red primaria necesaria para alimentar los transformadores, empleando una formulación del problema de Steiner.
Cossi A.M. [5], propone un problema de programación no lineal entero mixto que se resuelve, empleando un algoritmo evolutivo cuya representación se efectúa de manera trifásica.
Souza, C.H. [6], plantea el problema como un modelo no lineal entero mixto y lo resuelve, usando el algoritmo Búsqueda Tabú. Al igual que el trabajo anterior, el problema se representa considerando un modelo trifásico.
Mientras que en Marroquín O.A. [7], el modelo propuesto es de tipo no lineal entero mixto y se resuelve usando el algoritmo Colonia de Hormigas. En esta metodología, la ubicación de los elementos se conoce previamente, y se determina el dimensionamiento de transformadores de distribución y tramos de red. Adicionalmente, se realiza un equilibrio de cargas.
En este trabajo, el problema del planeamiento de sistemas secundarios de distribución se formula como un problema de programación no lineal entero mixto (PNLEM). La función objetivo considera costos de instalación de nuevos elementos (tramos de red y transformadores), repotenciación de tramos de red existentes y equilibrio de fases, y costos operativos relacionados con las pérdidas técnicas en los circuitos. El conjunto de restricciones está compuesto por las ecuaciones de equilibrio nodal, capacidades máximas permitidas para los elementos del sistema, máxima caída de tensión permitida, radialidad de la red y recursos económicos disponibles para invertir en el proyecto.
Con el fin de considerar el equilibrio de fases en la solución del problema, se empleó un modelo trifásico de los componentes del sistema de distribución [8]. En la solución del problema se empleó un algoritmo genético de Chu-Beasley, y para evaluar las configuraciones propuestas por el algoritmo, se empleó un flujo de carga trifásico basado en el método de barrido iterativo [9].
La codificación planteada en este trabajo, considera de manera implícita las alternativas mencionadas anteriormente, restricciones de capacidad y número de elementos, garantizando a su vez, el cumplimiento de máxima inversión disponible.
El artículo fue organizado de la siguiente forma: al comienzo, se presenta la metodología propuesta en donde se ilustra la formulación del problema y los aspectos más relevantes de la técnica de solución empleada. Posteriormente, se presenta la aplicación sobre un sistema de prueba, y por último, se muestran las conclusiones más relevantes obtenidas en este trabajo.
1. METODOLOGÍA
1.1. FORMULACIÓN DEL PROBLEMA
El problema matemático del planeamiento de sistemas secundarios de distribución, puede ser formulado como un problema de programación no lineal entero mixto de la siguiente forma [10]:
En la función objetivo descrita en la ecuación (1), los tres primeros términos representan los costos de instalación de nuevos tramos de red, nuevos transformadores de distribución y la repotenciación de elementos existentes, respectivamente. Los siguientes dos términos consideran el costo de reubicar transformadores existentes y el equilibrio de fases. Los últimos dos términos involucran los costos operativos debido a las pérdidas de energía en las líneas nuevas y existentes, respectivamente.
La restricción (2), representa las ecuaciones de equilibrio nodal, que obedecen a un modelo trifásico. La siguiente restricción (3), establece los límites operativos del sistema para todas las líneas y transformadores.
La ecuación (4), garantiza el cumplimiento de la radialidad en todas las configuraciones propuestas. La ecuación (5), asegura que la regulación de voltaje del sistema esté dentro de unos límites permitidos. La ecuación (6), permite que sólo se involucren durante el proceso, configuraciones que tengan un costo inferior a los recursos disponibles para el proyecto.
Donde,
-
z: función objetivo.
-
k : tipo o calibre del conductor.
-
RDMAX: máximo recurso disponible para invertir en el proyecto.
-
M: tipo de transformador de acuerdo con su capacidad.
-
CRECij,k: costo de reconductorizar un tramo de red i-j, con conductor tipo k
-
CFij,k: costo fijo de un tramo de red entre los nodos ij, con conductor tipo k
-
CFi,M: costo de inversión de un transformador de distribución en el nodo i , tipo M.
-
CFBi : costo fijo del equilibrio de cargas.
-
CTi,M: costo fijo de reubicar un transformador existente tipo M.
-
Ckwh: costo de la energía expresada en [$/kWh].
-
T: período de planeamiento en horas.
-
Rij,k-abc: resistencia del conductor tipo k entre los nodos ij, para las fases a-b-c
-
X ij,k-abc : reactancia del conductor tipo k entre los nodos ij, para las fases a-b-c.
-
Iij-abc : corriente entre los nodos i-j para las fases a-b-c.
-
Iji-abc : corriente entre los nodos j-i, para las fases a-b-c.
-
Imaxij-abc: corriente máxima permitida entre los nodos ij, para las fases a-b-c.
-
Vi-abc: caída de voltaje en el nodo i para las fases a-b-c.
-
Vj-abc: caída de voltaje en el nodo j para las fases a-b-c.
-
Vmaxi-abc : máximo voltaje permitido en los nodos del sistema, para las fases a-b-c.
-
Vmin i-abc : mínimo voltaje permitido en los nodos del sistema, para las fases a-b-c.
-
ΩAN: conjunto de tramos de red nuevos del sistema.
-
ΩAF: conjunto de tramos de red existentes del sistema.
-
ΩA: ΩAN U QAE
-
ΩTN: conjunto de transformadores nuevos del sistema.
-
ΩTE: conjunto de transformadores existentes del sistema.
-
ΩT: ΩTN U ΩTE
-
ΩR: conjunto de tramos de red del sistema por reconductorizar.
-
ΩB: conjunto de puntos que representan las posiciones de las cargas en las fases.
-
n: número total de nodos.
-
nfex : número de tramos de red existentes.
-
ntex : número de transformadores existentes.
-
δij,k : variable de decisión para instalar un conductor tipo k, en la ruta i-j.
-
δi,M : variable de decisión para instalar un transformador tipo M, en el nodo i.
-
δRECij,k: variable de decisión para reconductorizar en ij, con conductor tipo k
-
δCTiM: variable de decisión para reubicar transformadores existentes, tipo M.
-
δi: variable de decisión binaria para realizar equilibrio de cargas.
-
Pini-abc : potencia activa inyectada al nodo i .
-
Qini-abc: potencia reactiva inyectada al nodo i .
-
Pci-abc : potencia activa consumida en el nodo i .
-
Qci-abc: potencia reactiva consumida en el nodo i.
-
Gij-ik-abc: conductancia del conductor tipo k en la ruta ij, para las fases a-b-c.
-
Bij,k-abc: susceptancia del conductor tipo k en la ruta ij, para las fases a-b-c.
-
PTi-abc: potencia activa nominal del transformador en el nodo i .
-
QTi-abc : potencia reactiva nominal del transformador en el nodo i .
1.2. ALGORITMO PROPUESTO
La técnica de optimización propuesta para solucionar el problema del planeamiento de la expansión de sistemas secundarios de distribución, es un Algoritmo Genético de Chu-Beasley (AGCB), que fue desarrollado y adaptado para este problema en particular. A continuación, se describe en forma general el AGCB y los aspectos que se tuvieron en cuenta por este metodo.
1.2.1. Algoritmo Genético De Chu-Beasley
En los años 90, los Algoritmos Genéticos (AG), tomaron gran popularidad y desde entonces, han sido mundialmente acogidos para resolver problemas complejos de optimización matemática [11]. Sin embargo, en 1997 surge una versión modificada, planteada por Chu y Beasley [12], que lo mejora en alto grado al aplicar de forma efectiva, el concepto de diversidad en los algoritmos genéticos, en cuanto a la orientación de la búsqueda hacia un óptimo global del problema y con una disminución notable del tiempo computacional, por lo cual se considera como una técnica metaheurística y como un algoritmo muy competitivo para evaluar sistemas de gran tamaño, y de gran complejidad matemática. De igual manera que el AG, el AGCB se vale de los operadores de selección, crossover y mutación. Básicamente en el AGCB, se ha tomado como prioridad, garantizar la diversidad entre los cromosomas que conforman la población durante todo el proceso, reemplazando solo un individuo (cromosoma), por cada ciclo generacional, bajo unas condiciones de optimalidad y/o factibilidad establecidas.
1.2.2. Codificación del problema
La codificación empleada en este trabajo, utiliza un vector que por medio de variables enteras, representa los elementos y sus características operativas. Una de las ventajas que presenta esta codificación es que maneja de forma implícita, algunos de los límites descritos en el modelo matemático en la ecuación (3). El esquema de codificación se presenta en la Figura 1. En la primera parte, se representan la ubicación y el dimensionamiento de nuevos tramos de red, y el cambio de calibres de conductores existentes. En la segunda parte, se incorpora la ubicación y dimensionamiento de nuevos transformadores de distribución y reubicación de transformadores existentes. La tercera considera el equilibrio de fases.
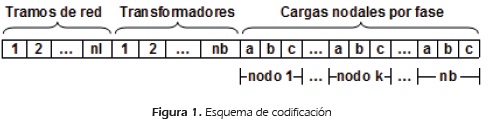
El anterior esquema de codificación se puede interpretar como sigue:
-
Las posiciones 1, 2, ..., nl identifican conductores nuevos y/o existentes en cada una de las ramas del circuito, donde nl es el número de tramos de red.
-
Las posiciones 1, 2, ..., nb representan transformadores de distribución nuevos y/o existentes, donde nb es el número de nodos del sistema.
-
Las posiciones 1, 2, ..., nb identifican las cargas conectadas en los nodos, donde los números uno, dos y tres indican la carga en la fase a, b y c, respectivamente.
1.2.3. Generación de la población inicial
Las configuraciones de la población inicial pueden ser construidas aleatoriamente o utilizando técnicas heurísticas constructivas que usan factores de sensibilidad.
En este trabajo, se generan aleatoriamente las configuraciones iniciales, iniciando con la selección de transformadores de distribución y a partir de estos las ramas que conforman la red, también de forma aleatoria, garantizando la radialidad de las topologías. Estos valores corresponden a las dos primeras partes del vector de codificación. La tercera parte del vector de codificación también se genera de forma aleatoria, es decir, la posición que va a tomar la carga en cada una de las fases. Los pasos para formar el vector de la codificación inicial son:
-
En cada posición de la primera parte del vector, se genera aleatoriamente un número entero que pertenece al conjunto de calibres considerados.
-
En cada posición de la segunda parte del vector, se genera aleatoriamente un número entero que pertenece al conjunto de transformadores considerados.
-
Para la última parte del vector, se generan para cada nodo, tres posiciones escogidas aleatoriamente, que representan las cargas conectadas a las fases a, b y c, respectivamente.
1.2.4. Evaluación de las configuraciones
Para cada topología del sistema, se calcula una función de adaptación a partir del esquema de codificación, considerando la función objetivo y las restricciones del problema. Esta función modela los costos de instalación de tramos de red y transformadores de distribución, costos operativos y costos por penalizaciones debido a la violación de las restricciones de regulación de voltaje y restricciones de las capacidades de las líneas y transformadores secundarios. En forma genérica, la función de adaptación está dada por la ecuación (7):
Donde FO(x ) es el valor de la función objetivo y fp el factor de penalización. Por lo tanto, la función objetivo penalizada puede ser escrita de la siguiente forma:
Donde: fpv, fpf y fps son los factores de penalización para límites de tensión, sobrecargas en los tramos de red y sobrecargas en transformadores de distribución. El valor de Vlim se obtiene a partir de la suma de (Vnom + ΔV ).
1.2.5. Parámetros de control
Los parámetros de control seleccionados, es decir, número de generaciones, tamaño de la población, tasas de recombinación y mutación, se obtienen por ensayo y error, a partir de diversas pruebas y teniendo en cuenta el tamaño del sistema estudiado.
1.2.6. Criterio de parada
El criterio de parada considerado en este trabajo, está basado en la comparación de la solución incumbente, es decir, si esta no mejora después de un número predefinido de iteraciones, se da por terminado el proceso.
1.2.7. Metodología
La metodología planteada se describe a continuación:
-
Generar la población inicial.
-
Evaluar las soluciones por medio la función de adaptación descrita en la ecuación (8). Por lo tanto:
-
Ejecutar el flujo de carga.
-
Verificar las restricciones de capacidades en tramos de red y transformadores de distribución (ecuación 3).
-
Determinar el cumplimiento de la regulación máxima permitida (ecuación 4).
-
Verificar la restricción financiera (ecuación 6).
-
-
Verificar el criterio de parada.
-
Si cumple, parar e imprimir resultados.
-
En caso contrario, ir al paso 4.
-
Implementar los operadores del algoritmo genético.
-
Volver al paso 2.
2. APLICACIÓN Y RESULTADOS
Para verificar la metodología propuesta, se empleó un sistema de prueba cuya topología se ilustra en la Figura 2, donde las líneas punteadas corresponden a tramos de red propuestos y los triángulos negros a posibles ubicaciones de transformadores de distribución. Para implementar la estrategia planteada, se empleó el software MATLAB. En las Tablas 1 y 2, se presentan los datos de las demandas del sistema y de los tramos de red, respectivamente.

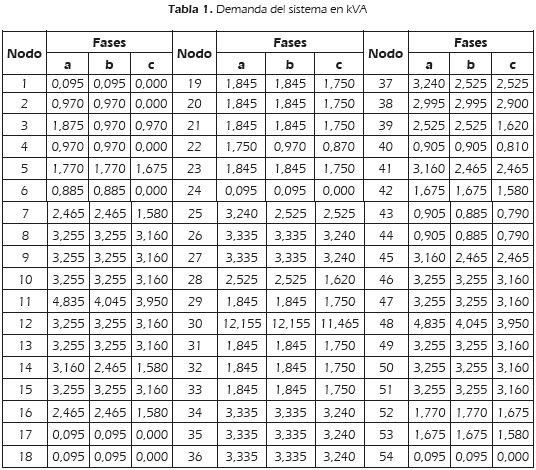
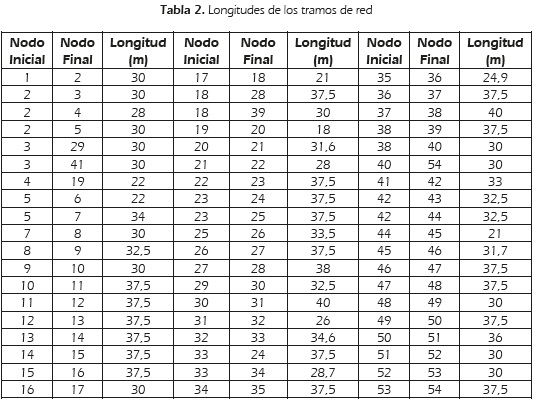
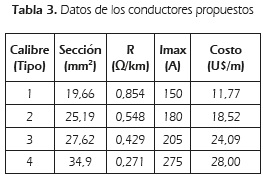
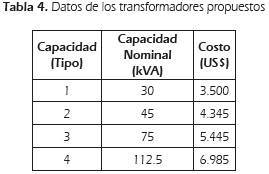
Los datos de conductores y transformadores de distribución propuestos, se ilustran en las Tablas 3 y 4, respectivamente.
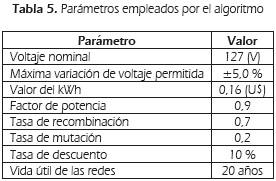
Los parámetros empleados por el algoritmo se presentan en la Tabla 5.
En la Tabla 6, se ilustran las mejores respuestas encontradas por la metodología bajo un modelo trifásico, considerando dos escenarios: con y sin equilibrio de fases. De los resultados obtenidos, se concluye la importancia de emplear un modelo trifásico de los elementos de la red, teniendo en cuenta el equilibrio de fases. Este desequilibrio influye de manera directa en el cálculo de las pérdidas en las tres fases, neutro y tierra, presentando grandes diferencias respecto del escenario en donde se tiene en cuenta.

En la Figura 3, se observa la configuración encontrada por el algoritmo al considerar el equilibrio de corrientes que circulan por el sistema, donde los tipos de conductores seleccionados se presentan entre paréntesis, al lado de cada tramo de red. Los transformadores seleccionados se encuentran ubicados en los nodos: 2 (45 kVA), 11 (75 kVA), 27 (45 kVA), 30 (75 kVA), 37 (112.5 kVA), 45 (75 kVA) y 51 (45 kVA).

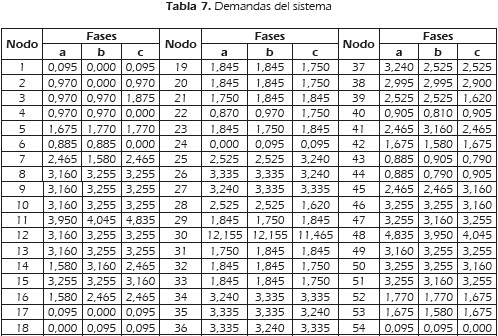
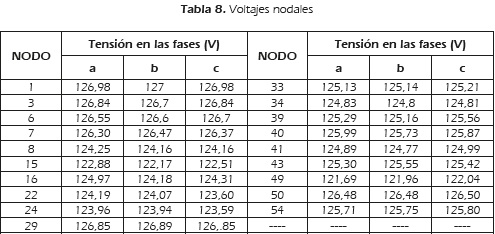
Las demandas del sistema y los voltajes nodales para los nodos al final de cada circuito, se presentan en las Tablas 7 y 8, respectivamente.
3. CONCLUSIONES
En este artículo, se presenta la solución al problema del planeamiento de redes secundarias empleando un algoritmo genético de Chu-Beasley. La metodología propuesta fue aplicada a un sistema de prueba de 54 nodos y 57 líneas propuestas. La red obtenida presenta adecuados niveles de tensión, equilibrio de corrientes por las fases, bajo nivel de pérdidas y no presenta sobrecargas. El bajo nivel de pérdidas es el resultado de una efectiva localización de transformadores, una adecuada selección del calibre de conductores y un buen equilibrio de fases.
El esquema de codificación planteado en esta investigación, presenta gran atractivo en la solución de este problema debido a su simplificación, al considerar de manera implícita algunas de las restricciones que, facilitan la representación completa de todo el sistema.
La técnica de solución empleada es de fácil implementación y presenta resultados de excelente calidad, lo cual se puede verificar, al observar los resultados de las variables consideradas en el modelo matemático.
La representación trifásica del sistema y el modelo no lineal permiten un acercamiento más real y preciso al modo operativo de estas redes, considerando el desequilibrio y la asimetría de algunos de los elementos que componen este sistema.
En la solución del problema de planeamiento de redes secundarias de distribución, además de la representación trifásica de los elementos, se debe considerar el equilibrio de cargas en el sistema, con el fin de incluir la situación operativa real de la red respecto de las pérdidas.
La finalidad de este artículo es transferir este conocimiento a las empresas del sector eléctrico. Por tal razón, se recomienda aplicar esta metodología, usando información de redes de distribución suministrada por empresas del sector, y compararla con los resultados obtenidos con los métodos tradicionales.
REFERENCIAS BIBLIOGRÁFICAS
[1] Gonen T. (1987). Electric power distribution system engineering. Singapore: McGraw Hill International, 318p. [ Links ]
[2] Galeano Ossa A.A. y Tapias Isaza, C.J. (2009). Planeamiento de sistemas secundarios de distribución usando el algoritmo Branch and Bound. Pereira: 19 p. Trabajo de Grado (Ingeniería Eléctrica). Universidad Tecnológica de Pereira Facultad de Ingeniería. [ Links ]
[3] Costa A.M. and França P.M. (2002). Planejamento de Redes Secundárias de Distribuição de Energia Elétrica; En: XV Congresso Brasileiro de Automática, Natal, pp. 2563-2568. [ Links ]
[4] García V.C., Morelato P., Vizcaino J.F., Yoshimoto E. and Lyra C. (2003). GRASP para o problema de planejamento de redes Secundárias de distribuição de energia elétrica; En: XXXV SBPO A pesquisa Operacional e os Recursos Renováveis, Natal, pp. 1427-1437. [ Links ]
[5] Cossi A.M. (2005). Planejamento de circuitos secundários de distribuçao usando algoritmo evolutivo especializado; Ilha Solteira, 7 p. Trabajo de Grado (Maestría en Ingeniería Eléctrica). Universidade Estadual Paulista, Brasil. Faculdade de Engenharia. [ Links ]
[6] Souza C.H. (2006). Planejamento e projecto de circuitos secundários de distribuição de energía eléctrica utilizando algoritmo busca tabu; Ilha Solteira, 26 p. Trabajo de Grado (Maestría en Ingeniería Eléctrica). Universidade Estadual Paulista, Brasil. Faculdade de Engenharia. [ Links ]
[7] Marroquín O.A. (2008). Planeamiento de redes secundarias de distribución usando un algoritmo de optimización basado en colonia de hormigas. Pereira, 14 p. Trabajo de Grado (Ingeniería Eléctrica). Universidad Tecnológica de Pereira. Facultad de Ingeniería. [ Links ]
[8] Kersting W.H. (2007). Distribution System Modeling and Analysis. Florida. CRC Press, 145p. [ Links ]
[9] Garcés A., Granada M. and Gallego R. (2004). Flujo de carga trifásico para sistemas radiales de distribución; En: Revista Scientia et Technica, Año X (24), pp. 19-24. [ Links ]
[10] González J.D., Gallego R.A. and Hincapié R.A. (2009). Modelamiento matemático del problema del planeamiento de sistemas secundarios de distribución. En: Revista Colombiana de Tecnologías de Avanzada, Vol.2 (14), pp.89-95. [ Links ]
[11] Gallego R.; Escobar A. and Toro E. (2008). Técnicas Metaheurísticas de Optimización. Pereira. Textos Universitarios Universidad Tecnológica de Pereira, 77p. [ Links ]
[12] Beasley, J.E. and Chu, P.C. (1997). A Genetic Algorithm for the Generalized Assignment Problem; En: Computers Operations Research, Vol.24 (1), pp. 17-23. [ Links ]