METODOLOGÍA PARA ESTIMAR CONCENTRACIONES DE SST EN TIEMPO REAL EN HIDROSISTEMAS URBANOS A PARTIR DE MEDICIONES DE TURBIEDAD

TURBIDITY-BASED METHODOLOGY FOR REAL-TIME TSS CONCENTRATIONS ESTIMATES IN URBAN WATER SYSTEMS

Andrés Torres
PhD en Hidrología Urbana, INSA-Lyon (Francia), MSc. En Ingeniería Civil, INSA-Lyon (Francia)
, Ingeniero Civil, Pontificia Universidad Javeriana, Bogotá. Profesor Asociado, Pontificia Universidad Javeriana, Bogotá, Colombia.
andres.torres@javeriana.edu.co.

Julio Mario Araújo Acosta.
Ingeniero Civil, Pontificia Universidad Javeriana, Bogotá.
araujoj@javeriana.edu.co

Mauricio González Acosta.
Ingeniero Civil, Pontificia Universidad Javeriana, Bogotá.
gonzalez.mauricio@javeriana.edu.co

Andrés Vargas Luna.
Magíster en Recursos Hidráulicos, Universidad Nacional de Colombia. Ingeniero Civil, Universidad Nacional de Colombia.
Profesor Asistente, Pontificia Universidad Javeriana, Bogotá, Colombia.
avargasl@javeriana.edu.co

Jaime Andrés Lara-Borrero.
PhD en Ingeniería de Caminos, Canales y Puertos, Universidad Politécnica de Madrid (España).
MSc. Ingeniería y Gestión Ambiental, Universidad Politécnica de Cataluña, (España).
Ingeniero Civil, Pontificia Universidad Javeriana, Bogotá. Profesor Asociado, Pontificia Universidad Javeriana, Bogotá, Colombia.
laraj@javeriana.edu.co

Lugar de la investigación: Bogotá, Colombia
Origen de subvenciones: Pontificia Universidad Javeriana, sede Bogotá. Resultados derivados del proyecto de investigación titulado Caracterización hidrodinámica de cargas contaminantes en hidrosistemas de saneamiento con código PS3544.
Periodo de ejecución: 15 de enero de 2010 a 14 de julio de 2011.

Fecha de recepción: 27 de septiembre de 2012 Fecha de aprobación: 15 de mayo de 2013

RESUMEN

Las mediciones de turbiedad in situ y en continuo pueden ser utilizadas para estimar concentraciones en tiempo real de Sólidos Suspendidos Totales (SST) en hidrosistemas urbanos. Con el fin de obtener resultados confiables de SST a partir de mediciones de turbiedad in situ y en continuo, se desarrollaron una serie de métodos orientados a: (i) estimar concentraciones e incertidumbres asociadas en muestras instantáneas analizadas mediante métodos estándar de laboratorio, (ii) detectar muestras con baja representatividad mediante análisis de outliers multivariados, (iii) establecer relaciones funcionales entre SST y valores de turbiedad que puedan ser explotadas para obtener concentraciones en tiempo real, teniendo en cuenta las incertidumbres. Con base en los elementos mencionados arriba, se desarrolló una metodología para estimar concentraciones de SST a partir de mediciones de turbiedad in situ y en continuo, la cual fue codificada en Mat-Lab®, obteniendo como resultado un programa llamado DROP (Data Relationships Of water Pollutants).

Palabras clave: Incertidumbre, Mediciones en tiempo real, Outliers, SST, Turbiedad.

ABSTRACT

Continuous in situ turbidity measurements can be used to estimate real-time TSS (Total Suspended Solids) concentrations in urban water systems. In order to obtain reliable TSS results from continuous in situ turbidity measurements, a set of methods were developed directed to: (i) assess concentrations and associated uncertainties for instantaneous samples applying lab reference methods, (ii) detect samples with low representativeness by means of multivariate outliers analysis, (iii) establish regression functions between TSS and turbidity values that could be used for obtaining real-time concentrations, accounting for uncertainties. Based on the above elements, a methodology for assessing TSS concentrations based on in situ and continuous turbidity measurements was constructed and coded in MatLab®, obtaining a program untitled DROP (Data Relationships Of water Pollutants).

Keywords: Outliers, Real-time measurements, TSS, Turbidity, Uncertainty.

INTRODUCCIÓN

Colombia ha conocido un crecimiento urbano considerable desde mediados del siglo 20: en el censo de 1973 se contabilizó una población urbana de 59 % sobre la población total (14 millones de habitantes) Murad Rivera [1] y en el censo de 2005 se contabilizó una población urbana de 74 % sobre la población total (32 millones de habitantes) Colombia, Departamento Administrativo Nacional de Estadística (DANE) [2]. Dicho crecimiento, usualmente incontrolado y con brechas en la planeación, trae como consecuencia que los medios acuáticos urbanos estén sometidos a flujos contaminantes cada vez mayores. En efecto, las concentraciones de los contaminantes asociados a los vertimientos urbanos pueden llegar a ser muy importantes, así como nocivas para los medios acuáticos más sensibles y variables espacio-temporalmente en función de los usos del suelo y de la dinámica hidrológica Chocat et al. [3]. La gestión, la operación y la rehabilitación, así como el mejoramiento de la calidad físico-química y ecológica de los hidrosistemas urbanos requieren del conocimiento de concentraciones de contaminantes a distintas escalas de tiempo.

Se ha demostrado que numerosos contaminantes transportados en hidrosistemas urbanos están presentes en fase particular y por lo tanto la concentración de Sólidos Suspendidos Totales (SST), más allá de su interés intrínseco, constituye un indicador global de la carga contaminante presente. En efecto, varios estudios de caracterización de sólidos en suspensión han mostrado que una serie de microcontaminantes se fijan usualmente a dichos sólidos Barrett et al. [4]; Wu et al. [5]; Becouze-Lareure [6], y que los comportamientos de la acumulación de contaminantes depende de los tamaños de los sólidos en suspensión Pitt et al. [7]: la mayoría de los contaminantes se fijan a partículas con diámetros que van desde unas pocas micras a 2 mm, con tamaños medios entre no mayores de 40 µm Chebbo [8]; Ashley et al. [9]; Torres et al. [10]. En particular, las concentraciones de contaminantes urbanos en los sedimentos, como hidrocarburos y metales pesados, han sido reportados como mayores en las partículas más finas de sedimentos Krein et al. [11]; Lee et al. [12]; Zhao et al. [13]. En nuestro medio, es práctica habitual estimar las concentraciones de SST y Demanda Química de Oxígeno (DQO) a partir de análisis de laboratorio efectuados sobre muestras puntuales recolectadas in situ. Esta práctica otorga resultados que no garantizan una información precisa, suficientemente representativa de la dinámica de los fenómenos ni completa para estimar de manera fiable los flujos de contaminantes a diferentes escalas de tiempo Winkler et al. [14].

Una de las alternativas posibles para limitar dichos inconvenientes consiste en utilizar captores in situ, capaces de proporcionar informaciones a alta frecuencia (del orden de una medición por minuto) que puedan traducirse en términos de concentraciones equivalentes de SST y eventualmente de DQO. Entre los captores actualmente disponibles, los turbidímetros pueden utilizarse in situ con un nivel de confianza satisfactorio Henckens et al. [15], Bertrand-Krajewski et al. [16]. Sin embargo, dado que estos captores no proporcionan directamente valores de concentraciones de SST, es necesario desarrollar y poner en práctica métodos específicos para evaluar dichas concentraciones equivalentes, así como su variabilidad y las incertidumbres asociadas. Esto otorga la posibilidad de tener mediciones en tiempo real de concentraciones equivalentes de contaminantes comúnmente utilizados para evaluar la calidad físico-química de los medios acuáticos urbanos (como los SST), lo cual facilita su manejo y gestión soportados en modelos suficientemente representativos temporalmente de las dinámicas hídricas particulares de cada hidrosistema.

Este artículo presenta una metodología para estimar concentraciones de SST a partir de mediciones de turbiedad in situ y en continuo, por medio de relaciones funcionales construidas teniendo en cuenta las incertidumbres experimentales asociadas y la representatividad de las muestras utilizadas.

1. MATERIALES Y MÉTODOS

Para la estimación de concentraciones equivalentes de SST a partir de mediciones in situ y en continuo de turbiedad, se propone una metodología que comprende cuatro fases, las cuales se describen a continuación. Como resultado de la aplicación de esta metodología, se obtiene una relación funcional y sus incertidumbres asociadas aplicable a mediciones en continuo de SST a partir de mediciones de turbiedad. Dicha relación contempla incertidumbres experimentales y representatividad de las muestras puntuales utilizadas para su construcción, lo cual representa ventajas con respecto a las prácticas comúnmente utilizadas en este campo (construcción de relaciones funcionales en hoja de cálculo sin tener en cuenta incertidumbres ni outliers).

a. Cálculo de valor promedio e incertidumbre para cada muestra

El primer paso de la metodología contempla el establecimiento de concentraciones de SST y DQO de referencia medidas en muestras puntuales mediante métodos estándar de laboratorio. Dado que la turbiedad se define como una “reducción de la transparencia de un líquido causada por la presencia de materia no disuelta” International Organization for Standardization [17], únicamente se establecen correlaciones con SST, pero sin aspirar a obtener equivalencias exactas. Las concentraciones de DQO de referencia se obtienen únicamente con el propósito de clasificar las muestras según su contenido de materia oxidable. Esta clasificación será utilizada en el paso 3 de la metodología (eliminación de outliers). El método plantea tomar muestras instantáneas de 1 L para la mayor diversidad de situaciones posibles en el hidrosistema estudiado, de tal forma que se obtenga un amplio rango de concentraciones, por lo cual se recomienda realizar el muestreo en diferentes horas del día y para días con diversas condiciones meteorológicas (luego de una lluvia, tiempo seco,tiempos de lluvia, etc.). Una vez tomadas las muestras, éstas son analizadas en laboratorio con el fin de estimar las concentraciones de SST y DQO de acuerdo con métodos estándar de laboratorio American Public Health Association et al. [18]. A partir de cada muestra de un litro, luego de homogeneizar manualmente, deben prepararse y analizarse individualmente al menos tres sub-muestras por cada muestra, y los resultados obtenidos se consideran como réplicas. Los valores correspondientes de concentraciones de SST y DQO de cada sub-muestra permiten calcular las concentraciones promedio de la muestra SST_p y DQO_p, así como las incertidumbres asociadas u(SST_p). Para lograr esta tarea, las réplicas son un insumo fundamental, puesto que la medición de concentraciones es muy sensible al sub-muestreo y a las incertidumbres analíticas (ver por ejemplo Bertrand-Krajewski et al. [16]).

Antes de realizar los análisis estándar de laboratorio, el turbidímetro de campo se sumerge directamente en cada muestra de 1 L, la cual es agitada en permanencia mediante un agitador magnético. Para cada muestra se toman mediciones repetidas de turbiedad (alrededor de 20). Para calcular la incertidumbre de los datos de turbiedad se utiliza la precisión del turbidímetro.

Con el propósito de obtener la incertidumbre estándar compuesta u(SST_i) asociada al resultado de concentración SST_i de la submuestra i, se debe tener en cuenta la precisión de la balanza utilizada para medir las masas, así como la precisión de la probeta utilizada para medir el volumen de la submuestra i.

Teniendo en cuenta los valores medidos T_i y SST_i y las incertidumbres asociadas u(T_i) y u(SST_i) para cada réplica i, y asumiendo que las mediciones repetidas arrojan distribuciones de probabilidad normales en cada caso, es posible calcular un intervalo para el cual exista un 95 % de probabilidad de que la medición se encuentre en dicho intervalo. El cálculo de la incertidumbre asociada a cada réplica i es útil tanto para estimar la incertidumbre estándar compuesta como para depurar e interpretar los resultados en bruto obtenidos en laboratorio. Si se asume que los resultados de las mediciones de cada réplica siguen una distribución normal, se propone una comparación por pares mediante pruebas t de Student. De acuerdo con los resultados de dichas comparaciones, pueden existir tres casos: (1) no se elimina ninguna réplica al no detectar diferencias significativas; (2) no se elimina ninguna réplica porque se detectan diferencias significativas entre todas las réplicas; (3) se elimina una sola réplica porque se detectan diferencias significativas entre una réplica y las dos restantes.

Una vez validada o descartada cada réplica para cada muestra, es posible calcular un valor promedio y la incertidumbre asociada a cada muestra, tanto para los valores de Turbiedad, como para las concentraciones de SST. Esto se puede realizar mediante métodos analíticos como la ley de propagación de incertidumbres o mediante métodos numéricos Greenland [19]; Smith [20] como el método de Monte Carlo, el cual fue seleccionado en el marco del presente trabajo, al seguir el método de Torres-Abello [21]. Finalmente, se cuenta con pares de valores promedio (T_p, SST_p) y sus incertidumbres (u(T_p), u(SST_p)) para cada muestra de 1 L, las cuales se utilizan en los siguientes pasos de la metodología propuesta.

b. Eliminación de muestras por alta incertidumbre

Con el fin de desarrollar relaciones funcionales utilizadas como leyes de comportamiento, parece fundamental que éstas sean construidas a partir de datos fiables o con incertidumbres no muy elevadas. Estudios previos (ver por ejemplo Cloirec et al. [22]) sugieren tener en cuenta únicamente aquellos datos cuyas incertidumbres relativas sean menores o iguales a 25 % sobre el valor medido. Siguiendo las recomendaciones anteriores, se sugiere eliminar aquellas muestras cuyos datos posean incertidumbres relativas superiores al 25 % sobre los valores de T o SST_p.

c. Eliminación de outliers

Cuando se pretende obtener reglas o leyes generales a partir de observaciones o mediciones, es necesario diferenciar observaciones ligadas a comportamientos generales del fenómeno de aquellas resultantes de situaciones especiales, para que no sean incluidas en el proceso de construcción de dichas reglas o leyes de comportamiento. El calificativo de outlier lo recibe una observación de acuerdo con sus características, pero sobre todo teniendo en cuenta la relación entre dicha observación y las otras observaciones de la serie.

Se desarrolló un algoritmo basado en el método propuesto por Rousseeuw et al. [23], el cual permite la detección de outliers debido a valores de Turbiedad, SST o DQO fuera de lo común, considerando todos los valores a la vez, con un 95 % de confianza. Este método se basa en el cálculo de la distancia robusta de Mahalanobis RD, utilizando el algoritmo FAST-MCD Rousseeuw et al. [23].

Algunas pruebas preliminares utilizando este método mostraron que la detección de outliers era muy sensible a efectos de borde para juegos de datos dispersos. Para eliminar este problema, se plantea una metodología en la que se estiman outliers parciales a partir de subjuegos de datos. El método consiste en estimar candidatos a outliers para todos los posibles juegos de datos parciales con un número particular de observaciones contiguas: estos subjuegos son grupos de n observaciones (cada observación tiene un valor característico de turbiedad y los valores correspondientes de concentraciones de SST y DQO), donde n va de dos al número total de observaciones de la serie, organizadas en forma creciente en función del valor de turbiedad. Para cada número específico n seleccionado, se recorre la serie incluyendo en cada subjuego n observaciones, desde aquellas con menores valores de turbiedad hasta aquellas con mayores valores de turbiedad. Para cada subjuego, se aplica el algoritmo FAST-MCD de Rousseeuw et al. [23], el cual determina qué muestra del subjuego es considerada como candidato a outlier. Cualquier observación detectada como candidato a outlier en más del 95 % de las veces en que ésta es evaluada en subjuegos parciales de datos es catalogada como outlier.

d. Establecimiento de las relaciones funcionales

Además de la utilización de la incertidumbre para la eliminación de observaciones por alta incertidumbre, ésta se utiliza adicionalmente para la construcción de la relación funcional SST = f (T). Lo anterior se tiene en cuenta para darle mayor peso o influencia en la construcción de la relación funcional f a aquellas muestras que presentan menor incertidumbre, y menor peso a aquellas muestras que presentan mayor incertidumbre. Este peso se determinó arbitrariamente como inversamente proporcional a la incertidumbre de cada muestra. Para la muestra con mayor incertidumbre se le asigna por defecto un peso igual a la unidad, mientras que el peso asignado a las demás aumenta proporcio-nalmente a medida que la incertidumbre disminuye. El peso de una muestra es representado mediante la generación aleatoria de un número de puntos igual a dicho peso, dentro del rango de incertidumbre calculado, para un nivel de confiabilidad de 95 %.

Con la priorización de las muestras realizada, se procede a generar la relación SST = f (T ). Dicho ajuste pasa predominantemente por aquellas muestras que contengan mayor cantidad de puntos, es decir menor incertidumbre. Debido a la incertidumbre que presenta cada muestra, se sugiere emplear el método de Montecarlo para generar aleatoriamente varias relaciones funcionales, variando la ubicación de los puntos necesarios para su construcción, dentro del intervalo de confianza asociado a cada muestra, y así hallar la ecuación que mejor se ajuste a cada una de estas variaciones, así como su variabilidad: para hallar la ecuación de mejor ajuste definitiva y su incertidumbre, se calcula respectivamente el promedio aritmético y la desviación estándar de todos los coeficientes calculados para cada regresión establecida.

2. RESULTADOS Y DISCUSIÓN

La metodología descrita anteriormente fue codificada en MatLab®, obteniendo como resultado un programa llamado DROP (Data Relationships Of water Pollutants).

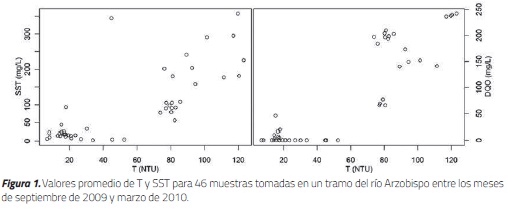
Para propósitos ilustrativos, este programa fue aplicado al Río Arzobispo, el cual se encuentra ubicado en la localidad de Teusaquillo. El 35 % de esta localidad está situada sobre la cuenca del Río Salitre o Juan Amarillo, la cual cuenta con una densidad poblacional de 97 hab/ha para el año 2005. El Río Arzobispo nace a 3200 metros sobre el nivel del mar en los cerros orientales y es canalizado sobre la carrera quinta (5ª) con calle treinta y nueve (39) pasando por los barrios Santa Teresita, La Magdalena, La Soledad, Palermo y Belalcazár, en un tramo de longitud aproximada de 1.8 kilómetros. Entre la Avenida Circunvalar y la carrera 5a. se encuentra con la Quebrada Pardo Rubio, la cual vierte aguas servidas y contaminadas al cauce Rivero Lopez [24]. Entre la carrera séptima y la carrera 13, se tomaron un total de 46 muestras. Dichas muestras fueron obtenidas y analizadas entre los meses de septiembre de 2009 y marzo de 2010. En cada muestreo se tomaron un mínimo de tres y un máximo de cinco muestras compuestas, teniendo en consideración la disponibilidad de equipos en el Laboratorio de Pruebas y Ensayos de la Facultad de Ingeniería de la Pontificia Universidad Javeriana (sede Bogotá) para realizar ensayos simultáneos. Los muestreos se realizaron sobre un tramo de 200 m del Río, distintos días de la semana, a diferentes horas del día y precedidos por condiciones climáticas variadas con la intención de obtener relaciones funcionales representativas espacio-temporalmente de la mayor cantidad de situaciones posibles. Los resultados de las concentraciones promedio, teniendo en cuenta la totalidad de las réplicas para cada muestra y sin realizar análisis complementarios, se muestran en la Figura 1.

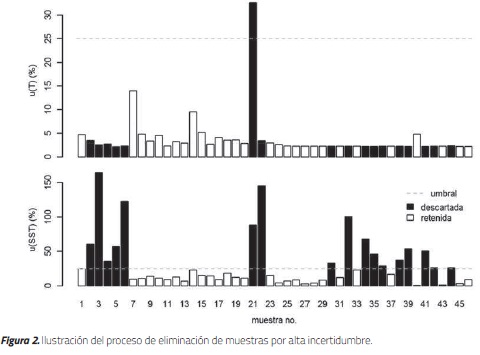
Posteriormente, dichos valores se some-T o SST se encontraban por encima del umtieron a la depuración por alta incertidum-bral fijado (25 %), de las 46 obtenidas inicialbre en la que se definió un valor límite de mente. La Figura 2 indica en blanco aquellas 25 %, según lo recomienda la metodología muestras que fueron validadas (29) y en planteada. Esta depuración eliminó un total negro aquellas descartadas (17). La cantide 17 muestras cuyas incertidumbres para dad de muestras descartadas es significativamente elevada, por lo que se recomienda tomar la mayor cantidad de muestras posibles para tener una cantidad considerable de datos con los cuales trabajar luego de la primera depuración. La alta variación de los valores de incertidumbre observada en la Figura 2 se debe probablemente a diferencias importantes en las concentraciones de las réplicas para cada muestra, lo cual puede provenir de diferencias en la manipulación de las muestras (por ejemplo homogeneización, submuestreo) antes de realizar análisis en laboratorio, puesto que el análisis de incertidumbre utilizado Torres-Abello [21] incluye no solamente la precisión de los instrumentos de laboratorio sino también el submuestreo y la manipulación de muestras y aparatos de laboratorio.

Los 29 datos validados fueron sometidos al análisis de outliers explicado anteriormente. Como resultado de este proceso depurativo se eliminaron cuatro muestras adicionales de las 29 muestras validadas en el paso anterior.

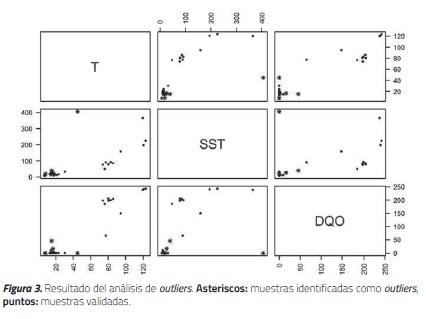
La Figura 3 ilustra las posibles relaciones entre los tres parámetros medidos, así mismo indica en asterisco las muestras que fueron calificadas como outliers. Finalmente, con las 25 muestras restantes se elaboraron las relaciones acorde con lo estipulado en la metodología propuesta, paso d). La relación definitiva SST=f (T ) obtenida fue la siguiente:

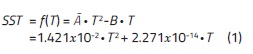
Donde la concentración de SST se expresa en mg/L y el valor de T se expresa en NTU. Adicionalmente, el método de Montecarlo permitió obtener los valores de las incertidumbres asociados a los coeficientes promedio de la ecuación anterior: 2.508x10^-4 para A y 5.323x10^-15 para B.

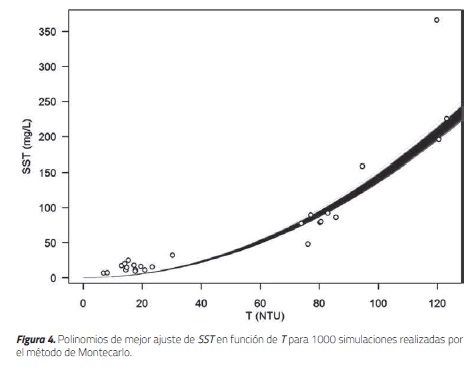
La Figura 4 ilustra los polinomios de mejor ajuste, calculados con el método de mínimos cuadrados para 1000 simulaciones realizadas por el método de Montecarlo para una relación entre datos de Turbiedad (abscisas) y Sólidos Suspendidos Totales (ordenadas).

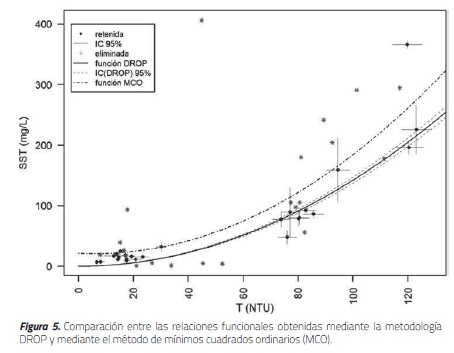
La Figura 5 muestra en línea continua el polinomio de mejor ajuste correspondiente a la relación definitiva SST = f (T ), calculada como el promedio de las 1000 simulaciones. Las líneas punteadas delimitan el intervalo de confianza de dicha función, para una confiabilidad de 95 %. Los puntos negros representan los valores promedio de turbiedad y SST para las 25 muestras validadas en los pasos anteriores y las líneas grises sus respectivas incertidumbres asociadas, para una confiabilidad de 95 %. Adicionalmente, en esta figura se muestra una comparación entre la relación funcional definitiva obtenida al aplicar la metodología DROP descrita anteriormente y aquella relación funcional que se hubiera obtenido al aplicar el método de mínimos cuadrados ordinarios (MCO) a todos los datos sin tratamientos matemáticos adicionales y sin contemplar incertidumbres experimentales. En esta figura se observa que la relación funcional MCO tiende a sobreestimar las concentraciones equivalentes de SST en relación con aquella obtenida mediante DROP para un mismo valor de turbiedad. Estas diferencias, mayores a 17 % para cualquier valor de turbiedad, podrían generar diferencias muy importantes para resultados de cargas contaminantes acumula-das en series temporales prolongadas y en particular para valores altos de turbiedad. Adicionalmente, la metodología planteada podría constituirse en una etapa preliminar para lograr mediciones en relativo tiempo continuo (valores en intervalos cortos de tiempo, del orden de una medición por minuto), in situ y en tiempo real de concentraciones equivalentes más representativas de contaminantes comúnmente utilizados para evaluar la calidad físico-química de los hidrosistemas urbanos, como los SST.

3. CONCLUSIONES

El presente trabajo tenía como objetivo desarrollar una metodología para la estimación de concentraciones de Sólidos Suspendidos Totales (SST) a partir de mediciones de turbiedad en hidrosistemas urbanos en operación. Esta metodología logró establecerse a partir de protocolos de laboratorio y campo acoplados con análisis de datos, contemplando incertidumbres experimentales, análisis de outliers y simulaciones de Montecarlo. Adicionalmente, a manera de síntesis de dicha metodología, ésta fue codificada en MatLab®, obteniendo como resultado un programa llamado DROP (Data Relationships Of water Pollutants). La metodología planteada y el programa DROP se aplicaron a muestras de agua extraídas en una sección del Río Arzobispo, obteniendo una relación funcional entre la turbiedad y la concentración de Sólidos Suspendidos Totales (SST). Esta relación se comparó con una función calculada mediante el método de mínimos cuadrados ordinarios (MCO), sin tratamientos matemáticos adicionales y sin contemplar incertidumbres experimentales. De esta comparación se obtuvo que la relación obtenida mediante MCO sobreestima los valores de concentraciones de SST en más de 17 % para cualquier valor de turbiedad con respecto a los valores de concentraciones obtenidos mediante DROP. Esto podría generar diferencias muy importantes para resultados de cargas contaminantes acumuladas en series temporales prolongadas y en particular para valores altos de turbiedad.

Al proponer relaciones funcionales entre turbiedad y SST que contemplen incertidumbres experimentales y representatividad de los datos utilizados para construirlas, se abre la posibilidad de realizar mediciones en relativo tiempo continuo, in situ y en tiempo real. Lo anterior ofrece ventajas importantes en varios niveles: (i) ventajas experimentales, al disminuir los inconvenientes demostrados que presentan los ensayos estándar de laboratorio sobre muestras puntuales ligados a su recolección, manipulación y transporte [4]; (ii) ventajas de gestión, al tener un conocimiento oportuno y representativo de las dinámicas de las concentraciones, lo que puede constituirse en una herramienta poderosa de toma de decisiones en tiempo real o diferido; así mismo, al contar con polutogramas representativos de los fenómenos, se podrían estimar las cargas vertidas de contaminantes a diferentes escalas de tiempo, lo que otorga una información clave para el manejo de los cuerpos acuáticos receptores; (iii) ventajas científicas, al tener una cantidad importante de datos longitudinales de concentraciones de contaminantes, característicos de los hidrosistemas de drenaje urbano, con los que se pueda realizar análisis frecuenciales de dichas series de tiempo, proponiendo nuevos métodos para el filtrado, el almacenamiento, la transmisión y el pronóstico de concentraciones de contaminantes comúnmente utilizados.

AGRADECIMIENTOS

Los autores agradecen al Laboratorio de Pruebas y Ensayos de la Facultad de Ingeniería de la Pontificia Universidad Javeriana, sede Bogotá, por su apoyo en el análisis de muestras.

REFERENCIAS

[1] Murad Rivera (2003) Estudio sobre la distribución espacial de la población en Colombia, Santiago de Chile.         [ Links ]

[2] Colombia, Departamento Administrativo Nacional de Estadística (DANE) (2005) Censo Nacional 2005: Nivel Nacional, Bogotá: DANE.         [ Links ]

[3] Chocat, Bertrand-Krajewski, and Barraud (2007) Eaux pluviales urbaines et rejets urbains par temps de pluie. Les Techniques de l'Ingénieur p. 17.         [ Links ]

[4] Barrett, Jr., Jr., and Charbeneau (1998) Characterization of Highway Runoff in Austin, Texas, Area. Journal of Environmental Engineering 124, pp. 131-137.         [ Links ]

[5] Wu, Allan, Saunders, and Evett (1998) Characterization and Pollutant Loading Estimation for Highway Runoff. Journal of Environmental Engineering 124, pp. 584-592.         [ Links ]

[6] Becouze-Lareure (2010) Characterization and estimation of priority substances flows in urban wet-weather discharges on two experimental watersheds. Ph.D. Thesis.INSA, Lyon, Francia.         [ Links ]

[7] Pitt, Field, Lalor, and Brown (1995) Urban Stormwater Toxic Pollutants: Assessment, Sources, and Treatability. Water Environment Research 67, pp. 260-275.         [ Links ]

[8] Chebbo (1992) Solids in urban wet-weather discharges: Characterisation and potential of treatment. PhD. Thesis, École nationale des ponts et chaussées, Paris, Francia.         [ Links ]

[9] Ashley, Bertrand-Krajewski, Hvitved-Jacobsen, Verbanck, House, and Street (2004) Solids in sewers, IWA-Publ.         [ Links ]

[10] Torres and Bertrand-Krajewski (2008) Evaluation of uncertainties in settling velocities of particles in urban stormwater runoff. Water Sci. Technol. 57, pp. 1389-1396.         [ Links ]

[11] Krein and Schorer (2000) Road runoff pollution by polycyclic aromatic hydrocarbons and its contribution to river sediments. Water Research 34, pp. 4110-4115.         [ Links ]

[12] Lee, Shimizu, Matsuda, and Matsui (2005) Characterization of Polycyclic Aromatic Hydrocarbons (PAHs) in Different Size Fractions in Deposited Road Particles (DRPs) from Lake Biwa Area, Japan. Environ. Sci. Technol. 39, pp. 7402-7409.         [ Links ]

[13] Zhao, Li, Wang, and Tian (2010) Grain size distribution of road-deposited sediment and its contribution to heavy metal pollution in urban runoff in Beijing, China. J. Hazard. Mater. 183, pp. 203-210.         [ Links ]

[14] Winkler, Saracevic, Bertrand-Krajewski, and Torres (2008) Benefits, limitations and uncertainty of in situ spectrometry. Water Sci. Technol. 57, pp. 1651-1658.         [ Links ]

[15] Henckens, Veldkamp, and Schuit (2002) On Monitoring of Turbidity in Sewers. In Global Solutions for Urban Drainage American Society of Civil Engineers, pp. 1-13.         [ Links ]

[16] Bertrand-Krajewski, Winkler, Saracevic, Torres, and Schaar (2007) Comparison of and uncertainties in raw sewage COD measurements by laboratory techniques and field UV-visible spectrometry. Water Sci. Technol. 56, pp. 17-25.         [ Links ]

[17] International Organization for Standardization (1999) Standard ISO 7027: Water quality - Determination of turbidity, Ginebra.         [ Links ]

[18] American Public Health Association and American Water Works Association (1999) Standard Methods for the Examination of Water and Wastewater, American Water Works Association (AWWA).         [ Links ]

[19] Greenland (2001) Sensitivity analysis, Monte Carlo risk analysis, and Bayesian uncertainty assessment. Risk Anal. 21, pp. 579-583.         [ Links ]

[20] Smith (2006) Uncertainty Analysis. In Encyclopedia of Environmetrics John Wiley & Sons, Ltd.         [ Links ]

[21] Torres-Abello (2011) Metodología para la estimación de incertidumbres asociadas a concentraciones de Sólidos Suspendidos Totales mediante métodos de generación aleatoria. Tecno Lógicas pp. 181-200.         [ Links ]

[22] Cloirec, Baléo, Bourges, Courcoux, and Faur-Brasquet (2003) Méthodologie expérimentale: Méthodes et outils pour les expérimentations scientifiques, Tec & Doc Lavoisier.         [ Links ]

[23] Rousseeuw and Driessen (1999) A Fast Algorithm for the Minimum Covariance Determinant Estimator. Technometrics 41, pp. 212-223.         [ Links ]

[24] Rivero Lopez (2012) Requerimientos de operación y mantenimiento para el monitoreo en continuo de calidad de aguas en hidrosistemas urbanos. (Trabajo de grado Ingeniería Civil.). Pontificia Universidad Javeriana, Bogotá, Colombia.         [ Links ]