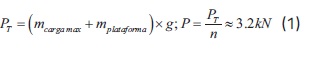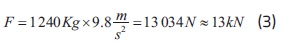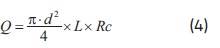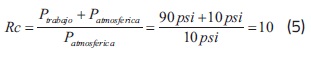Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Ciencia e Ingeniería Neogranadina
versão impressa ISSN 0124-8170
Cienc. Ing. Neogranad. vol.23 no.1 Bogotá jan./jun. 2013
EVALUACIÓN DEL DISEÑO DE UNA PEQUEÑA MESA VIBRATORIA PARA ENSAYOS EN INGENIERÍA SISMO-RESISTENTE
DESIGN EVALUATION OF A SMALL SHAKE TABLE FOR TESTS ON EARTHQUAKE-RESISTANT ENGINEERING
Julián Carrillo
Ing. Civil, Ph.D. Profesor e Investigador, Programa de Ingeniería Civil,
Universidad Militar Nueva Granada, UMNG, Bogotá, Colombia.
wjcarrillo@gmail.com.
Néstor M. Bernal Ruíz
Auxiliar de investigación, Programa de Ingeniería Civil, Universidad Militar Nueva Granada,
UMNG, Bogotá, Colombia.
u1801247@unimilitar.edu.co.
Pahola Porras
Ing. en Mecatrónica, Joven investigador, Programa de Ingeniería Civil,
Universidad Militar Nueva Granada, UMNG, Bogotá, Colombia.
paho756@gmail.com.
Fecha de recepción: 28 de noviembre de 2012 Fecha de aprobación: 15 de mayo de 2013
RESUMEN
Las consecuencias catastróficas de los sismos han incentivado la realización de estudios experimentales para mitigar los efectos de los sismos sobre las estructuras. En el artículo se presenta la evaluación de los diseños mecánico, neumático, estructural, de control y de adquisición de datos, de una pequeña mesa vibratoria uniaxial para ensayos de estructuras a escala reducida. Inicialmente se eligieron los elementos mecánicos que permiten el movimiento de la mesa. Luego se validó el desempeño del sistema a partir de herramientas de simulación. Finalmente se estudió la automatización de la mesa por medio de un control con sistema de lazo abierto, implementado en un micro-controlador. La mesa vibratoria propuesta es una herramienta versátil y económica para realizar pruebas experimentales orientadas al análisis y diseño de estructuras sometidas a eventos sísmicos. El dispositivo propuesto promoverá la investigación no sólo en nuevos materiales, sino en diseño y rehabilitación de viviendas, edificios y puentes sismo-resistentes.
Palabras clave: equipo de ensayo, estructuras, mesa vibratoria, sensores, sismo-resistente, sistema neumático, sistema de control.
ABSTRACT
The catastrophic consequences of earthquakes have encouraged to carrying out experimental studies for mitigating the effects of earthquakes on structures. This paper presents the assessment of the mechanic, pneumatic, structural, control and data acquisition designs of a small uniaxial shake table for testing of reduced-scale structures. Initially, the mechanical elements that allow the motion of the table were selected. Then, performance of the system was validated using simulation tools. Finally, the automation of the table was studied by using a control with an open-loop control system, which was implemented in a microcontroller. The proposed shake table is a versatile and economical facility for performing experimental tests aimed at analyzing and designing structures under seismic events. The proposed device will promote research not only on new materials, but also on design and rehabilitation of earthquake-resistant houses, buildings and bridges.
Keywords: test equipment, structures, shake table, sensors, earthquake-resistance, pneumatics system, control system.
INTRODUCCIÓN
En los últimos años han ocurrido eventos sísmicos devastadores, tales como el sismo de Haití de 2010 que dejó alrededor de 200 mil muertos y 295 mil casas o edificios destruidos [1]. En Colombia, los sismos de Armenia en 1999 (magnitud de 6.1) y de Popayán en 1983 (magnitud de 6.5) han demostrado la naturaleza sísmica de la región y han revelado la vulnerabilidad que presentan algunas estructuras ante un sismo de gran magnitud [2]. A pesar que desde hace varias décadas se han realizado estudios sobre el comportamiento sismo-resistente de estructuras [3], el crecimiento acelerado de las ciudades y las consecuencias de los sismos nuevamente han evidenciado la importancia de continuar estudiando el desempeño experimental de las construcciones ante eventos sísmicos.
En este artículo se presentan los resultados de la evaluación del diseño de una mesa vibratoria para estructuras a escala reducida. El estudio incluye los diseños mecánico, neumático, estructural, control y de adquisición de datos. Inicialmente, se discute el funcionamiento y el proceso de diseño de las mesas vibratorias, y se presentan los parámetros de diseño de la mesa vibratoria propuesta. La evaluación incluye el análisis de la durabilidad y efectividad de los elementos mecánicos, tales como rodamientos, placas, soportes y pernos, así como el tiempo de mantenimiento. Por último, se presentan las aplicaciones y limitaciones de la herramienta experimental desarrollada, y las posibles mejoras para simulaciones y diseños futuros.
1. ROL DE LAS MESAS VIBRATORIAS EN LA INGENIERÍA SISMO-RESISTENTE
Un sismo es la liberación de energía elástica almacenada durante años por movimientos relativos entre las placas tectónicas. Esta liberación se presenta como una ruptura en los contactos de las placas causando vibraciones en la corteza terrestre [4]. Un sismo libera gran cantidad de energía en el suelo y genera movimientos que se transmiten a las estructuras en términos de aceleraciones, desplazamientos y velocidades. Las consecuencias de los sismos significan anualmente no sólo numerosas pérdidas humanas, sino millonarias detrimentos en la infraestructura y en las invaluables construcciones históricas. Adicionalmente, la ocurrencia inesperada y su gran poder de destrucción [5] han convertido a los sismos en uno de los fenómenos naturales más temidos en el mundo.
Aunque actualmente no es posible predecir un sismo [6], sí se pueden minimizar sus efectos mediante la construcción de estructuras sismo-resistentes [7]. Las técnicas de análisis y diseño de estructuras sismo-resistentes pueden ser de tipo de-terminista o probabilista [8]. Dentro de las herramientas deterministas más utilizadas están los modelos matemáticos, los cuales se validan a partir de la comparación con resultados medidos en experimentos [9]. Sin embargo, este método no puede tener en cuenta todos los efectos aleatorios que se presentan en un sismo real, por lo que son denominados modelos idealizados. Para complementar la técnica determinista se han desarrollado métodos experimentales que permiten estudiar los efectos de los sismos sobre las construcciones, tales como ensayos dinámicos en mesas vibratorias, y ensayos seudo-dinámicos y cuasi-estáticos que usualmente utilizan un marco de carga o un muro de reacción [10].
1.1. EVOLUCIÓN DE LA MESAS VIBRATORIAS
Las primeras mesas vibratorias se desarrollaron a finales del siglo XIX. Tales mesas vibratorias generaban el movimiento de forma manual por medio de una rueda con manivela y una plataforma móvil sobre rieles. Unas décadas más adelante se utilizaron motores eléctricos para sustituir los mecanismos manuales. La siguiente generación de mecanismos nace con la propuesta de Jacobsen (1930), la cual es una mesa vibratoria que produce vibraciones a partir de un primer impulso. Este impulso es generado por un péndulo de impacto y el movimiento a la plataforma se transmite por medio de un resorte. Con la ayuda de modelos a escala reducida, este tipo de mesas fueron una herramienta clave para realizar numerosos avances en estructuras sismo-resistentes [11].
El principio de funcionamiento de las mesas vibratorias actúales inició con los avances logrados en la segunda guerra mundial. Las mesas vibratorias modernas usan actuado-res y sistemas de control avanzados para simular sismos reales o artificiales [12]. La primera mesa vibratoria de gran tamaño (6 California, Berkeley en 1972. La mesa fue construida con capacidad de movimiento horizontal y vertical, e inspiró el desarrollo de otras mesas vibratorias de gran tamaño con diferentes grados de libertad en todo el mundo [13]. En los últimos años, las mesas vibratorias se han convertido en una herramienta clave para estudiar los efectos de los sismos sobre estructuras [14]. Los resultados medidos en este tipo de ensayos dinámicos han sido fundamentales para validar, calibrar y complementar gran variedad de modelos de predicción que se utilizan para análisis, diseño y rehabilitación de viviendas, edificios, puentes, etc. [15].
1.2. CLASIFICACIÓN DE MESAS VIBRATORIAS
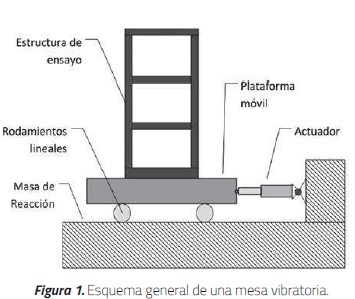
Una mesa vibratoria es una plataforma móvil que simula los movimientos de un sismo sobre un modelo estructural [17], tal como se observa en la Figura 1. Las mesas vibratorias pueden ser clasificadas según el tamaño, el tipo de actuador que genera el movimiento o los grados de libertad [12]. Los ensayos en mesa vibratoria generalmente involucran modelos a escala reducida. Sin embargo, en los últimos años se han llevado acabo ensayos de estructuras en escala real usando mesas vibratorias como las disponibles en el E-Defense en Japón o en la Universidad de San Diego en Estados Unidos. Estas mesas permiten simular movimientos hasta en seis grados de libertad.
2. PROGRAMA EXPERIMENTAL
Para desarrollar una mesa vibratoria, los movimientos producidos deben ser correctamente controlados para obtener la respuesta deseada [16]. Por otro lado, los modelos de ensayo deben mantener la similitud dinámica con la estructura real (prototipo), para que el escalamiento no afecte los resultados del ensayo [17][18].
2.1. PARÁMETROS DE DISEÑO DE LA MESA VIBRATORIA
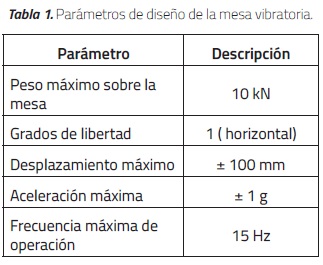
Los parámetros de diseño de la mesa vibratoria se muestran en la Tabla 1. En cuanto a las características de los movimientos que serán reproducidos y las demandas sísmicas transmitidas al modelo, se estudiaron los datos de amenaza sísmica en Colombia y los valores de aceleración pico efectiva (Aa), según la información registrada por Ingeominas [19]. De acuerdo con las características de frecuencia de los sismos que afectan la región Colombiana, para el movimiento del sistema se seleccionó una frecuencia de operación máxima de 15 Hz.
2.2. DISEÑO DE LA MESA VIBRATORIA
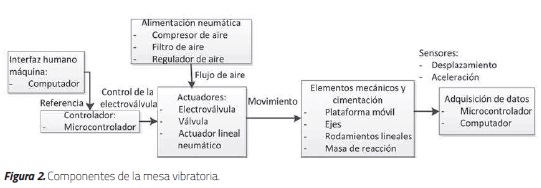
Los componentes de una mesa vibratoria se dividen básicamente en cinco grandes grupos: (i) elementos mecánicos y cimentación, (ii) fuente de alimentación, la cual puede ser eléctrica, hidráulica o neumática, (iii) actuadores, (iv) sistema de control, y (v) sistema de adquisición de datos [20]. El movimiento en una mesa vibratoria neumática se genera por medio de actuadores neumáticos (cilindros y válvulas), los cuales son alimentados por un compresor de aire. Las características del movimiento en términos de aceleración, velocidad y desplazamiento son controladas por medio de señales eléctricas en una electroválvula. Las señales son recibidas desde un controlador, el cual toma acciones en función de la orden dada por el usuario en el sistema de control. En la Figura 2 se observa la correlación entre los componentes de la mesa vibratoria en un sistema de control de lazo abierto.
En general, en el diseño de la mesa vibratoria se deben llevar a cabo cinco tipos de diseño: mecánico, neumático, estructural (cimentación), del sistema de control y del sistema de adquisición de datos. A continuación se describen las variables y el diseño de cada una de las componentes de la mesa vibratoria que se propone en este estudio.
2.2.1. Diseño mecánico
Los elementos mecánicos de una mesa vibratoria se pueden dividir en componentes móviles y estáticos. Entre los componentes móviles se encuentran la plataforma de ensayo y los rodamientos lineales que soportan la carga. Los componentes estáticos comprenden los rieles de los rodamientos lineales y los soportes. El diseño de los elementos mecánicos debe cumplir requerimientos de rigidez, resistencia, durabilidad y economía [21]. Los materiales más usados para este fin son magnesio, acero y aluminio. Por el bajo costo y maleabilidad, uno de los más utilizados es el acero SAE1020, cuyo esfuerzo último de tensión, fu 500 MPa (ASTM A-105) [22].
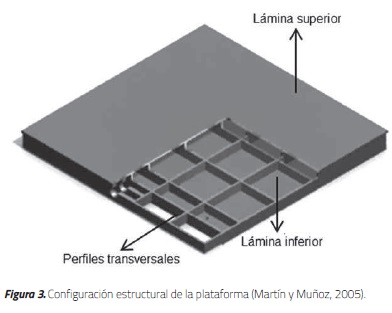
Para la mesa vibratoria de este estudio se consideró la utilización de una plataforma existente en el Laboratorio de Estructuras de la UMNG, la cual fue desarrollada por Martín y Muñoz [21]. La plataforma es una estructura en forma de cajón con dimensión cuadrada de 1.1 m de lado y espesor de 80 mm, tal como se muestra en la Figura 3. La plataforma está rigidizada por medio de perfiles transversales en las dos direcciones, una lámina superior y una lámina inferior. Este diseño minimiza el peso del cajón y ofrece un buen comportamiento bajo esfuerzos que actúan dentro y fuera del plano. El peso de la plataforma es de 2.4 kN sin carga. En el diseño de la plataforma se tuvieron en cuenta las siguientes variables: frecuencia natural del elemento, rigidez, resistencia, durabilidad y costo. El diseño se realizó con base en los esfuerzos admisibles propuestos en la Norma NSR-10 [8].
La plataforma debe soportar los esfuerzos dinámicos generados en la simulación de un sismo, con el peso máximo de 10 kN actuando sobre la mesa (ver Tabla 1). La plataforma se convierte en un elemento crítico en el diseño de la mesa vibratoria. Por tanto, su desempeño estático y dinámico se validó por el método de análisis en elementos finitos (FEM por sus siglas en inglés). Las simulaciones fueron implementadas en el programa Solidworks Simulation.
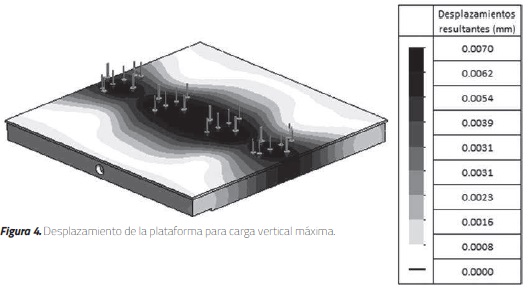
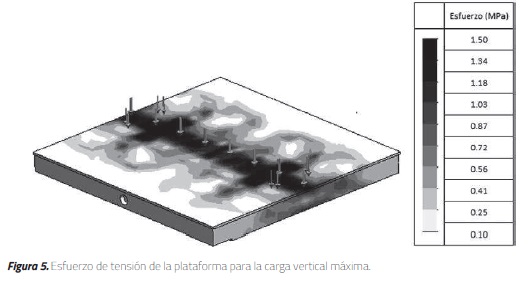
Las piezas y ensamblajes se modelaron utilizando un mallado con elementos sólidos de 4 puntos, 42 mm de espesor, dando un total de 15147 elementos finitos. Tomando en cuenta las demandas dinámicas sobre los elementos, el modelo de la pieza en CAD (Diseño asistido por computador, CAD por sus siglas en inglés) se realizó incluyendo las uniones del elemento, el material y el proceso de montaje. Para este caso, se tomaron en cuenta la unión a tope entre las piezas que componen la plataforma, así como el material de la plataforma (acero SAE-1020). En el caso del análisis estático, la masa correspondiente al peso máximo del modelo (10 kN) se aplicó como una carga distribuida en una sección de la plataforma. Para un caso crítico de servicio se seleccionó un espécimen con sección de 1.0 m 0.2 m, lo que representaría la sección transversal de un muro estructural. En los soportes de los rodamientos se consideró un desplazamiento nulo, proporcionando los ceros necesarios para la solución de la matriz de desplazamiento en el programa. Los diagramas de desplazamiento y esfuerzo de tensión de la plataforma bajo la carga vertical distribuida se muestran en las Figuras 4 y 5, respectivamente.
Tal como se esperaba, la configuración estructural de la plataforma genera que el desplazamiento máximo en la placa superior sea igual a 0.004 mm y ocurre en el centro de la plataforma (Figura 4.). El esfuerzo máximo de tensión en el punto crítico es de 8 MPa, el cual es significativamente inferior al esfuerzo máximo del acero empleado (fu 500 MPa), lo que indica que la estructura interna cumple su función de distribuir los esfuerzos en toda la plataforma.
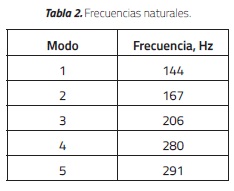
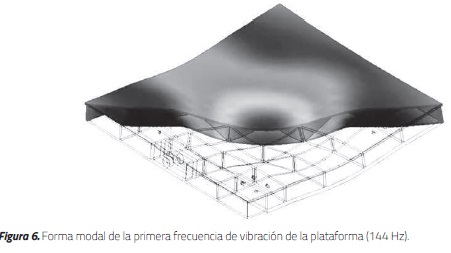
El análisis de los modos de vibración de un elemento permite conocer las frecuencias naturales donde se presentarán los mayores desplazamientos y esfuerzos en el elemento. Las deformaciones asociadas a las frecuencias de resonancia son mayores que las deformaciones estáticas, aunque éstas dependen de diferentes factores tales como la carga sobre la plataforma, la forma de la carga o las cargas adicionales. Las frecuencias de los modos de vibración de la plataforma se indican en la Tabla 2. En la tabla se observa que la frecuencia fundamental es de 144 Hz. Sin embargo, la frecuencia de simulación más alta de la mesa es de 15 Hz, es decir, se demuestra que no se presentará resonancia y, por tanto, no ocurrirán deformaciones que comprometan el desempeño del elemento. En la Figura 6 se muestra la forma modal de la primera frecuencia de vibración de la plataforma, la cual se presenta en la dirección de aplicación de la carga del modelo de ensayo.
Los rodamientos lineales y apoyos fueron seleccionados con base en los parámetros de diseño de la mesa y las recomendaciones del Manual Thomson para componentes lineales [23]. Para la selección del rodamiento lineal, la fuerza vertical que debe soportar cada rodamiento se calculó mediante la ecuación 1:
donde PT es la fuerza total en el sistema, n es el número total de rodamientos, y P es la fuerza horizontal en cada rodamiento. Los cuatro apoyos o rieles se deben escoger a partir del diámetro de los rodamientos, el cual se seleccionó de 20 mm, según el Manual Thomson [23]. De esta manera, se escogió el rodamiento lineal con referencia SSEPBOA-M20 DD con carga máxima de 4.4 kN, puesto que es la referencia con el valor más cercano al valor calculado de P (3.2 kN). Con base en las ecuaciones del Manual Thomson, el tiempo de servicio de estos elementos se estimó en 22.8 horas de operación continua.
2.2.2. Diseño neumático
El diseño neumático comprende la selección de un compresor de aire y de los actuadores para generar el movimiento de la plataforma. Para dimensionar adecuadamente el actuador neumático, es necesario conocer la fuerza que el actuador debe transmitir a la plataforma móvil. La fuerza necesaria es proporcional a la masa que estará en movimiento. Esta masa es igual a la suma de la masa del cajón, la masa de los rodamientos y la masa del modelo de ensayo; es decir, la masa en movimiento es aproximadamente igual a 1240 kg. La fuerza del actuador lineal está dada por la ecuación 2.
donde m es la masa total en movimiento del sistema, α es la aceleración máxima del sistema (+/- 0.3 g = 2.94 m/s2), F es la fuerza generada por el actuador lineal, N es la fuerza normal causada por m, y µfr es el coeficiente de fricción dinámico de los rodamientos. Si se supone un movimiento armónico simple con frecuencia de 10 Hz y desplazamiento máximo de 10 mm, la velocidad del sistema es igual a 400 mm/s. Teniendo en cuenta que la velocidad y el peso del sistema son relativamente bajos, es posible despreciar la fricción con el aire [24]. Por tanto, para calcular la fuerza máxima del actuador, la ecuación 2 se reduce a la ecuación 3, a partir de la cual se calcula la fuerza máxima necesaria para acelerar el sistema a 1 g, con una masa en movimiento de 1240 kg.
La fuerza máxima resultante es aproximadamente de 13 kN. Para seleccionar el actuador se utilizó la fuerza máxima calculada y se adicionó un 35% como factor de seguridad, es decir, 17 kN. Con base en el Manual Pneumatics, el actuador de 160 mm de diámetro y 100 mm de carrera es el que mejor se ajusta a las características de diseño. El actuador seleccionado es capaz de proporcionar una fuerza máxima de 30 kN, velocidad máxima de 500 mm/s, presión máxima de trabajo de 0.62 MPa (90 psi), y capacidad máxima de desplazamiento de 100 mm. El caudal del sistema neumático se calculó por medio de la ecuación 4.
donde d es el diámetro del cilindro (160 mm), L es la carrera del cilindro (100 mm) y Rc es la razón de compresión entre la presión de trabajo y la presión atmosférica. Para la Ciudad de Bogotá, Rc se calcula como se indica en la ecuación 5.
De esta manera, el caudal calculado con la ecuación 4 es de 100 l/s. Con base en el caudal se eligió una válvula de 5 vías, 2 posiciones (5/2), con puertos de ¾" (19 mm) de diámetro. Esta válvula será controlada por medio de una electroválvula 5/2 de alta velocidad a 24 VDC (voltaje de corriente directa, VDC por sus siglas en inglés) con puertos de ¼" (6.4 mm) de diámetro.
El flujo de aire necesario para el actuador neumático debe ser proporcionado por un compresor que permita una presión de operación asociada al caudal calculado (100 l/s). Por tanto, se seleccionó un compresor – Kaeser SK15 de 15 HP, el cual desarrolla una presión de trabajo de 0.55 MPa (80 psi).
2.2.3. Diseño estructural de la cimentación
Con base en la ley de acción y reacción de Newton, la fuerza aplicada a la masa móvil generará una fuerza de reacción de la misma magnitud en el sentido contrario de la fuerza de acción. De esta manera, la carga máxima de 13 kN (ecuación 3) debe ser soportada por una estructura de cimentación. Si el suelo no está debidamente preparado y la cimentación no está adecuadamente diseñada, el movimiento podría originar daños en edificaciones cercanas o el hundimiento del sistema. Por esta razón, fue necesario el diseño dinámico de una cimentación que sirva como masa de reacción. Esta masa de reacción debe proveer una base inercial que minimiza las vibraciones en el suelo [20].
Para el diseño de la cimentación se tuvieron en cuenta los dos principales problemas de estabilidad: el análisis de volcamiento y el análisis de deslizamiento en condiciones máximas [25]. También se atendieron todas las especificaciones, normas y pautas de la norma NSR-10 [27], y las recomendaciones indicadas en el documento ACI 351.3 R-04 [26]. En este último documento se proponen tres métodos de diseño para este tipo de estructuras no convencionales:
- Método empírico que consiste en un predimensionamiento y en la verificación del cumplimiento de varias condiciones estáticas preestablecidas. Este método se usa para maquinaria o estructuras pequeñas.
- Método de la carga estática equivalente donde se establecen cargas estáticas a partir de las características mecánicas de la maquinaria, las cuales son dadas por el fabricante. Se usa para maquinaria mediana de hasta 45 kN de peso.
- Método dinámico que consiste en establecer un modelo de comportamiento suelo-estructura mediante el uso de las propiedades dinámicas del equipo (dadas por el fabricante) y las propiedades dinámicas del suelo de cimentación obtenidas por un estudio de suelos orientado a encontrar parámetros dinámicos. Este método está orientado a maquinaria grande y/o pesada, o con requerimientos de funcionamiento a tolerancias mínimas.
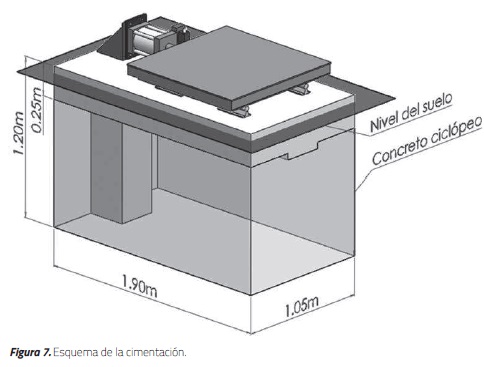
Con base a lo anterior, el método utilizado para este diseño fue el método empírico [29]. Para esto se realizó un predimensionamiento de la profundidad mínima de cimentación, que según el estudio de suelos es de 1.20 m. Adicionalmente, para efectos de mantenimiento y aislamiento de los equipos, la cimentación se dejó 50 mm por encima del nivel del suelo del laboratorio (ver Figura 7). Las cargas que actúan sobre la estructura fueron calculadas con base en el uso de la estructura, y de acuerdo con el Titulo B de la Norma NSR-10. Las cargas vivas para la placa plana son de 2 kN/m2 por mantenimiento y montaje. El diseño de car-gas horizontales está basado en las hipótesis de carga que incluyen sismo. Estas cargas sísmicas se calcularon de acuerdo con el Título A de la NSR-10 y los parámetros sísmicos corresponden a lo especificado en la Microzonificación Sísmica de Bogotá [28]. El periodo fundamental de la estructura no se puede obtener analíticamente por los métodos especificados en A.4.2 de la NSR10; sin embargo, con base en la gran rigidez del bloque sí se puede concluir que es muy bajo y que va a estar dentro de la meseta del espectro, muy por debajo de 1.5 s.
En general, la estructura de concreto es un bloque rígido de concreto ciclópeo enterrado en el suelo con dimensiones de 1.90 m de largo por 1.05 m de ancho, dentro del cual está embebido un semi-pórtico de concreto reforzado que consiste en una columna de sección 300mm que arranca en el fondo del bloque y remata en la superficie, donde se une con una viga de igual sección, con la que forman una "L" invertida.
La viga central soporta en toda su longitud la placa de concreto reforzado donde se anclan las guías de los rodamientos de soporte de la mesa vibratoria. En el nudo conformado por la unión de viga-columna se empotró una platina de acero para el montaje del actuador. El soporte metálico anclado a la viga central de concreto está diseñada para soportar las fuerzas cortantes dinámicas generadas en el movimiento horizontal del actuador y del espécimen montado en la mesa vibratoria.
2.2.4. Diseño de los sistemas de control y de adquisición de datos
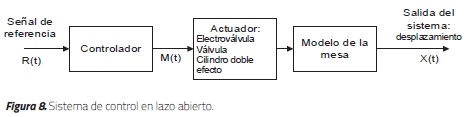
La mesa vibratoria se diseñó para un sistema control en lazo abierto que permita representar un sismo real ocurrido en Colombia, y que sea simple y fácil de instalar. La finalidad de este control es monitorear el funcionamiento adecuado de todos los componentes mecánicos y neumáticos.
En un control de lazo abierto, la variable de salida no tiene efecto sobre la acción de control y, por tanto, este control es muy sensible a perturbaciones. En general, es un sistema no realimentado en donde a cada entrada le corresponde una salida definida. Debido a que no existe una comparación entre la salida del sistema y la entrada, la exactitud dependerá de la calibración del controlador. En este estudio se planeó un sistema de lazo abierto, cuya representación se muestra en la Figura 8, en donde R(t), M(t) y X(t) son las señales de referencia, de salida del controlador y de salida del sistema, en función del tiempo, respectivamente. El sistema se diseñó con base en la velocidad de reacción del sistema neumático, ya que mientras la señal de realimentación es registrada, la válvula no alcanza a recorrer la totalidad de su carrera y, por tanto, el sistema neumático no logra conmutar la válvula para realizar el control esperado.
El modelamiento del sistema de la mesa se realizó tomando en cuenta los lineamientos recomendados por Conte y Trombetti [30]. En primer lugar, se realizó el modelo lineal de la electroválvula y la válvula. Luego, se obtuvo el modelo del actuador para estimar la función de transferencia del sistema neumático. Por último, se adicionaron los efectos de flexibilidad del actuador y los elementos mecánicos (incluida la cimentación).
El sistema de adquisición de datos está encargado de registrar el comportamiento de la mesa y de la estructura, sin llegar a influir en el movimiento. Para la adquisición de datos se seleccionó un sensor de aceleración capacitivo de alta sensibilidad de referencia MMA7361L, con intervalo de medición de +/-1.5 g a +/-6 g. Un microcontrolador de referencia PIC18F4550 se encargará de la conversión ADC de la señal del acelerómetro [31]. Tomando en cuenta que la separación entre la mesa vibratoria, el compresor de aire y la sala de control en el laboratorio de Estructuras de la UMNG es de aproximadamente 25 m, se realizó una comunicación serial inalámbrica usando módulos Xbee (módulo de radio-frecuencia), los cuales ofrecen un intervalo de operación de 30 m (en interiores).
2.3. ANÁLISIS DE COSTOS
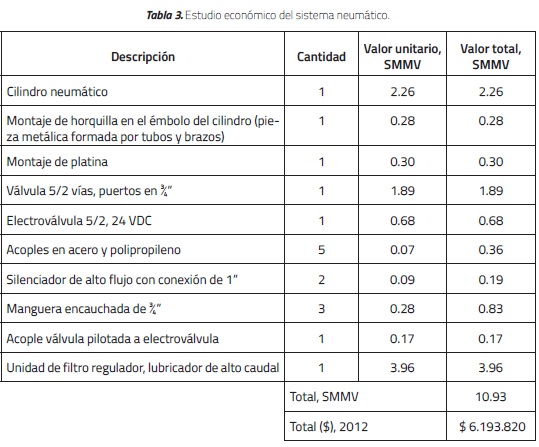
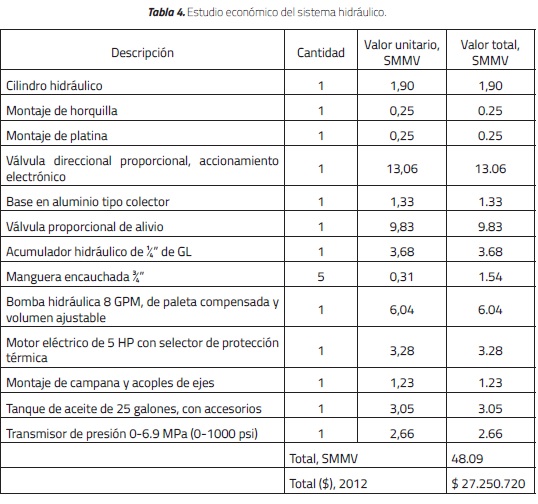
Para propósitos de comparación económica, en este estudio se realizó un análisis de costos de un sistema hidráulico y un sistema neumático, incluyendo el costo de cada elemento del sistema. Los resultados del análisis de costos de los dos sistemas se muestran en las Tablas 3 y 4. Para incluir la depreciación del peso colombiano, el análisis de costos se realizó en función del salario mínimo mensual vigente (SMMV) para el año 2012. En los costos se ha incluido el valor del Impuesto al Valor Agregado (IVA).
Como se muestra en las Tablas 3 y 4, el coscosto del sistema neumático equivale al 23% (10.93/48.09) del sistema hidráulico. Por tanto, el análisis de costos demuestra que, para mesas vibratorias pequeñas, la utilización del sistema neumático es una opción económicamente adecuada [32]. De esta manera, en pequeños centros de investigación o en universidades se podrá estudiar el desempeño dinámico de estructuras sometidas a efectos sísmicos.
3. CONCLUSIONES Y RECOMENDACIONES
En este artículo se han presentado los resultados de la evaluación de los diseños mecánico, neumático, estructural, de control y de adquisición de datos, de una pequeña mesa vibratoria uniaxial neumática, para ensayos dinámicos sobre estructuras en escala reducida. Este estudio representa una aplicación práctica de integración de la Ingeniería Civil y la Ingeniería Mecatrónica, en beneficio de la sociedad. La metodología del estudio se basó en la separación de las etapas de evaluación de diseño. Se considera que esta metodología fue adecuada y permitió un óptimo diseño de la mesa vibratoria, ya que fue posible delimitar el análisis de los elementos escogidos por medio de simulaciones.
La mesa vibratoria desarrollada consiste en una plataforma de 1.1 m2, la cual puede soportar una carga máxima de 10 kN y operar entre frecuencias entre 2 y 15 Hz. La mesa utiliza un control on-off en sistema de lazo abierto, el cual permite realizar pruebas con aceleración máxima de 1 g, velocidad de 40 m/s y desplazamiento de 100 mm. El diseño mecánico fue verificado satisfactoriamente por medio de software de análisis de elementos finitos. Los resultados de la plataforma móvil mostraron que el elemento tiene un factor de seguridad mayor que 10 y, por tanto, podrá soportar pruebas en condiciones máximas y por tiempos largos sin sufrir deformaciones considerables por fatiga.
Los resultados del estudio permitieron verificar las ventajas de un diseño neumático para aplicaciones sencillas en Ingeniería Civil, siendo este sistema versátil y económico para los laboratorios que desarrollan investigación sobre los efectos de los sismos en las estructuras. La mesa vibratoria servirá como apoyo tanto en las actividades académicas del Programa de Ingeniería Civil, como en los proyectos de investigación que se desarrollan en el Laboratorio de Estructuras de la UMNG. Por ejemplo, la herramienta de ensayo permitirá estudiar los efectos de los sismos y desarrollar recomendaciones para análisis, diseño y rehabilitación de estructuras sismo-resistentes.
REFERENCIAS BIBLIOGRÁFICAS
[1] Emergency Committee. (2012). Haiti Earthquake Facts and Figures. Consultada en marzo de 2012. En: http://www.dec.org.uk/haiti-earthquake-facts-and-figures. [ Links ]
[2] Vargas C., Nieto M., Monsalve H., Montes L. y Valdes M. (2008). The Abaníco del Quindío alluvial fan, Armenia, Colombia: Active tectonics and earthquake hazard; En: Journal of South American Earth Sciences, Vol. 25(1), pp. 64-73. [ Links ]
[3] Ozaki M. y Hayashi S. (1978). Earthquake resistant design of offshore building structures; En: IEEE Journal of Oceanic Engineering, Vol. 3(1), pp. 152-162. [ Links ]
[4] Sarria A., (1995). Ingeniería sísmica. Bogotá, Colombia. Ediciones Uniandes y Ecoe Ediciones, 56-120 p. [ Links ]
[5] Latchman S. (2009), Modeling catastrophes; En: Plus magazine, Vol. 53. [ Links ]
[6] Zafarani H., Noorzad A., Ansari A. y Bargi K. (2009). Stochastic modeling of Iranian earthquakes and estimation of ground motion for future earthquakes in Greater Theran; En: Soil Dynamics and Earthquake Engineering, Vol. 29(4), pp. 722-741. [ Links ]
[7] Marazzi F. y Tirelli D. (2010). Combating earthquakes: design and testing anti-seismic building; En: Science in School, Vol. 15, pp. 55-59. [ Links ]
[8] Moreno N. (2011). Estructuración de la Norma sismo resistente 2010 â NSR â 10 basada en el modelo de estados límite de diseño. En: Latin American and Caribbean Conference for Engineering and Technology. Medellin, Colombia, Corporación Universitaria de la Costa, CUC. [ Links ]
[9] Trombetti T. y Conte J. (2002). Shaking table dynamics: result from a test-analysis comparison study; En: Journal of Earthquake Engineering, Vol. 6, pp. 513-551. [ Links ]
[10] Carrillo J. y Alcocer S. (2012). Experimental investigation on dynamic and quasi-static behavior of low-rise RC walls; En: Earthquake Engineering and Structural Dynamics. DOI: 10.1002/eqe.2234. [ Links ]
[11] Severn R., Stoten D. y Tagawa. (2012), The Contribution of Shaking Tables to Earthquake Engineering; En: 15th World Conference On Earthquake Engineering. Lisboa, Portugal. [ Links ]
[12] Baran T., Tanrikulu A., Dundar C. y Tanritulu A. (2011). Construction and performance test of a low-cost shake table; En: Experimental Techniques, Vol. 35, No. 4, pp. 8â16. [ Links ]
[13] Severn R. (2011). An assessment of the use and value of shaking tables; En: Experimental Vibration Analysis for Civil Engineering Structures. Varenna, Italia. [ Links ]
[14] Carrillo J. y Alcocer S. (2011). Improved external device for a mass- carrying sliding system for shaking table testing; En: Earthquake Engineering & Structural Dynamics, Vol. 40, pp.393â411. [ Links ]
[15] Xilin L. (1995). Application of identification methodology to shaking table test on reinforced concrete columns; En: Engineering Structures, Vol. 17, pp. 505-511. [ Links ]
[16] O'Hagan J. y Ma Q. (2012). Experimental assessment of PID control for a uniaxial shake table; En: 15th World Conference On Earthquake Engineering. Lisboa, Portugal. [ Links ]
[17] Anastasopoulos I., Georgarakos T., Georgiannou V., Drosos V. y Kourkoulis R. (2010). Seismic performance of bar-mat reinforced-soil retaining wall: Shaking table testing versus numerical analysis with modified kinematic hardening constitutive model; En: Soil Dynamics and Earthquake Engineering, Vol. 30(10), pp. 1089-1105. [ Links ]
[18] Tashkov L., Krstevska L., Safak E., Cakti E., Edincliler A. y Erdik M. (2012), Comparative Study of Large and Medium Scale Mosque Models Tested on Seismic Shaking Table; En: 15th World Conference On Earthquake Engineering. Lisboa, Portugal. [ Links ]
[19] Ingeominas: Servicio Geológico Colombiano. (2012). Mapa de Amenaza sísmica y Valores de Aa de Colombia. Consultada en febrero del 2012. En: http://www.seisan.ingeominas.gov.co. [ Links ]
[20] Muhlenkamp M. (1997). Analysis, design y construction of a shaking table facility; Houston, 114p. Trabajo de grado (Master in Sciences). Rice University. [ Links ]
[21] Martin L. y Muñoz R. (2005). Diseño de una mesa vibratoria de un grado de libertad para simulación de sismos; Bogotá, 121 p. Trabajo de Grado (Ingeniero en Mecatrónica). Facultad de Ingeniería, Universidad Militar Nueva Granada. [ Links ]
[22] ASTM. (2011). Standard Specification for Carbon Steel Forgings for Piping Applications, ASTM A105. [ Links ]
[23] Danaher Motion. (Agosto 2004), Advance linear motion metric components. Vol. 1, pp. 22-31. [ Links ]
[24] Idrobo L, Patiño M., Racedo F., Dorado P, Escobar P, (2006). Diseño y construcción de un riel de aire automatizado para el estudio del movimiento utilizando sensores magnéticos; En: Revista de la Sociedad Colombiana de Física, Vol. 38, pp. 695-698. [ Links ]
[25] Uribe Escamilla J, Barbosa Jerez R, Pérez Ruiz P, Saavedra Quiroga P, Báiz Cueto M y Moreno Garzón J. (2006), Diseño y fabricación de mesas vibratorias para el estudio del comportamiento dinámico de modelos estructurales a escala reducida; En: Revista De La Escuela Colombiana de Ingeniería, Vol. 64, pp. 13-20. [ Links ]
[26] ACI Comité 351 (2004). Foundations for Dynamic Equipment. American Concrete Institute, ACI. Farmintong Hills, EE.UU., 63 pp. [ Links ]
[27] Asociación Colombiana de Ingeniería Sísmica. (2010). Reglamento Colombiano de Construcción Sismo Resistente de 2010, NSR-10. Ministerio de Ambiente, Vivienda y Desarrollo Territorial, Capitulo A.13. [ Links ]
[28] Alcaldía Mayor de Bogotá. "Decreto N° 523: Microzonificación sísmica de Bogotá D.C". Bogotá, Colombia. 16 de diciembre de 2010. [ Links ]
[29] Díaz A. (2013). Cimentación Mesa Vibratoria - Laboratorio de Ingeniería de la Universidad Militar Nueva Granada. Memorias de cálculo estructural. Bogotá, Colombia. [ Links ]
[30] Conte J. y Trombetti T. (2000). Linear dynamic modeling of a uni-axial servo-hydraulic shaking table system; En: Earthquake Engineering & Structural Dynamics, Vol. 29, pp. 1375-1404. [ Links ]
[31] Y. Xu, H. Hua y J. Han. (2007). Modeling a controller design of a shaking table in an active structural control system; En: Mechanical Systems and Signal Processing Vol. 22, pp. 1917-1922. [ Links ]
[32] Crewe A. y Severn R. (2001). The European collaborative program on evaluating the performance of shaking tables; En: The Royal Society. [ Links ]