INTRODUCCIÓN
Debido al alto crecimiento de la industria textil y la diversificación de los productos fabricados, es necesario diseñar métodos que permitan garantizar la calidad, con el fin de lograr ser competitivo en el mercado global, donde esta se ha convertido en el eje primordial [1]-[2]. El control de calidad se define como el grado de conformidad del producto con respecto a sus especificaciones, dichas especificaciones pueden ser objetivas y formales, sin embargo, en las fábricas donde se realiza tejido de punto, es un proceso subjetivo y difícil de definir [3].
En la actualidad se fabrican productos textiles para diferentes propósitos, como lo son la protección contra el frío, la absorción de líquidos, el diseño de modas, entre otros propósitos. A esto se le conoce como tecnologia textil y su clasificación varía según el patrón, lo que en muchos casos determina la calidad del producto [4]. Con el fin de garantizar la calidad en la fabricación de tejido de punto, se han propuesto diferentes métodos para realizar la inspección del producto, que van desde la revisión por operarios expertos, hasta el diseño de sistemas automáticos de inspección [1]-[9].
Los métodos de clasificación manual son ampliamente utilizados en las pequeñas empresas, aunque son de baja inversión y fácil implementación, no resultan efectivos debido a errores humanos como, por ejemplo, la percepción de colores y texturas. Adicionalmente se debe considerar que la materia prima, en este tipo de empresas, es diversa y se presenta en grandes cantidades lo que genera desgaste en los operarios y propicia los errores.
Dada esta situación, se han ideado diferentes técnicas para la identificación de errores en los textiles, tales como la inspección a través de máquinas. Esta ha demostrado resultados satisfactorios, sin embargo, su detección se limitada a una pequeña cantidad de tipos de telas, además de requerir una alta inversión. Otros enfoques proponen el uso de cámaras con el fin de determinar los defectos presentes en las telas por medio de técnicas de visión por computador, resaltando el uso de morfología matemática [10], método fractal [11], redes neuronales artificiales [12], entre otros.
En el estado del arte se han diseñado un gran número de metodologías para el reconocimiento de patrones, sin embargo, muchas de estas estrategias requieren de ambientes controlados (iluminación, escala, rotación, entre otros) y en los entornos industriales no siempre se cuenta con la posibilidad de garantizar esta clase de condiciones. Esto genera que este tipo de enfoques sean limitados para la solución del problema [13]-[14]. Ejemplo de ello se evidencia con enfoques de caracterización por color, los cuales presentan fallas cuando se generan cambios en la iluminación [15], por lo que se requiere de una iluminación externa que evite estos cambios [16]. Otros enfoques proponen el uso morfológico de los patrones presentes en la escena, métodos que a pesar de ser invariantes al cambio de color e iluminación, presentan dificultades cuando se generan oclusiones parciales causadas por factores externos como sombras u otros objetos [17].
Otro planteamiento, son los enfoques de textura los cuales se basan en transformaciones espacio-frecuencia. Estos cobran fuerza debido a que las telas producidas, a partir de estos materiales, presentan patrones periódicos que pueden ser ampliamente descritos en un espacio ortogonal [18]-[19], lo anterior permite robustez en las variaciones de color siendo potenciales para la implementación en ambientes con iluminación no controlada.
En otros trabajos se aborda el problema de control de calidad bajo un paradigma de diagnóstico en donde, por medio de técnicas de visión por computador por caracterización de textura, se identifican errores en un lote de producción. Sin embargo, estos solo se concentran en la segmentación del área afectada, por lo tanto el método sufre problemas con datos muy alejados a los valores de referencia [20]-[23].
Por otro lado, existen métodos basados en técnicas de aprendizaje de máquina que buscan patrones de textura dada una imagen de entrada. Si bien estos métodos logran agrupar un conjunto de pixeles, en una respectiva textura, este no puede ser denominado como un proceso de clasificación, sino como un problema de segmentación. Lo anterior porque repite el enfoque de los métodos anteriores, es decir en la literatura, se ha abordado tradicionalmente este problema de control de calidad como un paradigma de asignación de etiquetas, y no bajo un enfoque de comparación dado un patrón [24]-[31]. Otra estrategia busca, por medio de un modelo de aprendizaje de máquinas, seleccionar productos textiles; sin embargo, la documentación es limitada y los estudios realizados son exploratorios [12]. En este trabajo se propone aplicar técnicas de aprendizaje supervisado para clasificar productos textiles y caracterización espacio-frecuencia para la detección automática de tejidos terminados, utilizando imágenes digitales. El método involucra la construcción de una base de datos anotada con diez tipos de telas. A este conjunto de datos se le extrae las características relevantes por medio de FFT- (Fast Fourier Transform), Wavelet y la Transformada corta en espacio de Fourier SSFFT (Short Space Fast Fourier Transform) [18]-[19]. Por medio de estos, se evalúan tres métodos del estado del arte utilizados para clasificar datos, como son RNA, SVM y GP. Todo esto con el fin de determinar el desempeño de la metodología, dado un cambio en el modelo de aprendizaje.
Este trabajo se organiza de la siguiente manera, por etapas:
- Sección 1: Revisión del estado del arte en identificación de patrones, en productos textiles.
- Sección 2: Materiales y Métodos, el cual consta de una etapa para la construcción de una base de datos anotada, otra de extracción de características y otra de entrenamiento y clasificación de métodos de aprendizaje de máquina.
- Sección 3: Análisis y Resultados, en donde se tiene como objetivo la validación de los métodos propuestos.
- Sección 4: Conclusiones, en la que se busca determinar el comportamiento de estos métodos, para el problema específico de identificación de productos textiles.
2. ESTADO DEL ARTE
La industria textil es una de las que más genera ingresos a nivel mundial [20], pese a esto, también produce grandes pérdidas debido a los defectos de sus textiles. Generalmente, la calidad de las telas producidas es evaluada por un inspector humano que, debido a factores como cansancio, falta de tiempo, errores propios, entre otros, califica como aprobados un gran porcentaje de productos que contienen imperfectos [21]. La solución a este problema se ha planteado desde el área de reconocimiento de patrones y el procesamiento de imágenes digitales.
Los enfoques clásicos de reconocimiento patrones en imágenes digitales, utilizan una gran variedad de técnicas de caracterización, resaltándose como las más importantes el color, la forma y la textura. Las representaciones de color como los espacios RGB, CMYK, LAB, entre otros, permiten detectar patrones en una escena bajo las diferencias de color que cada objeto pueda tener en la escena; este tipo de enfoques son robustos frente a la deformación y oclusiones parciales. Sin embargo, al existir cambios de iluminación en la escena, los descriptores de color comienzan a presentar inconvenientes debido a que son sensibles a las variaciones fotométricas [19]. Otros enfoques clásicos como los descriptores SIFT, SURF, extraen las características morfológicas del objeto sin que las variaciones fotométrcas de la escena afecten el rendimiento de estas técnicas, pero al presentarse cambios en la forma del objeto, se pueden generar problemas en la clasificación, ya que estos descriptores no son aptos frente a oclusiones parciales o deformaciones del objeto [10].
Para clasificar los colores de la escena por clase, se utilizan métodos de aprendizaje de máquinas como redes neuronales artificiales multi-clase RNA, presentando aceptables rendimientos computacionales. Los métodos de agrupamiento muestran resultados satisfactorios, siempre y cuando no se presenten dependencias entre las dimensiones de representación. Otros enfoques como las máquinas de soporte vectorial - SVM, clasificador bayesiano lineal, procesos Gaussianos, entre otros, ofrecen grandes ventajas para modelar grandes volúmenes de información, pero su costo computacional es alto [32],[6].
Específicamente en trabajos de identificación automática de telas se han propuesto diversos métodos cuyo objetivo principal es encontrar defectos en las producidas como: la segmentación de una imagen de alta definición del producto a inspeccionar, para su posterior procesamiento, mediante técnicas de color; filtros de media adaptativos; y clasificación a través del uso de Redes Neuronales. De esta manera se obtienen resultados cuyo porcentaje de acierto varía entre 70 % y 93 % [20],[33].
También se han utilizado técnicas que buscan el análisis del producto mediante la observación de sus componentes de frecuencia [7]-[9],[12]. La Transformada de Fourier, en su variación discreta (DFT), es planteada como herramienta de apoyo para un sistema autónomo de búsqueda y detección de defectos en productos, trabajando mediante la extracción de características a través de la correlación cruzada para mejorar los resultados de la examinación de estructura frecuencial, del material probado [8],[21],[29]-[30].
Métodos que combinan factores como frecuencia estadística y espacial combinada, de resolución múltiple; matriz de campo aleatorio de Markov; matrices de nivel de grises; co-ocurrencia; entre otros; también han sido formulados como solución a la problemática de la detección de errores en productos textiles, obteniendo resultados de hasta el 96,6 % por cada 25 muestras [22],[27].
Metodologías basadas en Bandas Regulares, cuyo fin es analizar el patrón de textura, mediante el cambio de la intensidad del píxel; filtrado con Wavelet de Gabor, realizando un análisis morfológico; análisis de textura con Transformada Wavelet y redes neuronales LVQ, efectuando la evaluación de los materiales según técnicas de densidad Gaussiana y segmentación; y visión por computador y análisis digital de imágenes. Todas estas también han sido utilizadas en la búsqueda de un desenlace a esta problemática, sin embargo, a pesar de que algunas de estas metodologías presenten resultados correctos hasta del 99,4 %, otras tantas difícilmente alcanzan sobrepasar el umbral de 80 % de acierto [24]-[28].
La combinación de sistemas adaptativos de deducciones borrosas, basado en neuronas (ANFIS, por sus siglas en inglés) y Transformada Wavelet, han sido objeto de implementación, pero no han obtenido resultados mayores al 73 % de acierto. Otra combinación puesta a prueba, la convergencia de redes neuronales y Transformada Wavelet, obtuvo resultados similares a los primeros obtenidos [12],[25]-[26].
También se presenta un estudio para la detección de textiles empleando las características espaciales de textura GLCM - (Grey Level Co-Occurrence Matrix), GLRLM (Gray Level Difference Matrix) y NGLDM (Neighboring Gray Level Dependence Matrix), y Máquinas de Soporte Vectorial. Aunque los resultados de este trabajo son porcentajes de acierto mayores al 80 %, se considera que no es un porcentaje apto para considerar fiable la metodología, además de ser un número bajo de telas a detectar, solo con cinco clases [6].
3. MATERIALES Y MÉTODOS
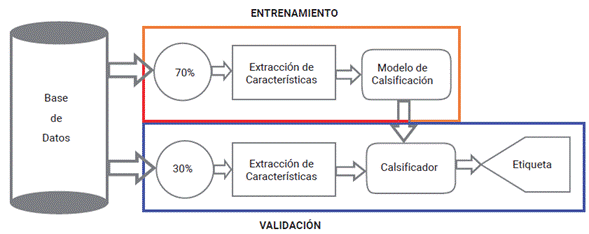
En esta sección se enseña la estructura metodológica de trabajo, la cual está compuesta por tres procesos. En primer lugar, se tiene el conjunto de imágenes anotadas a clasificar (base de datos); en segundo, una etapa que tiene como objetivo la extracción de características de cada imagen, utilizando descriptores de espacio frecuencia y parámetros estadísticos; y por último, una etapa de entrenamiento y validación que determina la clase de cada observación. En la figura 1, se enseña la metodología en diagrama de bloques.
3.1 Construcción base de datos
En el estado del arte existen diferentes bases de datos con imágenes de variación de texturas y productos textiles, tales como imágenes con arbustos, nubes, piedras, vidrios, arena, textiles, entre otros [34]-[35]. Específicamente, las bases de datos estándar para la inspección de productos textiles presentan el inconveniente de no estar disponibles, lo cual restringe la réplica y la comparación con trabajos similares. Por otro lado, estás se utilizan para la identificación de errores en el producto terminado, lo cual contrasta con el enfoque de este trabajo, el cual busca la selección automática del tejido [36].
Otra limitación, reportada en trabajos del estado del arte, es el incumplimiento de las características de anotación requeridas y la cantidad de muestras necesarias por clase, que debe tener la base de datos para asegurar validación estadística en los resultados. Además, las bases de datos comunes sólo consideran un tipo de tejido, lo anterior naturalmente restringe el comportamiento de la metodología para diferentes productos textiles. Por lo tanto, se realiza la construcción de una base de datos anotada que cumpla con estas características requeridas, por este trabajo.
Para la captura de las imágenes, se utilizó un teléfono inteligente con cámara digital de resolución de 1080 x 1920 Mpx; la base de datos se conforma de diez telas comunes, con diferentes patrones en el cocido, lo anterior con el propósito de observar el aporte de cada descriptor. Para cada clase de tela se capturaron 100 imágenes, obteniendo un total de 1.000 fotografías; se resalta que estas capturas se realizaron en diferentes momentos y sin un entorno controlado de iluminación, además no se asume calibración de la cámara. En la figura 2 se resumen las diferentes clases de telas.
3.2 Extracción de características
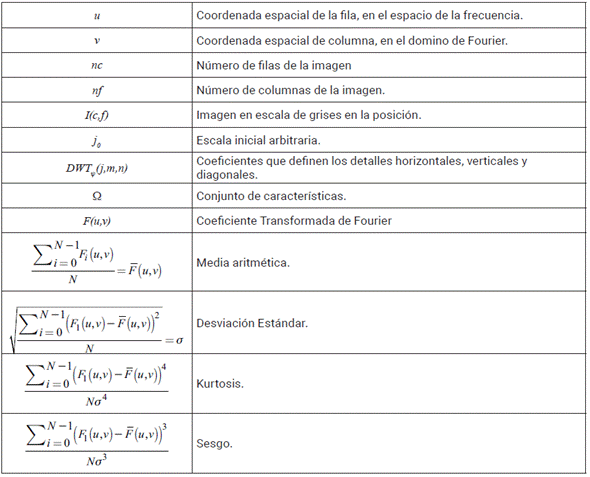
Este proceso se inicia transformando cada imagen de la base de datos a escala de grises, debido a que en un análisis de textura el color es irrelevante. Luego, esta es transportada a un dominio de frecuencia, utilizando la Transformada Rápida de Fourier, en dos dimensiones (FFT); la Transformada discreta de Wavelet; en dos dimensiones (DWT); y un método propuesto denominado Adaptación de la Transformada corta en tiempo de Fourier para imágenes (SSFT), el cual se propone y evalúa de forma exploratoria. Nótese que la metodología inicia computando un conjunto de coeficientes que describen la imagen real, en el dominio de la frecuencia, para cada uno de los descriptores que hacen parte del análisis. En la tabla 1 se enseña la nomenclatura a utilizar para la descripción de extracción de características [37].
Es de aclarar que el cálculo de parámetros estadísticos es aplicable de igual manera a los coeficientes dwt Ψ ,. Para el análisis acá presentado se ignora el componente imaginario de las transformaciones.
Las transformaciones permiten calcular el espectro y las variaciones de frecuencia de la imagen en escala de grises, las cuales vienen dadas por un vector de coeficientes y dwt Ψ Luego, a partir de este se procede a encontrar los parámetros estadísticos de la transformación, estos son: media, desviación estándar, sesgo y Kurtosis [37]. De esta forma, por cada imagen, la metodología computa un conjunto de características Ω, de dimensiones 4x1, para los descriptores FFT y DWT.
Para el cálculo del descriptor SSFT se procede inicialmente con recortar la fotografía en ventanas cuadradas iguales, tal como se enseña en la figura 3. Luego se aplica la transformación F(u,v) en cada uno de los recortes, obteniendo un vector de coeficientes en el dominio de la frecuencia. Al final se calcula el vector de parámetros estadísticos, el cual tiene dimensión 4Lx1 donde L es el número de ventanas cuadradas de la imagen.
3.3 Entrenamiento y clasificación
En esta etapa las características entregadas por los diferentes descriptores y sus respectivas etiquetas son dadas al clasificador, el 70 % de los datos son utilizados para el entrenamiento, el restante para validación, fraccionados aleatoriamente por medio de una distribución Gaussiana. La validación se realiza por medio de un experimento de MonteCarlo con el propósito de cuantificar el desempeño del clasificador. Para este trabajo se utilizaron tres métodos de entrenamiento supervisado: una Red Neuronal Multicapa (ANN), una Máquina de Soporte Vectorial (SVM) y un Proceso Gaussiano (GP), como modelos de aprendizaje.
Teniendo en cuenta que las SVM son un método de clasificación binario, se implementa la estrategia de clasificación multi-clase Uno vs Todos. Este método cuenta con el algoritmo de optimización mínima secuencial (OMS) para el entrenamiento del modelo [38]. Con el fin de realizar un análisis de separabilidad del espacio de características, se propone el uso de tres Kernels (Lineal, Polinomial y Gaussiano con radio adaptativo), para lograr la implementación de este algoritmo se utiliza la función Fitcecoc de Matlab® y para la clasificación con el método binario GP, se implementa una estrategia uno vs todos [37]. Al igual que el método anterior, se propone el uso de dos Kernels (Gaussiano y Exponencial cuadrado). Con el objetivo de lograr la implementación, se utiliza el toolbox GPML Matlab® versión 4.1 usando como método de inferencia una regresión con probabilidad Gaussiana [8]; para la ANN se utiliza el algoritmo Backpropagation con dos capas ocultas y 20 neuronas por capa, la selección de parámetros se realiza con la heurística del mejor desempeño.
Finalmente, el criterio de convergencia del algoritmo de Montecarlo, es el cálculo de similitud provisto por la distancia diag(k)-dia g(k-1) <0.001, donde diag(k) es el vector generado por la diagonal de la matriz de confusión y k es el valor de iteración actual. Las estadísticas obtenidas en el experimento consisten en el cálculo de la matriz de confusión, y el comportamiento promedio de la tasa de éxito, y su desviación estándar.
Con el objetivo de realizar comparaciones metodológicas y cuantificar el aporte de este trabajo, se propone aplicar variaciones a los modelos de aprendizaje de máquinas incluyendo el uso de Kernels Lineales, Gaussianos y Polinomiales. Además de comparar un instrumento de caracterización de textura del estado del arte como lo es SFTA (Segmentation-based Fractal Texture Analysis) [9].
4. ANÁLISIS Y RESULTADOS
Debido a la cantidad de experimentos realizados, solo se documentan las diagonales de la matriz de confusión correspondientes al porcentaje de acierto de cada clase. En las tablas 2, 3 y 4 se enseñan los resultados de identificación para el caso de las SVM el GP, en un experimento de Montecarlo variando la función de covarianza y el tipo de descriptor. En estas se presenta el desempeño de acierto promedio, que consiste en calcular el valor medio del vector de etiquetas resultante de la matriz de confusión, tal y como se puede observar al final de las tablas 2, 3 y 4.
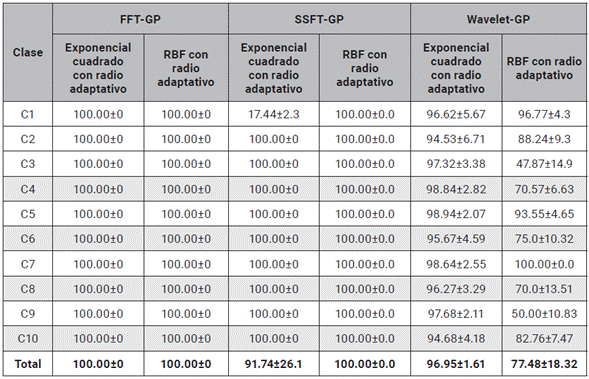
Tabla 2 Diagonal principal de las matrices de confusión de todos los métodos FFT Y SSFT implementados utilizando SVM.
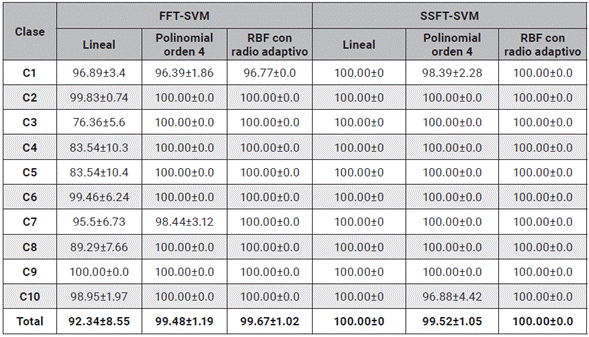
Tabla 3 Diagonal principal de las matrices de confusión de todos los métodos Wavelet y SFTA implementados utilizando SVM.
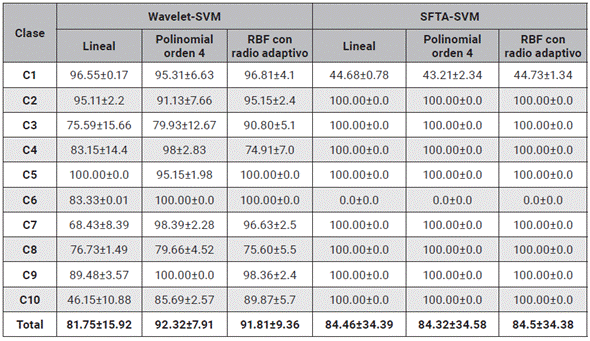
En las tablas 2 y 3 se evidencia el resultado de los experimentos de Montecarlo utilizando el enfoque de máquinas de soporte vectorial (SVM). Se puede observar que para este conjunto de experimentos se utilizan tres kernels (Lineal, Polinomial y Gaussiano Radial -RBF) y se computan los desempeños de acierto promedio. De las tablas 2 y 3 se puede ver un alto rendimiento para la detección de las diferentes telas, con porcentajes de acierto mayores al 75 %, para los diferentes experimentos propuestos. Se exceptúan de este análisis el kernel lineal con Wavelet y el Kernel lineal con SFTA, donde se obtuvieron los desempeños más inferiores (46.15±10.88 %, 44.73±1.34 %). Se puede observar que en general la utilización de un kernel RBF con radio adaptativo permite, en la separación de los datos, obtener los mayores rendimientos (FFT=99.67±1.02 %, SSFT=100.00±0.0 % y Wavelet=91.81±9.36 %). También se percibe que el kernel lineal evidencia los desempeños más bajos (FFT=92.34±8.55 % y Wavelet=81.75±15.92 %), sin embargo, se resalta que este enfoque presenta un rendimiento del 100 % utilizando la SSFT. El método Wavelet presenta porcentajes de acierto confiables del 90 %, sin embargo, se observa que las clases 4, 6, 8 y 10 presentan bajos rendimientos menores al 85 %, lo cual indica que la metodología no da garantía para detectar este tipo de patrones. Los resultados sugieren que el descriptor SFTA con SVM no es un candidato apto para la identificación de texturas, ya que no permite extraer características relevantes que permitan al clasificador computar un plano de separación para cada una de las clases, esto se puede observar en la tabla 3 donde la clase 3 presenta desempeños del 0 %.
Para el caso del GP al igual que en las SVM, se propone el uso de kernels para la mejora en la separación de los datos. De este se resalta que al hacer pruebas con los kernels lineal y polinomial, los desempeños de clasificación fueron no confiables con aciertos menores al 50 %, concluyendo que para este tipo de clasificador no garantizan una correcta separación y por el contrario, traslapan el espacio de entrenamiento. Por lo tanto, solo se documentan los resultados obtenidos con el kernels Exponencial cuadrado con radio adaptativo y Gaussiano Radial -RBF.
De la tabla 4 se aprecia que el GP genera un alto rendimiento para la detección estos patrones, con porcentajes de acierto mayores al 90 % para los diferentes experimentos propuestos. Se exceptúan de este resultado el método de caracterización SSFT con kernel Exponencial cuadrado, con un porcentaje de acierto del 17.44±2.33 % para la clase 1 y el método Wavelet con kernel RBF con bajo desempeño, para la mayoría de sus clases. Al igual que en los experimentos con SVM, se puede observar que el uso de un kernel RBF mejora la separación de los datos, obteniendo los mejores desempeños (FFT=100 %, SSFT=100.00 %). Sin embargo, se puede ver que en la metodología Wavelet, el desempeño 78.48±18.32 %, es un porcentaje bajo para garantizar confiabilidad del método. Esto ayuda a reafirmar, al igual que en los experimentos anteriores, que el método caracterización con Transformada Wavelet no es adecuado para garantizar una correcta clasificación de los datos. Por razones similares no se reporta la combinación del método SFTA con GP.
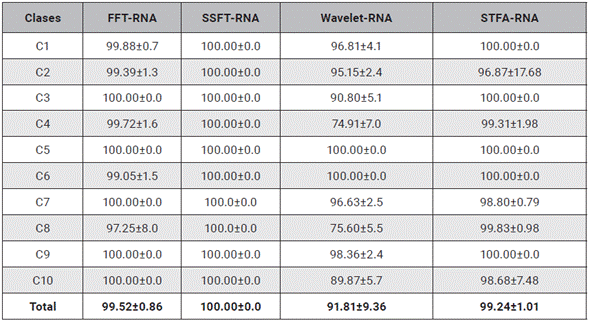
En la tabla 5 se enseña el cotejo entre los diferentes descriptores utilizados con el clasificador RNA, obteniendo un desempeño disperso comparado con las SVM y el GP. Esto se puede apreciar en Wavelet-RNA, en las clases cuatro y ocho que presentan un porcentaje de acierto menor al 80 % y se muestra que el mejor desempeño lo tiene la SSFT-RNA. De la tabla 5 se evidencia que los métodos con mejor desempeño son los que utilizan el descriptor SSFT, logrando un desempeño ideal del 100 % para la base de datos propuesta; aunque estos desempeños son ideales, se observa que los métodos de caracterización que utilizan la FFT, presentan desempeños similares del 99 %, por lo tanto, se puede ver que el método es confiable. También se evidencia que la transformada Wavelet tiene un desempeño mayor al 90 %, sin embargo la desviación estándar es grande, lo cual muestra que el método presenta problemas para ser utilizado como descriptor de textura, en este tipo de telas, tal y como se presenta en los otros métodos de clasificación. Por otro lado, el método de caracterización SFTA brinda un espacio de separación adecuado para clasificar con RNA, esto se observa al obtener un desempeño promedio de 99.24±1.01 %. Cabe resaltar que este descriptor, con un clasificador SVM, no presentó un desempeño adecuado, por lo que este clasificador muestra dependencia del método de aprendizaje escogido.
Al comparar los desempeños de las diferentes metodologías se evidencia que el descriptor SSFT corresponde al de los mejores desempeños con porcentajes de acierto del 100 %, esto muestra que la caracterización local de frecuencias, es adecuada para la caracterización de patrones en productos textiles. También es importante resaltar que la FFT presenta resultados de acierto confiables del 99 % lo que permite concluir que es un método estadísticamente similar a la SSFT.
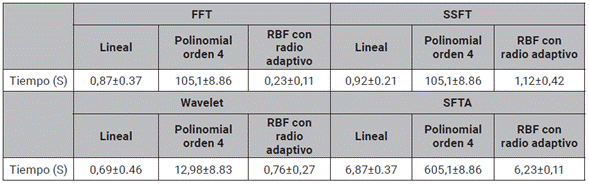
A continuación, se procede a realizar un estudio de costo computacional de cada una de las variantes que hacen parte del análisis. Para ello se cuantifica la cantidad de tiempo requerido para computar cada descriptor y una iteración de Montecarlo utilizando SVM, GP y RNA (ver tabla 6, 7 y 8), cabe resaltar que estos experimentos se llevaron a cabo en un computador con 16GB de RAM y un procesador Core I7.
La tabla 7 muestra que el método de caracterización con transformada FFT presenta el menor costo computacional, al obtener tiempos de ejecución de 0,23±0,11 [s]. Por otro lado el descriptor SSFT requiere de un costo computacional mayor. Esto se debe a que el método SSFT aumenta considerablemente el número de dimensiones de características. Aunque este consume una cantidad de recursos considerable, es importante resaltar que cuando se utiliza un kernel lineal, este tiempo es relativamente bajo (0,92±0.21).
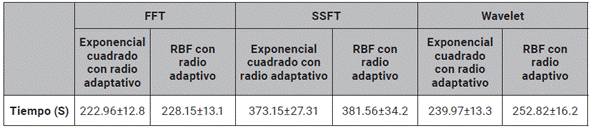
En la tabla 8 se observa el tiempo de cómputo en los experimentos de Montecarlo con el método de clasificación GP. Aunque esta variante presenta resultados confiables en su desempeño, los recursos que requiere para su ejecución son elevados, comparados con los requeridos por la SVM.
Para las RNA se observa un comportamiento similar al obtenido por la SVM, respecto a la comparación entre descriptores. También cabe resaltar que, en general, la SVM presento menores tiempo de computo que la RNA (ver tabla 9).
5. CONCLUSIONES
Se realizó un estudio detallado de la caracterización espacio frecuencia para la identificación de patrones de textura, utilizando métodos clásicos de aprendizaje supervisado como como SVM, GP y RNA. Este enfoque permite hacer uso de los patrones espaciales de textura, de una imagen digital, y ser caracterizados por medio transformadas como FFT, SSFT y Wavelet, obteniendo un espacio de representación que cuantifica las variaciones de frecuencia y son descritos por momentos estadísticos, la media, la desviación estándar, el sesgo y la Kurtosis.
Por medio de estos procesos se logran resultados confiables mayores al 90 % de eficiencia, para una base de datos anotada de 10 telas diferentes. En este trabajo se consigue cuantificar el rendimiento de algunos métodos de aprendizaje de máquinas supervisado, comunes en la literatura (SVM, RNA y GP), para un problema de selección de productos textiles; lo anterior es muy importante debido a la limitada documentación presente en la literatura que aborda el problema de inspección de textiles, bajo un paradigma de clasificación.
Basados en los resultados se logra identificar que el éxito se asocia al Kernel utilizado; esto indica que su elección permite mejorar la eficiencia en la identificación del patrón. Se resalta que la representación con un Kernel lineal genera bajos rendimientos tal y como se observa en las tablas 2, 3 y 4. Sin embargo para el caso de clasificación SVM generan resultado de alta confiabilidad.
Los métodos de SSFT-SVM, SSFT-GP y SSFT-RNA lograron un desempeño del 100 % demostrando ser unas metodologías adecuada para este tipo de aplicaciones. Sin embargo, se debe tener en cuenta el alto costo computacional asociado a la alta dimensión del descriptor.
En la Transformada Wavelet con SVM y RNA, el desempeño es mayor al 90 %, sin embargo, la incertidumbre es alta, ya que muestra un rango que no es aceptable para considerar este descriptor en una aplicación real. Esta observación también se puede apoyar en los diferentes Kernels, donde ninguno de los experimentos que realizó con este tipo de descriptor, logró que todas las clases tuvieran porcentaje de acierto mayores al 90 % tal y como se observa en las tablas 2, 3, 4 y 5.
Por último, el resultado que se obtuvo con el método de la FFT con SVM y RNA, presentaron un desempeño del 99 %, con un mínimo error y un costo computacional significativamente menor respecto a los demás descriptores, por lo tanto, se puede considerar que este es un candidato para ser implementado, debido a que estadísticamente presenta un funcionamiento similar al del mejor rendimiento (SSFT), con un costo de cómputo razonable.
Por otro lado, se puede observar que el método de caracterización SFTA brinda un espacio de separación adecuado para identificar productos textiles utilizando RNA, lo cual se evidenció al obtener un desempeño promedio de 99.24±1.01 %. Por esta razón este descriptor no debe ser descartado para la caracterización de este tipo de texturas, aunque con otros tipos de clasificadores su desempeño sea bajo (SVM y GP).