Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Facultad Nacional de Agronomía Medellín
Print version ISSN 0304-2847
Rev. Fac. Nac. Agron. Medellín vol.59 no.1 Medellín Jan./June 2006
EFECTO DE LA VARIABILIDAD SISTEMÁTICA DE LA PRODUCCIÓN DE FRÍJOL EN EXPERIMENTOS DE FERTILIZACIÓN. SEGUNDA SIEMBRA.
EFFECT OF SYSTEMATIC VARIABILITY IN FERTILIZATION EXPERIMENTS WITH BEANS. SECOND SOWING
Daniel Francisco Jaramillo Jaramillo1
1 Profesor Titular. Universidad Nacional de Colombia, Sede Medellín. Facultad de Ciencias. A.A. 3840. Medellín, Colombia. <djaramal@unalmed.edu.co>
Recibido: Abril 28 de 2005; aceptado: Noviembre 24 de 2005.
RESUMEN
Se evaluó el impacto que podía tener la variabilidad sistemática de la producción de dos variedades de fríjol, mediante análisis de tendencia y de semivariografía, sobre los resultados de los análisis de varianza realizados en un experimento de fertilización orgánica y con microorganismos, en una segunda siembra, en un diseño de bloques completos al azar con siete tratamientos y cuatro replicaciones, ubicado en el Centro de Investigación La Selva, de CORPOICA, municipio de Rionegro, Oriente Antioqueño-Colombia.
Se presentó un efecto diferencial en el comportamiento de las dos variedades de fríjol. En la variedad ICA Viboral, los anavas mostraron que sí hubo efecto significativo de los tratamientos sobre la producción. En la variedad CORPOICA 106 no se presentó variabilidad espacial de la producción y no hubo efecto significativo de los tratamientos sobre ella, ni con los datos originales ni con los residuales de los análisis de tendencia. El efecto específico de cada tratamiento en el análisis de varianza se distorsiona al ir eliminando componentes espaciales de la variabilidad.
Con lo observado en este estudio y en el de la primera siembra (Jaramillo, 2005) cabe recomendar que en los sitios que se van a utilizar para investigación agropecuaria, se hagan estudios detallados de suelos, en los cuales se incluya el conocimiento de su variabilidad espacial y temporal, de modo que puedan hacerse interpretaciones adecuadas de los experimentos que se conduzcan en ellos.
Palabras claves: Variabilidad espacial, geoestadística, análisis de tendencia, análisis de varianza, diseño experimental, producción de fríjol.
ABSTRACT
An evaluation was made on the impact that systematic variability could have on the production of two varieties of beans, by means of analysis of spatial tendency and semi-variography, on the results of the analyses of variance of an experiment of organic fertilization and with microorganisms in a second sowing. The experimental design was a complete random blocks design with 7 treatments and 4 replications, located in La Selva Research Center of CORPOICA, Rionegro, eastern Antioquia – Colombia .
A differential effect was found in the varieties of beans. In the ICA Viboral variety, the analysis conducted showed significant effects of the treatments on production. In the variety CORPOICA 106 there was no spatial variability, nor was there any significant effect of the treatments or of the blocks, with either the original data or with the residual analyses of spatial tendency and variability. The specific effect of each treatment in the analysis of variance was distorted when the components of the variability were eliminated.
With the observations in this study, it is possible to recommend that in sites that are going to be used for farming research, detailed soil surveys should be made, in which the knowledge of spatial variability is included, in order to be able to make proper interpretations of the tests conducted in them.
Key words: Spatial variability, geostatistics; analysis of tendency, analysis of variance, experimental design, production of beans.
 MATERIALES Y MÉTODOS
MATERIALES Y MÉTODOS
 RESULTADOS Y DISCUSIÓN
RESULTADOS Y DISCUSIÓN
 COMENTARIO FINAL
COMENTARIO FINAL
 CONCLUSIONES Y RECOMENDACIONES
CONCLUSIONES Y RECOMENDACIONES
 AGRADECIMIENTO
AGRADECIMIENTO
 BIBLIOGRAFÍA
BIBLIOGRAFÍA
El modelo estadístico lineal que define un diseño experimental en bloques completos al azar, con i tratamientos, j bloques y k unidades experimentales, es:
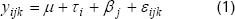
Donde:
yijk es la ijk-ésima observación.
m es el promedio general de la población.
ti s el efecto del i-ésimo tratamiento del experimento.
bj representa el efecto del j-ésimo bloque del experimento.
eijk es el componente aleatorio del error experimental.
Cuando se hace una regresión lineal simple, el modelo estadístico lineal que define una observación yi, en función de una variable de regresión xi, es:
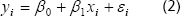
Donde b0 y b1 son los parámetros de la recta y son constantes y desconocidos y ei es el componente aleatorio del error experimental.
Si el análisis de regresión es lineal y cuadrático, el modelo de la Ecuación [2] se convierte en:
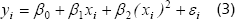
En todos los casos mencionados anteriormente, los errores deben tener una distribución normal (N), estar independientemente distribuidos (ID), tener una media igual a cero y una varianza constante, pero desconocida, s2. Éstos son los supuestos en que se basan los análisis de varianza y de regresión y el incumplimiento de alguno de ellos puede afectar el nivel de significancia y/o la sensibilidad de las pruebas para detectar diferencias reales entre los tratamientos (Gómez 1997). Estos supuestos se pueden representar, según Montgomery 1991, como sigue:
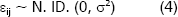
El error experimental lo define Gómez 1997, como aquel conjunto de variaciones en los resultados debidas a factores no conocidos o no controlados en el experimento. Para garantizar la independencia se recomienda la aleatorización y para reducir el tamaño y el tipo de error, se recomienda hacer un buen número de replicaciones en los tratamientos.
Montgomery 1991, establece como pilares fundamentales del diseño experimental la inclusión de replicaciones, con lo que se pretende conocer el error experimental y mejorar la precisión de la estimación del efecto de los factores que se estudian; la aleatorización, para garantizar la independencia de las observaciones o los errores y el análisis por bloques, para incrementar la precisión del experimento.
Martínez 1994 y Schabenberger y Pierce 2002, sostienen que la aleatorización de los tratamientos, en las unidades experimentales, debe ser capaz de neutralizar el efecto de la correlación espacial que se pueda presentar entre unidades experimentales vecinas, la que puede invalidar los resultados de los análisis de varianza que se realicen con ellas, debido a que los supuestos en que descansan estos análisis no se cumplen.
Como se mencionó anteriormente, el error experimental recoge todas las variaciones que se presentaron en el experimento y que no fueron controladas con el diseño experimental. Aunque en un determinado experimento las causas del error experimental no se conozcan, las variaciones producidas por ellas pueden ser aleatorias o sistemáticas. Upchurch y Edmonds 1991, señalan que cuando la variabilidad no puede relacionarse con causas conocidas, se define como variabilidad aleatoria o debida al azar; mientras que si la variabilidad puede ser atribuida a causas conocidas, entendibles y predecibles, se denomina variabilidad sistemática. A su vez, Samra et al. 1990, fraccionan la variabilidad sistemática en dos componentes: uno de tendencia relacionada con la localización de las unidades experimentales y que puede llamarse tendencia espacial (T), y otro de dependencia espacial (DE). Con los conceptos anteriores, la variabilidad total puede expresarse así:
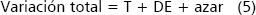
La dependencia espacial se caracteriza porque las propiedades que la presentan adquieren valores diferentes dependiendo del espaciamiento entre las muestras y/o de la dirección en que ellas sean recolectadas. Cuando este comportamiento está presente, no se satisface el supuesto de independencia de los errores, por lo que los procedimientos de la estadística paramétrica clásica no son adecuados para su estudio.
El efecto de la tendencia puede estudiarse mediante análisis de regresión simple o compuesta (Schabenberger y Pierce 2002) y el de la dependencia espacial se estudia mediante técnicas de la geoestadística, cuya herramienta básica es el análisis de semivariografía. Para las variables regionalizadas, es decir, que presentan dependencia espacial, se supone que hay una distribución normal (Cressie 1984) de los datos y, además, que hay estacionaridad de segundo orden. La estacionaridad de segundo orden, según Cressie 1984 y Upchurch y Edmonds 1991, se puede suplir con la hipótesis intrínseca, que sólo es violada cuando hay una tendencia obvia en la variable regionalizada. El producto fundamental del análisis de semivariografía o de semivarianza es el semivariograma, una gráfica que relaciona la semivarianza de las observaciones de pares de puntos que están separados a una determinada distancia, con los incrementos en la distancia de separación entre puntos. La semivarianza se estima con la siguiente expresión, tomada de Upchurch y Edmonds 1991:
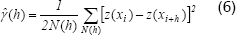
Donde:
(h) es la semivarianza
N es el número de pares de puntos separados por una determinada distancia h
z(xi) es el valor de la variable en una localidad x
z(xi+h) es el valor que toma la variable en otra localidad ubicada a una distancia h de x
Con los diseños experimentales, toda la variabilidad que no es debida a los factores que se están estudiando, se asume que es recogida por el error experimental pero, como se ha visto en párrafos anteriores, no toda esa variabilidad es aleatoria o debida al azar: puede tener un componente de variabilidad sistemática (Ecuación 5) que, en el caso de que ella sea espacial, se puede violar el supuesto de independencia en las observaciones. Igual sucede con los análisis de regresión: no toda la variabilidad que asume el error es, necesariamente, aleatoria y puede haber en ella un componente de dependencia espacial.
Para involucrar el efecto de la variabilidad sistemática en los modelos estadísticos que definen el análisis de varianza de un diseño de bloques completos al azar, con base en lo que se ha presentado hasta aquí, se puede plantear el siguiente modelo estadístico:
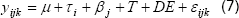
La variabilidad de las propiedades del suelo es una condición inherente al mismo y depende, aparte del tipo de suelo, de la propiedad que se analice. Hay menor variabilidad en las propiedades del suelo en su condición natural, que cuando ha estado sometido a uso. Aquellas propiedades que más se alteran por el manejo del suelo serán las que presenten la mayor variabilidad (Ovalles 1992 y Paz-González Vieira y Taboada Castro 2000).
El uso histórico del suelo tiene grandes efectos sobre la variabilidad de sus propiedades. Diferencias en el manejo de los fertilizantes y de los abonos orgánicos, tanto en el tipo como en la forma de aplicarlos, generan diferencias en la variabilidad de los contenidos de nutrientes en el suelo. Los cambios en el laboreo también producen efectos similares (Cambardella et al. 1994, Mallarino 1996, Cambardella y Karlen 1999 y Paz-González,Vieira y Taboada Castro 2000).
Ovalles y Comerma 1991, sostienen que en la selección de sitios experimentales es indispensable tener una alta homogeneidad en las propiedades de los suelos relacionadas con lo que se va a investigar. Además, que el conocimiento de la variabilidad del suelo es requisito indispensable para seleccionar tanto el sitio como el diseño experimental y recomiendan las técnicas geoestadísticas como las mejores para determinar el tamaño, la localización y la orientación de las parcelas experimentales.
Conociendo la variabilidad espacial que se presente en las unidades experimentales se puede hacer una mejor interpretación de los resultados que se obtengan. Puede presentarse el caso en que la interpretación de los resultados cambie drásticamente luego de considerar el efecto de la variabilidad espacial sobre ellos, como lo demostraron Bhatti et al. 1991.
Saldarriaga 2002, encontró dependencia espacial en la producción de fruta fresca de palma de aceite en un lote experimental en los Llanos Orientales de Colombia, donde se estaban evaluando varios sistemas de adecuación de tierras para ese cultivo. Al hacer los análisis de varianza sin eliminar la variabilidad espacial, para 10 ciclos de cosecha, se presentó diferencia significativa entre adecuaciones en 8 de los 10 ciclos, mientras que eliminando dicha dependencia, sólo se conservó la diferencia significativa entre adecuaciones en uno de los 10 ciclos de producción evaluados.
Antes de este trabajo, se realizó una primera siembra, en la cual se evaluó el efecto de 7 tratamientos de fertilización orgánica y con microorganismos, sobre la producción de las variedades de fríjol ICA Viboral y CORPOICA 106 (Jaramillo 2005). En ese trabajo se encontró un efecto diferencial, por variedad de fríjol, de la variabilidad sistemática sobre los resultados de los análisis de varianza. En la variedad ICA Viboral, el ANAVA hecho con los datos originales no mostró efectos significativos de los tratamientos sobre la producción pero, al quitar los componentes de tendencia y de variabilidad espacial, el ANAVA detectó que sí había efecto altamente significativo de los tratamientos sobre la producción. En la variedad CORPOICA 106 no se presentó efecto significativo de los tratamientos, ni con los datos originales, ni con los residuales de los análisis de tendencia y de variabilidad espacial.
En varios de los estudios citados anteriormente se observa cómo la variabilidad espacial del suelo puede enmascarar los efectos de los tratamientos que se están estudiando, llevando a conclusiones erróneas acerca de la necesidad o no de llevar a cabo alguna práctica de manejo de los cultivos.
Con el presente estudio se pretende establecer si persiste el efecto de la variabilidad sistemática sobre los resultados de los análisis de varianza hechos en un experimento de fertilización orgánica y con microorganismos, en dos variedades de fríjol, en una segunda siembra hecha exactamente con igual distribución y en el mismo lote experimental en que se hizo la primera, con un diseño de bloques completos al azar.
Localización. El trabajo se llevó a cabo en un lote experimental del Centro de Investigación La Selva de CORPOICA, ubicado en el sector de Llano Grande, municipio de Rionegro, oriente Antioqueño-Colombia. Se accede al Centro, desde Medellín, por una carretera pavimentada de 27 km de longitud, aproximadamente (Figura 1).
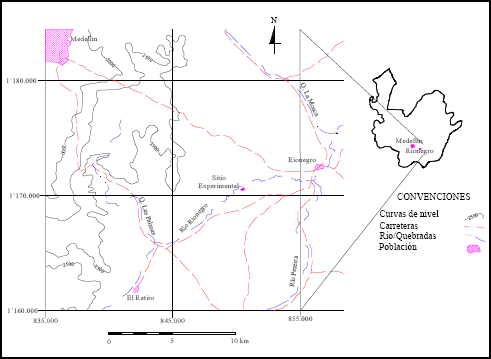
Figura 1. Localización del C.I. “La Selva” – CORPOICA. Rionegro, Oriente Antioqueño-Colombia.
El lote se encuentra localizado sobre una terraza aluvial baja del río Rionegro, plana, con pendiente menor al 3%, pobremente drenada. El suelo se ha desarrollado a partir de cenizas volcánicas que están recubriendo un aluvión fino y se clasificó como Typic Endoaquand.
Materiales experimentales. El experimento se hizo con dos variedades volubles de fríjol: Fríjol ICA Viboral y Fríjol CORPOICA 106. Los materiales fueron sembrados en dos parcelas experimentales contiguas de 16 m x 35 m cada una. Diseño experimental. Para cada una de las variedades de fríjol utilizadas se diseñó un experimento con arreglo en bloques completos al azar de siete tratamientos con cuatro replicaciones. La unidad experimental correspondió a una parcela compuesta por 4 surcos de 5 m de longitud; la distancia de siembra entre surcos fue de 1 m, y entre plantas, de 25 cm.Las siembras se hicieron en el mismo lote experimental en el que se realizó una primera siembra, con las mismas variedades de fríjol, a la que se le aplicaron directamente los tratamientos de fertilización. Con esta segunda siembra se quiso evaluar si había algún efecto residual de los tratamientos de fertilización que se habían aplicado a la primera siembra, sobre la producción de las dos variedades de fríjol mencionadas anteriormente, por lo que en este ciclo de cosecha no se aplicó ningún fertilizante ni enmienda al cultivo.
La cosecha de este experimento se llevó a cabo 1 año después de que se hizo la aplicación de los tratamientos de fertilización al primer ensayo y habían transcurrido aproximadamente 6 meses desde la cosecha de la primera siembra.
Los tratamientos de fertilización aplicados a la primera siembra y cuyo efecto residual se quería conocer en esta segunda siembra fueron:
- Tratamiento 1 (T1): Corresponde al testigo comercial del agricultor, en el cual se aplicaron 35 g de 10-30-10 m-1 de surco + 200 g de gallinaza m-1 de surco.
- Tratamiento 2 (T2): 200 g de gallinaza m-1 de surco + 20 g de inóculo de micorrizas por planta.
- Tratamiento 3 (T3): 200 g de gallinaza m-1 de surco + 20 g de inóculo de Rhizobium kg-1 de semilla.
- Tratamiento 4 (T4): 200 g de gallinaza m-1 de surco + 50 g de roca fosfórica m-1 de surco.
- Tratamiento 5 (T5): 200 g de gallinaza m-1 de surco + 20 g de inóculo de micorrizas por planta + 20 g de inóculo de Rhizobium kg-1 de semilla.
- Tratamiento 6 (T6): 200 g de gallinaza m-1 de surco + 20 g de inóculo de Rhizobium kg-1 de semilla + 50 g de roca fosfórica m-1 de surco.
- Tratamiento 7 (T7): 20 g de inóculo de micorrizas por planta + 20 g de inóculo de Rhizobium kg-1 de semilla.
Aparte de los tratamientos anteriores, en todas las unidades experimentales se adicionaron 50 g de cal agrícola por metro de surco y, excepto en las unidades experimentales correspondientes al testigo comercial, se aplicaron 20 g de KCl por metro de surco. Para suministrar las micorrizas se utilizó un producto comercial conocido con el nombre de Glomales de Antioquia, el cual ofrece una mezcla de inóculos de hongos de los géneros Acaulospora, Glomus y Scutelospora.
Variables evaluadas. Se midió la producción de grano seco de fríjol (con 14% de humedad, aproximadamente), en el metro central de cada surco, el cual se cosechó por separado en cada replicación y en cada tratamiento. Para el estudio de variabilidad espacial, al punto central de cada surco se le asignaron coordenadas planas (x, y) con base en un origen arbitrario, que georreferenciaron la producción en el respectivo surco cosechado.
Análisis estadísticos. A los datos de producción originales se les hizo inicialmente un análisis exploratorio, para ver su distribución y para detectar posibles desviaciones de los supuestos del análisis de varianza. Luego se hizo un análisis de varianza convencional, seguido de una prueba de comparación de medias de Duncan. A los residuales de este análisis se le chequearon los supuestos de homogeneidad de varianzas (valor p de la prueba de Bartlett o de Levene > 0,05, si los residuales presentaban o no distribución normal, respectivamente) y de normalidad (valor p de la prueba de Shapiro – Wilk > 0,05), como lo recomienda Montgomery 1991. Cuando estos supuestos se cumplían, ahí terminaba el análisis de varianza, pero cuando no, se hacía una transformación de los datos y se repetía el análisis de varianza hasta que se cumplieran tales supuestos. En caso de que no se cumpliera la normalidad se aceptaba que la distribución fuera solamente simétrica.
Terminado el análisis de varianza inicial, se hacia un análisis de tendencia (en este caso, de tendencia espacial porque se relaciona la producción de fríjol con las coordenadas) de los valores originales de producción en cada surco, mediante un análisis de regresión múltiple entre ella y los valores de las coordenadas (x, y), incluyendo la interacción entre las mismas, con un modelo del estilo Producción = a + b(x) + c(y) + d(xy). Si el modelo estudiado resultaba estadísticamente significativo, a los residuales de esta regresión también se les hacía la confirmación de los supuestos. En este caso también se chequeaban los supuestos de normalidad y de homogeneidad de varianza, como se indicó en el párrafo anterior.
Si con el análisis de tendencia se encontraba un modelo de regresión significativo, se utilizaban sus residuales para realizar el análisis de variabilidad espacial que se hace a continuación. Si no había tendencia en los valores de la producción, el análisis de semivariografía se llevaba a cabo con los datos originales o transformados utilizados para el análisis de varianza inicial. Después de este análisis espacial, los supuestos de los residuales también se verificaban como se ha expuesto antes.
Como se quería ver si había efecto de la variabilidad espacial sobre los resultados de los análisis de varianza del experimento, tanto después del análisis de tendencia, como después del análisis de semivariografía, se hicieron los correspondientes análisis de varianza y las comparaciones de las medias respectivas. Después de cada análisis de varianza realizado, se hizo un análisis de los residuales correspondientes para verificar que los supuestos de distribución normal, o por lo menos simétrica, y de igualdad de varianza se cumplían.
Todos los análisis mencionados anteriormente se llevaron a cabo para cada una de las dos variedades de fríjol estudiadas. Los análisis estadísticos se hicieron con ayuda de los programas de computador Statgraphics Plus 5.0 y GS+ 3.1.
Comportamiento general de la producción de fríjol en las dos variedades. Las Figuras 2 y 3 muestran la distribución de la producción en las parcelas experimentales y proporcionan información acerca de la variabilidad de la misma, por tratamiento, en las dos variedades. En la Figura 2 se observa que hay una alta variabilidad de la producción al interior de las replicaciones de los tratamientos: hay diferencias en el tamaño de los círculos que representan la producción por surco dentro de la parcela (el tamaño del círculo es directamente proporcional a la producción).
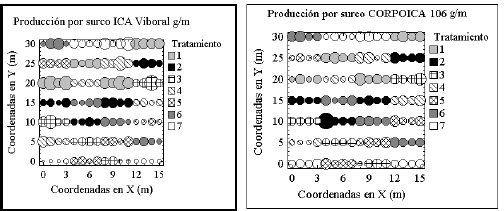
Figura 2. Distribución de la producción de fríjol en las parcelas experimentales, por surco. El tamaño de los círculos es proporcional a la producción.
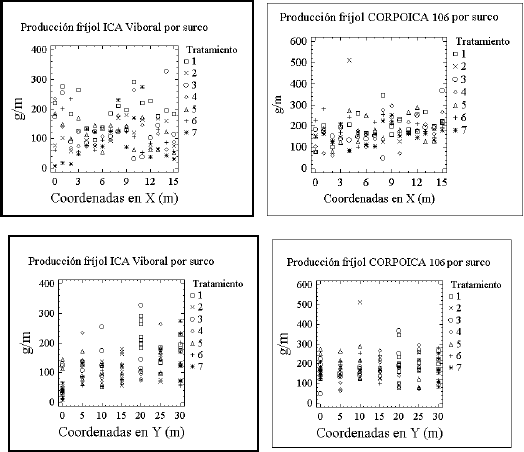
Figura 3. Distribución de los valores de la producción de las dos variedades, por tratamiento, en las parcelas experimentales, teniendo en cuenta la ubicación de los surcos con respecto a las coordenadas.
La distribución de la producción es variable, según la variedad, cuando se mira teniendo en cuenta las coordenadas de las parcelas (Figura 3) y los valores de producción en los tratamientos presentan mayor amplitud en la variedad ICA Viboral que en la CORPOICA 106, en ambas coordenadas. En ninguno de los casos, sin embargo, se aprecia una tendencia espacial bien definida en la distribución de la producción de fríjol en este experimento.
Producción del fríjol ICA Viboral. Una vez realizados los análisis exploratorios de los resultados se procedió a hacer el análisis de tendencia espacial de la producción con los valores originales de ella y aunque se obtuvo un modelo significativo de regresión, sus residuales no cumplieron con ninguno de los supuestos estadísticos por lo que fue necesario hacer varias transformaciones de los datos originales de producción y repetir el análisis de tendencia hasta encontrar un modelo que fuera satisfactorio. Dicho modelo se obtuvo cuando se transformaron los valores de la producción a raíz cuadrada y los resultados de este análisis de tendencia fueron:
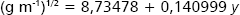
Los estadísticos del modelo anterior fueron: valor p del modelo = 0,0000, R2 = 21,96% y estadístico de Durbin-Watson = 1,87957. Los valores de los supuestos de los residuales de este análisis de tendencia fueron: valor p de Shapiro-Wilk = 0,481749 (distribución normal) y el valor p de Bartlett (porque hubo normalidad en la distribución de los residuales) fue de 0,810661 (varianzas homogéneas). Con los residuales del análisis de tendencia se hizo un análisis de variabilidad espacial que dio los resultados que se exponen en la Tabla 1.
Tabla 1. Parámetros del análisis de variabilidad espacial de los residuales de la tendencia de la producción de fríjol ICA Viboral en el metro central del surco de 5 m de longitud (lag activo = 10 m).
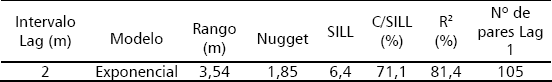
Al observar los resultados de la Tabla 1 se aprecia que hay una alta dependencia espacial de la producción (C/Sill = 71,1 %) y que dicha dependencia es de rango corto ( 3,54 m). En esta segunda siembra se incrementó el efecto de la variabilidad espacial sobre la producción, en comparación con lo encontrado con la misma variedad, en una primera siembra, por Jaramillo 2005; el grado de dependencia es mayor y el rango es menor en la segunda siembra. Lo anterior está confirmando las apreciaciones de Cambardella et al. 1994, Mallarino 1996, Cambardella y Karlen 1996 y PazGonzález et al. 2000, sobre el efecto del uso y del manejo del suelo sobre la variabilidad espacial de sus propiedades y de la producción de lo que en él se cultive.
Luego de terminar los análisis de tendencia y de variabilidad espacial, se llevaron a cabo los respectivos análisis de varianza, cuyos resultados se encuentran en la Tabla 2 y permiten ver que en todos los casos hubo efecto significativo de los tratamientos (aunque en el límite de significancia con los datos originales) sobre la producción de fríjol.
Tabla 2. Resumen de los análisis de varianza realizados para la producción de fríjol ICA Viboral en el metro central de surcos de 5 m de longitud, con datos originales y depurados para algunos efectos espaciales sobre la producción.
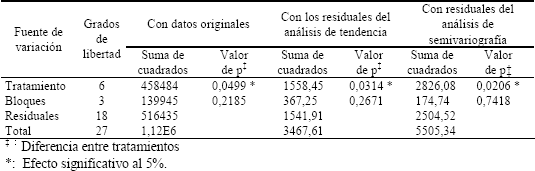
Al hacer la comprobación de los supuestos con los residuales de los ANAVAS realizados, se obtuvo normalidad e igualdad de varianzas en todos ellos: valor p de Shapiro-Wilk de 0,653649, 0,762835 y de 0,65927 y valor p de Bartlett de 0,65676, 0,302775 y de 0,650524, para los análisis de varianza hechos con los datos originales, con los residuales del análisis de tendencia y con los residuales del análisis de semivariografía, respectivamente. Después de los análisis de varianza se hicieron las correspondientes pruebas de comparación de medias por Duncan, las que dieron los resultados que se exponen en la Tabla 3.
Tabla 3. Prueba de Duncan para comparación de medias, con base en los diferentes análisis de varianza realizados para la variedad de fríjol ICA Viboral.
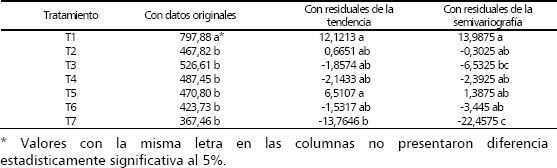
En la comparación de promedios anterior se aprecia que, como en la primera siembra (Jaramillo 2005), el tratamiento 7 es el de menor promedio de producción y que se presentan diferencias en el ordenamiento relativo de los tratamientos en los diferentes ANAVAS hechos.
Teniendo en cuenta los resultados del análisis de variabilidad espacial, también aquí, como en la primera siembra, es posible que se haya violado el supuesto de independencia de los errores, debido a que el rango de la variabilidad espacial es mayor que el espaciamiento que se dejó entre los surcos de las parcelas experimentales, al momento de establecer el experimento. Atendiendo las precisiones que hace Montgomery 1991, acerca de los supuestos que se deben cumplir para que el análisis de varianza se convierta en una prueba exacta para las hipótesis de igualdad de medias en los tratamientos, puede decirse que el comportamiento observado en los análisis de varianza hechos con los datos originales y con los residuales de la tendencia, por no cumplir con el supuesto de la independencia en los errores, no tienen validez y que el única análisis de varianza que es válido, es el que se hizo con los residuales de la semivariografía.
Producción del fríjol CORPOICA 106. Cuando se hizo el análisis de tendencia de la producción original se encontró un modelo que no satisfizo ninguno de los supuestos en sus residuales, por lo que se debieron hacer transformaciones, siendo la mejor la logarítmica base 10. El modelo que finalmente se produjo fue: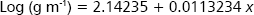
Los estadísticos del modelo de regresión anterior fueron: valor p del modelo = 0,0006, estadístico de Durbin
Watson = 1,76713 y R2 = 9,26 %. Los residuales del análisis de tendencia anterior cumplieron con los supuestos de normalidad: valor p de Shapiro-Wilk = 0,471729 y de igualdad de varianzas: valor p de Bartlett = 0,334912.
El análisis de semivarianza realizado con los residuales del análisis de tendencia (Tabla 4) muestra que no hubo dependencia espacial de la producción de fríjol en esta siembra: modelo de Nugget Puro, es decir, que toda la variabilidad fue aleatoria, situación muy diferente a lo ocurrido en la primera siembra, aunque en ésta el rango fue demasiado corto, lo que sugiere que la variabilidad espacial también fue de poca importancia (Jaramillo 2005).
Tabla 4. Parámetros del análisis de variabilidad espacial de la producción de fríjol CORPOICA 106 en el metro central de los surcos de 5 m de longitud (lag activo = 10 m).
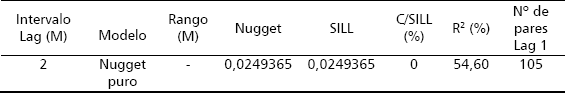
Una vez terminado el análisis de semivarianza, se procedió a llevar a cabo los análisis de varianza con los valores originales de la producción y con los residuales del análisis de tendencia, cuyos resultados se encuentran en la Tabla 5. Con esta variedad se mantuvieron los resultados obtenidos en la primera siembra (Jaramillo 2005), en el sentido de que no hubo diferencia significativa entre tratamientos ni con los datos originales de producción ni con los residuales de la tendencia.
Tabla 5. Resumen de los análisis de varianza realizados para la producción de fríjol CORPOICA 106 en el metro central de surcos de 5 m de longitud, con datos originales y depurados para algunos efectos espaciales sobre la producción.
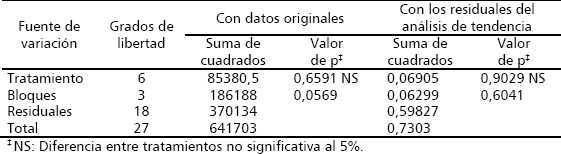
Al hacer la comprobación de los supuestos con los residuales de los ANAVAS realizados, se obtuvo normalidad e igualdad de varianzas en todos ellos: valor p de Shapiro-Wilk de 0,188034 y 0,475752 y valor p de Bartlett de 0,743937 y de 0,331693, para los análisis de varianza hechos con los datos originales y con los residuales del análisis de tendencia, respectivamente.
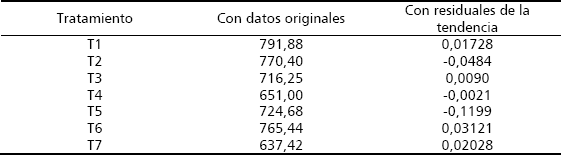
Aunque no se presentaron diferencias significativas entre tratamientos, se hizo un análisis de comparación de medias en los ANAVAS anteriores. En la Tabla 6 se observa la distribución relativa que presentaron las medias de los tratamientos y, como en la primera siembra de las dos variedades analizadas (Jaramillo 2005) y en la segunda siembra de la variedad ICA Viboral, presentada en el aparte anterior de este documento, se presentan diferencias en el ordenamiento relativo de los promedios de producción por tratamiento en los diferentes anavas hechos.
Tabla 6. Medias de la producción por tratamiento en los diferentes análisis de varianza realizados para la variedad de fríjol CORPOICA 106.
En esta segunda siembra, al eliminar las diferentes formas de la variabilidad espacial y hacer nuevamente los análisis de varianza, como ocurrió en la primera siembra (Jaramillo 2005), también se presentaron cambios en el efecto de los tratamientos sobre la producción de las variedades de fríjol utilizadas. En la Tabla 3 se aprecia que para la variedad de fríjol ICA Viboral cambió el ordenamiento relativo de las medias y la significancia de las comparaciones entre ellas.
Contrario a lo ocurrido en la primera siembra, en la variedad de fríjol CORPOICA 106 no hubo dependencia espacial de la producción en la segunda siembra. Lo anterior puede estar mostrando el efecto del uso del suelo sobre su variabilidad sistemática, como anotan Cambardella et al. 1994, Mallarino 1996, Cambardella y Karlen 1999 y Paz-González, Vieira y Taboada Castro 2000.
Como en los análisis hechos para los resultados de la primera siembra del experimento estudiado Jaramillo 2005, también en este trabajo se encontró una respuesta diferencial marcada en el comportamiento de los componentes sistemáticos de la variabilidad entre los dos lotes experimentales, a pesar de la alta homogeneidad topográfica y de suelos que se aprecia en toda la terraza sobre la que se ubicaron los experimentos analizados y de que ellos se sembraron uno contiguo al otro. Lo anterior sugiere que hay una diferencia importante entre las variedades de fríjol estudiadas frente a la respuesta que dan a la manera como se distribuyen, en el campo, algunos de los factores que controlan su producción.
El comportamiento observado en este trabajo muestra que ni la aleatorización de los tratamientos ni el establecimiento de bloques, fueron capaces de eliminar totalmente la variabilidad sistemática en este experimento. Lo anterior se debe, probablemente, a que el rango de la dependencia espacial, donde se presentó ésta, fue menor que el tamaño de las unidades experimentales puesto que, como sostienen Schabenberger y Pierce 2002, la aleatorización es capaz de neutralizar tendencias en fertilidad que se presenten en áreas experimentales que no son neutralizadas por los bloques, pero a la escala de las unidades experimentales, no a escalas mayores o menores que aquella.
Lo anterior ratifica la necesidad de conocer la variabilidad espacial de todas aquellas propiedades del suelo que se relacionan con la producción en aquellos sitios que van a ser utilizados como campos experimentales, de modo que se pueda hacer una distribución y ubicación óptimas de las parcelas y unidades experimentales en ellos que permita hacer una adecuada interpretación de los resultados que se produzcan. Schabenberger y Pierce 2002, afirman que es más conveniente utilizar un análisis que involucre explícitamente la variabilidad espacial de las unidades experimentales que utilizar uno que supone que dicha variabilidad no existe.
Lozano et al. 2004, mediante análisis geoestadísticos identificaron la estructura de la dependencia espacial de varias propiedades del suelo en un campo experimental; con esos modelos establecieron mapas de isolíneas para dichas propiedades que les permitieron diseñar la distribución más adecuada de las parcelas experimentales para estudiar cambios en el suelo producidos por el manejo.
En las estaciones experimentales en que no se tenga la información espacial, es recomendable que la cosecha de los ensayos se controle espacialmente, es decir, se georreferencie, de manera que se pueda hacer la evaluación de la variabilidad espacial, por lo menos de la producción, siguiendo una metodología como la que se ha presentado en este trabajo que permita hacer los ajustes necesarios a la interpretación de los resultados que se obtengan con los diseños experimentales trabajados.
CONCLUSIONES Y RECOMENDACIONES 
Los análisis llevados a cabo con la segunda siembra de fríjol permiten afirmar que, en el experimento evaluado, la variabilidad espacial generó diferencias en el comportamiento de los análisis de varianza de la producción en la variedad ICA Viboral, pero no en la variedad CORPOICA 106.
El efecto de dicha variabilidad espacial, aparte de ser diferencial con respecto a las variedades de fríjol utilizadas para el experimento, no sólo se manifiesta en el enmascaramiento del efecto de los tratamientos sobre la producción sino que, además, distorsiona la magnitud del mismo: después de eliminar por partes dicha variabilidad, luego de llevar a cabo el ANAVA respectivo, se obtiene un ordenamiento diferente de los promedios de los tratamientos, variando así su importancia dentro del experimento.
Se recomienda que en los sitios destinados a hacer investigación para el sector agropecuario se hagan estudios detallados de suelos que involucren, no sólo las propiedades del suelo que se relacionan directamente con los factores de producción que se quieren evaluar, sino que, además, incluyan su variabilidad espacial.
Se agradece a los Ingenieros Agrónomos Álvaro Tamayo Vélez y Luis Germán Peláez Valencia, Inves-tigadores de CORPOICA en el Centro de Investigación La Selva (Rionegro, Oriente Antioqueño-Colombia), por permitirme evaluar los resultados de sus experimentos. Al profesor Kenneth Roy Cabrera Torres por su colaboración en la aclaración de algunos puntos del trabajo.
Bhatti, A. U., Mulla, D. J., Koehler, F. E. y Gurmani, A. H. 1991. Identifying and removing spatial correlation from yield experiments. En: Journal of the American Society of Soil Science. Vol. 55; p. 1523-1528. [ Links ]
Cambardella, C. A y Karlen, D. L. 1999. Spatial analysis of soil fertility parameters. En: Precision Agriculture. Vol. 1, no. 1; p. 5-14. [ Links ]
________. Moorman, T. B., Novak, J. M., Parkin, T. B., Karlen, D. L., Turco, R. F. and Konopka, A. E. 1994. Fieldscale variability of soil properties in central Iowa soils. En: Journal of the American Society of Soil Science. Vol. 58; p. 1501-1511. [ Links ]
Cressie, N. 1984. Towards resistant geostatistics. p. 21-44. En: Verly G., David, M., Journel, A. G. and. Marechal, A., eds. Geostatistics for natural resources characterization: part 1. Dordrecht, Boston : Reidel. [ Links ]
Gómez López, Hernán. 1997. Estadística experimental con aplicaciones a las ciencias agrícolas. Medellín: Universidad Nacional de Colombia, 571 p. [ Links ]
Jaramillo, J. D. F. 2005. Efecto de la variabilidad sistemática en experimentos de fertilización con fríjol: primera siembra. En: Revista Facultad Nacional de Agronomía Medellín. Vol. 58, no. 1; p. 2717-2732. [ Links ]
Lozano, P. Z., Bravo, C., Ovalles, F., Hernández, R. M., Moreno, B., Piñango, L. y Villanueva, J. G. 2004. Selección de un diseño de muestreo en parcelas experimentales a partir del estudio de la variabilidad espacial de los suelos. En: Bioagro. Vol. 16, no.1; p. 61-72. [ Links ]
Mallarino, A. P. 1996. Spatial variability patterns of phosphorus and potassium in notilled soils for two sampling scales. En: Journal of the American Society of Soil Science. Vol. 60; p.1473-1481. [ Links ]
Martínez, R. 1994. Control de la correlación espacial en experimentos de campo en el sector agrícola. En: Agronomía Colombiana. Vol. 11, no. 1; p. 83-89. [ Links ]
Montgomery, D. C. 1991. Diseño y análisis de experimentos. México: Iberoamérica. 589 p. [ Links ]
Ovalles, F. 1992. Metodología para determinar la superficie representada por muestras tomadas con fines de fertilidad. Maracay: FONAIAP-CENIAP. 44 p. [ Links ]
________ . y Comerma, J.1991. Metodología para la selección y caracterización de sitios experimentales agropecuarios.Maracay: FONAIAP -CENIAP. (Serie B; no 18.). 44 p. [ Links ]
Paz-González, A., Vieira, S. R. y Taboada Castro, Ma. T. 2000. The effect of cultivation on the spatial variability of selected properties of an umbric horizon. En: Geoderma. Vol. 97; p. 273-292. [ Links ]
Saldarriaga L., M. M. 2002. Efecto de la variabilidad espacial en los resultados del análisis de varianza de la producción de palma joven (Elaeis guineensis Jacq.). Medellín. 66 h. Trabajo de grado en Ingeniería Agronómica. Universidad Nacional de Colombia. Facultad de Ciencias Agropecuarias. [ Links ]
Samra, J. S., Richter, J., Gill, H. S y. Anlauf, R. 1990. Spatial dependence of soil sodicity and tree growth in a Natric Haplustalf. En: Journal of the American Society of Soil Science. Vol. 54; p. 1228-1233. [ Links ]
Schabenberger, O. y Pierce, F. J. 2002. Contemporary statistical models for the plant and soil sciences. New York: CRC Press, 738 p. [ Links ]
Upchurch, D. R. and Edmonds, W. J. 1991. Statistical procedures for specific objectives. p. 49-71. En: Spatial variabilities of soils and landforms. 2 ed. Madison: SSA; (SSSA Special Publication; no. 28). [ Links ]














