Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Facultad Nacional de Agronomía Medellín
Print version ISSN 0304-2847
Rev. Fac. Nac. Agron. Medellín vol.64 no.1 Medellín Jan./June 2011
INFERÊNCIA BAYESIANA NA ANÁLISE DE TESTES REGIONAIS DE ARROZ EM DOIS SISTEMAS DE CULTIVO
BAYESIAN INFERENCE IN REGIONAL TRIALS ANALYSES WITH RICE UNDER TWO CROPPING SYSTEMS
Lina Maria Ramos Molina1; Adhemar Sanches2 y José Miguel Cotes Torres3
1 Engenheira Agrônoma. Estudiante Doctorado en Genética y Mejoramiento de Plantas,. Universidade Estadual Paulista "Júlio de Mesquita Filho". Faculdade de Ciências Agrárias e Veterinárias. Departamento de Ciências Exatas. Via de acesso Prof. Paulo Donato Castellane, s/n. CEP 14884-900. Jaboticabal, SP, Brasil. <limaramo@gmail.com>
2 Professor Adjunto. Universidade Estadual Paulista "Júlio de Mesquita Filho". Faculdade de Ciências Agrárias e Veterinárias. Departamento de Ciências Exatas. Via de acesso Prof. Paulo Donato Castellane, s/n. CEP 14884-900. Jaboticabal, SP, Brasil. <adhesan@fcav.unesp.br>
3 Profesor Asociado. Universidad Nacional de Colombia, Sede Medellín. Facultad de Ciencias Agropecuarias. Departamento de Ciencias Agronómicas. A.A. 3840, Medellín, Colombia. <jmcotes@unal.edu.co>
Recibido: Marzo 26 de 2010; aceptado: Mayo 13 de 2011
Resumo. O objetivo principal desta pesquisa foi utilizar a metodologia Bayesiana, a variância de estabilidade fenotípica de Shukla e um índice Bayesiano de Rendimento-Estabilidade (BYS), para avaliar o comportamento de genótipos de arroz na Colômbia. Para verificar a presença da interação genótipo-ambiente, foi feita a análise de variância conjunta. Quanto à média dos genótipos, os resultados mostraram que o melhor genótipo foi o 400094. O método Bayesiano na estimação dos parâmetros pelo método de Shukla não evidenciou diferença dos genótipos de forma eficiente, provavelmente devido à proximidade entre a produtividade dos genótipos avaliados. Os genótipos com menores variâncias, ou seja, os mais estáveis segundo a metodologia de Shukla foram 350405, 350406, 400090 e 400099, e o índice Bayesiano (BYS) identificou o genótipo 400094 como o de melhor comportamento, não apresentando diferença quando comparado com os outros genótipos.
Palavras-chave: Interação genótipo-ambiente, Metodologia Bayesiana, Variância de Shukla, Indice Bayesiano de Rendimento-Estabilidade.
Abstract. The main objective of this research was to analyze the behavior of 12 rice (Oryza sativa L.) genotypes from Colombia in five environments during 2005 and six environments during 2006. The Bayesian methodology was used to estimate genotype yield averages, Shukla’s variance to determine phenotypic stability and the Bayesian Yield-Stability (BYS) index for estimating yield stability.
Genotypic averages showed that greatest grain yield was obtained with genotype 400094. The genotypes with the least phenotypic variability according to Shukla’s methodology were 350405, 350406, 400090 and 400099. Numerically, the BYS index of genotype 400094 ranged above the averages of the other genotypes, but no statistically significant differences were found.
Key words: Genotype-environment interactions, Bayesian methodology, Shukla’s variance, Bayesian Yield-Stability.
Aproximadamente 75% da população mundial inclui o arroz na sua alimentação diária, superando em alguns casos o consumo de outros cereais tais como o milho e o trigo. A produção mundial de arroz supera 500 milhões de toneladas. As variedades de arroz cultivadas nos últimos anos apresentam uma gradual renovação das mais antigas, em função das melhores características, dado que as novas oferecem melhores rendimentos, uma maior resistência às pragas e enfermidades, altura mais baixa (resistência ao acamamento) e melhor qualidade de grãos (Franquet e Borrás, 2004).
O arroz tem a facilidade de se adaptar a diferentes climas, solos e condições de umidade. Na América Latina, cerca de 55% do cultivo é semeado em áreas úmidas, das quais dois terços são produzidos em condições de arroz irrigado. Os outros 45%, denominado arroz de sequeiro, são cultivados com a água de chuva (condições temporais) (CIAT, 2007). Desta forma, a avaliação da estabilidade fenotípica na cultura do arroz constitui-se numa das etapas importantes nos programas de melhoramento genético, antecedendo à recomendação de novos cultivares melhorados com características agronômicas, fisiológicas e morfológicas, superiores aos materiais originais, além de responder às necessidades dos agricultores.
As diferentes manifestações das características fenotípicas é o resultado da ação do genótipo sob influência do meio (Cruz et al., 1997). Numa série de ambientes, além dos efeitos genéticos e ambientais, existem os efeitos das interações. A avaliação da interação genótipo-ambiente é de grande importância para o melhorista, dado que existe a possibilidade do melhor genótipo num ambiente não o ser em outro.
Allard e Bradshaw (1964) discutiram os mecanismos que promovem a estabilidade da produção e concluíram que existem duas maneiras de escapar da interação. A primeira, o cultivar pode ser composto por um grande número de genótipos, adaptados a diferentes ambientes e, a segunda, os próprios indivíduos podem ser bem adaptados e cada membro da população ser bem adaptado em vários ambientes.
Nos Estados de Huila, Tolima e Meta na Colômbia, o programa de melhoramento genético de arroz é conduzido nos dois sistemas do cultivo (arroz irrigado e arroz de sequeiro). Dessa forma, é esperada a ocorrência da interação genótipo-ambiente.
A metodologia proposta por Shukla (1972), pode ser uma alternativa para se estudar a estabilidade de genótipos. O método da Máxima Verossimilhança Restrita (REML), desenvolvido por Patterson e Thompson (1971), é uma alternativa para a estimação dos componentes de variância em testes regionais desbalanceados (Piepho, 1997; Magari e Kang, 1997; Piepho, 1999), e pode ser implementado em metodologias como a proposta por Shukla (1972), utilizada para determinar a estabilidade dos genótipos. Outro método utilizado na atualidade para a estimação de dados desbalanceados é a estatística Bayesiana. Silva e Benavides (2001) afirmam que os resultados obtidos pelos métodos Bayesianos permitem uma maior informação e utilidade quando comparados com os métodos convencionais, além de melhor interpretação dos resultados.
A inferência Bayesiana utiliza três conceitos básicos que são: (i) uma informação inicial (probabilidade a priori), a qual geralmente é assumida como uma lei de probabilidade conjunta sobre os parâmetros, antes de se obter a particular amostra y1,...,yn da variável aleatória; (ii) o modelo probabilístico da variável aleatória resposta y, com o qual se obtém a verossimilhança da amostra, e (iii) o teorema de Bayes (Vázquez y Martel, 2000). Assim, no contexto Bayesiano, os parâmetros passam a ser interpretados como variáveis aleatórias, com uma lei de probabilidade (distribuição a priori) que reflete a informação inicial (ou a falta de informação) sobre eles, independente do que os dados possam mostrar.
A inferência Bayesiana para os componentes de variância é feita com base na chamada distribuição a posteriori conjunta desses parâmetros, que é obtida como uma combinação da distribuição a priori conjunta dos parâmetros e da verossimilhança da amostra. Uma estimativa de Bayes de um parâmetro pode ser determinada como a média ou mediana da distribuição a posteriori marginal desse parâmetro. No contexto de Teoria da Decisão, essa média (que é a média da distribuição a posteriori marginal) é o valor que minimiza o risco de Bayes quando se usa a função de perda quadrática. Quando se usa a função de perda absoluta, é a mediana (mediana da distribuição a posteriori marginal) que minimiza o risco de Bayes (Mood et al., 1974).
Silva y Benavides (2001) afirmam que os resultados obtidos pelos métodos Bayesianos, permitem uma maior informação e utilidade quando comparados com os métodos convencionais, além de permitir melhor interpretação dos resultados. Embora possam existir dificuldades nos cálculos numéricos, o fato é que as mesmas são possíveis de serem solucionadas mediante os programas computacionais modernos disponíveis aos usuários.
Estudos feitos em batata, trigo e milho (Cotes et al., 2006), utilizando o método Bayesiano, observaram que mediante esta metodologia, os programas de melhoramento de plantas podem ter a possibilidade de selecionar os melhores genótipos em determinados ambientes, obtendo uma estimativa mais precisa onde a informação a priori é utilizada.
De acordo com Blasco (2001), tanto os métodos frequentistas (REML) quanto os métodos Bayesianos possuem fundamentações teóricas consistentes e a escolha de um deles depende da capacidade e da facilidade de resolução de cada caso, bem como de preferências pessoais dos pesquisadores interessados.
O objetivo do presente trabalho consistiu em analisar a aplicação da metodologia Bayesiana na avaliação de genótipos de arroz em testes regionais, na estimação das médias dos genótipos, da variância de estabilidade fenotípica de Shukla, bem como no uso do índice Bayesiano de Rendimento-Estabilidade (BYS), através de dados de doze genótipos de arroz obtidos em onze ambientes diferentes da Colômbia, durante os anos 2005 e 2006, e em dois sistemas de cultivo (irrigado e de sequeiro).
MATERIAL E MÉTODOS
Testes regionais. Foram avaliados 11 experimentos no leste da Colômbia, da seguinte forma: no estado de Meta (em solo inundado na localidade de La Libertad e San Cayetano e não inundado na localidade de Tanane), no Tolima (Escobal, solo inundado) e Huila (Juncal, solo inundado), no ano de 2005. Em 2006, os genótipos foram avaliados nas localidades de Meta (solo inundado na localidade de La Libertad e não inundado nas localidades de Tanane, La Marina e San Vicente), no Tolima (Escobal, solo inundado) e Huila (Juncal, solo inundado). As informações das coordenadas geográficas dos locais, junto com o sistema do cultivo estão apresentadas na Tabela 1.
Tabela 1. Coordenadas geográficas e altitude das localidades de condução dos experimentos na Colômbia.
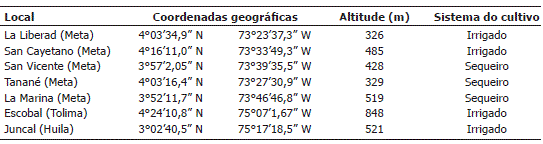
A variável resposta foi a produtividade de grãos (Kg ha-1) de oito novos genótipos da empresa SEMILLANO Ltda. (identificados como 350356, 350361, 350405, 350406, 350411, 400090, 400094 e 400099) e quatro cultivares comerciais utilizadas como testemunhas (Bonanza 6-30, Fedearroz 50, Fortaleza 5-30 e Progreso 4-25), num total de 12 genótipos avaliados. Houve dificuldade nos testes regionais quanto à disponibilidade de semente e, por isso, apresentam desbalanceamento dos materiais nos diferentes ambientes nos dois anos de estudo.
Delineamento experimental. Em cada localidade utilizou-se o delineamento de blocos ao acaso com quatro repetições. A unidade experimental foi constituída por 20 linhas de 5 m de comprimento, com 0,25 m de espaçamento entre linhas e uma densidade de 20 g de semente por linha. As práticas culturais adotadas foram as usuais da cultura, segundo o local, e estes experimentos foram estabelecidos na época do ano ótima para cada localidade. Realizou-se a análise de variância para cada experimento e, posteriormente, a análise conjunta dos ambientes, com a finalidade de determinar a significância da interação genótipo-ambiente.
Análise combinado. Neste trabalho onde foi considerado um grande número de dados desbalanceados, a análise de variância conjunta para verificar a presença da interação genótipo-ambiente, foi feita pelo método REML (Máxima Verossimilhança restrita) descrito por Patterson e Thompson (1971), método disponível no procedimento Mixed Procedure (PROC MIXED) do sistema computacional Statistical Analysis System (SAS) versão 9.1 (SAS, 2004). O REML é uma generalização da ANOVA para situações mais complexas, permitindo uma maior flexibilidade na modelagem por não supor a independência dos erros, estimando os componentes de variância (parâmetros genéticos) com maior precisão. Esse procedimento foi utilizado no ajuste do modelo linear misto para a análise dos testes regionais.
Análise bayesiana. Para o modelo foram considerados testes regionais de arroz com a ambientes (i=1,2,...,a), ri blocos por ambiente (j=1,2,...,b; onde b=Σri), g genótipos (k=1,2,...,g), ni observações por ambiente,nk número de ambientes avaliados para o k-ésimo genótipo e n=Σnρ número total de observações. Assim, para o vetor y de observações fenotípicas, de ordem n x 1, considera-se o seguinte modelo linear misto:

Para realizar a estimação Bayesiana dos parâmetros no modelo [1], supõe-se que a distribuição condicional de y
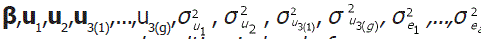
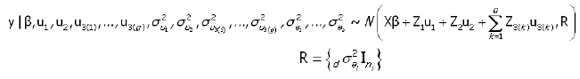
onde Ini é a matriz de identidade de ordem ni. Uma característica especial da metodologia Bayesiana, e que a diferencia da metodologia clássica, é a incorporação da informação a priori no modelo probabilístico. Assim, para o modelo [1] foram consideradas as seguintes informações a priori:
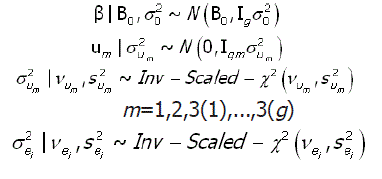

A notação Inv-Scaled-χ2 (Gelman et al., 1995) indica a distribuição qui-quadrado invertida com um parâmetro de escala.
Os valores 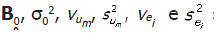 são denominados de hiper-parâmetros.
são denominados de hiper-parâmetros.
Multiplicando-se as distribuições a priori pela função de verossimilhança foi obtida a distribuição a posteriori conjunta:
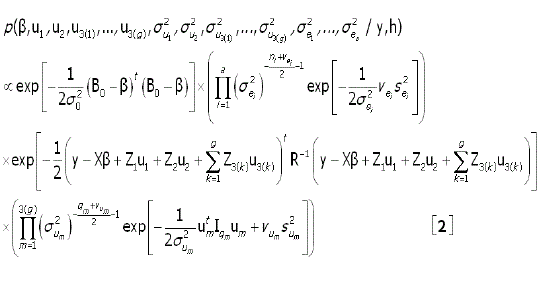
Onde h representa o vetor dos hiper-parâmetros. Nesta pesquisa, assumiu-se uma relativa ignorância a priori sobre os parâmetros β e os componentes de variância, colocando-se os hiper-parâmetros como: σ02=1x108; vum = 1;s2um =1x10-6; Vei=1; =1; s2ei=1 x10-6 e o vetor B0=(0,1) x 1g.
Algoritmo de GIBBS. Para o uso deste algoritmo é necessário reconhecer todas as distribuições condicionais da distribuição a posteriori conjunta [2]. Por conveniência, visando maior facilidade na programação do algoritmo, considerou-se a seguinte reparametrização:
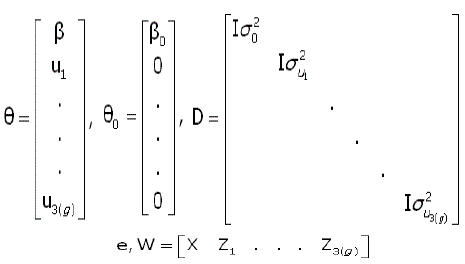
Assim, a distribuição a posteriori condicional para θ fica:
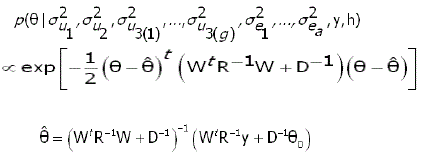
onde, Isto é, θ distribui-se condicionalmente como uma normal multivariada, ou seja
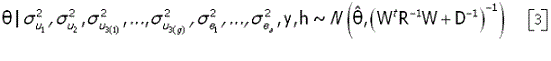
As distribuições a posteriori condicionais para são identificadas como uma qui-quadrado invertida escalonada, isto é,
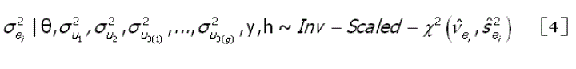
onde
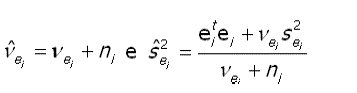
De modo semelhante, as distribuições a posteriori condicionais para são também identificadas como uma qui-quadrado invertida escalonada, ou seja
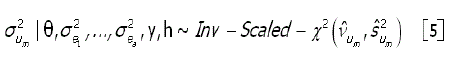
onde
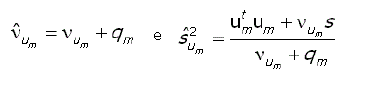

Nesta pesquisa, foram descartados os primeiros 15.000 vetores gerados correspondentes ao período de “burn-in” (ou período de aquecimento), que é o período no qual a cadeia de Markov (programada no algoritmo de GIBBS) foi estabilizada, segundo a interpretação visual dos gráficos para diagnóstico de convergência. Após esse período, e devido à correlação existente entre os vetores gerados, pegou-se um vetor a cada 10 vetores gerados (Wang et al., 1993). Procedendo-se assim foi obtida uma amostra de tamanho s, da distribuição a posteriori conjunta [2]. Amostras das distribuições a posteriori marginais, 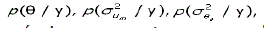 foram obtidas desses próprios s vetores gerados, pegando-se os componentes θ, e de cada um desses vetores, respectivamente.
foram obtidas desses próprios s vetores gerados, pegando-se os componentes θ, e de cada um desses vetores, respectivamente.
O algoritmo de GIBBS foi programado no SAS IML (SAS, 2004). Para os testes regionais foi obtida uma amostra de tamanho s=100000 vetores da distribuição a posteriori conjunta [2].
Análise de estabilidade fenotípica. A variância de Shukla é um indicativo de estabilidade dos genótipos, quando os mesmos são avaliados em vários ambientes. Assim, nesta pesquisa com o objetivo de estabelecer a estabilidade de um genótipo foi utilizado o parâmetro:

Ond ek corresponde ao genótipo de interesse e k ’ corresponde ao genótipo com a menor variância de Shukla. O genótipo k ’ é determinado como aquele que tem a menor estimativa de Bayes da variância de Shukla, porém esse genótipo é declarado estável dentro do grupo de genótipos avaliados.
Em seguida, com o objetivo de se determinar outros genótipos possíveis de serem também declarados estáveis, determina-se a distribuição a posteriori do parâmetro BSk e calcula-se a probabilidade a posteriori P(BSk=1). Quando esta probabilidade é maior ou igual a 5%, o genótipo k é também considerado estável.
A distribuição a posteriori do parâmetro BSk foi determinada a partir da amostra de tamanho s obtida pelo algoritmo de GIBBS da distribuição a posteriori conjunta [2], pegando-se os componentes 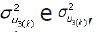 e , e calculando-se a razão entre eles para cada vetor dessa amostra. Com isso, obteve-se uma amostra de s valores de BSk com a qual a probabilidade P(BSk =1) foi estimada como a freqüência relativa do evento "BSk =1" nessa amostra.
e , e calculando-se a razão entre eles para cada vetor dessa amostra. Com isso, obteve-se uma amostra de s valores de BSk com a qual a probabilidade P(BSk =1) foi estimada como a freqüência relativa do evento "BSk =1" nessa amostra.
Análise de rendimento e estabilidade fenotípica. Como ultimo critério de seleção de genótipos, propõe-se o índice Bayesiano de Rendimento-Estabilidade BYS (iniciais do inglês Bayesian Yield-Stability) (Cotes, 2004) de um genótipo como BYS=m-σ, onde m é a média populacional e σ é a raiz quadrada da variância de Shukla, para o genótipo considerado.
O BYS é um parâmetro que leva em conta, simultaneamente, o rendimento e a estabilidade de cada genótipo. Segundo o BYS, considera-se como o melhor genótipo, àquele que apresenta o maior valor desse índice. Assim, o uso do BYS vai de encontro ao interesse do produtor, no sentido que seleciona genótipos com altas expectativas de rendimento mínimo.
Cotes (2004) afirma que é importante notar que o BYS, também pode ser estimado por outras metodologias estatísticas, mas a metodologia Bayesiana oferece vantagens importantes. A estimativa do BYS de cada genótipo foi determinada como a média da distribuição a posteriori desse parâmetro. Essa média foi obtida a partir da amostra de GIBBS gerada da distribuição a posteriori conjunta [2], calculando-se o BYS pelos componentes correspondentes à média e a variância de Shukla do respectivo genótipo em cada um dos s vetores gerados e, a seguir, obtendo-se a média aritmética dos s valores do BYS assim obtidos. Esses s valores do BYS correspondem a uma amostra de tamanho s da distribuição a posteriori marginal desse parâmetro, com base na qual foram determinados os intervalos de credibilidade ao 90%, além da própria estimação da distribuição a posteriori marginal do BYS.
RESULTADOS E DISCUSSÃO
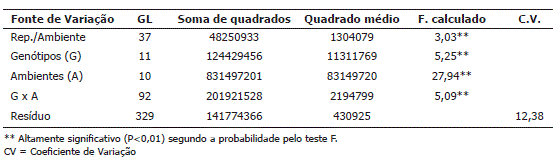
A análise de variância conjunta para produção de grãos indicou pelo teste F, que houve efeitos altamente significativos (P≤0,01) dos genótipos, dos ambientes e da interação genótipo-ambiente (Tabela 2). A diferença significativa dos genótipos e dos ambientes determina que existem diferenças genéticas entre os indivíduos, assim como entre os ambientes em estudo. A presença da interação significativa indica que o desempenho dos genótipos não foi consistente nos locais avaliados. Esse resultado reflete a sensibilidade dos genótipos às diversas condições dos ambientes avaliados, que neste estudo incluem sistema do cultivo, ano e localidade. Assim, há o interesse na identificação dos genótipos de comportamento previsível e que sejam responsivos às variações do ambiente. O coeficiente de variação do resíduo foi de 12,38%, considerando-se aceitável para a cultura do arroz.
Tabela 2. Análises de variância conjunta para a variável produção de arroz (Kg•ha-1) de 12 genótipos de arroz avaliados em cinco ambientes no ano de 2005 e seis em 2006, no leste da Colômbia.
Nas avaliações dos genótipos de arroz, considerando as estimativas das médias da produtividade, pode-se observar que o genótipo 400094 teve a maior média seguida da cultivar Fedearroz-50. Informações obtidas pelo Centro Internacional de Agricultura Tropical (CIAT, 2001) indicam que a cultivar Fedearroz 50 tem tido grandes êxitos, desde que foi levada ao mercado, apresentando uma produtividade média de 5 a 7 ton•ha-1, dependendo das condições climáticas.
Assim, pode-se destacar que o genótipo 400094 é tão bom como Fedearroz 50 quanto à produtividade, embora tenha outras características morfológicas favoráveis que não são apresentadas neste trabalho. Ao observar os intervalos de credibilidade (90%) entre os limites inferiores e superiores, nota-se que são muito semelhantes entre todos os genótipos, não apresentando uma diferença significativa entre eles quando comparados com a 400094, à exceção do genótipo 350405 onde seus intervalos foram muito baixos (Tabela 3).
Tabela 3. Estimativas de Bayes para as médias de produção e a variância da estabilidade fenotípica de Shukla, para 12 genótipos de arroz avaliados em cinco ambientes no ano de 2005 e seis em 2006, no leste da Colômbia.
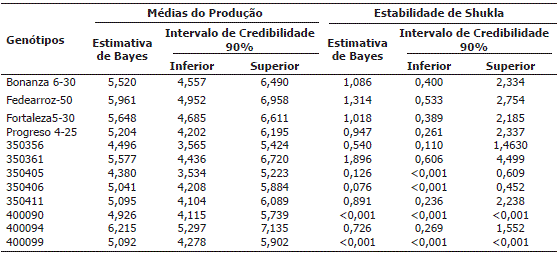
A estimativa da variância, segundo a metodologia de Shukla, é apresentada também na Tabela 3, onde os resultados indicam que os genótipos com menores variâncias, ou seja, os mais estáveis são 400099, 400090, 350406 e 350405 e os que têm maiores variâncias (possivelmente instáveis) são 350361 e Fedearroz 50. Assim, pode-se observar que os genótipos com média de produção alta, não foram segundo a metodologia de Shukla os mais estáveis.
Os resultados obtidos baseados no parâmetro Bayesiano de rendimento-estabilidade (BYS) indicam que os genótipos 400094 e 400099 apresentam os maiores valores. Quando se observam os intervalos de credibilidade, destaca-se que não há diferenças significativas entre estes genótipos e os restantes (Tabela 4). Desta forma o parâmetro BYS, analisado pelos intervalos de credibilidade, não foi conclusivo para a seleção de genótipos nestes testes regionais. Este resultado é diferente do encontrado por Cotes (2004) que, analisando testes regionais de batata em 10 localidades e 15 genótipos, encontrou que este parâmetro ajudava eficientemente na seleção de genótipos, confirmando de igual forma os estudos feitos em investigações desenvolvidas por Silva e Benavides (2001).
Tabela 4. Análise do índice Bayesiano de Rendimento-Estabilidade (BYS), para 12 genótipos de arroz, avaliados em cinco ambientes no ano de 2005 e seis em 2006, no leste da Colômbia.
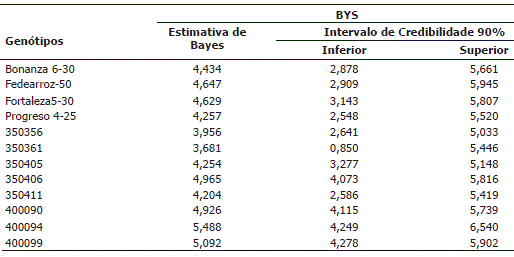
Os resultados de produtividade obtidos neste trabalho possivelmente indicam que os genótipos obtidos no programa de melhoramento tradicional em arroz têm pouco incremento em nível produtivo, ou seja, pode-se pensar que esse sistema de melhoramento pode estar chegando a um patamar quanto à produtividade. Ou também outra hipótese pode ser a possibilidade da falta de uma alta variabilidade genética nos cruzamentos entre os materiais em estudo quanto a produção. Desse modo, forna-se importante a busca de alternativas de melhoramento em arroz como é a tecnologia dos híbridos (Yuan y Fu, 2003).
CONCLUSÕES
Os dados das médias dos genótipos e o índice Bayesiano de rendimento-estabilidade indicaram o genótipo 400094, como o de melhor comportamento entre os genótipos em estudo, embora não tenham diferença significativa quando comparado com os outros genótipos avaliados.
A metodologia de Shukla foi útil para determinar a estabilidade dos genótipos em estudo, considerando-se que os materiais mais estáveis foram 400099, 400090, 350406 e 340405.
O parâmetro Bayesiano BYS não conseguiu diferenciar, neste caso, os genótipos de forma eficiente devido devido, provavelmente, à proximidade entre a produtividade dos genótipos avaliados.
BIBLIOGRAFIA
Allard, R.W. and A.D. Bradshaw. 1964. Implications of genotype-environmental interactions in applied plant breeding. Crop Science 4(6): 503-508. [ Links ]
Blasco, A. 2001.The Bayesian controversy in animal breeding. Journal of Animal Science 79(8): 2023-2046. [ Links ]
Centro Internacional de Agricultura Tropical (CIAT). 2001. Mejoramiento de arroz, resultadossobresalientes. Em: http://www.ciat.cgiar.org/riceweb/esp/resultados. htm; 162 p. consulta: fevereiro 2007. [ Links ]
Centro Internacional de Agricultura Tropical (CIAT). 2007. Mejoramiento de arroz CIAT, http://www.fitomejoramientocolombia.org/documentos/Mejora mientodearrozciat.doc; 27 p. consulta: julho 2008. [ Links ]
Cotes, J.M. 2004. Analise Bayesiana da interação genótipo-ambiente na seleção de genótipos por estabilidade fenotipica e por rendimento-estabilidade. Tese Doutorado em Genética e Melhoramento de Plantas. Universidade Estadual Paulista, Brasil. 64 p. [ Links ]
Cotes, J.M., J. Crossa, A. Sanches, and P.L. Cornelius. 2006. A bayesian approach for assessing the stability of genotypes.Crop Science 46(6): 2654-2665. [ Links ]
Cruz, C.D., A.J. Regazzi e P.C. Souza. 1997. Modelos biométricos aplicados ao melhoramento genético, volume 1. Segunda edição. Editora UFV, Viçosa. 390 p. [ Links ]
Franquet, M. y C. Borrás. 2004. variedades y mejora del arroz (Oriza sativa L.). Universitat Internacional Catalunya. Cataluña, España. 445 p. [ Links ]
Gelman, A., J.B. Carlin, H.S. Stem and D.B. Rubin. 1995. Bayesian data analysis. Fourth edition. Chapman and Hall, London. 526 p. [ Links ]
Magari, R. and M.S. Kang.1997. SAS-STABLE: Stability Analyses of Balanced and Unbalanced Data. Agronomy Journal 89(6): 929-932. [ Links ]
Mood, A.M., F.A. Graybill and D.C. Boes. 1974.Introduction to the teory of statistics. Thirth edition. McGraw Hill, Tokyo, Japan. 564 p. [ Links ]
Patterson, H.D. and R. Thompson. 1971. Recovery of inter-block information when block sizes are unequal.Biometrika 58(3): 545-554. [ Links ]
Yuan, L.P. y X.Q. Fu. 2003. Tecnología para la producción de arroz híbrido, http://www.fao.org/docrep/003/V4730S/v4730s01.htm#TopOfPage; consulta: fevereiro 2007. [ Links ]
Piepho, H.P. 1997. Analyzing genotype-environment data by mixed model with multiplicative terms. Biometrics 53(2): 761-766. [ Links ]
Piepho, H.P. 1999. Stability análisis using the SAS System. Agronomy Journal 91(1): 154-160. [ Links ]
SAS INSTITUTE. 2004. SAS CD ROM versão 9.1.3. SAS/STAT. Cary. [ Links ]
Shukla, G.K. 1972. Some statistical aspects of partitioning genotype-environment components of variability. Heredity 29: 237-245. [ Links ]
Silva, L.C. y A. Benavides. 2001. El enfoque bayesiano: otra manera de inferir. Gac Sanit 15(4): 341-346. [ Links ]
Vázquez, F.J. y M.C. Martel. 2000. Sobre la enseñanza de rudimentos de estadística bayesiana con aplicaciones en economía y empresa. ASEPUMA. Asociación Española de Profesores Universitarios de Matemáticas aplicadas a la Economía y la Empresa, http://150.214.55.100/asepuma/sevilla2000/m4-04.pdf. 8 p.; consulta fevereiro 2008. [ Links ]
Wang, C.S.; J. Rutledge and D. Gianola. 1993. Marginal inferences about variance components in a mixed linear model using Gibbs sampling. Genetics Selection Evolution GSE 25(1): 41-62. [ Links ]














