Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Revista Facultad Nacional de Agronomía Medellín
versão impressa ISSN 0304-2847
Rev. Fac. Nac. Agron. Medellín vol.65 no.2 Medellín jun./dez. 2012
DETERMINATION OF A MATHEMATICAL MODEL TO ESTIMATE THE AREA AND DRY WEIGHT OF THE LEAF LIMBO OF Prunus persica CV. Jarillo
DETERMINACIÓN DE UN MODELO MATEMÁTICO PARA LA ESTIMACIÓN DEL ÁREA FOLIAR Y PESO SECO DEL LIMBO DE Prunus persica CV. Jarillo
Enrique Quevedo García1; Martha Esperanza Arévalo González2 y Giovanni Orlando Cancino Escalante3
1 Associate Professor. Universidad de Pamplona, Faculty of Agrarian Sciences - Department of Agronomy. km 1 vía Bucaramanga el Buque, Pamplona, Norte de Santander, Colombia. <dagronomia@unipamplona.edu.co>
2 Biologist. B.Sc. Pamplona, Norte de Santander, Colombia. <fresiazucena@hotmail.com>
3 Associate Professor. Universidad de Pamplona - Faculty of Basic Sciences - Department of Biology and Chemistry. km 1 vía Bucaramanga el Buque, Pamplona, Norte de Santander, Colombia. <gcancino@unipamplona.edu.co>
Received: June 12, 2012; accepted: October 01, 2012.
Abstract. A study was conducted to determine the variables that estimated the leaf limbo area and the leaf limbo dry weight of peach Prunus persica (L.) Batsch cv. Jarillo. Fifty leaves, aged 2.5 months, were selected and measured: leaf limbo length and width, petiole length, leaf length, petiole diameter, leaf limbo fresh weight, petiole fresh weight, leaf fresh weight, leaf limbo dry weight, petiole dry weight, leaf dry weight, length/width limbo, petiole length/limbo length and leaf limbo area. The results allowed to obtain regression equations for estimating the leaf area and the limbo dry weight. Using the lineal models LA = b1 + b2 (LLL x LLW) and LA= b1+ b2LLL + b3LLW a leaf area equation was determined. Alternative models to calculate limbo dry weight were evaluated LLDW = -b1+ b2 LLFW and LLDW= - b1 + b2LLL + b3PL. The best equations found with an R2 of 0.99 were LA = 1.572 + 0.65169(LLL x LLW), LA=-23.106+2.8064LLW + 3.6761LLL and LLDW = -0.002+0.401(LLFW).
Key words: Fruits, regression models, leaf limbo length, leaf limbo width.
Resumen. Se realizó un estudio para determinar las variables que estimaran el área del limbo foliar y el peso seco del limbo de durazno Prunus persica (L.) Batsch cv. Jarillo. Se seleccionaron cincuenta hojas con 2,5 meses de edad, fueron medidos: ancho del limbo, longitud del limbo, longitud del peciolo, longitud hoja, diámetro peciolo, peso fresco del limbo, peso fresco del peciolo, peso fresco de la hoja, peso seco del limbo, peso seco peciolo, peso seco de la hoja, longitud /ancho limbo, longitud del peciolo/longitud del limbo, área foliar del limbo. Los resultados alcanzados permitieron obtener ecuaciones de regresión para estimar el área foliar del limbo y el peso seco del limbo. Se halló una ecuación para la determinación del área foliar del limbo con los modelos lineales LA = b1 + b2 (LLL x LLW) y LA= b1 + b2LLL + b3LLW. También se evaluaron modelos alternativas para calcular el peso seco del limbo, LLDW = -b1+ b2LLFW y LLDW= - b1 + b2LLL + b3PL. Las mejores ecuaciones encontradas con un R2 del 0,99 fueron LA = 1,572 + 0,65169(LLL x LLW), LA=-23,106+2,8064LLW + 3,6761LLL y LLDW = -0,002+0,401(LLFW).
Palabras clave: Frutales, modelos de regresión, largo del limbo foliar, ancho del limbo foliar.
Mathematical models are a simplified representation of real systems allowing one to understand, explain, estimate or predict the reality (Heiner, 2007; Thornley, 1976, cited by Curiel et al., 2007). In this regard, linear and multiple regression methods and experimental variables data associated with plant organs, such as leaf area and dry weight among others, enables the construction of mathematical models to estimate the plants photosynthetic capacity. Studies on the methods of estimating the leaf limbo area are in most cases costly, time consuming and sometimes it may cause severe plant damage. Casierra et al. (2008) claims that the leaves length and width are reliable values and when applied in regression equations it accurately reflects the leaf limbo area. It is, therefore, important to establish mathematical models based on simple measures that can estimate the area and dry weight of the leaf limbo without damaging plant material.
There is a close relationship between the leaf limbo area and its linear parameters (e.g. length and width), and such relationship can be described by regression equations (Simón and Trujillo, 1990; Venturieri, 1996; Murillo et al., 2004; Muñoz et al., 2008; Espitia et al., 2006; Ruiz et al., 2007; Galindo and Clavijo, 2007; Cardona et al., 2009; Ruiz et al., 2010; Wang and Zhang, 2012). Factors that can predict the production of dry weight, such as the amount of chlorophyll, temperature and photoperiod, have been directly related to the leaf area (Campostrini and Yamanishi 2001; Birch et al., 2003).
Several authors have shown that the variation of the leaf area is the most significant factor in the variation of dry weight accumulated by plants (Gutiérrez and Lavín, 2000; Astegiano et al., 2001; Disegna et al., 2005; Muñoz et al., 2008). It has also been shown that the plants photosynthesis capacity is directly related to the limbo surface expressed as leaf area index (Kozlowski et al., 1991; Calderón et al., 2009). In the case of peach [Prunus persica (L) Batsch] its photoassimiliate production is mainly in leaves and its size corresponds to the leaf area (Marquínez and Corchuelo, 1998). The leaf area index (LAI) is one of the most commonly used parameters for the structural analysis of crop canopy and it relates the plants leaf area with the section of ground area (Arias et al., 2007). Full grown peach crop intercepts 95% of incident light with different LAI values. The LAI of this specific percentage is known as critical leaf area index and is determined by leaf area per plant (Montaldi, 1995; De la Casa et al., 2007; Acosta et al., 2008; Tinoco et al., 2008). Therefore, the aim of this study was to generate an empirical mathematical model applying multiple linear regression techniques, in order to estimate the leaf limbo area and leaf limbo dry weight of peach plants [P. persica (L.) Batsch cv. Jarillo].
MATERIALS AND METHODS
Characteristics of the experimental farm. The geo-referenced position of the peach trees (P. persica (L) Batsch cv. Jarillo) and their crop age (four to six years) were considered for the selection of the Las Delicias farm, located in the Province of Pamplona, Colombia (Chíchira). Fifty sample leaves, aged 2.5 months of five random trees, were selected and their characteristics are given in Table 1.
Estimated leaf area using non-destructive method. The leaf limbo length (LLL) and the leaf limbo width (LLW) of fifty photosynthetically active and mature peach leaves were determined according to the reported procedure (Kumar, 2009). The product of the combination of LLL x LLW was the area of a rectangle that has as its base the leaf limbo length (LLL) and as its height the leaf limbo width (LLW).
The leaf limbo area was measured using an electronic scanner (Area Meter® AM300). Statistical analysis was performed with the aid of the statistical software package R and a scatter diagram was generated according to Murillo et al. (2004) and Ruiz et al. (2010) in Vigna unguiculata. The X-axis represents the product (length x width) of the leaf limbo area and the Y-axis the leaf limbo area. In order to estimate the leaf area the models used by Bianco et al. (2008a), Bianco et al. (2008b), Burgos et al. (2010) and Muñoz (1987) were considered:

An alternative model by Ruiz et al., 2007 was also considered:

Estimated dry weight using non-destructive method. The dry weight of the fifty leaves was measured using a forced air circulation oven and an electronic scale.
A total of fourteen variables were used according to the methodology applied by Venturieri in 1996 in order to obtain an estimated dry weight model:
LLW = Leaf limbo width (cm); LLL = Leaf limbo length (cm); PL = Petiole length (cm), LL = Leaf length (LLL + PL) (cm); PD = Petiole diameter (cm); LLFW = Leaf limbo fresh weight (g); PFW = Petiole fresh weight (g); LFW = Leaf fresh weight (LFW + PFW) (g); LLDW = Leaf limbo dry weight (g); PDW = Petiole dry weight (g); LDW = Leaf dry weight (LLDW+ PDW) (g); LLL/LLW = Leaf limbo length/width (cm); PL/LLL = Petiole length/ Leaf limbo length (cm); LA = Leaf limbo area (cm2).
Statistical analysis was performed with the aid of the statistical software package R. Correlation, simple and multiple linear regression analysis and Stepwise was used according to Bendel and Afifi ( 1977).
RESULTS AND DISCUSSION
Regression methods to determine leaf area of plants are an economic and useful tool in agronomic and plant physiology research (Casierra et al., 2008; Fallovo et al., 2008). It is also used to calculate the source-sink strength of leaf area and dry weight (Marquínez y Corchuelo, 1998). As were reported for many species, such as P. persica (Demirsoy et al., 2004), Pisum sativum (Galindo y Clavijo, 2007 y Ruiz et al., 2007), Malus domestica (Curiel et al., 2007) and Zea mays (Sezer et al., 2009), estimating leaf area from equations using leaf area measurement is a reliable and nondestructive method for accurately assessing leaf area. Therefore, in accordance with previous studies, the most appropriate mathematical approach to develop regression estimators and equations by using measured leaf parameters such as length and width were used.
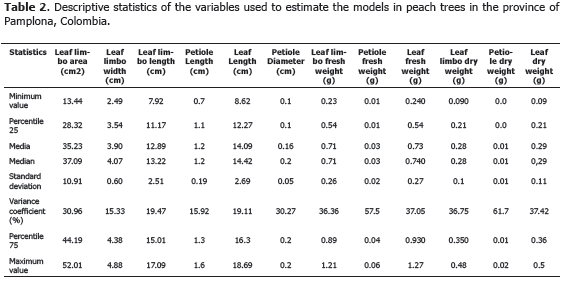
As a result, the present study indicates that the leaf limbo length and width of P. persica (L.) Batsch cv. Jarillo presented the lowest coefficient variation values (<20%), considered low in agreement with previous findings of Zamora (1989). The regression equations generated from the leaf limbo and leaf limbo dry weight were obtained using descriptive statistics: minimum value, 25th percentile, mean and median, standard deviation, coefficient of variation, 75th percentile and maximum value (Table 2). It is important to highlight that the analyses of the fourteen variables using the Pearson coefficient (Table 3) showed that there was close relationship between them, thus allowing the selection of the independent variables more accurately: leaf limbo area and dry weight (Sokal y Rohlf, 1981).
A Stepwise regression procedure was used to calculate the leaf limbo area and dry weight of P. persica (L.) Batsch cv. Jarillo and the independent variables are given in Tables 2 and 3. The statistical results of the thirteen estimation models obtained from such procedure are shown in Tables 4, 5, 6 and 7. It should be noted that the R2 in all models were equal to 0.99 (P<0.01) and the inclusion of a large number of independent variables did not improve the model's adjustment, as were reported in other species such as Xanthosoma sagittifolium (Simón y Trujillo, 1990). Therefore, from a statistical perspective any of the applied methods can be used to estimate leaf limbo area and dry weight of P. persica (L.) Batsch cv. Jarillo. Nevertheless, from a practical point of view, the ones that take into account the leaf's limbo length and width are considered optimal. It is also important to emphasize that the models obtained from the present study confirms the assumptions of simple and multiple regressions methods such as normality errors, non-autocorrelated errors and homogeneity of variance, similar to those in Carica papaya (Cardona et al., 2009).
In order to determine a mathematical model to predict nondestructive leaf limbo area of P. persica cv. Jarillo, six equations were generated and evaluated (Tables 4 and 5). The first regression model analyzed, when using the product of the leaf's limbo length and width (LLL x LLW) with a proportional coefficient (b2), as found in other species such as Persea bombycina (Chattopadhyay et al., 2011), Mangifera indica (Ghoreishi et al., 2012) and Jatropha curcas (Pompelli et al., 2012), was LA = b1 + b2 (LLL x LLW). The second multiple lineal regression model used to estimate the leaf limbo area with two proportional coefficient (b2) and (b3); also found in Vitis vinifera (Legorburo et al., 2007); Theobroma grandiflorum (Venturieri, 1996), S. rebaudiana (Espitia et al., 2006), Ocimum basilicum (Ruiz et al., 2007), P. sativum (Galindo and Clavijo, 2007), Merremia cissoides (De Carvalho et al., 2011) and Triticum aestivum (Cogliatti et al., 2010), was LA = b1 + b2 LLL + b3LLW.
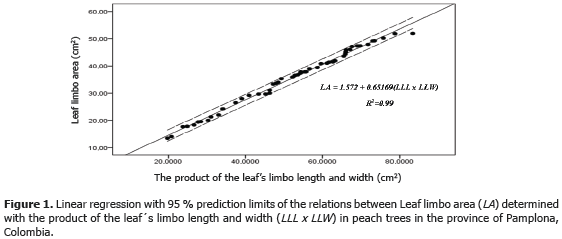
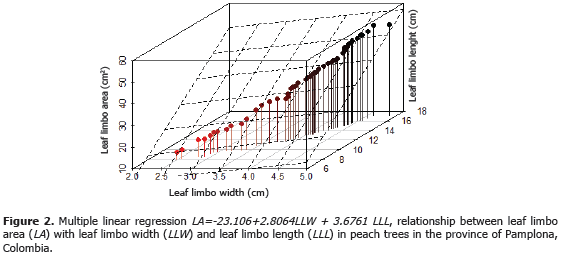
In this regard, when evaluating the results of the above equations, the 0.99 coefficient of determination obtained in P. persica (L.) Batsch cv. Jarillo and in other varieties of P. persica (Demirsoy et al., 2004) suggests that 99 of the observed points is due to a high level of statistical significance (P<0.01). These findings are similar to those of Nicotiana tabacum (Bozhinova, 2006), Actinidia deliciosa (Mendoza et al., 2007), Psidium guajava (Singh, 2007), Sida rhombifolia y Sida cordifolia (Bianco et al., 2008a), Ageratum conyzoides (Bianco et al., 2008b) and Xanthium strumarium (Bianco et al., 2010). Therefore, the results reported in the present study, together with previous reports in other species such as O. basilicum (Ruiz et al., 2007), have shown that the two best equations to calculate the leaf limbo area of P. persica (L.) Batsch cv. Jarillo with an R2 of 0.99 were: LA = 1.572 + 0.65169 (LLL x LLW) (Figure 1) and LA=-23.106+2.8064LLW + 3.6761LLL (Figure 2). This confirms that leaf length and width measurements are the most frequently dimensions used to estimate leaf limbo area as it can be easily used in the field due to its simplicity and accuracy (Mendoza et al., 2007).
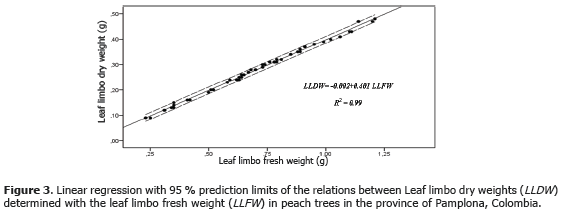
As mentioned previously Stepwise analysis regression was also performed to predict dry weight of P. persica (L.) Batsch cv. Jarillo leaves and seven equations were generated and evaluated (Tables 6 and 7). Results showed that the best equation to calculate dry weight with a 0.99 R2 was LLDW = -0.002+0.401(LLFW) (Figure 3). These findings confirm those of O. basilicum (Ruiz et al., 2007).
To summarize we can conclude that the present study validated the models and methodology (Demirsoy et al., 2004) used to estimate the leaf area and dry weight of P. persica (L.) Batsch cv. Jarillo. It is important to highlight that these models meet statistical parameters and are adjusted to the Colombian tropical conditions.
CONCLUSIONS
The models analyzed in this study can be used to estimate the leaf area and dry weight of peach trees.
The most practical options to estimate the limbo leaf area of peach plants, P. persicae (L.) Batsch cv. Jarillo were: a) LA =1.572 + 0.65169(LLL x LLW) and b) LA = -23.106+2.8064 LLW + 3.6761LLL and for the leaf limbo dry weight: LLDW= -0.002+0.401(LLFW).
The simple lineal and multiple regressions showed that the chosen variables to calculate the models are linearly related to the leaf limbo area.
ACKNOWLEDGEMENTS
The authors would like to thank the Universidad de Pamplona and the Ministerio de Agricultura y Desarrollo Rural (Project 2007L4757-502) for their financial support. They are also grateful to ASOHOFRUCOL, CORPONOR, IICA and ASPROBABEGA (Silos, Norte de Santander, Colombia), for their collaboration. The authors would also like to thank Susan Cancino MBA for her time, insight, dedication, corrections and translation.
BIBLIOGRAPHY
Acosta, D.E., G.J. Acosta, R.M. Amador y R.J. Padilla. 2008. Relación entre índice de área foliar y rendimiento en frijol bajo condiciones de secano. Agricultura Técnica en México 34 (1): 13-20. [ Links ]
Arias, D., J. Calvo and A. Dohrenbusch. 2007. Calibration of LAI-2000 to estimate leaf area index (LAI) and assessment of its relationship with stand productivity in six native and introduced tree species in Costa Rica. Forest Ecology and Management 247(1-3): 185-193. [ Links ]
Astegiano, E.D., J.C. Favaro y C.A. Bouzo. 2001. Estimación del área foliar en distintos cultivares de tomate (Lycopersicon esculentum Mill.) utilizando medidas foliares lineales. Investigación Agraria Producción y Protección Vegetal 16(2): 249 -256. [ Links ]
Bendel, R.B. and A.A. Afifi. 1977. Comparison of stopping rules in forward "stepwise" regression. Journal of the American Statistical Association 72(357): 46-53. [ Links ]
Bianco, S., L.B. De Carvalho and M.S. Bianco. 2008a. Estimativa da área foliar de Sida cordifolia e Sida rhombifolia usando dimensões lineares do limbo foliar. Planta Daninha 26(4): 807-813. [ Links ]
Bianco, S., M.S. Bianco e L.B De Carvalho. 2008b. Estimativa da área foliar de Ageratum conyzoides usando dimensões lineares do limbo foliar. Acta Scientiarum Agronomy 30(4): 519-523. [ Links ]
Bianco, S., M.S. Bianco, L.B. De Carvalho and V.G. Cury. 2010. Estimativa da área foliar de Xanthium strumarium L. usando dimensões lineares do limbo foliar. p. 1163-1166. Em: Memórias. XXVII Congresso Brasileiro da Ciência das Plantas Daninhas. Centro de Convenções Ribeirão Preto. São Paulo. [ Links ]
Birch, C.J., J. Vos and P.E. Van der Putten. 2003. Plant development and leaf area production in contrasting cultivars of maize grown in a cool temperate environment in the field. European Journal Agronomy 19(2): 173-/188. [ Links ]
Bozhinova, R.P. 2006. Coefficients for determination of the leaf area in three Burley tobacco varieties. Journal Central European Agriculture 7(1): 7-12. [ Links ]
Burgos, A.M., M.M. Avanza, C.N. Balbi, J. Prause y J.A. Argüello. 2010. Modelos para la estimación no destructiva del área foliar de dos cultivares de mandioca (Manihot esculenta Krantz) en la Argentina. Agriscientia 27(1): 55-61. [ Links ]
Calderón, A., F. Soto, M. Calderón y L.R. Fundora. 2009. Estimación de área foliar en posturas de mango (Manguifera indica L.) y aguacatero (Persea spp) en fase de vivero a partir de las medidas lineales de las hojas. Cultivos Tropicales 30(1): 43-48. [ Links ]
Campostrini, E. y O. Yamanishi. 2001. Estimativa da área foliar do mamoeiro utilizando o comprimento da nervadura central. Scientia Agrícola 58(1): 39-42. [ Links ]
Cardona, A.C., H.T. Araméndiz y C.C. Barrera. 2009. Estimación del área foliar de papaya (Carica papaya L.) basada en muestreo no destructivo. Actualidad y Divulgación Científica 12(1): 131-139. [ Links ]
Casierra, P.F., G.R. Peña y J.E. Peña. 2008. Estimación indirecta del área foliar en Fragaria vesca L, Physalis peruviana L., Acca sellowiana (Berg.) Burret, Rubus glaucus L., Passiflora mollisima (Kunth). L.H. Bailey y Ficus carica L. Actualidad y Divulgación Científica 11(1): 95-102. [ Links ]
Chattopadhyay, S., A. Tikader and N.K. Das. 2011. Nondestructive, simple, and accurate model for estimation of the individual leaf area of som (Persea bombycina). Photosynthetica 49(4): 627-632. [ Links ]
Cogliatti, D.H., M.F. Cataldi y F. Iglesias. 2010. Estimación del área de las hojas en plantas de trigo bajo diferentes tipos de estrés abiótico. Agriscientia 27(1): 43-53. [ Links ]
Curiel, A., J.R. Espinoza, J.P. Cruz, G. Almaguer. 2007. Modelos de regresión para estimar área de la hoja y biomasa de órganos en árboles jóvenes de manzano. Revista Chapingo. Serie Horticultura 13(2): 171-177. [ Links ]
De Carvalho, B.L., S. Bianco, V.C. Galati and A.R. Panosso. 2011. Determination of Merremia cissoides leaf area using the linear measures of the leaflets. Acta Scientiarum Agronomy 33(3): 473-476. [ Links ]
De la Casa, A., G. Ovando, L. Bressanini, Á. Rodríguez y J. Martínez. 2007. Uso del índice de área foliar y del porcentaje de cobertura del suelo para estimar la radiación interceptada en papa. Agricultura Técnica 67(1): 78-85. [ Links ]
Demirsoy H., L. Demirsoy, S. Uzun and B. Ersoy. 2004. Non-destructive Leaf area estimation in peach. European Journal Horticultural Science 69(4): 144-146. [ Links ]
Disegna, E., A. Coniberti y E. Dellacassa. 2005. Medición de área foliar de la vid: una herramienta para producir vinos de calidad. Revista INIA 4: 18-20. [ Links ]
Espitia, M.M., R.A. Montoya, J.R. Robles, C.C. Barbosa y C.A. Vergara. 2006. Modelo estadístico para estimación del área foliar en Stevia rebaudiana Bertoni en el Sinu medio. Temas Agrários 11(2): 45-51. [ Links ]
Fallovo, C., V. Cristofori, E. Mendoza de-Gyves, C.M. Rivera, R. Rea, S. Fanasca, C. Bignami, Y. Sassine and Y. Rouphael. 2008. Leaf area estimation model for small fruits from linear measurements. HortScience 43(7): 2263-2267. [ Links ]
Galindo, J.R. y J. Clavijo. 2007. Modelos alométricos para estimar el área de los foliolos de arveja (Pisum sativum L.). Ciencia y Tecnología Agropecuaria 8(1): 37-43. [ Links ]
Ghoreishi, M., Y. Hossini and M. Maftoon. 2012. Simple models for predicting leaf area of mango (Mangifera indica L.). Journal of Biology and Earth Sciences 2(2): 845-853. [ Links ]
Gutiérrez, T.A. y A.A. Lavín. 2000. Mediciones lineales en la hoja para la estimación no destructiva del área foliar en vides cv. Chardonnay. Agricultura Técnica 60(1): 69-73. [ Links ]
Heiner, L. 2007. Using crop models to develop production management tools for flower grower. p.197-210. En: Memorias. II Congreso Colombiano de Horticultura. Colombia hortícola: retos y oportunidades. Sociedad Colombiana de Ciencias Hortícolas. Bogotá D.C. [ Links ]
Kozlowski, T., P. Kramer and S. Pallardy. 1991. The physiological ecology of woody plants. Academic Press, San Diego. 657 p. [ Links ]
Kumar, R. 2009. Calibration and validation of regression model for non - destructive leaf area estimation of saffron (Crocus sativus L.). Scientia Horticulturae 122(1): 142-145. [ Links ]
Legorburo, A., J.A. de Juan, F.J. Montero y M.R. Picornell. 2007. Selección del modelo matemático de estimación del área foliar en cinco cultivares de Vitis vinifera L. p.166-169. En: XI Congreso SECH. Albacete. Actas de Horticultura No. 48. Sociedad Española de Ciencias Hortícolas. España. [ Links ]
Marquínez, X. y G. Corchuelo. 1998. Metabolismo y asignación de fotoasimilados en los cultivos. Comalfi 25(1-3): 59-80. [ Links ]
Mendoza, M., Y. Rouphael, V. Cristofoti and F.R. Mira. 2007. A non-destructive simple and accurate model for estimating the individual leaf area of kiwi (Actinidia deliciosa). Fruits 62(3): 171-176. [ Links ]
Montaldi, E. 1995. Capítulo 19: Bases fisiológicas del rendimiento. pp. 271-287. En: Principios de Fisiología Vegetal. Ediciones Sur, La Plata, Argentina. 298 p. [ Links ]
Muñoz, J.E. 1987. Estimación del área foliar por método no destructivo. ERGOS 1(1): 23-32. [ Links ]
Muñoz, F., M. Espinosa, J. Cancino, R. Rubilar y M. Herrera. 2008. Efecto de poda y raleo en el área foliar de Eucalyptus nitens. Bosque 29(1): 44-51. [ Links ]
Murillo, B., N.Y. Ávila, J.L. García, R. López, E. Troyo and C. Caya. 2004. Short Communication. Relationship between a nondestructive and an extraction method for measuring chlorophyll contents in cowpea leaves. Journal of Plant Nutrition Soil Science 167(3): 363-364. [ Links ]
Pompelli, M.F., W.C. Antunes, D.T. Ferreira, P.G. Cavalcante, H.C. Wanderley and L. Endres. 2012. Allometric models for non-destructive leaf area estimation of Jatropha curcas. Biomass and Bioenergy 36: 77-85. [ Links ]
Ruiz, F.H., B.A. Murillo, J.L. García, E. Trayo, A. Palacios, A. Beltrán, L. Fenech, S. Zamora, P. Marrero, A. Nieto y O. Cruz de la Paz. 2007. Mediciones lineales en la hoja para la estimación no destructiva del área foliar en albahaca (Ocinum basilicum L.). Revista Chapingo Serie Horticultura 13(1): 29-34. [ Links ]
Ruiz, F.H., B. Murillo, J.L. García, L. Fenech, E.O. Rueda, E. Troyo, C. Kaya, and A. Beltrán. 2010. Field evaluation of the relationship between chlorophyll content in basil leaves and a portable chlorophyll meter (Spad-502) readings. Journal of Plant Nutrition 33(3): 423-438. [ Links ]
Sezer, I., F. Oner and Z. Mut. 2009. Non-destructive leaf area measurement in maize (Zea mays L.). Journal of Environmental Biology 30(5): 785-790. [ Links ]
Simón, M. y A. Trujillo del Leal. 1990. Determinación del área foliar en cinco clones de ocumo (Xanthosoma sagittifolium (L.) O. Schott). Revista Facultad de Agronomía 16: 147-158. [ Links ]
Singh, A. 2007. Approximation of leaf area by using leaf dimensions in guava. I International Guava Symposium. Acta Horticulturae 735: 321-324. [ Links ]
Sokal, R.R. and F.J. Rohlf. 1981. Biometry. W.H. Freeman and Co., Nueva York. 859 p. [ Links ]
Tinoco, A.C., F.A. Ramírez, F.E. Villarreal y C.A. Ruiz. 2008. Arreglo espacial de híbridos de maíz, índice de área foliar y rendimiento. Agricultura Técnica en México 34(3): 271-278. [ Links ]
Thornley, J.H. 1976. Mathematical models in plant physiology. Ed. Academic Press. England. 318 p. Citado por: Curiel, A., J.R. Espinoza, J.P. Cruz and G. Almaguer. Revista Chapingo Serie Horticultura. 13(2): 171-177, 2007. [ Links ]
Venturieri, G.A. 1996. Estimativa da área foliar e do peso de folhas secas de plantas jovens de cupuaçu (Theobroma grandiflorum (Will. Ex Spreng.) Schum. - Sterculiaceae) por métodos não destrutivos. Acta Amazónica 25(1 -2): 3-10. [ Links ]
Wang, Z. and L. Zhang. 2012. Leaf shape alters the coefficients of leaf area estimation models for Saussurea stoliczkai in central Tibet. Photosynthetica 50(3): 337-342. [ Links ]
Zamora, F.C. 1989. Caracterización de 17 familias de pejibaye (Bactris gasipaes) pertenecientes a la colección Costa Rica, del CATIE. Trabajo de grado. Escuela de Fitotecnia, Facultad de Agronomía Universidad de Costa Rica. 121 p. [ Links ]