Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Facultad Nacional de Agronomía Medellín
Print version ISSN 0304-2847
Rev. Fac. Nac. Agron. Medellín vol.65 no.2 Medellín June/Dec. 2012
DINÁMICA DEL AGUA EN ANDISOLES BAJO CONDICIONES DE LADERA
SOIL WATER DYNAMICS IN ANDISOLS UNDER HILLSLOPE CONDITIONS
Edgar Hincapié Gómez1 y Conrado Tobón Marín2
1 Investigador Científico I, Disciplina de Suelos. Centro Nacional de Investigaciones de Café (CENICAFÉ). Sede Planalto, km 4 vía Chinchiná, Caldas, Colombia. <Edgar.Hincapie@cafedecolombia.com>
2 Profesor Asociado. Universidad Nacional de Colombia - Sede Medellín - Facultad de Ciencias Agrarias. A.A. 1779, Medellín, Colombia. <ctobonm@unal.edu.co>
Recibido: Mayo 09 de 2012; aceptado: Septiembre 22 de 2012.
Resumen. El flujo de agua en el suelo es calificado como un proceso dinámico que regula reacciones químicas y eventos físicos y biológicos, que a su vez influyen en la nutrición, crecimiento y desarrollo de las plantas; es considerado de interés ambiental, ya que influye en la regulación hidrológica, en la distribución y transmisión de agua, solutos y contaminantes a través de la zona no saturada del suelo. El objetivo de este estudio fue evaluar la dinámica de la humedad volumétrica y del potencial matricial del suelo a lo largo de un periodo de secado, en dos Andisoles, localizados en terrenos de ladera en los municipios de Chinchiná (Caldas) y Quimbaya (Quindío) - Colombia. En cada localidad se seleccionaron y aislaron tres monolitos de suelo de 1,5 m de ancho y 6,0 m de largo, con diferente grado de pendiente (20, 40 y 70%, en Chinchiná y 20, 40 y 75%, en Quimbaya). Se instalaron sensores de humedad y tensiómetros a diferentes profundidades y se monitoreó simultáneamente la humedad volumétrica y el potencial mátrico del suelo durante un periodo de 80 días y se obtuvieron las curvas de secamiento del suelo. El modelo potencial se ajustó mejor al comportamiento de la humedad volumétrica con relación al tiempo; en general, la humedad volumétrica se redujo drásticamente durante la primera etapa del drenaje (0-24 horas); posteriormente, le siguió un drenaje lento en el cual los cambios en la humedad volumétrica a través del tiempo fueron mínimos. La tasa de secamiento del suelo aumentó conforme se incrementó el ángulo de inclinación de la pendiente, lo que se atribuye a una refracción del flujo de agua, considerando que el potencial gravitacional está influido por la inclinación de la pendiente y a la vez indica que la pendiente del terreno afecta el movimiento del agua en el suelo.
Palabras clave: Flujo de agua, geomorfología, drenaje, propiedades hidráulicas.
Abstract. Soil water flux is qualified as a dynamic processes that regulate soil chemical reactions, physical and biological events, which in turn influence plant growth and nutrition. Water flow in soils is considered of environmental importance, since it influences the distribution and transmission of water, solutes and contaminants through the vadose zone. The aim of this study was to evaluate the water dynamics and the matric potential of an Andisols, which were determined over a period of wetting and drying of soil monlith, located on a hillslope area close to Chinchiná (Caldas) and Quimbaya (Quindío) - Colombia. At each site, we selected and isolated three soil monoliths of 1.5 m wide and 6.0 m long, with different slope (20, 40 and 70% in Chinchiná and 20, 40 and 75% in Quimbaya). Soil moisture sensors and tensiometers were installed at different soil depths. The soil volumetric moisture and the matric potential were monitored simultaneously, during 80 days, from which we obtained the drying curves. The resulting potential model fitted the best to the soil volumetric moisture behavior in relation to time. In general, volumetric moisture declined faster during the first drying step (0-24 hours), followed by a slow drainage in which the volumetric moisture changes over time were minimum. The rate of soil drying increased as the increased the slope angle, attributed to a refraction of the water flow, whereas the gravitational potential is influenced by the hillslope of the slope and at the time this indicates that this slope controls the soil water movement.
Key words: Soil water flow, geomorphology, soil drainage, soil hydraulic properties.
Los suelos derivados de cenizas volcánicas son aquellos formados a partir de la meteorización de depósitos de materiales provenientes de eyecciones volcánicas, los cuales han sido denominados Andisoles (Soil Survey Staff, 1999), nombre derivado de ando soil; etimológicamente an significa oscuro y do significa suelo en lenguaje japonés (Wada, 1985; Shoji et al., 1993). El concepto central de los Andisoles abarca dos aspectos fundamentales: (1) material parental de origen volcánico (cenizas, poma, escorias, piroclastos) y (2) suelos cuya fracción coloidal es dominada por materiales no cristalinos. Los Andisoles se encuentran distribuidos en Europa, África, algunas islas del Pacífico, Asia y en América desde Alaska hasta Argentina (Shoji et al., 1993). En Colombia los suelos derivados de cenizas volcánicas representan alrededor del 11,6% del territorio nacional, ocupando zonas de ladera principalmente, los cuales se extienden desde los departamentos de Antioquia, Caldas, Risaralda, Quindío, Valle del Cauca, Cauca, Huila, Nariño, Cundinamarca y Tolima (IGAC, 1995).
Las características y propiedades de los Andisoles, están estrechamente relacionadas con los procesos de formación y evolución que los tipifican, lo cual hace que estos suelos presenten propiedades únicas. Las propiedades físicas, hídricas, mecánicas y químicas de estos suelos, hacen que sean considerados de gran importancia a nivel mundial por su alto potencial productivo, alta acumulación de carbono y nitrógeno, y su alta capacidad de almacenamiento de agua (Shoji y Takahashi, 2004). Una de las características que diferencia a los Andisoles de otros suelos, es su alta capacidad de retención de humedad y almacenamiento de agua, lo cual a su vez determinada la dinámica del agua tanto a nivel superficial como dentro del perfil del suelo (Tobón et al., 2001; Tobón et al., 2010).
La dinámica del agua en el suelo, y a través de la pendiente, juega un papel fundamental en la disponibilidad de agua en el suelo y la distribución de los nutrientes, define la tasa de ocurrencia de procesos microbiológicos y de crecimiento vegetal, gobierna la transpiración, afecta la recarga de acuíferos subterráneos y controla la escorrentía superficial, de allí que su estudio debe integrarse al balance hídrico dentro de los balances hídricos y flujos de energía en los ecosistemas. El flujo de agua en suelos no saturado es el proceso que ocurre en el suelo cuando este está sujeto a cualquier condición de humedad menor que la de saturación (Tobón et al., 2001). Es considerado un proceso dinámico que afecta reacciones químicas y procesos físicos y biológicos que ocurren dentro del suelo e influyen en la nutrición, crecimiento y desarrollo de las plantas, en el almacenamiento de agua en el suelo y en la regulación hidrológica, entre otros; es también considerado de interés desde el punto de vista ambiental, ya que influye en procesos como distribución y transmisión de agua, solutos y contaminantes a través de la zona no saturada del suelo (Hillel, 1971).
El conocimiento de la dinámica del agua en el suelo, tanto a escala global como regional y del perfil del suelo, permite entender y abordar problemas relacionados con la disponibilidad de agua en cuencas hidrográficas, la disminución y contaminación de las fuentes de agua, la dinámica de nutrientes dentro del suelo y su disponibilidad para las plantas y la degradación de los suelos. Sumado a esto, la creciente demanda de agua de calidad para consumo humano y uso agrícola, resaltan la importancia de estudios relacionados con la caracterización de la dinámica del agua en el suelo. Por ende, el estudio de la tasa de humedecimiento y secamiento del suelo y el conocimiento sobre la capacidad de retención de humedad por los suelos, permiten evaluar el efecto de las propiedades físicas e hidráulicas del suelo y del gradiente de pendiente, sobre el movimiento del agua en el suelo, lo cual implica identificar y cuantificar los parámetros que controlan esta dinámica del agua en los suelos ubicados en zonas de ladera.
El flujo de agua en el perfil del suelo puede describirse mediante la estimación de las curvas de drenaje del suelo o modelarse a través de la aplicación de las ecuaciones que explican el movimiento de fluidos a través de medios porosos (Grohmann y Reichardt, 1976; Hillel, 1982; Hillel, 1998). Generalmente, las curvas de drenaje se obtienen mediante el ajuste de funciones tipo potencial, exponencial o logarítmica a los datos de humedad volumétrica registrados a través del tiempo durante un periodo de secamiento del suelo en condiciones controladas (Hewlett y Hibbert, 1963; Hillel, 1998), mientras que el modelamiento del flujo de agua en suelos no saturados se realiza mediante la aplicación de la ley de Darcy-Buckingham y la ecuación de Richards (Richard, 1931), para lo cual es necesario definir las funciones hidráulicas de retención de humedad (q-h) y de conductividad hidráulica (K). La función q-h se conoce como curva de retención de humedad (CRH) y se define como la variación de la succión con la capacidad de retención del agua en los poros del suelo; la K, expresa la capacidad intrínseca del suelo para transmitir agua en diversas condiciones. Características del suelo como la distribución de partículas, geometría de los poros, magnitud y composición mineralógica de la fracción fina, y el contenido de materia orgánica en el suelo son determinantes en la forma e inclinación de la CRH (Fredlund y Xing, 1994; Hillel, 1998); mientras que la distribución de poros según su tamaño, la conectividad entre estos y la tortuosidad, así como la densidad y viscosidad del fluido que se desplaza, determinan la magnitud de K (Gardner, 1958; Hillel, 1998; Warrick, 2003).
En condiciones de suelos de ladera, el movimiento del agua está influido por el grado de la pendiente, ya que este determina la magnitud de procesos hidrológicos como la infiltración, escorrentía superficial y subsuperficial (Philip, 1991; Miyazaki, 1993; Gavin y Xue, 2007); además, en terrenos inclinados opera la conductividad hidráulica horizontal debido al efecto de la pendiente (Ritsema et al., 1996). Otros factores como la presencia de capas impermeables, cambios significativos en las propiedades hidrofísicas de los horizontes del perfil del suelo, también influyen en el movimiento del agua en el suelo (Hewlett y Hibbert, 1963; DiCarlo et al., 1999; Harden y Scruggs, 2003; Bujang et al., 2006).
A pesar de su importancia, existe poca información relacionada con el efecto de la pendiente del terreno sobre la dinámica del agua y las propiedades hidráulicas del suelo, siendo esta información aún más escasa para Andisoles de ladera en el trópico. Dunne y Black (1970), midieron el flujo subsuperficial de agua en canales en una ladera en Vermont, USA; Mosley (1982), midió las propiedades hidráulicas en una ladera excavando canales en el contorno de un bloque de suelo y aplicando agua; Torres et al. (1998), utilizaron tensiómetros, piezómetros y lisímetros para identificar las vías de flujo de agua subsuperficial y Tobón et al. (2010), determinaron los flujos de agua en suelos de ladera en Costa Rica, mediante la caracterización de las propiedades hidrofísicas de Andisoles y el monitoreo continuo de la humedad del suelo.
En el caso especial de los Andisoles de la zona cafetera colombiana, no existen estudios relacionados con las interacciones entre la geomorfología del paisaje, las características de las precipitaciones, las propiedades superficiales y el uso del suelo, y su relación con la magnitud y velocidad del flujo del agua en el suelo. De acuerdo con lo anterior, la presente investigación tuvo como objetivo caracterizar la dinámica del agua en Andisoles, ubicados en zonas de ladera, y determinar el efecto de la pendiente del terreno sobre dicha dinámica, en suelos derivados de cenizas volcánicas de la región central cafetera de Colombia.
MATERIALES Y MÉTODOS
Para evaluar la dinámica del agua en el suelo, se seleccionaron dos clases de suelos derivados de cenizas volcánicas clasificados como unidad Chinchiná (CH) (Typic Hapludand) y unidad Montenegro (MN) (Typic Melanudand), los cuales son representativos de la región central cafetera de Colombia (Grisales et al., 1982). Los suelos objeto del estudio se ubicaron en la Estación Experimental Naranjal del Centro Nacional de Investigaciones de Café "Cenicafé" (unidad Chinchiná) en Chinchiná - Caldas a 4°59' N, 79°39' O y 1400 msnm y en la hacienda Maracay (unidad Montenegro) localizada en Quimbaya - Quindío a 4°36' N, 75°44' O y 1402 msnm.
En cada localidad se seleccionó un terreno con diferentes grados de pendiente y en este se localizaron y seleccionaron tres unidades de medición con diferente grado de la pendiente. Unidades CH-I, CH-II y CH-III con pendiente del 20, 40 y 70%, en Naranjal, respectivamente y MN-I, MN-II y MN-III, con pendientes del 20, 40 y 75%, en Maracay, respectivamente.
En cada clase de suelos se excavaron tres calicatas de 1,5 m de ancho, 1,0 m de largo y 1,5 m de profundidad y se realizó muestreo de suelos en cada uno de los horizontes diagnóstico del perfil, hasta una profundidad de 1,2 m. Se tomaron muestras disturbadas y sin disturbar para determinar las propiedades físicas e hidráulicas del suelo, en el laboratorio de suelos del Centro Nacional de Investigaciones de Café, Cenicafé. De acuerdo con el protocolo establecido por el laboratorio de Cenicafé y descrito por Hincapié y Tobón (2010), se determinaron propiedades como la textura del suelo, la densidad aparente, la porosidad total, la curva de retención de humedad a diferentes tensiones y la conductividad hidráulica saturada.
Asimismo, en cada una de las unidades de medición se aisló un monolito de suelo de 1,5 m de ancho, 6,0 m de largo y 1,6 m de profundidad; para ello se excavaron zanjas alrededor del monolito hasta una profundidad de 1,8 m y se cubrieron sus paredes con plástico, aislándolos del resto del continuo suelo. Una vez aislados los monolitos, e instalados los instrumentos, se cerraron nuevamente las zanjas con el suelo extraído. En cada monolito se instalaron los siguientes dispositivos:
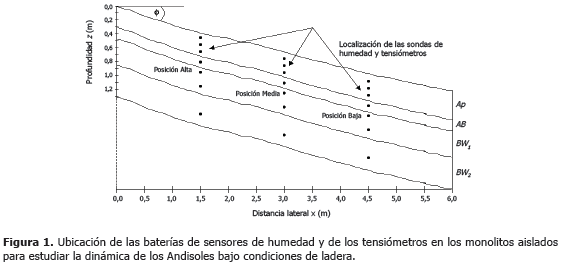
Sensores de humedad modelo Trase 6005 Waveguide Soilmoisture® de 20 cm de longitud con tres varillas para medir humedad volumétrica del suelo (q), con el equipo TDR (Time Domain Reflectometry) fueron insertados horizontalmente en el eje z del perfil del suelo a 10, 20, 30, 45, 60, 80 y 120 cm de profundidad en Naranjal y a 10, 30, 45, 60, 80 y 120 cm de profundidad en Maracay. Estas profundidades incluyeron los horizontes diagnóstico Ap, AB, BW1 y BW2. Cada una de las baterías de sensores se ubicó en las posiciones alta (A), media (M) y baja (B) del monolito de suelo a una distancia del eje x de 1,5; 3,0 y 4,5 m del borde superior de cada monolito (Figura 1). Tensiómetros con transductor electrónico Eijkelkamp® Tensior 4 con capsula porosa de 4 cm para medir la tensión h (potencial mátrico del suelo), fueron instalados a un lado de cada uno de los sensores de humedad del suelo y a la misma profundidad de estos, para la generación de datos pareados.
Una vez instalados los sensores y tensiometros, cada una de las paredes del monolito se cubrió con lámina plástica, con el fin de aislar el área del ingreso y salida de agua. Posteriormente, todas las excavaciones se taparon con el mismo suelo. Luego, se aplicó agua en el suelo hasta saturación de cada perfil, lo cual se logró cuando la tensión (h) registrada en cada uno de los tensiómetros presentó un valor h ≈ 0. Después de la saturación, el monolito se cubrió permanentemente con barbecho y luego con lámina plástica para impedir la evaporación y a la vez el ingreso de agua lluvia dentro del perfil del suelo.
Mediante la medición de los sensores TDR y tensiometros, se monitoreó simultáneamente la humedad volumétrica y el potencial mátrico del suelo a través del tiempo, durante 90 días, cuando el nivel del agua en el suelo fue el mínimo posible en campo. Se realizó una primera lectura antes de la saturación del suelo y después de esta a saturación a 0 horas, luego a las 1, 4, 6, 20, 24 horas; posteriormente cada 24 horas, durante 5 días, y luego cada 5 días durante un periodo de 85 días, para un total de 90 días de monitoreo continuo de la humedad y la tensión de humedad del suelo. A partir de la información colectada en cada profundidad de los perfiles de suelo o monolitos, se obtuvieron las curvas de drenaje o secamiento del suelo.
Estimación de las curvas de drenaje del suelo. Las curvas de drenaje del suelo, se obtuvieron mediante el ajuste de los datos de humedad volumétrica registrados a través del tiempo a un modelo no lineal. El criterio de decisión para seleccionar el mejor modelo fue la raíz del cuadrado medio del error (RCME) y el Pseudo-R2. El modelo seleccionado, se ajustó a los datos de humedad volumétrica registrados a través del tiempo para cada una de las posiciones y profundidades en cada uno de los monolitos, mediante estimación de los parámetros de ajuste. Este ajuste se realizó por el método Marquardt en el programa SAS®, el algoritmo iterativo de estimación fue Newton con un parámetro lambda (?) de convergencia.
Análisis estadístico. Con el fin de valorar si existen diferencias del comportamiento de la humedad del suelo debidas al efecto de la pendiente del terreno, así como debidas a los cambios en los horizontes del perfil, se compararon los modelos que describen las curvas de drenaje del suelo. Para esto se utilizó el método basado en el principio de la suma de cuadrados reducida y prueba de estadístico F (Schabenberger y Pierce, 2002).
Comparación entre modelos globales. Para estimar los parámetros de ajuste, de cada uno de los modelos y sus intervalos de confianza, así como para realizar las pruebas de hipótesis, se empleó el método nlin del paquete SAS®. Los intervalos de confianza se construyeron a partir del modelo único. Para el cálculo se incluyó en el modelo único una función indicador I, que retorna el valor de 1 si determinada condición es cierta y 0 en caso contrario:
![]()
Por ejemplo, si las observaciones corresponden al monolito 1, entonces I (j=1) toma el valor de 1, en caso contrario toma el valor de 0. Bajo la hipótesis nula, el modelo global de drenaje de los tres monolitos de cada localidad, está dado por un único modelo:
![]()
Si la hipótesis nula no es válida, entonces existen dos o tres modelos globales de drenaje del suelo en cada localidad.
Para realizar la comparación de los modelos por localidad, se estimaron los parámetros del modelo general, que minimizan la suma de cuadrados del error en el ajuste con las n observaciones (SCETotal).
Posteriormente, se estimaron los parámetros de los modelos individuales (por cada monolito) que independientemente minimizan la suma de cuadrados del error en el ajuste de las nI, nII, nIII,, observaciones, es decir SCEI, SCEII y SCEIII, respectivamente.
Donde,
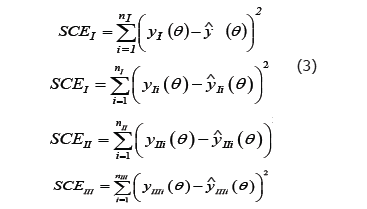
donde, yi(q) corresponde al conjunto de las n mediciones de humedad volumétrica registradas a través del tiempo (en los tres monolitos); yi(q) es el ajuste realizado al conjunto de los n datos; yIi (q); yIIi (q); yIIIi (q) corresponde a las mediciones individuales realizadas a través del tiempo en los monolitos I, II y III, respectivamente, y yIi (q); yIi (q); yIi (q) corresponde al ajuste realizado en los nI, nII, nIII, datos de los monolitos I, II y III, respectivamente.
Mediante la prueba F, se explica las diferencias entre monolitos y dentro de los monolitos así:
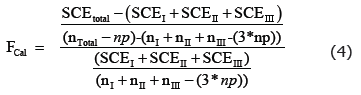
Donde, SCETotal - (SCEI + SCEII + SCEIII) es la suma de cuadrados de errores "entre" las pendientes (monolitos) que tienen (ntotal - p)-(nI+nI+nIII-3*p) grados de libertad, esta suma de cuadrados está asociada al modelo reducido y (SCEI + SCEII + SCEIII ) = SCE, es la suma de cuadrados de errores "dentro" de las pendientes (monolitos) y tiene ntotal - p) - nI + nI + nIII - 3*p) grados de libertad, esta suma de cuadrados está asociada al modelo completo.
Si bajo el estadístico F, las curvas de drenaje del suelo comparadas, presentaron diferencias, se realizó comparación individual de parámetros. Para ello, se construyó un modelo único con una función indicador I:
![]()
Para comparar los parámetros de los modelos, se expresó el parámetro a comparar en función del otro; por ejemplo, para comparar el parámetro a de los modelos, CH-I y CH-II, la expresión es: a1 vs a2 así: a2 = a + d; si el intervalo e confianza de d no contiene el cero, indica que estadísticamente d ≠ 0 y por lo tanto, a1 ≠ a2.
RESULTADOS Y DISCUSIÓN
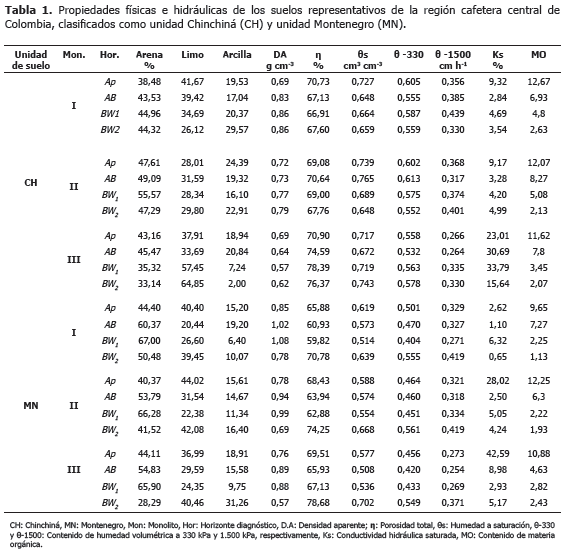
Propiedades hidrofísicas de los Andisoles de ladera. En la Tabla 1, se presenta la caracterización física e hidráulica de los suelos y el contenido de materia orgánica de cada uno de los horizontes diagnóstico en los seis monolitos de suelo estudiados.
De acuerdo con la Tabla 1, en los suelos estudiados predomina la textura franca en superficie; sin embargo, a profundidad se presenta un cambio de la textura, por un ligero incremento en el contenido de arcilla. Este cambio en la distribución de partículas, entre los horizontes AB a BW1 y BW1 a BW2, puede generar gradientes en las propiedades hidráulicas y por lo tanto en la dinámica del agua en el suelo. Existe una baja variabilidad en la textura entre los tres monolitos, donde las arenas son la fracción que menos variabilidad presenta en profundidad.
En términos generales, la densidad aparente de estos suelos es baja (Tabla 1) en los primeros horizontes y aumenta a partir del horizonte BW, mientras que la porosidad total disminuye con la profundidad. La excepción a esta tendencia se presenta en el perfil CH-II, donde a medida que se incrementa la profundidad del suelo la densidad aparente disminuye y la porosidad aumenta, estas diferencias pueden explicarse por las variaciones en los contenidos de arena en dichos perfiles; dado que en los horizontes que presentan mayor contenido de arena, el valor de la densidad aparente es el más alto. Con referencia al contenido de materia orgánica, en estos suelos se observa la misma tendencia, a medida que aumenta la profundidad del suelo, disminuye su contenido, desde 13% en el primer horizonte, hasta cerca del 2% en el límite inferior a 120 cm de profundidad. De acuerdo con lo descrito por Hincapié y Tobón (2010), las propiedades que presentan los Andisoles estudiados favorecen la circulación de agua y aire en el suelo.
Por su parte, la humedad a saturación presenta valores superiores a 0,6 cm3 cm-3, en todas las profundidades evaluadas, lo cual corresponde con el rango de valores reportados para suelos derivados de cenizas volcánicas (Henao et al., 1997; Fontes et al., 2004). La conductividad hidráulica saturada (Ks), presenta valores de mayores a 18 cm h-1, la cual se califica como muy rápida, asociada con su alta porosidad (>69%), baja densidad aparente (<0,7 g cm-3) y menor retención de humedad. Esta Ks disminuye a medida que se profundiza en el perfil del suelo, aunque se presentan pequeñas discontinuidades hidrológicas en los horizontes de transición, lo cual coincide con cambios en la distribución de partículas del suelo. Los análisis estadísticos indican diferencias significativas en la mayoría de las propiedades evaluadas, tanto entre los horizontes en cada perfil, como entre los monolitos (Hincapié y Tobón, 2010).
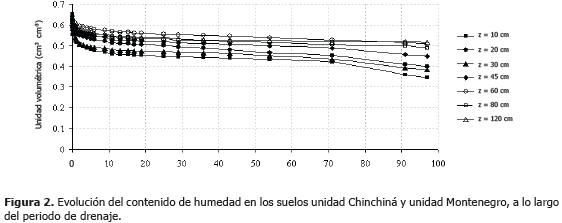
Comportamiento hidrodinámico del agua en el suelo. En la Figura 2, se presenta la evolución del contenido de agua en el suelo en función del tiempo. En general, la humedad volumétrica del suelo, al inicio de las mediciones, se redujo drásticamente durante la primera etapa del drenaje (0-24 horas), en esta etapa, principalmente los poros de mayor tamaño son los que conducen el agua (Hillel, 1998), de allí que en los horizontes con mayor proporción de macroporos (horizontes Ap y AB) los cambios en la humedad fueron mayores en las primeras 24 h. Posteriormente, sigue un drenaje lento en el cual los cambios en la humedad volumétrica a través del tiempo fueron mínimos. Reducciones lentas de la humedad en suelos, han sido registradas por Dirksen (1991) y están relacionadas con la alta capacidad de retención de humedad propia de los Andisoles, la cual parece ser mayor en el horizonte BW (a una profundidad entre 80 y 120 cm) que permanece a humedad cercana a saturación durante todo el tiempo de evaluación.
A escala del perfil, en el horizonte Ap (0-45 cm) la humedad del suelo se redujo cerca del 38% durante 90 días aproximadamente, de esta reducción de humedad, alrededor del 20% ocurrió durante las primeras 24 h del periodo de drenaje. Similar comportamiento se presentó en las demás profundidades evaluadas, excepto en el horizonte BW2 a 120 cm de profundidad, donde la humedad del suelo se redujo aproximadamente un 20% durante todo el periodo de drenaje, de la cual del 8 y 10% se produjo en las primeras 24 h.
Los suelos estudiados se caracterizaron por presentar alta humedad en profundidad, en este caso el flujo de agua no es necesariamente pequeño a bajos gradientes de humedad, lo que indica claramente que el potencial gravitacional controla el flujo de agua, ya que cuando la humedad entre capas subyacentes es alta, el gradiente matricial tiende a ser pequeño, por lo tanto el movimiento tiende a estar bajo la influencia de la gravedad.
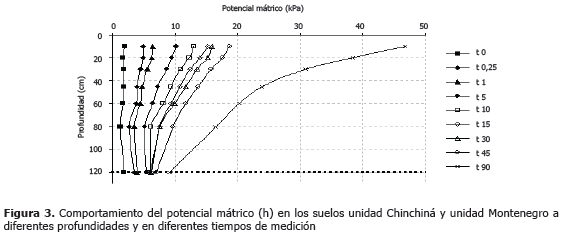
Potencial mátrico del suelo. En la Figura 3, se muestra el comportamiento del potencial mátrico (h) a diferentes profundidades y en diferentes tiempos de medición. Se puede observar como en todo el perfil del suelo, se alcanza un grado de humedad cercano al punto de saturación (h ≈ 0 kPa), el cual corresponde al día 0, o etapa inicial de la medición; posteriormente, se inicia un proceso de drenaje o redistribución del agua en el suelo, el cual se caracteriza por el incremento en el potencial mátrico. Durante los días donde el suelo estuvo alrededor del punto de saturación, h es casi idéntico a lo largo de todo el perfil, en estas condiciones el gradiente de potencial mátrico es casi nulo y por lo tanto el movimiento del agua en el suelo está determinado solamente por el potencial gravitacional e influido por la pendiente del terreno (Miyazaki, 1993). A partir del día 5, h se incrementa notoriamente, dicho incremento es mayor a nivel superficial, mientras que a la profundidad de 120 cm los cambios de h fueron mínimos (entre 5 y 20 kPa). Lo anterior indica la formación de una capa que puede permanecer casi saturada durante un largo periodo de tiempo y que influye en los procesos de la dinámica del agua en estos suelos, tales como flujos preferenciales, flujos laterales y ascenso capilar.
Las variaciones del potencial mátrico encontradas a través del perfil del suelo, pueden estar relacionadas con los cambios en las propiedades físicas e hidráulicas de los diferentes horizontes del perfil del suelo. En los horizontes Ap y AB, el alto contenido de materia orgánica, baja densidad aparente, alta porosidad y presencia de macroporos y fisuras por efecto de la alta presencia de raíces, determinan mayor dinámica del agua en estos horizontes; mientras que el cambio textural, la menor porosidad, mayor densidad aparente, menor conductividad hidráulica y alta retención de humedad, determinan la acumulación de humedad en los horizontes profundos.
Ajuste de las curvas de drenaje. Los resultados del ajuste de las curvas de drenaje del suelo, mostraron que el modelo potencial (ecuación 6) permitió describir con mejor precisión, el comportamiento de la humedad volumétrica con relación al tiempo (RCME<0,001; R2>0,96):
![]()
Donde, qi,j corresponde a las mediciones de humedad volumétrica realizadas en el tiempo ti,j, a y b son parámetros de ajuste del modelo relacionados con el contenido inicial de humedad y la tasa de drenaje del suelo, respectivamente. Valores de a altos, implican un contenido de humedad inicial alto, mientras que valores de b bajos, implican menor tasa de drenaje del suelo y viceversa.
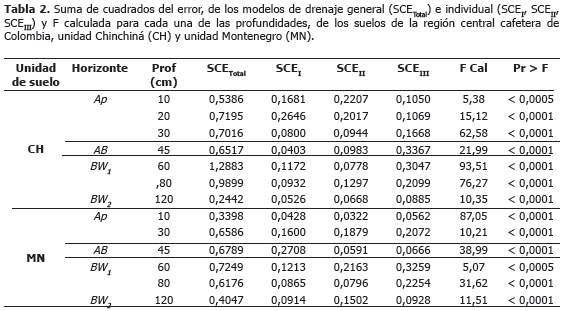
En la Tabla 2, se presentan los valores de la suma de cuadrados del error del modelo general obtenido a partir de los n valores de humedad volumétrica vs tiempo registrados en cada suelo y la suma de cuadrados del error del modelo obtenido a partir de los n valores de humedad volumétrica vs tiempo registrados en cada monolito de cada suelo.
Al comparar las curvas de drenaje del suelo entre monolitos (pendientes) por profundidad, se encontró evidencia estadística, que tanto en los suelos de la unidad Chinchiná como en Montenegro, en todas las profundidades evaluadas, las curvas de drenaje del suelo difieren entre pendientes. Por lo cual, se procedió a la comparación de parámetros individuales, para ello se empleó la ecuación 6. Para estimar los parámetros de ajuste a y b, y los intervalos de confianza del modelo para cada una de las condiciones evaluadas, se empleó la ecuación 7:
![]()
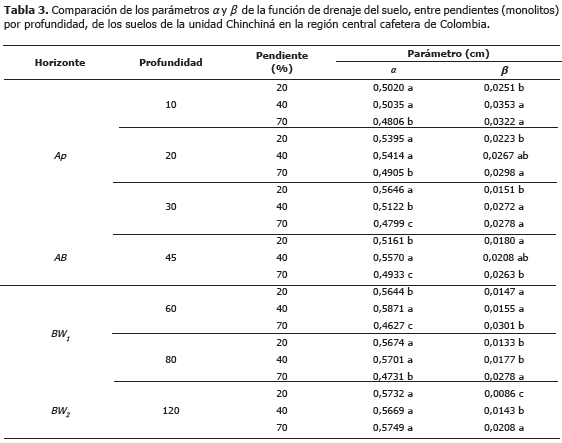
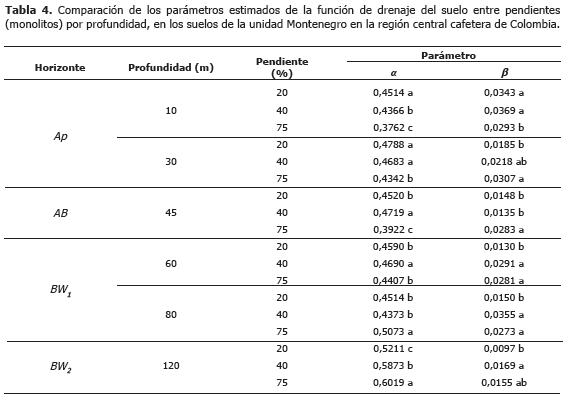
En las Tablas 3 y 4, se presentan los valores de los parámetros a y b de los modelos de drenaje del suelo, para cada una de las profundidades y pendientes evaluadas en los dos suelos. En general, los valores del parámetro a fueron mas altos en los suelos de la unidad Chinchiná, comparados con Montenegro, lo que implica mayores valores de la humedad cercana al punto de saturación en los suelos de la unidad Chinchiná y puede explicarse por el efecto de algunas propiedades del suelo tales como porosidad total, densidad aparente y contenido de arena (Tabla 1). En ambos suelos los valores de a aumentaron a medida que se incrementó la profundidad del suelo, los menores valores se encontraron en los suelos de mayor pendiente, excepto a las profundidades de 120 cm. Estadísticamente, el parámetro a presentó diferencias entre las pendientes evaluadas, principalmente entre la pendiente menor (20%), comparada con la mayor (>70%).
Al comparar la tasa de drenaje (parámetro b), entre pendientes por profundidad en cada suelo, se pudo observar que en todas las profundidades evaluadas existen diferencias estadísticas entre las pendientes, principalmente entre 20% y 70%. Los mayores valores del parámetro b se asocian con las pendientes mayores, lo cual indica que tanto en los suelos de la unidad Chinchiná como en Montenegro, la tasa de drenaje del suelo es mayor en los suelos de mayor pendiente, esto puede obedecer al hecho que el flujo de agua en terrenos pendientes está influido por la conductividad hidráulica horizontal que comienza a operar por efecto del gradiente de pendiente y generar flujos de agua laterales.
En terrenos pendientes la fuerza de gravedad que actúa en forma descendente durante el proceso de infiltración del agua en el suelo, se resuelve de acuerdo al coseno del ángulo de la pendiente y actúa perpendicular a esta (Miyazaki, 1993; Ritsema et al., 1996). De otro lado, en terrenos inclinados, el flujo de agua está afectado por la resistencia friccional o viscosa, dado que el agua tiende a avanzar más adherida a las paredes de los poros a medida que aumenta el grado de la pendiente, este proceso es descrito como refracción del flujo de agua (Miyazaki, 1993; Hillel, 1998).
Algunos autores han observado disminución de la conductividad hidráulica no saturada al aumentar el ángulo de inclinación de la pendiente (Bodhinayake et al., 2004; Casanova et al., 2009), lo cual puede obedecer al efecto de la conductividad hidráulica horizontal. De allí que la inclinación de la pendiente, sumado a la variabilidad espacial de las propiedades físicas e hidráulicas, puede controlar el movimiento de agua en el suelo (Daniels et al., 1987; Venterea et al., 2003; Tsui et al., 2004).
Implicación de los resultados en la determinación de los flujos de agua y nutrientes en suelos Andisoles bajo condiciones de ladera. En los suelos estudiados, bajo condiciones de mínima pendiente o casi planos, el movimiento del agua dentro del suelo está determinado por las funciones hidráulicas del suelo, asociadas con las propiedades físicas de este; sin embargo, en condiciones de ladera el movimiento del agua está adicionalmente controlado por la pendiente del terreno, lo cual puede inducir flujos laterales de agua en el suelo, generando variaciones en el contenido de humedad. Asimismo, la presencia de capas impermeables o cambios significativos de las propiedades hidrofísicas de los horizontes del suelo, parecen ser los responsables de la generación de flujos laterales de agua y asociados a estos flujos de agua, se mueven los nutrientes solubles en los suelos Andisoles de ladera.
Como se observa, estos suelos se caracterizan por presentar alta humedad en profundidad, en este caso el flujo de agua no es necesariamente pequeño a bajos gradientes de humedad, lo que indica claramente que el potencial gravitacional controla el flujo del agua, ya que cuando la humedad entre capas subyacentes es alta, el gradiente matricial tiende a ser pequeño, por lo tanto el movimiento tiende a estar bajo la influencia de la gravedad. Durante el tiempo de evaluación, el contenido de humedad del suelo no se redujo por debajo de 0,34 cm3 cm-3, lo que bajo condiciones de la medición corresponde a un potencial matricial de aproximadamente 300 kPa. Lo anterior se convierte en una limitación del método del perfil instantáneo, para el modelamiento del flujo del agua en estos suelos, dado que los valores de conductividad hidráulica no saturada que se obtienen, sólo son válidos para un rango estrecho de potenciales, pero a su vez expresaría las condiciones reales de estos suelos.
Estos resultados, muestran que dentro del mismo horizonte del suelo, existe una relativa homogeneidad de las variables que determinan la retención de humedad del suelo, por lo tanto la variación lateral de la humedad volumétrica y de los flujos de agua en estos suelos, puede originarse por otros factores tales como el grado de inclinación del terreno. Lo anterior implica que el gradiente de inclinación o pendiente del terreno controla gran parte de los flujos de agua en los suelos Andisoles bajo condiciones de ladera, lo que a su vez controla los flujos de solutos en el suelo, en dirección de la pendiente.
CONCLUSIONES
Se pudo verificar que existe un incremento en la magnitud del movimiento del agua en los Andisoles a medida que el ángulo de inclinación de la pendiente del terreno es mayor, lo cual es independiente de los cambios en las propiedades del suelo determinadas por cada uno de los horizontes del perfil suelo. De acuerdo con los resultados, se observó que a medida que se incrementa la pendiente del terreno se disminuye la densidad aparente y se incrementa la porosidad y la conductividad hidráulica saturada. La relación de estas propiedades con la pendiente del terreno puede originarse por el efecto de una mayor infiltración de agua lluvia en el suelo en terrenos planos, la cual actúa como un factor natural de compactación, que puede generar cambios en la densidad aparente, porosidad y conductividad hidráulica.
Al determinar el ajuste de las funciones que describen la tasa de drenaje del suelo, el modelo potencial permitió describir con mejor precisión, el comportamiento de la humedad volumétrica con relación al tiempo; en dicho modelo, los valores mas altos del parámetro b se asociaron con las determinaciones realizadas en los suelos de mayor pendiente y en los horizontes superficiales (Ap), lo cual indica que para estos casos el proceso de drenaje fue más rápido y puede obedecer al hecho que el flujo de agua en terrenos de alta pendiente, está influido por la conductividad hidráulica horizontal y la ocurrencia de flujos laterales de agua.
Es posible estudiar la dinámica del agua en suelos de ladera, directamente en condiciones de campo con la mínima alteración del suelo, mediante procesos de humedecimiento y secado del suelo y el monitoreo de la humedad volumétrica y del potencial mátrico con sensores de humedad y tensiómetros, a escalas temporales muy cortas. Esto generará nuevo conocimiento sobre la dinámica del agua en el suelo y permite entender mejor, no solo la dinámica del agua en suelos Andisoles bajo condiciones de ladera, sino igualmente la dirección y magnitud de los flujos de nutrientes solubles en estos suelos, lo cual se convierte en una herramienta de manejo de los cultivos y la fertilidad de estos suelos.
AGRADECIMIENTOS
Se agradece el apoyo brindado por Cenicafé y la Universidad Nacional de Colombia, lo cual hizo posible la realización de la investigación que permitió la elaboración de este artículo.
BIBLIOGRAFÍA
Bodhinayake, W., S.B. Cheng and K. Noborio. 2004. Determination of hydraulic properties in sloping landscapes from tension and double-ring infiltrometers. Vadose Zone Journal 3(3): 964-970. [ Links ]
Bujang, B.K., H.J. Faisal and T.H. Low. 2006. Water infiltration characteristics of unsaturated soil slope and its effect on suction and stability. Geotechnical and Geological Engineering 24(5): 1293-1306. [ Links ]
Casanova, M.P., G.O. Salazar, S.O. Seguel and A.V. Noguer. 2009. Hydraulic conductivity on soil monoliths of Central Chile. Journal Soil Science and Plant Nutrition 9(3): 210-221. [ Links ]
Daniels, W.L., L.W. Zelazny and C.J. Everett. 1987. Virgin hardwood forest soil of the southern Appalachian mountains: II. Weathering, mineralogy and chemical properties. Soil Science Society of American Journal 51(3): 730-738. [ Links ]
DiCarlo, D.A., T.W. Bauters, C.J. Darnault, T.S. Steenhuis and J.Y. Parlange. 1999. Lateral expansion of preferential flow paths in sands. Water Resources Research 35(2): 427-434. [ Links ]
Dirksen, C. 1991. Unsaturated hydraulic conductivity. pp. 209-269. In: Smith, K.A. and C.E. Mullins. (eds.). Soil analysis physical methods. New York. 620 p. [ Links ]
Dunne, T. and R.D. Black. 1970. An experimental investigation of runoff production in permeable soils. Water Resources Research 6(2): 478-490. [ Links ]
Fontes, J.C., L.S. Pereira and R.E. Smith. 2004. Runoff and erosion in volcanic soils of Azores: simulation with OPUS. Catena 56(1-3): 199-212. [ Links ]
Fredlund, D.G. and A. Xing. 1994. Equations for the soil-water characteristic curve. Canadian Geotechnical Journal 31(3): 521-532. [ Links ]
Gardner, W.R. 1958. Some steady state solutions of unsaturated moisture flow equations with applications to evaporation from water table. Soil Science 85(4): 228-232. [ Links ]
Gavin, K. and J. Xue. 2007. A simple method to analyze infiltration into unsaturated soil slopes. Computers and Geotechnics 35(4): 223-230. [ Links ]
Grohmann, F. e K. Reichardt. 1976. Metodos de determinaçao da conductividades hidraulica do solo. Campinas. Instituto Agronomico Circular No. 53. Brasil. 28 p. [ Links ]
Grisales, G.A, O.J. Álvarez, J. Chavarriaga, O. Olarte y A. Quevedo. 1982. Estudio de zonificación y uso potencial del suelo en la zona cafetera del departamento de Caldas. Federacafé. FNC, Bogotá. 309 p. [ Links ]
Harden, C.P. and D.P. Scruggs. 2003. Infiltration on mountain slopes: a comparison of three environments. Geomorphology 55: 5-24. [ Links ]
Henao, M.C., B. Delvaux y S. Suárez. 1997. Comparación de dos métodos de análisis granulométrico aplicados en Andisoles de la zona cafetera central de Colombia. Cenicafé 48(1): 12-25. [ Links ]
Hewlett, J.D. and A.R. Hibbert. 1963. Moisture and energy conditions within a sloping soil mass during drainage. Journal of Geophysical Research 68(4): 1081-1087. [ Links ]
Hillel, D. 1971. Soil and water: physical principles and processes. Academic Press. New York. 288 p. [ Links ]
Hillel, D. 1982. Introduction to soil physics. Academic Press. New York. 364 p. [ Links ]
Hillel, D. 1998. Environmental soil physics. Academic Press. New York. 413 p. [ Links ]
Hincapié, E. y C. Tobón. 2010. Caracterización de las propiedades hidrofísicas de los Andisoles en condiciones de ladera. Suelos Ecuatoriales 40(2): 156-169. [ Links ]
Instituto Geográfico Agustín Codazzi. IGAC. 1995. Suelos de Colombia. Origen, evolución, clasificación, distribución. IGAC, Santafé de Bogotá. 632 p. [ Links ]
Mosley, M.P. 1982. Subsurface flow velocities through selected forest soils South Island, New Zeland. Journal of Hydrology 55(1-4): 65-92. [ Links ]
Miyazaki, T. 1993. Water flow in soils. Marcel Dekker, New York. 296 p. [ Links ]
Philip, J.R. 1991. Infiltration and downslope unsaturated flows in concave and convex topographies. Water Resources Research 27(6): 1041-1048. [ Links ]
Richards, L.A. 1931. Capillary conduction of liquids through porous mediums. Journal of Applied Physics 1(5): 318-333. [ Links ]
Ritsema, C.J., K. Oostindie and J. Stolte. 1996. Evaluation of vertical and lateral flow through agricultural loessial hillslopes using a two-dimensional computer simulation model. Hydrological Processes 10(8): 1091-1105. [ Links ]
Schabenberger, O. and F.J. Pierce. 2002. Contemporary statistical models for the plant and soil sciences. CRC Press, Washington, D.C. 730 p. [ Links ]
Shoji, S., M. Nanzyo and R. Dahlgren. 1993. Volcanic ash soils: genesis, properties and utilization. Elsevier, Amsterdam. 288 p. [ Links ]
Shoji, S. and T. Takahashi. 2004. Environmental and agricultural significance of volcanic ash soils. Global Environmental Research. Association of International Research Initiatives for Environmental Studies (AIRIES) Japan 6(2): 113-135. [ Links ]
Soil Survey Staff. 1999. Soil taxonomy. Second edition. USDA-NRCS. Agriculture Handbook No. 436. 328 p. [ Links ]
Tobón, C., L.A. Bruijnzeel, K.F. Frumau and J.C. Calvo. 2010. Changes in soil physical properties after conversion of tropical montane cloud forest to pasture in northern Costa Rica. pp. 502-515. In: Bruijnzeel, L.A., F.N. Scatena and L.S. Hamilton (eds.). Tropical Montane Cloud Forests: Science for Conservation and Management. Cambridge University Press, Cambridge, UK. 768 p. [ Links ]
Tobón, C., W. Bouten and J. Sevink. 2001. Monitoring and modelling soil water dynamics in entire forest ecosystems in northwest Amazonia. Hydrology and Earth System Sciences 56: 145-156. [ Links ]
Torres, R., W.E. Dietrich, D.R. Montgomery, S.P. Anderson and K. Loague. 1998. Unsaturated zone processes and the hydrologic response of a steep, unchanneled catchment. Water Resources Research 34(8): 1865-1879. [ Links ]
Tsui, C., Z.S. Chen and C.F. Hsieh. 2004. Relationships between soil properties and slope position in a lowland rain forest of southern Taiwan. Geoderma 123(1-2): 131-142. [ Links ]
Venterea, R.T., G.M. Lovett, P.M. Groffman and P.A. Schwarz. 2003. Landscape patterns of net nitrification in a northern hardwood conifer forest. Soil Science Society of American Journal 67(2): 527-539. [ Links ]
Wada, K. 1985. The distinctive properties of Andosols. Advances in Soil Science 2: 173-229. [ Links ]
Warrick, A. W. 2003. Soil water dynamics. Oxford University Press, 391 p. [ Links ]