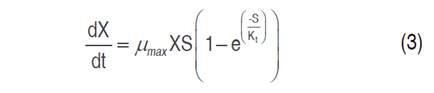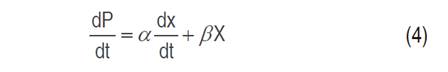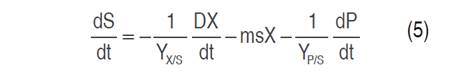Hemicellulose, the second most abundant polysaccharide in nature is used to generate value-added products such as xylitol, widely used in the food industry, as well as in products for oral hygiene, pharmaceuticals and cosmetics (Prakasham et al., 2009) . The use of lignocellulosic material such as oil palm empty fruit bunch (OPEFB) is an alternative for the production of this sugar alcohol. Colombia is the largest producer of oil palm in Latin America and the fourth largest producer in the world (Fedepalma, 2014). The OPEFB constitutes 21% of the total weight of harvested fruits and is one of the most promising resources of biomass waste, because they can be used as a substrate for the production of different compounds with chemical and biochemical processes, such as xylitol (Manjarres-Pinzon et al., 2017). During the hydrolysis, the polymers present in the hemicellulosic fraction are broken until obtaining xylose, a sugar that is converted to xylitol by fermentation. Xylitol yield and substrate consumption must be high and the production costs low for the xylitol industrial application (Yewale et al., 2017). In the market, xylitol is produced chemically based on a catalytic reduction of pure xylose, which is generally obtained from lignocellulosic residues, under high pressure and temperature using expensive catalyst (usually Ni-catalyst) (Rao et al., 2016). Currently, the commercial production of xylitol from lignocellulosic wastes is not made by biotechnological route; however, biotechnological production of xylose to xylitol offers a better alternative in terms of energy intensity of the production process of xylitol and overall process cost.
Mathematical modeling is an important tool to simulate and predict the operating conditions of a process. The mathematical model is important to deduce if there is inhibition by substrate or by production of a metabolite product, and to show the metabolic behavior of a strain; therefore, in the case of the biotechnological production of xylitol, the mathematical model can indicate the phase of growth where occurs more metabolite production, and what is the behavior at the numerical level to be able to predict results at the experimental level with different fermentation conditions. However, it is necessary to properly understand the biochemical principles of a biotechnological process to build a suitable model (Aguiar et al., 2002). It is important to qualitatively describe the system where the problem is evidenced to develop a mathematical model from flask-scale experimental data showing yeast growth, xylose consumption and xylitol production. Furthermore, the fundamental laws that govern the system, the aim of the model, the specification of input and output variables, the accuracy degree, the application scope and the factors during the fermentation process that support the model must be taken into account.
There is few information on modeling the kinetics of xylitol production. Moreover, it has focused on growth prediction of C. guilliermondii using non-linear methods (Aguiar et al., 2002), as well as on the development of a model with C. parapsilosis subjected to limited oxygen conditions (Aranda-Barradas et al., 2000) of a growth model of C. mogii with the presence of glucose as a co-substrate to facilitate xylitol production (Tochampa et al., 2005) and of a C. tropicalis growth model, based on the initial concentration of xylose and oxygen that is related to the agitation rate (Mohamad et al., 2016).
The diversity of raw materials and the complexity of fermentation processes mean that there are many ways to approach the mathematical description of these processes. There are two main types of mathematical models of growth kinetics: structured and unstructured. Structured models take into account the cell basic aspects and its chemical species in question. Conversely, unstructured models consider microorganisms and/or cells have a simple and fixed composition, and ignores changes in the culture medium resulting from the cell mass concentration (Esener et al., 1983). Moreover, models can also be classified into segregated and non-segregated type models. The segregated models refer to a heterogeneous microorganisms population, where different entities with dissimilar ages, shapes, sizes and internal compositions are distinguished in the population; whereas, the non-segregated models consider the cellular behavior is close to that of a single average cell that allows fixing the performance of certain variables during fermentation (Ghosh et al., 2012; Kucharska et al., 2018).
If complex such as inhibition are excluded, the functions that describe the growth rate of microorganisms can be classified into two main types, depending on whether they involve only the resource concentration in the medium containing the culture, as in the case of the Monod model, or substrate and biomass densities as in the case of the Contois or Tessier model (Krichen et al., 2017). Monod’s equation is applied to the substrates degradation at the concentration that partially saturates the microbial cells activity. The Contois model assumes that the half saturation rate depends on the biomass concentration, while the Tessier model is based on an exponential function (Sakthipriya et al., 2018).
At present, there are no studies showing models of cell growth and xylitol production with OPEFB. Monod, Contois and Tessier models in synthetic media have been adjusted to the growth of yeasts of the genus Candida (Aguiar et al., 2002). The aim of this study was to propose an unstructured and non-segregated model that adequately describes cell growth, xylose consumption and xylitol production in both synthetic medium and in non-detoxified OPEFB hydrolysate at flask scale using C. tropicalis.
MATERIALS AND METHODSE
Microorganism and culture medium
The Candida tropicalis (ATCC 96745) strain was stored at 4°C in agar of yeast extract, peptone and xylose (YPX) with a concentration of 20 g L-1 of each compound. The strain was subcultured in the same agar at 30 °C for 48 h before carrying out the pre-inoculum. Final pH was 5.6 and the fermentation medium was non-detoxified OPEFB hydrolysate (Manjarres-Pinzon et al., 2017).
Pre-inoculum and fermentation conditions
The pre-inoculum was performed in 100 mL Erlenmeyer flasks with 40 mL of medium and 20 g L-1 of xylose substrate. They were incubated at 30 °C and 120 rpm for 18 h. At the end, the Erlenmeyer flasks were inoculated with non-detoxified OPEFB hydrolysate as a fermentation medium aiming at studying their kinetics and modeling their behavior as well. The fermentations were also carried out in 100 mL Erlenmeyer flasks with 40 mL of YPX synthetic medium. The inoculum concentration was 1.6 g L-1, the ratio of medium volume and Erlenmeyer flask volume was 0.4, pH 5.6 and 120 rpm of agitation rate. For the kinetic study, the fermentations with non-detoxified OPEFB hydrolysates were performed for 96 h.
Analytical methods
Cellular concentration was determined by optical density spectrophotometry at 620 nm (Genesys 20, Thermo Scientific, Waltham, MA) and correlated with the dry weight method (Manjarres et al., 2018). Xylose and xylitol quantification was performed using an HPLC system (Shimadzu Prominence, Canby, OR), with IR detector, equipped with an Aminex HPX-87H column (Biorad). Elution was carried out with aqueous H2SO4 (0.005 M) at a flow rate of 0.6 mL min-1. The oven temperature was maintained at 65 °C. The injection volume was 20 μL (Manjarres-Pinzon et al., 2017). Samples were prepared in duplicate and filtered.
Fermentation models
Cell growth, substrate consumption and xylitol production kinetics were studied in flask scale with 100 mL capacity. The models studied for cell growth were Monod (Equation 1), Contois (Equation 2) and Tessier (Equation 3); Luedeking-Piret model (Equation 4) was applied for xylitol production and the general mass balance equation of substrate consumption was used for xylose consumption (Equation 5) (Aguiar et al., 2002).
Where, the estimated parameters were μmax, B, α, β, YX/S and YP/S, KS and Kt, according to the model used. The experimental maximum specific growth rate (μmax) was calculated from the slope of the regression line of the natural logarithm of the cell numbers (LnX) in the increasing phase as a time function (Mohamad et al., 2016). YX/S is the biomass yield based on substrate consumption and it was considered that the entire substrate was used for cell growth. KS is the saturation or substrate utilization constant, numerically equal to the substrate concentration where μ=μmax/2. In the Tessier model, growth inhibition by substrate depletion is included, thus, μ is nullified or tends to zero with low substrate concentrations. Kt is the substrate growth inhibition constant.
The exponential phase, where xylitol is produced, and the stationary phase were used for modeling. The substrate consumption was oriented to cell growth. In a batch system, the change in cell concentration depends solely on cell growth. The cell can consume the substrate in three ways: cell growth, cell maintenance and metabolite production. In the substrate equation (Equation 5), ms is the cellular maintenance proportional to the biomass present, YX/S -1 is the substrate fraction used for cell growth and YP/S -1 is the substrate fraction used to produce xylitol. In the Luedeking-Piret model (Equation 4), the first term is oriented to the ability of the cell during cell growth to produce the metabolite (growth or exponential phase); whereas, the second term indicates the metabolite production based on the biomass present in the environment (cellular maintenance or stationary phase). If the product is obtained mainly during cell growth, β must have a low value, and α a high value. Primary metabolites are produced in the growth phase, where xylitol is one of them; on the contrary, secondary metabolites are generally obtained in the stationary phase.
Unstructured kinetic model
Experimental data for kinetic parameters estimation were used. The modeling protocol consists of defining a mathematical model, making a numerical solution scheme, applying numerical solution methods and checking the numerical stability of the model. The latter implies that the model represents the real values of a process, or that the solution be consistent and real. The aim of the modeling protocol is to find a routine that is stable and consistent when applied in solving the differential equations that represent the phenomenology under study.
The parameter estimation process was carried out using the software Berkeley Madonna 8.0, where the parameters of both cell growth models, substrate consumption and xylitol production models must be introduced. The software Berkeley Madonna 8.0 implies a numerical solution scheme, generates alerts and makes the modeling protocol as well. After the model numerical stability is done, the study can start. Furthermore, this software has an internal routine that allows calibrating the model and its constants. Model calibration consists of selecting all the variables that are coupled and adjusting the numerical solution that this software gives to the observed data, in order to find the most suitable magnitudes of the constants included in the model. The software, based on the root mean square error (RMSE) and the coefficient of variation (CV), generates a comparison between the observed and estimated data, also begins to generate random values of all the variables, makes iterations and evaluations of RMSE and CV until gets the combination of factors that results in the lowest CV.
The estimation procedure involved the variation of different parameter values for minimizing the differences between the experimental or observed data and those predicted by the model. The applied numerical solution method was Runge-Kutta of order 4 (RK4), which takes the average of 4 slopes and that is the value used to perform the iteration. Parameters initial data were chosen according to the data reported in the literature for this type of fermentation. For instance, the maximum specific growth rate of yeast was taken with values in the range of 0.2-1 h and 0.5-1 h, yields between 0 and 1, parameter B, KS and Kt were 1.88, 599 and 305, respectively (Aguiar et al., 2002).
RESULTS AND DISCUSSION
Cell growth kinetics
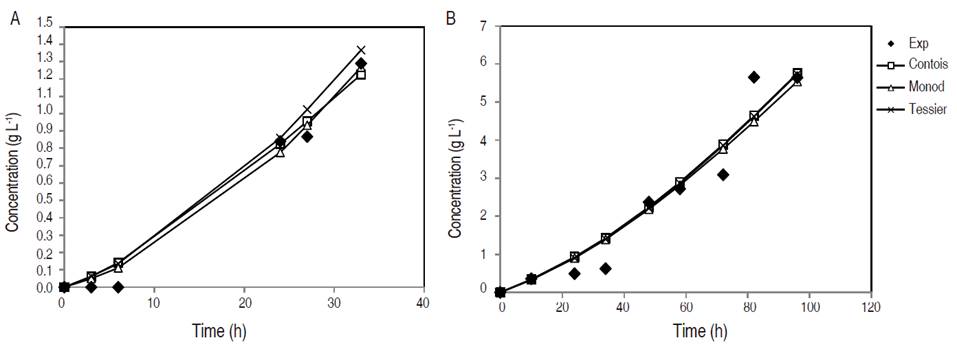
Biomass concentration with respect to fermentation time in YPX synthetic medium and in non-detoxified OPEFB hydrolysate is featured in Figure 1. It is important to note that fermentation in synthetic medium took 33 h, while in non-detoxified OPEFB hydrolysate took 96 h given that this medium contained different inhibitors and nutrients, which prolonged the yeast adaptation phase. Furthermore, no tests were made between 7 to 25 h since in initial experiments, Candida tropicalis reached the exponential phase in the YPX synthetic medium at that time. Thus, the aim was to evaluate the different growth phases of this yeast in the medium, and to try to model the fermentation results. The Contois model adequately predicts the experimental values of cell growth in synthetic medium. However, the behavior of all models predicts cell growth in the first 24 h in non-detoxified OPEFB hydrolysate and after that time, the values of the models tend to be lower than the experimental ones. The considerations that would improve the prediction of the model could be: more precise methods for the cell growth determination such as colony forming unit (CFU) and adjust only two variables for the model instead of three variables (biomass, substrate and product), as was done in this study. Therefore, the type of culture medium was a factor that affected the parameters sensitivity of a kinetic growth model.
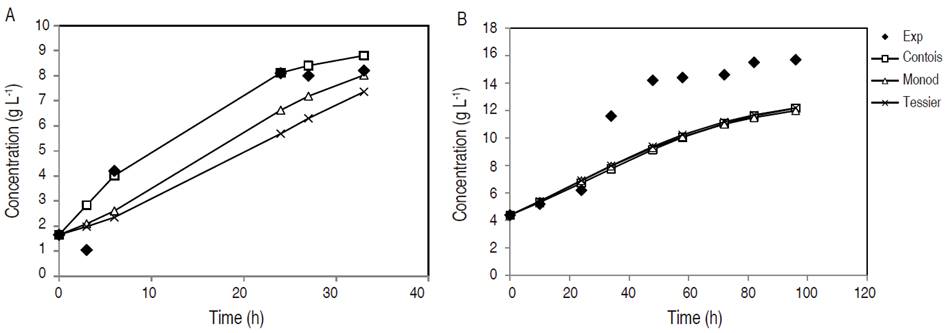
Figure 1 Cell mass concentration during fermentation in synthetic medium YPX (A) and non-detoxified OPEFB hydrolysate (B).
In another study, the application of the Contois model in the cell growth of C. guilliermondii using a synthetic medium was suitable with small deviations (Aguiar et al., 2002). On the other hand, the non-detoxified OPEFB hydrolysate, outside of xylose, has other sugars such as glucose that can contribute to the increase in biomass production. In addition, the non-detoxified OPEFB hydrolysate was supplemented with different salts, such as 4 g L-1 yeast extract, 3 g L-1 (NH4) 2SO4, 0.5 g L-1 MgSO4 7H2O and 0.1 g L-1 CaCl2 2H2O, which help to improve the Candida metabolism (Manjarres-Pinzon et al., 2016).
Xylose consumption kinetics
Xylose consumption during fermentation in synthetic medium and in non-detoxified OPEFB hydrolysate is depicted in Figure 2. Xylose concentration gradually decreased over time in both media. Xylose was consumed by 50% in YPX and 70% in non-detoxified OPEFB hydrolysate according to experimental data. Xylitol concentration increased mainly during the rapid xylose consumption period, which confirmed xylitol accumulation due to imbalance factors of the enzymatic activities that involved xylose consumption in the cells (Mohamad et al., 2016).
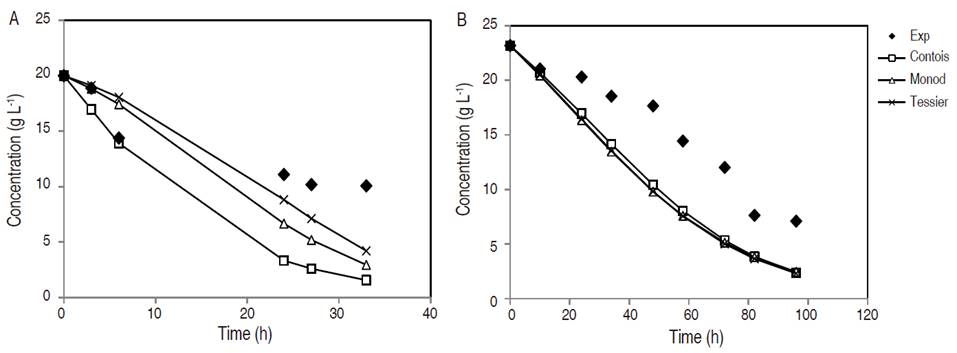
Figure 2 Xylose concentration during fermentation in synthetic medium YPX (A) and non-detoxified OPEFB hydrolysate (B).
In synthetic media, both Monod and Tessier models adequately predicted experimental values in the first 3 h of fermentation; but after 24 h, the models distanced themselves from the experimental values, being the Tessier model the closest in terms of the reported values. The values estimated by the models behave similarly in non-detoxified OPEFB hydrolysate, where it can be emphasized that the estimated results were similar between the models and completely away from the experimental ones. It is necessary to highlight that the modeling of substrate consumption was based on Equation 5, which is closely related to the growth kinetics variables of each model studied.
Xylitol production kinetics
Xylitol production during fermentation in synthetic medium and in non-detoxified OPEFB hydrolysate is shown in Figure 3. All the models were similar to each other and adequately predicted the xylitol production, especially in synthetic medium. However, it should be kept in mind that the base equation in all models for the development of this kinetic was Luedeking-Piret equation, although they also depend on other parameters, which are found both in cell growth and in substrate consumption. The Luedeking-Piret equation is a function of cell growth and cell maintenance to describe product formation (Veeravalli and Mathews, 2018). The Luedeking-Piret equation was originally developed to explain the fermentation kinetics of glucose to lactic acid secretion based on instantaneous growth of bacterial rate and to the bacterial density. Nonetheless, it has been modified to relate the production rate of any metabolite with substrate consumption rate and substrate concentration (Mahdinia et al., 2019). Xylitol concentration was higher in non-detoxified OPEFB hydrolysate with a value around 6 g L-1 compared to the synthetic medium that was 1.3 g L-1. Studies have shown that xylitol production is affected by many factors such as the type of microorganism, the medium composition, such as initial xylose concentration, inhibitors, etc., and the environmental conditions such as pH, temperature, agitation and aeration (Mohamad et al., 2016; Pappu and Gummadi, 2016).
Model comparison
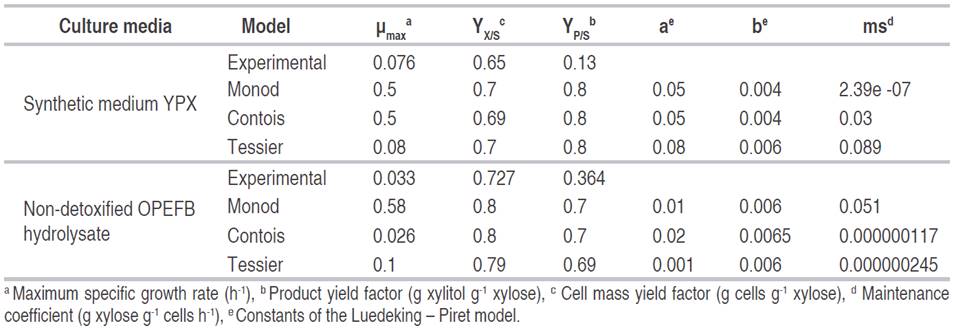
A kinetic model is helpful to understand and optimize a fermentation process (Zhu et al., 2016). Table 1 shows the estimated parameters of each model during fermentation of C. tropicalis in two culture media. Mathematical modeling of cell growth behavior is highly investigated to control, predict and design the processing, stability and safety of food and bioproducts (Guo et al., 2018; Pappu and Gummadi, 2016). The equations of Monod and Tessier are normally used to describe growth with a low cell population; while the Contois model usually works better in cultures with high cell density (Aguiar et al., 2002).
Table 1 Estimated values of the parameters of cell growth, xylose consumption and xylitol production during Candida tropicalis fermentation in different culture media using unstructured models.
Monod kinetics, expressed as substrate degradation resulting from microbial uptake and cell concentration, has a great effect on degradation rates. Contois kinetics considers the fact that a high concentration of cells adhered to the surface of the particles could inhibit substrate degradation. Tessier kinetics takes into account the maintenance energy for cellular activity, which means that the maximum growth rate will be reduced when the substrate concentration is lower and microorganisms compete for food sources (Wang and Witarsa, 2016).
It is necessary to highlight that the experimental value of μmax in the synthetic medium was similar to that reported by the Tessier model, whereas it was closer to the Contois equation in non-detoxified OPEFB hydrolysate (Table 1). The experimental value of μmax was higher in the synthetic medium than in the non-detoxified OPEFB hydrolysate, which indicates that the medium influences the cell growth potential. Generally, yeast extract provides good growth factors and organic nitrogen for microorganisms. In addition, the activities of enzymes involved in cell growth are inhibited by changes in the culture medium (Zhu et al., 2016).
The μmax of yeast is usually between 0.2 and 0.5 h-1. In C. guilliermondii growth using a synthetic medium for the production of xylitol, a value of μmax was found for the Contois model of 0.25 h-1 (Aguiar et al., 2002). Nevertheless, in other works, the value has been below than what was previously reported. In xylitol production with C. parapsilosis in synthetic medium, μmax was between 0.1 to 0.13 h-1 (Aranda-Barradas et al., 2000); value of 0.12 h-1 was reported with C. tropicalis in synthetic medium (Mohamad et al., 2016) and with Debaryomyces nepalensis in synthetic medium were values from 0.029 to 0.078 h-1 (Pappu and Gummadi, 2016). The values of this latter study were close to the experimental values reported in the present study. This indicates that μmax experimentally depends on the fermentation conditions and the microorganisms used as well.
Experimental values of xylitol yield (YP/S) and cellular yield (YX/S) were higher in the non-detoxified OPEFB hydrolysate than in the synthetic medium. Data of the models were closer to the experimental results of YX/S than of YP/S; the latter being similar among the models. This is probably due to the fact that the base equation used for product modeling was the same for all models as mentioned above. YX/S and YP/S values were found between 0.09 to 0.15 (g g-1) and between 0.13 to 0.41 (g g-1), respectively, for xylitol production with C. tropicalis in synthetic medium (Mohamad et al., 2016). Regarding the xylitol production with D. nepalensis in synthetic medium, YX/S and YP/S values were reported between 0.1 to 0.6 (g g-1) and 0.1 to 0.5 (g g-1), respectively (Pappu and Gummadi, 2016). The experimental values of the present study were slightly higher for YX/S, whereas the YP/S data were in the literature range.
Non-growing or slowly growing microbial cultures can recycle much of the metabolic energy derived from initial fermentation of a polysaccharide to boost the additional production of a secondary metabolite (Singh et al., 2019). In order to determine if this could be happening in this study, the amount of substrate used for biomass in the non-growth phase and the maintenance coefficient (ms) for C. tropicalis in synthetic medium and in non-detoxified OPEFB hydrolysate were determined (Table 1). The ms indicates the portion of substrate consumed for the maintenance of cellular function and is used as a correction for the microbial growth kinetics (Wang and Witarsa, 2016). In synthetic media, the estimated values of the ms showed that in the Tessier model more xylose was used for its non-growing components, which contributed to xylitol formation; while in the non-detoxified OPEFB hydrolysate, the Monod model showed greater use of xylose for its non-growing components. The estimated values of the ms were low compared to the literature (Pappu and Gummadi, 2016; Singh et al., 2019), which could assume that xylitol is mainly produced during the cell growth phase.
The estimated product formation coefficient (α), which represents xylitol production associated with growth, was always higher in all models in both media, except for the Tessier model in non-detoxified OPEFB hydrolysate. This indicates that xylitol formation depends on cell growth. The xylitol production in the stationary phase is represented by β, which is the coefficient of non-growth product. A comparatively low β value suggests that xylitol production remains low in non-growing conditions (Ghosh et al., 2012). These results agreed with what was previously reported for the ms.
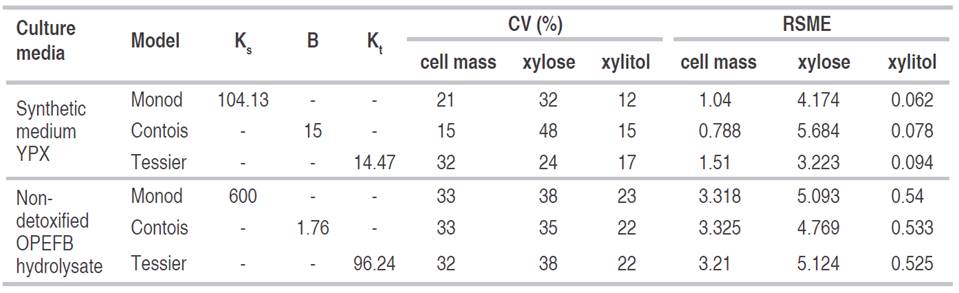
Statistical criteria to validate fit of data to models, CV and RSME of the models are portrayed in Table 2. CV and RSME were lower in synthetic medium than in non-detoxified OPEFB hydrolysate, except for CV and RSME of Contois model substrate that reported a value of 48% and 5.684, respectively. Lower CV and RSME values represent the best fit of the model (Pappu and Gummadi, 2016). If we focus only on these values, the Monod model would be the most representative in synthetic medium and the Contois model in the non-detoxified OPEFB hydrolysate. Nonetheless, taking into account the experimental values of μmax and YX/S, the models that are closest to reality were Tessier in synthetic medium and Contois in non-detoxified OPEFB hydrolysate. The latter is essential to clarify, since a model is the mathematical representation of a phenomenon or process, and apparently, it can have a good predictive capacity represented in different statistical comparisons and experimental errors; but first of all, the model must be in accordance with the adequate prediction of what happens in reality. The Tessier model in synthetic medium and Contois in non-detoxified OPEFB hydrolysate had a CV in the growth kinetics of 32 and 33%, respectively. This means that the kinetic behavior of the experimental values can be predicted in the conditions posed in this study by around 67%. This may be due to the way the cell concentration was determined and the different assumptions used to apply the models.
Table 2 Estimated parameters and deviations of the models applied in the Candida tropicalis fermentation in different culture media.
Since fermentation is a complex bioprocess, it is difficult to obtain a complete profile to reveal what really happens during the entire process and predict the cell growth kinetics and metabolism under certain conditions. Although a huge amount of research on mathematical modeling of microbial processes has been carried out, the applicability of biological concepts into the models remained limited (Tian et al., 2018). It is necessary to keep in mind that these types of processes are complex and depend on various variables.
CONCLUSION
Unstructured models for cell growth, xylose consumption and xylitol production were applied in fermentation by C. tropicalis in synthetic medium and in non-detoxified OPEFB hydrolysate. According to the experimental values and the evaluation of model performances, the Tessier model predicted better results in a synthetic environment and the Contois model had a better fit in non-detoxified OPEFB hydrolysate. However, the prediction of these models had an estimate of 67% which coincided with the assumed value with the experimental growth kinetics. Xylitol was a metabolite associated with cell growth.