Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista de la Academia Colombiana de Ciencias Exactas, Físicas y Naturales
Print version ISSN 0370-3908
Rev. acad. colomb. cienc. exact. fis. nat. vol.35 no.135 Bogotá Apr./June 2011
FÍSICA
César A. Valenzuela-Toledo1, Yeinzon Rodríguez2,3
1 Departamento de Física, Universidad del Valle, Ciudad Universitaria Meléndez, Santiago de Cali 760032, Colombia, Correo electrónico: cesar.valenzuela@correounivalle.edu.co
2 Vicerrectoría de Ciencia, Tecnología, e Innovación, Universidad Antonio Nariño, Cra. 3 Este # 47A-15, Bogotá D.C. 110231, Colombia, Correo electrónico: yeinzon.rodriguez@uan.edu.co
3 Escuela de Física, Universidad Industrial de Santander, Ciudad Universitaria, Bucaramanga 680002, Colombia, Correo electrónico: yrodrig@uis.edu.co
Resumen
Se estudian los descriptores estadísticos (nivel de anisotropía estadística y niveles de no gaussianidad)de la perturbación primordial en la curvatura  para modelos cosmológicos inflacionarios que incluyen campos escalares y vectoriales, estos últimos propuestos para incluir violaciones de la isotropía estadística. Para estos modelos se encuentra que es posible obtener relaciones de consistencia entre los descriptores estadísticos, los cuales poseen una contraparte observacional y que por ende permiten validar o desechar un modelo teórico. Finalmente se muestra que los resultados obtenidos están de acuerdo con los datos observacionales más recientes. Como un subproducto de este estudio, presentamos en este artículo la definición del verdadero principio cosmológico.
para modelos cosmológicos inflacionarios que incluyen campos escalares y vectoriales, estos últimos propuestos para incluir violaciones de la isotropía estadística. Para estos modelos se encuentra que es posible obtener relaciones de consistencia entre los descriptores estadísticos, los cuales poseen una contraparte observacional y que por ende permiten validar o desechar un modelo teórico. Finalmente se muestra que los resultados obtenidos están de acuerdo con los datos observacionales más recientes. Como un subproducto de este estudio, presentamos en este artículo la definición del verdadero principio cosmológico.
Palabras clave: cosmología, anisotropía estadística, no gaussianidad, perturbación primordial en la curvatura.
Abstract
We study the statistical descriptors (the leve! of statistical anisotropy and the levels of nongaussianity) of the primordial curvature perturbation  for cosmological inftationary models that include scalar fields as well as vector fields, the Iatter being proposed to include violations of the statistical isotropy. It is found for these models that it is possible to obtain consistency relations among the statistical descriptors, which possess an observational counterpart and that therefore allow us to keep or reject a theoretical model. Finally, we show that the obtained results agree with the most recent observational data. As a byproduct of this study, we present in this paper the definition of the true cosmological principie.
for cosmological inftationary models that include scalar fields as well as vector fields, the Iatter being proposed to include violations of the statistical isotropy. It is found for these models that it is possible to obtain consistency relations among the statistical descriptors, which possess an observational counterpart and that therefore allow us to keep or reject a theoretical model. Finally, we show that the obtained results agree with the most recent observational data. As a byproduct of this study, we present in this paper the definition of the true cosmological principie.
Key words: Cosmology, Statistical anisotropy, Non-gaussianity, Primordial curvature perturbation.
l. Introducción
El desarrollo de la cosmología moderna centra sus cimientos en el principio cosmológico, aquél que señala que el Universo luce igual en todas las direcciones (isótropo) con respecto a cualquier región de volumen superior a 106 Mpc3 , y en consecuencia luce igual en cada una de estas regiones (homogéneo)4 . Generalmente se piensa que el principio cosmológico tuvo sus origenes en la observación, pero es bien sabido que las observaciones de la distribución de galaxias en escalas mayores a 100 Mpc datan de no más de dos décadas atrás, así como los datos de radiación cósmica de fondo (RCF) datan desde la década de los 60's. En realidad el principio cosmológico es resultado de una línea de pensamiento filosófico establecida en la época de los antiguos griegos, el cual coincidencialmente terminó siendo coherente con las observaciones modernas. Sin embargo, qué podemos entender como un Universo isótropo con respecto a todas las regiones (y por lo tanto homogéneo) a grandes escalas? Si dividimos el Universo en cubos de volumen de unos pocos Megaparsecs cúbicos, encontraremos que la densidad de energía puede variar considerablemente de cubo a cubo; esto por supuesto implica que el Universo a esta escala no es homogéneo y por ende no es isótropo con respecto a todos los cubos. Por el contrario, si se divide el Universo en cubos de volumen superior a los 106 Mpc3 , se podrá observar que en promedio el Universo luce homogéneo e isótropo con respecto a todos los cubos. Lo anterior nos invita a fundamentar todos nuestros desarrollos en cosmología: la métrica de Friedmann-Robertson-Walker (FRW), las ecuaciones de Friedmann y de continuidad, la evolución postinflacionaria del Universo, el proceso de nucleosíntesis, etc., a partir del sacro principio cosmológico. Con respecto al primer punto, la métrica de FRW se construye a partir de la simetría de invarianza ante rotaciones espaciales (Weinberg, 1972) (la cual realmente es la definición formal de isotropía) con respecto a todos los puntos, que a su vez implica la simetría de invarianza ante translaciones espaciales (Mukhanov, 2005) (la cual realmente es la definición formal de homogeneidad). La estructura a gran escala que observamos hoy en día es el resultado de la evolución de perturbaciones en la densidad de energía en un fondo absolutamente isótropo con respecto a todos los puntos y por consiguiente homogéneo (de ahí que dicho fondo venga descrito por la métrica de FRW). El principio cosmológico, como un producto de la observación y no de la filosofía, no corresponde al conjunto de simetrías descritas anteriormente asociadas al fondo sino al mismo conjunto de simetrías asociadas a la estructura a gran escala observada. Puesto que en este caso este conjunto de simetrías no se respeta, pero aún así podemos hablar en promedio de homogeneidad e isotropía con respecto a todos los cubos, es necesario definir claramente qué entendemos por principio cosmológico.
La primera parte de este artículo (Sección 2) está dedicada a la formulación clara del principio cosmológico en términos de lo que se denomina la homogeneidad e isotropía estadística. Para ello se introducirán los correladores de n puntos en perturbaciones cosmológicas que son base fundamental para el estudio de los mecanismos que dan origen a las estructuras a gran escala. Estos correladores describen la estadística de las estructuras presentes y por consiguiente pueden darnos información acerca de posibles desviaciones del (no tan) sacro principio cosmológico, así como del carácter gaussiano o no gaussiano de tales esctructuras. En la actualidad poseemos pistas que nos conducen a pensar que existen violaciones tanto de la homogeneidad como de la isotropía estadística hasta un máximo relativo del 10% (Groeneboom, Ackerman, Wehus, & Eriksen, 2010; Hansen et. al., 2009; Hoftuft et. al., 2009). Tales pistas serán discutidas en la Sección 3.
Si bien violaciones en la homogeneidad estadística son posibles de acuerdo a lo discutido en la Sección 3, son las violaciones en la isotropía estadística las que más se han estudiado hasta el momento (debido a que la ausencia de homogeneidad estadística nos impediría contrastar los resultados derivados de los diferentes modelos cosmológicos con las observaciones vía el teorema ergódico5). La anisotropía estadística se genera simultáneamente por cierto monto de expansión anisótropa pero también por la naturaleza anisótropa de los campos involucrados en el mecanismo de expansión inflacionaria. Varios tipos de campos han sido estudiados hasta el momento con el fin de generar este efecto: campos vectoriales (véase por ejemplo (Golovnev, Mukhanov, & Vanchurin, 2008b)), campos espinoriales (Böhmer & Mota, 2008), p-formas (Germani & Kehagias, 2009), pero en este artículo sólo nos concentraremos en el primer tipo, realizando en la Sección 3 una introducción a la anisotropía estadística y la no gaussianidad en modelos inflacionarios que involucran campos vectoriales.
La distribución de las estructuras a gran escala en el Universo ha sido bien estudiada por las sondas galácticas (Aihara et. al., 2011) y por las misiones espaciales dedicadas a estudiar la RCF (Komatsu et. al., 2011). Se ha concluido que el perfil de distribución de densidad de energía, así como el de temperatura de la RCF, es prácticamente gaussiano. Sin embargo, los mismos resultados observacionales son consistentes con pequeñas desviaciones con respecto a la gaussianidad exacta, con una cota superior del orden de una parte en 103 (Komatsu et. al., 2011). Normalmente los modelos inflacionarios convencionales (aquéllos basados en campos escalares y que por consiguiente respetan la homogeneidad e isotropía estadística a través del teorema del no cabello cósmico (Starobinsky, 1983; Wald, 1983) pueden desviarsen de la gaussianidad exacta hasta en una parte en 107 (Komatsu, 2010), haciendo que sea imposible someterlos a la prueba observacional y discriminar entre ellos en vista de la actual precisión experimental. En contraste, los modelos inflacionarios que involucran campos vectoriales pueden fácilmente generar niveles de no gaussianidad apreciables, altamente anisótropos, pero aún consistentes con las cotas observacionales (Karciauskas, Dimopoulos & Lyth, 2009; Valenzuela-Toledo & Rodríguez, 2010; ValenzuelaToledo, Rodríguez, & Lyth, 2009), perteneciendo de esta manera al selecto grupo de modelos que pueden ser discriminados mediante estas pruebas. En las Secciones 4 y 5 se discuten los aspectos más importantes concernientes a la generación de no gaussianidad primordial en modelos inflacionarios con campos vectoriales, enfatizando en la Sección 5 en la tremenda utilidad que tendrían las relaciones de consistencia entre el nivel de anisotropía estadística y los niveles de no gaussianidad en la puesta a prueba de los modelos inflacionarios que involucran campos vectoriales a la luz de las observaciones.
2. El principio Cosmológico: homogeneidad e isotropía estadística
Las existencia de galaxias, cúmulos, supercúmulos, filamentos, pero también de regiones de espacio vacío claramente nos enseña que nuestro Universo no es homogéneo y en consecuencia no es isótropo con respecto a todos los puntos. Por esta razón nuestro Universo no puede ser descrito mediante la métrica de FRW. Sin embargo, las mismas observaciones nos han enseñado también que las estructuras presentes pueden ser descritas adecuadamente a través de perturbaciones en esta métrica. El procedimiento a seguir es asignar un sistema coordenado cartesiano a nuestro espaciotiempo de tal manera que en cada hipersuperficie de tiempo t constante la densidad de energía sea uniforme, exigir que las líneas descritas por coordenadas espaciales x constantes sean líneas de mundo de observadores típicos en caída libre, y hacer uso de la suposición de universos separados (Dimopoulos, Karciauskas, Lyth & Rodríguez, 2009; Lyth & Liddle, 2009) que permite describir cada punto del espacio en escalas de superhorizonte como si fuese un universo separado el cual evoluciona localmente de forma homogénea. Así, la parte espacial de la métrica de FRW perturbada viene descrita por:
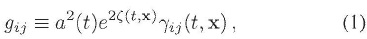
en donde a(t) es el parámetro de expansión global,  es la perturbación en la curvatura, y
es la perturbación en la curvatura, y 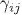 es una cantidad que da cuenta de las perturbaciones tensoriales y cuyo determinante es igual a uno6. La perturbación en la curvatura (es la cantidad más importante en cosmología; es mediante ella que podemos describir la estadística de las estructuras a gran escala, y es precisamente ella la que nos permitirá definir adecuadamente el principio cosmológico.
es una cantidad que da cuenta de las perturbaciones tensoriales y cuyo determinante es igual a uno6. La perturbación en la curvatura (es la cantidad más importante en cosmología; es mediante ella que podemos describir la estadística de las estructuras a gran escala, y es precisamente ella la que nos permitirá definir adecuadamente el principio cosmológico.
Como se discutió en la Introducción, si dividimos el Universo en cubos de volumen mayor a 106 Mpc3 encontraremos que la distribución del contenido energético es en promedio similar en cada cubo. De allí que digamos que el Universo es homogéneo, pero esta palabra "homogéneo" debemos entenderla en relación con la homogeneidad estadística. De manera similar, podemos decir que el Universo es isótropo con respecto a todos los cubos, pero esta palabra 'isótropo" debemos entenderla en relación con la isotropía estadística. La siguiente subsección presenta las respectivas definiciones de homogeneidad estadística e isotropía estadística que dan cuenta del verdadero principio cosmológico, así como la definición de gaussianidad que se empleará más adelante en este artículo.
2.1. Homogeneidad estadística, isotropía estadística, y gaussianidad
La mecánica cuántica sólo nos permite predecir las probabilidades de diferentes resultados después de un experimento en un ensamble de sistemas, en contraste con la mecánica clásica la cual sí nos permite predecir el resultado exacto después de un experimento en sólo un elemento del ensamble. Puesto que el mecanismo físico subyacente en la generación de perturbaciones cosmológicas es de naturaleza cuántica, los cosmólogos están más interesados en estudiar las propiedades estadísticas de un mapa de perturbaciones, dígase el mapa de la RCF o el mapa de la distribución de galaxias. La manera de hacer esto es vía los correladores de n puntos de las perturbaciones en el espacio real. Realicemos una expansión en integral de Fourier de 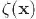 en el espacio real:
en el espacio real:
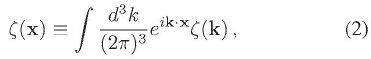
en donde 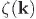 es un modo de Fourier genérico de
es un modo de Fourier genérico de 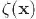 . Los correladores den puntos de
. Los correladores den puntos de 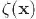 son promedios sobre el ensamble de los productos
son promedios sobre el ensamble de los productos  (x1)
(x1) (x2 ) ...
(x2 ) ...  (xn) en donde x1, x2 , ... , xn representan diferentes puntos en el espacio7 :
(xn) en donde x1, x2 , ... , xn representan diferentes puntos en el espacio7 :
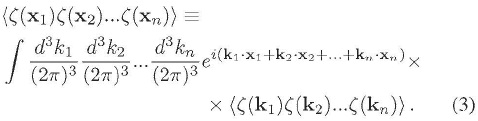
Así, las funciones de correlación en el espacio real pueden ser estudiadas vía las funciones de correlación en el espacio de momentum. Veamos ahora el significado de homogeneidad estadística, isotropía estadística, y gaussianidad.
Homogeneidad estadística
Por supuesto el mapa de perturbaciones no es homogéneo (i.e., invariante bajo translaciones espaciales), pero puede ser que la función de distribución de probabilidad que gobierna a 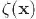 sí lo sea, lo cual es llamado homogeneidad estadística (Abramo & Pereira, 2010; Lyth & Liddle, 2009; Weinberg, 2008). Esto significa que los correladores de n puntos en el espacio real son invariantes bajo translaciones en el espacio, i.e.
sí lo sea, lo cual es llamado homogeneidad estadística (Abramo & Pereira, 2010; Lyth & Liddle, 2009; Weinberg, 2008). Esto significa que los correladores de n puntos en el espacio real son invariantes bajo translaciones en el espacio, i.e.
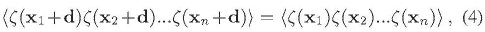
en donde d es algún vector en el espacio real que establece el monto de la translación espacial. La única forma de lograr esto, en vista de la Ec. (3), es expresar el argumento de la función exponencial dentro de la integral com la suma de varios términos de la forma ƒ(xi- xj). lo cual es a su vez posible (pero no es la única posibilidad) si los correladores de n puntos en el espacio de momentum son proporcionales a la función delta de Dirac:
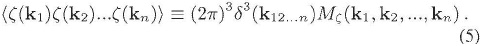
En la anterior expresión, k12... n significa k1 + k2 + ... + kn, y la función 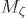 (k1, k2, ... , kn) es llamada el (n-1)-espectro. La homogeneidad estadística es absolutamente necesaria como una hipótesis del teorema ergódico (Weinberg, 2008); de otra manera, aunque sí disponemos de un marco teórico para hacer cálculos y aunque sí disponemos de un monto significativo de datos observacionales con precisión sin precedentes, no podríamos comparar lo uno con lo otro.
(k1, k2, ... , kn) es llamada el (n-1)-espectro. La homogeneidad estadística es absolutamente necesaria como una hipótesis del teorema ergódico (Weinberg, 2008); de otra manera, aunque sí disponemos de un marco teórico para hacer cálculos y aunque sí disponemos de un monto significativo de datos observacionales con precisión sin precedentes, no podríamos comparar lo uno con lo otro.
Isotropía estadística
Una vez la homogeneidad estadística ha sido asegurada, en la forma de la Ec. (5), nos preguntamos acerca de la invarianza ante rotaciones espaciales (i.e. isotropía). De nuevo por supuesto, el mapa de las perturbaciones no es isótropo, pero puede que la función de distribución de probabilidad que gobierna a 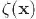 sí lo sea, lo cual es llamado isotropía estadística (Abramo & Pereira, 2010; Lyth & Liddle, 2009; Weinberg, 2008). Esto significa que los correladores de n puntos en el espacio real son invariantes bajo rotaciones en el espacio, i.e.
sí lo sea, lo cual es llamado isotropía estadística (Abramo & Pereira, 2010; Lyth & Liddle, 2009; Weinberg, 2008). Esto significa que los correladores de n puntos en el espacio real son invariantes bajo rotaciones en el espacio, i.e.
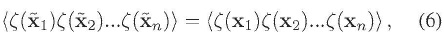
en donde 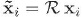 , siendo
, siendo 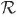 un operador de rotación. Para satisfacer el anterior requerimiento, el ( n - 1 )-espectro debe satisfacer la condición
un operador de rotación. Para satisfacer el anterior requerimiento, el ( n - 1 )-espectro debe satisfacer la condición
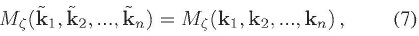
en donde las tildes sobre los momentums representan también una rotación espacial, parametrizada por 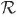 , en el espacio de momentum. Esta condición tiene consecuencias más explícitas en el espectro (1-espectro) y el biespectro (2- espectro):
, en el espacio de momentum. Esta condición tiene consecuencias más explícitas en el espectro (1-espectro) y el biespectro (2- espectro):
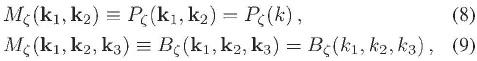
en donde en la primera línea k = |k1| = |k2|, y en la segunda línea ki = |ki|. A partir del tri espectro (3-espectro ), la condición en la Ec. (7) acerca de la isotropía estadística en todos los (n-1)-espectros de más alto orden no puede ser reducida a condiciones similares a aquéllas en las Ecs. (8) y (9), de tal manera que la forma mínima de parametrizar los (n-1)-espectros (con n ::;:, 4) será siempre en términos de todos los n vectores de onda.
Gaussianidad
La gaussianidad puede ser definida ya sea vía las perturbaciones 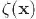 en el espacio real o vía las perturbaciones
en el espacio real o vía las perturbaciones 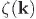 en el espacio de momentum. Hablemos primero acerca de las últimas y luego regresaremos sobre las primeras. Decimos que la función de distribución de probabilidad que gobierna a
en el espacio de momentum. Hablemos primero acerca de las últimas y luego regresaremos sobre las primeras. Decimos que la función de distribución de probabilidad que gobierna a 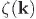 es gaussiana si para diferentes vectores de án correlacionadas:8
es gaussiana si para diferentes vectores de án correlacionadas:8
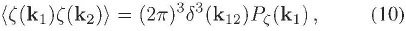
y si los correladores de n puntos, con n siendo impar, son cero, mientras que aquéllos con n siendo par son iguales a la suma sobre todas las formas de aparear 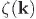 s con cada uno de los otros de un producto de correladores de dos puntos de los pares 9 (Lyth & Liddle, 2009; Weinberg, 2008):
s con cada uno de los otros de un producto de correladores de dos puntos de los pares 9 (Lyth & Liddle, 2009; Weinberg, 2008):
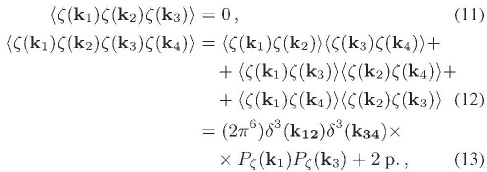
y así sucesivamente, en donde 2p. significa dos permutaciones. Las Ecs. (10) y (13) muestran claramente que la homogeneidad estadística es una condición necesaria mas no suficiente para que la función de distribución de probabilidad que gobierna a 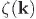 sea gaussiana (Dimopoulos, Karciauskas, Lyth & Rodríguez, 2009; Lyth & Liddle, 2009). Ahora, regresando a las perturbaciones
sea gaussiana (Dimopoulos, Karciauskas, Lyth & Rodríguez, 2009; Lyth & Liddle, 2009). Ahora, regresando a las perturbaciones 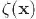 en el espacio real, es posible mostrar que la condición de gaussianidad expresada arriba implica que la función de distribución de probabilidad P(
en el espacio real, es posible mostrar que la condición de gaussianidad expresada arriba implica que la función de distribución de probabilidad P( 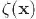 ) está dada por
) está dada por
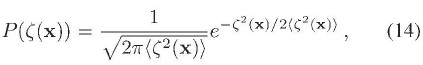
la cual es la definición usual de una función de distribución de probabilidad gaussiana. Sin embargo, exigiendo que las Ecs. (11), (12), y así sucesivamente se satisfagan para 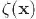 , en vez de para
, en vez de para 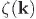 , también da lugar a la Ec. (14) sin requerir gaussianidad en los modos
, también da lugar a la Ec. (14) sin requerir gaussianidad en los modos 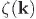 . En otras palabras, la gaussianidad en
. En otras palabras, la gaussianidad en 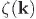 es una condición suficiente pero no necesaria para la gaussianidad en
es una condición suficiente pero no necesaria para la gaussianidad en  ( x); de hecho, vía el teorema del límite central (Adler, 1981; Karlin & Taylor, 1975),
( x); de hecho, vía el teorema del límite central (Adler, 1981; Karlin & Taylor, 1975), 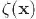 puede llegar a ser gaussiana simplemente si es expresada como una suma de cantidades no correlacionadas
puede llegar a ser gaussiana simplemente si es expresada como una suma de cantidades no correlacionadas  ((k)) incluso si ellas no son gaussianas.
((k)) incluso si ellas no son gaussianas.
Cuando las perturbaciones 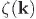 no son gaussianas, pero aún asumiendo homogeneidad estadística, los correladores de n puntos en el espacio de momentum, con n 6 ≥ 3, son expresados en términos de los correladores de n puntos "conectados" (identificados con el subíndice e) los cuales establecen la desviación de la condición de gaussianidad:
no son gaussianas, pero aún asumiendo homogeneidad estadística, los correladores de n puntos en el espacio de momentum, con n 6 ≥ 3, son expresados en términos de los correladores de n puntos "conectados" (identificados con el subíndice e) los cuales establecen la desviación de la condición de gaussianidad:
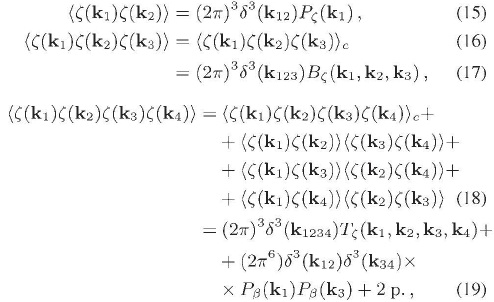
y así sucesivamente. En las anteriores expresiones, 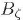 (k1, k2, k3) y
(k1, k2, k3) y  (k1, k3, k3, k4) son llamados el biespectro y tri espectro conectados de
(k1, k3, k3, k4) son llamados el biespectro y tri espectro conectados de  .
.
3. Anisotropía estadística y no gaussianidad en modelos inflacionarios que involucran campos vectoriales
Las propiedades de las anisotropías en la temperatura de la RCF se han convertido en uno de los campos de estudio más relevantes de la cosmología moderna (Lyth & Liddle, 2009; Weinberg, 2008), particularmente porque son utilizadas para discriminar entre los diferentes modelos cosmológicos propuestos para la formación de estructuras a gran escala (Aiabidi & Huston, 2010; Alabidi & Lidsey, 2008; Alabidi & Lyth, 2006a; Alabidi & Lyth, 2006b) a través de parámetros que pueden ser contrastados directamente con la observación. En el aspecto teórico de la cosmología, las propiedades de las anisotropías en la temperatura de la RCF se estudian a través de las propiedades de la perturbacion primordial en la curvatura  10(Lyth & Liddle, 2009; Weinberg, 2008). Las propiedades de
10(Lyth & Liddle, 2009; Weinberg, 2008). Las propiedades de  están descritas en términos de funciones espectrales, tales como el espectro, el biespectro, el triespectro, etc., quienes a su vez están dadas en función de los, así llamados, descriptores estadísticos de la función de distribución de
están descritas en términos de funciones espectrales, tales como el espectro, el biespectro, el triespectro, etc., quienes a su vez están dadas en función de los, así llamados, descriptores estadísticos de la función de distribución de  (Cogollo, Rodríguez, & ValenzuelaToledo, 2008). En estos términos, la parte isótropa del espectro
(Cogollo, Rodríguez, & ValenzuelaToledo, 2008). En estos términos, la parte isótropa del espectro 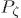 se encuentra parametrizada en función de una amplitud Pe, y del índice espectral
se encuentra parametrizada en función de una amplitud Pe, y del índice espectral 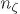 ,:
,:
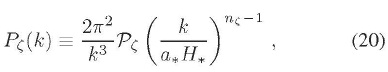
en donde a* y H* son el parámetro de expansión y el parámetro de Hubble evaluados a la salida del horizonte, el biespectro 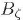 , se encuentra parametrizado en términos de productos del espectro y del nivel de no gaussianidad ƒNL
, se encuentra parametrizado en términos de productos del espectro y del nivel de no gaussianidad ƒNL
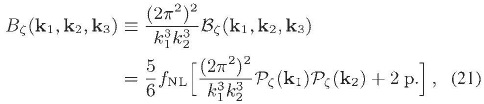
el triespectro  , se encuentra parametrizado como productos del espectro y de los niveles de no gaussianidad TNL y gNL:
, se encuentra parametrizado como productos del espectro y de los niveles de no gaussianidad TNL y gNL:
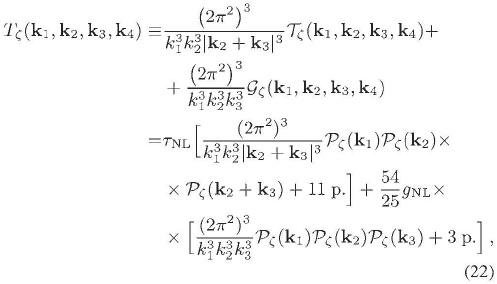
y así sucesivamente. Estas cantidades están fijadas por la observación o, por lo menos, poseen una cota observacional (Bunn & White, 1997; Komatsu e t. al., 2011 ; Smidt et. al., 2010): 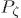 ,
,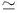 (5 x 10-5)2 ,
(5 x 10-5)2 , 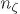 , = 0,968 ± 0,012, -10 <
, = 0,968 ± 0,012, -10 < 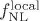 < 74, -0,6 X 104
< 74, -0,6 X 104 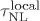 < 3,3 X 104, and -7,4 X 105 <
< 3,3 X 104, and -7,4 X 105 < 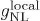 < 8,2 X 105 .
< 8,2 X 105 .
En la gran mayoría de los modelos cosmológicos propuestos para la formación de estructuras a gran escala, se asume que los correladores de n puntos, de los cuales derivan las funciones espectrales, son invariantes bajo rotaciones espaciales (isotropía estadística) y translaciones espaciales (homogeneidad estadística). Sin embargo, violaciones de tales invarianzas son objeto de estudio hoy en día puesto que podrían estar presentes en las observaciones (ver (Armendariz-Picon & Pekowsky, 2009; Groeneboom, Ackerman, Wehus, & Eriksen, 2010; Groeneboom & Eriksen, 2009; Hanson & Lewis, 2009; Hanson, Lewis & ChaIIinor, 2010; Ma, Efstathiou & Challinor, 2011; Sama!, Saha, Jain, & Ralston, 2009) para el caso de anisotropía estadística).
Una forma de caracterizar las violaciones a la isotropía estadística es incluir campos vectoriales en la dinámica inflacionaria (Armendariz-Picon, 2007; Dimopoulos, 2006; Dimopoulos, 2007; Dimopoulos & Karciauskas, 2008; Dimopoulos, Karciauskas, Lyth, & Rodríguez, 2009; Dimopoulos, Karciauskas, & Wagstaff, 2010a; Dimopoulos, Karciauskas, & Wagstaff, 2010b; Dimopoulos & Wagstaff, 2011; Dulaney & Gresham, 2010; Golovnev, 2010; Golovnev, Mukhanov, & Vanchurin, 2008a; Golovnev, Mukhanov, & Vanchurin, 2008b; Golovnev & Vanchurin, 2009; Gümrükcüoglu, Himmetoglu, & Peloso, 2010; Himmetoglu, 2010; Himmetoglu, Contaldi, & Peloso, 2009a; Himmetoglu, Contaldi, & Peloso, 2009b; Himmetoglu, Contaldi, & Peloso, 2009c; Kanno, Kimura, Soda & Yokoyama, 2008; Karciauskas, 2011; Karciauskas & Lyth, 2010; Koh & Hu, 2009; Maleknejad & SheikhJabbari, 201la; Maleknejad & Sheikh-Jabbari, 2011b; Watanabe, Kano, & Soda, 2009; Watanabe, Kano, & Soda, 2010; Yokoyama & Soda, 2008)11, lo cual implica modificaciones en los descriptores estadísticos para la perturbación primordial en la curvatura  (Ackerman, Carroll, & Wise, 2007; Dimopoulos, Karciauskas, Lyth, & Rodríguez, 2009; Bartolo, Dimastrogiovanni, Matarrese, & Riotto, 2009a; Bartolo, Dimastrogiovanni, Matarrese, & Riotto, 2009b; Dimastrogiovanni, Bartolo, Matarrese, & Riotto, 2010; Karciauskas, Dimopoulos, & Lyth, 2009; Valenzuela-Toledo & Rodríguez, 2010; Valenzuela Toledo, Rodríguez, & Lyth, 2009). Por ejemplo, para parametrizar la anisotropía estadística (asumiendo homogeneidad estadística), el espectro se modifica de tal manera que éste adquiere una dependencia explícita del vector de onda. En esta forma, el espectro incluye una parte isótropa P(k) y una parte anisótropa proporcional a P(k) (Ackerman, Carroll, & Wise, 2007):
(Ackerman, Carroll, & Wise, 2007; Dimopoulos, Karciauskas, Lyth, & Rodríguez, 2009; Bartolo, Dimastrogiovanni, Matarrese, & Riotto, 2009a; Bartolo, Dimastrogiovanni, Matarrese, & Riotto, 2009b; Dimastrogiovanni, Bartolo, Matarrese, & Riotto, 2010; Karciauskas, Dimopoulos, & Lyth, 2009; Valenzuela-Toledo & Rodríguez, 2010; Valenzuela Toledo, Rodríguez, & Lyth, 2009). Por ejemplo, para parametrizar la anisotropía estadística (asumiendo homogeneidad estadística), el espectro se modifica de tal manera que éste adquiere una dependencia explícita del vector de onda. En esta forma, el espectro incluye una parte isótropa P(k) y una parte anisótropa proporcional a P(k) (Ackerman, Carroll, & Wise, 2007):
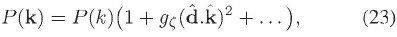
en donde 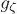 es un parámetro adimensional conocido como el nivel de anisotropía estadística en el espectro,
es un parámetro adimensional conocido como el nivel de anisotropía estadística en el espectro, 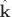 es el vector de onda unitario y
es el vector de onda unitario y 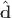 es un vector unitario a lo largo de la dirección preferencial.
es un vector unitario a lo largo de la dirección preferencial.
Un estudio reciente (Groeneboom, Ackerman, Wehus, & Eriksen, 2010; Groeneboom & Eriksen, 2009) de las anisotropías en la temperatura de la RCF, encuentra una débil evidencia de violaciones de la isotropía estadistíca en el quinto año de resultados del satélite WMAP de la NASA12. Mantiendo únicamente términos cuadrupolares en la ecuación (23), es decir:
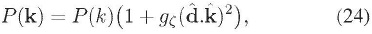
los autores de (Groeneboom, Ackerman, Wehus, & Eriksen, 2010; Groeneboom & Eriksen, 2009) encuentran que 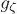
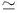 0,290 ± 0,031. Este resultado elimina la posibilidad de
0,290 ± 0,031. Este resultado elimina la posibilidad de 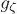 = 0 a más de
= 0 a más de 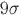 . Sin embargo, la dirección preferente (
. Sin embargo, la dirección preferente (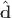 ) yace cerca al plano del sistema solar, lo cual hace pensar a los autores que este efecto podría ser debido a algún error sistemático sin resolver. A pesar del panorama expuesto anteriormente, algunos autores (Pullen & Kamionkowski, 2007) se han tomado el trabajo de calcular la incertidumbre asociada a
) yace cerca al plano del sistema solar, lo cual hace pensar a los autores que este efecto podría ser debido a algún error sistemático sin resolver. A pesar del panorama expuesto anteriormente, algunos autores (Pullen & Kamionkowski, 2007) se han tomado el trabajo de calcular la incertidumbre asociada a 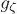 a la que llegarán los satélites encargados de medir la temperatura de la RCF en su estado de mayor rendimiento y que actualmente se encuentran en operación. Ellos encuentran (Pullen & Kamionkowski, 2007): |
a la que llegarán los satélites encargados de medir la temperatura de la RCF en su estado de mayor rendimiento y que actualmente se encuentran en operación. Ellos encuentran (Pullen & Kamionkowski, 2007): |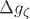 |
| 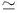 0,1 para el satellite de la NASA WMAP y |
0,1 para el satellite de la NASA WMAP y |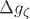 |
| 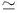 0,02 para el satellite de la ESA PLANCK13.
0,02 para el satellite de la ESA PLANCK13.
En algunos estudios diferentes (Hansen et. al., 2009; Hoftuft et. al., 2009), la perturbación cuadrática media en la temperatura de la RCF se ha medido en hemisferios opuestos con el fin de observar si existe alguna diferencia entre los hemisferios. Ellos encuentran una diferencia del orden de 10 %, para una cierta escogencia de los hemisferios, siendo estadísticamente significativa en un 99 %. Dada la dificultad en el manejo de los errores sistemáticos sería prematuro considerar la evidencia de asimetría hemiesférica como completamente abrumadora. Ahora bien, enfocándonos en un pequeño parche del cielo, la anisotropía estadística de  implica que la perturbación cuadrática media en la temperatura de la RCF en un pequeño parche dependerá en general de la dirección de ese parche. Lo anterior debido a que la perturbación cuadrática media en ese parche depende (en la aproximación de desacople repentino) de la perturbación cuadrática media en la curvatura en una pequeña región plana de espacio perpendicular a la línea de observación ubicada en la última dispersión. Sin embargo, la perturbación cuadrática media en la temperatura de la RCF será la misma en parches situados en direcciones opuestas del cielo debido a que ella explora a
implica que la perturbación cuadrática media en la temperatura de la RCF en un pequeño parche dependerá en general de la dirección de ese parche. Lo anterior debido a que la perturbación cuadrática media en ese parche depende (en la aproximación de desacople repentino) de la perturbación cuadrática media en la curvatura en una pequeña región plana de espacio perpendicular a la línea de observación ubicada en la última dispersión. Sin embargo, la perturbación cuadrática media en la temperatura de la RCF será la misma en parches situados en direcciones opuestas del cielo debido a que ella explora a 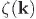 en el mismo k-plano y el espectro
en el mismo k-plano y el espectro 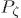 (k) es invariante bajo el cambio k
(k) es invariante bajo el cambio k 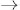 -k. Se concluye entonces que la anisotropía estadística de
-k. Se concluye entonces que la anisotropía estadística de  no puede por sí misma generar la asimetría hemiesférica y que, por ende, es la inhomogeneidad estadística la requerida para explicar dicho fenómeno. En virtud de las hipótesis requeridas para demostrar el teorema ergódico (Weinberg, 2008), si la evidencia de asimetría hemiesférica se torna contundente en los próximos años, nos estaríamos enfrentando a una crisis sin precedentes en los fundamentos de la cosmología como ciencia.
no puede por sí misma generar la asimetría hemiesférica y que, por ende, es la inhomogeneidad estadística la requerida para explicar dicho fenómeno. En virtud de las hipótesis requeridas para demostrar el teorema ergódico (Weinberg, 2008), si la evidencia de asimetría hemiesférica se torna contundente en los próximos años, nos estaríamos enfrentando a una crisis sin precedentes en los fundamentos de la cosmología como ciencia.
En el presente trabajo se utiliza el formalismo δN (Dimopoulos, Karciauskas, Lyth, & Rodríguez, 2009) para calcular las contribuciones a nivel árbol y a un lazo para el espectro 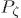 , el biespectro
, el biespectro 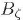 y el triespectro
y el triespectro  . de la perturbación primordial en la curvatura
. de la perturbación primordial en la curvatura  ,cuando se incluyen campos escalares y vectoriales en la dinámica inflacionaria; se integran de esta manera los resultados obtenidos en (ValenzuelaToledo, Rodríguez & Lyth, 2009) para el caso del biespectro y en (Valenzuela-Toledo & Rodríguez, 2010) para el caso del triespectro, para aquellos casos descritos en la próxima sección y que gozan de completa autoconsistencia. Debido a las restricciones observacionales se asumirá que el espectro está dominado por las contribuciones provenientes de perturbaciones en el campo escalar (denotadas con un subíndice (
,cuando se incluyen campos escalares y vectoriales en la dinámica inflacionaria; se integran de esta manera los resultados obtenidos en (ValenzuelaToledo, Rodríguez & Lyth, 2009) para el caso del biespectro y en (Valenzuela-Toledo & Rodríguez, 2010) para el caso del triespectro, para aquellos casos descritos en la próxima sección y que gozan de completa autoconsistencia. Debido a las restricciones observacionales se asumirá que el espectro está dominado por las contribuciones provenientes de perturbaciones en el campo escalar (denotadas con un subíndice ( Φ ya que su contribución al espectro es perfectamente isótropa. Además, se supondrá que el biespectro y el triespectro están dominados por contribuciones provenientes de las perturbaciones en el campo vectorial (denotadas con un subíndice
Φ ya que su contribución al espectro es perfectamente isótropa. Además, se supondrá que el biespectro y el triespectro están dominados por contribuciones provenientes de las perturbaciones en el campo vectorial (denotadas con un subíndice  A); esta suposición permite obtener niveles de no gaussianidad altamente anisótropos (lo cual está absolutamente permitido por las observaciones, en contraste a lo que ocurre con el espectro) y que fácilmente pueden ser contrastados con la observación. Finalmente, se calculan los niveles de no gaussianidad
A); esta suposición permite obtener niveles de no gaussianidad altamente anisótropos (lo cual está absolutamente permitido por las observaciones, en contraste a lo que ocurre con el espectro) y que fácilmente pueden ser contrastados con la observación. Finalmente, se calculan los niveles de no gaussianidad 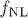 y
y 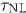 TNL y se relacionan con el nivel de anisotropía estadística en el espectro
TNL y se relacionan con el nivel de anisotropía estadística en el espectro 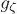 .
.
El formalismo δN (Dimopoulos, Karciauskas, Lyth, & Rodríguez, 2009; Lyth, Malik, & Sasaki, 2005; Lyth & Rodríguez, 2005; Sasaki & Stewart, 1996; Sasaki & Tanaka, 1998; Starobinsky, 1985) se ha convertido en una de las herramientas más usadas para calcular la perturbación primordial en la curvatura  y sus descriptores estadísticos. El caso más simple que permite violaciones a la isotropía estadística consiste en incluir en la dinámica inflacionaria un campo escalar y un campo vectorial; en este caso el formalismo δN brinda una fórmula para calcular
y sus descriptores estadísticos. El caso más simple que permite violaciones a la isotropía estadística consiste en incluir en la dinámica inflacionaria un campo escalar y un campo vectorial; en este caso el formalismo δN brinda una fórmula para calcular  hasta segundo orden (Dimopoulos, Karciauskas, Lyth, & Rodríguez, 2009):
hasta segundo orden (Dimopoulos, Karciauskas, Lyth, & Rodríguez, 2009):
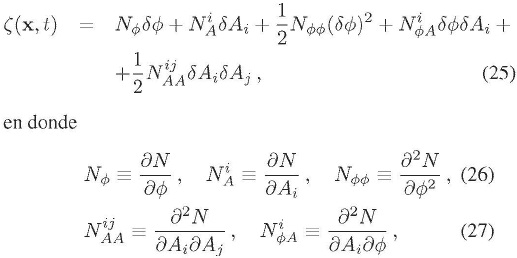
siendo N es el número de e-folds global desde una hipersuperficie de tiempo constante inicial t* en donde la geometría espacial es plana, hasta una hipersuperficie de tiempo constante final ten donde la densidad de energía es uniforme; Φ es el campo escalar y A es el campo vectorial con sus respectivas perturbaciones evaluadas en la hipersuperficie de tiempo constante inicial t*. Es de anotar que el tiempo inicial t* se escoge apropiadamente como unos pocos e-folds después de la salida del horizonte. Finalmente, el índice i corresponde a un índice espacial que corre de 1 a 3 14.
Por simplicidad, las expresiones (20), (21), y (22) se escriben como una suma, en la cual se encuentran términos que dependen solamente de perturbaciones escalares, otros que dependen de perturbaciones vectoriales y otros que dependen de contribuciones mixtas:
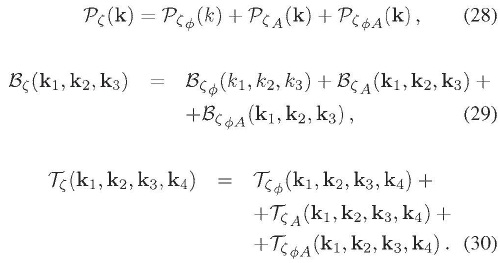
La ecuación (25) y las definiciones (15), (17) y (19), permiten calcular los diferentes descriptores estadísticos para  y a cualquier orden deseado en teoría de perturbaciones. Una característica importante de la perturbación primordial en la curvatura
y a cualquier orden deseado en teoría de perturbaciones. Una característica importante de la perturbación primordial en la curvatura  , es que se puede escribir como una serie de Taylor en las pertubaciones de los campos (ver ecuación (25)). Por lo anterior y en virtud de las definiciones (15), (17) y (19), las funciones espectrales para
, es que se puede escribir como una serie de Taylor en las pertubaciones de los campos (ver ecuación (25)). Por lo anterior y en virtud de las definiciones (15), (17) y (19), las funciones espectrales para  pueden ser obtenidas en términos de series. Según lo anterior, y utilizando el lenguaje de la teoría cuántica de campos, es posible identificar correcciones a nivel árbol (o correcciones de primer orden), correcciones a un lazo (o correcciones de segundo orden), correciones a dos lazos (o correcciones de tercer orden), etc., en cada una de las funciones espectrales (Beltrán Almeida, Rodríguez & Valenzuela-Toledo, 2011 ; Boubekeur & Lyth, 2006; Byrnes, Koyama, Sasaki, & Wands, 2007), por lo cual se hace necesario definir cuáles de estos términos son los dominantes (Cogollo, Rodríguez, & Valenzuela-Toledo, 2008; Rodríguez & Valenzuela-Toledo, 2010).
pueden ser obtenidas en términos de series. Según lo anterior, y utilizando el lenguaje de la teoría cuántica de campos, es posible identificar correcciones a nivel árbol (o correcciones de primer orden), correcciones a un lazo (o correcciones de segundo orden), correciones a dos lazos (o correcciones de tercer orden), etc., en cada una de las funciones espectrales (Beltrán Almeida, Rodríguez & Valenzuela-Toledo, 2011 ; Boubekeur & Lyth, 2006; Byrnes, Koyama, Sasaki, & Wands, 2007), por lo cual se hace necesario definir cuáles de estos términos son los dominantes (Cogollo, Rodríguez, & Valenzuela-Toledo, 2008; Rodríguez & Valenzuela-Toledo, 2010).
Cuando se buscan los términos dominantes en las funciones espectrales es necesario tener en cuenta las restricciones observacionales. Como se mencionó en la Sección 3, si la anisotropía estadística existe, ésta vendría cuantificada en el nivel de anisotropía estadística 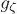 en el espectro
en el espectro 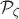 ; sin embargo, observacionalmente se sabe que este nivel es muy pequeño y por lo tanto es necesario asegurar que las contribuciones provenientes de los vectores en el espectro sean más pequeñas que las provenientes de las perturbaciones en los campos vectoriales. Lo anterior se satisface fácilmente si se asume que la corrección a nivel árbol en el primer término de la ecuación (28) domina sobre todos los demás. Adicionalmente, en el presente trabajo se asumirá que en los demás términos las correcciones asociadas a los campos vectoriales dominan sobre las contribuciones de los campos escalares y sobre los términos mixtos; lo anterior con el fin de obtener niveles de no gaussianidad altamente anisótropos que son, hasta el momento, observacionalmente permitidos.
; sin embargo, observacionalmente se sabe que este nivel es muy pequeño y por lo tanto es necesario asegurar que las contribuciones provenientes de los vectores en el espectro sean más pequeñas que las provenientes de las perturbaciones en los campos vectoriales. Lo anterior se satisface fácilmente si se asume que la corrección a nivel árbol en el primer término de la ecuación (28) domina sobre todos los demás. Adicionalmente, en el presente trabajo se asumirá que en los demás términos las correcciones asociadas a los campos vectoriales dominan sobre las contribuciones de los campos escalares y sobre los términos mixtos; lo anterior con el fin de obtener niveles de no gaussianidad altamente anisótropos que son, hasta el momento, observacionalmente permitidos.
Con las anteriores consideraciones y tomando la serie para  hasta orden dos, las ecuaciones (28), (29) y (30) se pueden separar de la siguiente manera:
hasta orden dos, las ecuaciones (28), (29) y (30) se pueden separar de la siguiente manera:
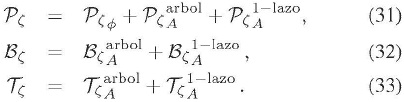
Finalmente, utilizando la ecuación (25) y las definiciones (15), (17) y (19), se obtinen los términos necesarios para la realización del presente trabajo:
a. Correcciones a nivel árbol:
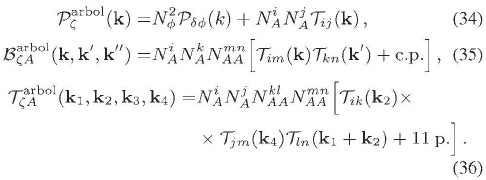
b. Correcciones a un lazo:
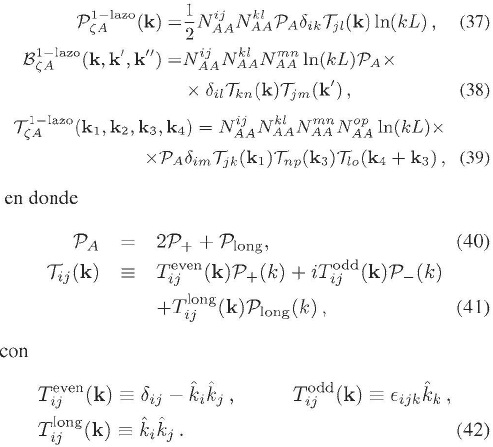
En las anteriores expresiones 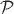 δΦ, representa el espectro asociado a las perturbaciones en el campo escalar,
δΦ, representa el espectro asociado a las perturbaciones en el campo escalar, 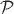 long representa el espectro para la polarización longitudinal del vector, y
long representa el espectro para la polarización longitudinal del vector, y 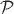 +y
+y 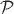 - representan los espectros que conservan y violan respectivamente la paridad:
- representan los espectros que conservan y violan respectivamente la paridad:
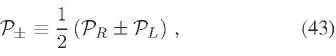
en donde 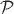 R y
R y 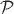 L denotan los espectros asociados a las componentes transversales del espectro del vector, con polarización circular derecha (R) y polarización circular izquierda (L) respectivamente. La sigla c.p. significa permutaciones cíclicas, y la cantidad L es el tamaño de la caja sobre la cual se realizan las integraciones correspondientes a las correcciones a un lazo; excepto cuando se consideren multipolos bajos en la RCF, el tamaño de la caja debe ser fijado a L
L denotan los espectros asociados a las componentes transversales del espectro del vector, con polarización circular derecha (R) y polarización circular izquierda (L) respectivamente. La sigla c.p. significa permutaciones cíclicas, y la cantidad L es el tamaño de la caja sobre la cual se realizan las integraciones correspondientes a las correcciones a un lazo; excepto cuando se consideren multipolos bajos en la RCF, el tamaño de la caja debe ser fijado a L 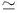 H0 (Kohri, Lyth, & Valenzuela-Toledo, 2010; Kumar, Leblond, & Rajaraman, 2010) (siendo H0< el parámetro de Hubble hoy en día), lo cual da ln(kL) ∼ 1 para las escalas cosmológicas relevantes.
H0 (Kohri, Lyth, & Valenzuela-Toledo, 2010; Kumar, Leblond, & Rajaraman, 2010) (siendo H0< el parámetro de Hubble hoy en día), lo cual da ln(kL) ∼ 1 para las escalas cosmológicas relevantes.
Es de anotar que se ha supuesto que la expansión es isótropa: de esta manera los espectros asociados al campo escalar y a las diferentes polarizaciones del campo vectorial dependen únicamente del número de onda; adicionalmente, los correladores de dos puntos entre el campo escalar y alguna de las componentes del campo vectorial se hacen iguales a cero debido a la invarianza ante rotaciones espaciales.
5. Cálculo de los niveles de no gaussianidad 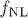 Y
Y 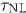
En esta sección se estimarán los descriptores estadísticos 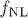 y
y 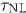 , conocidos en la literatura como niveles de no gaussianidad. Se asumirá que éstos son generados por la parte anisótropa de la perturbación primordial en la curvatura
, conocidos en la literatura como niveles de no gaussianidad. Se asumirá que éstos son generados por la parte anisótropa de la perturbación primordial en la curvatura  y se considerará que la parte no gaussiana de
y se considerará que la parte no gaussiana de  es producida únicamente por las perturbaciones en los campos vectoriales. En virtud de las ecuaciones (31 ), (32) y (33), se estudiarán las siguientes posibilidades autoconsistentes las cuales integran los resultados obtenidos en Valenzuela-Toledo, Rodríguez, & Lyth, 2009) para el caso del biespectro y en (ValenzuelaToledo & Rodríguez, 2010) para el caso del triespectro15:
es producida únicamente por las perturbaciones en los campos vectoriales. En virtud de las ecuaciones (31 ), (32) y (33), se estudiarán las siguientes posibilidades autoconsistentes las cuales integran los resultados obtenidos en Valenzuela-Toledo, Rodríguez, & Lyth, 2009) para el caso del biespectro y en (ValenzuelaToledo & Rodríguez, 2010) para el caso del triespectro15:
l. Espectro (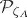 ) y biespectro (
) y biespectro (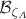 ) de las perturbaciones en los campos vectoriales dominados por términos a nivel árbol.
) de las perturbaciones en los campos vectoriales dominados por términos a nivel árbol.
2. Espectro (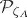 ) y biespectro (
) y biespectro (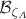 ) de las perturbaciones en los campos vectoriales dominados por términos a un lazo.
) de las perturbaciones en los campos vectoriales dominados por términos a un lazo.
3. Espectro (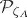 ) y tri espectro (
) y tri espectro (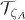 ) de las perturbaciones en los campos vectoriales dominados por términos a nivel árbol.
) de las perturbaciones en los campos vectoriales dominados por términos a nivel árbol.
4. Espectro (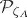 ) y tri espectro (
) y tri espectro (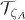 ) de las perturbaciones en los campos vectoriales dominados por términos a un lazo.
) de las perturbaciones en los campos vectoriales dominados por términos a un lazo.
5.1. Espectro (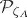 ) y biespectro (
) y biespectro (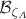 ) de las perturbaciones en los campos vectoriales dominados por términos a nivel árbol.
) de las perturbaciones en los campos vectoriales dominados por términos a nivel árbol.
En este caso el parámetro de no gaussianidad 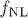 viene ón:
viene ón:
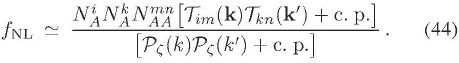
Lo que se quiere en este artículo es obtener el orden de magnitud de los niveles de no gaussianidad, así que se se asumirá, con una buena aproximación, que 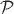 Long
Long 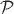 +, y
+, y 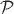 -- son todos del mismo orden de magnitud, además de considerar que el espectro es invariante de escala. Así,
-- son todos del mismo orden de magnitud, además de considerar que el espectro es invariante de escala. Así, 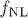 se puede escribir de la siguiente forma:
se puede escribir de la siguiente forma:

Finalmente, si se asume que 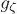 ∼
∼ 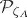 /
/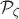 , y tomando el valor observacional para
, y tomando el valor observacional para 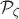 ,
, 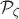 1/2,
1/2, 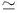 5 x 10-5 (Bunn & White, 1997), se puede encontrar que:
5 x 10-5 (Bunn & White, 1997), se puede encontrar que:
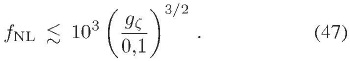
El anterior resultado, da una cota superior para el valor de 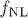 en términos del nivel de anisotropía estadística. Se puede observar que nuestro resultado está de acuerdo con las más recientes cotas observacionales sobre
en términos del nivel de anisotropía estadística. Se puede observar que nuestro resultado está de acuerdo con las más recientes cotas observacionales sobre 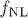 , por ejemplo -10 <
, por ejemplo -10 < 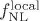 < 74 (Komatsu et. al., 2011), aunque podría llegar a excederlas.
< 74 (Komatsu et. al., 2011), aunque podría llegar a excederlas.
5.2. Espectro (Pc,A) y biespectro (Bc,A) de las perturbaciones en los campos vectoriales dominados por contribuciones a un lazo.
En esta situación 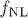 toma la forma:
toma la forma:
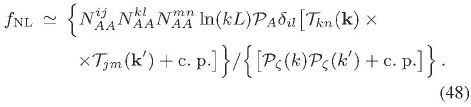
Nuevamente, asumiendo que las componentes del espectro son todas del mismo orden y además que son invariantes de escala, se tiene que:
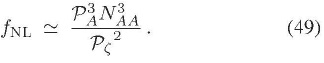
Como se está considerando que el espectro está dominado por correcciones a un lazo, (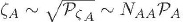 . Así, se puede encontrar que:
. Así, se puede encontrar que:
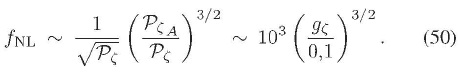
Esta ecuación muestra una relación directa entre el parámetro de no gaussianidad 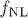 y el nivel de anisotropía estadística
y el nivel de anisotropía estadística 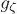 Como un ejemplo, y aprovechando la incertidumbre acerca del valor de
Como un ejemplo, y aprovechando la incertidumbre acerca del valor de 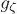 , se puede dar una cota superior para
, se puede dar una cota superior para 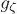 a partir de la actual cota superior para
a partir de la actual cota superior para 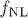 · Si
· Si 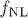 < 74, entonces
< 74, entonces 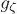 < 0,2 en este escenario.
< 0,2 en este escenario.
5.3. Espectro (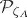 Pc,A) y triespectro (
Pc,A) y triespectro (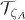 ) de las perturbaciones en los campos vectoriales dominados por términos a nivel árbol.
) de las perturbaciones en los campos vectoriales dominados por términos a nivel árbol.
En este caso el nivel de no gaussianidad 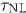 en el triespectro se escribe como
en el triespectro se escribe como
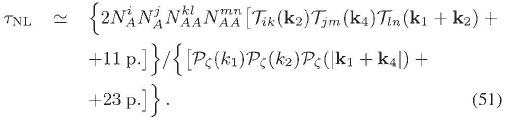
Si se asume que 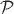 Long,
Long,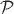 + y
+ y 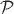 - son todos del mismo orden de magnitud y además que el espectro es invariante de escala,
- son todos del mismo orden de magnitud y además que el espectro es invariante de escala, 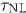 toma una forma más simple,
toma una forma más simple,
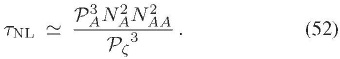
Ahora, utilizando el hecho de que  y que
y que 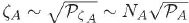 , fácilmente se puede llegar a:
, fácilmente se puede llegar a:

Finalmente, empleando 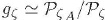 , se obtiene:
, se obtiene:
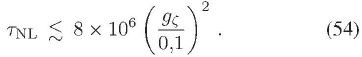
La anterior expresión brinda una cota superior para el el nivel de no-gaussianidad en el triespectro  , en función del nivel de anisotropía estadística en el espectro
, en función del nivel de anisotropía estadística en el espectro 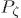 . Este resultado puede fácilmente exceder la cota observacional sobre
. Este resultado puede fácilmente exceder la cota observacional sobre 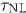 TNL: -0,6 X 104 <
TNL: -0,6 X 104 <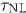 < 3,3 X 104 (Smidt et. al., 2010).
< 3,3 X 104 (Smidt et. al., 2010).
5.4. Espectro (Pe,A) y triespectro (T¿A) de las perturbaciones en los campos vectoriales dominados por contribuciones a un lazo
En esta situación 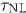 se escribe como:
se escribe como:
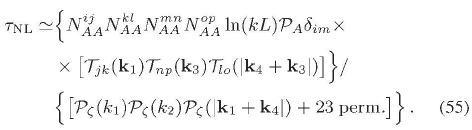
Nuevamente, asumiendo que los espectros son del mismo orden de magnitud e invariantes de escala, se obtiene:
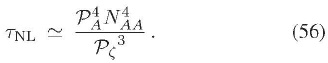
Utilizando las consideraciones sobre el espectro de la perturbaciones vectoriales de la Subsección 5.2, se puede obtener la siguiente relación para 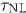 :
:
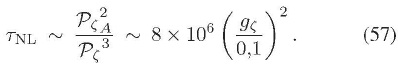
La anterior ecuación brinda una relación directa entre 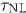 y el nivel de anisotropía estadística en el espectro. Finalmente, combinando las ecuaciones (50) y (57), se obtiene:
y el nivel de anisotropía estadística en el espectro. Finalmente, combinando las ecuaciones (50) y (57), se obtiene:
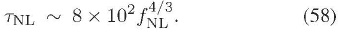
la cual brinda una relación de consistencia entre los niveles de no gaussianidad 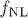 y
y 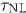 para este escenario en particular. Las relaciones dadas por las ecuaciones (50), (57) y (58) se pueden utilizar en el futuro para poner bajo prueba este escenario frente a los resultados observacionales.
para este escenario en particular. Las relaciones dadas por las ecuaciones (50), (57) y (58) se pueden utilizar en el futuro para poner bajo prueba este escenario frente a los resultados observacionales.
6. Conclusiones
Se estudió en este artículo el orden de magnitud de los niveles de no gaussianidad 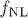 en el biespectro
en el biespectro 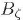 y
y 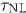 en el triespectro T(. cuando se consideran violaciones a la isotropía estadística por la presencia de campos vectoriales en la dinámica inflacionaria. Se encontró que es posible obtener valores observables de los niveles de no gaussianidad que incluso pueden superar los actuales límites observacionales (para el máximo valor posible de
en el triespectro T(. cuando se consideran violaciones a la isotropía estadística por la presencia de campos vectoriales en la dinámica inflacionaria. Se encontró que es posible obtener valores observables de los niveles de no gaussianidad que incluso pueden superar los actuales límites observacionales (para el máximo valor posible de 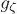 de acuerdo a los análisis observacionales más recientes (Groeneboom, Ackerman, Wehus, & Eriksen, 2010; Groeneboom & Eriksen, 2009)). Además se encontraron algunas relaciones de consistencia entre los tres descriptores estadísticos: los niveles de no gaussianidad
de acuerdo a los análisis observacionales más recientes (Groeneboom, Ackerman, Wehus, & Eriksen, 2010; Groeneboom & Eriksen, 2009)). Además se encontraron algunas relaciones de consistencia entre los tres descriptores estadísticos: los niveles de no gaussianidad 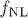 y
y 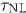 y el nivel de anisotropía estadística en el espectro
y el nivel de anisotropía estadística en el espectro 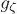 . Queremos enfatizar que tales relaciones de consistencia se pueden utilizar en el futuro para poner bajo prueba este escenario frente a los resultados observacionales; ellas permiten fijar dos de los descriptores estadísticos a partir del tercero.
. Queremos enfatizar que tales relaciones de consistencia se pueden utilizar en el futuro para poner bajo prueba este escenario frente a los resultados observacionales; ellas permiten fijar dos de los descriptores estadísticos a partir del tercero.
Como un subproducto del estudio realizado en este artículo, se presentó la definición del verdadero principio cosmológico: éste, como un producto de la observación y no de la filosofía, corresponde a la invarianza ante translaciones espaciales y rotaciones espaciales de la función de distribución de probabilidad que gobierna a la a la perturbación primordial en la curvatura  . En otras palabras, la homogeneidad e isotropía a grandes escalas debe entenderse como la homogeneidad estadística y la isotropía estadística asociadas
. En otras palabras, la homogeneidad e isotropía a grandes escalas debe entenderse como la homogeneidad estadística y la isotropía estadística asociadas  .
.
______________
4 En este caso se dice que el Universo es homogéneo e isótropo a gran escala. El conjunto de palabras "gran escala" hace referencia al hecho de que se está considerando regiones del Universo de volumen superior a 106 Mpc3.
5El teorema ergódico, y las hipótesis que conducen a éste, se presentan y discuten en (Weinberg, 2008).
6Cuando 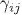 depende del tiempo, la expansión es anisótropa (Dimopoulos, Karciauskas, Lyth & Rodríguez, 2009).
depende del tiempo, la expansión es anisótropa (Dimopoulos, Karciauskas, Lyth & Rodríguez, 2009).
7El promedio sobre el ensamble dentro de la integral es sobre los modos de Fourier solamente puesto que ellos son las variables estocásticas.
8Para iguales vectores de onda, la condición de realidad sobre  (x) aplica y, por lo tanto, hay autocorrelación.
(x) aplica y, por lo tanto, hay autocorrelación.
9La suma sobre los apareamientos no distingue aquéllos que intercambian vectores de onda en un par, o que meramente intercambian pares.
10La relación entre estas dos cantidades es conocida como el efecto Sachs-Wolfe (Sachs & Wolfe, 1967).
11Una descripción de los resultados de cada uno de estos artículos está más allá de los propósitos del presente artículo. Sin embargo, el propósito de cada uno de ellos es esencialmente el mismo: contribuir a la expansión acelerada y/o a la generación de estructuras a gran escala a través de campos vectoriales.
12NASA's Wilkinson Microwave Anisotropy Probe homepage: http://wmap.gsfc.nasa.gov/.
13ESA's PLANCK mission homepage: http://planck.esa.int/.
14Como se muestra en (Dimopoulos, 2006), debido a que la inflación hace homogéneo el campo vectorial (∂iAµ=0) su componente temporal se hace cero. Adicionalmente, si el campo vectorial no tiene masa, se puede hacer la componente temporal igual a cero mediante una escogencia del gauge.
15Escenarios en donde una función espectral es dominada por términos a nivel árbol mientras que otra es dominada por términos a un lazo carecen de autoconsistencia (Valenzuela-Toledo & Rodríguez, 2010; Valenzuela-Toledo, Rodríguez, & Lyth, 2009).
Agradecimientos
C.A. V.-T. agradece a la Vicerrectoría de Investigaciones de la Universidad del Valle. Y.R. cuenta con el apoyo financiero de COLCIENCIAS mediante proyecto de investigación número 1102-487-25992 CT-460-2009, y de la DIEF (UIS) mediante proyecto de investigación número 5177.
Referencias
Abramo L. R. & Pereira T. S., 2010. Testing gaussianity, homogeneity, and isotropy with the cosmic microwave background, Adv. Astron. 2010, 378203. [ Links ]
Ackerman L., Carroll S. M., & Wise M. B., 2007. Imprints of a primordial preferred direction on the microwave background, Phys. Rev. O 75, 083502. [ Links ]
Adler R. J., 1981. The geometry of random fields, John Wiley & Sons, Chichester - UK. [ Links ]
Aihara H. e t. al., 2011. The eighth data release of the S loan Digital Sky Survey: First data from SDSS-III, Astrophys. J. Suppl. Ser. 193,29. [ Links ]
Alabidi L. & Huston l., 201O. An update on single field models of inftation in light of WMAP7, JCAP 1008, 037 (20 10). [ Links ]
Alabidi L. & Lidsey J., 2008. Single field inftation after the WMAP five-year data, Phys. Rev. D. 78, 103519. [ Links ]
Alabidi L. & Lyth D. H., 2006a. Inftation models after WMAP year three, JCAP 0608, 013. [ Links ]
Alabidi L. & Lyth D. H., 2006b. Inftation models and observation, JCAP 0605, 016. [ Links ]
Armendariz-Picon C., 2007. Creating statistically anisotropic and inhomogeneous perturbations, JCAP 0709, 014. [ Links ]
Armendariz-Picon C. & Pekowsky L., 2009. Bayesian limits on primordial isotropy breaking, Phys. Rev. Lett. 102, 03130 l. [ Links ]
Bartolo N., Dimastrogiovanni E., Matarrese S., & Riotto A., 2009a. Anisotropic bispectrum of curvature perturbations from primordial non-Abelian vector fields, JCAP 0910, 015. [ Links ]
Bartolo N., Dimastrogiovanni E., Matarrese S. & Riotto A., 2009b. Anisotropic trispectrum of curvature perturbations induced by primordial non-Abelian vector fields, JCAP 0911, 028. [ Links ]
Beltrán Almeida J. P., Rodríguez Y. & Valenzuela-Toledo C. A., 2011. Feynman-like rules for calculating n-point correlators of the primordial curvature perturbation, in preparation. [ Links ]
Bohmer C. G. & Mota D. F., 2008. CMB anisotropies and inftation from non-standard spinors, Phys. Lett. B 663, 168. [ Links ]
Boubekeur L. & Lyth D. H., 2006. Detecting a small perturbation through its non-gaussianity, Phys. Rev. D 73, 021301 (R). [ Links ]
Bunn E. F. & White M. J., 1997. The four-year COBE normalization and large-scale structure, Astrophys. J. 480, 6. [ Links ]
Byrnes C. T., Koyama K., Sasaki M., & Wands D., 2007. Diagrammatic approach to non-gaussianity from inftation, JCAP 0711, 027. [ Links ]
Cogollo H. R. S., Rodríguez Y., & Valenzuela-Toledo C. A., 2008. On the issue of the ( series convergence and loop corrections in the generation of observable primordial non-gaussianity in slow-roll inftation. Part 1: the bispectrum, .ICAP 0808, 029. [ Links ]
Dimastrogiovanni E., Bartolo N., Matarrese S. & Riotto A., 2010. Non-gaussianity and statistical anisotropy from vector field populated inftationary models, Adv. Astron. 2010, 752670. [ Links ]
Dimopoulos K, 2006. Can a vector field be responsible for the curvature perturbation in the Universe?, Phys. Rev. D 74, 083502. [ Links ]
Dimopoulos K, 2007. Supergravity inspired vector curvaton, Phys. Rev. D 76, 063506. [ Links ]
Dimopoulos K & Karciauskas M., 2008. Non-minimally coupled vector curvaton, .IHEP 0807, 119. [ Links ]
Dimopoulos K, Karciauskas M., Lyth D. H., & Rodríguez Y., 2009. Statistical anisotropy of the curvature perturbation from vector field perturbations, JCAP 090S, 013. [ Links ]
Dimopoulos K, Karciauskas M., & WagstaffJ. M., 2010a. Vector curvaton with varying kinetic function, Phys. Rev. D 81, 023522. [ Links ]
Dimopoulos K, Karciauskas M. & Wagstaff J. M., 2010b. Vector curvaton without instabilities, Phys. Lett. B 683, 298. [ Links ]
Dimopoulos K&. Wagstaff J. M, 201l. Particle production of vector fields: scale invariance is attractive, Phys. Rev. D 83, 023523. [ Links ]
Dulaney T. R. & Gresham M. l., 2010. Primordial power spectra from anisotropic inftation, Phys. Rev. D 81, 103532. [ Links ]
Germani C. & Kehagias A., 2009. p-form inftation, JCAP 0903, 028. [ Links ]
Golovnev A., 2010. Linear perturbations in vector inftation and stability issues, Phys. Rev. D 81, 023514. [ Links ]
Golovnev A., Mukhanov V., & Vanchurin V., 2008a. Gravitational waves in vector inftation, .ICAP 0811, O 18. [ Links ]
Golovnev A., Mukhanov V., & Vanchurin V., 2008b. Vector inftation, JCAP 0806, 009. [ Links ]
Golovnev A. & Vanchurin V., 2009. Cosmological perturbations from vector inftation, Phys. Rev. D 79, 103524. [ Links ]
Groeneboom N. E., Ackerman L., Wehus l. K., &. Eriksen H. K, 2010. Bayesian analysis of an anisotropic universe model: systematics and polarization, Astrophys. J. 722, 452. [ Links ]
Groeneboom N. E. & Eriksen H. K, 2009. Bayesian analysis of sparse anisotropic universe models and application to the 5-yr WMAP data, Astrophys. J. 690, 1807. [ Links ]
Gümrükcüoglu A. E., Himmetoglu B., & Peloso M., 2010. Scalar-scalar, scalar-tensor, and tensor-tensor correlators from anisotropic inftation, Phys. Rev. D 81, 063528. [ Links ]
Hansen F. K. et. al., 2009. Power asymmetry in cosmic microwave background ftuctuations from full sky to sub-degree scales: is the Universe isotropic?, Astrophys. J. 704, 1448. [ Links ]
Hanson D. & Lewis A., 2009. Estimators for CMB statistical anisotropy, Phys. Rev. D 80, 063004. [ Links ]
Hanson D., Lewis A. & Challinor A., 2010. Asymmetric beams and CMB statistical anisotropy, Phys. Rev. D 81, 103003. [ Links ]
Himmetoglu B., 2010. Spectrum of perturbations in anisotropic inftationary Universe with vector hair, JCAP 1003, 023. [ Links ]
Himmetoglu B., Contaldi C. R., & Peloso M., 2009a. Instability of the Ackerman-Carroll-Wise model, and problems with massive vectors during inftation, Phys. Rev. D 79, 063517. [ Links ]
Himmetoglu B., Contaldi C. R., & Peloso M., 2009b. Instability of anisotropic cosmological solutions supported by vector fields, Phys. Rev. Lett. 102, 11130 l. [ Links ]
Himmetoglu B., Contaldi C. R., & Peloso M., 2009c. Ghost instabilities of cosmological models with vector fields nonminimally coupled to the curvature, Phys. Rev. D 80, 123530. [ Links ]
Hoftuft J. et. al., 2009. Increasing evidence for hemispherical power asymmetry in the five-year WMAP data, Astrophys. J. 699, 985. [ Links ]
Kanno S., Kimura M., Soda J., & Yokoyama S., 2008. Anisotropic inftation from vector impurity, JCAP 0808, 034. [ Links ]
Karciauskas M., 2011. The primordial curvature perturbation from vector fields of general non-abelian groups, arXi v: 11 O 4 . 3 62 9 [astro-ph. CO]. [ Links ]
Karciauskas M., Dimopoulos K., & Lyth D. H., 2009. Anisotropic non-gaussianity from vector field perturbation, Phys. Rev. D 80, 023509. [ Links ]
Karciauskas M. & Lyth D. H., 2010. On the health of a vector field with (RA2)/6 coupling to gravity, JCAP 1011,023. [ Links ]
Karlin S. & Taylor H. M., 1975. A first course on stochastic processes, Academic Press, New York - USA. [ Links ]
Koh S. & Hu B., 2009. Timelike vector field dynamics in the early Universe, arXiv: 0901.042 9 [hep-th]. [ Links ]
Kohri K., Lyth D. H., & Valenzuela-Toledo C. A., 2010. On the generation of a non-gaussian curvature perturbation during preheating, JCAP 1002, 023. [ Links ]
Komatsu E., 2010. Hunting for primordial non-gaussianity in the cosmic microwave background, Class. Quantum Grav. 27, 12401 O. [ Links ]
Komatsu E. et. al., 2011. Seven-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: cosmological interpretation, Astrophys. J. Suppl. Ser. 192, 18. [ Links ]
Kumar J., Leblond L., & Rajaraman A., 2010. S cale dependent local non-gaussianity from loops, JCAP 1004, 024. [ Links ]
Lyth D. H. & Liddle A. R., 2009. The primordial density perturbation: cosmology, inftation, and the origin of structure, Cambridge University Press, Cambridge- UK. [ Links ]
Lyth D. H., Malik K. A., & Sasaki M., 2005. A general proof of the conservation of the curvature perturbation, JCAP 0505, 004. [ Links ]
Lyth D. H & Rodríguez Y., 2005. Inftationary prediction for primordial non-gaussianity, Phys. Rev. Lett. 95, 121302. [ Links ]
Ma Y.-Z., Efstathiou G. & Challinor A., 2011. Testing a direction-dependent primordial power espectrum with observations of the cosmic microwave background, Phys. Rev. D 83, 083005. [ Links ]
Maleknejad A. & Sheikh-Jabbari M. M. 2011a. Gauge-flation: inflation from non-abelian gauge fields, arXiv: 1102.1513 [hep-ph]. [ Links ]
Maleknejad A. & Sheikh-Jabbari M. M. 2011b. Non-abelian gauge field inflation. arXiv: 1102.1932 [hep-ph]. [ Links ]
Mukhanov V., 2005. Physical foundations of cosmology, Cambridge University Press, Cambridge - UK. [ Links ]
Pullen A. R. & Kamionkowski M., 2007. Cosmic microwave background statistics for a direction-dependent primordial power spectrum, Phys. Rev. D 76, 103529 [ Links ]
Rodríguez Y. & Valenzuela-Toledo C. A., 2010. On the issue of the C series convergence and loop corrections in the generation of observable primordial non-gaussianity in slow-roll inflation. Part II: the trispectrum, Phys. Rev. D. 81, 023531. [ Links ]
Sachs R. K. & Wolfe A. M., 1967. Perturbations of a cosmological model and angular variations of the microwave background, Astrophys. J. 147, 73. [ Links ]
Samal P. K., Saha R., Jain P., & Ralston J.P., 2009. Signals of statistical anisotropy in WMAP foreground-cleaned maps, Mon. Not. R. Astron. Soc.396, 511. [ Links ]
Sasaki M. & Stewart E. D., 1996. A general analytic formula for the spectral index of the density perturbations produced during inflation, Prog. Theor. Phys. 95, 71. [ Links ]
Sasaki M. & Tanaka T., 1998. Superhorizon scale dynamics of multiscalar inflation, Prog. Theor. Phys. 99, 763. [ Links ]
Smidt J. et al., 2010. A mesurement of cubic-order primordial non-gaussianity (gNL and TNL) with WMAP 5-year data, arXiv: 1001.5026 [astro-ph.CO]. [ Links ]
Starobinsky A. A., 1983. Isotropization of arbitrary cosmological expansion given an effective cosmological constant, Pis'ma Zh. Eksp. Teor. Fiz. 37, 55 [JETP lett. 37, 66]. [ Links ]
Starobinsky A. A., 1985. Multicomponent de Sitter (inflationary) stages and the generation of perturbations, Pis'ma Zh. Eksp. Teor. Fiz. 42, 124 [JEPT lett. 42, 152]. [ Links ]
Valenzuela-Toledo C. A. & Rodríguez Y., 2010. Non-gaussianity from the trispectrum and vector field perturbations, Phys. Lett. B 685, 120 (2010). [ Links ]
Valenzuela-Toledo C. A., Rodríguez Y., & Lyth D. H., 2009. Non-gaussianity at tree and one-loop levels from vector field perturbations, Phys. Rev. D 80, 103519. [ Links ]
Wald R. M., 1983. Asymptotic behavior of homogeneous cosmological models in the presence of a positive cosmological constant., Phys. Rev. D 28, R2118. [ Links ]
Watanabe M.-a., Kanno S., & Soda J., 2009. Inflactionary Universe with anisotropic hair, Phys. Rev. Lett. 102, 191302. [ Links ]
Watanabe M.-a., Kanno S., & Soda J., 2010. The nature of primordial fluctuations from anisotropic inflaction, Prog. Theor. Phys. 123, 1041. [ Links ]
Weinberg S., 1972. Gravitation and cosmology: principles and applications of the general theory of relativity, Jhon Wiley & Sons, New York - USA. [ Links ]
Weinberg S., 2008. Cosmology, Oxford University Press, Oxford - UK. [ Links ]
Yokoyama S. & Soda J., 2008. Primordial statistical anisotropy generated at the end of inflation, JCAP 0808, 005. [ Links ]
Recibido: marzo 23 de 2011. Aceptado para su publicación: mayo 2 de 2011.