Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en
SciELO
Similares en
SciELO -
 Similares en Google
Similares en Google
Compartir
Revista de la Academia Colombiana de Ciencias Exactas, Físicas y Naturales
versión impresa ISSN 0370-3908
Rev. acad. colomb. cienc. exact. fis. nat. vol.36 no.139 Bogotá abr./jun. 2012
MATEMÁTICAS
* Universidad Distrital Francisco José de Caldas, Bogotá, Colombia. Email: paacostas@udistrital.edu.co
**Universidad Nacional de Colombia, Bogotá, Colombia. Email: valbis@accefyn.org.co
AMS Classification 2010: 13B25, 13F25, 11T55.
Abstract
Known results on orthogonal systems and permutation polynomials vectors over finite fields are extended to modular algebras of the form 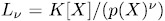 , where K is a finite field,
, where K is a finite field, 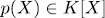 is an irreducible polynomial,
is an irreducible polynomial, 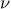 = 1, 2, . . ., and to the algebra of formal power series
= 1, 2, . . ., and to the algebra of formal power series 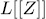 , where L1 = K[X]/(p(X)) = L.
, where L1 = K[X]/(p(X)) = L.
Key words: Permutation polynomial, orthogonal systems, permutation polynomial vectors
Resumen
Resultados sobre sistemas ortogonales y vectores de polinomios de permutación se extienden a las álgebras modulares de la forma 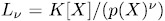 , donde K es un cuerpo finito,
, donde K es un cuerpo finito, 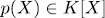 un polinomio irreducible,
un polinomio irreducible, 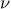 = 1, 2, . . . y al álgebra de las series potenciales formales
= 1, 2, . . . y al álgebra de las series potenciales formales 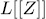 , donde L1 = K[X]/(p(X)) = L.
, donde L1 = K[X]/(p(X)) = L.
Palabras clave: Polinomio de permutación, sistemas ortogonales, vectores de polinomios de permutación.
1. Introduction
Let 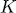 be a finite field,
be a finite field, 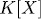 its ring of polynomials and
its ring of polynomials and 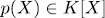 an irreducible monic polynomial. It is known that
an irreducible monic polynomial. It is known that 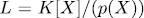 is a finite field an that
is a finite field an that 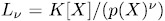 ,
, 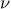 = 1,2,..., are L-algebras (see infra for details). In previous papers ([1] and [2]) the authors obtained results about permutation polynomial over the L-algebras
= 1,2,..., are L-algebras (see infra for details). In previous papers ([1] and [2]) the authors obtained results about permutation polynomial over the L-algebras 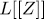 (formal series over L) and
(formal series over L) and  , analogos to some known results over finite fields, Galois rings
, analogos to some known results over finite fields, Galois rings 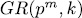 , and the rings
, and the rings 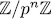 (see, for example, [5],[7],[8],[10],[13] and [14]). Permutation polynomial, find applications currently in cryptography and coding theory (see [4] for more references).
(see, for example, [5],[7],[8],[10],[13] and [14]). Permutation polynomial, find applications currently in cryptography and coding theory (see [4] for more references).
In this paper we deal with systems of polynomials in 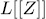 and
and  , obtaining results than in some cases lead to construct new permutation polynomials. The systems we are interested in are know as orthogonal systems has being studied by NIEDERREITER in [6] when the coefficients of the polynomials are in finite fields. Moreover, WEI & ZHANG in [12] and SHIUE, SUN & ZHANG in [8] extended some of these results to certain finite rings.
, obtaining results than in some cases lead to construct new permutation polynomials. The systems we are interested in are know as orthogonal systems has being studied by NIEDERREITER in [6] when the coefficients of the polynomials are in finite fields. Moreover, WEI & ZHANG in [12] and SHIUE, SUN & ZHANG in [8] extended some of these results to certain finite rings.
2. Preliminaries.
In this section we recall some properties of  and
and 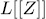 needed for the best undertading of what follows (see [3],[9]. Here the elements of
needed for the best undertading of what follows (see [3],[9]. Here the elements of  will be denoted by
will be denoted by
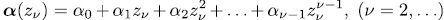
wher 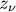 is the class of equivalence
is the class of equivalence 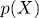 modulo
modulo 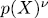 The elements of L will simply be denote by α It is know that
The elements of L will simply be denote by α It is know that
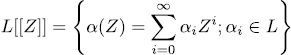
is a local ring with maximal ideal (Z), and
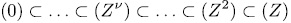
are the only ideals of
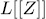 . Also,
. Also, 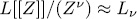 , and
, and  is a finite ring with
is a finite ring with 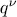 elements, (
elements, (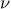 =1,2,...,) when L has q elements. Thus
=1,2,...,) when L has q elements. Thus 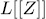 is the projective limit of the projective system of L-algebras
is the projective limit of the projective system of L-algebras 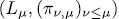 where
where
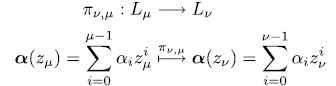
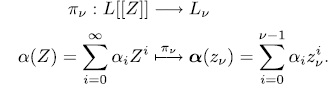
If 
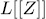 , its reduction
, its reduction  modulo
modulo 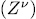 is the polynomial in
is the polynomial in 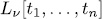 whose coefficients are the classes modulo
whose coefficients are the classes modulo 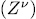 of the coefficients of
of the coefficients of 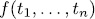 . Clearly, if
. Clearly, if 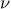 ≤ µ,
≤ µ, 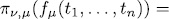

If
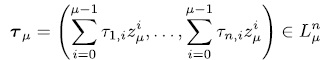
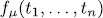 and
and 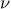 ≤ µ, we say that
≤ µ, we say that 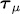 is a descendant of
is a descendant of 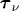 if
if 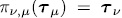 ; obviously, if that is the case,
; obviously, if that is the case, 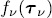 = 0, and we also say that
= 0, and we also say that 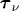 is an ascendantof
is an ascendantof 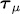 . Moreover, if
. Moreover, if 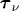 ∈
∈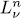 is a zero of
is a zero of  , then in
, then in 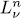 ,
, 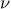 ≤ µ,
≤ µ, 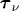 has ot most
has ot most 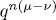 descendants, if any.
descendants, if any. A zero 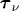 ∈
∈ 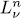 of
of  is said to be non-singular if
is said to be non-singular if
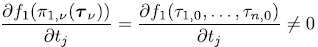
for some j= 1,...,n. Otherwise
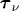 is called a singular zero. It is clear that any descendant (resp. ascendant) of a non-singular zero is a non-singular zero.
is called a singular zero. It is clear that any descendant (resp. ascendant) of a non-singular zero is a non-singular zero.
3. Orthogonal systems and permutation polynomial vectors.
In this section we introduce definitions and some results on the systems we are interested in. For a given commutative ring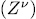 is also a regular polynomial in
is also a regular polynomial in 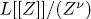 . More precisely, we prove that
. More precisely, we prove that 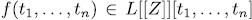 induces a permutation polynomial over
induces a permutation polynomial over  if, and only if, the equation
if, and only if, the equation 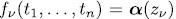 has exactly
has exactly 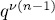 solutions for each
solutions for each 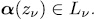
Accordingly to ZHANG ([11],[12]) this means that the polynomial 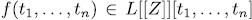 induces a permutation polynomial over
induces a permutation polynomial over  if, and only if,
if, and only if,  is a uniform map.
is a uniform map.
The system 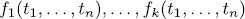 of polynomials in
of polynomials in 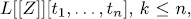 is said to be an orthogonal system over
is said to be an orthogonal system over  if the map
if the map  given by
given by 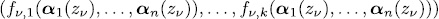 for
for 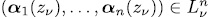 is a uniform map over
is a uniform map over  , i.e., if the system of equations
, i.e., if the system of equations
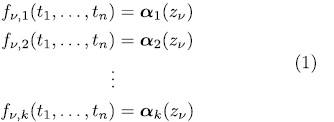
has 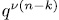 solutions in
solutions in 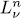 where
where 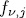 is the reduction of
is the reduction of 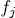 in
in 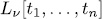 . If n = k the system is called permutation polynomial vector (PPV) over
. If n = k the system is called permutation polynomial vector (PPV) over 
Is clear that when k = 1, an orthogonal system is a permutation polynomial.
Proposition 3.1. Let 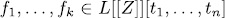 . If
. If  is an orthogonal system over
is an orthogonal system over  the it is and orthogonal system over
the it is and orthogonal system over 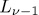 In particular, it is an orthogonal system over L.
In particular, it is an orthogonal system over L.
Proof. Let 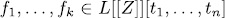 be an orthogonal system over
be an orthogonal system over  . Then the system
. Then the system
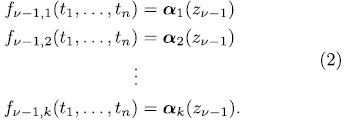
has solution 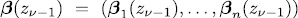 in
in 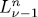 . Let N be the number of these solutions. Each of them has
. Let N be the number of these solutions. Each of them has 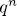 descendants. On the other hand, from (2) we see that there are
descendants. On the other hand, from (2) we see that there are 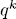 systems of the form
systems of the form
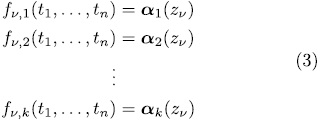
each of which has, by hypothesis, 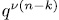 different solutions, i.e., taken altogether all the above
different solutions, i.e., taken altogether all the above 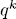 systems will have
systems will have 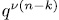
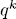 different solutions. Since each solution descends from
different solutions. Since each solution descends from 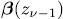 then
then
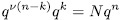
therefore, 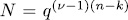 . So,
. So,  is an orthogonal system over
is an orthogonal system over 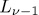 .
.
Corollary 3.1. Let 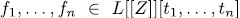 be a permutation polynomial vector over
be a permutation polynomial vector over  , then
, then  is a permutation polynomial vector over
is a permutation polynomial vector over 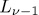 . In particular is a permutation polynomial vector over L.
. In particular is a permutation polynomial vector over L.
Proposition 3.2. let 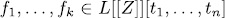 be an orthogonal system over L1 = L, and such that the zeroes of
be an orthogonal system over L1 = L, and such that the zeroes of 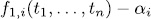 are nonsingular for all
are nonsingular for all 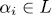 . Then
. Then  is an orthogonal system over
is an orthogonal system over  (
(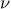 = 1,2,...).
= 1,2,...).
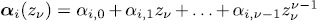 . We obtain the system
. We obtain the system 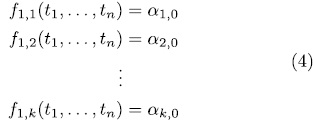
which has 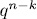 solutions. Since the zeroes of
solutions. Since the zeroes of 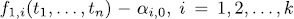 are non singular, each of the polynomial in (3) has exactly
are non singular, each of the polynomial in (3) has exactly 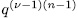 descendants in
descendants in  ([1, lem. 2.2 ]). All of them are not different, since otherwise each zero of (4) would have
([1, lem. 2.2 ]). All of them are not different, since otherwise each zero of (4) would have 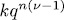 descendants and since each element of L can be viewed in
descendants and since each element of L can be viewed in 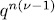 ways in
ways in  , then for k > 1, a zero of (4) would have more than
, then for k > 1, a zero of (4) would have more than 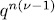 ways to be viewed in
ways to be viewed in 
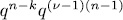 different solutions. Then the system would have
different solutions. Then the system would have
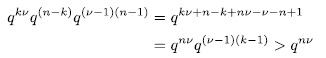
different solutions, thus for 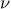 > 1, k >1. But this contradicts, the cardinality of
> 1, k >1. But this contradicts, the cardinality of 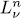 .
.
Therefore, the number of descendants, let us say D, contributed, by each polynomial in the system (4) to the solutions of system (3) is such that
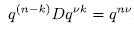 .
. Thus, 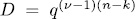 and the total number of solutions of (3) is
and the total number of solutions of (3) is 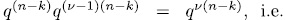
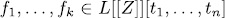 is an orthogonal system over
is an orthogonal system over 
Corollary 3.2. Let 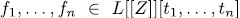 be a PPV over L such that the zeroes of
be a PPV over L such that the zeroes of 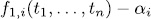 are nonsingular for all
are nonsingular for all 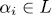 . Then
. Then  is a PPV over
is a PPV over  .
.
Proposition 3.3. Let 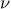 > 1 be,
> 1 be, 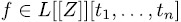 and
and 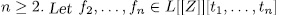 be polynomials such that
be polynomials such that 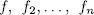 is a PPV over
is a PPV over  then,
then, 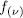 the projection of
the projection of 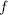 in
in 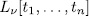 is a permutation polynomial.
is a permutation polynomial.
Proof. If 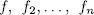 is a PPV over
is a PPV over  then, for all
then, for all 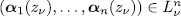 the system
the system
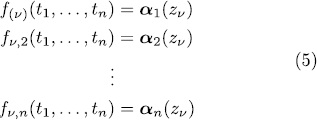
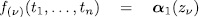 has at least one solution in
has at least one solution in  . Let
. Let 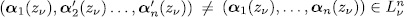 . The system
. The system 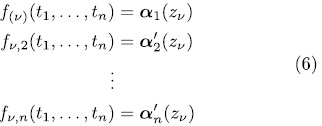
has again a unique solution, different to the solution of (5), because, otherwise,
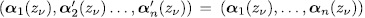 . But this can be done in
. But this can be done in 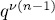 ways, i.e., for
ways, i.e., for 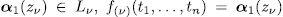 has at least
has at least 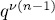 solutions. If there is one more solution, say
solutions. If there is one more solution, say  we can construct the system
we can construct the system
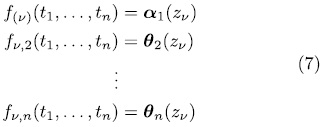
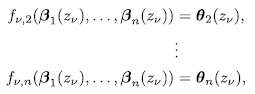
system that necessarily is one of previous system (6). Therefore
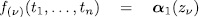 has exactly
has exactly 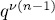 solutions, thus
solutions, thus 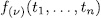 is a permutation polynomial.
is a permutation polynomial. Corollary 3.3. Every polynomial in a PPV is a permutation polynomial.
Proposition 3.4. Let 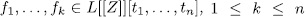 be an orthogonal system over
be an orthogonal system over  and
and 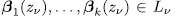 and at least one them a unit.
and at least one them a unit.
Then the polynomial

is a permutation polynomial over

Proof. Let be 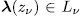 . We see that the number of solutions of
. We see that the number of solutions of
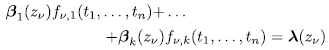
is
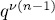 . By hypothesis, the system,
. By hypothesis, the system, 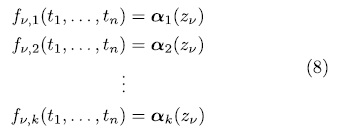
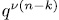 solutions, thus
solutions, thus 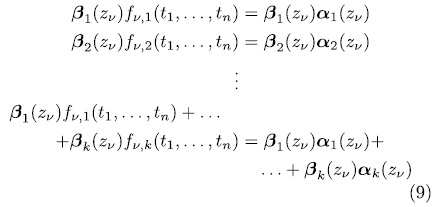
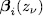 for some
for some 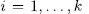 is a unit, then (9) has
is a unit, then (9) has 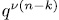 solutions, i.e.,
solutions, i.e., 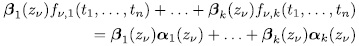
has at least 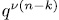 solutions. Now, the polynomial
solutions. Now, the polynomial 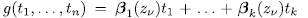 is a permutation polynomial, and for
is a permutation polynomial, and for 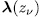 in
in  , the equation
, the equation 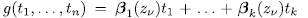 =
= 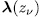 has qv(k-1) solutions.
has qv(k-1) solutions.
So, the equation
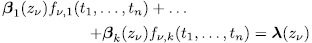
has
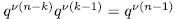 solutions.
solutions. Corollary 3.4. Every polynomial an orthogonal system is a permutation polynomial.
Proposition 3.5. If
 ,
,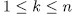 is a permutation polynomial over
is a permutation polynomial over  and the zeroes of
and the zeroes of 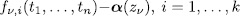 are non singular for all
are non singular for all 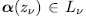 and
and 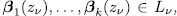 where at least one them is a unit, then
where at least one them is a unit, then 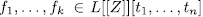 is an orthogonal system over
is an orthogonal system over  .
. Proof. If

is a permutation polynomial then  is also a permutation polynomial ([1, lem. 3.3]). By hypothesis, the zeroes of
is also a permutation polynomial ([1, lem. 3.3]). By hypothesis, the zeroes of 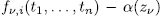 are non singular; then by the corollary to theorem 2 in [6], the system
are non singular; then by the corollary to theorem 2 in [6], the system  is an orthogonal system over L and by proposition 3.2
is an orthogonal system over L and by proposition 3.2  is an orthogonal system over
is an orthogonal system over  .
.
Proposition 3.6. Let 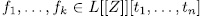 . If
. If  is an orthogonal system over
is an orthogonal system over  then for all permutation polynomial
then for all permutation polynomial 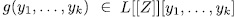 over
over  , the polynomial
, the polynomial
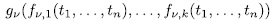
is a permutation polynomial.
Proof. Let be 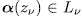 . Since
. Since 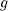 is a permutation polynomial,
is a permutation polynomial, 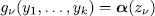 has
has 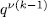 solutions
solutions  in
in  and the system
and the system
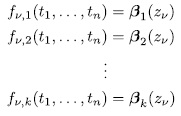
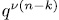 solutions. But
solutions. But  is an orthogonal system over
is an orthogonal system over  and, therefore,
and, therefore,
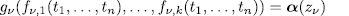
has
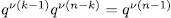 solutions, i.e,
solutions, i.e, 
is a permutation polynomial over
 .
. Proposition 3.7. Let
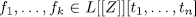 .
. If
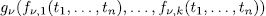
 for all permutation polynomial over
for all permutation polynomial over  ,
, 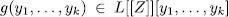 , and the zeroes of
, and the zeroes of 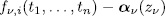 are non singular for all
are non singular for all 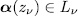 and
and 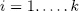 then
then  is an orthogonal system over
is an orthogonal system over  .
. Proof. Since 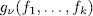 is a permutation polynomial, for all permutation polynomial, for all permutation polynomial
is a permutation polynomial, for all permutation polynomial, for all permutation polynomial 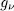 , in particular it is a permutation polynomial for
, in particular it is a permutation polynomial for 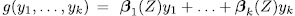 , where at least one
, where at least one 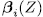 is a unit. Then by proposition 3.5, the system
is a unit. Then by proposition 3.5, the system  is an orthogonal system over
is an orthogonal system over  .
.
Proposition 3.8. Let 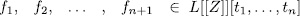 be a polynomials system. Then there exist coefficients
be a polynomials system. Then there exist coefficients 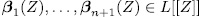 , where at least one of them is a unit, such that
, where at least one of them is a unit, such that
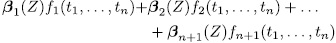
is not a permutation polynomial.
Proof. Let 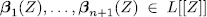 where at least one of them is a unit. If the polynomial
where at least one of them is a unit. If the polynomial
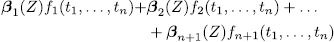
were a permutation polynomial, then the polynomial
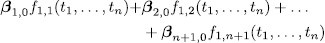
is also a permutation polynomial with
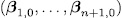 different from (0,â¦,0). This contradicts [6, theor. 4].
different from (0,â¦,0). This contradicts [6, theor. 4]. Proposition 3.9. If 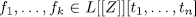 is an orthogonal system, then any of its nonempty subsystem is again an orthogonal system.
is an orthogonal system, then any of its nonempty subsystem is again an orthogonal system.
Proof. If  an orthogonal system then
an orthogonal system then
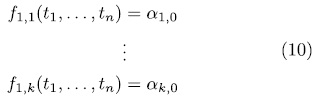
has
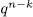 solutions. The lemma is proved, without lost of generality, if the system
solutions. The lemma is proved, without lost of generality, if the system
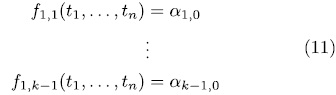
has
 solutions. Then, for all
solutions. Then, for all 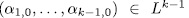 the equation (11) has at least
the equation (11) has at least 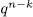 solutions, the same as (10). If we take
solutions, the same as (10). If we take 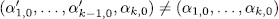 , then again for this
, then again for this 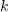 (10) has
(10) has 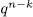 solutions, which are different to the initial ones; therefore for each
solutions, which are different to the initial ones; therefore for each 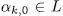 , the equation (11) has
, the equation (11) has 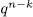 solutions more. In total (11) has
solutions more. In total (11) has 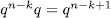 solutions.
solutions. Corollary 3.5. If 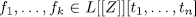 is a PPV, then any of its nonempty subsystems is an orthogonal system.
is a PPV, then any of its nonempty subsystems is an orthogonal system.
Proof. It is clear from proposition 3.9 and the definition of PPV.
Acknowledgements
We wish to express our thanks to Yuguang Lu for his help in the reading and understanding of [8], [10] and [14].
References
[1] Acosta, S. P. A. & Albis, V.S. Characterization of multivariate permutation polynomials in positive characteristic, Sao Paulo J. Math. Sci. 3 N. 1 (2009), 1-12. [ Links ]
[2] Acosta, S. P. A. & Albis, V.S. Permutation polynomials in one indeterminate over modular algebras, Rev. Acad. Colomb. Cienc. 30 Nº. 117 (2006), 541-548. [MR:2334082] [ Links ]
[3] Albis, V. S. & Chaparro, R. On a conjecture of Borevich and Shafarevich ,Rev. Acad. Colomb. Cienc. 21 (1997), 313-319. [MR:98g:11130] [ Links ].
[4] Laigle-Chapuy, Y. Permutations polynomials and applications to coding theory., Finite Fields Appl. 13 (2007), 58-70. [ Links ]
[5] Niederreiter, H. Permutation polynomials in finite fields, Proc. Japan Acad. 46 Nº. 9 (1970), 1001-1005. [MR: 44#5298] [ Links ].
[6] Niederreiter, H. Orthogonal system of polynomials in finite fields, Proc. Amer. Math. Soc. 28 (1971), 415-422. [MR: 45#230] [ Links ].
[7] Nöbauer, Wilfriend. Zur Theorie der polynomialsformationen und permutations polynome, Math. Annalen 157 (1964), 332-342. [ Links ]
[8] Shiue, P. J. S; Sun, Q. & Zhang, Q. Multivariate permutation polynomials and orthogonal systems over residue class rings, Chinese. Ann. Math. Ser. A. 17 Nº. 1 (1996), 43-46. [in Chinese] [MR: 97e:11152] [ Links ].
[9] Smits, T. H. . On the group of units of 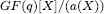 . Indag. Math. 44 (1982), 355-358. [ Links ]
. Indag. Math. 44 (1982), 355-358. [ Links ]
[10] Sun, Q. A note on permutation polynomials vectors over 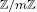 Adv. Math. (china) 25 Nº. 1 (1996), 311-314. . [in Chinese] [MR: 98h:11157] [ Links ].
Adv. Math. (china) 25 Nº. 1 (1996), 311-314. . [in Chinese] [MR: 98h:11157] [ Links ].
[11] Zhang, Q Polynomials functions and permutation polynomials over some finite commutative rings. J. Number Theory 105 (2004), 192- 202. [ Links ]
[12] Wei, Q. & Zhang, Q. On strong orthogonal systems and weak permutation polynomials over finite commutative rings, Finite Fields Appl. 13 (2007), 113-120. [ Links ]
[13] Zhang, Q. On the polynomials in several indeterminates which can be extended to permutation polynomial vector over 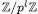 , Adv, Math.22 Nº.5 (1993), 456- 457. [ Links ]
, Adv, Math.22 Nº.5 (1993), 456- 457. [ Links ]
[14] Zhang, Q. Permutation polynomial in several indeterminates over 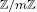 , Chinese An. Math. Ser. A. 16 Nº.2 (1995), 168-172. . [in Chinese] [MR: 96g:11143] [ Links ].
, Chinese An. Math. Ser. A. 16 Nº.2 (1995), 168-172. . [in Chinese] [MR: 96g:11143] [ Links ].
Recibido: 5 de marzo de 2012
Aceptado para publicación: 19 de abril de 2012