Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista de la Academia Colombiana de Ciencias Exactas, Físicas y Naturales
Print version ISSN 0370-3908
Rev. acad. colomb. cienc. exact. fis. nat. vol.36 no.141 Bogotá Oct./Dec. 2012
MATEMÁTICAS
* Trabajo presentado en las XV Jornadas en Estadística e Informática de la ESPOL en Guayaquil, Ecuador, 2008. Los resultados previos a este trabajo se obtuvieron en el marco del proyecto de investigación Cálculo Eficiente del Estimador Jackknife para MínimosCuadrados Lineales, inscrito en la Vicerrectoría de Investigación de la Universidad del Valle.
**Â Profesor Titular, AA 25360, Depto. de Matemáticas, Universidad del Valle. hector.martinez@correounivalle.edu.co
*** Profesora Titular, AA 25360, Depto. de Matemáticas, Universidad del Valle. ana.sanabria@correounivalle.edu.co
Resumen
En este artículo, extendemos al problema de mínimos cuadrados lineales de rango deficiente, el resultado presentado en [MaSa06], el cual reduce de 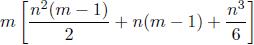 a m [3n + n2] el costo del algoritmo standard para calcular el estimador jackknife para mínimos cuadrados lineales de rango completo.
a m [3n + n2] el costo del algoritmo standard para calcular el estimador jackknife para mínimos cuadrados lineales de rango completo.
Palabras Claves: Estimador jackknife, Mínimos cuadrados lineales, Rango completo, Rango deficiente.
Abstract
In this article, we extend to the linear least squares problem of rank deficient, the result given in [MaSa06], which reduces from 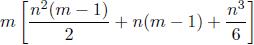 to m[3n + n2] the standard algorithm cost of computing the jackknife estimator for the linear least squares problem of full range.
to m[3n + n2] the standard algorithm cost of computing the jackknife estimator for the linear least squares problem of full range.
Key words: Jackknife estimator, Linear least squares problem, full range, rank deficient.
1. Introducción.
Los estimadores basados en técnicas de remuestreo como el jackknife, por sus propiedades estadísticas [Ef94], [Ko.e88], [ShTu96], son cada vez mas usados, tanto en general, como en particular, en el problema de mínimos cuadrados lineales [WeWe83], para reducir el sesgo de las estimaciones [Mi74], y estimar varianzas [Wo85] e intervalos de confianza [Kl.87], principalmente. Además, en las dos últimas décadas, este tipo de métodos han ganado importancia debido a las facilidades computacionales de los nuevos tiempos. Pero, como paralelamente ha aumentado la dimensión de los problemas a resolver, las facilidades computacionales no eximen de la necesidad de buscar algoritmos más eficientes para los cálculos. En [MaSa06], usando convenientemente propiedades básicas del álgebra lineal, se propone un algoritmo mucho más eficiente que el algoritmo standard para el cálculo de Estimador Jackknife para Mínimos Cuadrados Lineales (EJMCL), que funciona cuando el problema de estimación inicial es de rango completo.
En este artículo, proponemos una modificación al algoritmo propuesto en [MaSa06], de tal manera que conserve la eficiencia sin requerir condición alguna sobre el problema inicial ni sobre los subproblemas involucrados en la estimación jackknife.
Para lograr este propósito, inicialmente, recordamos la definición del estimador jackknife para el problema de mínimos cuadrados lineales de rango completo, luego presentamos el algoritmo standard para el cálculo del EJMCL y los aportes, en este sentido, hechos por Martínez y Sanabria [MaSa00] y [MaSa06]. Posteriormente, sin usar el supuesto de rango completo de la matriz inicial del Problema de Mínimos Cuadrados Lineales (PMCL), presentamos una nueva caracterización de la o las soluciones de los subproblemas de mínimos cuadrados (no necesariamente de rango completo), requeridas para el cálculo del EJMCL. Finalmente, con base en este resultado, proponemos la modificación al algoritmo planteado anteriormente, la cual es el objetivo central de este artículo.
2. Estimador Jackknife para Mínimos Cuadrados Lineales(EJMCL).
Como se planteó en [MaSa00] y [MaSa06], dado un parámetro 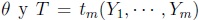 un estimador de este parámetro, se puede construir otro estimador utilizando la técnica de jackknife, la cual consiste en corregir el estimador inicial con base en el promedio de los m estimadores que se obtienen al aplicar el procedimiento inicial de estimación a cada una de las submuestras que resultan al eliminar una observación de la muestra inicial.
un estimador de este parámetro, se puede construir otro estimador utilizando la técnica de jackknife, la cual consiste en corregir el estimador inicial con base en el promedio de los m estimadores que se obtienen al aplicar el procedimiento inicial de estimación a cada una de las submuestras que resultan al eliminar una observación de la muestra inicial.
Formalmente, dada Y1, Y2, · · · , Ym, una muestra aleatoria de una población caracterizada por un parámetro 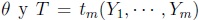 un estimador de q, se calculan los estimadores
un estimador de q, se calculan los estimadores 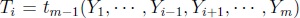 para i = i, ·Â ·Â ·Â , m y luego se calcula el estimador
para i = i, ·Â ·Â ·Â , m y luego se calcula el estimador
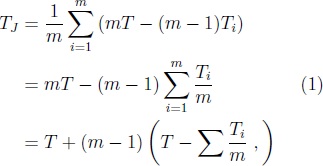
llamado estimador jackknife [BeYe91], [Ef94], [Mi74], [ShTu96], [Ko.e88].
En particular, dado el conjunto de observaciones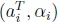 , para i = 1, ·Â ·Â ·Â , m, donde
, para i = 1, ·Â ·Â ·Â , m, donde 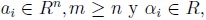 , el problema de estimar x tal que
, el problema de estimar x tal que 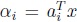 , por el método de los mínimos cuadrados, se reduce a encontrar
, por el método de los mínimos cuadrados, se reduce a encontrar 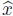 Â tal que
 tal que
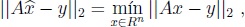
donde 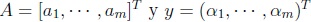 , lo cual se conoce como el Problema de Mínimos Cuadrados Lineales (PMCL).
, lo cual se conoce como el Problema de Mínimos Cuadrados Lineales (PMCL).
Así, el estimador jackknife para mínimos cuadrados es
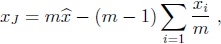
donde 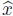 i  es tal que
i  es tal que
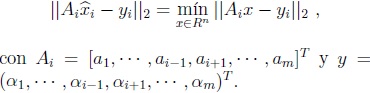
3. Algoritmos para calcular el EJMCL.
Por lo descrito en la sección anterior, el algoritmo para calcular el EJMCL se divide en tres pasos:
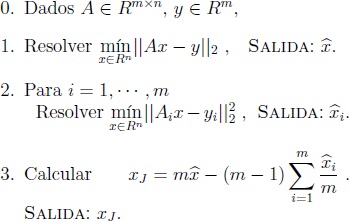
Si las matrices A y Ai, para i = 1, · · · , m, son todas de rango completo, los problemas de los Pasos 1 y 2 se reducen a encontrar las soluciones únicas de las ecuaciones
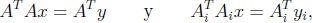
para i = 1, · · · , m, En otras palabras, a calcular
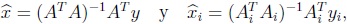
para i = 1, · · · , m.
Para este caso, en [MaSa00], los autores proponen un algoritmo que reduce el costo de los cálculos de 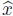 i, una vez
i, una vez 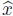 Â Â está calculado.
  está calculado.
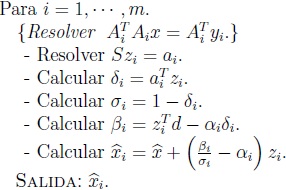
Como soporte teórico de este algoritmo, con base en ciertas relaciones entre las matrices y los vectores involucrados [MaSa00] y la propiedad de matrices invertibles dada por Shermann-Morrison-Woodbury [DeSc83], Martínez y Sanabria obtuvieron el siguiente resultado.
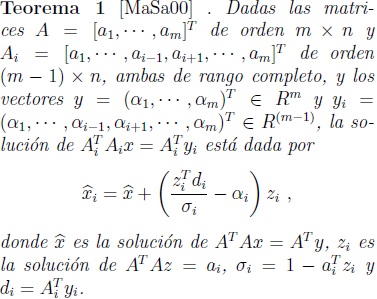
Más tarde, para fortalecer el resultado anterior, en [MaSa06], los autores encontraron una caracterización del conjunto solución de 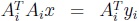 , basada en la solución
, basada en la solución 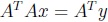 , independientemente de si la matriz Ai  es o no de rango completo.
, independientemente de si la matriz Ai  es o no de rango completo.
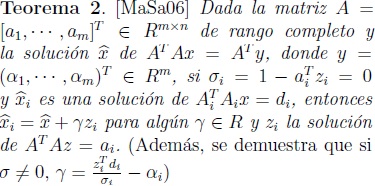
Este resultado, les permitió a Martínez y Sanabria implementar una ligera modificación del segundo paso del algoritmo propuesto en [MaSa00], para seguir siendo eficientes en el cálculo del estimador jackknife para mínimos cuadrados lineales con la condición única que A sea de rango completo [MaSa06]:

Como este último algoritmo solo está garantizado si la matriz A es de rango completo, nos vimos obligados a continuar con la búsqueda de resultados que nos permitieran una caracterización de la o las soluciones de 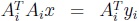 , basada en una solución de
, basada en una solución de 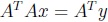 , independientemente de si las matrices A y Ai son o no de rango completo. A continuación, presentamos los resultados de esta búsqueda.
, independientemente de si las matrices A y Ai son o no de rango completo. A continuación, presentamos los resultados de esta búsqueda.
4. Caracterización del conjunto solución de 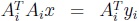 .
.

de donde resulta obvio que si 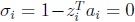 , entonces
, entonces 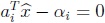 .
.

El Teorema 1 establece que si 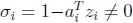 , entonces Ai  es de rango completo y
, entonces Ai  es de rango completo y
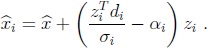
Al igual que en [MSa06] veamos que, en caso que si  = 0, utilizando el Lema anterior, podemos determinar algunas soluciones de 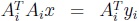 .
.
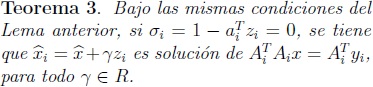
Demostración:Â Usando la misma notación que en la demostración del Lema anterior, sea g ∈ R,
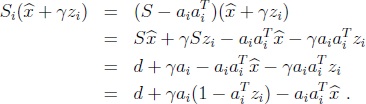
Usando la hipótesis si  = 0, por el Lema anterior, 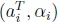 y por lo tanto
y por lo tanto
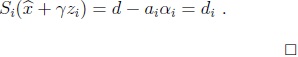
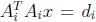 , obtuvimos el siguiente resultado.
, obtuvimos el siguiente resultado.

Demostración: Usando la misma notación que en la demostración del Lema anterior, si

entonces,
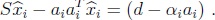
Por tanto,
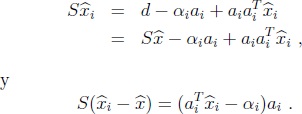
Así que
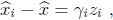
para algún gi ∈ R y un zi  tal que Szi  = ai. Como 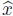 i  =
i  = 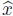  + gizi  es solución de Sxi  = di, entonces
 + gizi  es solución de Sxi  = di, entonces
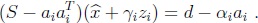
Y puesto que S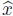 Â = d, entonces
 = d, entonces
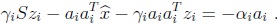
Ahora, como Szi  = ai, se tiene que
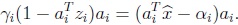
De aquí que 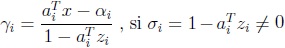 , por el Lema anterior, gi será cualquier número real, si si  = 0 (ver Teorema 3).
, por el Lema anterior, gi será cualquier número real, si si  = 0 (ver Teorema 3).

Es de anotar que, si el problema original es de rango completo; es decir, S es invertible, este gi  coincide con el escalar encontrado en [MaSa00]. En este caso, 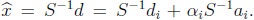 . Por lo tanto,
. Por lo tanto, 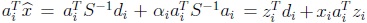 . Reemplazando este resultado en (2), tenemos que
. Reemplazando este resultado en (2), tenemos que
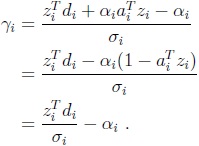
que es el escalar obtenido en el Teorema 1, demostrado en [MaSa00].
5. Algoritmo modificado y generalizado para el cálculo del EJMCL.
Los resultados anteriores nos permiten implementar una ligera modificación del algoritmo propuesto en [MaSa06] para seguir siendo eficientes en el cálculo del estimador jackknife para mínimos cuadrados lineales, aún en el caso que A sea de rango deficiente. Dicho algoritmo modificado y generalizado para calcular 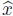 i  aparece a continuación.
i  aparece a continuación.

Al comparar este algoritmo con el propuesto en la Sección 5 de [MaSa06], podemos concluir que la diferencia aparece por la posibilidad que existe que A sea de rango deficiente y por lo tanto que el PMCL inicial tenga infinitas soluciones. En este caso, con base en una solución del problema inicial, podemos calcular una solución de los subproblemas requeridos para la estimación de jackknife, simplemente calculando una solución de AT Az = aiy un escalar apropiado (ver (2)).
Al igual que en [MaSa06], si si  = 0 (subproblema de rango deficiente), el subproblema tiene infinitas soluciones, en donde sugerimos tomar como solución la misma que se tomo para el problema inicial 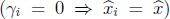 . En consecuencia, como se demostró en [MaSa00], este algoritmo reduce el costo de solución de los subproblemas aunque no sean de rango completo, de
. En consecuencia, como se demostró en [MaSa00], este algoritmo reduce el costo de solución de los subproblemas aunque no sean de rango completo, de 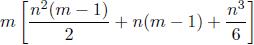 a m [3n + n2] el número de flops requeridos para el cálculo del estimador jackknife de mínimos cuadrados lineales (EJMCL) para un modelo lineal aún si este es de rango deficiente, siendo n el número de parámetros a estimar y m el tamaño de la muestra.
a m [3n + n2] el número de flops requeridos para el cálculo del estimador jackknife de mínimos cuadrados lineales (EJMCL) para un modelo lineal aún si este es de rango deficiente, siendo n el número de parámetros a estimar y m el tamaño de la muestra.
Es más, si no se necesitan los EMCL de cada una de las submuestras, se puede obtener el EJMCL sin calcular los EMCL, mediante la expresión
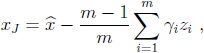
con la ventaja adicional de saber que algunos gi  son cero, lo cual simplifica la sumatoria de la expresión anterior.
6 . Conclusiones
En este artículo, se ha caracterizado completamente el conjunto solución de los subproblemas de mínimos cuadrados lineales que resultan en el cálculo del estimador jackknife de mínimos cuadrados lineales de un modelo lineal, aún en el caso que éste sea de rango deficiente.
Este resultado permite modificar el algoritmo propuesto en [MaSa06] para calcular el mencionado estimador, sin requerir que ninguno de los problemas involucrados (inicial o subproblemas) sean de rango completo, manteniendo la misma eficiencia de computo.
Al igual que en [MaSa00], este resultado permite hacer cálculos más eficientes siempre que el algoritmo que se utilice para resolver los diferentes subproblemas de mínimos cuadrados lineales requeridos por el estimador jackknife sea el mismo que se utilice para resolver el problema de mínimos cuadrados lineales inicial.
Queda como un reto para nosotros y nuestros lectores, desarrollar una teoría similar que permita caracterizar las soluciones de los subproblemas de mínimos cuadrados para el caso generalizado del estimador jackknife en el cual se elimina más de una observación de la muestra inicial para plantear los subproblemas (Estimador jackknife agrupado).
7 . Agradecimientos
Nuestros agradecimientos al Departamento de Matemáticas de la Universidad del Valle por el apoyo logístico y económico tanto para el desarrollo como para la divulgación del presente trabajo. También, nuestro reconocimiento y agradecimientos al evaluador anónimo de la version original de este trabajo por sus sugerencias para mejorar la presentación de los resultados.
Referencias
[BeYe91]Â Behar, R. y Yepes, M. (1991) Sobre algunas técnicas de remuestreo: El método de jackknife. Heurística, No 6, Págs. 49-58 [ Links ]
[DeSc83]Â Dennis, J.E. & Schnabel, R.B. (1983) Numerical methods for unconstrained optimization and nonlinear equations. Prentice Hall, New Jersey, USA. [ Links ]
[Ef94]Â Efron, B. (1994) The Jackknife, the Bootstrap and Other Resampling Plans CBMS-NSF Regional Conference Series in Applied Mathematics, No. 38, Sixth Edition, SIAM, Philadelphia, PA, USA. [ Links ]
[Kl.e87]Â Kleijuen, JPC., Karremans, P. Oortwinj, W., Van Groennendaal, W. (1987) Jackknifing estimated weighted least squares, Communications in Statistics: Theory and Methods v.16, Pags. 747-764. [ Links ]
[Ko.e88]Â Kovar, J., Rao, J. & Wu, CFJ. (1988) Bootstrap and other methods to measure errors in survey estimates, Canadian Journal of Statistics 16, Pág. 26-45. [ Links ]
[MaSa00] Martínez, H.J. y Sanabria A.M. (2000) Cálculo eficiente del estimador jackknife para mínimos cuadrados lineales bajo condiciones de unicidad. Matemáticas: Enseñanza Universitaria, Vol VIII, Nos 1 y 2, Págs. 29-43. [ Links ]
[MaSa06] Martínez, H.J. y Sanabria A.M. (2006) Cálculo eficiente del estimador jackknife para mínimos cuadrados lineales de Rango Completo. Revista de la Academia Colombiana de Ciencias Exactas, Físicas y Naturales, Vol XXX, Pág. 361-365. [ Links ]
[Mi74] Miller, R.G. (1974) The Jacknife: a review. Biometrika 61, Pags. 1-15. [ Links ]
[ShTu96] Shao, J. and Tu, D. (1996) The Jackknife and the Bootstrap, 2nd Printing, Springer Series in Statistics, New York. USA. [ Links ]
[WeWe83]Â Weber, N.C. & Welsh, A.H. (1983) Jackknifing the general linear model, Australian Journal of Statistics 25, No. 3, Pags. 425-436. [ Links ]
[Wo85] Wolter,  K.M., (1985) Introduction to variance estimation, First Edition, Statistics for Social and Behavioral Science, Springer, New York, USA. [ Links ]
Recibido: 10 de agosto de 2012
Aceptado para publicación: 5 de diciembre de 2012













