CIENCIAS FÍSICAS

¹ Observatorio Astronómico Nacional, Facultad de Ciencias, Universidad Nacional de Colombia, e-mail: jomurciap@unal.edu.co
² Observatorio Astronómico Nacional, Facultad de Ciencias, Universidad Nacional de Colombia, e-mail: jgportillab@unal.edu.co

Resumen

Se presenta el estudio de la trayectoria de vuelo de un cohete de tres etapas lanzado desde territorio colombiano con el propósito de posicionar un pequeño satélite en órbita baja terrestre. Para ello se consideraron las fuerzas que afectan el movimiento del cohete tales como la fuerza de empuje, la de la gravedad así como las que surgen cuando el objeto se desplaza a través de la atmósfera y, con valores específicos de rendimiento de cohetes que se pueden deriverar de la producción actual de la industria nacional, se estableció la masa y el tamaño de cada una de las tres etapas que conforman el cohete a través de un proceso de optimización. Se integraron las ecuaciones diferenciales que describen el movimiento del cohete por medio de un código computacional diseñado por los autores lo que permite determinar el estado dinámico de la carga útil (y de las etapas una vez se hayan desprendido) en cualquier instante de tiempo. La integración se extendió hasta alcanzar el momento de la entrada a órbita (inyección) lo que permite establecer los elementos orbitales del satélite.

Palabras clave. Satélite artificial, cohete, motor cohete, trayectoria de vuelo, vehículo lanzador.

Abstract

We present a study of the flight path trajectory of a three stage rocket launched from colombian territory with the purpose of placing a small satellite in Low Earth Orbit (LEO). Various forces that affect the motion of the rocket were considered such as thrust, gravity an those that arise from the movement through the atmosphere. Taking into account specific values related with the performance of rockets that could be derived from the output of the national industry, we calculated the mass and size of each one of the three stages by means of an optimization procesa. The differential equations were integrated using a Fortran code written by the authors which permits to calculate the dynamic state of the payload (and stages when discarged) at the desired time. The integration was extended until orbit insertion which permits to know the orbital elements of the satellite.

Key words. Artificial satellite, rocket, rocket motor, flight path trajectory, launcher.

l. Introducción

Colocar un objeto en órbita alrededor de la Tierra exige, en nuestro actual estado tecnológico, utilizar vehículos de masa variable que sean capaces de alcanzar velocidades cercanas a la decena del kilómetro por segundo. Para ello se apela al uso de un sistema de uno o varios motores diseñados para quemar grandes cantidades de material químico el cual, al entrar en combustión, genera en tiempos relativamente breves, una fuerza de empuje en dirección opuesta a la dirección del vehículo, esto es, del cohete. De este modo se comunica la velocidad necesaria para dejar orbitando una carga útil (satélite o nave espacial) alrededor del planeta Tierra.

Como es bien conocido, el primer satélite artificial fue el Sputnik 1 colocado por el misil balístico de alcance intercontinental R-7. Esto fue realizado por la Unión de las Repúblicas Socialistas y Soviéticas (URSS) el 4 de octubre de 1957. Desde entonces, otras naciones han desarrollado autónomamente la tecnología necesaria para llegar a órbita, con lo que, hasta ahora, se han llevado a cabo más de 6000 lanzamientos para colocar cargas orbitales con amplia diversidad de objetivos, lo que ha generado una industria sólida y en permanente crecimiento. Se estima que, en el presente, la industria espacial mundial posee volúmenes de ventas que se aproximan a los 270 miles de millones de dólares anualmente³ y su impacto e influencia en casi todas las áreas de las actividades humanas es directo y de gran visibilidad.

Lamentablemente Colombia ha hecho pocos esfuerzos para convertirse en una nación que genere desarrollo en tecnología astronáutica. Existe una comunidad marginal, fundamentalmente constituida por entusiastas aficionados, quienes han realizado al menos desde hace 40 años, y no con la debida continuidad, ensayos con pequeños cohetes. También existe una población minoritaria, con formación posgradual en el campo (lograda tanto nacional como internacionalmente) que poseen proyectos de investigación muy puntuales en algunas universidades o en los servicios de la fuerzas militares, en particular de la Fuerza Aérea. Pero cada uno trabaja aisladamente el uno del otro: nadie, con la debida autoridad e interés, ha canalizado estos esfuerzos para dirigirlos hacia un objetivo central y, menos aun, se ha generado una política decisiva en términos de asegurar presupuestos sustanciosos y continuos que sustente una diversidad de proyectos que hagan competitiva la nación frente a países del medio local.

La razón principal de esta situación, triste es decirlo, es la falta de interés de parte del Estado quien, al menos en teoría, está en la obligación de promover –con políticas serias y continuas y vigilando la asignación de sus correspondientes presupuestos– el establecimiento y desarrollo de la tecnología espacial en los servicios armados, universidades, institutos de investigación y la industria. Esta indiferencia ha conllevado, por supuesto, a una casi que total dependencia de las instituciones estatales y privadas usuarias de la tecnologías espaciales que, para efectos de cumplir con sus actividades, deben contratar con industrias extranjeras y someterse a sus arbitrios y condiciones.

Solo en poco más de la última década se ha venido presenciando un ligero incremento de la investigación astronáutica en algunas universidades y los servicios armados. Entre los años 2000 a 2002 surgieron, en la Universidad Nacional de Colombia, las primeras tesis en diseño de motores cohete de combustibles sólidos y, al poco tiempo, se realizaron investigaciones conjuntas en el Departamento de Ingeniería Mecánica de dicha Universidad sobre el modelamiento matemático, diseño, construcción y pruebas de un micromotor cohete de propelentes líquidos y se publican los primeros avances teóricos de cohetería en el país (Garzón, Duque & Roa, 2004; Achury, 2005). También en la misma universidad se creó, por esos mismos años, un grupo de investigación en cohetería hidráulica (GIPCUN).

En otras universidades bogotanas se ha presenciado un interés en temas de propulsión: la Universidad San Buenaventura ha adelantado investigaciones en la construcción y funcionamiento de motores cohete de propelentes sólidos a base de combustibles caseros (Gómez & Castro, 2006). En el año 2008 surgió un semillero de investigadores en la Universidad Libre para el desarrollo de motores cohete de combustible sólido y la integración de ingenieros aeronáuticos, mecánicos y electrónicos enfocados en el desarrollo de cohetes atmosféricos (Galindo & Murcia, 2009). En el año 2009 la Fundación Universitaria los Libertadores creó la primera tesis sobre el diseño conceptual y preliminar de un cohete portador de dos etapas para el transporte de carga útil de una tonelada lanzado desde el territorio colombiano a órbitas bajas de la Tierra (Calderón & Murcia, 2009); también se realizaron las dos primeras tesis sobre el diseño y estudio de motores cohete de propulsión iónica para los sistemas de posicionamiento de satélites (Escorcia, 2011; Robledo, 2011). La Universidad de los Andes formó el grupo de investigación Proyecto Uniandino Aeroespacial (PUA) que se ha enfocado en la investigación en temas de propulsión termoquímica, aerodinámica y, en general, comportamientos actitudinales propios de vehículos tipo cohete. El 9 de junio de 2009, con apoyo de la Fuerza Aérea Colombiana en la base de GAORI, se llevó a cabo el lanzamiento de la primera misión de cohetería experimental de PUA con un vehículo cohete propulsado por un motor de combustible sólido de 20 kg de empuje, equipado con sistemas de monitoreo y almacenamiento de datos (Urrego, 2009). En el campo satelital, el desarrollo más publicitado lo ha tenido el proyecto de la Universidad Sergio Arboleda con el picosatélite Libertad 1, un objeto en forma de cubo de 10 cm de lado, comprado y ensamblado por esta universidad y luego transportado a Kazajistán para su lanzamiento abordo de un cohete portador ruso para posicionarlo en órbita baja polar (Joya, 2007). El satélite, junto con varios otros, entró en órbita exitosamente en abril del 2007; duró en funcionamiento 21 días aunque aun permanece en órbita. A parte del evidente propósito propagandístico, permanece por aclarar cuales fueron los objetivos tecnológicos y científicos que se lograron con la puesta en órbita de este objeto (Portilla, 2013).

Varias universidades en Medellín no han sido ajenas a investigaciones de tipo astronáutica. En el 2006 se creó un grupo que fomenta la investigación aeroespacial denominado lnges Aerospace, con la participación conjunta de la Universidad de Antioquia, Eafit y Bolivariana y con una rama dedicada a la cohetería conocida como "Cohetería Paisa" , cuyo principal desarrollo es en el campo de la propulsión sólida con el diseño de cohetes por etapas⁴. La Universidad Pontificia Bolivariana (UPB) adelanta investigaciones en diseños aerodinámicos de toberas, diseños de motores cohete de 70 mm con propelentes sólidos, contando con la colaboración de la Fuerza Aérea Colombiana y empresas privadas (Escobar & Jaramillo, 2009).

A parte de estas investigaciones promovidas en las instituciones universitarias, también merecen citarse los proyectos de los servicios armados, industria militar e institutos gubernamentales. En el año 2008 la Fuerza Aérea Colombiana a través del Centro de Investigaciones en Tecnología Aeronáutica (CITA) propuso la creación de un cohete portador de tres etapas de propelentes líquidos con la capacidad de transportar pico satélites colombianos a órbitas bajas de la Tierra⁵. En la actualidad Indumil es la única empresa del Estado que se encarga de investigar y adelantar proyectos en el campo de los cohetes y misiles de propelentes sólidos de doble base, contando con los permisos militares exigidos y con las instalaciones necesarias para el almacenamiento, manipulación y producción de químicos altamente explosivos.

Finalmente, en el año 2006 y como iniciativa del Estado Colombiano, se creó la Comisión Colombiana del Espacio (CCE), una organización intersectorial con fines de consulta, coordinación y planificación de políticas nacionales sobre tecnología espacial. Poco después de su creación, la Secretaría de la CCE fue asignada al Instituto Geográfico Agustín Codazzi. Sin embargo, tanto por su condición de "comisión", así como su estructura y ubicación en el organigrama del estado, no le ha permitido rendir los mejores frutos por lo que sus logros, a sus siete años de creación, han sido más bien discretos. La intención de aquirir un satélite goestacionario para propósitos de comunicaciones no fue posible concretarla, pese a existir los recursos para ello y de haber convocado a licitación en dos ocasiones. Se esperaría que en este tipo de adquisiciones la CCE tuviera mucho en qué intervenir y acompañara la compra exitosa de dicho satélite. No fue ese el caso. Una segunda intención, esta vez de adquirir un satélite de observación terrestre, lleva en consideración más de dos años a la espera de que alguien ofrezca alguna explicación sobre en qué etapa del proceso se está. A finales del año 2012, la Secretaría de la CCE fue cedida a la Fuerza Aérea Colombiana, por lo que es de esperar que temas como los del satélite de observación terrestre así como la creación de una Agencia Colombiana del Espacio sean pronto una realidad.

Retornando a las investigaciones realizadas en el medio académico, ningún grupo a nivel nacional ha emprendido un estudio teórico que permita realizar un primer análisis del tipo de trayectoria de un cohete multietapas (lanzado desde un punto en particular del territorio colombiano) requerido para colocar pequeños satélites en órbitas bajas que permitan suplir algunas necesidades en el caso eventual que la nación adopte la decisión política de construirlos, no solo éstos sino también los cohetes que los coloquen en órbita. Por ello, esta comunicación se constituye en un primer estudio de exploración consistente en estudiar de forma preliminar la trayectoria de un pequeño cohete de tres estapas lanzado desde territorio colombiano para efectos de colocar una carga útil con masas cercanas a los 200 kg. De este modo, se estudian algunas posibles trayectorias que tendría el cohete para efectos de observar en donde se verifican los sitios de caída de sus dos primeras etapas, así como examinar el perfil de vuelo, esto es, estudiar el incremento de la velocidad y de la altura conforme transcurre el tiempo. Para dicho estudio se tuvieron en cuenta las principales fuerzas que afectan el movimiento de un cohete (empuje, gravedad, resistencia y sustentación), lo que exigió, para efectos de integrar las ecuaciones diferenciales de movimiento, desarrollar un programa en Fortran escrito por los propios autores con base en el integrador numérico Radau (Everhart, 1985).

La sección 2 de esta comunicación describe las fuerzas involucradas; las ecuaciones diferenciales de movimiento se examinan en la sección 3; la sección 4 contiene la optimización de las etapas del cohete, sus masas y dimensiones en tanto que la sección 5 presenta los resultados obtenidos. Finalmente, la sección 6 expone las conclusiones.

2. Fuerzas involucradas

Para modelar el movimiento de un cohete es necesario definir el tipo de fuerzas que actuan sobre el objeto. En este estudio se consideran cuatro fuerzas: aquellas que surgen a causa del movimiento a través de la atmósfera: el arrastre D y la sustentación L; adicionalmente, se considera la fuerza de propulsión (empuje) del cohete T y la fuerza de atracción gravitacional W.

2.1 Las fuerzas aerodinámicas

Generalmente (aunque no exclusivamente) los cohetes parten de la superficie terrestre, en donde la densidad atmosférica es un máximo. Por ello, en los primeros instantes del vuelo, ha de tenerse en cuenta las fuerzas que surgen por el movimiento del cohete a través del fluido. Conforme transcurre el tiempo la altura del vehículo se va incrementando por lo que la densidad comienza a decaer fuertemente y eventualmente, a partir de cierta altura, se reducen a cero.

Funcionalmente, la fuerza de arrastre D y de sustentación L están definidas por:

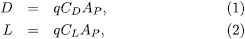
donde Ap es el área proyectada del vehículo, C_D y C_L son los coeficientes de resistencia y sustentación, respectivamente, y q es la denominada presión dinámica dada por:

en donde V es la velocidad y p es la densidad del aire en un punto determinado de la atmósfera considerándola ideal, sin influencia de los vientos o fenómenos meteorológicos. Para una descripción satisfactoria de la densidad atmosférica en función de la altura es indispensable contar con un modelo de atmósfera estándar.

Existen varios modelos matemáticos para la atmósfera terrestre que han sido creados a lo largo de los años, tales como la US Standard Atmophere, ISA (International Standard Atmosphere), Earth-GRAM (Earth Global Reference Atmospheric Model), MSISe (Mass Spectrometer Incoherent Scatter), ICAO (International Civil Aviation Organization), ARDC (Air Research and Development Comand), entre otros (ANSI, 2004). El más reciente y avanzado es el modelo de la NASA Earth Gram 2010⁶, un modelo global que depende de la latitud, longitud y achatamiento terrestre; también modela las corrientes que generan los vientos. Otro modelo utilizado actualmente por la organización de aviación civil internacional (OACI) es el ISA con límites de datos hasta los 32 km y el modelo completo hasta los 90 km de altitud (ANSI, 2004).

El modelo de atmósfera estándar US1976 cuenta con datos hasta los 1000 km de altitud, pero la descripción matemática que describe las variaciones de presión y densidad en función de la altitud no está completo. Una buena opción, por su persistencia, relativa sencillez y rango amplio de valores, es la utilización del modelo ARDC1959 (Zipler, 2007) sobre el que se realizaron con posterioridad el modelo atmosférico ISA y el US1976. Dicho modelo matemático es utilizado aun en aplicaciones aeroespaciales actuales. Debido a que Colombia no cuenta con investigaciones de una atmósfera estándar local, y por las razones atrás expuestas, se utilizó el modelo atmosférico ARDC1959 (Minzner et al, 1959). Otro motivo para su aplicación es que códigos como el CADAC o ALTOS de simulación de cohetes cuentan con este para el modelamiento atmosférico por su precisión y simplicidad (Zipfel, 2007).

El modelo ARDC1959 define el cambio de las propiedades del gas como lo son la temperatura molecular, la presión P y la densidad r en función del incremento de la altitud geométrica h_G y la variación de la gravedad g.

Utilizando los principios de la hidrostática (Minzner et al, 1959), considerando la atmósfera terrestre libre de rotación, fuerzas de Coriolis y centrípeta, vientos e incidencia de la radiación solar, la variación de la presión en función del cambio de altitud se representa como:

Con los datos obtenidos de cohetes sondas y globos meteorológicos se puede construir el modelo matemático de cada capa atmosférica (aquellas con gradiente térmico y aquellas que no lo tienen) obteniendo el comportamiento de las propiedades del fluido en función de la altitud geométrica. En particular, la Figura 1 muestra los valores de densidad r correspondientes a los valores de altura geométrica obtenidos con el modelo ARDC1959. Dicho perfil de densidad es el que se adoptó para este estudio.

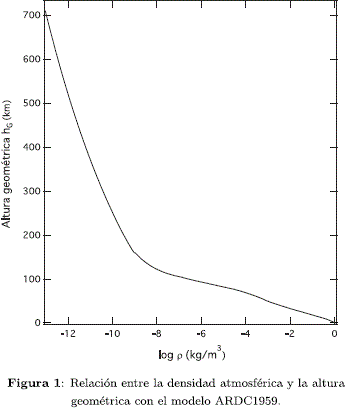
La dependencia funcional de C_D será vista en la sección 4 cuando se defina la dimensión y forma del cohete.

2.2 La fuerza gravitacional

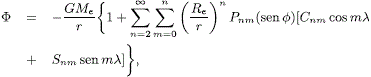
donde G = 6.67 × 10^-11 N m² kg^-2 es la constante de Cavendish, M_e es la masa de la Tierra (5,67×10²⁴ kg), C_nm y S_nm son los denominados armónicos esféricos (constantes adimensionales propias de cada cuerpo central) y P_nm (sen f) son los polinomios de Legendre. Para el caso de la Tierra el término adicional que más perturba el clásico potencial kepleriano (GM_e/r) es aquel que corresponde a C₂₀ = C₂ = -J₂, el cual es al menos mil veces más grande que todas las demás constantes que siguen en la serie. Por tal razón, el potencial gravitacional que se tendrá en cuenta aquí solo incluye el término de C₂₀, por lo que se reduce a (Tewari, 2007; Portilla, 2009):

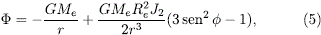
donde J₂ = 0.00108263 para la Tierra. Despreciando la atracción gravitacional del Sol y de la Luna, de tal suerte que la fuerza gravitacional 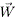sea solo debida a la fuerza de atracción gravitacional terrestre, tendremos que:

donde y son vectores unitarios en la dirección del radio vector y la latitud, respectivamente. Por lo tanto, tenemos:

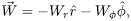
donde:

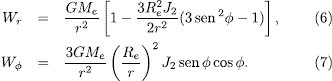
2.3 La fuerza de empuje

La fuerza de empuje está descrita por:

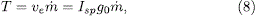
donde u_e es la velocidad de salida de los gases calientes (con respecto al cohete), I_sp es el impulso específico, g₀ el valor de la aceleración de la gravedad en la superficie terrestre y 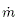es la tasa de salida (masa en la unidad de tiempo) de los mismos. Se ha supuesto que la contribución adicional del empuje originado por la diferencia de presión entre los gases de salida con la de la presión atmosférica es despreciable. Asumiremos que el grano que conforman los motores de combustible sólido se ha diseñado de tal modo que la tasa de salida de los gases sea constante.

3. Ecuaciones de movimiento

Como origen del sistema inercial se toma el centro de masas de la Tierra. Respecto a la superficie de la Tierra, el cohete se sitúa en un marco de referencia sobre la superficie del planeta que depende de las coordenadas esféricas de latitud f y longitud l (ver Figura 2).

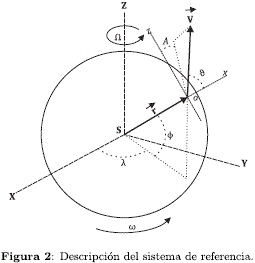
Con origen en el centro de masas de la Tierra (S), se definen los ejes cartesianos XY Z donde el plano del ecuador se encuentra sobre los ejes XY y el eje Z apunta al polo norte celeste. Sobre este sistema de referencia inercial se encuentra un punto o fijo sobre la superficie terrestre cuya distancia al centro de masas es r e inclinado respecto a los ejes del sistema de referencia inercial por un ángulo de latitud f (positivo hacia el PNC, negativo en caso contrario), y un ángulo de longitud l respecto al eje X; estas coordenadas se encuentran en movimiento debido al efecto de rotación de la Tierra a una velocidad angular 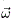sobre el ecuador. Por tal motivo se crea un sistema de referencia no inercial instantáneo de origen en o y con los ejes cartesianos xy z definidos de tal modo que el eje x está en dirección del radio vector posición 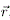, el eje z apuntando en dirección norte y el eje y hacia el este. El ángulo formado entre el eje z y la proyección del vector velocidad 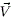en el plano yz se conoce como el azimut A o rumbo: es la dirección de movimiento del cohete respecto al norte geográfico de la Tierra. El ángulo que forman el vector posición con el vector velocidad sobre el eje x se denomina ángulo de trayectoria de vuelo J, ver Figura 2 (Tewari, 2007).

El conjunto de las seis ecuaciones diferenciales que definen el movimiento del cohete sobre dicho sistema de referencia son (Tewari, 2007):

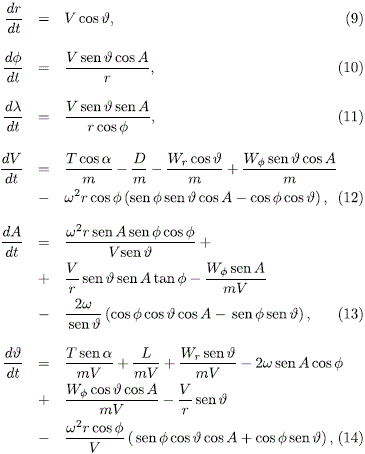
donde m es la masa instantánea del cohete, a es el denominado ángulo de ataque (aquel que existe entre el vector velocidad y el vector de empuje). Es claro que, dada la complejidad de las ecuaciones diferenciales, se ha de proceder para su solución a través de la utilización de un integrador numérico. Para tal efecto, hemos utilizado el integrador Radau escrito en Fortran 77 (Everhart, 1985).

Nótese que las ecuaciones no contienen términos que incluyan tanto la presencia de vientos como la existencia de ángulo de deslizamiento (ver Calise & Leung, 1995, para las ecuaciones completas). Tampoco se ha incluido un método de optimización de trayectoria. La inclinación que presenta el vehículo, esto es, a que el águlo J tienda a aumentar en el tiempo, es estrictamente de origen gravitacional.

4. El cohete portador

De proponérselo, el país podría estar en capacidad de desarrollar un pequeño cohete para colocar cargas útiles a órbitas bajas. Países como Brasil y Argentina están encaminados en esa dirección y en menos de un lustro esperan colocar satélites artificiales por sus propios medios.

Una opción que bien vale la pena considerar, en un inicio, es la colocación de minisatélites con masas cercanas a los 200 kg. De hecho, la Fuerza Aérea Colombiana ha propuesto un rango parecido de masa para un satélite de órbita baja. Para estos rangos de masa, y con los avances en miniaturización, se podrían elaborar satélites que satisfagan un amplio abanico de propósitos entre los que se encuentran la seguridad del territorio y vigilancia de fronteras, búsqueda de recursos naturales, prevensión y monitoreo de desastres naturales, etc. Dada la dificultad inherente en el desarrollo y puesta a punto de motores de combustible líquido no sería nada extraño que se adoptara como alternativa la utilización de motores de combustible sólido para cada una de las etapas que costituyen el cohete. Éstos son relativamente sencillos de construir y puede decirse que en el presente se dispone del propelente ya que el país elabora propelentes sólidos de doble base con un impulso específico⁷ de 220 s y una densidad de 1.67 g cm^-3. Este tipo de propelentes están siendo utilizados en aplicaciones militares a baja escala por lndumil.

Para efectos de estudio, se decidió adoptar una configuración de un cohete consistente en tres etapas, parecida a la del cohete Scout (Whitney et al., 1965) donde todas sus etapas están conformadas por motores de combustible sólido. Con el propósito de adoptar valores de masa iniciales (y, obviamente, de definir las dimensiones del vehículo) es preciso optimizar la relación de masas entre cada etapa, considerando la masa de la carga útil, la masa del propelente, la masa de la estructura y las velocidades de salida de los gases con relación al vehículo. Para tal efecto, se puede utilizar un procedimiento iterativo y de ese modo obtener los valores adecuados de relaciones de masa. Para el valor nominal que se ha escogido para la masa de la carga útil, teniendo en cuenta el valor del impulso especifico I_sp para propelentes sólidos que actualmente se desarrollan en el país por las industrias militares (que, como ya se dijo, están alrededor de 220 s) y que se toma como un estándar para cada una de las tres etapas. Partiendo de la ecuación ideal del movimiento del cohete que permite conocer el cambio de velocidad DV a través de:

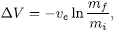
donde u_e es la velocidad de los gases de escape con relación al vehículo, m_i la masa inicial y m_f la masa final, se puede extender la misma para sucesivas etapas y así escribir (Koelle, 1961; Tewari, 2007):

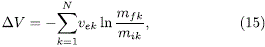
donde el subíndice k indica la etapa específica a analizar; en nuestro caso N = 3. Si se reemplazan las masas por los factores de carga estructural a1e, el factor de relación de masas iniciales y finales s_k, se encuentra que la ecuación anterior queda de la forma:

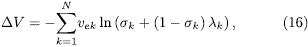
donde:

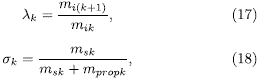
siendo m_sk la masa estructural de la etapa y m_propk la masa del propelente químico. Al relacionar el cambio de velocidad con la velocidad de gases de escape de la primera etapa, y la relación entre factores de masa a_k, la ecuación a iterar queda de la siguiente forma:

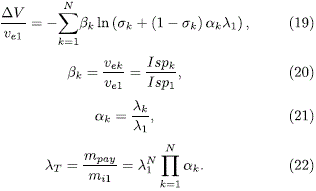
Para este caso, B_k representa la relación de velocidades de escape, l_T a relación entre la carga paga o carga útil m_pay (masa a transportar) con la masa inicial total del vehículo m_i1 (Lafieur, Fleming & Saleh, 2012).

Para el caso de estudio adoptamos una velocidad final del cohete ideal, al cabo de las tres etapas, de 9.7 kms^-1 que es 2 kms^-1 más de lo requerido para la velocidad orbital, pues a ese valor hay que restarle lo que se reduce en velocidad por pérdida de la presencia de la fuerza de gravedad y el arrastre atmosférico (Tewari, 2007). Se compararon datos estadísticos de otros cohetes lanzadores para órbitas bajas llegándose a adoptar como factor de masa estructural un valor de s_k = 0.1 que sería el peor episodio posible en cada una de las tres etapas, es decir, el cohete más pesado estructuralmente. De igual forma, se adoptó b_k = 1 por aquello de que todas las etapas tienen el mismo propelente e impulso específico (Humble, Henry & Larson, 1995). Los resultados que se obtuvieron del proceso iterativo a través de un código de optimización se presentan en la Tabla l.

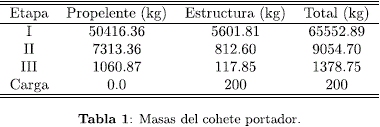
Con las masas halladas en el código de optimización se procedió a realizar un diseño conceptual de las dimensiones aproximadas del cohete portador para que se sea posible realizar valoraciones de carácter aerodinámico (como el C_D) y de ese modo incluir dichos datos en el código de trayectoria de vuelo. Es importante añadir que para el diseño final se tuvieron en consideración las dimensiones y características de cohetes construidos en otras latitudes con las mismas o similares características (Humble, Henry & Larson, 1995).

El primer parámetro que depende de las masas es la relacion de la fuerza de empuje a desarrollar por cada uno de los motores cohete. Para ello se buscaron valores de la relacion empuje/peso (T /W ) de cohetes históricos o de línea base (Humble, Henry & Larson, 1995; Sutton & Biblatz, 2010). Para los cohetes portadores usuales el valor de la relación T /W para las primeras etapas oscila entre 1.0 a 1.5. En el caso que nos ocupa se seleccionó un valor medio de 1.3. Para los motores de etapas superiores y de posicionamiento orbital el valor suele ser inferior a 1.0. Adoptamos entonces los valores de 0.9 y 1.1 para la segunda y tercera etapa, respectivamente. Sabiendo los valores de masa de cada etapa, tomando u_e= 2160 ms^-1, se puede utilizar la ecuación (8) con los valores se fuerzas de empuje y así determinar los flujos másicos y los tiempos de funcionamiento de cada etapa, ver Tabla 2.

Una de las ventajas tecnológicas de construir un cohete portador de varias etapas es que la estructura de todas ellas, exceptuando la última, pueden ser recuperadas mediante paracaídas una vez que se consume el propelente y ser reutilizadas en otro lanzamiento. La estructura de la etapa superior suele quedar en órbita baja y al cabo de un tiempo reingresar a la atmósfera terrestre donde se desintegra por efectos de fricción.

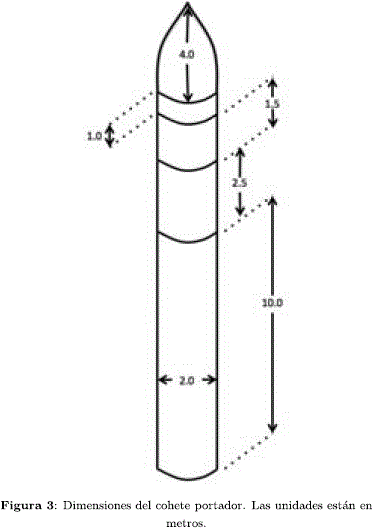
Teniendo los datos de las masas de cada etapa, el estimado de la densidad del propelente, el volumen de carga que ocupa y la referencia de los cohetes históricos, se estiman las dimensiones del cohete portador del presente estudio. En la Figura 3 se pueden observar las dimensiones del portador. El cohete tiene un diámetro de 2 m, longitud de fuselaje de 14 m y el cono de protección de la carga útil de 4 m, dando una altura total de 18 m. Para este caso se tienen en cuenta la densidad⁸ del propelente de 1.67 g cm^-3, y con las masas de la Tabla 3 de cada etapa se estima el volumen y longitud de las mismas, dando como resultado que la primera etapa tiene una longitud estimada de 10 m, 2.5 m la segunda, 1.5 m la tercera y un espacio de 1 m de longitud para computadoras y otros sistemas de vuelo.

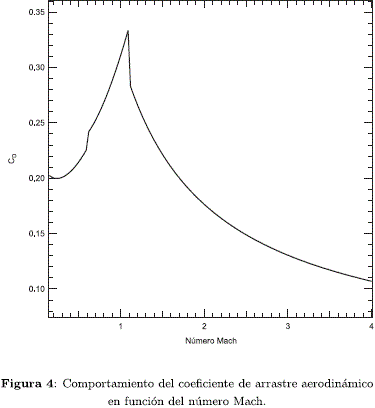
Una vez calculadas las dimenciones del cohete, se introdujeron como datos de entrada en un código computacional aerodimático obteniendo así el comportamiento del coeficiente de arrastre en función del número Mach, esto es, de la velocidad, tal y como se muestra en la Figura 4. Ahí se observa que el máximo coeficiente de arrastre del vehículo por onda de choque se obtiene alrededor de Mach 1 con un valor cercano a 0.34. Después de superar los efectos sónicos, el coefiente desciende a medida que aumenta el valor de número Mach siendo cercano a 0.10 para velocidades de 4 veces la del sonido y superiores. Con el propósito de evitar una variación notoria del coeficiente de arrastre con respecto al ángulo de ataque, asumiremos que existe un mecanismo de control que mantiene un valor nulo del ángulo de ataque.

En el momento del despegue, el cohete enciende el motor cohete de su primera etapa generando una fuerza de empuje constante de 834761 N durante un tiempo de 130.4 s. Cinco segundos antes del apagado del motor cohete principal (MECO, Main Engine Cut Off) se desprende la estructura de la primera etapa del cuerpo principal del cohete sólido de la segunda etapa que transmite una fuerza de empuje de 83831 N durante 188.4 s antes de ser desprendida de la estructura de la tercera etapa y carga útil (SECO, Second Engine Cut Off). Finalmente, se enciende la tercera etapa con una fuerza de empuje constante de 15271 N, la cual se puede diseñar de tal modo que el quemado proceda durante un tiempo de 150 s y cuyo propósito es generar la velocidad final de inserción (inyección) necesaria para que la carga útil quede orbitando a una altitud determinada. De acuerdo con los parámetros de diseño, el flujo másico se mantiene constante, siendo controlado con la cantidad de área quemada por el propelente constante en el tiempo que puede lograrse mediante la utilización de una configuración de estrella para la forma del grano.

Con el propósito de estudiar la trayectoria del cohete lanzado desde territorio continental colombiano, se eligió un sitio ubicado en el departamento de la Guajira sobre el mar Caribe con coordenadas geográficas de f = 12°3'20" norte y l = 72°9'35" oeste. Esta posible localización tiene la ventaja de estar ubicada en una zona desértica muy cerca al mar para aprovechar los recursos hídricos en las plataformas de lanzamiento. También se encuentra alejada de núcleos urbanos; la mayor parte de la trayectoria de vuelo puede realizarse sobre zona desértica y marítima; además, en esta zona se encuentra la más grande infraestructura ferroviaria del país por las minas de sal y carbón existentes en la región, contando con puertos marítimos y aeropuertos independientes que disponen de los medios para el transporte de maquinaria pesada. Entre las desventajas de este lugar se encuentran las altas velocidades de los vientos, razón por la cual allí se ubica el parque eólico de Colombia. Adicionalmente, es una de las zonas del territorio nacional más alejadas del ecuador con latitud superior a los 12° norte, lo que disminuiría el peso del lanzamiento de carga útil a órbitas geoestacionarias. Las posibles trayectorias del cohete que pueden cruzar por rutas aéreas de alto tráfico así como la posibilidad de sobrevuelo de territorio continental venezolano para cierto rango de azimuts de lanzamiento se constituyen también en factores de desventaja.

Para efectos de estudiar la trayectoria de vuelo del cohete, junto con cada una de las trayectorias de las etapas del mismo, una vez que éstas ya no hacen parte integral de la parte activa del cohete, se procedió a integrar numéricamente las ecuaciones (9) a (14), las cuales contienen términos que funcionalmente están definidos por las ecuaciones (1), (2), (3), (6), (7) y (8). La dependencia de la densidad del aire r frente a la altura está dada a través del modelo ARDC1959 (ver Figura 1) para lo cual se utilizaron valores tabulados en el correspondiente código. Del mismo modo se procedió frente a la dependencia funcional de C_D con respecto a la velocidad (ver Figura 4). Se asumió la existencia de un mecanismo de control de vuelo para asegurar un valor constante del ángulo de ataque a igual a cero. Así mismo, se adoptó un valor de C_L =O. El valor de la masa del cohete en todo tiempo se calculó asumiendo tasas de quemado constante en cada una de las etapas, esto es, m = M₀ - mt (ver Tabla 2) y teniendo en cuenta la expulsión de las etapas correspondientes. Las condiciones iniciales del vuelo corresponden al radio terrestre (r =R_e), la latitud y longitud del sitio del lanzamiento (citados atrás) y el azimut de lanzamiento que puede ser variable. Para términos que diverjan, los valores iniciales tanto de V como de J son igualados a un valor pequeño diferente de cero.

5. Resultados

En la Figura 5 se puede observar el comportamiento del valor de la presión dinámica (ver ecuación (3)) con respecto al tiempo. Se observa que el punto de mayor presión, conocido como q_max, se logra a los 65 s de vuelo (que corresponde a un valor de altitud de 10 km y una velocidad de 426 m s^-1). El valor de esa presión en tal punto es de 36000 Pa. Este factor es de vital importancia para el diseño estructural del vehículo, ya que es la máxima carga que debe soportar el cohete durante la fase de ascenso atmosférico.

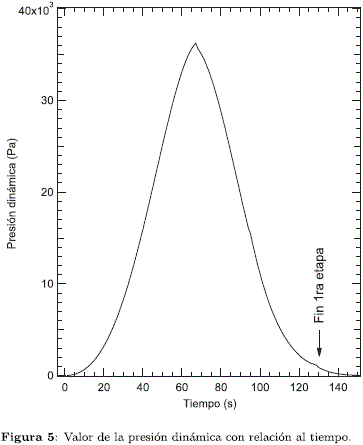
Durante el ascenso, el cohete aumenta la velocidad a medida que disminuye la masa, proporcionalmente a este aumento de velocidad se produce un aumento de presión hasta llegar a la zona de la atmósfera donde se vuelve significativo el descenso de la densidad del aire a medida que aumenta la altitud y velocidad del vehículo. Después de los 65 s de vuelo el valor de la densidad desciende considerablemente dando como resultado la disminución de la presión dinámica. Tan solo unos 20 segundos después del fin de la primera etapa se puede considerar que la presión dinámica es nula.

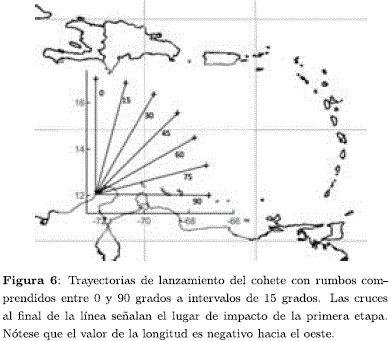
Posteriormente se analizaron las posibles trayectorias del cohete con un rumbo comprendido desde los O hasta los 90 grados a intervalos de 15 grados con el prósito de determinar si la primera y segunda etapas tienen el riesgo de impactar en o cerca de poblaciones pertenecientes a territorios de otros países.

Para este tipo de cálculos se hizo la suposición de que cada etapa en su caída hacia la tierra está orientada de "cabeza", esto es, el eje longitudinal de la etapa es paralelo a la dirección del vector de la fuerza de resistencia para que de ese modo se conserve el valor del área proyectada. Una suposición adicional y solo válida en una primera aproximación, es conservar el mismo comportamiento de C_D del de la primera etapa.

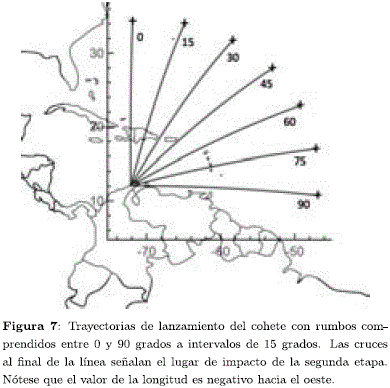
En la Figura 6 se muestran las trayectorias y los lugares de impacto de la primera etapa. Se observa que la mayoría de las trayectorias sobrevuelan el mar Caribe y el impacto de la primera etapa, salvo para rumbos de lanzamiento entre 75 y 90 grados, no representa preocupación para habitantes en tierra. En la Figura 7 se puede observar la continuación de la trayectoria y los lugares de impacto de la segunda etapa. Los valores de azimut comprendidos entre 0 40 grados sobrevuelan el algún momento territorio insular bien de Haití, República Dominicana y Puerto Rico. Valores de azimut entre 63 y 78 grados sobrevuelan las Antillas Menores. Ángulos de azimut cercanos a cero son especialmente sensibles debido a su relativa cercanía de sobrevuelo por territorio continental de la costa este de los Estados Unidos. Exceptuando ángulos de azimut inferiores a unos 5 grados, los lugares de impacto de la segunda etapa se verifican en sitios bien al interior del Océano Atlático. Si bien esto no representa riesgo a poblaciones en tierra, sí lo puede representar para barcos que estén atravesando el océano o aviones desplazándose a través de rutas aéreas al momento del despegue. Si se trata de minimizar el sobrevuelo de áreas relativamente pobladas, valores de azimut comprendidos entre 45 y 60 grados serían los más convenientes.

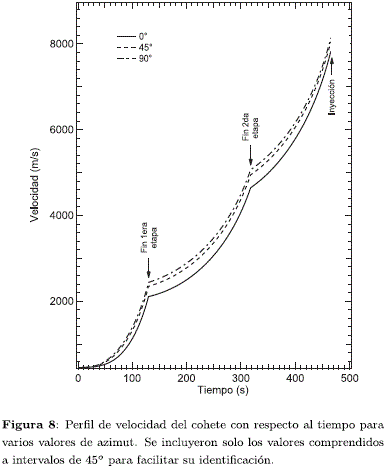
La Figura 8 muestra el correspondiente perfil de velocidad del cohete con relación al tiempo para varios valores de azimut de lanzamiento. Al final de la primera etapa se alcanzan a lograr velocidades comprendichul entre 2.05 a 2.45 km s^-1, mientras que al finalizar la segunda etapa las velocidades están en un rango entre 4.6 a 5.1 km s^-1. Los valores de velocidad en el momento de la inyección están en un intervalo comprendido entre 7.8 y 8.1 km s^-1. Es claro que los máximos valores de velocidad se logran con un ángulo de azimut de lanzamiento igual a 90° aunque la diferencia, con relación a los valores mínimos (de 0°), es de apenas unos 150 a 200 m s^-1 para la inserción orbital.

Los anteriores análisis fueron realizados con varios valores de rumbo comprendidos desde 0° hasta 90°. Para efectos de la continuación del análisis de la trayectoria y estudiar la colocación de un satélite en órbita baja, se seleccionó un valor representativo de azimut de 45°. Dejando los demás valores de condiciones iniciales sin modificar, se analiza primeramente el comportamiento de la altitud de cada una de las etapas en función del tiempo de vuelo. Esto se puede observar en la Figura 9. La primera etapa se agota en torno a los 130 s; después de la separación de ésta (para dar lugar al inicio del encendido de la segunda) continua ganando altura hasta alcanzar un valor cercano a los 150 km, lo que ocurre a los 270 s después del lanzamiento. Su impacto en el océano se verifica a los 450 s.

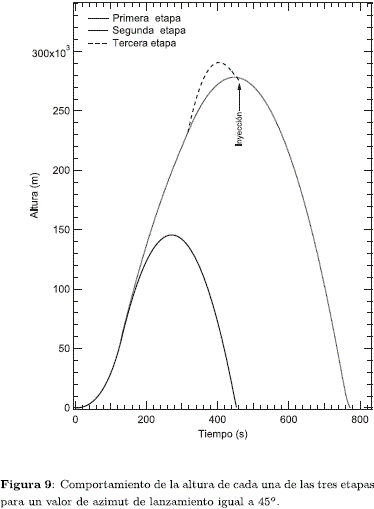
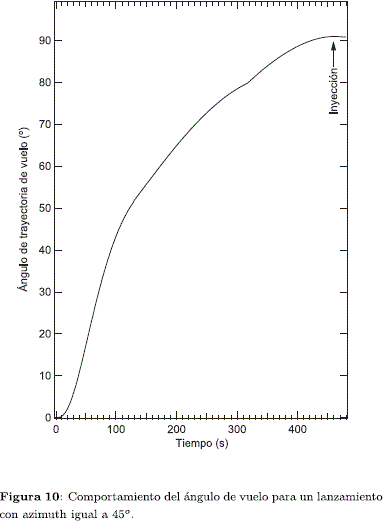
En cuanto a la segunda etapa, la cual se enciende estando a una altura de unos 55 km, termina agotándose al cabo de transcurridos 318 s a una altitud cercana a los 230 km; continua ganando altura hasta llegar a los 290 km (lo que ocurre a los 395 s) para, posteriormente, de regreso a tierra, impactar en el océano a los 775 s. La tercera etapa continua ganando un poco más de altura, alcanzado el máximo pico de altitud de 290 km a los 400 s. A partir de ahí, y aun ganando velocidad, comienza a dismunir la altura (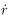 < 0) hasta llegar el momento de la inyección a los 470 s. En la Figura 10 se puede apreciar el comportamiento del ángulo de vuelo en función del tiempo. La inyección se verifica a un valor de J = 90.9: tanto la tercera etapa como la carga útil quedan en órbita. Sin embargo, esta última se puede desprender de la estructura de la tercera etapa con ayuda de resortes u otro mecánismo con lo que se altera muy ligeramente la trayectoria de la carga útil. La trayectoria de la tercera etapa será la misma que tiene el satélite en órbita en los primeros instantes de la inyección pero, por su mayor á.rea proyectada, experimenta nna fuerza mayor de resistencia y su descenso será más marcado que el que experimentará el satélite. Finalmente, por su cercanía con las capas densas de la atmósfera, se genera un aumento de temperatura por fricción de tal modo que se desintegra el objeto.

Examinemos las características orbitales del satélite en el momento en que ingresa a órbita terrestre. En la Tabla 3 están consignados los valores dinámicos en el momento de la inyección orbital para un lanzamiento de 45°, valores que corresponden al sistema inercial centrado en la Tierra.

En el caso que nos ocupa, el valor de la velocidad en el momento de la inyección (cut-off) es más del requerido para una órbita circular a una altura de 272 km (que es del orden de 7745 m s^-1), esto es, casi 300 m s^-1 más. De ahí que la órbita deba resultar con una excentricidad relativamente alta.

Los valores del semieje mayor a y excentricidad e de la órbita están dado entonces por (Portilla, 2009):

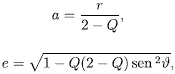
en donde:

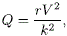
siendo 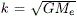= 107.10085 RT^3/2 d^-1. Los valores de la altura en el perigeo h_p y el apogeo h_a están dados por:

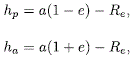
y el periodo orbital por:

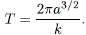
De igual modo, el valor de la inclinación orbital está dado por (Chobotov, 2002):

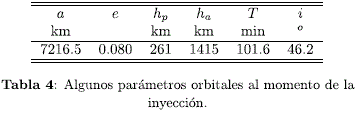
Los valores de algunos de los elementos orbitales del satélite en el momento de ingresar a órbita baja terrestre se presentan en la Tabla 4.

Claramente es posible explorar otra serie de azinmts de trayectoria para efectos de colocar satélites con objetivos claramente definidos. Es el caso, por ejemplo, de los satélites en órbita heliosincrónica, frecuentemente utilizados para observación terrestre y que requieren órbitas de tipo polar ligeramente superiores a los 90°. Nuestro código posee la facilidad de cambiar directamente datos de entrada que permitan calcular, y con ello examinar, la factibilidad en la escogencia de rumbos específicos así como valorar los tipos más adecuados de órbitas que se ajusten a las necesidades del país a mediano y largo plazo.

6. Conclusiones

En la presente comunicación se ha realizado el estudio de la trayectoria de vuelo para un cohete de tres etapas lanzado desde un sitio en territorio colombiano con fines de colocar un pequeño satélite (∼ 200 kg) a órbita baja. Para ello se integraron las ecuaciones diferenciales de movimiento en un sistema de referencia no inercial así como se definieron algunas características de diseño del vehículo el cual se optimizó a través de un proceso iterativo. Se tuvo en cuenta las fuerzas principales que afectan el movimiento del vehículo, tales como la atracción gravitacional (incluyendo el armónico zonal J₂) así como la fuerza de empuje y aquellas otras que se originan por el movimiento a través de un fluido. Para estas últimas fue preciso utilizar datos de densidad del aire en función de la altura para lo cual se utilizó un modelo atmosférico. Para la integración numérica de las ecuaciones diferenciales se utilizó un código computacional en lenguaje Fortran 77 elaborado por los autores basado en el integrador Radau. Se logró simular la trayectoria de vuelo desde el lanzamiento (ubicado en un sitio en el departamento de la Guajira) y determinar la trayectoria de vuelo para varios valores de azimut. Se determinaron los puntos de impacto de la primera y segunda etapas y se discriminaron de ese modo las trayectorias de vuelo que sobrevuelan por áreas pobladas o limítrofes con otros países. Se estableció que el mejor rango de azimut corresponde a valores entre 45 y 60°.

Este se constituye en el primer análisis realizado en Colombia que se ocupa de estudiar la trayectoria de un cohete (incluso sin apelar a códigos realizados en el extranjero) para posicionar un pequeño satélite de forma lo más realista posible, advirtiendo que son mucho los aspectos que habría que incluir para futuros análisis más detallados, tales como el estudio del perffi atmosférico en la zona próxima al lanzamiento, estudio de vientos, características de los materiales que integran el cohete, forma detallada del velúculo, etc. Tanto el vehículo de lanzamiento como el satélite bien pueden ser de fabricación autóctona, realizable a un corto plazo siempre y cuando el país adopte la decisión, fundamentalmente política, de hacerlo. El análisis es del todo premeliminar, básicamente enfocado en cual tendrían que ser las dimensiones del vehículo y cual tendrían que ser los azimuts de lanzamiento para minimizar los riesgos de caída de las etapas o de mal funcionamiento del vehículo. Estos resultados han de verse como una primera exploración tendiente a crear conciencia en el medio, de que este tipo de tecnologías pueden ser accequibles a un país como el nuestro, que a pesar de la problemática social y relativamente altos niveles de pobreza, los ejemplos de países en condiciones iguales o peores que el nuestro tales como Irán, Paquistán y Corea del Norte mues tran que es posible acceder al espacio por medios autóctonos.

_________________

³ http://www.vatp.iv1en/nekrizelv-large-potential-spa.ce-industry
⁴ http://ingesaerospace.blogspot.com
⁵ Presentación en el congreso de ciencia y tecnología aeroespacial CICTA 2007.
⁶ http://see.msfc.nasa.gov/tte/model_gram.htm
⁷ Comunicación personal con Indumil.
⁸ Dato suministrado por Indumil.

Bibliografía

Achury, V. 2005. Modelamiento por CFD Aplicado a un Micro Motor Cohete, Tesis de Pregarado en Ingeniería Mecánica, Universidad Nacional, Bogotá         [ Links ].

American National Standard Institute, ANSI. 2004. Guide to Reference and Standard Atmosphere Model.s. American lnstitute of Aeronautics and Astronautics, Reston, Virginia.         [ Links ]

Anderson, J. 2010. Introduction to Flight, McGraw Hill, Singapur.         [ Links ]

Bate, R., Mueller, D., & White, J.1971. Fundamental.s of Astrodynamics, Dover, New York.         [ Links ]

Calderón, O. & Murcia, J. 2009. Diseño Conceptual y Preliminar de un Vehículo que Transporta Carga Útil de una Tonelada a Órbitas Bajas, Tesis de Pregrado en Ingeniería Aeronáutica, Fundación Universitaria los Libertadores, Bogotá         [ Links ].

Calise, A. J. & Leung, M. S. K. 1995. Optimal. Guidance Law Development for an Advanced Launch System, NASA Contractor Report 4667.         [ Links ]

Chobotov, V. 2002. Orbital Mechanics. American Institute of Aeronautics and Astronautics, Reston, Virginia.         [ Links ]

Escobar, S. & Jaramillo, S. 2009, Diseño Conceptual de un Motor Cohete de 70 mm de Propelente Sólido. Tesis de Pregrado en Ingeniería Aeronáutica, Universidad Pontificia Bolivariana, Medellín.         [ Links ]

Escorcia, M. 2011. Estudio Dinámico de los Parámetros Generales de Rendimiento en un Motor Cohete de Propulsión Iónica Mediante el Lenguaje Computacional de Tipo M. Tesis de Pregrado en Ingeniería Aeronáutica, Fundación Universitaria los Libertadores, Bogotá         [ Links ].

Everhart, E. 1985. An Efficient lntegrator that Uses Gauss-Radau Spacings, Dynamics of Comets: Their Origin and Evolution, Carusi & Valsecchi (edi.): 185-202.         [ Links ]

Galindo, D. & Murcia, J. Diseño de Cohetes Atmosféricos, Segundo Congreso de Ciencia y Tecnología Aeroespacial, CICTA 2008, Bogotá         [ Links ].

Garzón, D., Duque, C. & Roa, M. 2004. Introducción General a la Tecnología de la Propulsión. Universidad Nacional de Colombia, Bogotá         [ Links ].

Gómez, S. & Castro, H. 2006. Diseño Preliminar de un Sistema de Propulsión Líquida con Hidrógeno Líquido como Combustible Adaptado a un Rocket Belt, Tesis de Pregarado en Ingeniería Aeronáutica, Universidad San Buenaventura, Bogotá         [ Links ].

Hwnble, R., Henry, G. & Larson, W.1995. Space Propulsion Analisys and Design. McGraw Hill, New York.         [ Links ]

Joya, R. 2007. Libertad 1, primer satélite colombiano en el espacio. Innovación y Ciencia, 14: 16-23.         [ Links ]

Kaula, W. M. 1966. Theory of satellite Geodesy. Blaisdell Pu. Co., Waltham, Massachusetts.         [ Links ]

Koelle, H.1961. Handbook of Astronautical Engineering. Mc-Graw Hill, New York.         [ Links ]

Lafl.eur, J., Fleming, S. & Saleh, J. 2012. Response Surface Equations for Expendable Launch Vehicle Payload Mass Capability, Journal of Spacecraft and Rockets, 49, (1): 185-189.         [ Links ]

Minzner, R., Champion, K. & Pond, H.1959. The ARDO Model Atmosphere, 1959. Air Force Surveys in Geophysics No. 115.         [ Links ]

Portilla, J. G.1996. El Problema de los dos Cuerpos y el Problema Principal del Satélite Artificial en Ecuaciones Diferenciales del Primer Orden. Rev. Acad. Colomb. Cien., 20, (76): 25-32.         [ Links ]

Portilla, J. G. 2001. Astronomía Para Thdos. Unibiblos, Bogotá         [ Links ].

Portilla, J. G. 2009. Elementos de Astronomía de Posición. Unibiblos, Bogotá         [ Links ].

Portilla, J. G. 2013. La órbita del satélite Libertad l. Aceptado para publicación en la Rev. Acad. Colomb. Cien.

Robledo, J. 2011. Diseño Conceptual de un Motor Cohete Iónico para Maniobras Espaciales, Tesis de Pregrado en Ingeniería Aeronáutica, Fundación Universitaria los Libertadores, Bogotá         [ Links ].

Sutton, G. & Biblatz, O. 2010. Rocket Propulsion Elements. John Wiley & Sons, New York.         [ Links ]

Tewari, A. 2007, Atmospherc and Space Flight Dynamics, Birkhii.user, Boston.         [ Links ]

Urrego, A. 2009. Investigaciones en Cohetería Experimental. Misión Séneca, Lanzamiento del Cohete Ainkaa 1, Tesis de Pregrado en Ingeniería Mecánica, Universidad de los Andes, Bogotá         [ Links ].

Weiland, C.. 2010. Computational Space Flight Mechanics. Springer, Heidelberg.         [ Links ]

Whitney, C. K., et al. 1965. Scout Motor Performance Analysis and Prediction Study (PAPS). NASA Contractor Report CR-336.         [ Links ]

Xu, G.. 2008. Orbits. Springer, Berlín.         [ Links ]

Zipfel, P.2007. Modeling and Simulation of Aerospace Vehicle Dynamics. American Institute of Aeronautics and Astronautics, Reston, Virginia.         [ Links ]

Recibido: 20 de junio de 2013
Aceptado para publicación: 16 de enero de 2014