MATEMÁTICAS

* Samara State Aerospace University named after Academician S.P. Korolev Samara, Russia
** Department of Mathematics, Faculty of Informatics, Universidad de Pinar del Río, Pinar del Río, Cuba
*** Instituto Universitario de Matemática Pura y Aplicada, Universitat Politècnica de València, València, Spain

ABSTRACT

In this paper we present, with a pedagogical aim, a method to calculate the associated Legendre functions and polynomials. The method uses stable recurrence relations involving these functions.

Keywords: legendre associated functions, Legendre polynomials, recurrence relations, stability.

RESUMEN

En este trabajo se presenta, con una finalidad pedagógica, un método para evaluar funciones y polinomios de Legendre. El método utiliza relaciones de recurrencia estables que involucran a estas funciones.

Palabras clave: funciones asociadas de Legendre, polinomios de Legendre, relaciones de recurrencia y estabilidad.

Introduction

Spherical harmonic functions and associated functions of Legendre of the first and second kind 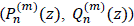[1,2] are related to most of the special functions of mathematical physics. For example, they appear in the computation of atomic electron configurations [4], in the representation of electromagnetic fields in materials and at surfaces and intefaces [5], and in the characterization of some forms of electromagnetic radiation [6]. Apart from these works, we refer to the reader to [11,12,13] and references therein for other applications and the recent discoveries about Legendre's functions. They are solutions of Legendre's equat.

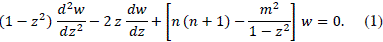
Solution of this equation are analytical in z, n and m. Usually n is called the degree and m the order. Solutions of this equation are polynomials for n integer and even, and m integer such that 0 ≤ m ≤ n. In the case of n odd they are not polynomials, although the whole set of solutions are known as Legendre Polynomials. If m = 0, then the solution are the well-known Legendre polynomials. Usually, when one uses these functions in applied problems, it is necessary to compute them for all n, m in a wide range, which is computationally expensive.

In the case of Legendre's Polynomials, there exists an explicit form of the polynomials P_n(z), given by the formula of Rodrigues,

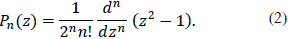
Expanding this formula, one obtains,

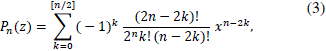
where [n/2] is the integer part of the number n/2.

Whereas for small values of n, the computation of Legendre's polynomials using (3) is trivial, when N » 1 several accuracy and stability problems arise. One should be tempted to use the recurrence relation,

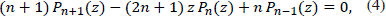
since P₀(z) = 1 and P₁(z) = z. However, the ascending recursion formula (4) is also unstable. This is related to the fact that in the interval (-1,1) the norm of the polynomial 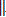P_n(z)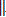 diminishes as 1/√(n) [6]. In other words, the use of a recursion that produces a monotonically descending sequence in norm, leads to a rapid accumulation of round-off errors.

In this paper we present a suitable algorithm to compute the associated Legendre functions P_n^(m)(z), which includes as especial case the Legendre polynomials P_n(z). In fact, P_n(z) = P_n^(m)(z) for m = 0 and n integer, since [1]

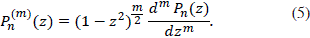
The formula (4) is computationally stable for the regular solutions P_n(z) of Legendre’s equation (1) using backward recursion. In this case, as the norm of polynomials P_n(z) and P_n-1 (z) is smaller than the norm of P_n-2 (z), there is not round-error accumulations. As there are not cancellations, the finiteness of the mantissa does not influence in the error of each step in the recursion.

Of course, if backward recursion has to be applied by using (4), one needs initial values P_N(z) and P_N-1(z). The evaluation of these values is very expensive for great values of N using formula (3). Furthermore, the computational implementation of (3) generates additional problems, related to the round-off error and also to accumulation of error in the subtraction of closed values.

The computation of the associated Legendre functions P_n^(m) (z) in physical and/or engineering problems results as frequent as those of Legendre polynomials P_n(z), so it is very useful that the algorithm computes both the polynomials and functions. Following the same strategy of [7,9,10] it is possible to find the functions P_n^(m)(z) and the polynomials P_n(z) in an unified algorithm.

Solutions of equation (1) [8] are subordinated to the recursion relations

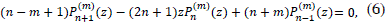
and

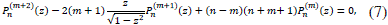
where initial values are given by

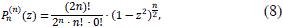
and

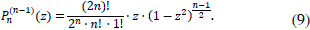
However, recursion (7) is computationally unstable backwards. The nature of this instability is the same as in the forward recursion (3) for Legendre's polynomials P_n(z). This is a consequence of the rapid accumulation of error on the computed value Y_n from the standard trinomial recursion relation

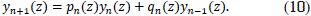
The associated function of Legendre P_n^(m)(z) is analytic on m, -n ≤ m ≤ n, and for a fixed value of n, the norm 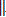P_n^(m)(z) 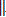monotonically increases with m. Connection between the associated functions of Legendre for the negative and positive values m it is given by the relationship, [1]

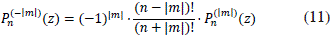
From the formulas (8), (9), (11) it follows that

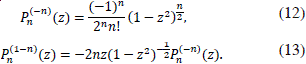
Using (11), (12) and (13) it is possible to find the initial values P^(-n)(z), P_n^(1-n)(z), which permits to compute Legendre P_n^(m)(z) for all 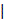m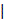 ≤ n on the basis of the steady ascending recursion (7).

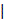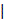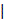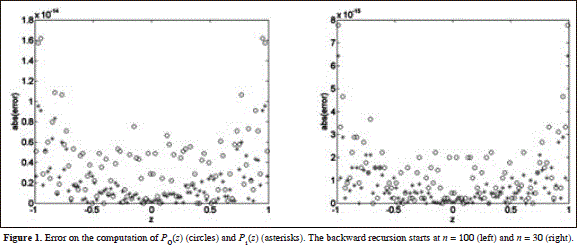
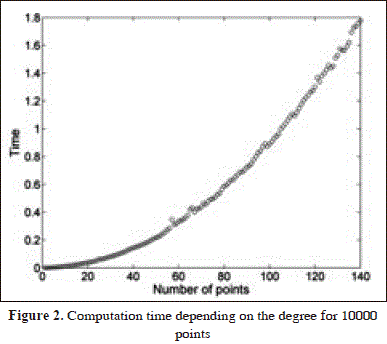
As a particular case, this formula is also useful to compute P^o_n(z) which can be readily used to compute P^o_o(z) backwards in a very fast and accurate way. Moreover, the error of the algorithm can be estimated by e = P_o ^appr (z) - 1 and e₁ = P₁ ^appr (z) - z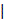. In Figure 1a and 1b we plot the errors for initial n = 100 and n = 30. Both errors are in the range 10^-14, i.e. close to the round-off error. As we can see from Fig. 2, typical time for a run is in the range of seconds for 10.000 points.

A last question: as we want to present this work with a methodological point of view, we only sketch the main problems of Legendre recurrence formulas. We refer to [11] or [14] for more formal comparisons.

Codes developed

The subroutine flgndr computes accurately the values of Legendre's function for any z ∈ (-1,1) and all m integer in -n ≤ m ≤ n. The maximum possible n is 120. This limitation is due to the small value of 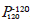, which cannot be accurately described in double precision.

In this subroutine, z is a column vector containing the points where Legendre's functions are going to be calculated, and n is the degree. Output is a matrix, pnm, of size [length(z), 2n + 1] containing the values of P_n^(m) for -n ≤ m ≤ n.

Using the previous routine, it is possible to compute P_n(z) and P_n-1(z), which allow us to compute Legendre polynomials. The inputs are the same that in the flgndr function, but the output contains the values for all the orders from 0 until n. This n is limited in double precision to 120 approximately.

Conclusion

In this work we have developed and described (with pedagogical aim) an algorithm which computes Legendre's functions and polynomials. Testing shows how this method can compute this function with a maximum error of 1e-14. The main limitation is due to the small value of P_n^(-n), which can be by-passed using 16 bytes precision. A generaliza- tion of this method to another orthogonal polynomials and functions are currently in progress.

Acknowledgements

Authors thank Universitat Politècnica de València funding under project SP 20120909.

Bibliografía

[1] Abramowitz M, and Stegun IA, Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, Dover, New York 1972.         [ Links ]

[2] Zwillinger D, Handbook of Differential Equations, Academic Press, Boston, 1997.         [ Links ]

[3] Olver FWJ, and Smith JM, Associated Legendre functions on the cut, Journal of computational Physics, 1983; 51, 502-518.         [ Links ]

[4] Slater JC, Quamtum Theory of Atomic Structure, Volume I, Mac-Graw-Hill, New York, 1960.         [ Links ]

[5] Jackson JD, Classical Electrodynamics, John Wiley and Sons, Inc., New York, 1998.         [ Links ]

[6] Aksenov EP, Special functions in the celestial mechanics, GlavnayaRedaktsiyaFiziko-MatematicheskojLiteratury, Nauka, Moskva, in Russian, 1986, 320 pages.         [ Links ]

[7] RatisYuL, and Fernández de Córdoba P, A code to evaluate (high order) Bessel functions based on the continued fractions method, Computer Physics Communications 1993; 76, 381-388.         [ Links ]

[8] Segura J, and Gil A, Evaluation of Associated Legendre functions off the cut and parabolic cylinder functions, Electronic transactions on numerical Analysis 1999; 9, 137-146.         [ Links ]

[9] Bastardo JL, Abrahamm Ibrahim S, Fernández de Córdoba P, Urchueguía JF, and RatisYuL, Evaluation of Fresnel integrals based on the continued fractions method, Applied Mathematics Letters, 2005; 18, 23-28.         [ Links ]

[10] Selezneva IA, A rapid algorithm for computing special functions in mathematical physics, Vital problems of contemporary natural science, Samara, Intercollegiate collection of scientific papers dedicated to Alexander IvanovichFedosov's memory, 2004; 1, 22-26.         [ Links ]

[11] Gil A, Segura J, and Temme N, Numerical Methods for special functions. SIAM, Philadelphia, PA, 2007.         [ Links ]

[12] Gil A, Segura J, and Temme N, Basic methods for computing special functions. Recent advances in computational and applied mathematics, 67-121, Springer, Dordrecht, 2011.         [ Links ]

[13] Olver FWJ, Lozier DW, Boisvert RF, and Clark CW, NIST Handbook of Mathematical Functions, U. S. Dept. Commerce, Washington. Cambridge University Press, New York, 2010.         [ Links ]

[14] Schneider I, Segura J, Gil A, Guan X, and Bartschat K, A new Fortran 90 program to compute regular and irregular associated Legendre functions. Comput. Phys. Comm. 181 (2010), no.12, 2091-2097.         [ Links ]

Recibido: 28 enero de 2013
Aceptado: 13 de noviembre de 2013