doi: http://dx.doi.org/10.18257/raccefyn.99

¹ Departamento de Física, Universidad de los Andes, Bogotá, Colombia * Correspondencia: Gabriel Téllez: gtellez@uniandes.edu.co
² Departamento de Física, Universidad del Valle, Cali, Colombia

Recibido: 20 de agosto 2014. Aceptado: 16 de abril 2015

Abstract

We analyse the classical and quantum behaviour of a particle trapped in a diamond-shaped billiard with rounded crown. We defined this billiard as a half stadium connected with a triangular billiard. A parameter x smoothly changes the shape of the billiard from an equilateral triangle (x = 1) to a diamond with rounded crown (x = 0). The parameter x controls the transition between the regular and chaotic regimes. The classical behaviour is regular when the control parameter x is one; in contrast, the system is chaotic when x ≠ 1 even for values of x close to one. Several quantities such as Lyapunov exponent and the entropy of the distribution of the incident angle are used to characterize the chaotic behaviour of the classical system. The average information preserved by the classical trajectories increases rapidly as x is decreased from 1 and the Lyapunov exponent remains positive for x < 1. The Finite Difference Method was implemented in order to solve the quantum counterpart of the billiard. The energy spectrum and eigenstates were numerically computed for different values of x < 1. The spacing distribution between adjacent eigenvalues is analysed as a function of x, finding a Poisson and a Gaussian Orthogonal Ensemble (GOE) distribution for regular and chaotic regimes respectively. Several scars and bouncing ball states are shown with their corresponding classical periodic orbits. On the other hand, the results found for the quantum billiard are in agreement with the Bohigas-Giannoni-Schmit conjecture and exhibits the standard features of chaotic billiards such as the scarring of the wavefunction.

Keywords: quantum chaos, quantum billiards, random matrices, finite difference method.

Resumen

Se estudia el comportamiento de una partícula en el interior de un billar triangular donde uno de sus lados toma de medio estadio que se llamó billar diamante con corona redondeada o DSRC por su siglas en inglés. Se definió un parámetro x que cambia suavemente la forma la frontera partiendo de un billar triangular x = 1 a un billar DSRC x = 1. Dicho parámetro controla la transición entre el régimen regular y caótico. Clásicamente, el sistema es regular cuando x = 1. Por otro lado, el sistema se torna caótico para x ≠ 1 incluyendo valores próximos a 1. Se calcula el coeficiente de Lyapunov y la entropía media de la distribución de los ángulos de incidencia para caracterizar el comportamiento caótico del sistema. Se observó un rápido crecimiento de la información de las trayectorias hasta saturar la entropía al cambiar levemente la frontera del billar triangular original. A su vez el coeficiente de Lyapunov se mantuvo positivo durante este proceso una vez que x se alejaba de 1. Se implementó el método de diferencias finitas FDM para obtener el espectro y los estados propios de la contraparte cuántica del sistema. La distribución de espaciamiento entre primeros vecinos para varios valores de x fue construida numéricamente para diferentes valores de x encontrando una distribución de Poisson y otra correspondiente al ensamble ortogonal gaussiano GOE dentro de las regiones clásica y caótica respectivamente. Se identificaron cicatrices en algunos de sus estados así como estados de "bola rebotadora" con sus correspondientes órbitas periódicas. El sistema exhibe un comportamiento que está de acuerdo a la conjetura BGS y presenta las características típicas de un billar caótico como la cicatrización de la función de onda.

Palabras clave: caos cuántico, billares cuánticos, matrices aleatorias, método de diferencias finitas.

1 Introduction

Billiards are one of the most used systems to analyse the quantum signatures of classical chaotic motion [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17]. Some advantages of the billiards are their extreme simplicity, their straightforward quantization and the possibility to measure many of the relevant quantities in laboratory experiments [18, 19, 20, 21, 22, 23, 24, 25].

Many aspects of classical and quantum chaos have been widely studied by means of billiards with different shapes [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17]. We offer a brief review about some commonly used methods to characterize the classical and quantum motion of particles inside billiards. For this purpose we use the diamond-shaped billiard with rounded crown which is described in next section. For the classical case, we focus on the determination of the trajectories, Lyapunov exponents and the entropy of the distribution of incident angles. In the quantum case, it is studied the spacing distribution between adjacent eigenvalues of the Hamiltonian and the scarring of the wave function.

Basically, a billiard is a system where a particle, with mass m, is trapped into a region D with perfect reflecting boundaries. The dynamics of the particle varies depending on the shape of the billiard boundary ∂D. The cardioid billiard, the Bunimovich billiard (stadium billiard) and non-equilateral triangular billiards are typical examples which exhibit classical chaos. The quantum problem is reduced to solve the Helmholtz equation for the wave function y()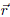

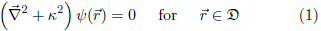
with the Dirichlet boundary condition y(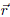) = 0 if 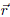∈ ∂D where k = 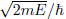is the wave vector and E is the energy. For Hamiltonian systems, the statistical properties of the energy levels can be studied taking borrow some results from the random matrix theory. For example, it is well known that the energy level spacing distributions of a system is Poissonian if its classical counterpart exhibits a regular motion. Some examples are billiards whose shape is a rectangle (particle in a two dimensional box), an equilateral triangle, a circle or an ellipse. On the other hand, if the classical counterpart has a chaotic motion, then the energy levels follow the same distribution of the eigenvalues of the Gaussian Orthogonal Ensemble (GOE) distribution [26, 27, 28, 29, 31]. Other non convex and chaotic two dimensional quantum cavities are the Sinai and the annular billiards where an inner disk of infinite potential is placed into a rectangular or circular billiard, respectively.

2 Geometrical considerations

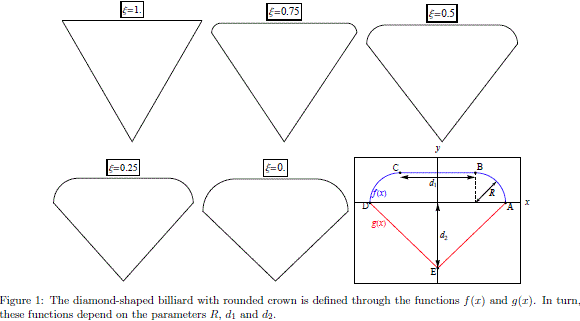
As mentioned before, this paper is devoted to the study of the motion of a particle inside of a diamond-shaped billiard with rounded crown (DSRC billiard) which is shown in Fig. 1. The shape of the upper boundary of the billiard is a half stadium defined by the equation y = f (x) with

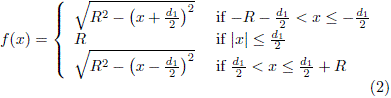
On the other hand, the shape of the lower boundary y =g(x) is given by

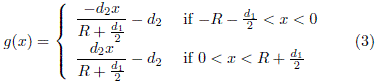
The parameters which determine the shape of the billiard R, d₁ and d₂ are functions of the control parameter x. Explicitly we define R(x) = R₀ (1 – x), d₁ (x) = (5/2 + x) R₀ and d₂ (x) = √3/4 d₁ (x). Henceforth, we take R₀ = 1. For x = 1 the shape of the billiard resembles a diamond with rounded crown and for x = 0 the shape is an equilateral triangle.

As shown in Fig. 1, for intermediate values of x there is a smooth interpolation between these two shapes. The boundary can be conveniently expressed in polar coordinates as follows

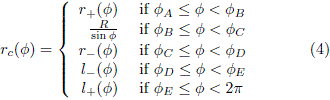
In Eq. (4), the left (-) and right (+) quarter of circles are cording to defined ac

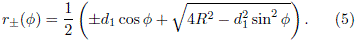
while the straight lines DE and EA are given by

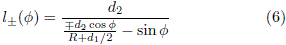
The f-coordinate of the points from A to E can be written as fA = 0, fB = arctan 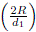fC = arctan 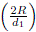+ 2 arctan 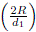, fD = p and fE = 3 p, respectively.

3 Classical diamond-shaped billiard with rounded crown

3.1 Trajectories

There are two degrees of freedom in the DSRC billiard, thus its phase space has four dimensions. The elastic collisions between the particle and the boundaries ensure the energy conservation reducing the number of dimensions to three. As usual, in order to obtain the dynamical information of the system, we construct the Poincaré section, and the dynamical behaviour of the particle can be described by a two-dimensional map. This method is equivalent to choose two variables which define where and how the collisions occur inside the billiard.

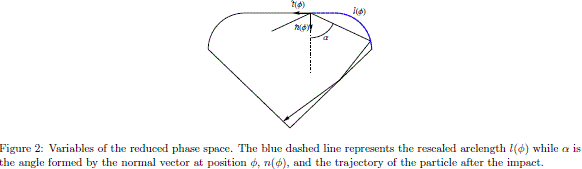
We choose a rescaled arclength l(f) and the angle a as the variables to describe the particle motion in the billiard. These variables are schematized in Fig. 2. The angle a gives the direction of the velocity after the impact and the rescaled arclength is defined as l(f) = 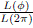where L(f) = 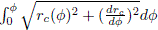is the arclength measured from the point A. Following the standard procedure, it is necessary to express the position and the incident velocity of the (n + 1)-th collision in terms of the of the position and velocity of the n-th collision. Let (x⁽ⁿ⁾ , y⁽ⁿ⁾ ) = (r_c (f⁽ⁿ⁾ ) , f⁽ⁿ⁾ ) and ⁽ⁿ⁾ = (v_x⁽ⁿ⁾ , v_y⁽ⁿ⁾ ) be position and the incident velocity of the n-th collision, respectively. The normal v_n⁽ⁿ⁾ and tangent v_t⁽ⁿ⁾ components of the velocity are calculated by projecting the velocity into the normal, 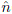(f), and the tangent, (f), unitary vectors of the boundary, see Fig. 2. As consequence of the elastic collisions with the boundary the normal component velocity changes its sign while the tangent component remains unchanged. Thus, one can obtain the velocity ⁽ⁿ⁺¹⁾ after the n-th collision which is also the incident velocity (n + 1)-th collision. In order to accomplish this calculation the components of the tangent vector 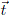d/df (r_c (f) cos f, r_c (f) sin f) = (T_x, T_y) are required. A simple calculation gives

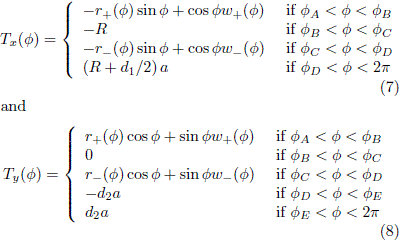
where we have defined

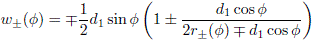
with

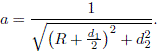
The normal vector is obtained by rotating the tangent vector = R (-p/2), hence n_x (j) = t_y (j) and n_y (j) = -t_x (j). On the other hand, the position of the (n + 1)-th collision is calculated as follows. The straight line which crosses through the points (x⁽ⁿ⁾ , y⁽ⁿ⁾ ) and (x⁽ⁿ⁺¹⁾ , y⁽ⁿ⁺¹⁾ ) is given by Y ⁽ⁿ⁾ (x) = m⁽ⁿ⁾ x + b⁽ⁿ⁾ . The slope and the y-intercept can be written as

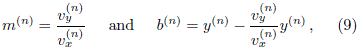
respectively. The x coordinate of the intersections of the line Y (x) with the boundary satisfy

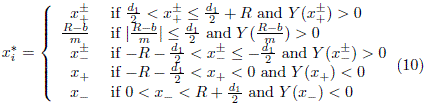
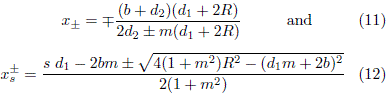
with s = {+, -}. The DSRC billiard is a convex billiard, then, Eq. (10) has two roots: x^*₁ and x^*₂. One of them is the position of the n-th collision, xⁿ = (x*₁)(n), which is already known. The second root gives the position of the (n + 1)-th collision

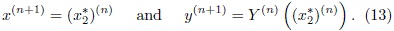
In general this procedure can be applied satisfactorily. Nonetheless, if the particle reaches one of the points {A, D, E} where vectors 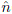and are not well defined, then the method described previously cannot be applied. This is an unlikely event, however, the problem can be avoided by taking the average of the normal and tangent vectors of the boundaries connected in those problematic points. Some trajectories of the particle inside the triangular and the DSRC billiards are shown in Fig. 3. These trajectories were found by using the procedure previously described in this section. For the triangular billiard (x = 1), we found regular and periodic trajectories. In contrast, for values of x close to one, e.g. x = 0.99 there are irregular trajectories. In order to obtain information about the motion of the particle, the trajectories were mapped into a Poincaré section defined by the collision angle and the arclength. The periodic orbits of the triangular billiard are represented as a set of two or more points in the Poincaré section. This is the case of the trajectories (a),(b),(c),(e),(g) and (h) shown in Fig. 3. Quasi-periodic orbits such as the ones of Figs. 3 (e) and (f )) are represented by a set of straight lines in the Poincaré section (see Fig. 4).

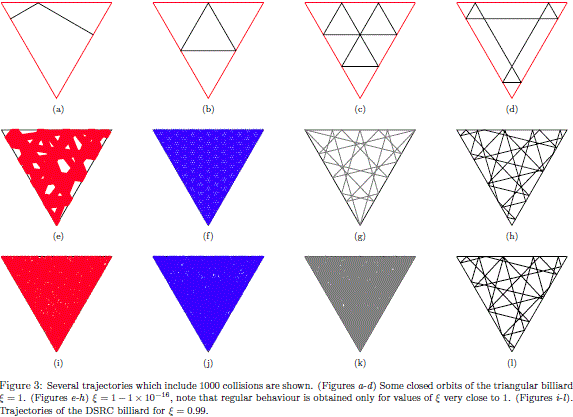
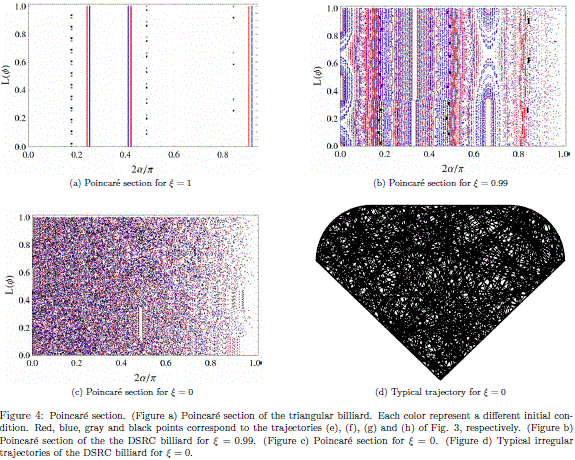
In order to illustrate the destruction of regular trajectories we have calculated the particle motion for the same initial conditions of Figs. 3 (e) to (h) but taking now x = 0.99. In this way, for Fig. 3 (i) we have used the same initial condition of Fig. 3 (e), (j) the same initial condition of (f ) and so on.If the shape of the triangular billiard is slightly changed, the trajectories shown in Figs. 3 (e)-(f ) become irregular as shown in Figs. 3 (i)-(k). However, the trajectory shown in Fig. 3 (h) remains regular for x = 0.99. Eventually, the regular trajectories can be immersed inside of a chaotic sea in the Poincaré section (black points in Fig. 4-(b)), this is the case of the periodic orbit of Fig. 3-(h).

3.1.1 Entropy

In the previous section, a simple methodology based on geometrical considerations was used to find the classical trajectories of the particle inside the billiard. This is not the more elegant way to find trajectories. In fact, it is possible to find a transformation or map which connects the variables of the reduced phase space of consecutive collisions of the DSRC billiard. In principle, for a given initial condition, the trajectory of the particle can be constructed if this map is known. Avoiding the very special cases of the periodic orbits, the degree of irregularity of a set of trajectories with different initial conditions depends only on the shape of the billiard. Let a_n be the incident angle with respect to the normal vector of the boundary. Note that a_i ∈ I and I = [-p/2, p/2]. This interval can be divided into M equal subintervals I_i . Then, for a given initial condition N collisions are generated and their respective incident angles a_n are calculated (n = 1, 2, 3,. .., N). We repeat this procedure for several different initial conditions. Let N_i be the number of angles a_n which belong to the interval I_i . Then, the probability to find an incident angle in the interval I_i is P (I_i) = N_i/N. The entropy S of the distribution (I_i) can be written as [32]

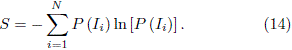
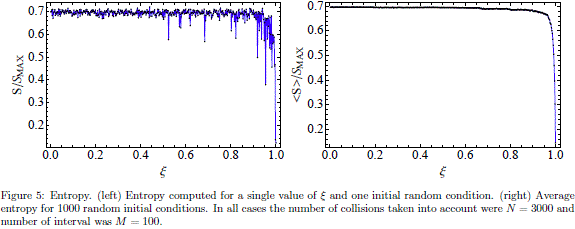
Note that, the maximum entropy is obtained when the set of generated incident angles {a_n} are uniformly distributed in the subintervals {I_i}. For this case, the probability is equal for each subinterval, i.e., P (I_i) = 1/M , and the entropy takes its maximum value S_max = ln(M). On the other hand, if all incident angles belongs to a single subinterval I_j , P (I_i) = d_ij and the entropy is zero. For a given control parameter, we have computed the average entropy for a set of 1000 different random initial conditions. The results are shown in Fig. 5. As expected, the smallest value of entropy is obtained when x is exactly one and the billiard is an equilateral triangle. The entropy grows quickly for values of x close to one. For example, lets consider x = 0.99 where the entropy is close to the 55% of its maximum theoretical value. For values of x close to zero, the entropy reaches its saturate value which is about the 70% of S_max. As shown in Fig. 3, for values of x close to zero (DSRC billiard) the trajectories of the particle are more complex than the ones found for x close to one (triangular billiard).

3.1.2 Lyapunov exponent

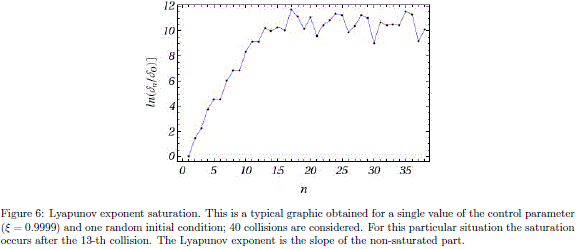
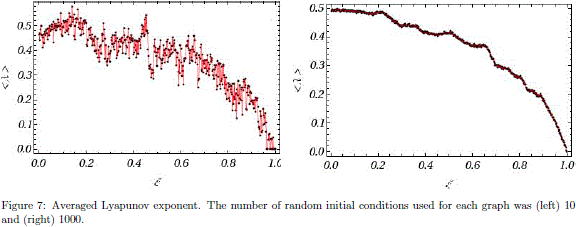
The Lyapunov exponent l is used as a measure of divergence between the trajectories of a couple of infinitesimal close initial conditions in the phase space. Usually, l is calculated as a function of time. However, the time is not a suitable parameter to compute l in billiard systems since the particle movement is linear between collisions and as consequence the distance between trajectories diverges linearly. Instead of the time, the collision index n was used as parameter. The sensibility to small changes in the initial conditions is characterized by d_n = d₀ exp (ln) where dn is the absolute value of the difference between the incident angles of nearby initial conditions after n collisions. The typical behaviour of l for a pair of nearby initial conditions is shown in Fig. 6. Note that after few collisions l reaches its maximal value, i.e., the exponent saturates. For a couple of close random initial conditions, the trajectories were generated and the Lyapunov exponent was computed, see Fig. 6 (left). In order to avoid the dependence with the initial conditions the Lyapunov exponent was averaged for several couples of initial conditions. The behaviour of l for different values of x is shown if Fig. 7 (right). Note that the Lyapunov exponent shown in Fig.7 (right) does not decrease monotonically and is not as smooth as the entropy of Fig. 5. This happens even if the number of pairs of initial conditions is increased. This is not an unexpected result because not all sets of initial conditions reach saturation after the same number of collisions. However, Fig. 7 captures an important feature of the billiard: as the half stadium appears over one side of the original equilateral triangle, then the Lyapunov exponent increases, indicating sensibility to the initial conditions, even for values of x close to one.

4 Quantum diamond-shaped billiard with rounded crown: Finite Difference Method Implementation

In previous section, the chaotic behaviour of the classical system was described in terms of the trajectories, the lyapunov exponents and the entropy of the distribution of incident angles. In the quantum version of the problem, the signatures of chaos are described in terms of the spacing distribution between adjacent eigenvalues and through the scarring of wave functions. The eigenvalues and eigen-functions of the Hamiltonian are typically calculated by using the finite element method (FEM) [33]. However, we prefer to use the finite difference method (FDM) to express the Hamiltonian as a matrix and then solve the resulting eigenvalue problem. The FDM is described in Appendix. In order to test the validity of the numerical results we compared them with the exact ones for the equilateral triangular billiard. The triangular billiard is integrable and the expression for the energy levels is well known [35]

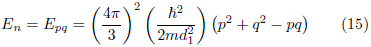
where d₁ is the edge length when x = 1, p and q are positive integers which satisfy q ∈ [1, p/2]. A comparison of the numerical and analytic energy levels is shown in Table 1. The relative error is small in all cases.

One advantage of the FDM lies in the fact that Hamiltonian is computed by the direct evaluation of the potential and some Kronecker deltas. As consequence, it is possible to build a Hamiltonian matrix with size 11000 × 11000 which in a personal computer (an i7 processor in our case) can be diagonalized with the Fortran Lapack package in less than 25 minutes. In order to check the accuracy of the results, a comparison with the energy staircase function N (E) with the Weyl-type formula was performed. N (E) gives the number of energy levels below the energy value E. N (E) is defined by

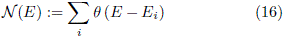
where q(x) is the step function. The analytical result for a two-dimensional billiard with area A and perimeter P is given by [36, 37, 38, 39]

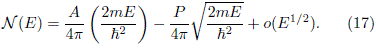
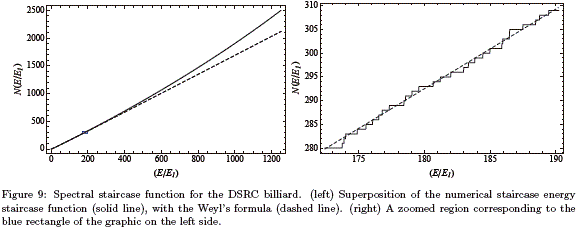
The Weyl formula is only valid in the semiclassical limit, i.e., for high energy levels. In Figure 9 we have superposed the numerical result of the energy staircase function with the one provided by (17). The agreement is very good for energy values E such E/E₁ < 500 where E₁ is the ground state. The differences between the numerical results and the theoretical prediction for high energies is due to the use of a discrete Hamiltonian with finite dimension instead of the exact Hamiltonian which has infinite dimension. Then, it is not surprising that the discretization procedure is not able to describe properly wavefunctions for high energies. These states have very small wavelength oscillations. For this reason, to calculate the wavefunctions for large energy it is necessary to increase of the number of points of the mesh. The number of points taken in our mesh is ∼ 11000, as consequence, only the first ∼ 200 computed states are reliable.

Other typical signature of chaos in quantum billiards is the scar identification in the semiclassical regime, i.e., for large values of energy. One of the most widely used method to scar identification is the improved Heller' s PWDM (Heller' s plane wave decomposition method) [40]. This method avoids the computation of the eigenvectors near to the ground state calculating directly the states with high quantum numbers. We used the finite difference method in order to diagonalize quantum DSRC billiard. Some of the first excited states of this billiard are shown in Fig. 8. This states are symmetric or antisymmetric with respect to the symmetry axis of the billiard. This ensures that the square of the wavefunctions is always symmetric with respect to this axis.

5 Quantum diamond-shaped billiard with rounded crown: level statistics

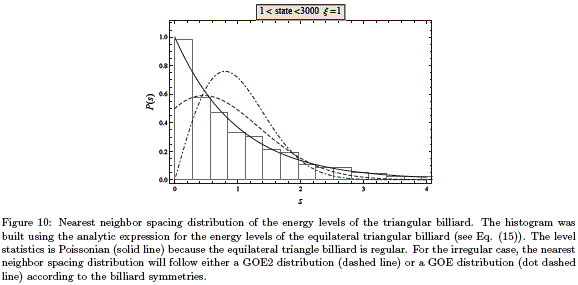
Several experiments with quantum hard wall billiards were performed in the nineties. One example is given by the microwave resonators, which use the equivalence between the stationary Scrödinger equation with the Helmholtz equation to study chaos in quantum billiards using electromagnetic waves [41]. Other devices used in the study of quantum chaos were the semiconductors billiards, which are essentially open quantum cavities that permit a current flow through two contact points. These systems are different from a quantum billiard, because the later is a completely closed system which confines the particle inside of it. However, if the size of the quantum open cavity is much smaller than the mean free path of the electrons, then the behaviour of both systems are similar. For example, they share the same energy level statistics and the scarring of the wavefunction [33]. For Hamiltonian systems such as the one described in this paper, the spacing distribution of the energy levels, P (s), is a feature which characterize the spectrum of a system with regular or chaotic classical analogue. According to the Bohigas-Giannoni-Schmit conjecture [42] the spectra of a time-reversal-invariant system with classical chaotic counterpart follows a Gaussian Orthogonal Ensamble (GOE) distribution. On the other hand, if the classical analogue is regular, the spectrum is characterized by a Poisson distribution (see Fig. 10). This conjecture has been tested in a variety of systems including billiards [1, 4, 5, 16, 7, 30].

The DSRC billiard has a mirror reflection symmetry axis. For this reason, there are two set of states each one related to a symmetry class. Lets name them for instance, odd and even eigenstates. The general expression of the nearest neighbour spacing distribution for a superposition of N independent spectra in the GOE statistics is given by [43]

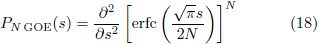
where s is the energy spacing between nearest neighbour levels, and erfc(s) is the complementary error function. The spacing distribution for N = 2 is

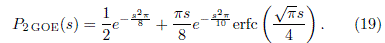
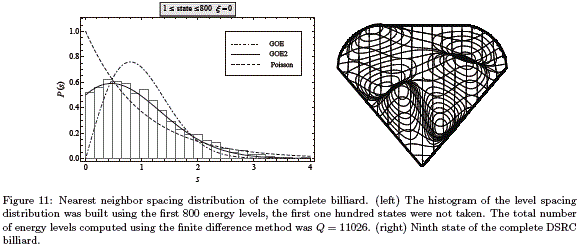
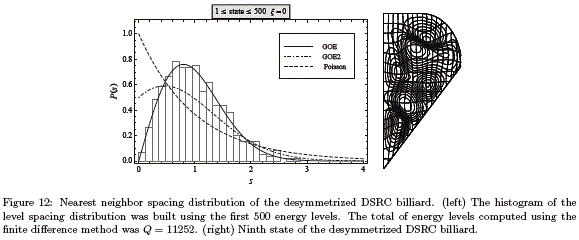
In Fig. 11 it is shown the nearest neighbour spacing distribution for the DSRC billiard which, as expected, is well fitted by the P_2GOE (GOE2) distribution. There are two ways to recover the GOE distribution: the first one is classify the energy levels according to the parity of the eigenstates and then build the corresponding histogram with one of these two sets. The disadvantage of this method is that only takes into account approximately the half of the energy levels computed. The second method consists in statistical study of the spectrum corresponding to the desymmetrized billiard. In this case the billiard is desymmetrized by taking a half of it following the symmetry axis. As shown in Fig 12, the statistical behaviour of the energy levels obeys a GOE distribution.

Another important feature of quantum billiards with chaotic classical counterpart is the high concentration of the wavefunction amplitude along the classical periodic orbits. The phenomenon was initially observed by McDonald and Kaufman [44], and posteriorly in the Bunimovich billiard by Heller [45]. Heller called this phenomena a scar. The scarring of wavefunction does not appear in regular billiards such as the ones with rectangular, circular or equilateral triangle shapes. This phenomena is exclusive for billiards where their classical counterpart has chaotic behaviour. As the quantum numbers are increased, we expect to recover the classical properties of the system, which is, in some sense, the idea behind the correspondence principle. In a classical chaotic billiard, a trajectory which evolves from an arbitrary initial condition tends to fill the whole billiard. As consequence, a typical wavefunction do not have a significant localization. This is the more common situation for the irregular billiards. Nonetheless, for the special case of an unstable periodic orbit, it is possible to find a high probability density underlying such classical trajectory. This can be intuitively understood at least in the semiclassical limit. Some scars and bouncing ball states are shown in Fig. 13. The bouncing ball states have a well defined momentum, but not position. Then we can associate a set of classical periodic orbits to a single bouncing ball state. In contrast, a scar is related to a single unstable periodic orbit.

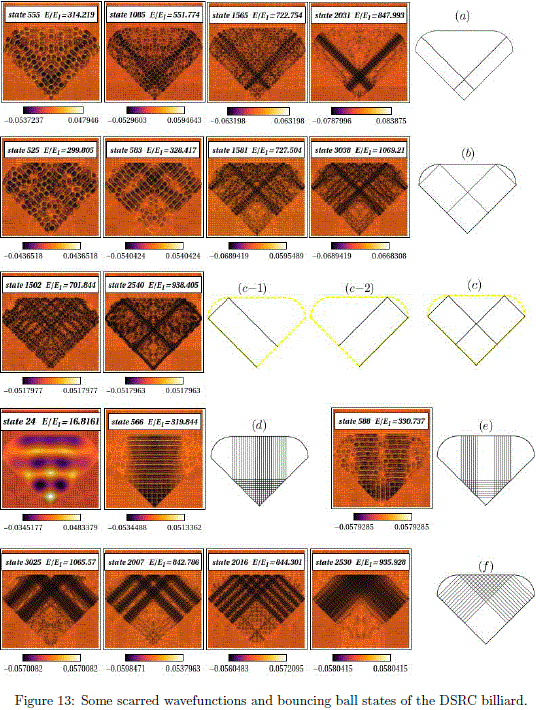
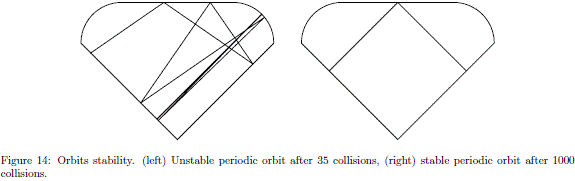
Example of scars are shown in Figs. 13-(a) and 13-(c). The stability of the orbits with lowest period is shown in Fig. 14.

6 Quantum diamond-shaped billiard with rounded crown: time evolution of the state vector

The time evolution of the state vector for quantum Hamiltonian systems is given by 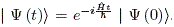. Expanding the state vector over the corresponding stationary states l Y (, 0)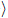 = S_s c_s l y^(s) 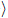, and taking the inner product with 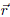l it is possible to find

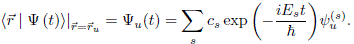
The components c_s can be calculated in the usual way. However, we prefer to use the lattice representation in order to calculate c_s in an easier way. Explicitly we found

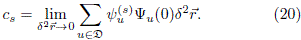
Since the eigenvectors of the Hamiltonian matrix, given by Eq. (29), are real, then the complex conjugation has been dropped. For large values of Q, it is possible to calculate cs from Eq. (6) ignoring the limit d²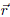 → 0. The same kind of approach can be used for the computation of the other expectation values. Using the index displacement transformations and central differences, the gradient evaluated at the point u(i, j) can be expressed as

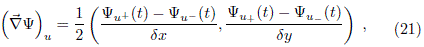
then, the mean value for momentum takes the form

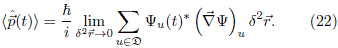
The real and imaginary part of Eq. (6) are given by

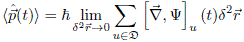
and

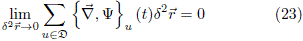
respectively. In Eq. (23) the following expressions were used

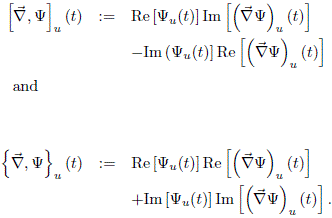
The imaginary part of (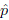(t)) is zero, then, we can use the second part of Eq. (23) to check the accuracy of the numerical solution. Similarly, for the mean value of the squared momentum we find

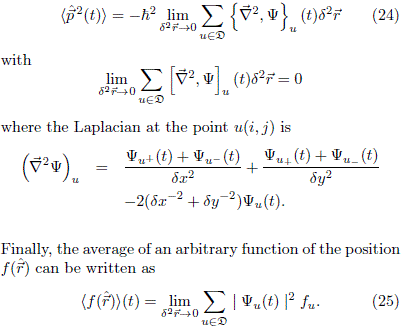
The time evolution of the expectation values of position for a system prepared in a well localized initial state at 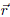⁰ = (x₀ , y₀ ) using a Gaussian wave packet

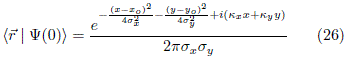
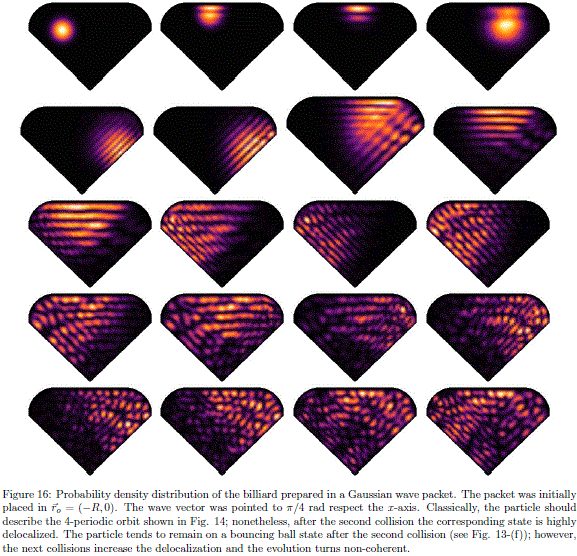
is shown in Fig. 15. = (k_x , k_y) is the wave vector, s_x and s_y are the standard deviations along x and y, respectively. As shown in Fig. 16, the wavepacket is destroyed after few collisions. However, this is not a consequence of the chaotic behaviour of the classical counterpart of the system. This irregular dynamics can be attributed to the non-coherent preparation of the initial state. This can be checked in the time evolution of the uncertainty products. The system must be prepared in a coherent state in order to reduce the uncertainty products to their minimum value 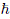/2. Nevertheless, even for simple cases (such as a particle in a rectangular domain) we do not have an analytical expression for the coherent states.

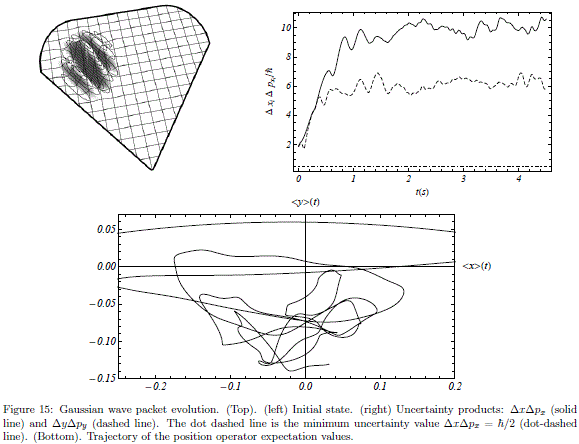
Classically, the chaotic behaviour of a specific system often emerges from the nonlinear nature of the system. Nevertheless, the classical and quantum billiards are an exception to this rule because of the absence of nonlinear terms in the equations that govern the dynamical behaviour of them. Indeed, the difficulty for quantum chaos determination does not lie in this lack of nonlinearity. The problem resides in the difficulty to find a correspondence between the classical and quantum behaviour far from the classical limit when the classical system evolves chaotically. The question is not solved by simply showing that the system satisfy the Bohigas-Giannoni-Schmit conjecture because the nearest neighbor spacing distribution is just a semiclassical result. The analysis of the time evolution of the expectation value of the position operator is an alternative to study the correspondence between the classical and quantum systems in the irregular regime. However, this approach frequently is not successful because quantum systems evolve in a non-coherent way when their classical counterparts are chaotic. For this reason sometimes the sensibility of quantum Hamiltonian systems is studied by perturbing the Hamiltonian instead of changing the initial state [46].

7 Concluding remarks

The classical and quantum DSRC billiard was studied through some quantities. In particular, we calculate the entropy, the Lyapunov exponent and some trajectories for the classical problem. The chaotic behaviour for the classical system emerges even for values of x close to one where the shape of the billiar is quite similar to an regular equilateral triangle. The entropy and the Lyapunov exponent grow when a half of stadium is introduced in one side of the triangular billiard. If the control parameter is set far enough from one, for example in the interval 0.8 ≤ x ≤ 1, then the entropy practically is a 70% of S_max. This en- tropy value is relatively far from its maximum because the DSRC billiard does not have dispersive frontiers as other billiards, e.g. Sinai billiard. Nonetheless, it is enough to ensure a great irregularity in the classical trajectories.

The finite difference method provides an alternative approach to solve the quantum problem. The DSRC shape billiard has a mirror reflecting symmetry. Because of this, the energy levels split in two different symmetry classes according to the wavefunction parity. As consequence, P (s) for the complete billiard is given by a GOE2 distribution. If DSRC billiard is desymmetrized, then the level statistics follows a GOE distribution. On the other hand, the classical behaviour is regular when the control parameter is set to one. Consequently, for x = 1 the distribution of energy levels is Poissonian for the quantum billiard. Therefore, the results are according to the Bohigas-Giannoni-Schmit conjecture.

We found scarred states in the quantum DSRC billiard, as well as bouncing ball states with their corresponding classical stable periodic orbits. These results agree with those reported previously for other Hamiltonian systems. In the last section, a practical method to compute the time evolution of the state vector was described. This method uses the lattice discretization along with the finite difference approach.

Acknowledgments

This work was supported by ECOS NORD/COLCIENCIAS- MEN-ICETEX. D. L. González was supported by the Vicerrectoría de investigaciones de la Universidad del Valle and the NSF-MRSEC at the University of Maryland, Grant No. DMR05-20471.

Appendix: The finite difference method

For simplicity we start with a rectangular domain. The discretization of the domain is shown in Fig. 17-left. A point at the position 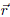ij can be labelled in one of these ways, with pair (i, j) or by using a single index u. The second option is used in order to avoid the impractical use of four indices in the Hamiltonian matrix. It is easy to build a single-valued function u = u(i, j) which maps the pair of indices (i, j) to the index u. We refer to this procedure as first indexing. The time independent Schrödinger equation is evaluated at the point u(i, j) according to

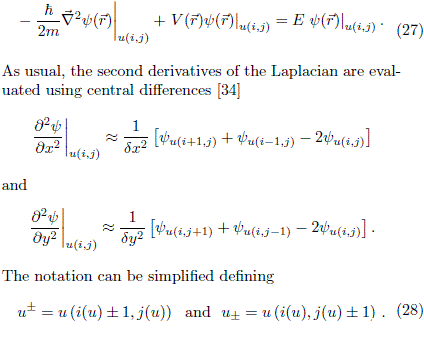
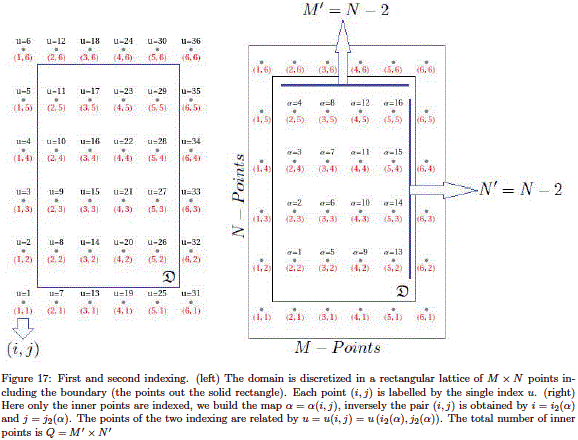
Note that u^± and u^± give horizontal and vertical displacements from the point (i, j) on the lattice, respectively. Using this notation, Eq. (27) can be written as

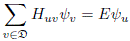
where H_uv is the discrete version of the Hamiltonian. Explicitly, H_uv is given by

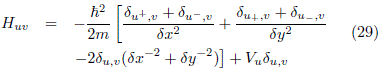
Note that repeated indices in the last term of Eq. (29) do not involve sum over them. For points along the boundary ∂D, we performed a second indexing (see Fig. 17-right). For these points, the eigenvalue equation can be written as

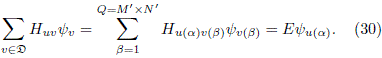
The eigenvalues and eigenvectors of the Hamiltonian H_ab are obtained numerically. Commonly, the packages of matrix diagonalization arrange the eigenvectors in a matrix, let us call it M_ab with a, b = 1,. .., Q. If the eigenvectors are arranged in the columns of such matrix, then the state s evaluated at the point a is y_a^(s) = M_as with (s = 1, 2,. .., Q). In order to return to the initial labelling we write y_ij^(s) = M_a(i,j),s if 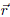_ij ∈ D, 0, otherwise. The generalization to billiards with different shapes does not represent considerable difficulties. It is possible to place the boundary of the billiard over a rectangular grid and take into account only the points inside of ∂D. After the identification of the boundary points, the inner points (say Q inner points) are enumerated first (u = 1, 2, ..., Q). Once this procedure is accomplished, the points along the boundary are enumerated. Some grids with different values of Q for the DSRC billiard are shown in Fig. 18.

Competing interests: The authors have declared that no competing interests exist.

References

[1] B. Dietz, T. Friedrich, M. Miski-Oglu, A. Richter, and F. Schfer. (2007) Spectral properties of Bunimovich mushroom billiards. Phys. Rev. E, 75, 035203.         [ Links ]

[2] B. Dietz, T. Friedrich, M. Miski-Oglu, A. Richter, T. H. Seligman, and K. Zapfe. (2006). Nonperiodic echoes from mushroom billiard hats. Phys. Rev. E, 74, 056207.         [ Links ]

[3] T. Miyaguchi. (2007). Escape time statistics for mushroom billiards. Phys. Rev. E, 75, 066215.         [ Links ]

[4] F. M. de Aguiar. (2008). Quantum properties of irrational triangular billiards Phys. Rev. E, 77, 036201.         [ Links ]

[5] T. Araújo Lima, S. Rodríguez-Pérez, and F. M. de Aguiar. (2013). Ergodicity and quantum correlations in irrational triangular billiards. Phys. Rev. E, 87, 062902.         [ Links ]

[6] T. Araújo Lima and F. M. de Aguiar. (2015). Classical billiards and quantum fluids. Phys. Rev. E, 91, 012923.         [ Links ]

[7] V. Lopac, I. Mrkonjíc and D. Radíc. (1999) Electron energy level statistics in graphene quantum dots. Phys. Rev. E, 59, 303.         [ Links ]

[8] V. Lopac and A. Simíc. (2011). Communications in Nonlinear Science and Numerical Simulation, Vol. 16, Issue 1        [ Links ]

[9] V. Lopac, I. Mrkonjíc and D. Radíc. (2001). Recurrence of particles in static and time varying oval billiards. Phys. Rev. E, 64, 016214.         [ Links ]

[10] V. Lopac, I. Mrkonjíc and D. Radíc. (2002). Phys. Rev. E, 66, 036202.         [ Links ]

[11] J. Chen, L. Mohr, Hong-Kun Zhang and Pengfei Zhang. (2013). Chaos, 23, 043137.         [ Links ]

[12] M. Sieber and F. Steiner. (1990). Physica D. Classical and quantum mechanics of a strongly chaotic billiard system. 44.         [ Links ]

[13] S. Ree and L. E. Reichl. (1999). Phys. Rev. E, 60, 1607.         [ Links ]

[14] T. Szeredi and D. A. Goodings. (1993). Classical and quantum chaos of the wedge billiard. II. Quantum mechanics and quantization rules. Phys. Rev. E, 48, 3529.         [ Links ]

[15] T. Szeredi and D. A. Goodings. (1993). Classical and quantum chaos of the wedge billiard. I. Classical mechanics. Phys. Rev. E 48, 3518.         [ Links ]

[16] A. Bäcker, F. Steiner, and P. Stifter. (1995). Phys. Rev. E 52, 2463.         [ Links ]

[17] Wenjun Li, L. E. Reichl, and Biao Wu. (2002). Quantum chaos in a ripple billiard. Phys. Rev. E 65, 056220.         [ Links ]

[18] A. Kudrolli, S. Sridhar, Akhilesh Pandey and Ramakrishna Ramaswamy. (1994). Signatures of chaos in quantum billiards: Microwave experiments. Phys. Rev. E 49, R11(R)        [ Links ]

[19] S. Hemmady, J. Hart, X. Zheng, T. Antonsen, E. Ott and S. Anlage. (2006). Phys. Rev. B, 74, 195326.         [ Links ]

[20] S. Schlunk, M. d' Arcy, S. Gardiner, D. Cassettari, R. Godun, and G. Summy. (2003).Phys. Rev. Lett., 90, 054101.         [ Links ]

[21] Y. H. Kim, M. Barth, H.J. Stöckmann. (2002), and J. P. Bird. Phys. Rev. B, 65, 165317.         [ Links ]

[22] L. Sirko and P. M. Koch. (1996). Phys. Rev. E 54, R21(R).         [ Links ]

[23] K. F. Berggren and Z. Li Ji. (1996). Chaos, 6, 543.         [ Links ]

[24] A. Kudrolli, V. Kidambi, and S. Sridhar. (1995). Phys. Rev. Lett., 75, 822.         [ Links ]

[25] S. Deus, P. Koch, and L. Sirko. (1995). Phys. Rev. E, 52, 1146.         [ Links ]

[26] T. Prosen and M. Robnik. (1993). J. Phys. A: Math. Gen., 26.         [ Links ]

[27] O. Bohigas, M.J. Giannoni and C. Schmit. (1981). Phys. Rev. Lett., 52.         [ Links ]

[28] T.A. Brody. (1973). Lett. Nuovo Cimento, 7 .         [ Links ]

[29] G. Cassati and T. Prosen. (1999). Physica D, 131.         [ Links ]

[30] V. Andreev, O. Agam, B. D. Simons, and B. L. Altshuler. (1996). Quantum Chaos, Phys. Rev. Lett. 76, 3947.         [ Links ]

[31] M. L. Mehta. (2004). Random Matrices, Academic Press, 2d Ed.         [ Links ]

[32] F. Haake. (2010). Quantum Signatures of Chaos. Springer-Verlag Berlin Heidelberg, 3rd Ed.         [ Links ]

[33] R. Akis and D. K. Ferry, (1998). Wave Function Scarring Effects in Open Ballistic Quantum Cavities, VLSI Design, 8, 307.         [ Links ]

[34] R. Garg. (2008). Analytical and Computational Methods in Electromagnetics, Artech House.         [ Links ]

[35] M. Brack, R. Bhaduri. (1997). Semiclassical Physics, Addison-Wesley Publishing Company.         [ Links ]

[36] H. Weyl, Göttingen Nach. (1911). 110.         [ Links ]

[37] H. Weyl. (1946). The Classical Groups: Their Invariants and Representations, Princeton university press        [ Links ]

[38] M. Kac. (1966). Can One Hear the Shape of a Drum?, Amer. Math. Month. 73, 1        [ Links ]

[39] R. W. Robinett. (2003). Quantum mechanics of the two-dimensional circular billiard plus baffle system and half-integral angular momentum, Eur. J. Phys. 24, 231-243         [ Links ]

[40] B. Li and B. Hu. (1998). Statistical Analysis of Scars in Stadium Billiard. J. Phys. A: Math. Gen. 31, 483.         [ Links ]

[41] H. J. Stockman and D. K. Ferry. (2006). Chaos in Microwave resonators, Séminaire Poincaré IX, 1        [ Links ]

[42] O. Bohigas, M. J. Giannoni, and C. Schmit. (1984) Characterization of Chaotic Quantum Spectra and Universality of Level Fluctuation Laws, Phys. Rev. Lett. 52, 14.         [ Links ]

[43] I. Kosztin and K. Schulten. (1997). Boundary Integral Method for Stationary States of Two- Dimensional Quantum Systems, Int. J. Mod. Phys. C 8, 293-325.         [ Links ]

[44] S. W. McDonald and A. N. Kaufman. (1979). Spectrum and eigenfunctions for a hamiltonian with stochastic trajectories, Phys. Rev. Lett. 42, 1189.         [ Links ]

[45] E. J. Heller. (1984) .Bound-State Eigenfunctions of Classically Chaotic Hamiltonian Systems: Scars of Periodic Orbits. Phys. Rev. Lett. 53, 1515.         [ Links ]

[46] D. A. Wisniacki, E. G. Vergini, H. M. Pastawski, and F. M. Cucchietti. (2002). Sensitivity to perturbations in a quantum chaotic billiard, Phys. Rev. E 65, 055206(R).         [ Links ]