doi: http://dx.doi.org/10.18257/raccefyn.185

Observatorio Astronómico Nacional, Facultad de Ciencias, Sede Bogotá, Universidad Nacional de Colombia. Bogotá, Colombia. * Correspondencia: José Gregorio Portilla, jgportillab@unal.edu.co

Recibido: 19 de enero de 2015; Aceptado: 18 de mayo de 2015.

Resumen

Presentamos una descripción de las tres soluciones analíticas del problema de los dos cuerpos clásico que corresponden al caso del momentum angular cero. Se presentan las constantes de integración y su relación con la forma y orientación de la trayectoria en el espacio. Igualmente se propone un método de determinación orbital para un objeto que cae en línea recta hacia el Sol con base en dos observaciones angulares realizadas desde la Tierra.

Palabras clave. Problema de dos cuerpos, movimiento rectilíneo, determinación orbital.

Abstract

We present a description of the three analytical solutions of the two-body problem associated to the case of angular momentum equal to zero. The constants of integration and their relationship with the shape and orientation of the trajectory are showed. Additionally, we propose a method for determining a rectilinear trajectory of a body plunging into the sun based on two angular observations performed from the Earth.

Key words. Two-body problem, rectilinear motion, orbit determination.

Introducción

El problema de los dos cuerpos es, en mecánica celeste clásica, el sistema más extensivamente estudiado, no solo por su simplicidad sino, además, por ser uno de los pocos problemas cuya solución completa se logra a través de la obtención de cantidades conservadas (denominadas integrales de movimiento). De hecho, algunas de las técnicas de perturbación desarrolladas para abordar problemas de tres o más cuerpos, descansan en la solución del problema de los dos cuerpos.

La ecuación diferencial de movimiento relativo de un cuerpo de masa m₂ con relación al cuerpo de masa m₁ es, en notación vectorial:

donde 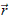es el vector de posición relativo (con componentes cartesianas x, y, z y la masa m₁ colocada en el origen de coordenadas), r su norma y m = G(m₁ + m₂) donde, a la vez, G es la constante de gravitación universal.

Como se sabe, la anterior ecuación admite la integral del momentum angular por unidad de masa , esto es,

donde 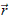es el vector velocidad (un punto sobre la cantidad representa la primera derivada temporal de dicha cantidad; dos puntos, dos derivadas temporales). La existencia de estas tres constantes (pues en el espacio tenemos que tiene por componentes h₁, h₂, h₃, de modo tal que h² = h₁² + h₂² + h₃²) indica que el movimiento se verifica en un plano y, por ende, el sistema puede resolverse utilizando dos grados de libertad. Ahora bien, nótese que el momentum angular puede ser cero, lo que ocurre de ser la velocidad nula o en dirección exclusivamente radial.

De forma casi que universal, la literatura describe extensivamente las soluciones que dan lugar a aquellas trayectorias que se obtienen cuando el momentum angular es diferente de cero que, como es bien conocido, corresponden a las secciones cónicas: elipse, parábola e hipérbola. En particular, se hace énfasis en la primera ya que con dicha solución es posible llegar a las consabidas leyes de Kepler. Sin embargo, son muy pocos (poquísimos) los autores que hacen referencia al caso más obvio y directo del que se pueda esperar de una ley de fuerza que es radial y de atracción: el movimiento en línea recta, el cual corresponde al caso del momentum angular nulo (ver Taff (1985), Chandrasekhar (1995)). La razón es simple: a pesar de que es un movimiento con el que alguien aquí en la Tierra está muy familiarizado –basta con observar objetos soltados desde determinada altura y que caen libremente en dirección al suelo–, no se ha registrado el caso de un objeto que describa una trayectoria en línea recta en dirección hacia el centro de Sol. Lo más parecido a esta situación, que se sepa, es el caso de los cometas rasantes al Sol los cuales, por su trayectoria fuertemente elíptica o parabólica, y su cercanía al Sol en instantes previos a su perihelio (algunos de los cuales resultan destruidos o seriamente afectados), pueden considerarse, en primer grado de aproximación, como objetos en caída libre hacia el Sol. De todas formas, sería prematuro descartar la existencia de objetos, posiblemente cometas, que puedan seguir trayectorias en caída libre en dirección al centro del Sol.

El propósito de esta comunicación es doble: primero, exponer con suficientemente generalidad el movimiento en línea recta de m₂ con relación a m₁; como veremos, dependiendo de las condiciones iniciales, se tendrá una situación análoga a la de las cónicas: puede darse un movimiento i) acotado (equivalente al caso elíptico), ii) de escape con velocidad mínima (equivalente al parabólico) y iii) de escape con exceso de velocidad (equivalente al hiperbólico). La exposición de tal solución se hace en términos de la obtención de todas las integrales de movimiento (energía, momentum angular y vector de Laplace-Runge-Lenz) y, a diferencia de las anteriores descripciones, se muestra la conexión entre las constantes y los ángulos que definen la orientación de la órbita en el espacio.

Segundo, se propone un método para obtener los parámetros orbitales que definen una trayectoria de un objeto en caída libre con respecto al Sol observado en dos tiempos distintos desde la Tierra. Hasta donde sabemos, los métodos de determinación orbital estudiados hasta ahora parten del supuesto de que el objeto en cuestión se desplaza en una cónica.

En lo que sigue se muestran inicialmente algunos aspectos básicos del problema de dos cuerpos, para luego continuar con una exposición de la generalidad del movimiento rectilíneo, describiendo los casos posibles que dependen de las condiciones iniciales del problema. Posteriormente se describe cómo es posible la determinación orbital de un objeto en movimiento rectilíneo (con velocidad nula en el infinito o, lo que es lo mismo, con velocidad de escape mínima en el infinito) siendo observado desde la Tierra en dos tiempos distintos incluyéndose, además, un ejemplo.

Movimiento en el plano

Se vio en la sección anterior que la existencia del vector , por ser constante (y ortogonal al plano formado por el vector posición y velocidad), implica movimiento en un plano. En términos de las componentes del vector posición y velocidad, las componentes cartesianas de dicho vector están dadas por:

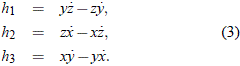
Adicionalmente, la ecuación (1) admite otra integral vectorial denominada vector de Laplace-Runge-Lenz, dado por:

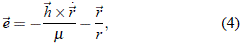
que se conoce también como vector excentricidad, el cual está contenido en el plano de la trayectoria y en dirección de la línea de las ápsides (la línea que une el centro de la cónica con los focos). Las componentes cartesianas de dicho vector (e₁, e₂ , e₃) de modo tal que: e² = e₁² + e₂² + e₃², están dadas entonces por:

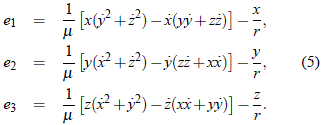
Puesto que es ortogonal al plano de la órbita y 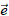está en dirección de dicho plano se tendrá que · 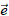= 0y así:

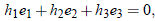
lo que significa que una de las constantes puede colocarse en términos de las otras cinco.

Utilizando coordenadas polares (r, q) y recordando que el vector velocidad en tales coordenadas es: 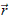= 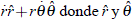son vectores unitarios en la dirección radial y tangencial a esta, respectivamente, se tiene, de acuerdo con (2):

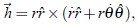
de la que se desprende que:

De igual modo, teniendo en cuenta la expresión del vector aceleración en coordenadas polares 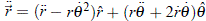, al reemplazar este vector en la ecuación (1), se tiene:

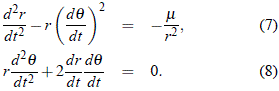
La literatura es rebosante en describir cómo, con estas dos últimas ecuaciones, y cuando h ≠ 0, es posible determinar no solo que el diferencial del área es proporcional al diferencial de tiempo (segunda ley de Kepler) sino además que el movimiento de m₂ con respecto a m₁ es una cónica con uno de los focos ubicado en m₁. Remitimos al lector interesado en ese aspecto a cualquier libro introductorio de mecánica celeste. En la presente comunicación nos concentramos solo en el caso cuando h = 0.

Movimiento rectilíneo

Es claro, de la ecuación (2), que h = 0 ocurre cuando el vector velocidad es nulo, o dicho vector está en la misma dirección del vector posición. Al mismo tiempo, se tendrá que (6) se convierte en dq /dt = 0, esto es, q = q₀ (q₀ siendo una constante), lo que significa que el movimiento se puede expresar con un único grado de libertad, esto es, el movimiento se verifica en línea recta. En tal caso, el problema se soluciona encontrando funcionalmente la variable r en términos del tiempo.

La solución es como sigue. Al tener q = 0, la ecuación (7) se reduce a:

y dado que es lícito hacer d²r/dt² = (dr/dt)(d²r/dt²)(dt/dr), entonces:

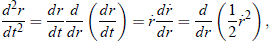
pero, al mismo tiempo, como:

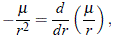
se deduce entonces que, al reemplazar estas dos últimas expresiones en (9), se obtiene:

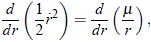
que al integrar da:

donde E' es una constante de movimiento que tiene unidades de energía sobre unidad de masa. Al multiplicar a ambos lados por la denominada masa reducida del sistema (m₁ m₂/(m₁ + m₂)), podemos escribir:

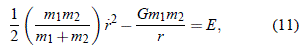
donde es claro que el primer término es la energía cinética; el segundo término es la energía potencial gravitacional y E = E'm₁m₂ /(m₁ + m₂) es entonces la energía total del sistema.

Dependiendo de los valores que se asuman para r y 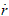en un instante de tiempo inicial t₀, esto es, para r₀ y 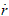₀, se tendrá que el valor de E puede ser positivo, negativo o cero. En el caso en el que E > 0 el objeto tiene energía cinética suficiente como para vencer la atracción gravitacional y escapará (es el equivalente de la órbita hiperbólica con h ≠ 0). Para el caso E = 0 el valor de la velocidad inicial es el mínimo suficiente como para que la energía potencial se haga cero en el infinito y, por lo tanto, también escapa (es el equivalente de la órbita parabólica con h ≠ 0). Por último, para el caso E < 0 la energía potencial es mayor que la cinética y, en consecuencia, el movimiento del objeto está acotado (es el equivalente de la órbita elíptica con h ≠ 0). Por supuesto, esto último implica una colisión entre ambos objetos. A continuación pasaremos a resolver cada uno de los tres casos.

Caso con E' = 0

Para este caso se puede presentar cualquiera de los siguientes dos escenarios: i) que el objeto tenga una velocidad cero en el infinito y que esté cayendo en dirección hacia m₁, en cuyo caso 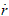< 0; ii) que el objeto posea una velocidad no nula en el tiempo t₀ y que sea justa la necesaria para que escape en el infinito, y se tendrá 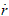> 0. Para ambas situaciones, el valor de la energía potencial es igual en valor absoluto a la energía cinética y la energía total es cero. De ese modo, la ecuación (10) queda convertida en:

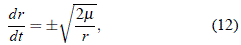
en donde el signo positivo se toma si el objeto está escapando hacia el infinito y el negativo si está cayendo en dirección hacia m₁.

Al separar las variables:

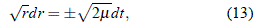
e integrando con los límites inferiores t₀ para un r₀, llegamos a:

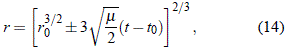
ecuación que permite obtener la distancia r en función del tiempo t para unas condiciones iniciales dadas y se ha de escoger adecuadamente el signo dependiendo de si el objeto está escapando o va en rumbo de colisión hacia m₁.

Caso con E' < 0

Cuando la energía potencial es mayor, en valor absoluto, a la energía potencial se tendrá que E' < 0 y en tal caso el cuerpo de masa m₂, con independencia de la dirección de la velocidad, estará condenado a chocar invariablemente con m₁. En tal caso, la ecuación (10) queda, haciendo explícito el signo del valor de la energía total por unidad de masa:

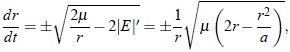
siendo

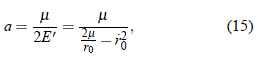
una constante que tiene unidades de distancia y que es positiva dado que en este caso 2m/r₀ > 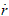₀². Una distribución conveniente de los términos permite escribir:

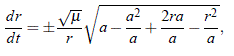
y de ese modo colocar:

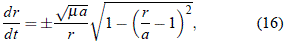
o mejor, al separar las variables:

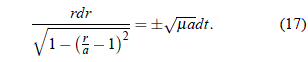
Introduciendo la variable auxiliar de integración f como

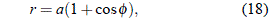
por lo que: dr = –a sen f df, y por lo tanto la ecuación (17) queda en la nueva variable como:

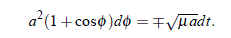
Integrando con límites inferiores f₀ (f₀ = cos^–1 [(r₀ /a) – 1)] para el tiempo t₀ obtenemos:

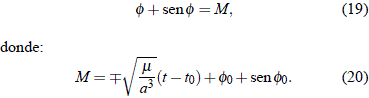
En la ecuación anterior, el signo positivo se toma si la velocidad inicial es negativa (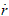₀ < 0) en tanto que el signo negativo se toma si la velocidad inicial es positiva (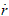₀ > 0).

La magnitud de la velocidad, dada por la ecuación (16), en términos de f es:

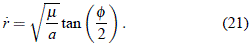
El procedimiento para hallar r (y 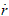) en función del tiempo es como sigue. Primeramente se calcula el valor de la constante a a partir de las condiciones iniciales de velocidad (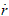₀ ) y posición (r₀) con ayuda de la ecuación (15); con ello, el valor de f₀ se calcula de inmediato. Seguidamente, por intermedio de (20), se determina la variable M, que es función lineal del tiempo. Luego se halla f mediante algún procedimiento numérico o iterativo en la ecuación (19) para luego determinar r mediante (18) y 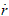mediante (21).

Un lector familiarizado con el caso del momentum angular no nulo puede advertir que tanto la variable M como la variable f desempeñan un rol equivalente al que hacen, respectivamente, la anomalía media y la anomalía excéntrica en la órbita elíptica, siendo la expresión (19) una variante de la denominada ecuación de Kepler.

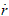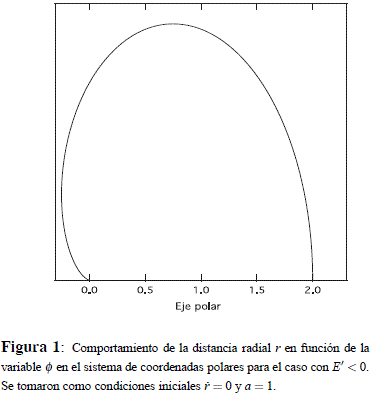
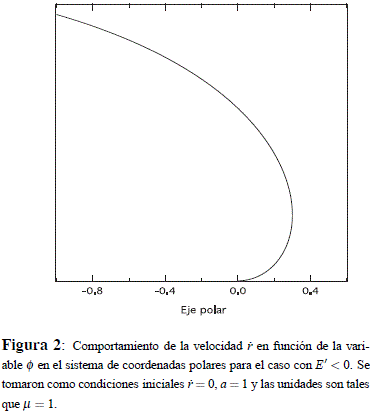
Un caso particular se tiene cuando la velocidad inicial es nula, esto es, ₀ = 0. En tal caso: a = r₀ /2; de ese modo f₀ = cos^–01(2 – 1), esto es, 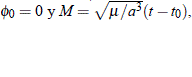ver las Figuras 1 y 2.

Caso con E' > 0

Este caso es semejante al anterior salvo que ahora hacemos explícito el signo positivo de E' , ya que la energía cinética es mayor que la energía potencial y, en consecuencia, si el objeto tiene la dirección correcta, escapa. Como antes, la ecuación (10) puede escribirse como (tomando solo el signo positivo, que es el que corresponde al caso práctico):

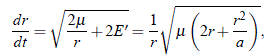
Siendo ahora

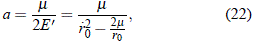
una constante positiva dado que 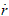₀² > 2m/r₀. Realizando, como antes, un acomodamiento conveniente de términos al interior del radicando podemos colocar:

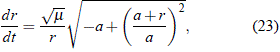
y al separar las variables se obtiene:

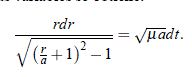
Introduciendo la variable auxiliar de integración F como

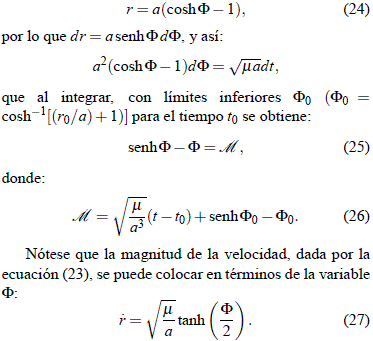
Un ejemplo

Para efectos de ilustrar el procedimiento de cálculo en las tres situaciones anteriores, mostramos a continuación un ejemplo. Supóngase que en un instante dado t₀ un objeto de masa infinitesimal está sometido a la atracción gravitacional del Sol y posee momentum angular nulo. Además, en dicho instante, se encuentra a 2 u.a. (unidades astronómicas) del Sol. Determinaremos la distancia a la que se encuentra dicho objeto en el instante t₀ + 20 días en cada una de las siguientes tres situaciones: i) = k (en u.a./d) en t₀; ii) = 0 en t₀; iii) = 2k (en u.a./d) en t₀, siendo k = √m = 0.01720209895 u.a.^3/2 d^–1, esto es, la conocida constante de Gauss.

El caso i) corresponde a E' = 0. De ahí que, de acuerdo con (14), se tenga que:

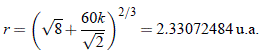
El caso ii) corresponde a E' < 0 dado que 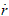= 0. Por lo tanto, a = 1 u.a., f₀ = 0 y M = 20k = 0.34404198. Utilizando un método numérico para la resolución de la ecuación (19), como, por ejemplo, el de Newton-Raphson (Pao, 1999) cuya convergencia es rápida, encontramos: f = 0.17244772. Nótese que los cálculos se están haciendo en radianes. Al reemplazar en (18) se tiene: r = 1.98516771 u.a.

El caso iii) corresponde a E' > 0. Es claro que a = 1/3 u.a., así como F₀ = cosh^–1 (7) = 2.63391579. Así, M = 6.08198200 y resolviendo numéricamente (25) se obtiene: F = 2.89038812; por lo tanto, de (24) se obtiene finalmente r = 2.67597486 u.a.

Constantes y la orientación en el espacio

Como ya se dijo, el movimiento rectilíneo implica momentum angular igual a cero (h = 0), esto es, cada constante del momentum angular cumple h₁ = h₂ = h₃ = 0. Pero, dado que h₁² + h₂² + h₃² = 0 se deduce que una de ellas, al menos funcionalmente hablando, puede expresarse en términos de las otras dos. Ahora bien, de las ecuaciones (4) y (5) se infiere que, si = 0, entonces: 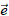= –rˆ, y así:

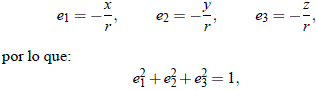
y de ese modo una de las componentes, digamos e₃, puede expresarse en términos de las otras dos (e₁ y e₂). Entonces, al definir una línea recta orientada de tal modo que pase por el origen, se requieren dos ángulos, que llamaremos W e i, expresados en un sistema de coordenadas cartesiano, tal y como se observa en la Figura 3; es evidente que:

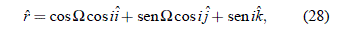
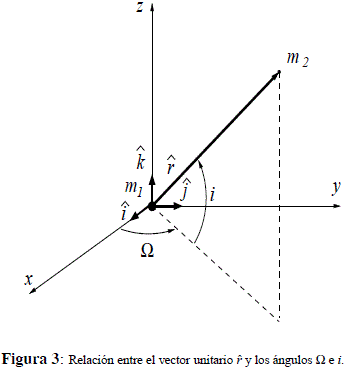
y de ese modo: e₁ = – cos W cos i, e₂ = – sen W cos i, e₃ = – sen i. Por lo tanto, la relación entre estos ángulos y las constantes e₁ y e₂ son:

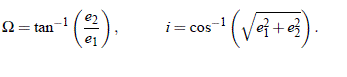
De ese modo, las seis constantes independientes que resuelven la ecuación (1) son: dos de las tres del momentun angular (digamos h₁ y h₂), dos de las tres del vector excentricidad (digamos e₁ y e₂), a, una distancia relacionada con la energía total (cuyo valor es infinito en el caso de escape con velocidad nula en el infinito) y la constante temporal t₀ que vincula los valores del vector posición y velocidad con una escala de tiempo dada. Por lo tanto, en el caso de la trayectoria rectilínea, podemos asumir que los elementos orbitales que definen la trayectoria del objeto están dados por: una distancia a (para los casos con E ' > 0 y E ' < 0), el valor de t₀ (para un r₀ dado) y los ángulos W e i. El caso de escape en el infinito (a = ∞) no requiere de un valor equivalente para hallar r o .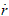

Determinado el valor de r para el tiempo requerido (según los casos particulares vistos en la sección anterior), los valores de las componentes cartesianas del vector posición respecto al sistema de coordenadas elegido, son:

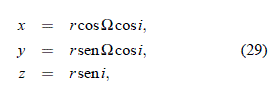
y, del mismo modo, con el valor dado de la velocidad para el tiempo de interés, los valores de las componentes del vector posición son:

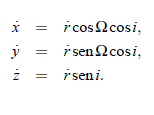
Determinación de una órbita rectilínea

Varios libros clásicos de mecánica celeste (por ejemplo Dubyago, 1961; McCuskey, 1963; Danby, 1970) exponen el problema de la determinación orbital consistente en hallar los elementos orbitales de un objeto sometido al campo gravitacional del Sol a partir de dos o más observaciones que se hacen del objeto visto desde la Tierra. De forma invariable dichos libros describen el método de Gauss y, algunos otros, el de Laplace, en los que se asume de entrada que el objeto se desplaza en órbita elíptica. Para algunos cometas se ajusta mejor asumir que la órbita es parabólica y se aplica el método de Olbers. El que se elija una u otra órbita lo determina qué también los elementos orbitales hallados permiten explicar los datos observacionales que se van realizando conforme transcurre el tiempo.

A continuación se propone un método de determinación de una trayectoria rectilínea de un objeto cayendo rumbo al Sol el cual es observado en dos ocasiones desde la Tierra. Para efectos de simplificar el procedimiento, se asume que el objeto viene cayendo desde el infinito (con velocidad nula), de modo tal que se puedan hacer las consideraciones vistas en el caso con E' = 0.

Supóngase que en dos instantes dados t₁ y t₂ se realizan observaciones de las coordenadas ecuatoriales absolutas, la ascensión recta y la declinación, i.e., a_k, d_k (con k = 1, 2) y, se suponen conocidos, para dichos tiempos, los vectores geocéntricos ecuatoriales del Sol ( con k = 1, 2) los cuales equivalen a _k = –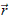'_TK), donde 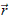'_TK son los vectores ecuatoriales heliocéntricos de la Tierra. Nótese que los vectores primados se están usando para indicar que están referenciados al plano del Ecuador Celeste. Como es costumbre en este tipo cálculos, la dificultad estriba en determinar las distancias geocéntricas y heliocéntricas en ambos tiempos de observación.

Por lo tanto, teniendo en cuenta la Figura 4, para ambas observaciones tenemos:

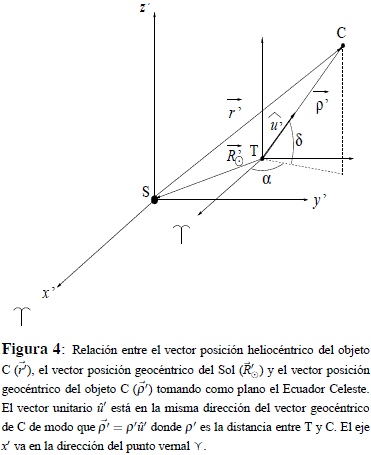
donde los vectores û'₁ y û'₂ son cantidades conocidas a través de:

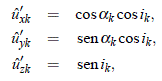
con k = 1, 2.

Como el movimiento es en línea recta, se tendrá que uno de los vectores heliocéntricos, digamos 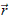' ₂, puede espresarse en términos del otro, del siguiente modo:

donde l es un número positivo. Por lo tanto, la ecuación para 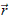'₂ puede escribirse entonces como:

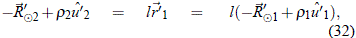
y eso permite escribir r₁û'₁ de la siguiente forma:

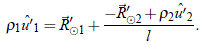
Multiplicando la anterior ecuación por û'₁· a ambos lados, tenemos:

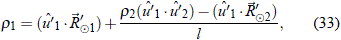
que tiene tres cantidades desconocidas: r₁ y r₂ y l. Pero, si ahora se multiplica la ecuación (32) por û'₂· a ambos lados se encuentra que:

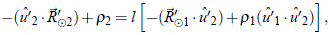
de la que, al despejar r₁, se obtiene:

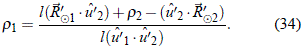
Igualando las expresiones (33) y (34), despejando r₂ y después de algo de álgebra, se obtiene:

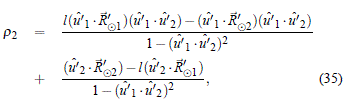
expresión de la que todos sus términos del lado derecho son conocidos exceptuando el valor de l.

Por otro lado, se puede relacionar geométricamente r₁ y r₁ junto con r₂ y r₂, con las distancias R'₁y R'₂del Sol del Sol a la Tierra, ver Figura 5, y de ese modo:

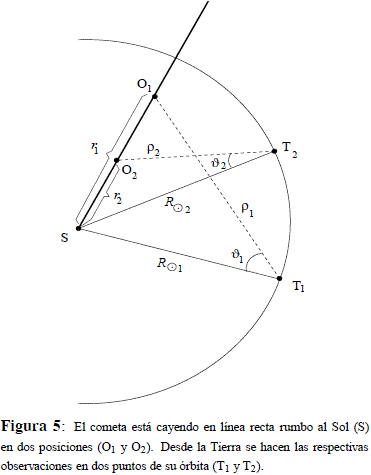
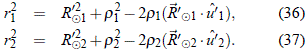
Como se supone que el objeto está cayendo con velocidad cero desde el infinito, existe una condición de carácter dinámico que relaciona r₁ y r₂, a saber, a través de la ecuación (14). De ese modo se tiene que:

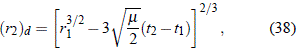
donde hemos colocado el signo negativo puesto que hemos asumido que el objeto se dirige hacia el Sol. El símbolo (r₂)_d indica el valor que ha de tener r2 basado en consideraciones dinámicas.

El proceso de la determinación de las cantidades r1, r1, r2, r2 se logra a través de un proceso iterativo. Se escoge un valor tentativo y realista de la cantidad l de forma tal que se pueda determinar r₂ a través de (35) y con éste, la cantidad r₁ y con éste,  se halla inmediatamente por medio de (34) lo que a la vez permite hallar las cantidades r₁ y r₂ a través de (36) y (37). El valor correcto de l (y de todas las demás cantidades) será aquel que permita satisfacer: r2 = (r2)_d.

Habiendo determinado las distancias geocéntricas r₁ y r₂, los vectores heliocéntricos ecuatoriales se pueden calcular a través de (30). Dado que se acostumbra a colocar los ángulos que definen la orientación de la órbita con respecto al plano fundamental (la Eclíptica), realizamos una rotación de cada uno de los vectores heliocéntricos un ángulo e alrededor del eje x', siendo e la oblicuidad e de la Eclíptica y obtener de ese modo los vectores heliocéntricos eclípticos 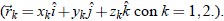Por lo tanto, ver por ejemplo Portilla (2009):

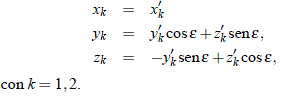
El cálculo de los ángulos W e i es inmediato, teniendo en cuenta las expresiones (29), y de ese modo:

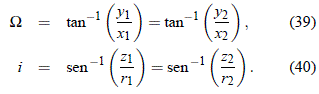
Como es fácil verificar, el tiempo en que ocurre el impacto con la superficie del Sol, suponiendo que el objeto aun no se haya sublimado por completo, es:

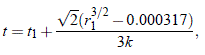
donde hemos tomado que el radio solar equivale a 0.00465 u.a.

Un ejemplo

El cometa ISON (C2012 S1) es un cometa de tipo rasante al Sol que se desintegró a finales del mes de noviembre de 2013. Numerosas observaciones indicaron que el objeto se ajustaba a una órbita de tipo hiperbólico con excentricidad de 1.000002. Su distancia al perihelio fue estimada en 0.01244 u.a., esto es, alrededor de 2.67 radios solares. Suponiendo que el objeto está cayendo en órbita rectilínea con velocidad nula en el infinito, determinar qué también se ajusta una trayectoria rectilínea frente a la trayectoria hiperbólica. Para tal efecto se hará uso de dos observaciones de varias realizadas realizadas al cometa¹ a mediados del mes de agosto de 2013 y que se escogieron libremente, ver Tabla 1, donde los tiempos están en fechas julianas (FJ).

Las componentes de los vectores heliocéntricos ecuatoriales de la Tierra, para ambos tiempos de observación, fueron tomados de la página de la Oficina de Longitudes² y pueden verse en la Tabla 2.

Con estos valores es directo obtener los términos conocidos de varias expresiones. De ese modo, las ecuaciones (35) y (34) quedan, respectivamente, como:

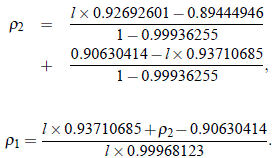
Igualmente, las ecuaciones (36) y (37) quedan como:

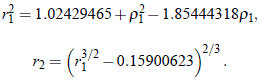
Ensayando diversos valores de l es fácil verificar que: r2 – (r₂)_d = 0 se logra con l = 0.96976273. De ese modo se obtiene entonces:

De ese modo, los valores de los vectores heliocéntricos eclípticos son, para ambos tiempos:

Conocidas estas componentes se pueden calcular los valores de W e i que, al tomar el promedio de los ángulos calculados con los dos vectores, dan: W = 112.48507610°, i = 5.44481777°. El tiempo de impacto, calculado con los valores de la primera observación, corresponde a una fecha juliana de 2456619.98027, esto es, a las 11^h 31^m de noviembre 23 de 2013. En realidad, el perihelio del cometa se verificó cinco días después, el 28 de noviembre. La tabla 4 contiene la posición del cometa ISON para el 5.051 de septiembre de 2013 (TU) calculada con los elementos aquí hallados y comparados con la posición observada en aquel día.

Nótese que al cabo de casi dos semanas de realizadas las observaciones, las diferencias entre los datos calculados (asumiendo solución lineal) con la trayectoria real del objeto ya son del orden de varios minutos de arco. Es de esperar una diferencia de este orden, ya que el cometa sí tiene momentum angular y se desplaza siguiendo una trayectoria hiperbólica. Sin embargo, si se tiene en consideración la enorme diferencia existente entre la complejidad del cálculo entre los métodos tradicionales de determinación orbital, con el mucho más simplificado método que aquí se ha propuesto, bien puede utilizarse como una primera introducción a la explicación de la determinación orbital para cometas que pasan rasantes al Sol.

Conclusiones

En esta comunicación se ha mostrado cómo encontrar la posición de un objeto en trayectoría en línea recta correspondiente al caso del momentum angular nulo en el problema de los dos cuerpos, para todo tipo de condiciones iniciales. Las soluciones se han obtenido de tal modo que guardan una analogía con las soluciones que corresponden al caso de momentum angular distinto de cero, esto es, a las cónicas. De igual modo, se hizo especial énfasis en visualizar la correspondencia entre las constantes del problema y su significado geométrico. Finalmente, se propuso un método para determinar la trayectoria de un objeto que se asume está en trayectoria de colisión rumbo al Sol, el cual puede, bajo cierto grado de aproximación, ser utilizado, sin invertir una gran dosis de cálculo, para determinar la órbita de un cometa rasante al Sol.

¹ http://www.minorplanetcenter.net/mpec/K13/K13Q27.html (consultado el 8 de noviembre de 2014).

² www.bdl.fr (consultado el 8 de noviembre de 2014).

Agradecimientos

El autor agradece las sugerencias y la lectura atenta del manuscrito por parte de un árbitro anónimo.

Conflicto de interés

El autor declara que no tienen ningún confiicto de interés.

Bibliografía

Chandrasekhar, S. 1995. Newton's Principia for the Common Reader, Clarendon Press, Oxford.         [ Links ]

Danby, J. M. A. 1970. Fundamentals of Celestial Mechanics, The MacMillan Co., New York.         [ Links ]

Dubyago, A. D. 1961. The Determination of Orbits, The MacMillan Co., New York.         [ Links ]

McCuskey, S. W. 1963. Introduction to Celestial Mechanics, Addison-Wesley Pub. Co., Reading, Massachusetts.         [ Links ]

Pao, Y. C. 1999. Engineering Analysis, CRC Press LLC, Boca Raton.         [ Links ]

Portilla, J. G. 2009. Elementos de Astronomía de Posición, Editorial Universidad Nacional de Colombia, Bogotá         [ Links ].

Taff, L. G., 1985. Celestial Mechanics, John Wiley & Sons, New York.         [ Links ]