Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista de la Academia Colombiana de Ciencias Exactas, Físicas y Naturales
Print version ISSN 0370-3908
Rev. acad. colomb. cienc. exact. fis. nat. vol.40 no.155 Bogotá Apr./June 2016
https://doi.org/10.18257/raccefyn.332
doi: http://dx.doi.org/10.18257/raccefyn.332
1 Escuela de Física, Universidad Industrial de Santander, Bucaramanga, Colombia. *Corresponding author: Guillermo A. González, guillermo.gonzalez@saber.uis.edu.co
2 Institute for Theoretical Physics, University of Amsterdam, Amsterdam, Netherlands
3 Departamento de Física, Universidade Federal de São Carlos, São Carlos, Brasil
Received: February 3, 2016. Accepted: May 2, 2016
Abstract
We present the derivation of distribution functions for the first four members of a family of disks, previously obtained in González and Reina (2006), which represent a family of axially symmetric galaxy models with finite radius and well-behaved surface mass density. In order to do this, we employ several approaches that have been developed starting from the potential-density pair and, essentially using the method introduced by Kalnajs (1976), we obtain some distribution functions that depend on the Jacobi integral. Now, as this method demands that the mass density can be properly expressed as a function of the gravitational potential, we can do this only for the first four disks of the family. We also find another kind of distribution functions by starting with the even part of the previous distribution functions and using the maximum entropy principle in order to find the odd part and so a new distribution function, as it was pointed out by Dejonghe (1986). The result is a wide variety of equilibrium states corresponding to several self-consistent finite flat galaxy models.
Key words: Stellar dynamics, Galaxies: kinemtics and dynamics.
Resumen
Se presenta la derivación de funciones de distribución para los primeros cuatro miembros de una familia de discos, obtenida previamente en González and Reina (2006), la cual representa a una familia de modelos de galaxias axialmente simétricas de radio finito y con densidad superficial de masa bien comportada. Para ello, se emplean varios enfoques desarrollados a partir del par potencial-densidad y, utilizando esencialmente el método introducido por Kalnajs (1976), se obtienen algunas funciones de distribución que dependen de la integral de Jacobi. Ahora, ya que este método exige que la densidad de masa se pueda expresar adecuadamente como una función del potencial gravitacional, sólo es posible hacer esto para los primeros cuatro discos de la familia. También encontramos otro tipo de funciones de distribución, comenzando con la parte par de las funciones de distribución anteriores y utilizando el principio de máxima entropía con el fin de encontrar la parte impar y por lo tanto una nueva función de distribución, como fue señalado por Dejonghe (1986). El resultado es una amplia variedad de estados de equilibrio correspondiente a varios modelos auto-consistentes de galaxias planas finitas.
Palabras clave: Dinámica estelar, Galaxias: cinemática y dinámica.
Introduction
The problem of finding self-consistent stellar models for galaxies is of wide interest in astrophysics. Usually, once the potential-density pair (PDP) is formulated as a model for a galaxy, the next step is to find the corresponding distribution function (DF). This is one of the fundamental quantities in galactic dynamics specifying the distribution of the stars in the phase-space of positions and velocities. Although the DF can generally not be measured directly, there are some observationally accesible quantities that are closed related to the DF: the projected density and the line-of-sight velocity, provided by photometric and kinematic observations, are examples of DF moments. Thus, the formulation of a PDP with its corresponding equilibrium DFs establish a self-consistent stellar model that can be corroborated by astronomical observations.
On the other hand, a fact that is usually assumed in astrophysics, see Binney and Tremaine (2008), is that the main part of the mass of a typical spiral galaxy is concentrated in a thin disk. Accordingly, the study of the gravitational potential generated by an idealized thin disk is a problem of great astrophysical relevance and so, through the years, different approaches has been used to obtain the PDP for such kind of thin disk models (see Kuzmin (1956) and Toomre (1963, 1964), as examples).
Now, a simple method to obtain the PDP of thin disks of finite radius was developed by Hunter (1963), the simplest example of disk obtained by this method being the Kalnajs (1972) disk. In González and Reina (2006), we use the Hunter method in order to obtain an infinite family of axially symmetric finite thin disks, characterized by a well-behaved surface density, whose first member is precisely the well-known Kalnajs disk. Also, the motion of test particles in the gravitational fields generated by the first four members of this family was studied in Ramos-Caro, López-Suspez and González (2008), and a new infinite family of self-consistent models was obtained in Pedraza, Ramos-Caro and González (2008) as a superposition of members belonging to the family.
We will consider at the present paper the derivation of some two-integral DFs for the first four members of the family obtained in González and Reina (2006). Now, as is stated by the Jeans theorem, an equilibrium DF is a function of the isolating integrals of motion that are conserved in each orbit and, as it has been shown, it is possible to find such kind of DFs for PDPs such that there is a certain relationship between the mass density and the gravitational potential. The simplest case of physical interest corresponds to spherically symmetric PDPs, which are described by isotropic DFs that depends on the total energy E. Indeed, as was be shown in Eddington (1916), it is possible to obtain this kind of isotropic DFs by first expressing the density as a function of the potential and then solving an Abel integral equation.
Jiang and Ossipkov (2007) found that a similar procedure can be performed in the axially symmetric case, where the equilibrium DF depends on the energy E and the angular momentum about the axis of symmetry Lz, i.e. the two classical integrals of motion. They developed a formalism that essentially combines both the Eddington formulae and the Fricke (1952) expansion in order to obtain the DF even part, starting from a density that can be expressed as a function of the radial coordinate and the gravitational potential. Once such even part is determined, the DF odd part can be obtained by introducing some reasonable assumptions about the mean circular velocity or using the maximum entropy principle.
On the other hand, another method appropriated to find DFs depending only of the Jacobi integral, Er = E â WÂLz, for axially symmetric flat galaxy models was introduced by Kalnajs (1976) for the case of disk-like systems and basically consists in to express the DF as a derivative of the surface mass density with respect to the gravitational potential. Such method does not demands solving an integral equation, but instead is necessary properly to express the mass density as a function of the gravitational potential, a procedure that is only possible in some cases.
In this paper we will use both of the mentioned approaches in order to obtain equilibrium DFs for some generalized Kalnajs disks. Accordingly, the paper is organized as follows. First, we present the fundamental aspects of the two methods that we will use in order to obtain the equilibrium DFs. Then, we present a summary of the main aspects of the generalized Kalnajs disks, and then we derive the DFs for the first four members of the family. Finally, we summarize our main results.
Formulation of the Methods
We assume that Âf and E are, respectively, the gravitational potential and the energy of a star in a stellar system. One can choose a constant  Âf0 such that the system has only stars of energy E < f0, and then define a relative potential Y = âÂfÂ+Âf0 and a relative energy e = âE+Âf0, see Binney and Tremaine (2008), such that e = 0 is the energy of escape from the system. Both the mass density r(r) and the DF f(r, v) are related to ÂYÂ(r) through the Poisson equation
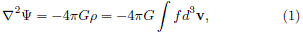
where G is the gravitational constant.
For the case of an axially symmetric system, it is customary to use cylindrical polar coordinates (R, j, z), where v is denoted by v = (vR, vj,vz). As it is well known, such system admits two isolating integrals for any orbit: the component of the angular momentum about thez-axis, Lz = Rvj, and the relative energy e. Hence, by the Jeans theorem, the DF of a steadystate stellar system in an axially symmetric potential can be expressed as a non-negative function of e and Lz, denoted by f(e, Lz). Such DF, that vanishes for e < 0, is related to the mass density through eq. (1).
In this subject, f(e, Lz) is usually separated into even and odd parts, f+(e, Lz) and f–(e, Lz) respectively, with respect to the angular momentum Lz, where
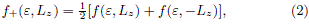
and
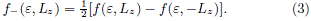
So, by using
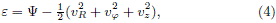
the integral given by (1) can be expressed, see Binney and Tremaine (2008), as
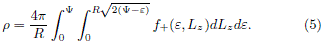
For a given mass density, this relation can be considered as the integral equation determining f+(e, Lz), while the odd part satisfies the relation
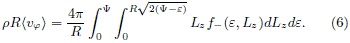
This integral equation was first found by Lynden-Bell (1962) and then applied by Evans (1993) into calculating the odd DF for the Binney model, under the assumption of  having some realistic rotational laws.
having some realistic rotational laws.
As  is not known, we cannot compute f–(e, Lz) directly by eq. (6) but what we can do is to obtain the most probable distribution functions under some suitable assumptions. Once f+(e, Lz) is known, f–(e, Lz), and therefore f(e, Lz), can be obtained by means of the maximum entropy principle, see Dejonghe (1986), and we obtain
is not known, we cannot compute f–(e, Lz) directly by eq. (6) but what we can do is to obtain the most probable distribution functions under some suitable assumptions. Once f+(e, Lz) is known, f–(e, Lz), and therefore f(e, Lz), can be obtained by means of the maximum entropy principle, see Dejonghe (1986), and we obtain
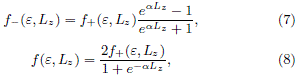
where a is the parameter depending on the total angular momentum. Obviously, çf–(e, Lz)ç ≤ çf+(e, Lz)ç. Also, the system is non-rotating when a = 0 and maximally rotating as a → ∞, i.e., for a → +∞, it is anticlockwise and f(e, Lz) = [1+sign(Lz)]f+(e, Lz), for a → –∞, the rotation is clockwise and f(e, Lz) = [1–sign(Lz)]f+(e, Lz). The parameter a reflects the rotational characteristics of the system.
As it was pointed out by Fricke (1952) and recently by Jiang and Ossipkov (2007), the implementation of integral equations (5) and (6) demands that one can express r as a function of R and yÂ. This holds indeed for the case of disk-like systems, which surface mass density SÂ is related to f through
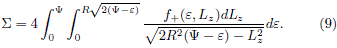
In order to incorporate the formalisms developed for the 3-dimensional case to deal with disk-like systems, we have to generate a pseudo-volume density 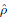 , see Hunter and Quian (1993), according to
, see Hunter and Quian (1993), according to
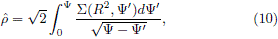
which must take the place of r in (5) and (6). In particular, when 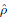 (Ây,R) =
(Ây,R) = 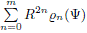 , see Jiang and Ossipkov (2007), the corresponding even DF is
, see Jiang and Ossipkov (2007), the corresponding even DF is
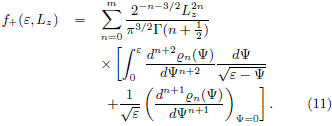
Another simpler method to find equilibrium DFs corresponding to axially symmetric disk-like systems, was introduced by Kalnajs (1976). Such formalism deal with DFs that depend on the Jacobi's integral Er = E â WÂLz, i.e. the energy measured in a frame rotating with constant angular velocity ÂW. It is convenient to define an effective potential FÂr = F Ââ ½W2R2 in such way that, if we choose a frame in which the velocity distribution is isotropic, the DF will be Lz-independent and, from (9), the relation between the surface mass density and the DF is reduced to
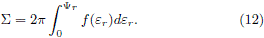
Here, yÂr = âÂF + ½W2R2 + FÂ0r and er = e+ÂWLz+FÂ0râÂF0, i.e. the relative potential and the relative energy measured in the rotating frame. Moreover, if one can express ÂS as a function of yÂr, differentiating both sides of (12) with respect to yÂr, we obtain
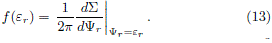
Note that in this formalism it is also necessary to express the mass density as a function of the relative potential.
DFs for the family of disks
The family of disk models. In González and Reina (2006), we obtain an infinite family of axially symmetric finite thin disks such that the mass surface density of each model (labeled with the positive integer m ≥ 1) is given by
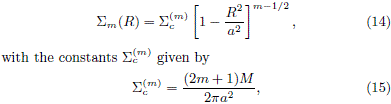
where M is the total mass and a is the disk radius. Such mass distribution generates an axially symmetric gravitational potential, that can be written as
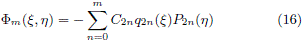
where P2n(h) and q2n(x) = i2n+1 Q2n(ix) are the usual Legendre polynomials and the Legendre functions of the second kind respectively, and C2n are constants given by
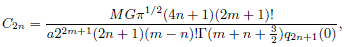
where G is the gravitational constant. Here, â1 ≤ h ≤ 1 and 0 ≤ x < ∞ are spheroidal oblate coordinates, related to the usual cylindrical coordinates (R, z) through the relations
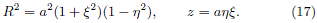
In particular, we are interested in the gravitational potential at the disk, where z = 0 and 0 ≤ R ≤ a, so x = 0 and 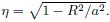
Ifwe choose Â0m in such a way that Âm ≥ 0, the corresponding relative potential for the first four members will be
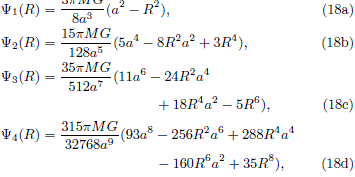
We shall restrict our attention to these four members. The formulae showed above defines the relative potentials that will be used to calculate the DFs by the implementation of the methods sketched in previous section.
DFs for the m = 1 disk. Given the mass surface distribution (14) and the relative potential (18a), we can easily obtain the following relation:
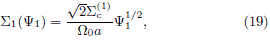
where –W0 = [3pGM/(4a3)]1/2. As we are dealing with disk-like systems, it is necessary to compute the pseudo-volume density 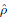 by eq. (10) in order to perform the integral (5),
by eq. (10) in order to perform the integral (5),
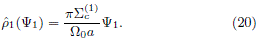
By using the right part of eq. (11) with n = 0, which is equivalent to calculate the Fricke component of (20), we obtain the even part of a DF which depends only on the relative energy
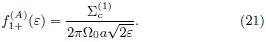
At this point, we may notice that this f1+(e) corresponds to the DF formulated by Binney and Tremaine (2008) when –W = 0. (Note that there is a difference of constants as a result of a different definition of the relative potential and relative energy.)
To obtain a full DF, we use the maximum entropy principle by means of eq. (8) and the result is To obtain a full DF, we use the maximum entropy principle by means of eq. (8) and the result is
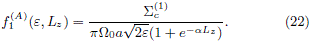
In figure 1 we shown the contours of f1(A) for different values of a: we take α = 10 in figure 1(a), α = 1 in figure 1(b), α = 0.1 in figure 1(c) and α = 0 in figure 1(d). As it is shown in the figures, α determines a particular rotational state in the stellar system (from here on we set G = a = M = 1 in order to generate the graphics, without loss of generality). As α increases, the probability to find a star with positive Lz increases as well. A similar result can be obtained for α < 0, when the probability to find a star with negative Lz decreases as α decreases, and the corresponding plots would be analogous to figure 1, after a reflection about Lz = 0.
We can generalize this result if we perform the analysis in a rotating frame. At first instance, it is necessary to deal with the effective potential in order to take into account the fictitious forces. Choosing conveniently F0r, the relative potential in the rotating frame takes the form
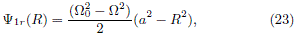
so the corresponding mass surface density and the pseudovolume density can be expressed as
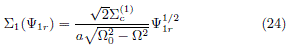
and
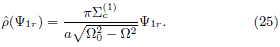
The resulting even part of the DF in the rotating frame is
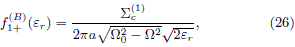
and it can be derived following the same procedure used to find
f1+(A) (e) or by the direct application of eq. (13).
Finally, one can come back to the original frame through the relation between er, e and Lz to obtain
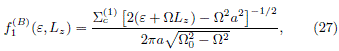
which is totally equivalent to the Binney and Tremaine (2008) DF for the Kalnajs disk. Its contours, showed in figure 2 for different values of WÂ, reveals that the probability to find stars with e < WÂÂ2a2/2 â WÂÂLz is zero, while it has a maximum when e ÂWÂ2a2/2 â WÂÂLz (this defines the white strip shown in the figure) and decreases as e increases. We take WÂÂ = âp/4 in figure 2(a), WÂÂ = âp/16 in figure 2(b), Â WÂ = p/4 in figure 2(c) and WÂÂ = p/16 in figure 2(d). Nevertheless, this f1(B) (e, Lz) is quiet unrealistic as it represent a state with 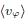 = WÂR and it means that the behavior of the system, in disagreement with the observations, behaves like a rigid solid.
= WÂR and it means that the behavior of the system, in disagreement with the observations, behaves like a rigid solid.
However, we can generate a better DF if we took only the even part of (27) and using the maximum entropy principle to obtain
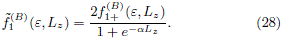
As it is shown in figure 3, where we plot the contours of  1(B) for W = p/4 with a = 1 in figure 3(a) and a = 10 in figure 3(b), and for W = p/16 with a = 1 in figure 3(c), and a = 10 in figure 3(d), there is a zone of zero probability, just in the intersection of black zones produced by
1(B) for W = p/4 with a = 1 in figure 3(a) and a = 10 in figure 3(b), and for W = p/16 with a = 1 in figure 3(c), and a = 10 in figure 3(d), there is a zone of zero probability, just in the intersection of black zones produced by 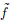 1(B) (e,±Lz), and there are also two maximum probability stripes. The variation of the W parameter leads to the change of inclination of the maximum probability stripes and it is easy to see that the DF would be invariant under the sign of W, by the definition of the even part. Furthermore, a plays a similar role than in figure 1, increasing the probability of finding stars with high Lz as a increases and vice versa.
1(B) (e,±Lz), and there are also two maximum probability stripes. The variation of the W parameter leads to the change of inclination of the maximum probability stripes and it is easy to see that the DF would be invariant under the sign of W, by the definition of the even part. Furthermore, a plays a similar role than in figure 1, increasing the probability of finding stars with high Lz as a increases and vice versa.
DFs for the m = 2 disk. Working in a rotating frame we found that the relative potential is given by
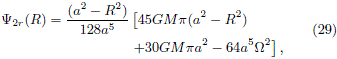
while the surface mass density is given by (14) when m = 2. This case is a little more complicated than the usual Kalnajs disk, because the analytical solution of the pseudo-volume density cannot be performed with total freedom. We will need to operate in a rotating frame conveniently chosen in such a way that the relation between the mass surface density and the relative potential becomes simpler.
From eq. (29) it is possible to see that if we choose the angular velocity as
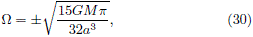
the relative potential is reduced to
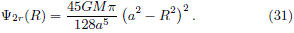
Now, we can express the surface mass density easily in terms of the relative potential by the relation
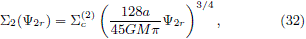
and the integral for the pseudo-volume density can be performed and we obtain
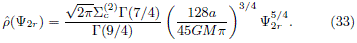
Using then eq. (11), the resulting even part of the DF in the rotating frame and the full DF in the original frame are
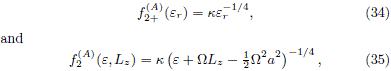
respectively, where W could take the values according to (30) and k is the constant given by
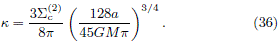
Moreover, using the same arguments given in section (), it's convenient to take the even part of (35) and obtain a new DF using eq. (8), which is given by
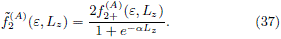
A more general case can be derived without the assumption (30) if we use the Kalnajs method in order to avoid the pseudovolume density integral. Here we work in terms of the spheroidal oblate coordinates to obtain more easier the relation between the mass surface density and the relative potential, which can be expressed as
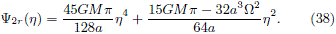
Now, it is possible to rewrite this expression as
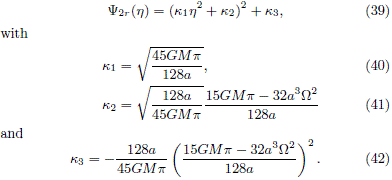
Then, as ÂS can be expressed in terms of h in the form
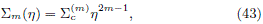
the relation between ÂS2 and y2r is
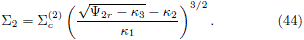
Now, by using eq. (13), we obtain
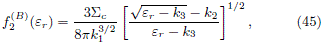
and the result in the original frame is
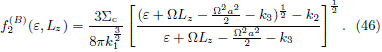
Obviously, this DF is the same as (35) when the condition (30) is satisfied. Finally, by eq. (8), the resulting DF with maximum entropy is given by
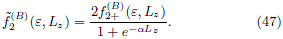
We can see the behavior of these DFs in figures 4 and 5. In figures 4(a) and 4(b) we show the contours of f2(A) for the two rotational states given by eq. (30). Such DF is maximum over a narrow diagonal strep, near to the zero probability region, and the probability decreases as ε increases, similarly to the case showed in figure 3. The corresponding contours of 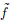 2(A), given by eq. (37), are plotted in 4(c), for a = 1, and 4(d), for a = 10.
2(A), given by eq. (37), are plotted in 4(c), for a = 1, and 4(d), for a = 10.
The DFs for stellar systems characterized by different W Â are shown in figures 5(a) and 5(b), where we plot the contours of f2(B) for the two rotational states given by (30). Note that f2(B) equals to f2(A) when WÂ is given by (30). In this case the DF varies more rapidly as W decreases, originating narrower
bands. The corresponding contours of 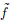 2(A) and
2(A) and 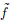 2(A) for different values of the parameter α are shown in figures 5(c) and 5(d), showing a similar behavior than
2(A) for different values of the parameter α are shown in figures 5(c) and 5(d), showing a similar behavior than 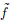 2(A) . We take a = 1 for 5(c) and a = 10 for 5(d).
2(A) . We take a = 1 for 5(c) and a = 10 for 5(d).
DFs for the m = 3 disk. Once again, if we want to use the Kalnajs method, it is necessary to derive the relation ÂS3(Ây3r) and, according to (43), it is posible if we can invert the equation of the relative potencial, which in this case is given by
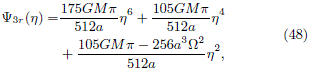
in order to obtain h(y3r). To solve it, we must deal with a cubic equation and with its non-trivial solutions; fortunately, we still have W as a free parameter.
One can easily note that it is possible to write (48) as
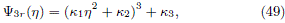
with
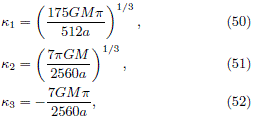
and W has be chosen as
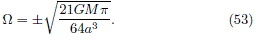
Now, by replacing (43) into (49), we obtain
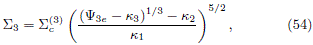
and, by using eq. (13),
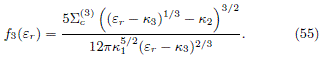
Coming back to the original frame, the result is
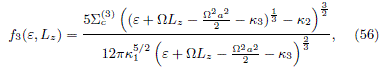
while the respective DF with maximum entropy is
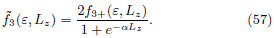
In figure 6(a) we show the contour of f3, while in figures 6(b), 6(c) and 6(d) are plotted the contours of 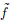 3 for different values of a. We can see that the behavior of these DFs is opposite to the previous cases. As the Jacobi's integral icreases, the DF also increases.
3 for different values of a. We can see that the behavior of these DFs is opposite to the previous cases. As the Jacobi's integral icreases, the DF also increases.
DFs for the m = 4 disk. As we saw in section , in order to find a DF using the Kalnajs method, we must find h as a function of the relative potential in order to obtain ÂS(yr). For the m = 4 disk, the relative potential can be expressed as
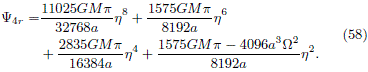
Now, although we have to deal with a quartic equation, it is possible to rewrete (58) as
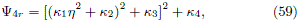
where
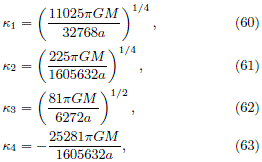
and W must to be chosen as
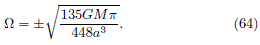
Finally, by using (43) and (49), we find the expression
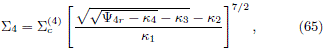
which, by means of eq. (13), can be used to derive the even part of the DF in the rotating frame,
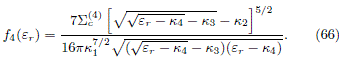
Therefore, the corresponding DF in the original frame is given by
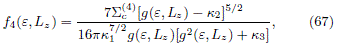
where
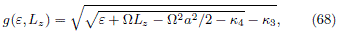
and the respective DF with maximum entropy is given by
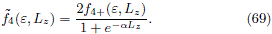
In figure 7(a) we show the contour of f4, while in figures 7(b), 7(c) and 7(d) are plotted the contours of 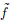 4 for different values of a. As we can see, the behavior is analogous to the showed at figure 6.
4 for different values of a. As we can see, the behavior is analogous to the showed at figure 6.
Concluding Remarks
We presented the derivation of two-integral equilibrium DFs for some members of the family of disks previously obtained by González and Reina (2006). Such two-integral DFs were obtained, esentially, by expresing them as functionals of the Jacobi integral, as it was sketched in the formalism developed by Kalnajs (1976). Now, since such formalism demands that the surface mass density can be written as a potential-dependent function, the above procedure can only be implemented for the first four members of the family, the disks with m = 1, 2, 3, 4. Indeed, the procedure requires that the expression given the relative potential yÂr as a function of the spheroidal variable h can be analytically inverted in order to express the surface mass density SÂ as a function of the relative potential. So, we can do this in a simple way for the disks with m = 1 to 4. However, when m > 4 we must to solve an equation of grade larger than four, whose analytical solution do not exists.
For the first two members of the family, the disks with m = 1, 2, we also use the method introduced by Jiang and Ossipkov (2007) in order to find the even part of the DF and then, by introducing the maximum entropy principle, we can determines the full DF. This procedure was also used for the other three disks, starting from the Kalnajs (1976) method, so defining another class of two-integral DFs. Such kind of DFs describes stellar systems with a preferred rotational state, characterized by the parameter a. This paper can be considered as a natural complement of the work previously presented by González and Reina (2006) and Ramos-Caro, López-Suspez and González (2008), where the PDP formulation and the kinematics, respectively, of the disks were analyzed. Now, by the construction of the corresponding two-integral DFs, the first four members of this family can be considered as a set of selfconsistent stellar models for axially symmetric galaxies.
Acknowledgments. GAG was supported in part by VIEUIS, under grants number 1347 and 1838, and COLCIENCIAS, Colombia, under grant number 8840.
Bbliografía
Binney, J. and Tremaine, S. (2008). Galactic Dynamics. 2nd ed. Princeton University Press. [ Links ]
Dejonghe, H. (1986). Stellar dynamics and the description of stellar systems. Phys. Rep., 133, 217. [ Links ]
Eddington, A. S. (1916). The distribution of stars in globular clusters. MNRAS, 76, 572. [ Links ]
Evans, N. W. (1993). Simple galaxy models with massive haloes. MNRAS, 260, 191. [ Links ]
Fricke, W. (1952). Dynamic justification of the speed distribution in the star system. Astron. Nachr., 280, 193. [ Links ]
González, G. A. and Reina, J. I. (2006). An infinite family of generalized Kalnajs disks. MNRAS, 371, 1873. [ Links ]
Hunter, C. (1963). The structure and stability of selfgravitating disks. MNRAS, 126, 299. [ Links ]
Hunter, C. and Quian, E. (1993). Two-integral distribution functions for axisymmetric galaxies. MNRAS, 262, 401. [ Links ]
Jiang, Z. and Ossipkov, L. (2007). Two-integral distribution functions for axisymmetric systems. MNRAS, 379, 1133. [ Links ]
Kalnajs, A. J. (1972). The equilibria and oscillations of a family of uniformly rotating stellar disks. Astrophys. J., 175, 63. [ Links ]
Kalnajs, A. J. (1976). Dynamics of flat galaxies. III. Equilibrium models. Astrophys. J., 205, 751. [ Links ]
Kuzmin, G. (1956). A stationary galaxy model admitting triaxial velocity distribution. Astron. Zh., 33, 27. [ Links ]
Lynden-Bell, D. (1962). Stellar dynamics: Exact solution of the self-gravitation equation. MNRAS, 123, 447-458. [ Links ]
Pedraza J. F., Ramos-Caro J. and González G. A. (2008). An infinite family of self-consistent models for axisymmetric flat galaxies. MNRAS, 390, 1587. [ Links ]
Ramos-Caro J., López-Suspez F. and González G. A. (2008). Chaotic and Regular Motion Around Generalized Kalnajs disks. MNRAS, 386, 440. [ Links ]
Toomre, A. (1963). On the Distribution of Matter Within Highly Flattened Galaxies. Astrophys. J., 138, 385. [ Links ]
Toomre, A. (1964). On the gravitational stability of a disk of stars. Astrophys. J., 139, 1217. [ Links ]













