doi: http://dx.doi.org/10.18257/raccefyn.376

¹ Escuela de Física, Universidad Industrial de Santander, Bucaramanga, Colombia. *Corresponding author: Guillermo A. González, guillermo.gonzalez@saber.uis.edu.co
² Departamento de Ciencias Básicas, Universidad Santo Tomás-Bucaramanga, Bucaramanga, Colombia

Received: 13 de abril de 2016. Accepted: 10 de agosto de 2016

Abstract

A family of analytical potential-density pairs for flat galaxies with spheroidal halos is presented. The potential are obtained by means of the sum of two independent terms: a potential associated with a thin disc and a potential associated with a spheroidal halo, which are expressed as appropriated superpositions of products of Legendre functions, in such a way that the model implies a linear relationship between the masses of the thin disc and the spheroidal halo. By taking a particular case for the halo potential, we found that the circular velocity obtained can be adjusted very accurately to the observed rotation curves of some specific galaxies, so that the models are stable against radial and vertical perturbations. Two particular models for the galaxies NGC4389 and UGC6969 are obtained by adjusting the circular velocity with data of the observed rotation curve of some galaxies of the Ursa Mayor Cluster, as reported in Verheijen and Sancisi (2001). The values of the halo mass and the disc mass for these two galaxies are computed obtaining a very narrow interval of values for these quantities. Furthermore, the values of obtained masses are in perfect agreement with the expected order of magnitude and with the relative order of magnitude between the halo mass and the disc mass.

Key words: Potential Theory; Disk Galaxies; Celestial Mechanics; Galactic Mass.

Resumen

Se presenta una familia de pares analíticos potencial-densidad para galaxias planas con halos esferoidales. Los potenciales son obtenidos por medio de la suma de dos términos independientes: un potencial asociado al disco delgado y un potencial asociado al halo esferoidal, los cuales son expresados apropiadamente como la superposición de productos de funciones de Legendre, de tal manera que el modelo implica una relación lineal entre las masas del disco delgado y el halo esferoidal. Tomando un caso particular para el potencial del halo, encontramos que la velocidad circular obtenida puede ser ajustada muy precisamente con la curva de rotación de algunas galaxias específicas, de tal manera que los modelos son estables contra perturbaciones radiales y verticales. Dos modelos particulares para las galaxias NGC4389 y UGC6969 son obtenidos ajustando la velocidad circular del modelo con datos de la curva de rotación observada de algunas galaxias del Cluster de la Osa Mayor, reportados en Verheijen and Sancisi (2001). Los valores de la masa del halo y la masa del disco para estas dos galaxias son calculados obteniendo un intervalo muy estrecho de valores para dichas cantidades. Además, los valores de masa aquí obtenidos están en perfecto acuerdo con el orden de magnitud esperado y con el orden de magnitud relativo entre la masa del halo y la masa del disco.

Palabras clave: Teoría del Potencial; Galaxias de Disco; Mecánica Celeste; Masa de Galaxias.

Introduction

One of the oldest and most important problems in galactic dynamics is the determination of the mass distribution based on the observations of the circular velocity or rotation curve (Pierens and Hure, 2004), defined as the speed of the stars moving in the galactic plane in circular orbits around the center. Now, if we assume a particular model for the composition of the galaxy, the fit of that model with the rotation curve of a particular galaxy can, in principle, completely determine the distribution of mass. So then, the rotation curve provides the most direct method to measure the distribution of mass of a galaxy (Binney and Tremaine, 2008).

Currently, the most accepted description of the composition of spiral galaxies is that a significant portion of its mass is concentrated in a thin disc, while the other contributions to the total mass of the galaxy come from a spherical halo of dark matter, a central bulge and, perhaps, a central black hole (Binney and Tremaine, 2008). Now, since all components contribute to the gravitational field of the galaxy, obtaining appropriate models that include the effects of all parts is a problem of great difficulty. However, the contribution of each part is limited to certain distance scales, so in a reasonably realistic model it is not necessary to include the contribution of all components (Faber, 2006).

In particular, the gravitational influence of the central black hole is appreciable only within a few parsecs around the center of the galaxy (Schödel, et al., 2002), so it can be completely neglected when studying the dynamics of the disc, or in regions outside the central bulge, while the bulge mainly dominates the inner region of the galaxy to a few kiloparsec. So then, the main contributions to the gravitational field of the galaxy come from the galactic disc and the dark matter halo (Faber, 2006). However, it is commonly accepted that many aspects of galactic dynamics can be described, in a fairly approximate way, using models that consider only the contribution of a thin galactic disc (Binney and Tremaine, 2008).

Accordingly, the study of the gravitational potential generated by an idealized thin disc is a problem of great astrophysical relevance and so, through the years, different approaches have been used to obtain such kind of thin disc models (see Binney and Tremaine (2008) and references therein). So, once an expression for the gravitational potential has been derived, corresponding expressions for the surface mass density of the disc and for the circular velocity of the disc particles can be obtained. Then, if the expression for the circular velocity can be adjusted to fit the observational data of the rotation curve of a particular galaxy, the total mass can be obtained by integrating the corresponding surface mass density.

However, although most of these thin disc models have surface densities and rotation curves with remarkable properties, many of them mainly represent discs of infinite extension and thus they are rather poor flat galaxy models. Therefore, in order to obtain more realistic models of flat galaxies, it is better to consider methods that permit obtaining finite thin disc models. Now, a simple method to obtain the gravitational potential, the surface density and the rotation curve of thin discs of finite radius was developed by Hunter (1963), the simplest example of a disc obtained by this method being the well known Kalnajs (1972) disc.

In a previous paper (González and Reina, 2006) we used the Hunter method in order to obtain an infinite family of thin discs of finite radius with a well-behaved surface mass density. This family of disc models was derived by requiring that the surface density behaves as a monotonously decreasing function of the radius, with a maximum at the center of the disc and vanishing at the edge. Furthermore, the motion of test particles in the gravitational fields generated by the first four members of this family was studied in Ramos-Caro, López-Suspez and González (2008). So, although the mass distribution of this family of discs presents a satisfactory behaviour in such a way that they could be considered adequate as flat galaxy models, their corresponding rotation curves do not present a so good behavior, as they do not reproduce the flat region of the observed rotation curve.

On the other hand, in Pedraza, Ramos-Caro and González (2008) a new family of discs was obtained as a superposition of members of the previously obtained family, by requiring that the surface density be expressed as a well- behaved function of the gravitational potential, in such a way that the corresponding distribution functions can be easily obtained. Furthermore, besides presenting a well-behaved surface density, the models also presented rotation curves with a better behavior than the generalized Kalnajs discs. However, although these discs are stable against small radial perturbations of disc star orbits, they are unstable to small vertical perturbations normal to the disc plane. Then, apart from the stability problems, these discs can be considered as quite adequate models in order to satisfactorily describe a great variety of galaxies.

Based on these works, in González, Plata-Plata and Ramos-Caro (2010) were obtained some thin disc models in which the circular velocities were adjusted to very accurately fit the observed rotation curves of four spiral galaxies of the Ursa Major cluster, galaxies NGC3877, NGC3917, NGC3949 and NGC4010. These models presented well- behaved surface densities and the obtained values for the corresponding total mass agree with the expected order of magnitude. However, the models presented a central region with strong instability to small vertical perturbations. Now, this result was expected as a consequence of the fact that the models only consider the thin galactic disc. Therefore, more realistic models must be considered including the non-thin character of the galactic disc or the mass contribution of the spheroidal halo.

In agreement with the above considerations, in this paper we will consider a family of models obtained by expressing the gravitational potential as the superposition of a potential generated by the thin galactic disc and a potential generated by the spheroidal halo, in such a way that the model implies a linear relationship between the masses of the thin disc and the spheroidal halo. By adjusting the corresponding expression for the circular velocity to the observed data of the rotation curve of some specific galaxies, some particular models will be analysed. Then, from the corresponding expressions for the disc surface density and the density of the halo, estimate values for the total mass of the disc and the total mass of the halo will be obtained. The paper is organised as follows. First we present the thin disc plus halo model. Then, we obtain the corresponding expressions for particular models, and then the models are fitted to data of the observed rotation curve of some galaxies of the Ursa Mayor Cluster, as reported in Verheijen and Sancisi (2001). Finally, we discuss the obtained results.

The Thin Disc Plus Halo Model

In order to obtain galaxy models consisting of a thin galactic disc and a spheroidal halo, we begin considering an axially symmetric gravitational potential F = F (R, z), where (R, j, z) are the usual cylindrical coordinates. Also, besides the axial symmetry, we suppose that the potential has symmetry of reflection with respect to the plane z = 0,

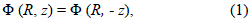
which implies that the normal derivative of the potential satisfies the relation

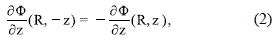
in agreement with the attractive character of the gravitational field. We also assume that ∂ F / ∂z does not vanish on the plane z= 0, in order to have a thin distribution of matter that represents the disc.

On the other hand, in order to separately describe the thin disc and the spheroidal halo, we consider that the gravitational potential can be written as the superposition of two independent components

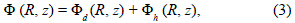
where F_d (R, z) is the part of the potential generated by the thin galactic disc, while F_h (R, z) corresponds to the spheroidal halo component. The disc component F_d (R, z) must be a solution of the Laplace equation everywhere outside the disc,

while the halo component F_h (R, z) satisfies the Poisson equation

where Q(R, z) is the mass density of the halo.

So, given a potential F (R, z) with the previous properties, we can easily obtain the circular velocity u_c (R), defined as the velocity of the stars moving at the galactic disc in circular orbits around the center, through the relationship

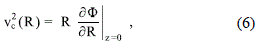
while the surface mass density S(R) of the thin galactic disc is given by

which it is obtained by using the Gauss law and the reflection symmetry of F (R, z).

Accordingly, in order that the potential of the spheroidal halo does not contribute to the disc surface density, we will impose the condition

Furthermore, in order to have a surface density corresponding to a finite disclike distribution of matter, we impose boundary conditions in the form

in such a way that the matter distribution is restricted to the disc z = 0, 0 ≤ R ≤ a, where a is the radius of the disc.

In order to properly pose the boundary value problem, we introduce the oblate spheroidal coordinates, whose symmetry adapts in a natural way to the geometry of the model. These coordinates are related to the usual cylindrical coordinates by the relation (Morse and Fesbach, 1953)

where 0 ≤ x < ∞ and -1 ≤ h < 1. The disc has the coordinates x = 0, 0 ≤ h² < 1. On crossing the disc, the h coordinate changes sign but does not change in absolute value. The singular behaviour of this coordinate implies that an even function of h is a continuous function everywhere but has a discontinuous h derivative at the disc.

Now, in terms of the oblate spheroidal coordinates, the Laplace operator acting over any axially symmetric function F (x, h) gives

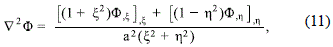
Whereas the boundary condition (8) is equivalent to

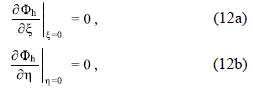
and the boundary conditions (9a) and (9b) reduce to

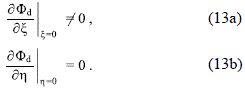
Moreover, in order for the gravitational potential to be continuous everywhere, F (x, h) must be an even function of h, which grants also the fulfilment of conditions (12b) and (13b).

Accordingly, by imposing the previous boundary conditions over the general solution of the Laplace equation in oblate spheroidal coordinates, we can write the gravitational potential of the galactic disc as (Bateman, 1944)

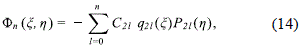
where n is a positive integer, which it defines the model of disc considered. Here P₂₁ (h) are the usual Legendre polynomials and q₂₁ (x) = i^2l+1Q₂₁ (ix), with Q₂₁ (x) the Legendre functions of second kind (see Arfken and Weber (2005) and, for the Legendre functions of imaginary argument, Morse and Fesbach (1953), page 1328). The coefficients C₂₁ are, in principle, arbitrary constants, though they must be specified to obtain any particular model. We will do this later on, by adjusting the circular velocity of the model with the observed data of the rotation curve of some specific galaxies.

With this expression for the gravitational potential of the disc, the surface density is given by

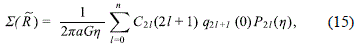
where, as 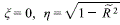, with 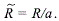Then, by integrating on the total area of the disc, we find the value

for the total mass of the disc. Now, it is clear that the surface density diverges at the disc edge, when h = 0, unless that we impose the condition (Hunter, 1963)

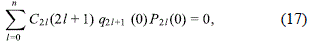
that, after using the identities

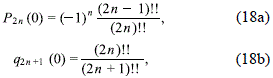
which are easily obtained from the properties of the Legendre functions, leads to the expression

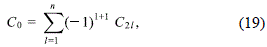
which gives, through (16), the value of the disc mass M_d in terms of the constants C₂₁, with l ≥ 1.

Now, to properly choose the gravitational potential of the spheroidal halo, we consider the superposition

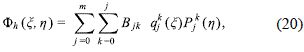
where m is a positive integer, which defines the model of halo considered, and the coefficients B_jk are arbitrary constants which must be specified to obtain any particular model. Here (Lamb, 1945)

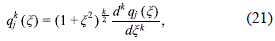
are the solutions of the differential equation

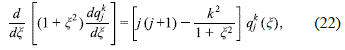
while the associated Legendre functions (Arfken and Weber, 2005),

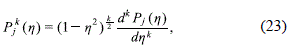
are the solutions of the differential equation

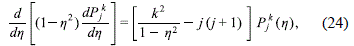
where j and k are integers, with j ≥ k. On the other hand, due to the discontinuous character of h, F_h (x, h) will be continuous everywhere only if we take (j - k) as an even number in order that P^k_j(h) be an even function of h.

With the previous expressions, and using the Laplace operator in oblate spheroidal coordinates (11) in the Poisson equation (5), we obtain for the mass density of the halo the expression

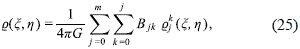
Where

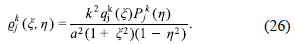
Now, from (23) and (26) it is easy to see that at the z axis, when h = ±1, the function Q^k_j(x, h) diverges for k = 1 and vanishes for k > 2. Accordingly, in order to have a well behaved mass density for the halo, we only consider in expression (20) the terms with k = 0 and k = 2 and so, in order to grant the continuity of the potential, we must take j as an even number. Furthermore, in order to have a nonzero mass density for the halo, we must consider models with m ≥ 2. Finally, as P^k_j(h) is finite at the interval -1 ≤ h ≤ 1 and q^k_j(x) goes to zero when x → ∞, Q(x, h) properly vanishes at infinity.

A simple possibility for the halo potential in agreement with the above considerations is given by taking (20) with m = 4,

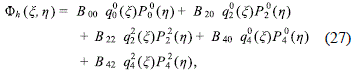
in such a way that at least two terms in (25) contribute to the mass halo density. Then, after using the explicit expressions for q^k_j(x) and P^k_j(h), the halo density can be written as

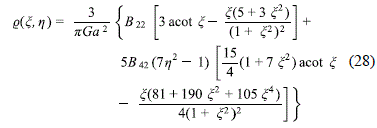
which is maximum at the disc surface, when x = 0, and then fastly decreases being constant at the oblate spheroids defined by x = cte.

By integrating over all the space, we obtain the expression

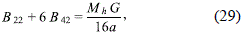
Where M_h is the total mass of the halo. Furthermore, from the condition (12a), we obtain the relations

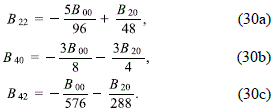
Finally, solving the system of equations (29) and (30), we obtain

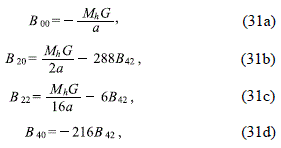
and so all the constants in (27) are expressed in terms of the halo mass M_h and the coefficient B₄₂.

On the other hand, if we restrict to particles moving in the thin disc, the circular velocity is written in terms of the spheroidal coordinates as

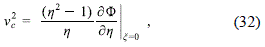
which, by using (3), (14), (27) and the properties of the Legendre functions, reduces to

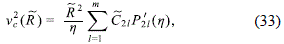
where

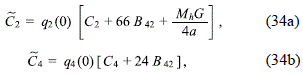
and

for l ≥ 3. Then, by using (19), (34a), (34b) and (35), it is easy to establish that

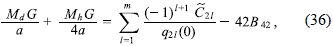
and thus the model implies a linear relationship between M_d and M_h, where the independent term is determined by the constants ˜C₂₁, with l ≥ 1, and the coefficient B₄₂. Now, it is clear that the above relationship makes sense only if the right hand side it is positive, which should be checked for every set of constants ˜C₂₁ corresponding to any particular model. The coefficient B₄₂ must be chosen in such a way that the model represent galaxies with a surface density mass and vertical frequency with a physically acceptable behavior.

Obtaining Particular Models

In order to obtain particular models, we must specify the constants ˜C₂₁ of the general model. So, we will adjust these constants in such a way that the circular velocity u²_c(˜R) fits with the data of the rotation curve of some particular galaxy. As expression (33) for the circular velocity only involves derivatives of the Legendre polynomials of even order, it can be written as the rotation law (González, Plata-Plata and Ramos-Caro, 2010)

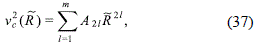
where the A₂₁ constants are related with the previous constants ˜C₂₁, for l ≠ 0, through the relation

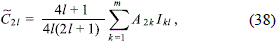
where

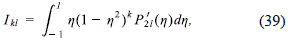
which is obtained by equaling expressions (33) and (37) and by using the orthogonality properties of the associated Legendre functions (Arfken and Weber, 2005).

Then, if the constants A₂₁ are determined by a fitting of the observational data of the corresponding rotation curve, the corresponding values of the coefficients ˜C₂₁ can be determined by means of relation (38), obtaining then a particular case of (36) corresponding to a specific galaxy model, which can be written in terms of the constants A₂₁ as

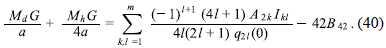
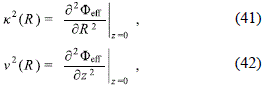
However, this relation does not determine completely the values of M_d and M_h, but only gives a linear relationship between them. So, in order to restrict the allowed values of these masses, it is needed to analyse the behaviour of some other quantities characterizing the kinematics of the model. These features are the epicycle or radial frequency, k²(R), and the vertical frequency, n²(R), which describe the stability against radial and vertical perturbations of particles in quasi-circular orbits (Binney and Tremaine, 2008). These frequencies, which must be positive in order to have stable circular orbits, are defined as

Where

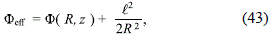
is the effective potential and l = Rn_c is the specific axial angular momentum. Then, by using expression (6) for the circular velocity, we can write the above expressions as

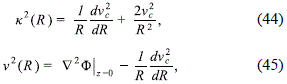
where we also used the expression for the Laplace operator in cylindrical coordinates.

Now, by using (37), the epicycle frequency can be cast as

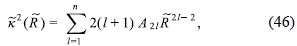
where ˜k= ak. It is easy to notice that the above expression is completely determined by the set of constants A₂₁, which are fixed by the numerical fit of the rotation curve data, such that it is not possible to find a relation between the disc and halo masses that can be adjusted by requiring radial stability. On the other hand, by using the Poisson equation (5), the expression (28) for the halo density and the expression (37) for the circular velocity, we find that the vertical frequency can be written as

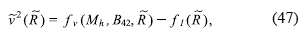
where ˜n = an,

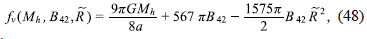
and

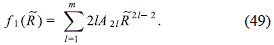
Thus, as ˜n² must be positive everywhere at the interval 0 ≤ ˜R ≤ 1 in order to have vertically stable models, it must satisfy that

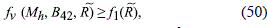
which give us a range for M_h y B₄₂ such that ˜n² ≥ 0.

Now, we also need to consider the behavior of the surface mass density, which by using the condition (17) and replacing (34a) and (34b) in (15), can be written as

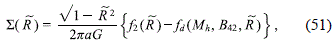
where

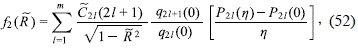
and

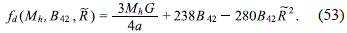
So, in order for the surface mass density to be positive in the interval 0 ≤ ˜R ≤ 1, it must be met that

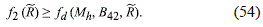
The relation (54) give us another range of values, not necessarily equal to the relation (50), for which we obtain a surface density mass with a acceptable behavior. Then, in order that the model make sense, we must verify that it meets the relation

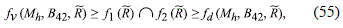
which should be checked for every set of constants corresponding to any particular model.

Adjusting Data to Models

In order to illustrate the above model to the real observed data, we have taken a sample of spiral galaxies of the Ursa Major cluster. We pick the corresponding data out from Table 4 of the paper by Verheijen and Sancisi (2001), which presents the results of an extensive 21 cm-line synthesis imaging survey of 41 galaxies in the nearby of the Ursa Major cluster using the Westerbork Synthesis Radio Telescope. The mean distance between this telescope and the cluster is 18.6 Mpc. At this distance, 1 arcmin corresponds to 5.4 kpc.

For each rotation curve data, we take as the value of a, the value given by the last tabulated radius, i.e. we are assuming that the radius of each galaxy is defined by its corresponding last observed value. Although this assumption about the galactic radius do not agrees with the accepted standard about the edge of the stellar disc (Binney and Merrifield, 1998), we will make it since we are assuming that all the stars moving in circular orbits at the galactic plane are inside the disc and that there are no stars moving outside the disc. Thereafter we take the radii normalized in units of a to fit the rotation curve of every galaxy by mean of the model (37).

The fits are made through a non-linear least squares fitting using the Levenberg-Marquardt algorithm, implemented internally by ROOT version 5.28 (Brun and Rademakers, 1997), which minimizes the weighted sum of squares of deviations between the fit and the data. We assigned weights to the data points inversely proportional to the square of their errors. These errors corresponding to 2vDv being Dv the galaxy velocity measurement error. For each galaxy, initially we look for all the possible fits starting at m = 1 up to m = N - 1, with N the number of measured data pairs (R, v²), hence we find a value for m such that we get the minimum reduced chi square c²_r(the best fit). Now we can discard the galaxies that do not pass the reduced chi squared test with a confidence level of 95% (Bevington and Keith, 2003).

The ˜C₂₁ constants are calculated by using the relations (19), (35) and (38). Therefore, by using this set of constants in (49) and (52) we find for each galaxy the functions f₁ and f₂. Finally, through a routine made in Mathematica 8.0., we check for each galaxy of the sample the validity of the condition (55). However, when we check the consistency of the adjust, we found that only the fit of the data for the galaxies NGC4389 and UGC6969 it agrees with these conditions, whereas that for all the other galaxies we found that the solution interval for M_h and B₄₂, given by (55), is empty.

In Table 1 we present the values of the constants A₂₁, in units of 10⁶m²s^-2, obtained by the numerical adjust with the rotation curve data for galaxies NGC4389 and UGC6969. With this values for the constants, we obtain, from (40), for the galaxy NGC4389 the relationship

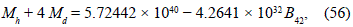
and for the galaxy UGC6969 the relationship

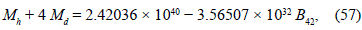
where all the quantities are in kg.

In Figure 1, we present the region that represent the solution interval of the condition (55) for the galaxies NGC4389 and UGC6969. This region represent the values that the halo mass and the coefficient B₄₂ can take, in order to obtain galaxy models with a vertical frequency always positive and with a surface density that has a maximum value at the disc centre and then decreases as ˜R increases, vanishing at the disc edge.

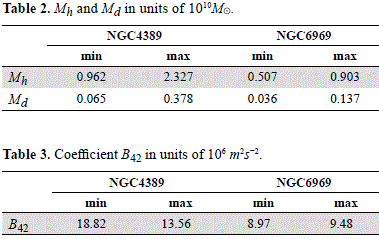
In Table 2 we present, based on the values obtained by the condition (55) and plotted in the Figure 1, the minimum and maximum values for the halo mass of each galaxy and the disc mass calculated from the relations (56) and (57), in units of 10¹⁰M·o, whereas in Table 3 we present the respectives values of the coefficient B₄₂, in units of 10⁶ m²s^-2.

In Figure 2, we show the adjusted rotation curve for these two galaxies. The points with error bars are the observations as reported in Verheijen and Sancisi (2001), while the solid line are the circular velocity determined from (37) and the A₂₁ parameters given by the best fit. As we can see, for the two galaxies we get a fairly accurate numerical adjustment with the observational rotation curve.

In figure 3 we show the epicycle frequency for the two galaxies. It is easy to see that this quantity is always positive, which means that the galaxies are stable against radial perturbations. In figure 4 we present the vertical frequency for the two models. For the two galaxies, the solid line represent the vertical frequency by taking the minimum value for the halo mass, whereas the dashed line represent the vertical frequency by using the maximum value for the halo mass. As can be notice in the figure, for the two galaxies the vertical frequency is positive over the entire range of ˜R, so the models are stable against vertical perturbations. It is easy to verify that for any other value of the halo mass and the corresponding parameter B₄₂, as determined from figure 1, the vertical frequency remains positive in all range ˜R.

In Figure 5 we present the corresponding plots of the surface mass density for the two galaxies. As in the previous case, for both galaxies the solid line represents the behavior of the surface mass density by taking the minimum value for the halo mass, while the dashed line is the surface mass density for the maximum value of the halo mass. The behavior of this quantity is similar for both galaxies, i.e. the surface mass has a maximum value at the disc centre and then decreases as ˜R increases, vanishing at the disc edge.

Finally, from (28), in figure 6 we show the contours of the halo density distribution for the galaxy NGC4389. In plot (a), the contours are drawn using the minimum value for the halo mass, while in plot (b) we present the contours using the maximum value for the halo mass. Similarly, in figure 7 we show the same quantities, but for the galaxy UGC6969. In both cases, the density profiles are positive and do not have discontinuities in all range ˜R, z, taking a maximum value at center and smoothly decreasing to zero when ˜R → ∞.

Concluding Remarks

We have presented a family of analytical potentials for flat galaxies with spheroidal halos characterised by a linear relationship between the halo mass and the disc mass. The models are stable against radial and vertical perturbations, and their circular velocities can be adjusted very accurately to the observed rotation curves of some specific galaxies. The here presented models are a generalisation of the models presented in González, Plata-Plata and Ramos-Caro (2010), where only models with a thin galactic disc are considered. The generalisation was obtained by adding to the gravitational potential of the thin disc the gravitational potential corresponding to a spheroidal halo, in such a way that we have solved the problem of vertical unstability presented by the previous models.

Two particular models were obtained by a numerical fit of the general expression (37) for the circular velocity with the observed data of the rotation curve of galaxies NGC4389 and UGC6969. For these two galaxies we have obtained a fairly accurate numerical adjustment with the rotation curve and, from the constants A₂₁ obtained with the numerical fit, we compute the values of the halo mass, the disc mass and the total mass for these two galaxies in such a way that we obtain a very narrow interval of values for these quantities. Furthermore, the values of masses here obtained are in agreement with the expected order of magnitude, between about 10⁸ and 10¹² M·o, and with the relative order of magnitude between the halo mass and the disc mass, M_d / M_h ≈ 0.1, (Ashman, 1990). Accordingly, we believe that the values of mass obtained for the two studied galaxies may be taken as a very accurate estimate of the upper and lower bounds for the mass of the galactic disc and for the mass of the spheroidal halo in these two galaxies. Additionally, the density profiles obtained satisfy several conditions which are necessary to describe real galactic systems, i.e. they are positive and not have discontinuities in all range ˜R, z, taking a maximum value at center and smoothly decreasing its value to zero when ˜R → ∞.

However, although we tested the applicability of the present model with all the galaxies reported by Verheijen and Sancisi (2001), consistent models were obtained only for the two galaxies NGC4389 and UGC6969, whereas for all the other galaxies were obtained models with values of the halo mass such that the condition (55) is not satisfied. Now, it can be considered that this result occurs as a consequence of the simple halo model that we have taken here. Indeed, as we can see from expressions (26) and (27), only one term of the gravitational potential of the halo contributes to their density, what leaves only one free constant to be determined in order to fit the model to the imposed consistency conditions. This constant is precisely the mass of the halo, M_h, which is determined by requiring the positiveness of the vertical frequency and the surface mass density. On the other hand, if we consider additional terms in expression (27) for the halo potential, we will have new free parameters that perhaps allow to better adjust the model to properly describe the behavior of other galaxies besides the two considered here.

In agreement with the above considerations, we can consider the simple set of models here presented as a fairly good approximation to obtaining quite realistic models of galaxies. In particular, we believe that the values of mass obtained for the two galaxies here studied may be taken as a very accurate estimate of the upper and lower bounds for the mass of the galactic disc and for the mass of the spheroidal halo in these two galaxies. Accordingly, we are now working on a more involved model, obtained by including additional terms in expression (27) for the halo potential, in order to get some particular models that can be properly adjusted with the observed data of the rotation curve of some other galaxies besides the two here considered.

Acknowledgments

The authors were supported in part by VIE-UIS, under grant number 1838, and COLCIENCIAS, Colombia, under grant number 8840. JIR wants to thank the support from VicerrectoríaAcadémica, Universidad Santo Tomás, Bucaramanga.

Conflict of interest

The authors declare that they have no conflict of interest.

References

Arfken, G. and Weber, H. (2005). Mathematical Methods for Physicists. 6th ed. Academic Press.         [ Links ]

Ashman, K. M. (1990). The origin of mass, disk-to-halo mass ratio and L-V relation of spiral galaxies. Astrophys. J., 359, 15.         [ Links ]

Bateman, H. (1944). Partial Differential Equations. Dover.         [ Links ]

Bevington, P. and Keith, D. (2003). Data Reduction and Error Analysis for the Physical Sciences. 3rd Ed., Mc Graw Hill.         [ Links ]

Binney, J. and Merrifield, M. (1998). Galactic Astronomy. Princeton University Press.         [ Links ]

Binney, J. and Tremaine, S. (2008). Galactic Dynamics. 2nd ed. Princeton University Press.         [ Links ]

Brun, R. and Rademakers, F. (1997). ROOT - An object oriented data analysis framework. Nucl. Instrum. Meth. in Phys. Res. A, 389, 81.         [ Links ]

González, G. A., Plata-Plata, S. and Ramos-Caro, J. (2010). Finite thin disk models of four galaxies in the Ursa Major cluster: NGC3877, NGC3917, NGC3949 and NGC4010. MNRAS, 404, 468.         [ Links ]

González, G. A. and Reina, J. I. (2006). An infinite family of generalized Kalnajs disks. MNRAS, 371, 1873.         [ Links ]

Faber, T. (2006). Galactic halos and gravastars: static spherically symmetric spacetimes in modern general relativity and astrophysics, M. Sc. Thesis in Applied Mathematics, Victoria University of Wellington.         [ Links ]

Hunter, C. (1963). The structure and stability of self-gravitating disks. MNRAS, 126, 299.         [ Links ]

Kalnajs, A. J. (1972). The equilibria and oscillations of a family of uniformly rotating stellar disks. Astrophys. J., 175, 63.         [ Links ]

Lamb, H. (1945). Hydrodynamics. Dover.         [ Links ]

Morse, P. M. and Fesbach, H. (1953). Methods of Theoretical Physics, Mc Graw Hill.         [ Links ]

Pedraza J. F., Ramos-Caro J. and González G. A. (2008). An infinite family of self-consistent models for axisymmetric flat galaxies. MNRAS, 390, 1587.         [ Links ]

Pierens, A. and Hure, J. (2004). Rotation curves of galactic disks for arbitrary surface density profiles: a simple and efficient recipe. Astrophys. J., 605, 179.         [ Links ]

Ramos-Caro J., López-Suspez F. and González G. A. (2008). Chaotic and Regular Motion Around Generalized Kalnajs disks. MNRAS, 386, 440.         [ Links ]

Schödel, R. et al. (2002). A star in a 15.2-year orbit around the supermassive black hole at the centre of the Milky Way. Nature, 419, 694.         [ Links ]

Verheijen, M. A.W. and Sancisi, R. (2001). The Ursa Major cluster of galaxies. IV. HI synthesis observations. Astron. Astrophys., 370, 765.         [ Links ]