doi: http://dx.doi.org/10.18257/raccefyn.351

¹ Department of Mathematics, Western Illinois University, 476 Morgan Hall, 1 University Circle, Macomb, IL 61455, U.S.A., CF-Ealy@wiu.edu
² Departamento de Matemáticas, Universidad de los Andes, Cra 1 No. 18A-10, Edificio H, Bogotá, Colombia, aonshuus@uniandes.edu.co *Corresponding autor: Alf Onshuus, aonshuus@uniandes.edu.co

Received: March 11, 2016. Accepted: December 2, 2016

Abstract

We use the construction of an independence relation to prove that þ-forking is equivalent to forking of a stable formula (in the sense of st-forking, see Definition 1.3) in all theories, and to show that from þ-dividing one can always achieve strong dividing over a base which is in the definable closure of the parameter set.

Key words: Stable Forking Conjecture, þ-Forking.

Resumen

Usamos una contrucción particular de una relación de independencia para demostrar que en cualquier teoría þ-bifurcación es equivalente a bifurcación con una fórmula estable (en el sentido específico de st-bifurcación dada en la Definición 1.3). También demostramos que si tenemos þ-división podemos lograr división fuerte sobre una base que pertenece a la clausura algebraica del conjunto parámetro.

Palabras clave: Conjetura de Bifurcación Estable, þ-Bifurcación.

1. Introduction

Notions of size and dimension have been key invariants in mathematics for a long time. It was "Peano's Curve", a continuous surjective mapping from the interval (0, 1) to the whole plane, which was so counterintuitive that trying to understand this phenomenon prompted great contributions to general topology.

This concept of dimension has been generalized within model theory by abstract independence notions, starting with Morley's rank (Morley (1965)) which then turned into Shelah's definition of forking (see for example Shelah (1990)) which turned out to be the most important notion in the development of stable and simple theories. For a long time forking was seen as the correct generalization of topological dimension, but it had the limitation of only working in the appropriate contexts: simple and stable theories.

In the early 2000's, we started studying a new independence notion called þ-forking (see for example Onshuus (2006)). The construction was similar to Shelah's forking, except that instead of requiring sets indexed by an indiscernible sequence to be "almost disjoint" (k-inconsistent), we required sets with parameters varying over definable families to be k-inconsistent. This lead to a notion of independence which captured both forking in stable theories and topological independence in o-minimal theories. It was later that we understood, when analyzing the role of forking and þ-forking in the context of the real numbers, that forking was much closer to a notion of "largeness" derived from measure theory than the notion of geometric dimension it was thought to generalize. The reason that in stable contexts forking gave us a notion of dimension was simply there these two notions coincided. Let us explain what we mean by this.

In the real plane, lines and points are "smaller" than the whole plane, and this is captured by having smaller dimension (þ-forking). The unit square, however, also has dimension 2 but it is still smaller than the plane in the sense that it has finite measure: finitely many translates of the box cannot cover the plane. Bounding a set in the sense of measure causes forking, and forking-wise the box is smaller than the plane. Making it smaller in the sense of dimension causes þ-forking, and while the line and a point are smaller than the plane in the sense of þ-forking, the box is not.

The reason that for many years model theorists believed forking (and Morley rank) was a generalization of dimension is that in the right context, (such as algebraic geometry) the two notions coincide: Given a (complex) algebraic group (G, ·) and an algebraic subset X of the same dimension as G, we know that G is always covered by finitely many cosets of X (sets of the form a · X with a∈ G). More generally, given an algebraic variety X (over the complex field C), then one cannot find infinitely many disjoint subvarieties of X of the same dimension. The reader should compare this fact with the example in the paragraph above: Not only can one find infinitely many dis-joint squares with sides of length 1 in R² , but one needs infinitely many sets of the form a¯ + [0, 1]² to cover the group (R² , +).

One context in which the two relations agree is that of stable theories. This was made explicit in Onshuus (2006) and can even be stated at a local level (as stated in Fact 3.2). And the fact that the two notions agree in stable theories is a very strong property of this class of theories, as is proved in the first author's Ph.D. thesis (Ealy (2004)) and also in Adler (2009): in any theory any notion of independence (in the sense of Kim and Pillay (1997), Definition 4.1) is stronger than þ-forking and weaker than forking. Thus, if þ-forking and forking coincide then they define the only possible abstract independence relation in the theory.

In this paper we continue the study of forking and þ-forking. In particular, we will focus on the role of stable formulas. In many theories with a well-behaved independence relation, one finds that dependence is often witnessed by stable formulas. Most famously, one has the Stable Forking Conjecture for simple theories*, but this phenomena extends beyond simple theories. For instance, in a real closed field, o-minimal dependence (i.e. þ-forking) is always witnessed by a stable formula.

One approach would be simply to define an independence relation using, in some sense, only stable formulas. However, here a few obstacles immediately present themselves. Whether or not a formula is stable depends not only on the formula itself, but also on how the variables are divided into parameter and object variables. For this (and other reasons), the set of stable formulas changes as the language is expanded by constants. When model theorists say a set is "definable", quite often "definable with parameters" is the default meaning, and one says "empty set definable" if one means definable without parameters.

In this paper, we explore stable forking understanding the precise use of parameters. We assume the reader is familiar with the basic model theoretical terms. We will use upper case letters A, B, C to denote sets, while lower case letters a, b, c will denote tuples of elements. Variables x and y will be used as tuples of variables.

1.1. Results

Definition 1.1. Let T be a theory with language L, and let M be a model of T. For B⊂ M, denote by L_B the language L expanded by constant symbols for elements of B.

• A formula j(x, y) in L(B) is stable if there are no B-indiscernible w-sequences áa_iñ and ác_iñ such that M ç= j(a_i , c_j ) if and only if i ≤ j.
• Given formula j(x, y) in L(B), some parameter c∈ M and some A, we say that j(x, c) divides over A if there is a ( A∪ B)-indiscernible sequence ác_iñ with c= c₀ such that

is inconsistent with Th(M).

Definition 1.2. Denote by L_B the language L expanded by constant symbols for elements of B. If the following two conditions hold

(1) there is B such that j(x, c) is a stable L_B formula
(2) j(x, c) divides over A (again, in L_B)

then we say j(x, c) stably divides with parameters (w.p.) over A.

A type tp(a/C) with A⊆ C stably divides (w.p.) over A if it contains a formula j(x, c) which stably divides (w.p.) over A.

If tp(a/C) implies a disjunction of formulas, each of which stably divides (w.p.) over A we say tp(a/C) stably forks (w.p.) over A. We write a 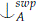C to mean tp(a/AC) does not stably fork (w.p.) over A.

The following is the main result of this paper.

Theorem 3.3 Suppose A⊆ C. Then tp(a/C) þ-forks over A⊆ C if and only if tp(a/C) stably forks (w.p) over A. Furthermore, if tp(a/C) stably divides (w.p.) over A, the parameters witnessing this, B, may always be taken A⊆ B⊆ C.

The right to left direction of the theorem was proved in the thesis of the second author (Onshuus (2002)) and is explicitly quoted in Fact 3.2. The left to right direction is proved in this paper.

Theorem 3.3 has the following weak version of the Stable Forking Conjecture as a corollary, as þ-forking and forking coincide in simple theories that eliminate hyperimaginaries. (This latter class, one recalls, is known to include large classes of simple theories, such as supersimple theories, and conjecturally includes all simple theories.)

Corollary 3.4 In a simple theory that eliminates hyperimaginaries, if tp(a/C) forks over A⊆ C, then it stably forks (w.p.) over A. Furthermore, if tp(a/C) stably divides (w.p.) over A, the parameters witnessing this may always be taken A⊆ B⊆ C.

In addition, we explore what our methods can say about stable forking without additional parameters. To this end we make the following definition.

Definition 1.3. Now we will give a new notion of "stable dividing" which we will call "st-dividing". A formula j(x, c) st-divides over A if there is a tuple b∈ C, a definable function (without parameters) f(x, y), and a stable q(w, y) such that

(1) j(x, c) implies q( f(x, b), c)
(2) q(w, c) divides over Ab.

Given a type tp(a/C) with A⊆ C st-divides over A if it contains a formula which st-divides over A. Finally, if tp(a/C) implies a disjunction of formulas which st-divide over A, then we will say that tp(a/C) st-forks over A.

We write a 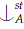C to mean tp(a/ AC) does not st-fork over A.

We have the following theorem and corresponding corollary:

Theorem 3.6 Suppose A⊆ C. Then tp(a/C) þ-forks over A⊆ C if and only if tp(a/C) st-forks over A.

Corollary 3.7 In a simple theory that eliminates hyperimaginaries, if tp(a/C) forks over A⊆ C, then it st-forks over A.

Finally, we observe that the method of proof for Theorems 3.3 and 3.6 also yields new information about þ-dividing. Recall that a formula j(x, c) þ-divides over A when there is a tuple b so that j(x, c) strongly divides over Ab.

Corollary 4.2 If a formula j(x, c) þ-divides over A then the tuple b so that j(x, c) strongly divides over Ab may be taken from dcl(Ac).

2. *-independence

In this section, we will work with *-independence, where the * is to be understood as a wildcard, later to replaced with "stable (w.p.)" or "st" or þ. First, we will prove a general statement about independence relations (understood just as a ternary relation with additional properties we will explicitly mention), and then we will describe a method of obtaining independence relations satisfying the properties we desire, before turning to particular independence relations in subsequent sections.

Recall the definition of þ-forking.

Definition 2.1. Let j(x, c) be any formula. We say j(x, c) strongly divides over A if cis not algebraic over A and there is an A-formula q(y) satisfied by c such that

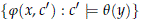
is k-inconsistent for some k. We say j(x, c) þ-divides over A if it strongly divides over Ab for some b. Finally, j(x, c) þ-forks over A if it implies a disjunction of formulas, each of which þ-divides over A.

One says that tp(a/C) strongly divides over A if it contains a formula that does so. Note that this is the same as saying there is c∈ C such that c∈ acl(Aa) \ acl(A).

We assume the reader is familiar with the properties of monotonicity and extension, but the reader may also refer to Lemmas 2.6 and 2.7, respectively, for the definitions.

Definition 2.2. An independence relation for a theory is a automorphism invariant ternary relation on small (compared to the saturation) subsets of a monster model of that theory.

Note that this is a far weaker definition than a notion of independence in the sense of Kim and Pillay (1997) mentioned in the introduction.

Definition 2.3. If a 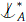C whenever there is c∈ C with c∈ acl(aA) \ acl(A) then we say 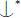is antireflexive.

Theorem 2.4. Let *-independence be an independence relation. Then, for any element a and B⊂ C the following hold.

(1) If tp(a/C) does not *-fork over B and *-independence is antireflexive, then tp(a/C) does not strongly divide over B.
(2) If tp(a/C) does not *-fork over B and *-independence satisfies monotonicity, extension, and anti-reflexivity, then tp(a/C) does not þ-fork over B.

In particular, if a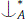 b then a 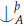b.

Proof. (1). Since strong dividing gives us c∈ C with c∈ acl(aA) \ acl(A), this is simply anti-reflexivity.

(2). First we show that tp(a/C) does not þ-divide over B. Assume otherwise, so that by definition there is some c∈ C, a formula j(x, y) such that j(a, c) holds, and some tuple dsuch that j(x, c) strongly divides over Bd.

Since a 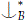c, by extension there is some a' such that a' 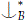cd and such that a' satisfies the same type as a over Bc (so in particular j(a' , c) holds). Thus tp(a' /Bcd) strongly divides over Bd, and by (1) this implies that a' 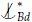cd, and by monotonicity, a' 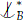cd, a contradiction.

That *-independence implies þ-independence now follows immediately from extension.

Now we will describe how to build from a basic notion of independence, an independence relation satisfying mono- tonicity and extension. We will call our basic notion *- strong-dividing, in analogy to the definition of þ-forking. Then we will modify it to get *-dividing which will satisfy monotonicity, and finally go from *-dividing to *-forking, in the traditional fashion, to ensure extension.

Suppose we have a notion of what it means for a formula j(x, c) *-strong dividing over a set A, such that when- ever j(x, c) *-strong divides over A there is a finite tuple a¯ ∈ A such that j(x, c) *-strong divides over A₀ for any a¯ ⊆ A₀ ⊆ A.

Definition 2.5. We will say that a formula j(x, c) *- divides over A if there are tuples c¯, b¯ ∈ C, an A-definable function f(x, y) and a formula q(z, c¯) such that

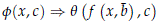
and q(z, c¯) *-strong-divides over Ab¯ .

We will say that tp(a/C) *-divide s over A if it has a formula which *-divides over A.

We will say that a type tp(a/C) *-forks over A, with A⊂ C, if it implies a finite disjunction of formulas, each of which *-divides over A. We will in general say that a 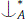B if tp(a/ A ∪ B) does not *-fork over A.

The following then holds by construction

Lemma 2.6 (Monotonicity). If tp(a/C) is a type and A⊂ B⊂ C, then tp(a/C) *-divides over A whenever tp(a/C) *-divides over B or when tp(a/B) *-divides over A. The corresponding statement for *-forking holds as well.

Proof. Let A⊆ B⊆ C. If tp(a/B) *-divides over A then it implies a formula which *-divides over A, and so does tp(a/C). Likewise, if tp(a/B) *-forks over A, so does tp(a/C).

Now, if tp(a/C) *-divides over B then by definition there are tuples d¯, c¯ and a formula q (f (x, d¯) , c¯) where f(x, y) is a B-definable function, and q(z, c) *-strong divides over Bd¯.

By hypothesis on *-strong dividing, there is a tuple b¯₀ such that q(z, c) *-strong divides over Ab¯₀ d¯. Let b¯₁ be a tuple in B such that f(x, y) = f_A(x, y, b¯1 ) where f_A is A-definable. Let k¯ = b¯₀^b¯₁^d¯. Then:

• We can write q (f (x, d¯) , c¯) as q (f (x, k¯) , c¯), and
• q (f (x, k¯) , c¯) *-strong-divides over Ak¯ .

Since tp(a/C) l= q (f (x, k¯) , c¯), we have that tp(a/C) *- divides over A, as required.

Suppose that tp(a/C) *-forks over B, i.e. there is an E⊇ C such that each extension of tp(a/C) to E*-divides over B. By monotonicity of *-dividing, each such extension also *-divides over A. Thus tp(a/C) *-forks over A.

Lemma 2.7 (Extension). If A ⊂ B ⊂ C and p(x) is a type with parameters in B which does not *-forks over A, then we can extend p(x) to a type p_C(x) with parameters in C and which does not *-fork over A.

Proof. This is word by word the same proof as in the dividing-forking case, see for example Theorem 1.4 in Chapter III of Shelah (1990).

In the following sections, we will be concerned with *- dependence derived from two *-strong-dividing notions. The first, where *-strong-dividing is stable dividing, will give rise to st-forking. The second notion is where we take *-strong dividing is strong dividing (see Onshuus (2006)); we will prove that this latter notion is equivalent to þ-forking, which should not be quite surprising since the definition makes the notion very close to þ-forking, but we will be able to understand properties for þ-forking which were previously unknown.

Up until now, we were emphasizing what the *- construction gave us in terms of monotonicity. However, when *-strong-dividing is stable dividing, it already has monotonicity, and the additional information achieved by the *-construction comes in terms of anti-reflexivity. Specifically we have the following complement to Theorem 2.4.

We start with the following definition.

Definition 2.8. We will say that a *-strong-dividing notion respects algebraicity if q(x, b) *-strong-divides over C for any any b∉ acl(C) whenever q(x, y) is a formula without parameters such that

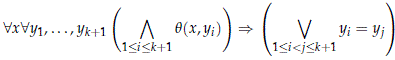
for some k∈ N.

Theorem 2.9. Any *-independence notion constructed (as described above) from a *-strong-dividing notion which respects algebraicity satisfies anti-reflexivity.

So if a *-strong-dividing notion respects algebraicity, then the related *-independence notion satisfies monotonicity, extension and anti-reflexivity and therefore implies þ-independence.

Proof. Assume otherwise, so that a 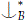c but c∈ acl(aB) \ acl(B). Let j(a, b, c) witness such algebraicity with b∈ B, and let j' (xy, z) be the formula (over M^eq ) which groups the first and second variables and the third one as imaginaries (instead of tuples). Since *-strong-dividing respects algebraicity we have that j' (xy, c) must *-strong-divide over B, but by definition this implies that tp(a/Bc) *- divides over B, as required.

The rest follows from Theorem 2.4.

3. Stable Forking

First we will prove Theorem 3.3. Although the result might not seem as strong as the other statements we prove, the proof is short and illustrates why the methods in this paper do not yield the full Stable Forking Conjecture.

Lemma 3.1. Let a be an element and B⊂ C. Then if a 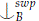B C then a 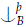C

Proof. Stable dividing (w.p.) clearly satisfies monotonicity, and by the proof of Lemma 2.6, we see that stable forking (w.p.) satisfies monotonicity as well, and of course, it satisfies extension. Thus it remains only to show that it satisfies anti-reflexivity. Suppose that c ∈ acl(Ba) \ acl(B), witnessed by a(c, ba) where b is a tuple in B and such that a(z, b' a' ) has only finitely many realizations. The formula a(z, yx) is of course a stable formula, but a(zy, x) need not be. But adding the constant b to the language means that algebraicity is witnessed by the a(c, a), and a(c, x) witnesses anti-reflexivity of stable forking (w.p.).

The converse of Lemma 3.1 follows from Theorem 5.1.1 in Onshuus (2006):

Fact 3.2. Let T be any theory, M be any model of T and A= acl( A) be any subset of M, and a and b be tuples in M and let j(x, y) be a stable formula without parameters. Suppose that p(x) is a type over Ab containing a j-formula (boolean combination of y-instances of j) which forks over A. Then p(x) þ-forks over A.

Theorem 3.3. tp(a/C) þ-forks over A⊆ C if and only if tp(a/C) stably forks (w.p) over A. Furthermore, if tp(a/C) stably divides (w.p.) over A, the parameters witnessing this, B, may always be taken A⊆ B⊆ C.

Proof. Left to right is Lemma 3.1. Right to left is Fact 3.2 together with the observation that, unlike stable forking, removing parameters from the language can only increase the amount of þ-forking. The restriction that A ⊆ B ⊆ C may be obtained by adding this to the definition of stable dividing (w.p.) and noting that monotonicity, extension, and antireflexivity still hold.

Since by Ealy (2004) in any simple theory which eliminates hyperimaginaries forking and þ-forking coincide, this provides a proof of a weak Stable Forking Conjecture in simple theories which eliminate hyperimaginaries.

Corollary 3.4. In a simple theory that eliminates hyperimaginaries, if tp(a/C) forks over A⊆ C, then it stably forks (w.p.) over A. Furthermore, if tp(a/C) stably divides (w.p.) over A, the parameters witnessing this may always be taken A⊆ B⊆ C.

We will now prove that st-independence is equivalent to þ-forking. One direction follows easily from Theorem 2.9.

Lemma 3.5. Let a be an element and B⊂ C. Then if a 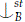C the a 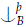C.

Proof. Note that st-forking is just the independence relation obtained by letting *-strong dividing be dividing witnessed by a stable formula. Thus, by Theorem 2.9, we just need to show that stable dividing respects algebraicity. But this is clear since any formula q(x, y) without parameters satisfying

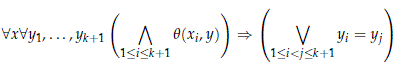
is a stable formula, and q(x, c) divides (in the usual sense) over A whenever c ∉ acl(A).

Theorem 3.6. Let T be any theory, M be any model of T and A= acl(A) be any subset of M, and a and b be tuples in M. Then

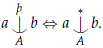
Corollary 3.7. In a simple theory that eliminates hyperimaginaries, if tp(a/C) forks over A⊆ C, then it st-forks over A.

Proof. One direction is Lemma 3.5. For the converse, we will first prove the following lemma.

Lemma 3.8. Suppose that tp(a/ Ab) st-divides over A. Then a 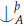b.

Proof. By definition, there is a stable formula q(x, y) and some b0 ∈ dcl( Ab) and some definable function f(x, w) such that

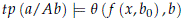
and q(x, b) divides over Ab₀. By Fact 3.2 we have f(a, b₀) 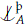b₀ b which implies a 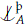b by monotonicity and partial left transitivity, (Lemmas 2.1.3 and 2.1.6 in Onshuus (2006)).

The rest is pretty standard. If a 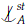b then for some finite tuple e we have that every extension of tp(a/ Ab) to Abe st-divides over A. By the lemma, this implies that every extension from tp(a/ Ab) to Abe þ-forks over A, but þ-independence always satisfies extension, so a 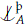bas required.

Observation: There is a caveat when going from stable dividing to st-dividing, which is particularly problematic when looking for canonical bases, as can be seen in Pillay's example of an o-minimal theory without canonical bases, which we will now describe: bases, which we will now describe:

Let R be a non standard real closed field, and let a be a transcendental real number. Let R_a be the reduct of R where we preserve only addition and the restriction of multiplication by a to the open unit interval. Now, let b, cbe infinite (meaning larger than any integer number) numbers in R_a such that (b - c) ∈ (0, 1), and let d= a(b - c)+ a. Then tp(a/bcd) has no canonical bases.

To understand what happens with st-forking and why this cannot help us with canonical bases, let j(x, y, z, w) := w= a(y - z) + x, and notice that j(a, b, c, d) witnesses that ac 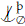bd.

So tp(ac/bd) ⇒ j(x, b, z, d), the formula j' (xyz, w) := j(x, y, z; w) is stable and j' (xyz, d) divides over bc, so tp(a/bcd) st-forks over Ø. But the canonical parameter of j' (xyz, d) is ditself which is too small to be definable from what the canonical base of tp(a/bcd) should be.

4. On þ-forking

Combining the definitions of strong dividing and þ-dividing given in the previous section (together with compactness), we have that j(x, c) þ-divides over A if for some bvwe have c∉ acl(Ab) and

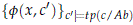
is k-inconsistent for some k.

A long standing question was whether we could say something about where to find the parameter b which allowed us to go from þ-dividing to strong dividing. We can now answer this.

Start with the definition of strong dividing, and since it is clear that strong dividing respects algebraicity, if we apply the *-construction to strong dividing we get, by Theorem 2.9, an independence notion which implies þ- independence.

Conversely, it is also clear that the dividing notion we get implies þ-dividing: the *-definition of "dividing" is more restrictive since it requires the extra parameter to come from the parameter set of the type.

By analyzing precisely what is going on, we get the following.

Theorem 4.1. If we redefine þ-forking by defining a formula j(x, c) þ-divides over A if there is some b∈ dcl(Ac) such that j(x, c) strongly divides over Ab, then the corresponding notion of þ-independence is equivalent to þ-forking.

Proof. If we take the dividing notion corresponding to strong dividing (according to Definition 2.5), then we have that a formula j(x, c) *-divides over A if there are tuples c¯, b¯ ∈ dcl( Ac), an A-definable function f(x, y) and a formula q(z, c¯) such that

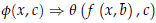
and q(z, c¯) strong-divides over Ab¯ .

By definition c ∉ acl(Ab¯) and there is some Ab¯-definable p(y) such that p(c) holds and

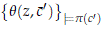
is k-inconsistent.

But of course this implies that both

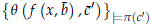
and

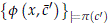
are k-inconsistent.

It follows that if a formula *-divides then it þ-divides and we can find the elements that makes it strongly divide from the definable closure of the parameter set which is a big improvement in our understanding of þ-forking. This proves the following corollary.

Corollary 4.2. If a formula j(x, c) þ-divides over A then the tuple b so that j(x, c) strongly divides over Ab may be taken from dcl(Ac).

Observation: It is important to notice that our result is just for þ-dividing and not for þ-forking. For example, take the projective plane with sorts for points and lines and the incidence relation ∈ between the sort (where p ∈ L if p is a point in the line L).

Let p and L be a point and a line with p∈ L. Then clearly, p 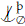L (the formula x∈ L þ-forks over Ø). If q us any other point in L, then this þ-forking can be witnessed b

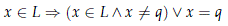
and both this formulas þ-divide over Ø. The formula x∈ L∧ x ≠ q strongly divides, as indicated by Theorem 4.1, over q.

We do not believe, however, that the formula x∈ L implies formulas which strongly divide over some subset of dcl(L). A þ-forking version of Theorem 4.1, is that in any theory and given any a, a model M and a subset A⊂ M then a 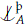M can always be witnessed by a disjunction of formulas over with parameters in Meach of which þ-divides over M. This is true, but it follows mainly from the fact that all the instances in the definition of þ-forking can be found in a w-saturated model M. One can then drop the w-saturation assumption using Theorem 4.1.

___________

* Whether or not an instance of forking in simple theories can always be witnessed by a stable formula is probably the most important open question in simple theories. We refer to Kim (2001) and Kim and Pillay (2001) for a good review of the subject, and Palacín and Wagner (2013) for the most recent advances in the conjecture.

References

Adler, H. (2009). A geometric introduction to forking and thorn-forking. J. Math. Log., 9(1):1-20.         [ Links ]

Ealy, C. (2004). Thorn Forking in Simple Theories and a Manin-Mumford Theorem for T-Modules. Thesis (Ph.D.)- University of California, Berkeley.         [ Links ]

Kim, B. (2001). Simplicity, and stability in there. J. Symbolic Logic, 66(2):822-836.         [ Links ]

Kim, B. and Pillay, A. (1997). Simple theories. Ann. Pure Appl. Logic, 88(2-3):149-164. Joint AILA-KGS Model Theory Meeting (Florence, 1995).         [ Links ]

Kim, B. and Pillay, A. (2001). Around stable forking. Fund. Math., 170(1-2):107-118. Dedicated to the memory of Jerzy Łosss´.         [ Links ]

Morley, M. (1965). Categoricity in power. Trans. Amer. Math. Soc., 114:514-538.         [ Links ]

Onshuus, A. (2002). Thorn-forking in rosy theories. ProQuest LLC, Ann Arbor, MI. Thesis (Ph.D.)-University of California, Berkeley.         [ Links ]

Onshuus, A. (2006). Properties and consequences of thorn-independence. J. Symbolic Logic, 71(1):1-21.         [ Links ]

Palacín, D. and Wagner, F. O. (2013). Elimination of hyperimaginaries and stable independence in simple CM- trivial theories. Notre Dame J. Form. Log., 54(3-4):541-551.         [ Links ]

Shelah, S. (1990). Classification theory and the number of non-isomorphic models, volume 92 of Studies in Logic and the Foundations of Mathematics. North-Holland Publishing Co., Amsterdam, second edition.         [ Links ]