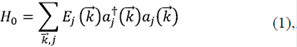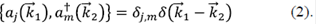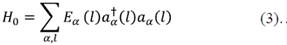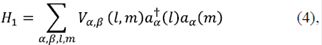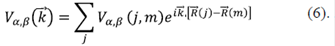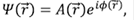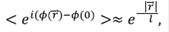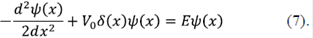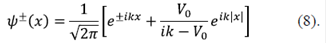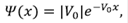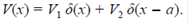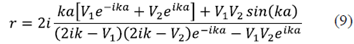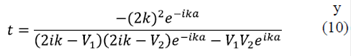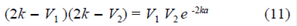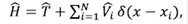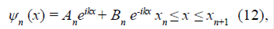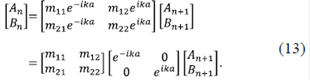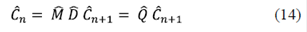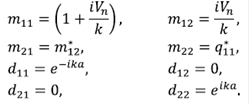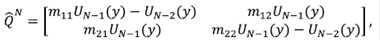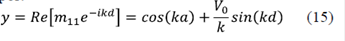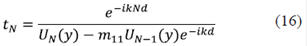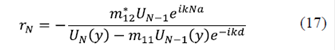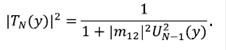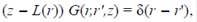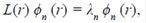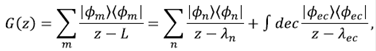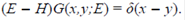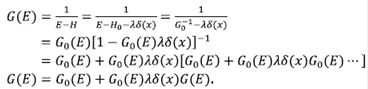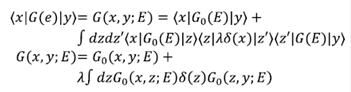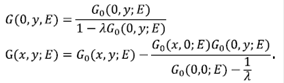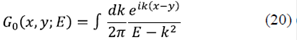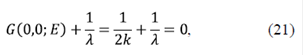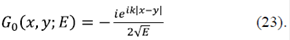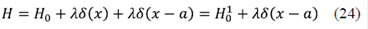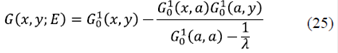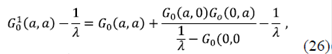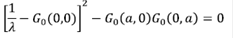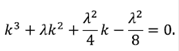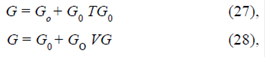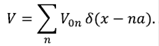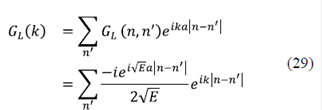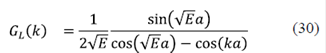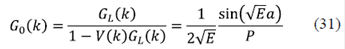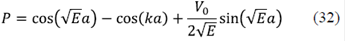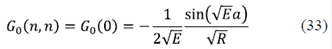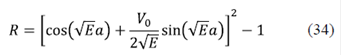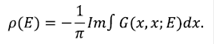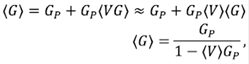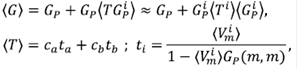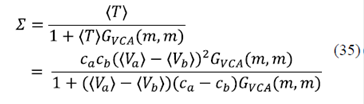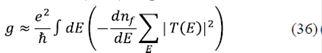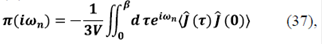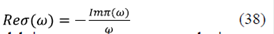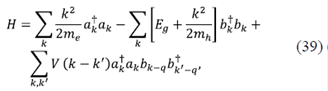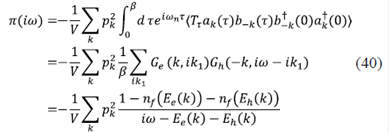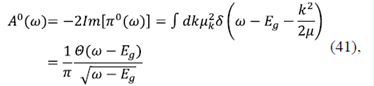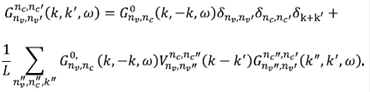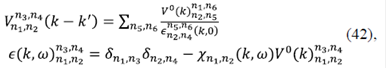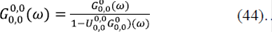Introducción
Los sistemas de materia condensada, como los sólidos, los líquidos y los gases, constituyen el laboratorio natural para estudiar las propiedades clásicas y cuánticas de la interacción entre la radiación y la materia. Específicamente en sistemas de estado sólido, los átomos están arreglados en estructuras muy ordenadas, o cristales. Estos cristales se pueden organizar de forma natural en estructuras tridimensionales que obedecen a ciertas formas básicas, las cuales ayudan a minimizar la energía de configuración. Se sabe que existen cinco formas básicas en estructuras bidimensionales y 18 en estructuras tridimensionales. Sin embargo, recientemente se han creado y fabricado estructuras unidimensionales que se han podido manipular en distintas dimensiones (desde 0 hasta tres dimensiones). En cualquier dimensión, estas estructuras tienen propiedades electrónicas ópticas y de transporte que no son explicables mediante teorías clásicas, y que han llamado la atención de los físicos experimentales y de los teóricos. Entre dichas propiedades cabe mencionar las siguientes: 1) que los estados de energía están localizados en estructuras unidimensionales y no en dos o tres dimensiones (P. W.Anderson, 1958), y 2) que no existen transiciones de fase en sistemas unidimensionales a temperatura finita con interacciones de corto alcance (L. D.Landau, E. M. Lifshitz, 1980). Sin embargo, algunos resultados demuestran que puede controlarse la existencia de transiciones de fase en sistemas unidimensionales muy específicos bajo la presencia de campos externos unidimensionales (Van Hove, 1950; D. Ruelle, 1989, J. A.Cuesta & A. Sánchez, 2002).
Cuando se aumenta la dimensión, se presentan fenómenos como el paso de la luz a través de sistemas sólidos bidimensionales que contienen agujeros en sus estructuras. Este fenómeno es importante, pues se ha logrado demostrar experimentalmente que la luz incidente con una longitud de onda mayor que la del tamaño de los agujeros puede atravesar el sólido y no ser reflejada, como se esperaría que sucediera. La explicación teórica de este fenómeno se fundamenta en la distribución espacial de los agujeros en el sólido bidimensional (Pendry, 1993). Estos fenómenos tan raros y exóticos solo pueden explicarse mediante la teoría cuántica.
Por otra parte, se presentan fenómenos en los que muchas partículas, después de interactuar con pocos átomos, pueden llegar a organizarse de una forma colectiva y ser observables macroscópicamente, como sucede con la superconductividad y la condensación de Bose-Einstein, entre otros. Estas manifestaciones forman parte de un área muy interesante denominada “física de muchos cuerpos”. Son problemas de la ciencia de frontera que nos ofrece la naturaleza y cuyo estudio teórico y experimental es muy interesante.
El propósito de este artículo es estudiar algunos de dichos fenómenos de la física de muchos cuerpos que dan idea del alcance de la mecánica cuántica y de sus manifestaciones a nivel macroscópico, entre ellos, la forma en que el orden puede surgir del desorden. Una de las cuestiones más importantes es saber sí cuanto más desordenado sea un sistema, más señales organizadas colectivamente y de largo alcance pueden aparecer, ya que no todo lo que se presenta de forma ordenada constituye la mejor posibilidad de obtener una propiedad colectiva. Para dar respuesta a estas preguntas se presentarán los resultados sobre transporte en sistemas de un solo cuerpo que interactúan con muchos potenciales y las propiedades ópticas en sistemas interactivos de muchos cuerpos modeladas por una interacción de contacto. Estos dos problemas se abordan mediante las técnicas de las funciones de Green (FG) para así establecer la conexión con los experimentos.
Primero, se presentan los estudios relacionados con la interacción de una partícula con muchos potenciales, los cuales pueden cambiar las propiedades de transporte. En particular, se calculan los coeficientes de transmisión y la densidad de estados en sistemas ordenados o desordenados. Dichos coeficientes son importantes para caracterizar estas propiedades en sistemas unidimensionales. En segundo lugar, se analiza una situación un poco diferente, en la que muchas partículas interactúan con un potencial cuasiuniforme, y se demuestra que, como fenómeno colectivo, las propiedades ópticas cambian mucho. Por último, se describe la teoría que conecta los fenómenos de transporte con los ópticos, se calcula el espectro de emisión de luz y se estudia la respuesta óptica de un hilo cuántico para un sistema cuasi-unidimensional que confina muchas partículas. En resumen, se exploran dos límites: sistemas de una partícula y de muchas. Algunos de estos resultados provienen de mi trabajo de tesis de pregrado y de doctorado en física, en la cual se resume una parte de mi actividad como científico en Colombia.
El artículo está organizado en diferentes secciones: inicialmente se presenta una muy breve motivación para estudiar los sistemas unidimensionales; se hace a continuación una introducción al modelo teórico y se desarrolla la teoría que estudia los fenómenos de transporte desde el punto de vista de las matrices de transferencia para diferente número de potenciales de interacción. Después se introduce el concepto de funciones de Green y se demuestra su utilidad para calcular las propiedades ópticas y de transporte de un sistema de muchos cuerpos en interacción con un potencial producido por un hueco en la banda de valencia para, finalmente, presentar las principales conclusiones.
Sistemas electrónicos unidimensionales
Con base en los avances tecnológicos de los últimos años, los sistemas unidimensionales en materia condensada se pueden construir de manera muy detallada, y permiten explorar vertientes muy interesantes de la física, por ejemplo, el bien conocido fenómeno de la inestabilidad de Peierls (1955). Peierls demostró que en sistemas unidimensionales metálicos, es decir, cuya banda de conducción esté parcialmente llena, los electrones pueden reducir colectivamente su energía cinética, de tal forma que por un rompimiento espontáneo de simetría, la banda de conducción se abre en bandas más pequeñas, totalmente llenas y completamente vacías, es decir que un sistema con estas propiedades puede pasar de metálico a semiconductor. Otros resultados demuestran que cuando la banda está a medio llenar, el estado fundamental es aislante, siempre y cuando la longitud de correlación de la interacción entre electrones se aumente ( Lieb & Wu, 1968). También se ha demostrado que, a diferencia de los sistemas tridimensionales y bidimensionales, cuando el electrón interactúa con varios potenciales que varían su intensidad de forma aleatoria, o cuando los átomos con los cuales interactúa están dispuestos de forma aleatoria, los estados son localizados (Anderson, 1958). Pero la física en sistemas unidimensionales de carácter claramente metálico no necesariamente lleva a este tipo de transiciones. Se ha demostrado que en los sistemas magnéticos unidimensionales, los llamados compuestos A15, existen propiedades muy interesantes: cuando el nivel de Fermi se encuentra ubicado cerca del borde de una banda, se produce una transición de fase que se explica por el efecto Jahn-Teller, el cual permite entender el fenómeno de superconductividad a temperaturas altas críticas en algunos compuestos (Jahn & Teller, 1937; Englman, 1972).
Los resultados experimentales no son el único interés, pues los fenómenos que se predicen recurriendo a las nuevas teorías desarrolladas en el campo de los sistemas unidimensionales, en especial en los desordenados, han generado nuevas formulaciones que pueden aplicarse en diferentes áreas de la física. Por ejemplo, el desarrollo de técnicas computacionales para estudiar sistemas desordenados a gran escala, o perturbativas, en las cuales las funciones de Green (Mahan, 1990) constituyen una herramienta fundamental, al no tener que resolver directamente la ecuación de Schrödinger, e, incluso más, cuando se quiere estudiar la dinámica de un observable determinado. Las funciones de Green permiten establecer un método directo para calcular observables que después pueden ser comparados con el experimento. En general, el problema de los sistemas desordenados y de muchos cuerpos ha sido un tema de gran interés teórico y experimental en la comunidad científica en las últimas décadas.
Modelo teórico
En muchas situaciones de la física, se parte de un hamiltoniano que contenga la mayor cantidad de posibles interacciones y que se pueda resolver de la manera más exacta. Si se logra resolver, entonces es posible desarrollar nuevas técnicas teóricas para describir todas las interacciones mediante un modelo efectivo de una sola partícula no interactiva, pero cuya energía renormalizada tenga en cuenta las interacciones más importantes. El hamiltoniano siempre tendrá dos partes: una que corresponde al caso de una partícula libre, y otro término que corresponde a la interacción. Por ejemplo, si un electrón está dentro de un cristal tal que en cada posición haya un átomo que puede aceptar electrones o no, el electrón tendrá una parte de energía cinética que ocupará los niveles de energía permitidos por el cristal. De aquí surge el concepto de bandas de energía según el teorema de Bloch: los orbitales de una sola partícula se pueden asignar a un vector 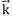 y a un índice de banda m. En un cristal perfecto, es decir, aquel en el que los átomos sean los mismos, o en el que estos se organicen en estructuras periódicas y, por lo tanto, exista una simetría de traslación, el hamiltoniano de una partícula no interactuante, H0, se puede escribir como:
y a un índice de banda m. En un cristal perfecto, es decir, aquel en el que los átomos sean los mismos, o en el que estos se organicen en estructuras periódicas y, por lo tanto, exista una simetría de traslación, el hamiltoniano de una partícula no interactuante, H0, se puede escribir como:
donde cualquier excitación se describe por medio de una banda j y un vector de onda 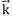 , y pertenece a la primera zona de Brillouin, debido a la simetría de traslación. La energía Ej(
, y pertenece a la primera zona de Brillouin, debido a la simetría de traslación. La energía Ej(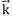 ) se asocia con la (j,
) se asocia con la (j, 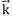 ) - ésima excitación, y aj†(
) - ésima excitación, y aj†(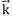 ) y aj(
) y aj(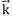 )son los operadores de creación y destrucción fermiónicos que satisfacen las relaciones de anticonmutación:
)son los operadores de creación y destrucción fermiónicos que satisfacen las relaciones de anticonmutación:
Si se desea describir la física de un sistema complicado como si fuera el de una sola partícula, entonces la partícula se “viste” de todas las interacciones y adquiere una nueva energía, que puede ser compleja, y los operadores se convierten en unos nuevos que crean o destruyen las diferentes excitaciones. Esta imagen permite tratar el caso de electrones que interactúan con una red. La red se representa por una serie de sitios, y se describen, entonces, operadores que crean o destruyen excitaciones particulares en celdas unitarias del cristal, lo cual puede lograrse mediante una transformación a una base completa denominada funciones de Wannier (Wannier, 1962). Esta base tiene la característica que representa las funciones de Bloch sobre el espacio real de orbitales localizados y asigna como números cuánticos el vector de la red 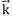 de la celda donde los orbitales están localizados, junto con un índice de banda m. Usando esta transformación, el hamiltoniano se convierte en:
de la celda donde los orbitales están localizados, junto con un índice de banda m. Usando esta transformación, el hamiltoniano se convierte en:
Si, además, se incluye la interacción entre partículas, esta se puede describir con el hamiltoniano H1
donde Eα(l) corresponde a la energía de partícula libre y Vα,β(l,m) representa el término de interacción, el cual depende de la celda unitaria l y de la posición relativa entre diferentes puntos de la red: 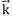 (l) -
(l) - 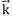 (m). Con el hamiltoniano total se pueden escribir las ecuaciones de Heisenberg en el tiempo para determinar las propiedades dinámicas o estacionarias de los operadores fermiónicos y deducir los estados de energía del sistema. Mediante la representación de Wannier se puede demostrar que los niveles de energía se describen a partir de una ecuación secular:
(m). Con el hamiltoniano total se pueden escribir las ecuaciones de Heisenberg en el tiempo para determinar las propiedades dinámicas o estacionarias de los operadores fermiónicos y deducir los estados de energía del sistema. Mediante la representación de Wannier se puede demostrar que los niveles de energía se describen a partir de una ecuación secular:
En general, y dependiendo del problema, se puede trabajar tanto en el espacio real como en el espacio recíproco. El primero es muy útil para problemas de transporte, en tanto que el segundo es fundamental para estudiar fenómenos ópticos.
Transporte en sistemas unidimensionales
El estudio del comportamiento de un electrón en presencia de un potencial periódico uniforme se cuenta entre los problemas básicos en la física del estado sólido. Este problema se usa bastante para modelar una red perfecta de átomos dispuestos en un arreglo determinado como primera aproximación. Un arreglo periódico de potenciales lleva a lo que conocemos usualmente como modelos tipo Kronig- Penney (Kronig & Penney, 1931). En particular, cuando se quieren describir potenciales atómicos de corto alcance se usan como modelos los potenciales de tipo δ. Asimismo, estos potenciales pueden emplearse para simular impurezas en cristales periódicos. Para un cristal con muchas impurezas, como sucede en los sistemas reales, la solución total y exacta del problema se vuelve complicada e inmanejable, por lo que, claramente, se requieren una serie de aproximaciones para comenzar a entender la física del problema.
Uno de los trabajos pioneros en sistemas desordenados unidimensionales fue el trabajo de Anderson, (1958) “Absence of diffusion in certain random lattices”, en el cual se ocupó del problema del movimiento de un electrón en un potencial desordenado. Anderson demostró por primera vez el fenómeno denominado posteriormente como “localización de Anderson”. Las conclusiones principales se fundamentan en que si la intensidad del desorden es débil, las funciones de onda se comportarán como las de una onda plana, pero sobre una escala de longitud corta. La longitud sobre la cual la fase de la función de onda difiere apreciablemente de la de una onda plana, se denomina ruta de camino libre medio. Sin embargo, cuando el desorden aumenta progresivamente, las fluctuaciones en la amplitud de probabilidad comienzan a ser grandes. Cuando estas fluctuaciones son del orden de la separación entre átomos, o mayor, las amplitudes de las funciones de onda asociadas a los estados propios del sistema comienzan a decaer exponencialmente, produciendo así estados localizados. Es de esperar que, físicamente, los estados localizados aparezcan cuando la longitud libre del camino medio se compara con la longitud de onda del electrón.
Para ilustrar este concepto más fácilmente, se puede pensar en escribir la función de onda en un potencial periódico perfecto como:
donde la amplitud A(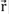 ) es una función periódica de
) es una función periódica de 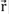 y la fase ϕ(
y la fase ϕ(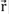 ) =
) = 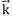 .
.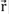 presenta una coherencia perfecta. Sin embargo, si el desorden existe, tanto la amplitud como la fase se deberían ver afectadas. Si el desorden es débil, se asume que la amplitud no varía mucho, pero sí la fase. Se puede, entonces, hacer un promedio estadístico de las fluctuaciones de la fase, y así se demuestra el término:
presenta una coherencia perfecta. Sin embargo, si el desorden existe, tanto la amplitud como la fase se deberían ver afectadas. Si el desorden es débil, se asume que la amplitud no varía mucho, pero sí la fase. Se puede, entonces, hacer un promedio estadístico de las fluctuaciones de la fase, y así se demuestra el término:
donde l = vfτ es la longitud de coherencia de la fase para una velocidad de Fermi vF y un tiempo de recorrido libre medio τ. A partir de esta fórmula se ve claramente que la coherencia de fase se pierde en un punto 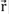 que esté a una distancia mayor o igual a la longitud de coherencia. La importancia de la demostración de Anderson es que permite ver cómo los estados evolucionan hacia estados extendidos cuando el desorden se incrementa. A partir de este trabajo aparecen conceptos como la localización de la función de onda, la fractalidad, los ejes de movilidad en los bordes de zona, etc., los cuales comenzaron a estudiarse ampliamente en la física teórica y experimental de sistemas desordenados. El desorden afecta tanto la densidad de estados como las funciones de onda.
que esté a una distancia mayor o igual a la longitud de coherencia. La importancia de la demostración de Anderson es que permite ver cómo los estados evolucionan hacia estados extendidos cuando el desorden se incrementa. A partir de este trabajo aparecen conceptos como la localización de la función de onda, la fractalidad, los ejes de movilidad en los bordes de zona, etc., los cuales comenzaron a estudiarse ampliamente en la física teórica y experimental de sistemas desordenados. El desorden afecta tanto la densidad de estados como las funciones de onda.
Con el fin de ilustrar este fenómeno más detalladamente con un modelo sencillo, en este trabajo se soluciona el problema de una partícula en presencia de una o dos impurezas muy localizadas de dos maneras: mediante la función de onda y mediante la función de Green. La diferencia entre estas dos técnicas es que la segunda permite tener una imagen física más detallada y más comparable con los experimentos.
Potencial δ en una dimensión
Para comenzar a entender el fenómeno de localización, se soluciona el problema de una partícula libre en interacción con un potencial localizado de tipo δ, es decir V(x) = V0 δ(x). Al solucionar la ecuación de Schrödinger para un potencial repulsivo, la función de onda se deslocaliza, y cuando el electrón interactúa con dicho potencial, se produce un corrimiento de fase y el coeficiente de transmisión puede llegar a ser uno.
La ecuación de Schrödinger para un electrón se escribe como (ℏ = 1, masa del electrón m = 1):
En el caso de energías en las que E > 0, las partículas libres se dispersan debido a la interacción con el potencial y las soluciones a las funciones de onda, con E = 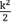 , se pueden escribir como:
, se pueden escribir como:
Con base en la teoría de la dispersión (scattering), se pueden identificar claramente los coeficientes de transmisión y reflexión, T(k) = 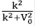 y R(K) =
y R(K) = 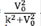 y deducir que, como es de esperar, cuanto mayor sea la energía de la partícula, la probabilidad de transmisión aumenta y la de reflexión disminuye; además, estos coeficientes son independientes del signo del potencial. Sin embargo, el caso más interesante aparece cuando consideramos el caso de energías en las que E < 0. En este caso la solución a la ecuación de Schrödinger es:
y deducir que, como es de esperar, cuanto mayor sea la energía de la partícula, la probabilidad de transmisión aumenta y la de reflexión disminuye; además, estos coeficientes son independientes del signo del potencial. Sin embargo, el caso más interesante aparece cuando consideramos el caso de energías en las que E < 0. En este caso la solución a la ecuación de Schrödinger es:
y para una energía E0 = - 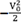 , se obtiene un estado ligado. Esta solución, tanto para la función de onda como para la energía, es muy parecida a la de un átomo de hidrógeno en tres dimensiones. Si, por el contrario, el potencial es atractivo, la función de onda se localiza cerca del potencial y se produce un estado ligado. Se presentan, así, características interesantes, como el concepto de estados ligados o localizados.
, se obtiene un estado ligado. Esta solución, tanto para la función de onda como para la energía, es muy parecida a la de un átomo de hidrógeno en tres dimensiones. Si, por el contrario, el potencial es atractivo, la función de onda se localiza cerca del potencial y se produce un estado ligado. Se presentan, así, características interesantes, como el concepto de estados ligados o localizados.
En resumen, se ha demostrado que un potencial genera un único estado ligado, sin importar la intensidad que pueda tener la constante V0 y que, entonces, no pueden existir estados excitados. Si se le proporciona esta energía a una partícula atrapada en un potencial de tipo δ, lo único que puede suceder es que la partícula quede completamente libre y, por lo tanto, pase a ocupar estados excitados de un continuo de energías.
Dos potenciales de tipo δ
El problema cuya solución se busca corresponde al incremento del número de centros que pueden dispersar al electrón. En este caso, el sistema es más interesante, ya que podemos controlar separadamente dos potenciales: de manera repulsiva y atractiva. Se asume una distancia de separación entre ellos:
Al solucionar la ecuación de Schrödinger con las apropiadas condiciones de frontera, se obtienen los resultados para los coeficientes de reflexión y transmisión:
Cuando el denominador de los coeficientes de reflexión, r, o de transmisión, t, llegan a cero, se encuentran los polos o estados ligados. Si se hace un cambio de variables: Vi → -Vi y k → ik, se encuentra una solución que se puede escribir como:
En la figura 1, se muestran los resultados para los coeficientes de transmisión. Cuando la intensidad del potencial es muy pequeña o muy grande, solamente se observa un estado ligado, lo cual correspondería a tener el equivalente de un solo potencial. Sin embargo, existe un régimen intermedio de energías en el cual se pueden observar dos estados ligados. Es decir, las soluciones confirman que nuestro resultado analítico es correcto: como máximo pueden existir dos estados ligados. Para E ≥ 0, el número de ceros se puede incrementar, pero el máximo valor del coeficiente de transmisión debe ser uno. Cada cero del denominador de r o t nos indica las energías de resonancia.
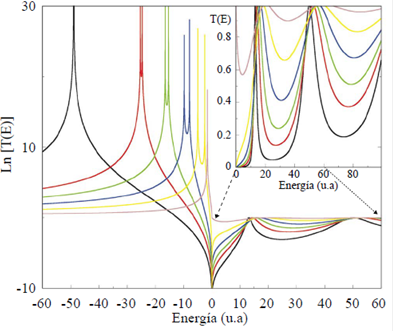
Figura 1 Logaritmo natural de los coeficientes de transmisión para intensidades de potencial V1 = V2 = -14 (curva negra), -10 (curva roja), -8 (curva verde), -6 (curva azul), -4 (curva amarilla), -2 (curva marrón). En el recuadro se muestran los resultados del coeficiente de transmisión para energías positivas.
Varios potenciales δ
En las secciones anteriores se ha demostrado que se pueden crear estados ligados en sistemas de uno y dos potenciales δ, o no. Ahora ampliamos el problema: se simula un cristal en el cual puede haber N potenciales δ. Dicho sistema corresponde a un cristal perfecto en el cual se introducen impurezas. Se supone que un electrón de masa m incide sobre la red de potenciales, cuya intensidad puede variar de forma aleatoria, y como resultado de la interacción la onda asociada al electrón comienza a reflejarse y a transmitirse produciendo fenómenos de interferencia múltiple, descrita como una superposición lineal de funciones de onda que entran y salen después de interactuar con el i - ésimo potencial. Para resolver este problema se usó un modelo estudiado en la física matemática (Morse & Feshbach, 1953), y también en óptica cuántica (Born & Wolf, 1963), que se denomina el formalismo de matriz de transferencia.
El hamiltoniano de este sistema se puede escribir como:
donde 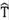 representa el operador de energía cinética,
representa el operador de energía cinética, 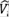 , y el potencial de interacción, el i - ésimo potencial de tipo δ (positivo o negativo) en la posición xi. Para cada una de las n + 1 zonas en las cuales existe un potencial δ en la posición N, la función de onda se puede escribir como:
, y el potencial de interacción, el i - ésimo potencial de tipo δ (positivo o negativo) en la posición xi. Para cada una de las n + 1 zonas en las cuales existe un potencial δ en la posición N, la función de onda se puede escribir como:
donde k es el vector de onda asociado a la energía de la partícula E = k2, definido en esta parte del artículo como 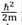 = 1. Teniendo en cuenta que para el caso de potenciales de tipo δ, la función de onda debe ser continua y la derivada discontinua, se puede llegar a demostrar que los coeficientes, antes y después de interactuar con el n-ésimo potencial δ, están relacionados como:
= 1. Teniendo en cuenta que para el caso de potenciales de tipo δ, la función de onda debe ser continua y la derivada discontinua, se puede llegar a demostrar que los coeficientes, antes y después de interactuar con el n-ésimo potencial δ, están relacionados como:
En general este sistema se puede escribir como:
donde
En la ecuación 14, la matriz de coeficientes 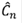 puede escribirse en términos de una matriz Q, que a su vez se descompone en dos matrices, M y D, las cuales dan cuenta de la interacción y de la periodicidad espacial de la red. Po lo tanto, si se quieren evaluar los coeficientes de transmisión para una red de N potenciales, es necesario calcular la matriz
QN
. Suponiendo por el momento que todas las intensidades de los potenciales son iguales:
Vn
=
V0
, y combinando esto con los resultados de la óptica cuántica, esta matriz se puede escribir como (Born & Wolf, 1963):
puede escribirse en términos de una matriz Q, que a su vez se descompone en dos matrices, M y D, las cuales dan cuenta de la interacción y de la periodicidad espacial de la red. Po lo tanto, si se quieren evaluar los coeficientes de transmisión para una red de N potenciales, es necesario calcular la matriz
QN
. Suponiendo por el momento que todas las intensidades de los potenciales son iguales:
Vn
=
V0
, y combinando esto con los resultados de la óptica cuántica, esta matriz se puede escribir como (Born & Wolf, 1963):
donde UN (y) representan los polinomios de Tchebychev de segunda clase y es una variable que tiene en cuenta la estructura de bandas de un sistema unidimensional perfecto, descrita por:
En el modelo se han usado condiciones de periodicidad de cadena cerrada, lo que quiere decir que las funciones de onda se vuelven continuas y su derivada discontinua cuando se une el sitio 1 de la cadena con el N. Esta aproximación se justifica plenamente cuando el número de sitios de la cadena es grande. Bajo esta condición, la variable está relacionada con los valores de energía para los cuales el polinomio de Tchebychev puede calcularse. Este polinomio se puede expresar como UN (x) = 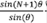 con x = cos (θ). Claramente, θ tendría sentido en el rango de [-1,1]. Si el argumento de esta función está afuera de este rango, los polinomios no están definidos. Físicamente significa que los estados de energía no son permitidos y, por lo tanto, se presenta una estructura de bandas y brechas de energía. En la figura 2 se ha graficado el coeficiente de transmisión que claramente muestra zonas cuyo valor es 1 (transmisión perfecta) para un sistema finito de N=10 potenciales, y otras zonas que valen cero. Estas zonas representan estados de energía prohibidos. En el lado derecho se representa la variable y (ecuación 15), la cual da cuenta de los valores para los cuales se puede encontrar entre [1,-1].
con x = cos (θ). Claramente, θ tendría sentido en el rango de [-1,1]. Si el argumento de esta función está afuera de este rango, los polinomios no están definidos. Físicamente significa que los estados de energía no son permitidos y, por lo tanto, se presenta una estructura de bandas y brechas de energía. En la figura 2 se ha graficado el coeficiente de transmisión que claramente muestra zonas cuyo valor es 1 (transmisión perfecta) para un sistema finito de N=10 potenciales, y otras zonas que valen cero. Estas zonas representan estados de energía prohibidos. En el lado derecho se representa la variable y (ecuación 15), la cual da cuenta de los valores para los cuales se puede encontrar entre [1,-1].
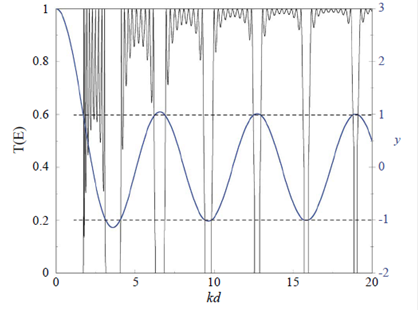
Figura 2 El lado izquierdo del eje representa los coeficientes de transmisión, el lado derecho, el argumento del polinomio de Tchebychev (Ec. ([dispersion])). Cuando este valor es mayor que 1 o menor que -1, se encuentra una brecha, de lo contrario, los estados son permitidos. Las líneas punteadas sirven como referencia para observar cuándo sale del rango.
Con estas propiedades es posible calcular analíticamente las amplitudes de los coeficientes de transmisión y reflexión para un sistema de N potenciales
y el coeficiente de transmisión para cualquier δN potencial es:
Este sistema ya se puede perturbar con una o varias impurezas. Sin embargo, hacer un cálculo en términos de matriz de transferencia se puede convertir en algo mucho más complicado matemática y numéricamente. Por lo tanto, se usó una técnica muy bien estudiada, las funciones de Green, las cuales permiten estudiar de manera mucho más clara sistemas perfectamente ordenados, así como sistemas desordenados.
Funciones de Green
Hasta este punto se han estudiado algunos sistemas que presentan un orden (sistemas infinitos) y algunos sistemas finitos de pocos potenciales δ, que ilustran el fenómeno de localización y deslocalización de la función de onda. Aunque este es un modelo muy simple, sin duda da una idea de lo que puede suceder en sistemas más complejos con muchos potenciales de tipo δ, organizados ya sea de forma regular o aleatoria. Estos modelos idealizados han suscitado mucho interés, pues, aunque son sencillos, son importantes para entender la física del problema. Una primera solución analítica del problema de transporte en sistemas desordenados fue la propuesta por Dyson (1953), quien, teniendo en cuenta una cadena unidimensional desordenada, pudo encontrar una expresión para la densidad de estados usando el método de las funciones de Green (FG). Este modelo general se aplicó a un sistema clásico de masas diferentes y unidas por resortes. Aunque el modelo no puede explicar efectos cuánticos, el formalismo teórico sí puede emplearse. Con esta metodología se desarrolló el uso de las matrices de transferencia (Schmidt, 1957), y se pudieron obtener resultados muy parecidos a los ya publicados por Dyson. La esencia de estos dos métodos es la posibilidad de calcular las matrices de transferencia que tienen una analogía muy cercana con la matriz de transmisión. Cuando estas técnicas se usan en sistemas de muchos potenciales, se puede demostrar que el espectro presenta brechas de energía (Hori, 1968). Además, es posible calcular la densidad de estados, la que, por razones conceptuales, es muy importante para describir la posible ocupación de estados de energía, pero no es muy accesible desde el punto de vista experimental. Sin embargo, se describe el método requerido, ya que son muchos los observables que pueden obtenerse de las funciones de Green.
En este trabajo se presenta la teoría de las funciones de Green independientes del tiempo, con el fin de estudiar fenómenos que se encuentren en el régimen estacionario. En general, la función de Green puede escribirse como:
donde esta función depende de dos puntos espaciales, r,r',z =λ + is, y L(r) es un operador diferencial hermítico tal que
y el conjunto completo de funciones propias del operador, L(r) y ϕ n (r), satisfacen las condiciones de frontera de la G(r,r') y son ortonormales. Si todos los valores propios de z - L son diferentes de cero, entonces puede escribirse la FG en términos de los valores propios de energía, tanto los discretos como los continuos, de la siguiente manera:
donde las sumas y las integrales corren sobre estados discretos y estados continuos de energía, respectivamente.
Primero se aplica este formalismo al caso de un potencial δ considerando un hamiltoniano H, que puede ser el de una partícula libre o el de una partícula en un medio perfecto de potenciales de tipo δ. La ecuación para la FG es:
Si los estados propios de H son En y las funciones propias se denotan por ψn (x), entonces,
Para el caso de un potencial δ, el hamiltoniano se escribe como H = H0 + λ(x)δ(x). H0 puede ser el hamiltoniano de partícula libre o de un cristal perfecto, es decir, un H que se puede resolver exactamente. Suponiendo que la función de Green asociada al hamiltoniano H0 es G0(x,y:E), entonces G0(E) = 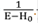 . La FG asociada a H puede escribirse como:
. La FG asociada a H puede escribirse como:
Esta ecuación es similar a la ecuación de Dyson y puede representarse en el espacio real mediante la relación de completitud como:
Si se supone que x = 0, y se usan las propiedades de la función δ, se puede escribir de forma más simplificada como:
Las ecuaciones descritas representan, en general, la función de Green en dos sitios (Rodríguez, 1988), lo cual depende mucho de la FG calculada para un medio conocido, G0 (0,0). Es evidente que si se considera una partícula libre, es posible observar la presencia de un polo en la FG, es decir, cuando G0 (0,0;E) = 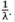 . En este caso, H0 =
. En este caso, H0 = 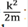 y las funciones propias de este hamiltoniano son ondas planas, por lo tanto,
y las funciones propias de este hamiltoniano son ondas planas, por lo tanto,
Es especialmente importante calcular los polos, los cuales se definen usando la función de Green G(0,0;E). Esta integral es muy sencilla de resolver, y se encuentra que,
donde se ha asumido que para estados ligados k = 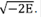 Por lo tanto, el potencial debe ser atractivo para que existan estados ligados, lo que confirma los resultados teóricos ya presentados. Se puede calcular exactamente la FG de una partícula libre resolviendo la ecuación 20, y se obtiene:
Por lo tanto, el potencial debe ser atractivo para que existan estados ligados, lo que confirma los resultados teóricos ya presentados. Se puede calcular exactamente la FG de una partícula libre resolviendo la ecuación 20, y se obtiene:
Esta función vale tanto para un sistema continuo como para uno discreto (con x = na), siendo n un entero y a la separación de los puntos de red. El procedimiento se puede extender al caso de dos potenciales de tipo δ, pero, en este caso, tomando como hamiltoniano el siguiente:
La ventaja de separar este hamiltoniano con el término 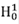 es que ya conocemos la FG para él. Después del algebra necesaria, esta se puede calcular como:
es que ya conocemos la FG para él. Después del algebra necesaria, esta se puede calcular como:
donde 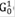 (x, y) es la FG ya calculada para el caso de una partícula libre. Con la expresión arriba descrita, se pueden calcular los polos de la FG como (G(0,0)=G(x,x)):
(x, y) es la FG ya calculada para el caso de una partícula libre. Con la expresión arriba descrita, se pueden calcular los polos de la FG como (G(0,0)=G(x,x)):
Mediante las definiciones de G(x,y,E), y teniendo que G0(0,0) = 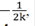 se puede demostrar que para obtener los polos se debe resolver una ecuación de tercer orden dada por
se puede demostrar que para obtener los polos se debe resolver una ecuación de tercer orden dada por
Es evidente que el método de las funciones de Green puede dar una idea más clara de los estados ligados y, también, de la densidad de estados. Si se conoce la FG de un medio, en principio se podría calcular la FG para un sistema perturbado, como lo describe la ecuación 19, la cual admite una representación gráfica más intuitiva, representada por el diagrama de Feynman (figura 3).
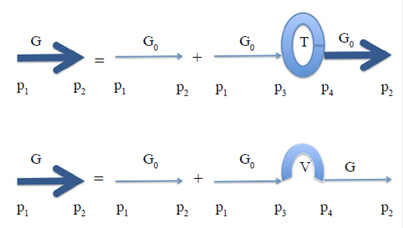
Figura 3 Propagador de Feynman que tiene en cuenta la matriz de transferencia o la interacción particular
Dicha ecuación también puede escribirse en términos de operadores como:
donde T representa la matriz de transferencia y V está asociado al potencial. Usando esta formulación podemos calcular la FG de un modelo unidimensional periódico no perturbado.
Función de Green de un medio periódico no perturbado
Se calcula a continuación la FG de un medio que obedece una periodicidad espacial en una dimensión. Se considera un sistema de N átomos en un arreglo unidimensional de longitud L y de constante de red tal que cada sitio de la red esté descrito por un potencial δ:
Con la ecuación 23, pero escribiéndola en la base discreta y realizando su transformada de Fourier, se tiene que:
Con esta FG de partícula libre, GL, en el espacio real y en k, se puede calcular la FG del medio periódico perfecto, G0, usando las fórmulas de la ecuación 28:
Los ceros de la función P, determinarán los polos de la FG y, por lo tanto, las bandas y las brechas de energía. Al transformar de forma inversa, se puede calcular la FG local, así:
Función de Green de un medio periódico con perturbaciones: desorden
Como ya se mencionó, el desorden es una situación común en cualquier sistema realista de estado sólido. Uno de los sistemas experimentales de mayor interés consiste en aleaciones binarias donde los “átomos” son colocados aleatoriamente sobre los sitios regulares de la red. Estos sistemas han llamado mucho la atención y se han estudiado ampliamente con base en diferentes teorías (Faulkner, 1970, Buttler, 1976).
El interés se ha centrado especialmente en el cálculo de la densidad local de estados del sistema, la cual está directamente relacionada con la parte imaginaria de la FG, como:
Según se ha demostrado, la FG se puede calcular exactamente para un modelo unidimensional periódico de potenciales de tipo δ. Sin embargo, cuando existe desorden, por ejemplo en aleaciones, la FG debe calcularse como el promedio estadístico de diferentes tipos de configuraciones de todo el sistema. Para calcular dicho promedio, se usan varios métodos que se pueden agrupar en dos familias: perturbativos y autoconsistentes. Cualquiera de ellos resulta bastante complicado computacionalmente, por lo que se prefieren algunos métodos más rápidos y efectivos, especialmente los que recurren a aproximaciones: la aproximación de cristal virtual (VCA), la aproximación promedio de la matriz de transferencia (ATA) y la aproximación de potencial coherente (CPA), las cuales se describen brevemente a continuación.
1. VCA: en esta aproximación se separan las correlaciones que puedan existir entre el potencial y la FG, es decir, se asume que en la ecuación 28:
donde GP es la FG promedio del medio que se conoce y el promedio 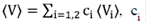 es la concentración de potenciales de tipo i tal que
es la concentración de potenciales de tipo i tal que 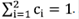 Físicamente, esto significa que todo el sistema tiene en promedio un potencial 〈V〉, lo cual se da sencillamente sumando un potencial promedio al potencial del medio perfecto o periódico. Por lo tanto, bajo esta aproximación, los estados que producen las impurezas se mezclan con los estados del continuo, y no debería observarse un gran cambio en la densidad de estados.
Físicamente, esto significa que todo el sistema tiene en promedio un potencial 〈V〉, lo cual se da sencillamente sumando un potencial promedio al potencial del medio perfecto o periódico. Por lo tanto, bajo esta aproximación, los estados que producen las impurezas se mezclan con los estados del continuo, y no debería observarse un gran cambio en la densidad de estados.
2. ATA: esta aproximación va un poco más allá de la VCA. Se usa la primera fórmula del propagador en la ecuación 28 y se promedia la matriz de transferencia para cada átomo i de la aleación binaria a, b, así,
donde se ha tomado como 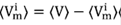 y la FG GP (m,m) está asociada a un centro de dispersión, lo cual ya fue calculado en la sección [transporte]. Este método es muy interesante porque permite definir un medio efectivo de potencial, Σ, que está directamente relacionado con la matriz promedio de transferencia,
y la FG GP (m,m) está asociada a un centro de dispersión, lo cual ya fue calculado en la sección [transporte]. Este método es muy interesante porque permite definir un medio efectivo de potencial, Σ, que está directamente relacionado con la matriz promedio de transferencia,
es decir, las FG calculadas mediante las aproximaciones ATA y VCA están correlacionadas, solamente que se toma un corrimiento en la energía dada por Σ: GATA(E) = GVCA(E - Σ). Debe señalarse, asimismo, que cuando las concentraciones ci son muy bajas, el medio no tiene mucho efecto y los resultados de la aplicación de las dos aproximaciones deberían ser los mismos.
3. CPA: esta aproximación es perturbativa y, además, autoconsistente. En esta aproximación la FG promedio se calcula usando un hamiltoniano efectivo, el cual se caracteriza por la creación de un potencial efectivo periódico que depende de la energía y usualmente puede ser complejo. Por lo general, este modelo toma el medio totalmente desordenado y lo reemplaza por un medio que tenga la misma matriz efectiva de transferencia 〈T〉en todos los sitios. Como resultado, se puede demostrar que cada sitio de la red está descrito por un potencial promedio (complejo), y que en el origen de la cadena puede estar presente una impureza real a o b; es decir que la CPA es realmente una aproximación por sitio.
Aquí se muestran los resultados más importantes de la aproximación CPA. Para una explicación más detallada del problema, se asume que el sistema unidimensional se subdivide en pequeñas celdas tales que na = L/N, donde n es un número entero arbitrario. La concentración de los sitios será 1/n y estos están aleatoriamente ocupados.
En la figura 4 se presentan los resultados de la densidad de estados para diferentes concentraciones de desorden x. La curva negra representa el modelo unidimensional totalmente ordenado (x = 1) y corresponde a la parte imaginaria de la FG (ecuación 34), y en ella aparecen claramente la brecha y las singularidades de Van Hove en los bordes de banda. Cuando aumenta el desorden (x = 0,7), se produce un corrimiento de banda y muchos de los estados que estaban en ella aparecen como ‘minibandas’ en las regiones en donde antes había brechas. En el caso del modelo altamente desordenado (x = 0,02), el carácter unidimensional permanece muy cerca del borde de banda, pero la densidad de estados de energía se convierte en una sola banda.
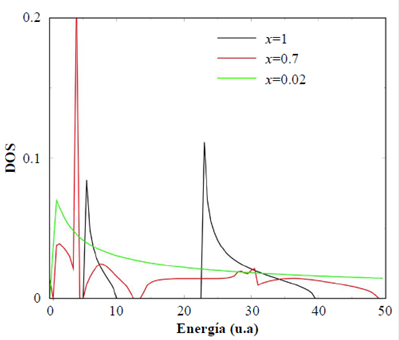
Figura 4 Densidad de estados como función de la energía para un sistema unidimensional del tipo de Kronig-Penney en el cual las impurezas se colocan de forma desordenada. El potencial de contacto es V0 = 8 para diferentes tipos de concentración de impurezas. Curva negra: (ordenado); curva roja: (parcialmente desordenado); curva verde: (muy desordenado)
Para finalizar esta parte del artículo, la pregunta es: ¿para qué sirve calcular una densidad de estados y unos coeficientes de transmisión, ya que estos no se miden experimentalmente? La respuesta es que ello obedece a que así se pueden obtener las propiedades de transporte tales como la conductancia electrónica de una forma muy directa a partir de las cantidades ya calculadas.
Por ejemplo, la conductancia en sistemas unidimensionales según Landauer (1970), se puede escribir como:
donde g es la conductancia y nf es la distribución de Fermi- Dirac. Estas fórmulas generalmente pueden escribirse desde un punto de vista cuántico en el cual un sistema cualquiera responde a un estímulo externo como un campo eléctrico. Es posible, bajo el mismo formalismo de la FG, estudiar las funciones de correlación de campos y deducir tanto propiedades ópticas como de transporte (Mahan, 1990; Kubo, Hasegawa, Hashitsume, 1959).
Con las ideas básicas sobre la FG ya discutidas, se presentan ahora los resultados de las propiedades ópticas en sistemas unidimesionales. Se considera un sistema de muchos electrones interactivos, los cuales comienzan a interactuar con un potencial muy fuerte producido por un hueco en la banda de valencia. En este caso, tenemos un problema similar a los anteriores, en el cual las impurezas simulan el potencial creado por una perturbación externa. Este problema fue inicialmente formulado por Mahan (1967) en sistemas aislantes tridimensionales. Se predecía que se podía crear un estado ligado entre un electrón y un hueco bajo el umbral de absorción óptico. Con el fin de resolver este problema, se consideró la presencia de un excitón en semiconductores de brecha directa, en donde la banda de conducción pueda considerarse como un sistema de Fermi degenerado. La pregunta que debería resolverse era: ¿cómo un excitón normal podría interactuar con un mar de Fermi de muchas partículas? A diferencia de lo comentado en las secciones anteriores, este problema no corresponde a uno de una partícula individual, sino a uno de muchos electrones que interactúan bajo la presencia de un potencial externo. Es decir, es un problema de muchos cuerpos, y es la base para estudiar las propiedades ópticas de sistemas unidimensionales realistas tales como los de hilos cuánticos.
Propiedades ópticas de muchas partículas
La conductividad eléctrica puede calcularse usando la fórmula de Kubo (Mahan, 1990; Kubo, Hasegawa, Hashitsume, 1959), la cual tiene en cuenta la correlación entre dos operadores de corriente 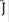 y está escrita como la FG retardada π(ω):
y está escrita como la FG retardada π(ω):
donde iωn → ω + iσ y β es el inverso de la temperatura. La conductividad se puede calcular como σ = minω→0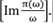 La parte real de la función de correlación está relacionada directamente con el proceso de absorción óptica y puede calcularse como:
La parte real de la función de correlación está relacionada directamente con el proceso de absorción óptica y puede calcularse como:
El hamitoniano del sistema que tiene en cuenta las interacciones entre muchas partículas, se puede escribir como:
donde Eg es la brecha de energía, y 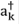 y
y  representan los operadores de creación de electrones de conducción y valencia, respectivamente. La interacción entre los electrones de conducción puede tenerse en cuenta usando un formalismo de renormalización de la energía, que para nuestro caso no tendrá muchos efectos, pues la densidad electrónica es muy alta. Con el hamiltoniano ya escrito se puede calcular la función de correlación de Kubo para π(iω), cuando la interacción es nula:
representan los operadores de creación de electrones de conducción y valencia, respectivamente. La interacción entre los electrones de conducción puede tenerse en cuenta usando un formalismo de renormalización de la energía, que para nuestro caso no tendrá muchos efectos, pues la densidad electrónica es muy alta. Con el hamiltoniano ya escrito se puede calcular la función de correlación de Kubo para π(iω), cuando la interacción es nula:
donde Pk = 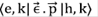 representa el elemento dipolar óptico que tiene en cuenta la interacción de la luz con la materia.
representa el elemento dipolar óptico que tiene en cuenta la interacción de la luz con la materia. 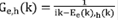 representa las mismas funciones de Green calculadas anteriormente para electrones y huecos, respectivamente. nf (Ee(k)) y nf (Eh(k)) representan las funciones de Fermi, tanto para electrones como para huecos. Es muy fácil calcular la absorción óptica como:
representa las mismas funciones de Green calculadas anteriormente para electrones y huecos, respectivamente. nf (Ee(k)) y nf (Eh(k)) representan las funciones de Fermi, tanto para electrones como para huecos. Es muy fácil calcular la absorción óptica como:
donde μ es la masa reducida del electrón y el hueco. Aquí se hace evidente que el espectro de absorción óptica es proporcional a la densidad de estados del sistema.
En la figura 5 se detalla el proceso de absorción por el cual el sistema es excitado con muchas frecuencias que van desde la brecha de energía EG hasta el borde superior de estados de energía EG + EF.
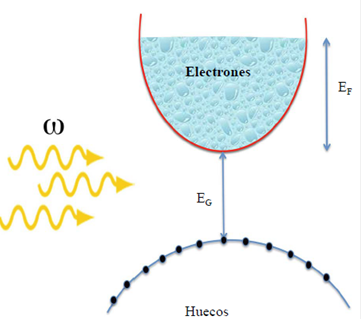
Figura 5 Interacción de la luz de frecuencia ω con un semiconductor dopado tipo n. Los electrones de la banda de conducción pueden someterse a excitación con una frecuencia E g + E F , y el mar de Fermi puede absorber luz de la energía de Fermi o emitir luz desde el borde inferior de la banda de conducción o desde el nivel de Fermi.
Sin embargo, el problema empieza a complicarse cuando se considera que la banda de conducción es ocupada por un mar de Fermi de electrones. Entonces la interacción entre electrón y hueco es apantallada por las interacciones entre electrón y electrón del mar de Fermi. En este caso es necesario calcular una serie de diagramas de Feynman que van más allá del primer diagrama mostrado, en el cual se calcula la absorción sin interacción (figura 6).
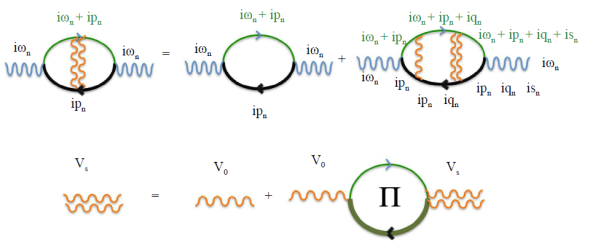
Figura 6 Diagramas de Feynman que se deben calcular para tener en cuenta las interacciones del hueco de la banda de valencia con los electrones del mar de Fermi
Matemáticamente, estos diagramas se pueden escribir usando la función de Green (Rodríguez, 1994) en la ecuación 28, pero ahora representada en el espacio de momentum k, como:
Esta ecuación también se conoce como la ecuación de Bethe-Salpeter. La interacción está descrita como:
donde la primera ecuación describe que la interacción directa V0 entre el electrón y el hueco está apantallada por la constante dieléctrica del mar de Fermi de electrones ϵ. Es decir, tanto el electrón como el hueco ven un medio efectivo de electrones que puede tener excitaciones de todas las clases, como, por ejemplo, plasmones de frecuencia ω. Para resolver de forma más sencilla esta ecuación, se supondrá que, al igual que en el caso del transporte de electrones, la interacción efectiva es un potencial δ en el espacio k, es decir:  . De esta forma, se llega a un modelo muy simple que ilustra la presencia de un estado ligado descrito por la siguiente ecuación:
. De esta forma, se llega a un modelo muy simple que ilustra la presencia de un estado ligado descrito por la siguiente ecuación:
El hueco podría considerarse, entonces, como un centro de dispersión de electrones, y el espectro óptico podría describirse fácilmente por los desplazamientos de fase de los electrones del fondo de la banda de conducción y de los que están ceca al nivel de Fermi. En la figura 7 se muestra el espectro de fotoemisión para un sistema con una energía de Fermi Ef ≈ 4meV y a una temperatura T = 2° K (Rodríguez, 1994, Rodríguez & Tejedor, 1993).
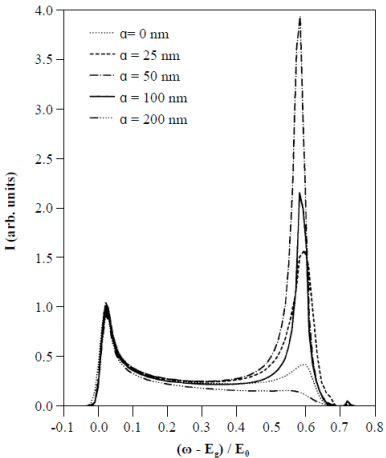
Figura 7 Singularidad de la energía de Fermi para diferentes anchos de un hilo unidimensional. Cuanto más ancho sea el hilo, más disminuye la interacción, y, por lo tanto, la singularidad se hace menos evidente.
Se detectan dos picos: el de más baja energía representa la emisión de luz por la recombinación de pares de electrón y hueco que están en la brecha de energía. La forma demuestra claramente la singularidad de Van Hove típica de sistemas unidimensionales, la cual viene determinada por la densidad unidimensional de estados. El segundo pico demuestra el comportamiento colectivo de muchos cuerpos al nivel de la energía de Fermi. Este efecto se detectó experimentalmente (Calleja, Goñi, Pinczuk, Dennis, Weiner, Pfeiffer, West, 1995) en sistemas unidimensionales y nuestra teoría explica muy bien dichos resultados: se produce una rápida creación de pares de electrón y hueco en la banda de conducción que, acoplados con el hueco de la banda de valencia, les permiten un mecanismo eficiente de recombinación llevando al comportamiento singular del espectro de emisión conocido como singularidad de Fermi.
Conclusiones
En este trabajo se ha demostrado la utilidad de las funciones de Green en sistemas unidimensionales para describir tanto las propiedades de transporte como las ópticas en sistemas de materia condensada. El formalismo permite realizar cálculos teóricos que pueden compararse directamente con los resultados experimentales. Aunque los coeficientes de transmisión son difíciles de obtener experimentalmente, estos están directamente relacionados con la conductancia electrónica, que sí es fácil de medir experimentalmente. Con esta técnica es posible calcular las propiedades de transporte más complicadas, incluido el desorden. Se demostró que cuando estos efectos se incluyen, se producen estados en las brechas de energía que dan cuenta del fenómeno de localización. Se calcularon los espectros de emisión de luz en estos sistemas y se demostró que se obtienen dos singularidades que compiten en intensidad: una asociada al carácter puramente unidimensional de partículas que no interactúan y otra que se asocia al fenómeno colectivo de interacción de muchas partículas. Se usó el mismo formalismo para el estudio de las propiedades de transporte como de las ópticas con funciones de Green representadas en el espacio real y recíproco, respectivamente. Se demostró la presencia de estados ligados tanto en sistemas de pocas partículas como en los de muchas.