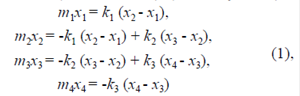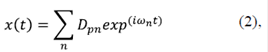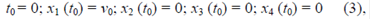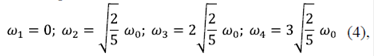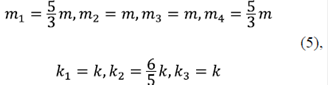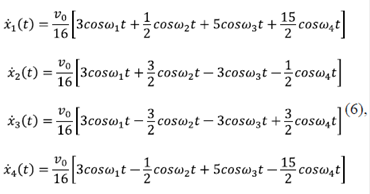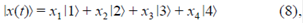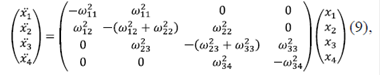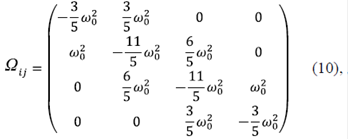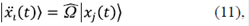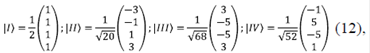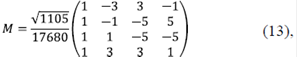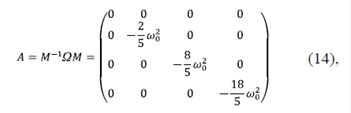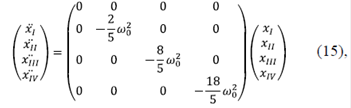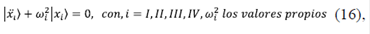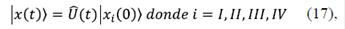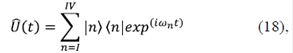Introducción

Tradicionalmente, la mecánica clásica se considera como la puerta de entrada a la física y a su enseñanza, lo cual se sustenta por su relación con campos disciplinarios tales como la termodinámica, el electromagnetismo, y otros. Esta relación se debe a que en dichos campos se utilizan modelos explicativos sustentados en las elaboraciones que están en la base de los sistemas mecánicos, por lo cual se considera que un fenómeno es comprensible si es posible explicarlo en términos mecánicos (^{Schmid, 1983}).

Por otra parte, Dirac evidencia en su tratado (1968) la necesidad de abandonar las ideas clásicas, ya que, aunque el esquema clásico es elegante y logra explicar un gran número de sistemas a escala macroscópica, sus predicciones teóricas a nivel atómico no concuerdan con los datos experimentales, por lo que sugiere construir un nuevo esquema para la descripción de los fenómenos a escala atómica. Este nuevo esquema establece un límite en torno a lo que se considera pequeño y grande y, por consiguiente, la necesidad de darle al tamaño un carácter absoluto (^{Dirac, 1968}).

La idea de grande y pequeño pasa a ser fundamental en física, ya que todo sistema considerado como grande está sujeto al principio de causalidad y su comportamiento queda descrito por ecuaciones diferenciales dependientes del tiempo. Por otra parte, si el sistema se considera pequeño con respecto a la perturbación producida, ello implica establecer una relación causal entre las condiciones de una situación inicial en un instante dado y las condiciones en otro instante posterior mediante una ecuación diferencial. En otras palabras, cuando se conoce el vector de estado del sistema en un instante inicial, éste evoluciona en el tiempo de manera determinista mientras no se perturbe el sistema. En el caso de un proceso de medida, ésta representa una perturbación que altera la evolución temporal del vector de estado.

La diferencia entre pequeño y grande, aunque no provee elementos que permitan hacer una teorización de la naturaleza a nivel atómico, sí constituye una nueva forma de mirarla, caracterizada por el hecho de que la observación que se hace sobre el sistema conlleva un grado de perturbación de su estado.

La física del siglo XX ha modificado nuestra imagen clásica del mundo gracias a la cosmovisión que nos ofrecen la mecánica cuántica y la relatividad general. La nueva comprensión del mundo se fundamenta en estas dos teorías. Ambas exigen una modificación radical de nuestra manera de conocer y de las ideas convencionales acerca del mundo, poniendo de manifiesto un revolucionario alcance conceptual. La mecánica cuántica entraña una visión del mundo en la que, como ya se dijo, la observación que se haga de un sistema lo perturba de maneras que no pueden controlarse, es decir, el observador afecta y define la realidad que estudia.

Esta visión rompe con el paradigma clásico que ha imperado e influido nuestro pensamiento y nuestra manera de ver el mundo desde el siglo XVII, y es una de las razones por la que es importante enseñarla y enfrentar las dificultades de los estudiantes a la hora de apropiarse de los conceptos en los que se fundamenta.

Una de las mayores dificultades para la enseñanza de la mecánica cuántica radica en que los fenómenos cuánticos no son directamente perceptibles y, por lo tanto, son contrarios a la intuición nacida de la observación de los estudiantes, más aún cuando se abordan desde una perspectiva teórica formalista que no resalta las implicaciones de la visión cuántica del mundo.

En este contexto, se presenta un análisis detallado de un sistema de osciladores acoplados, tema de gran importancia, ya que a partir de él se describen, por un lado, fenómenos mecánicos, electromagnéticos, y otros, y, además, se abre la puerta al estudio de sistemas con un gran número de grados de libertad y a la transición a una descripción en términos de grados de libertad continuos, y, por otro, se proporciona una estrategia metodológica para introducir conceptos del algebra lineal y obtener una solución usando la notación braket, en la que el número de coordenadas generalizadas para resolver el problema se relaciona con el conjunto de vectores propios que sirven para determinar de manera unívoca la configuración del sistema de osciladores.

Esta estrategia brinda la oportunidad de realizar una presentación alternativa de la solución del problema, con una discusión complementaria que tiene que ver más con la física involucrada que con el método a seguir, como lo establece ^{Rozo (2016)} al exponer una forma alternativa, didáctica y sólida para el tratamiento de la dinámica de una partícula en rotación, lo cual se conecta con un tópico conocido de la mecánica clásica.

La motivación es la de familiarizar al estudiante con los conceptos y los procedimientos para resolver problemas de mecánica cuántica tales como el de valores propios, aspecto que constituye una dificultad para la mayoría de los estudiantes. En este sentido, se describe en detalle la dinámica del comportamiento de cuatro osciladores acoplados utilizando el espacio vectorial generado por una base estándar. Este planteamiento permite obtener la dinámica del sistema de osciladores y, a la vez, ilustra el uso del método algebraico como un primer paso para mejorar el aprendizaje de las nociones, fundamentos y formalismos de la mecánica cuántica.

Esquema clásico

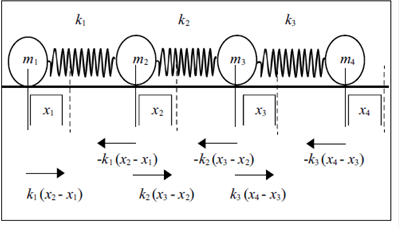
Se estudia en detalle la transmisión de energía en el sistema de osciladores acoplados sugerido por ^{Herrmann & Schmalzle en su artículo (1981)}. El sistema de osciladores se considera como una cadena lineal de esferas con movimiento unidimensional, la cual sirve como medio de propagación de una deformación. El sistema se encuentra constituido por un conjunto de cuatro osciladores acoplados, con diferente masa (m) y diferente coeficiente de acoplamiento (k). Los resortes interactúan elásticamente con los osciladores y su estado de movimiento se representa en la figura 1.

Figura 1 Estado de movimiento de un sistema de cuatro osciladores acoplados 

El sistema de osciladores obedece las siguientes ecuaciones de movimiento, (^{Marion, 1992}), (^{Berkeley, 1994}):

donde x ₁, x ₂, x ₃, x ₄, son los desplazamientos de las masas con respecto a su posición de equilibrio. La dinámica del sistema de osciladores se describe mediante la solución de las ecuaciones de movimiento (1) dada por ^{Symon (1968)} y ^{Sposito (1976)}:

donde ^_Dpn = ^_ApnCn es el producto de dos coeficientes: ^_Apn , que representa los modos normales de oscilación, y las constantes ^_Cn que se obtienen a partir de las condiciones iniciales:

Las frecuencias normales de oscilación del sistema están dadas por:

donde ω0 = 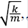obtenidas a partir de los valores dados para las masas y constantes de acoplamiento sugeridos por ^{Herrmann (1981)}:

Por último, la dinámica del sistema se rige por las siguientes ecuaciones de movimiento:

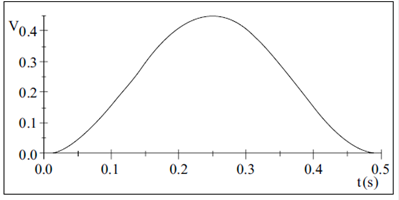
La figura 2 muestra el comportamiento del sistema de osciladores a partir de las soluciones dadas en (6). Cuando el primer oscilador se saca de su posición de equilibrio y se deja libre (excitación inicial externa), se propaga una oscilación con una velocidad que va disminuyendo a través del sistema de osciladores como lo muestra la curva roja punteada. A través del movimiento de oscilación del segundo y del tercer oscilador alrededor de su posición de equilibrio, se propaga un pulso que se desplaza por el sistema y que se muestra en las curvas en negro (asterisco negro) y en azul (punto azul) hasta el último oscilador del lado opuesto, en el cual la velocidad de oscilación aumenta hasta alcanzar la misma con la que se excitó inicialmente el sistema, lo cual se evidencia con la curva verde (símbolo de x verde), sin que los osciladores se hayan trasladado.

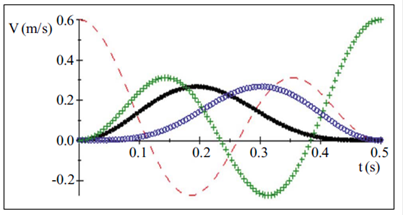
Figura 2 Comportamiento del sistema de osciladores cuando el primer oscilador se saca de su posición de equilibrio 

Por lo tanto, al considerar el medio como el conjunto de osciladores acoplados, la excitación inicial externa se propaga a través de la oscilación del sistema de osciladores alrededor de su posición de equilibrio hasta el último oscilador del lado opuesto. El comportamiento de la deformación se debe a las fuerzas elásticas que actúan sobre los osciladores y provocan que éstas se propaguen con cierta velocidad. La deformación representa un transporte de energía, ya que el trabajo que realiza la fuerza externa durante el momento de la excitación inicial se reparte por el sistema en forma de energía elástica (cinética y potencial) a medida que la deformación avanza por él y trabaja en su contorno para producirla (^{Berkeley, 1994}), (^{French, 1974}).

Por último, a través del sistema se propaga un pulso que pasa de un oscilador a otro transmitiendo la energía para que se efectúen las deformaciones hasta el último oscilador del lado opuesto, como se muestra en la figura 3.

Figura 3 Propagación de un pulso entre el sistema de osciladores 

Esquema del álgebra lineal

La solución del problema anterior puede obtenerse usando conceptos del álgebra lineal, con el fin de familiarizar a los estudiantes con los procedimientos que se utilizan en la solución de problemas de valores propios, y, además, recurriendo a la notación utilizada en el esquema de la mecánica cuántica. Este planteamiento permite tender un puente entre los conceptos ya adquiridos por los estudiantes y los utilizados en mecánica cuántica.

Como en el caso anterior, el problema se reduce a hallar los valores de x ¹ (t), x ² (t), x ³ (t), x ⁴ (t) conociendo las condiciones iniciales. El espacio vectorial se genera a través de la base estándar definida de la siguiente forma:

Los vectores |1>, |2>, |3>, |4> se toman como el conjunto de estados de base bien definidos para el análisis del comportamiento del sistema de osciladores. Además, el concepto de estado tiene un papel importante en el análisis, ya que permite hacer una descripción de la evolución temporal del sistema (^{Gillespie, 1991}).

En este sentido, al analizar la definición de la palabra estado de la ^{Real Academia Española (2017)}: “Situación en que se encuentra alguien o algo, y en especial cada uno de sus sucesivos modos de ser o estar”, se rescatan dos elementos importantes. Primero, ese alguien o algo aludirían al sistema y, segundo, los modos de ser o estar serían los diferentes estados en los que éste se puede encontrar en el transcurso del tiempo. Por lo tanto, el estado del sistema se puede definir como las diferentes maneras de estar, caracterizadas por las variables dinámicas de posición y momentum, las cuales tienen el papel de observables del sistema.

Por último, el estado de un sistema se caracteriza con relación a una cualidad, la cual permite referirse a una propiedad específica del sistema. En otras palabras, el estado del sistema queda dado en relación con una cualidad específica que puede ser de movimiento, térmica, eléctrica, etc., sin que el sistema pierda su identidad. Por lo tanto, el concepto de estado es la estrategia que el sujeto elabora para referirse a las diferentes formas de estar del sistema con relación a una cualidad determinada.

La formalización del estado del sistema se hace usando un vector normalizado, es decir que a todo posible estado físico del sistema se le hace corresponder un ket normalizado, existiendo una relación biunívoca entre vectores normalizados y estados físicos (^{Gillespie, 1991}). Por lo tanto, el estado del sistema en cualquier instante de tiempo puede expresarse como una combinación lineal de los estados de base:

donde cada uno de los coeficientes varía en el tiempo, y los estados que componen la superposición no pierden su identidad, lo cual significa que la superposición se da con relación al resto de elementos superpuestos. En otras palabras, el estado del sistema puede considerarse como el resultado de estar simultáneamente en cada uno de los estados de base que se hayan seleccionado |1>, |2>, |3>, |4> (^{Feynman, 1964}). La superposición es, entonces, una relación entre los estados constitutivos con respecto a una cualidad dada, en este caso de movimiento, de forma que el estado resultante queda determinado por los pesos relativos de los estados que se superponen.

Por otro lado, las ecuaciones de movimiento (1) se pueden reescribir en una representación matricial como:

y los elementos 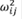de la matriz anterior se obtienen explícitamente a partir de los valores dados en (3), obteniéndose la matriz _^Ωij

donde 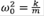es la frecuencia natural de oscilación del sistema. Haciendo uso de la representación matricial, las ecuaciones de movimiento pueden escribirse como:

siendo la matriz ^_Ωij la representación matricial del operador denominado 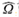, y los coeficientes xj (t) los elementos que caracterizan el vector de estado |x (t)>.

La base estándar (|1>, |2>, |3>, |4>) así definida es conveniente para interpretar los coeficientes x1 (t), x2 (t), x3 (t), x4 (t) como los desplazamientos de cada uno de los osciladores alrededor de su posición de equilibrio, sin embargo, esta definición no permite obtener la solución directa de las ecuaciones de movimiento (9), ya que este es un sistema acoplado, como lo muestran los elementos que se encuentran fuera de la diagonal de la matriz Ωij. Por lo tanto, para desacoplar el sistema de ecuaciones es necesario encontrar un conjunto de vectores propios de la matriz Ωij.

El problema, entonces, se reduce a hallar los vectores propios (^{Bronson, 1991}) del operador 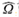con el fin de construir una matriz que permita diagonalizar la matriz Ωij y, así, desacoplar las ecuaciones de movimiento.

En este orden de ideas, los vectores propios del operador 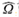son:

los cuales cumplen con la condición de ortonormalización: 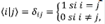y forman un conjunto de estados de base que es conveniente para describir los estados del sistema de osciladores. A partir de los vectores de base |I >, |II >, |III >, |IV > se construye la matriz

que diagonaliza la matriz ^_Ωij (^{Bronson, 1991}), (^{Grossman, 2012}):

Los vectores propios de la matriz (A) son los vectores de la base estándar definidos anteriormente (|1>, |2>, |3>, |4>). Usando la matriz similar (A), las ecuaciones de movimiento se desacoplan fácilmente para obtener:

Los valores propios de la matriz (A) que se encuentran en la diagonal se identifican con las frecuencias normales de oscilación del sistema, es decir, existe una relación biunívoca entre el valor propio y la frecuencia normal de oscilación del sistema. La obtención del conjunto de vectores propios |I >, |II >, |III >, |IV >, permite desacoplar de manera sencilla las ecuaciones de movimiento, así como identificar cada vector propio con el modo normal de oscilación correspondiente a cada frecuencia normal de oscilación del sistema. Por último, la solución del sistema (16) tiene una simple dependencia temporal en forma de exponencial como la dada en (2).

Aun cuando la evolución temporal del vector de estado del sistema queda especificada por la ecuación (16), se puede establecer un operador que también permite obtener la evolución temporal del sistema, así:

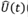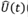lo cual significa que el operador actúa sobre el vector de estado inicial | ^_xi (0)> para producir un nuevo vector de estado |x (t)> cuando transcurre un tiempo (t), es decir, el estado final |x (t)> es lo que resulta cuando el operador actúa sobre el estado inicial | ^_xi (0)> (^{Feynman, 1964}; ^{Gillespie, 1991}). El operador 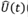es independiente del estado inicial del sistema y debe satisfacer la condición 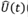= 1. Su representación se obtiene sustituyendo (17) en (16):

El operador 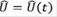se denomina operador de evolución temporal o propagador del estado del sistema (^{Townsend, 2000}; ^{Gillespie, 1991}), ya que al conocer el estado inicial se puede determinar el estado futuro del sistema. Por lo tanto, si se halla la evolución temporal del sistema, se determina la solución completa del problema.

Este análisis permite que los problemas abordados usualmente desde el contexto de la mecánica clásica también lo pueden ser haciendo uso del algebra lineal, lo que conduce a introducir conceptos como vector de estado, principio de superposición, operador, vectores propios, valores propios, transformación de similitud y otros, que son la base para el estudio de la mecánica cuántica. Además, con el procedimiento utilizado se muestra que la notación empleada bra y ket no es exclusiva de la mecánica cuántica, lo cual permite un acercamiento más rápido y una mayor familiarización de los estudiantes con la manera de proceder cuando se abordan problemas desde el contexto de la mecánica cuántica. Asimismo, se elaboró un cuadro comparativo del análisis usual mediante el esquema clásico y el que se propone haciendo uso del algebra lineal (Tabla 1).

Tabla 1 Comparativa entre el esquema clásico y el esquema del álgebra lineal 

Conclusión

La representación matricial de las ecuaciones de movimiento y la definición de la base estándar tiene las siguientes ventajas: permite hacer uso de conceptos del algebra lineal para hallar la solución del sistema de ecuaciones y, por lo tanto, conocer la evolución temporal del sistema; asimismo, la estrategia metodológica plantea una forma diferente, novedosa y didáctica para deducir las ecuaciones de movimiento del sistema de osciladores acoplados, lo cual permite, además, familiarizar a los estudiantes con el álgebra lineal y con la notación bra-ket ampliamente utilizada en mecánica cuántica.

En el esquema clásico el intercambio de energía entre los osciladores se considera continuo y depende del acoplamiento entre ellos. En el contexto cuántico existe un nivel de energía bien definido y no continuo correspondiente a cada uno de los estados bien definidos del sistema, el cual es un efecto estrictamente cuántico.

Esta estrategia de enseñanza adquiere especial importancia, pues permite tender un puente entre conceptos ya adquiridos por los estudiantes y los conceptos utilizados en mecánica cuántica, y, además, mostrar los procedimientos empleados para resolver problemas de valores propios.

Brinda, asimismo, un enfoque diferente para abordar problemas de la mecánica clásica, lo que constituye una forma novedosa de obtener los mismos resultados y de familiarizar más rápidamente a los estudiantes con el formalismo de la mecánica cuántica. Se sugiere incentivar a los docentes a replantear la enseñanza de la física, en particular la de la mecánica clásica, bajo un enfoque diferente al usual, que permita evidenciar formas alternativas de resolver problemas y, a la vez, introduzca una formalización que considere el contexto y permita a los estudiantes de formación inicial acceder a un conocimiento moderno y al pensamiento crítico. Esta perspectiva permite la formación de los estudiantes como investigadores y contribuye a la de los docentes de física, promoviendo un cambio de paradigma de las prácticas de enseñanza.