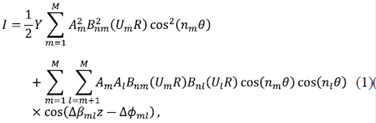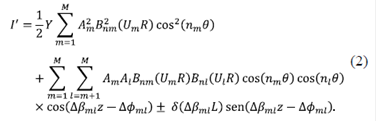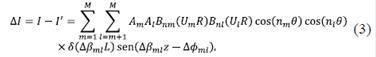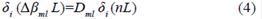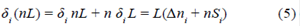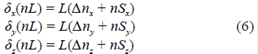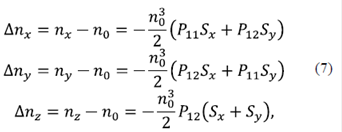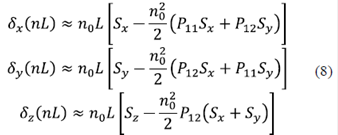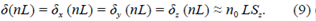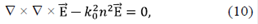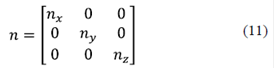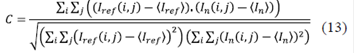Introducción
Cuando la radiación laser es insertada en una fibra óptica multimodo, los efectos de propagación producen a la salida de la fibra un patrón de speckle (moteado), el cual contiene información sobre el estado espacial de la fibra óptica y que puede ser usado en aplicaciones metrológicas (Arístizabal, Vélez, Rueda, Gómez, & Gómez, 2016; Efendioglu, 2017; Gasvik, 2002; Hung, 1978; R. Jones and C. Wykes, 1989; Saleh & Teich, 1991; Yu & Yin, 2002). De esta manera, pequeñas perturbaciones sobre la fibra multi-modo producirán cambios en la distribución espacial del patrón de speckle que pueden ser detectados mediante cambios locales de intensidad o técnicas de correlación (Crammond, Boyd, & Dulieu-Barton, 2013; Liu & Wei, 2007; B. Wang, Huang, Guo, & Yu, 2003). Los sistemas de sensado basados en patrones de speckle producidos en fibras ópticas multimodo son conocidos como Sensores de Specklegramas de Fibra Óptica (FSS por sus siglas en inglés).
Los FSS han sido ampliamente estudiados mediante arreglos holográficos cuyo medio de registro es un material fotorrefractivo (Gmez, Lorduy G., & Salazar, 2011; Gómez, Lorduy G., & Salazar, 2011; Gómez & Salazar, 2012; Wu, Yin, & Yu, 1991; Yu, Yin, Zhang, & Guo, 1994; Yu, Zhang, Yin, & Ruffin, 1995), sin embargo, más recientemente, se ha explorado la importancia de este tipo de sistemas en esquemas no-holográficos, en la medición de múltiples parámetros de interés en ingeniería (Fujiwara, Marques dos Santos, & Suzuki, 2017; Fujiwara, Wu, dos Santos, Schenkel, & Suzuki, 2017; Fujiwara, Wu, & Suzuki, 2012; Kumar, Varshney, Antony C, & Sharma, 2003; Li, Cai, Geng, Qu, & Fang, 2007; Malki, Gafsi, Michel, Labarrère, & Lecoy, 1996; Rodriguez-Cobo, Lomer, & Lopez-Higuera, 2015; B. Wang, Guo, Yin, & Yu, 2004; Y. Wang, et al., 2008; Yu, Wen, Yin, & Uang, 1993). Principalmente, dos posibilidades han sido reportadas alrededor de los arreglos no-holográficos. En el primer caso, se han usado herramientas de procesamiento de imágenes para calcular la correlación entre los patrones de speckle perturbados que son capturados mediante cámaras CCD a la salida de la fibra multimodo (Malki, et al., 1996; B. Wang, et al., 2004; Yu, et al., 1993). En el segundo caso, se han usado esquemas experimentales de fibras mono-multi-mono modo para generar y filtrar el patrón de speckle que se genera en la fibra multimodal, lo que permite configurar esquemas de FSS interrogados por variación de potencia óptica (V.H. Aristizabal, Hoyos, Rueda, Gomez, & Gomez, 2015; Darío Gómez & Gómez, 2013). Esta estrategia presenta ventajas de simplicidad, estabilidad y bajo costo (Zhang & Ansari, 2006), pero la correlación entre la distribución espacial de los patrones de speckle y el estado de la fibra óptica se pierde, ya que la salida del sensor es puntual.
En este trabajo exploramos numéricamente la generación de patrones de speckle a la salida de una fibra óptica y el uso del cálculo de valores de correlación entre los patrones de speckle para la medición de perturbaciones físicas, específicamente, esfuerzos mecánicos.
Análisis teórico
En aproximación de campo cercano, la distribución espacial de intensidad del campo a la salida de una fibra óptica multimodo se puede escribir en coordenadas polares en el punto como (Darío Gómez & Gómez, 2013):
donde Δ
βml
=
βm
-
βl
es la diferencia de las constantes de propagación, Δ
ϕml
=
ϕm
-
ϕl
es la diferencia de las constantes de fase,
Am
y
Al
son las amplitudes de los modos m y l, respectivamente. R = a ⁄ r es el radio normalizado siendo a el radio del núcleo de la fibra óptica, Y = n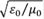 es la admitancia característica del núcleo donde n es el índice de refracción del núcleo,
Um
=
es la admitancia característica del núcleo donde n es el índice de refracción del núcleo,
Um
= 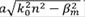 es el parámetro modal,
k0
= 2
π⁄λ0
es el número de onda de la luz en el vacío,
λ0
es la longitud de onda en el vacío y B
nm
(U
m
R) es la función de Bessel de primera especie.
es el parámetro modal,
k0
= 2
π⁄λ0
es el número de onda de la luz en el vacío,
λ0
es la longitud de onda en el vacío y B
nm
(U
m
R) es la función de Bessel de primera especie.
Cuando la fibra es perturbada, se asume que los cambios en el patrón de speckle se deben principalmente a cambios de fase y que la intensidad total del patrón de speckle en la fibra es constante (Darío Gómez & Gómez, 2013). Ahora, teniendo en cuenta lo dicho anteriormente y considerando que al sensor de specklegramas a fibra o FSS (Fiber Specklegram Sensor) se le aplica una perturbación en una pequeña región de longitud L, los cambios de fase entre el modo m y l se pueden escribir como δ( ΔβmlL ). De esta manera, si las variaciones de fase son pequeñas, la nueva distribución de intensidad del patrón a la salida de la fibra multimodo en el punto (r,θ) es:
Entonces, para calcular los cambios en el patrón de intensidad ΔI se usan las ecuaciones (1) y (2):
De (3) se puede concluir que las variaciones en el patrón de intensidad son debidos a las diferencias de fase de los modos m y l. Entonces, los cambios de fase se pueden escribir como Δβml = nDml , donde Dml es una constante proporcional asociada con el cambio de fase entre los modos m y l. De esta forma, los cambio en la constante de propagación en la dirección i (i = x, y o z) debido a una perturbación en un segmento L sobre la fibra se puede expresar como
En la ecuación (4) se puede observar que los cambios en las constantes de propagación de los modos que viajan a través de la fibra se deben a cambios en la longitud de camino óptico δi (nL). Es posible demostrar que cuando una perturbación es aplicada al segmento de fibra multimodo δi (nL) está dado por
donde,
Δni
=
ni
─ n
0 ≈ 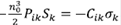 (aquí se indica en notación tensorial) es el cambio del índice de refracción siendo el material isotrópico en un momento inicial con índice
n0
,
Si
es la deformación mecánica (mechanical strain en inglés) y σ
i
es la tensión o esfuerzo mecánico (mechanical stress en inglés) en la dirección principal i.
Pik
es el tensor de deformación mecánica y
Cik
es el tensor de esfuerzo mecánico (Arístizabal,
et al.,
2016). En forma más simplificada:
(aquí se indica en notación tensorial) es el cambio del índice de refracción siendo el material isotrópico en un momento inicial con índice
n0
,
Si
es la deformación mecánica (mechanical strain en inglés) y σ
i
es la tensión o esfuerzo mecánico (mechanical stress en inglés) en la dirección principal i.
Pik
es el tensor de deformación mecánica y
Cik
es el tensor de esfuerzo mecánico (Arístizabal,
et al.,
2016). En forma más simplificada:
donde bajo la suposición de deformación plana (plane strain approximation en inglés), es decir Sz = 0 se tiene que los cambios de índice de refracción debido a efectos mecánicos son (Arístizabal, et al., 2016; Mase & Mase, 1999):
donde P 11 y P 12 son conocidos como coeficientes Pockels. Entonces, las ecuaciones en (6) quedan
En las ecuaciones (8), si las deformaciones mecánicas son pequeñas del orden de 10-3 en fibras ópticas (Gianino & Bendow, 1981), se puede despreciar el término que contiene los coeficientes Pockels debido a que estos son mucho menores que uno (Arístizabal, et al., 2016; Victor H.Aristizabal, Velez, & Torres, 2006), obteniéndose la ecuación simplificada:
En la ecuación aproximada (9), Sz se puede estimar como la deformación unitaria de ingeniería que se define como (L - L 0)/L 0. Al reemplazar la ecuación (9) en (3), se puede observar que los cambios de la intensidad en el patrón de speckle varía linealmente con la deformación mecánica producida en la fibra óptica. En conclusión, cuando la fibra óptica es perturbada, el patrón de speckle a la salida de la fibra es ligeramente modificado por los cambios de fase en la fibra óptica multimodo. Estas modificaciones producen variaciones locales de intensidad lo que genera pequeñas deformaciones en el patrón de speckle de la fibra. Este tipo de comportamiento se ilustra en (Arístizabal, et al., 2016) donde la intensidad es perturbada localmente deformando ligeramente el patrón de speckle de la fibra para el caso de una perturbación mecánica.
En este trabajo se empleará un método alternativo para calcular las intensidades definidas en las expresiones (1) y (2). Primero, para calcular las distribuciones de intensidad del campo eléctrico para una fibra multimodo bajo la aplicación de una línea de carga mecánica (Arístizabal, et al., 2016; Victor H.Aristizabal, et al., 2006), se soluciona numéricamente mediante el método de los elementos finitos la ecuación de onda vectorial para una onda monocromática (V.H. Aristizabal, Vélez, & Torres, 2004, 2006; Torres, Aristizábal, & Andrés, 2011):
dónde n es la distribución del índice de refracción de la fibra y se puede expresar como:
siendo nx , ny y nz los índices definidos en (7). n 0 para el núcleo se calculó usando la ecuación de Sellmeier para el Sílice fundido (Arístizabal, et al., 2016):
y n
0 para el revestimiento se computó desde la ecuación (12) y la apertura numérica de la fibra bajo estudio (NA =  De esta manera se obtienen el campo vectorial de los modos y las constantes de propagación para el sistema perturbado mecánicamente. Todos los modos calculados se suman vectorialmente para hallar la intensidad del campo resultante, obteniéndose finalmente el patrón de speckle (Arístizabal,
et al.,
2016).
De esta manera se obtienen el campo vectorial de los modos y las constantes de propagación para el sistema perturbado mecánicamente. Todos los modos calculados se suman vectorialmente para hallar la intensidad del campo resultante, obteniéndose finalmente el patrón de speckle (Arístizabal,
et al.,
2016).
Ya que los cambios de intensidad por perturbaciones se dan a una escala local cercana a la del tamaño del grano de speckle, estos cambios no se pueden cuantificar adecuadamente por medio del promedio de la intensidad del patrón speckle completo. Así, cuando se tienen imágenes, regularmente se usan técnicas de correlación para esta cuantificación. La implementación algebraica de esta técnica se puede llevar a cabo por medio de varias expresiones similares. (Efendioglu, 2017; Gubarev, Li, Klenovskii, & Glotov, 2016), aunque la más común es el coeficiente de correlación (C) dado por:
donde 〈 Iref 〉 y 〈 In 〉 corresponden a las intensidades promedio del patrón de speckle a la salida de la fibra en un estado de referencia y perturbada, respectivamente.
Resultados y discusión
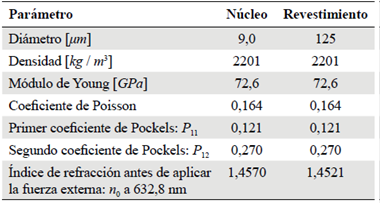
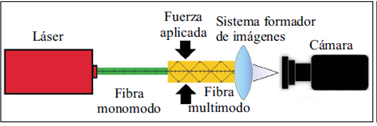
Siguiendo la metodología explicada anteriormente, se calculó y simuló el patrón de speckle para una fibra multimodo (MMF) Thorlabs 1550BHP, con los parámetros descritos en la Tabla 1, donde la fuente de luz tiene una distribución gaussiana y el campo eléctrico polarizado en x. A la fibra multimodo se le aplicó una fuerza en dirección contraria a y. En la Figura 1 se ilustra la situación física que se simula. Los patrones de la Figura 2 muestran el speckle obtenido mediante la superposición de pocos modos para diferentes valores de la fuerza de perturbación, alrededor de 16 modos que son los que se propagan en la fibra estudiada. En este caso, debido a que la fibra que estudiamos sólo soporta 16 modos de propagación, la distribución de puntos brillantes y oscuros no corresponde a la de un patrón de speckle bien comportado, sino una distribución de intensidades con una modulación más suave extendida sobre toda la salida de la fibra. Así, estas imágenes hacen evidente la interferencia entre los modos de propagación y el intercambio de energía entre ellos al perturbar la fibra.
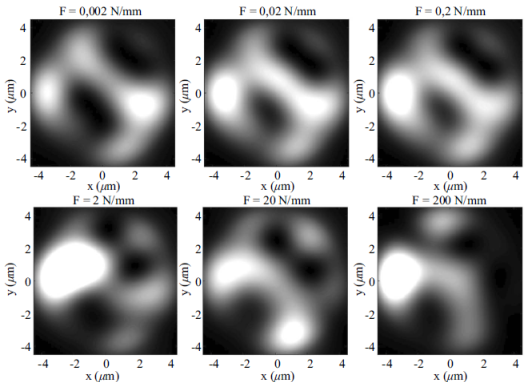
Figura 2 Imágenes de patrones de speckle en una fibra multimodo simulados numéricamente a 650 nm para varios valores de fuerza por unidad de longitud aplicada.
Al analizar la evolución de estos patrones completos usando la medida de correlación entre ellos en diferentes estados de perturbación, se encuentran varios comportamientos para los diferentes rangos de fuerza por unidad de longitud aplicada. El coeficiente de correlación se comporta linealmente para ciertos rangos, como lo muestra la Figura 3b y 3c, pero en otros no existe un comportamiento lineal, ni siquiera monotónico (Figura 3a y 3d). Adicionalmente, la sensibilidad también es dependiente del rango de fuerzas analizado, por ejemplo, la sensibilidad es más alta en la Figura 3c que en la Figura 3b o 3d, si en esta última se redujera el rango de trabajo a la zona lineal de la curva.
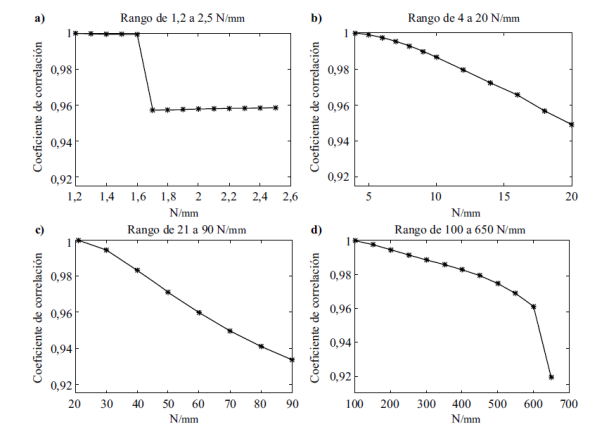
Figura 3 Curvas de correlación entre patrones de speckle a la salida de la fibra para diferentes rangos de fuerza por unidad de longitud aplicada.
La medida de correlación es dependiente de que tan grandes son los cambios en la distribución de intensidades del patrón al cambiar la fuerza aplicada. Ante cambios grandes en la intensidad del patrón se pueden generar comportamientos no monotónicos como de discontinuidad de las curvas de correlación. Una propuesta para evitar estos inconvenientes es la redefinición del patrón de intensidades usado como referencia en los cálculos de correlación, lo que equivale a una recalibración del sistema, pero también es algo que permite aprovechar zonas específicas dónde el comportamiento de la curva de correlación sea el adecuado. En la Figura 3b se muestra la curva de correlación en la que el patrón de referencia usado es el proveniente de la fuerza por unidad de longitud de 4 N/mm y con respecto a este patrón es que se calculan las correlaciones de los demás puntos en esa figura.
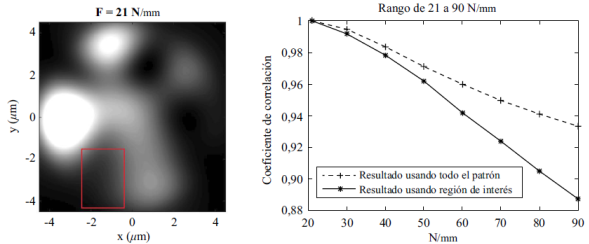
Si se hace una división en regiones del patrón de intensidades, como por ejemplo la región del rectángulo rojo en la figura 4a, y se analiza la correlación para esta región en diferentes patrones de intensidad (diferentes fuerzas aplicadas), se puede mejorar el comportamiento de las curvas de respuesta en correlación. De esta manera, se puede mejorar en la capacidad de sensado del sistema según sea el requerimiento. La figura 4b muestra la curva de correlación para el rango de fuerzas entre 21 N/mm y 90 N/mm (antes mostrado en la figura 3c), usando la zona del rectángulo rojo mencionado, el cual tiene una mayor sensibilidad manteniendo una alta linealidad. Este caso muestra las posibilidades de mejorar las características metrológicas del sensor al usar diferentes zonas del patrón de salida. Finalmente, se puede observar que la sensibilidad y el rango dinámico dependerán de cómo cambia el patrón de intensidades para cada zona elegida. Así, se pueden encontrar zonas que mejoren ostensiblemente el desempeño del sensor como otras que producen comportamientos no monotónicos o discontinuidades en un rango de fuerza requerido.
Conclusiones
En este trabajo se llevó a cabo la simulación numérica de la acción de una fuerza de perturbación sobre una fibra óptica y la respuesta en el patrón de intensidades a la salida de ésta. Los resultados son cercanos a los observados experimentalmente y mostrados en la literatura. Sobre estos patrones se realizó análisis de correlación como método de cuantificación/ interrogación del sistema al ser usado como sensor de perturbaciones físicas. Se mostró que esta metodología es útil y que la división del patrón de intensidades puede mejorar las características metrológicas del sistema como sensor.