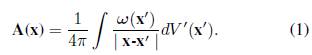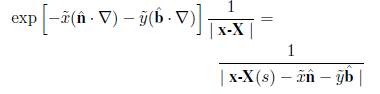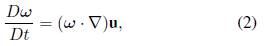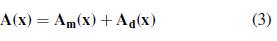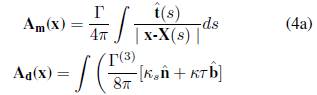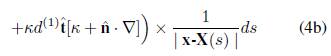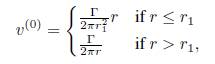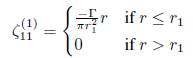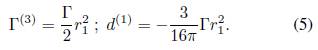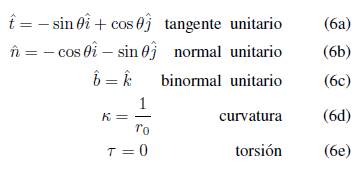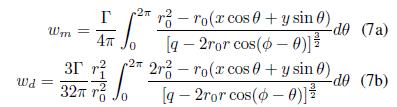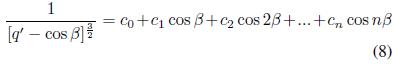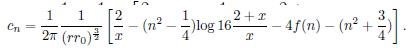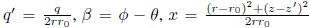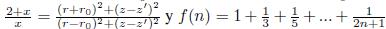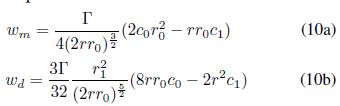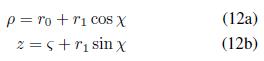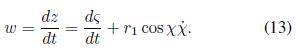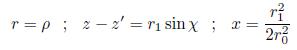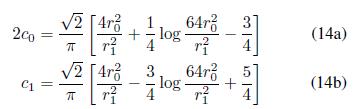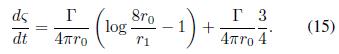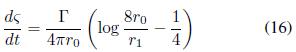Introducción
El estudio de los flujos vorticales obtuvo algunas de sus principales contribuciones con las investigaciones de Helmholtz (1858), donde se establece la existencia de estos flujos al plantear la imposibilidad que tiene un fluido acotado bajo la condición de impenetrabilidad del contorno de ser un flujo potencial. En su trabajo, Helmholtz, además de establecer los principales teoremas que satisfacen las regiones con vorticidad, caracteriza el movimiento de un filamento anular. Las conclusiones de Helmholtz se desarrollan basadas en la constancia de la energía; empero, ninguna expresión analítica fue suministrada.
El interés por las estructuras vorticales se intensificó, tras la sugerencia de W. Thomson (Lord Kelvin) (1867) de suponer que los vórtices anulares en el éter correspondían con los verdaderos átomos. Sugerencia que fue desestimada tras el posterior éxito de los modelos atómicos de J.J. Thomson, E. Rutherford y N. Bohr. No obstante, aún la teoría de vórtices es parte fundamental, no solo de la teoría hidrodinámica, sino del estudio de la generación del sonido como indica Muller (1988), y los fenómenos de transporte y mezcla como indica Mungal (1984).
Tras las conclusiones de Helmholtz sobre el movimiento de filamentos anulares, W.Thomson (1867) establece, sin demostración, a partir de primeros principios, la primera expresión analítica de la velocidad de traslación, Г/4πr 0[log(8r 0 /r 1) − 1/4] , para un vórtice anular de radio de línea central r 0, radio de sección transversal r 1 y con circulación , suponiendo en la sección transversal una distribución lineal de vorticidad, debido a la curvatura del vórtice. Para el mismo vórtice anular estudiado por W. Thomson, J.J. Thomson (1883) establece un método analítico,- importante en el estudio aquí presentado- con el cual determina la velocidad de traslación, Г/4πr 0[log(8r 0 /r 1) − 1], para el vórtice anular. La diferencia entre ambos resultados radica en que el método desarrollo por J.J. Thomson considera, en primer lugar, un vórtice delgado con una distribución de vorticidad uniforme en su sección trasversal; omitiendo así los efectos que la curvatura tiene sobre dicha distribución y, en segundo lugar, establece la velocidad de traslación resolviendo explícitamente la ley de Biot-Savart, para su evaluación posterior en la autoinducción presente. Otras investigaciones clásicas que calculan la velocidad de traslación bajo la consideración de distribución de vorticidad uniforme en la sección transversal del vórtice se encuentran en los trabajos de Lewis (1879) y Joukovskii (1907).
El primer método analítico para calcular la velocidad de traslación de vórtices anulares que considera una distribución lineal en la sección transversal del vórtice, fue desarrollado por Hicks (1885); en el método se emplea la función de corriente de Stokes, expresada en términos de armónicos toroidales (soluciones de las ecuaciones de Laplace para un dominio toroidal). Otros métodos reportados para la misma distribución se encuentran en los trabajos de Dyson (1893), Gray (1914) y Basset (1961).
La teoría de los vórtices anulares ha dado origen a un gran número de investigaciones, no solamente referidas al problema de la traslación. Por ejemplo, en términos observacionales y experimentales los vórtices anulares han concentrado los esfuerzos de muchos hombres de ciencia. Velasco Fuentes (2014) relata las primeras observaciones y experimentos sobre la interacción, formación y reconección asociadas a vórtices anulares; temas que han sido áreas activas de investigación durante las últimas dos décadas. Otras propiedades de los vórtices anulares también han sido estudiadas teórica y experimentalmente por Lamb (1932), Norbury (1973), Kambe & Oshima (1975), Saffman (1992) y Shariff & Leonard (1992) donde se discuten propiedades del vórtice anular como su circulación, impulso, energía cinética e incluso su evolución, desde su generación hasta decaimiento bajo efectos de la viscosidad. Numéricamente, importantes desarrollos han sido reportados con el fin de visualizar y ratificar las propiedades teóricamente obtenidas y encontrar unas nuevas como puede verse en las investigaciones de Stanaway (1988), Mohseni & Ghatib (1998), Kaplanskii & Rudi (1999), Fukumoto & Moffat (2000) y Fukumoto & Kaplanskii (2008). La extensión y el estado del arte asociado al problema general de los vórtices anulares son tan amplias, que para un esquema más detallado sería necesario remitirnos a V.V. Meleshko (2012). En esta sección solo se pretende mostrar el estado del arte acerca de las distribuciones de vorticidad más relevantes -a juicio del autor que han sido consideradas históricamente en el cálculo de la velocidad de traslación de vórtices anulares.
Es de notar cómo el problema de la traslación de vórtices anulares y sus métodos, ha sido investigado por más de un siglo. Sin embargo, la extensión de estos métodos a estructuras vorticales más complejas en general se encuentra limitada por la especial simetría que presentan los vórtices anulares.
En este estudio se presenta un método para determinar la velocidad de traslación de vórtices anulares, aplicable a estructuras más complejas. Así, en la sección II se formulará el modelo matemático, el campo de velocidad inducido y la velocidad de traslación del vórtice anular, en la sección III se realizará la discusión de los resultados encontrados y en la sección IV se concluirán las ventajas que presenta el modelo teórico empleado.
Traslación de un vórtice anular
La traslación de un vórtice anular se da como consecuencia de los efectos de autoinducción que tiene la distribución de vorticidad del vórtice sobre sí mismo. Dicho efecto puede ser determinado a partir del campo de velocidad asociado al vórtice, el cual se calcula desde el potencial vectorial asociado a la ley de Biot-Savart, bajo la condición de que todas las variables físicas sean continuas en todo el espacio. Así, los campos de velocidad no solo dependerán de la distribución interna de vorticidad sino también de su geometría.
En la Figura 1 se presentan los parámetros que caracterizan la configuración investigada, correspondientes al vórtice anular; en lo que sigue se presenta el método de expansión multipolar utilizado para conocer el campo de velocidad de la configuración en cualquier punto circundante al vórtice anular.
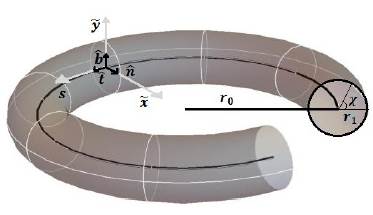
Figura 1 Representación geométrica de un vórtice anular con radio de la línea central r
0, radio de sección transversal del vórtice respecto a la línea central r
1 y χ el ángulo en la sección transversal del vórtice. Adicionalmente, se ilustra el sistema coordenado local de Frenet-Serret (
 ) con sus correspondientes vectores unitarios
) con sus correspondientes vectores unitarios
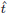 (tangente),
(tangente),
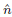 (normal) y
(normal) y
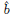 (binormal).
(binormal).
Método de expansión multipolar
El método de expansión multipolar es entendido como el desarrollo en serie de potencias del potencial vectorial, A(x), asociado a la ley de Biot-Savart en términos del parámetro de relación de aspecto, que determina el grosor trasversal del vórtice. En este método el vórtice se encuentra descrito en términos de un sistema coordenado local, como indica Callegari (1978), que permite conocer los efectos del vórtice, independientemente de su movimiento, en el medio.
El cálculo del campo de velocidad inducido por la región con vorticidad se determina indirectamente, calculando el rotacional del potencial vectorial. Para esto, primero se realiza la expansión multipolar del potencial vectorial asociado, A(x), el cual se define como
sujeto a la condición de normalización,
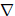 = 0, relacionada con el flujo nulo de vorticidad en la superficie del vórtice. Donde ω es la vorticidad, x es la posición sobre la cual se distribuye la vorticidad en el espacio, y x la posición exterior al vórtice donde se manifiestan los efectos inductivos del vórtice.
= 0, relacionada con el flujo nulo de vorticidad en la superficie del vórtice. Donde ω es la vorticidad, x es la posición sobre la cual se distribuye la vorticidad en el espacio, y x la posición exterior al vórtice donde se manifiestan los efectos inductivos del vórtice.
Para la expansión asintótica del potencial, Y. Fukumoto & V. L.Okulov (2005) expresan la posición de un punto dentro del vórtice en un sistema coordenado de Frenet-Serret (entiéndase como un sistema que se mueve con el vórtice y cuyos ejes coordenados son
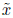 a lo largo del vector normal,
a lo largo del vector normal,
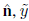 a lo largo del vector binormal,
a lo largo del vector binormal,
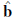 , y s la longitud de arco a lo largo del vector tangente,
, y s la longitud de arco a lo largo del vector tangente,
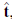 , asociados a la línea central del vórtice y desde el cual es posible definir el sistema cilíndrico (r, θ, s)), y con ello re-escribir parte del potencial mediante el operador de desplazamiento de Dyson (1893)
, asociados a la línea central del vórtice y desde el cual es posible definir el sistema cilíndrico (r, θ, s)), y con ello re-escribir parte del potencial mediante el operador de desplazamiento de Dyson (1893)
Donde el vector posición de un punto del vórtice se expresa como
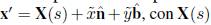 , con X(s) la posición de la línea central del vórtice respecto a un sistema fijo. Luego, una expansión en Taylor del operador desplazamiento es posible, donde cada orden retenido en esta expansión representa los diferentes efectos del grosor del vórtice que pueden ser retenidos en el calculo de la velocidad de traslación del vórtice anular, en este estudio los términos retenidos en la expansión son de hasta primer orden.
, con X(s) la posición de la línea central del vórtice respecto a un sistema fijo. Luego, una expansión en Taylor del operador desplazamiento es posible, donde cada orden retenido en esta expansión representa los diferentes efectos del grosor del vórtice que pueden ser retenidos en el calculo de la velocidad de traslación del vórtice anular, en este estudio los términos retenidos en la expansión son de hasta primer orden.
Adicionalmente, en la expansión asintótica del potencial vectorial la vorticidad se desarrolla como una serie de Fourier, como indica Fukumoto (2000, 2005); donde la componente de vorticidad longitudinal,
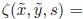
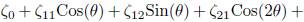 , se considera dominante por el hecho de que los vórtices anulares no presentan giro. Los coeficientes de la serie de Fourier se determinan mediante la solución de la componente longitudinal (a lo largo de la línea central) de la ecuación de vorticidad de Helmholtz, Ec. (2), para una expansión asintótica en el parámetro
, se considera dominante por el hecho de que los vórtices anulares no presentan giro. Los coeficientes de la serie de Fourier se determinan mediante la solución de la componente longitudinal (a lo largo de la línea central) de la ecuación de vorticidad de Helmholtz, Ec. (2), para una expansión asintótica en el parámetro
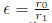 (ver Figura 1), donde resultan los coeficientes dependientes del perfil inicial de velocidad. La expansion asintótica de la ecuación de vorticidad consiste en encontrar los coeficientes de la expansión de Fourier de la componente longitudinal de la vorticidad,
(ver Figura 1), donde resultan los coeficientes dependientes del perfil inicial de velocidad. La expansion asintótica de la ecuación de vorticidad consiste en encontrar los coeficientes de la expansión de Fourier de la componente longitudinal de la vorticidad,
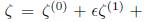 ..., lo cual se logra solucionando la ecuación de Helmholtz para un fluido incompresible y sin viscosidad,
..., lo cual se logra solucionando la ecuación de Helmholtz para un fluido incompresible y sin viscosidad,
sin perder de vista que el orden conocido de los coeficientes en la expansión asintótica representa el grado de precisión con el que se deseen modelar los efectos de la distribución de vorticidad, presentes por la existencia del grosor del vórtice y, en general por la geometría del mismo.
Para la componente de vorticidad longitudinal a orden cero se encuentra que;
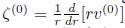 . Donde v
(0) corresponde a la componente angular de la velocidad a orden cero, es decir el perfil inicial de la velocidad con el que empieza la traslación el vórtice anular. Para la ecuación de Helmholtz a primer orden, la solución se obtiene a partir de los campos de velocidad dados en términos del potencial vectorial (encontrándose la componente tangencial de la vorticidad expresada en términos de una función de corriente que se obtiene a partir de la ecuación para la componente longitudinal de vorticidad) -el desarrollo de estas soluciones no se hace explícito ya que su extensión y detalle desviarían el artículo de su propósito- para más detalle ver Fukumoto (2005) y Gonzalez (2013) . Así, el coeficiente a primer orden se expresa como
. Donde v
(0) corresponde a la componente angular de la velocidad a orden cero, es decir el perfil inicial de la velocidad con el que empieza la traslación el vórtice anular. Para la ecuación de Helmholtz a primer orden, la solución se obtiene a partir de los campos de velocidad dados en términos del potencial vectorial (encontrándose la componente tangencial de la vorticidad expresada en términos de una función de corriente que se obtiene a partir de la ecuación para la componente longitudinal de vorticidad) -el desarrollo de estas soluciones no se hace explícito ya que su extensión y detalle desviarían el artículo de su propósito- para más detalle ver Fukumoto (2005) y Gonzalez (2013) . Así, el coeficiente a primer orden se expresa como
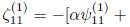
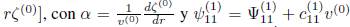 donde
donde
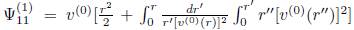 y
y
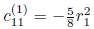 valor asignado para el caso en que el origen se encuentre en un punto a lo largo de la dirección normal al vórtice y donde su sección transversal sea simétrica como indica Fukumoto (2000). Establecidas las expansiones anteriores y, reteniendo los efectos a primer orden correspondientes a la distribución de vorticidad debido a la curvatura del vórtice, la expresión para el potencial (1) toma la forma:
valor asignado para el caso en que el origen se encuentre en un punto a lo largo de la dirección normal al vórtice y donde su sección transversal sea simétrica como indica Fukumoto (2000). Establecidas las expansiones anteriores y, reteniendo los efectos a primer orden correspondientes a la distribución de vorticidad debido a la curvatura del vórtice, la expresión para el potencial (1) toma la forma:
Donde
Donde κ y τ son la curvatura y la torsión a lo largo de la línea central, κ
s
la derivada de la curvatura del vórtice respecto a la longitud de arco, Г es la circulación y
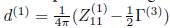 . Siendo,
. Siendo,
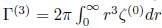 y
y
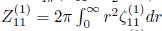 , los momentos de vorticidad en términos de
, los momentos de vorticidad en términos de
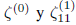 , los coeficientes de vorticidad de orden 0 y 1, respectivamente.
, los coeficientes de vorticidad de orden 0 y 1, respectivamente.
Las ecuaciones anteriores expresan el potencial vectorial A mediante dos contribuciones principales; Am (monopolar) y Ad (dipolar), para vórtices con relación de aspecto pequeña. La contribución monopolar está referida a los efectos de inducción de un vórtice infinitamente delgado, cuyos efectos por grosor son ausentes, mas los de forma no. De otra parte, la contribución dipolar hace referencia a los efectos de inducción debidos a la reorganización de la vorticidad en el interior del vórtice como consecuencia del estiramiento y doblamiento del mismo, por la presencia de la curvatura y la torsión en la Ec.(4b), reconociéndose como efectos propios del grosor del vórtice.
Campos de velocidad
El campo de velocidad asociado a la distribución de vorticidad del vórtice anular es, por definición, como indica Bachelort (2000) u =
 × A. El cálculo del campo de velocidades se obtiene explícitamente una vez que se establece el perfil inicial de vorticidad, ζ
(0), el cual se toma constante, correspondiente al perfil inicial de velocidad (ver Figura 2)
× A. El cálculo del campo de velocidades se obtiene explícitamente una vez que se establece el perfil inicial de vorticidad, ζ
(0), el cual se toma constante, correspondiente al perfil inicial de velocidad (ver Figura 2)
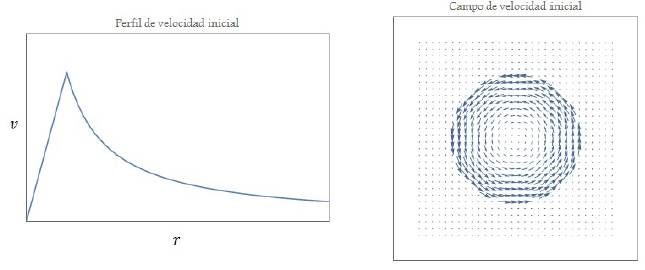
Figura 2 Perfil de velocidad inicial a orden cero (panel izquierdo). Representación vectorial del perfil de velocidad, a orden cero, de una sección transversal del vórtice anular (panel derecho).
con esto, el coeficiente de vorticidad a orden uno es
y por tanto, los momentos de vorticidad quedan expresados como
Además de la distribución de vorticidad, también la geometría es fundamental en la determinación de las contribuciones monopolar, Am, y dipolar, Ad, como se deduce de las Ecs. (4a) y (4b). Para el caso del vórtice anular la geometría es caracterizada por
La traslación de un vórtice anular es establecida respecto a la componente de velocidad vertical al plano de la configuración, w. Esta componente, propia de la inducción, se calcula reteniendo los efectos que la forma (en la contribución monopolar) y el grosor (en la contribución dipolar) tienen en la evolución del vórtice. A partir de la geometría anteriormente dada, se establece Am(x) y Ad(x), donde
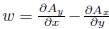 . El cálculo explícito de w como de las otras componentes del campo de velocidad son desarrolladas, para el vórtice anular, por Jeasson F. Gonzalez (2013). Encontrándose para las contribuciones monopolar, w
m
, y dipolar, w
d
, de la componente de la velocidad w las siguientes expresiones integrales:
. El cálculo explícito de w como de las otras componentes del campo de velocidad son desarrolladas, para el vórtice anular, por Jeasson F. Gonzalez (2013). Encontrándose para las contribuciones monopolar, w
m
, y dipolar, w
d
, de la componente de la velocidad w las siguientes expresiones integrales:
Donde las cordenadas (r
0
, θ, z’ ) corresponden a un punto sobre el vórtice anular, las coordenadas (r, φ, z) a un punto arbitrario fuera del vórtice y
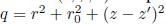 .
.
Para desarrollar las integrales (7a) y (7b) se realizará la siguiente expansión en Fourier,
Con
Obteniendose para las contribuciones monopolar y dipolar las expresiones
luego, el campo inducido total queda expresado como la superposición de las contribuciones monopolar, (10a), y dipolar, (10b), tal que
La expresión encontrada, compuesta de dos términos, permite distinguir la naturaleza de las contribuciónes a la traslación de un vórtice anular por medio de la autoinducción; primero, w m , resalta la contribución que tiene la forma del vórtice y, segundo, w d , la contribución que se tiene por el grosor del vórtice.
Velocidad de traslación
Para determinar la traslación del vórtice anular se sigue la consideración clásica de que la superficie del vórtice es una superficie material. Luego, los cambios en el tiempo de la superficie del vórtice coinciden con el campo de velocidad evaluada en la superficie del mismo, hecho que es de esperarse ya que la traslación del vórtice se origina por medio de un proceso de autoinducción. La determinación de la velocidad vertical de la superficie material del vórtice se establece como sigue: primero se determina la geometría de la superficie (ver Figura 1), la cual se expresa como
donde ς es la altura del plano sobre el cual yace el vórtice anular; segundo, se determina por diferenciación respecto del tiempo de (12b) la velocidad vertical de la superficie material. La cual queda definida como
Con lo que se hacen evidentes dos contribuciones, independientes a la velocidad vertical. La primera propia de la traslación del vórtice, evidenciada en el primer término de la Ec. (13), y la segunda, evidenciada en el segundo término, debida a los efectos de rotación internos al vórtice.
Por otra parte, la evaluación del campo inducido sobre la superficie material es establecida teniendo en cuenta las siguientes relaciones
Así, los coeficientes de Fourier, tal como se deduce de la Ecs. (8) y (9), pueden ser escritos como
Donde se ha tomado a f (0) = 0 y a f (1) = 1.
Para la velocidad de traslación del vórtice se realiza la comparación entre los resultados de la Ec. (13) y la Ec. (11) con los coeficientes de Fourier (14a) y (14b). Omitiéndose en (13) el término χ˙ ya que se supone que el vórtice no tiene giro como indica Moffatt (1988). Por todo lo anterior, se encuentra para la velocidad de traslación del vórtice la expresión
De este modo, la velocidad de traslación del vórtice anular se expresa como la suma de las contriuciones monopolar y dipolar en el primer y segundo término del lado derecho de la Ec. (15) respectivamente. La primera propia de la forma del vórtice y la segunda correspondiente al efecto que tiene la distribución de vorticidad por la curvatura del vórtice, con lo que se considera el efecto que tiene el grosor en el vórtice.
Discusión
La expresión (15) resalta como el primer término a la derecha resulta ser la contribución a la traslación debida al efecto puramanete monopolar (equivalente al resultado de Thomson 1883). Donde se considera el promedio de la vorticidad en la sección transversal del vórtice concentrada a lo largo de su línea central.
Por otra parte, el segundo término a la derecha de (15) representa la contribución a la traslación debida al efecto dipolar. La cual tiene en cuenta la distribución de vorticidad en la sección transversal del vórtice, debido a los efectos de curvatura del mismo. Finalmente, la suma de ambas contribuciones, resulta en la expresión
que equivale al resultado de Kelvin (1867), para la traslación del vórtice anular. La importancia del resultado presentado en este estudio, más que la obtención correcta de las expresión analítica (16), es la interpretación física asociada a cada término de (15). Adicionalmente, es importante notar como a partir de la consideración inicial de una distribución de vorticidad uniforme, el resultado del método de expansión multipolar concuerda con el modelo de Kelvin; para el cual la distribución de vorticidad lineal era considerada como una condición inicial estacionaria como indica Fukumoto (2000).
Conclusiones
Se investigó mediante un método analítico alternativo, los efectos que el grosor de un vórtice anular tiene para la traslación del mismo. Encontrándose que en la contribución del grosor, recae la redistribución de vorticidad en la sección transversal del vórtice debido a la curvatura del mismo, como se evidencia en la expresión que define al potencial dipolar, Ad, en la Ec. (4b). Además, el efecto del grosor hace al vórtice anular más veloz que cuando se considera a éste con una distribución de vorticidad uniforme, propia del efecto monopolar donde se omite la contribución del grosor, lo cual se verifica desde la contribución que tiene el segundo término al lado derecho de (15).
La ventaja que recae sobre el método presentado radica en el hecho de que es igualmente válido a la hora de aplicarse sobre estructuras vorticales más complejas, como son por ejemplo los vórtices anudados o helicoidales, una vez que pueda determinarse de modo analítico la geometría de la estructura vortical.
Los campos de velocidad asociados con el vórtice se encontraron siguiendo el método de expansión multipolar para la ley de Biot-Savart y se evaluaron para efectos de traslación siguiendo el método de J.J. Thomson. La solución encontrada, Ec. (16), corresponde al resultado clásicamente ya reportado por W. Thomson (1867); sin embargo, permite discutir de manera más profunda la interpretación del mismo mediante los efectos monopolares y dipolares. Así, el método presentado tiene como ventaja la capacidad de distinguir la naturaleza de los efectos que contribuyen a la velocidad de traslación de vórtices anulares y, mas ampliamente, de estructuras vorticales mas complejas.
Para una aproximación de primer orden en r 1 /r 0 en la expansión multipolar de la ley de Biot-Savart, se obtuvo que el campo inducido asociado al vórtice de interés, se encuentra influenciado principalmente por dos aspectos; el primero, la geometría del vórtice, el segundo, la distribución de vorticidad en la sección transversal del vórtice debido a la curvatura del mismo.
Lo anterior aclara la relación entre la distribución de vorticidad -asumida en la sección transversal de los vórtices- y el grado de precisión de la descripción empleada. Ya que aunque la distribución uniforme y lineal resultan ser distribuciones independientes, correspondientes a efectos dominantes de órdenes de importancia diferentes, su superposición resulta ser solo una aproximación del perfil real de la distribución de vorticidad en la sección transversal del vórtice. Con esto la distribución de vorticidad en la sección transversal de un vórtice no es impuesta arbitrariamente según la complejidad que quiera considerarse, sino que corresponde directamente con el número de efectos que quieran tenerse en cuenta en la evolución del vórtice, debidos esencialmente, a la geometría (forma) del mismo; esto es, los efectos que tiene su curvatura, su torsión y su grosor en la evolución del vórtice.