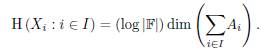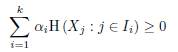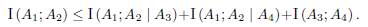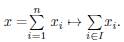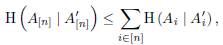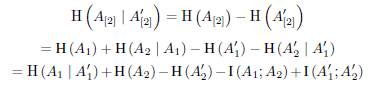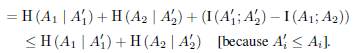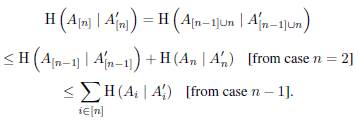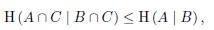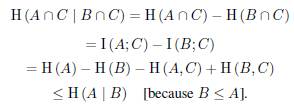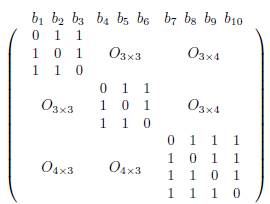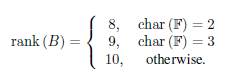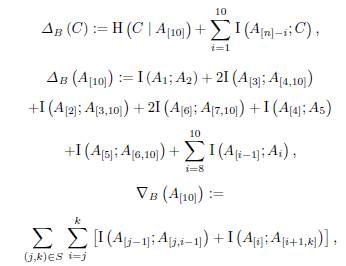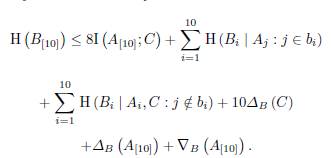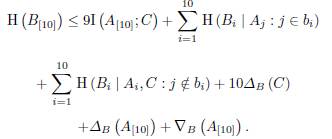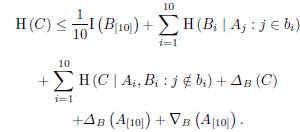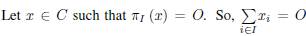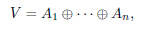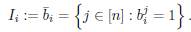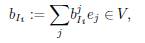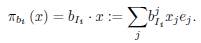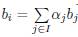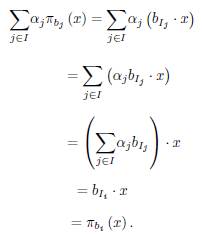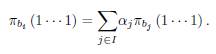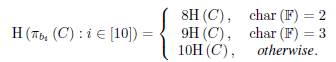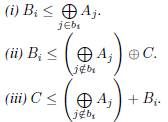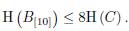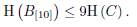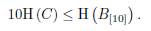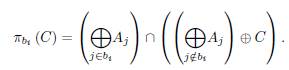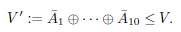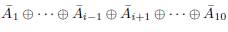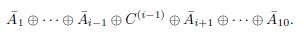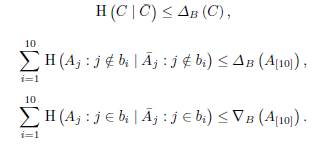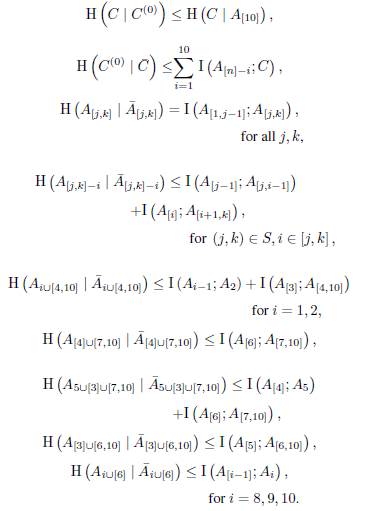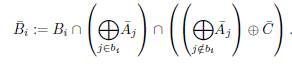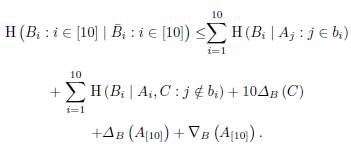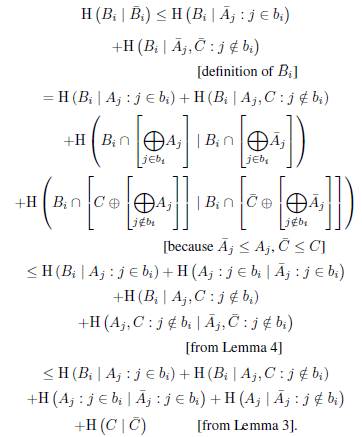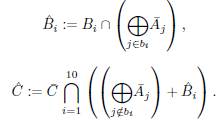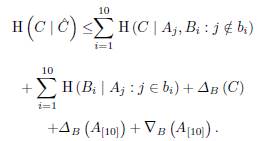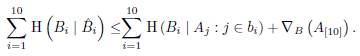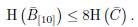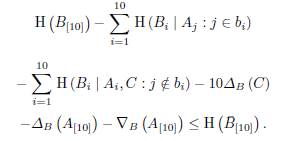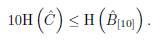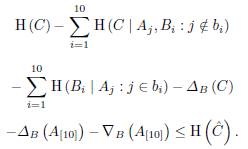Entropy and inequalities in Linear Algebra

In the following, we introduce the necessary concepts to understand this paper. Let A, B, A ₁ , A _n be vector sub-spaces of a finite dimensional vector space V over a finite field 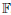. Let 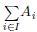be the span of A _i , i e I. There is a correspondence between inequalities satisfied by dimensions of spans of vector spaces and inequalities satisfied by entropies of certain class of random variables induced by vector spaces (A. ^{Shen, et al., 2000}, Theorem 2). We explain that: let f be chosen uniformly at random from the set of linear functions from V to F. For A _i , A _n define the random variables X ₁ = f \ _a1 , X _n = f | _An . For I ⊆ [n]: = {1,...,n}, we have

The random variables X ₁ , X _n are called linear random variables over 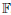. For simplicity, we identify the entropy of linear random variables with the dimension of the associated subspaces, i.e. H(A₁: i Є I), the entropy of A_i, i e I, is dim 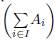. With this notation, the mutual information of A and B is given by I(A; B) = dim (A ∩ B). The codi-mension of A in V is given by codimy (A) = dim (V) - dim (A). We have H(A | B) = codim_A (A ∩ B). In a similar way conditional mutual information is expressed.

We give the following definition in order to fix ideas about inequalities.

Definition 1. Let P be a proper subset of primes, and let Ii, I _k be subsets of [n]. Let α ₁ Є ℝ, for 1 ≤ i ≤ k .A linear inequality of the form

- is called a characteristic-dependent linear rank inequality if it holds for all jointly distributed linear random variables X₁, X _n finite fields with characteristic in P, and does not in general hold over fields with other characteristic.

- is called a linear rank inequality if it holds for all jointly distributed linear random variables over all finite field.

- is called an information inequality if the inequality holds for all jointly distributed random variables.

By definition of linear random variables, we note any information inequality is an inequality which is also satisfied by dimensions of spans of vector spaces. The following inequality is the first linear rank inequality which is not information inequality.

Example 2. (^{Ingleton, 1969}) For any A₁, A₂, A₃, A₄ sub-spaces of a finite dimensional vector space,

We can think a characteristic-dependent linear rank inequality like a linear rank inequality that is true over some fields.

We say that A + B is a direct sum, denoted by A ⊕ B, if A ∩ B = O. In case that V = A ⊕ B, the members of this sum are called (mutually) complementary subspaces in V. Alternatively, A ₁ , ... , A _n are mutually complementary subspaces in V if every vector of V has an unique representation as a sum of elements of A₁, A_n. In this case, п _I denotes the I-projection function 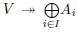given by

The inequalities of the following lemmas, that we will use later, are valid for linear random variables that hold some additional conditions.

We remark that we use the following notation of intervals: [j, k] := {i Є ℕ : j ≤ i ≤ k}, [k] = [1,k]. The sum A _j +… + A _k is denoted by A _[tk], and A₀: = A_Ø: = O.

Lemma 3. For any subspaces A ₁ , ..., A _n , A ₁ , ..., A _n of a finite dimensional vector space V such that Ai ≤ A ₁ , we have

with equality if and only if Ai+1 ∩ A _[i] = A' _i+1 ∩ A’ _[i] for all i.

Proof. By induction over n. In case n =2, we have

The equality holds if and only if I (A ₁ ; A₂ )= I (A’ ₁; A’₂). In other words, A ₁ ∩ A ₂ = A’ ₁ ∩ A’₂ because A’₁ ≤ A_i. Now, we suppose the case n - 1 is true. We have

The equality holds if and only if I (A _i+1 ; A _[i] ) =

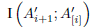. Since A’ _i ≤ A _i for all i, we have A _i+1 ∩ A _[i] = A’ _i+1 ∩ A’ _[i]

Lemma 4. For any subspaces A, B , C of a finite dimensional vector space V such that B ≤ A, we have

with equality if and only A + C = B + C.

Proof. We have

The equality holds if and only if H(A, C)=H(B, C).

Since B ≤ A, it follows that A + C = B + C.

Producing inequalities

Let B be the following 10 x 10 binary matrix

We calculate the rank of the matrix B over different fields to find:

For a column b _i of B, the set {j : b ^j _¡ = 1} ⊆ [10] is denoted by b_i; if there is no confusion, by abuse of notation, we identify bi and b _i . The notation is the same for row and column vectors. We define:

where S is the set of the three points (1,3), (4, 6), (7,10).

The theorem of this paper shows three characteristic-dependent linear rank inequalities. The proof is guided by the matrix B; we choose this matrix because it is the smallest binary matrix, which we find, whose rank is different over at least three different finite fields. We hope that the arguments presented in the demonstration can be used to produce other inequalities taking matrices that have similar properties to this matrix.

Theorem 5. Let A ₁ , A ₂ , A ₃ , A ₄ , A ₅ , A ₆ , A ₇ , A ₈ , A ₉ , A ₁₀ , B ₁ , B ₂ , B ₃ , B ₄ , B ₅ , B ₆ , B ₇ , B ₈ , B ₉ , B ₁₀ , C be vector subspaces of a finite dimensional vector space V over a finite field F. The following inequalities are characteristic-dependent linear rank inequalities: - If the characteristic of 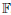is 2, then

- If the characteristic of 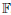is neither 2, then

- If the characteristic of 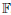is neither 2 nor 3, then

We remark that these inequalities do not in general hold over other fields whose characteristic is different to the described characteristic. A counterexample would be in V = GF (p) ¹⁰ . Take the vector subspaces: A _i = (e _i ), the span of each vector of the canonical basis in V; B _i = (b _i ), the span of each column of the matrix B; and C = {(1 … 1)), the span of the vector with 1 in all entries. Then, if p =2, the first inequality does not hold; if p = 2, 3, the second inequality does not hold; if p =2or 3, the third inequality does not hold.

The proof is given at the end of the section. Before, we introduce some propositions and lemmas that will help its development.

Let V = A ₁ ⊕ … ⊕ A _n , and take a vector subspace C of V such that A ₁ h-----h A _i-1 + C + A _i+1 h-----h A _n is a direct sum for all i. We say that (A ₁ ,...,A _n ,C) is a tuple of complementary vector subspaces in V.

Proposition 6. A subspace C as above described holds H(п _i (C)) =H(C) ≤ H(A ₁ ),forall Ø #= I ⊆ [n].

Proof. .

Hence, x e 0 A_i. By property of the tuple of complementary vector subspaces, x = O. In other words, п _I (C) and C are isomorphic or have the same dimension.

As a consequence a non-zero element of C can be written uniquely as a sum of non-zero elements of A ₁ , ... , A _n .

Consider any n x m binary matrix B', with columns denoted by b_i. Let п _bi be the I _i -projection of

Where

Take

where (e _j ) _j is the canonical basis in V; and b ^j _It . is 1 if ej ∈ A _k for some k such that b _k = 1, and 0 in otherwise. If 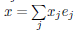, then we have

We have the following proposition.

Proposition 7. Let V = A ₁ ⊕ … ⊕ A _n , A _i # O, and let B ^' be a n x m binary matrix. For all i and I, we have 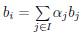if and only if .

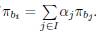Proof. We note 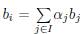if and only if .

Now, let . For x ∈ V,

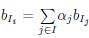The other implication is obtained from

Example 8. 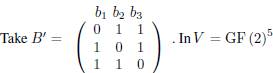, define 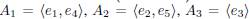. We have 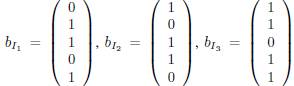. One can check that b ₁ = b ₂ + b ₃ and b _I3 = b _I2 + b _I3 .

As a consequence of Proposition 6, if each A _i and C are one-dimensional vector spaces, then C is isomorphic to the span of (1 … 1), and each п _b1 . (C) is isomorphic to {b _Ii ). From this and the last proposition, we have the following proposition that is a stronger version of this fact:

Corollary 9. Let (A ₁ ,...,A _n ,C) be a tuple ofcomplementary vector subspaces in V over with C # O, and let B ^' be a n x m binary matrix with columns denoted by bi. We have {b _i } _i ∈ _I is an independent set if and only if is a direct sum.

If we take B' := B, the 10 x 10 binary matrix defined above, in the last corollary, we obtain:

Corollary 10. If (A ₁ ,..., A₁₀,C) is a tuple of complementary vector subspaces of V, then

In the rest of the paper, we only work with the matrix B. The Corollary 10 is used immediately to find three inequalities which are true over vector spaces that hold some conditions. We note that the desired conditions are described by the dependency relationships of the columns of B.

Proposition 11. Let A _x , A ₂ , A3, A4, A ₅ , A _e , A ₇ , A ₈ , A ₉ , A₁₀, B₁, B₂, B₃ , B ₄ , B ₅ , B ₆ , B _r , B ₈ , B ₉ , B ₁₀ , C vector subspaces of a finite dimensional vector space V over a finite field F such that (A ₁ ,..., A₁₀,C) is a tuple of complementary vector subspaces. Consider the following conditions:

We have the following implications:

1. If conditions (i) and(ii) hold, and the characteristic of 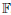is 2, then

2. If conditions (i) and(ii) hold, and the characteristic of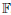is 3, then

3. If conditions (i) and (iii) hold, and the characteristic of 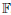is neither 2 nor 3, then

Proof. To proof 1 and 2, we can use

Therefore, using conditions (i) and (ii), we have Bi ≤ п _bi (C). Then we apply the last corollary. To proof 3, using conditions (i) and (iii), we can derive п _bt . (C) ≤ B _i . Then we apply the last corollary.

Define 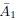: = A₁, and for i > 1, take a vector subspace of Ai which is complementary to 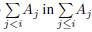, denote this subspace by 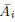. We have

Let C ⁽⁰⁾ = V' ∩ C. Recursively, for i, denote by C ⁽ⁱ⁾,a subspace of C ^(i-1) which is a complementary subspace to

in

Let Ċ denote the subspace C ⁽¹⁰⁾. The tuple ( 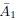,..., 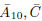) is not unique but from now on we fix one of these tuples.

Lemma 12. ( 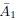,..., 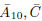) is a tuple of complementary vector subspaces in V ^' that holds the following inequalities:

Proof. The given tuple is a tuple of complementary vector subspaces in V' by definition. Furthermore, using Lemma 3, we have the following inequalities:

One can use all (hese inequalities along with the definitions of ∆ _B (C), ∆ _B (A[₁₀]), ∇ _B (A[₁₀]) (these definitions were previously given) to obtain the described inequalities.

Lemma 13. For each i, let

We have the subspaces 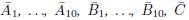satisfy conditions (i), (ii) of Proposition 11, and the following inequality holds

Proof. The subspaces satisfy conditions (i) and (ii) of Proposition 11 by definition. Also, we have

Then, we apply the inequalities from Lemma 12.

Lemma 14. For each i, let

We have the subspaces 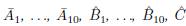satisfy conditions (i), (iii) of Proposition 11, and the following inequality holds

Proof. The subspaces satisfy conditions (i) and (iii) of Proposition 11 by definition. Also,we have

Hence,

Then, we apply the inequalities from Lemma 12 and the inequality presented at the beginning of the proof.

Proof of Theorem 5

To prove the inequality 1, from Lemma 13, the vector sub-spaces 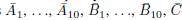satisfy Proposition 11 with condition 1 if the characteristic of the field F is 2. We have

One can note H (C) < I (A[ ₁₀ ]; C), and the inequality given in Lemma 13 can be write as

Using all these inequalities we obtain the desired inequality.

The inequality 2 is obtained in a similar way; and from the inequality 1, it is easy to note that the inequality 2 also holds over fields whose characteristic is 2.

To prove the inequality 3, from Lemma 14, the vector subspaces 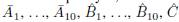satisfy Proposition 11 with condition 3 if the characteristic of the field F is neither 2 nor 3, we have

One can note 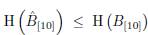, and the inequality given in Lemma 14 can be write as

Using all these inequalities we obtain the desired inequality.