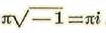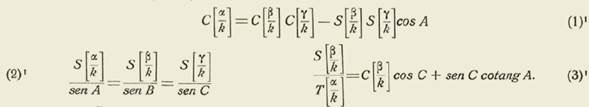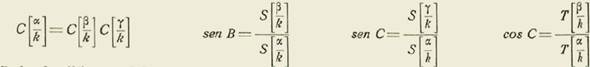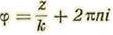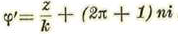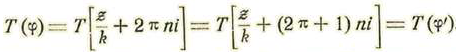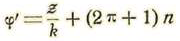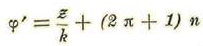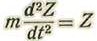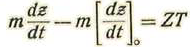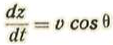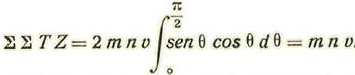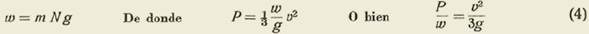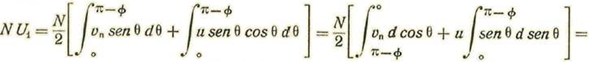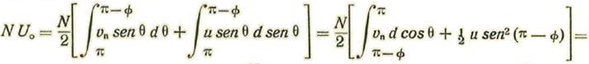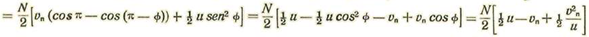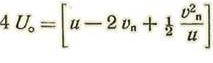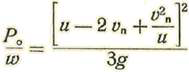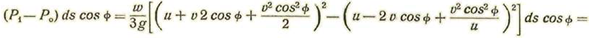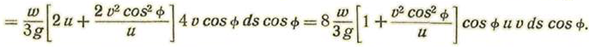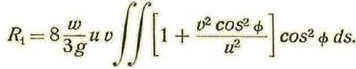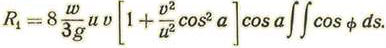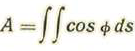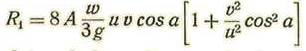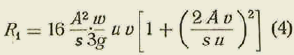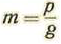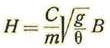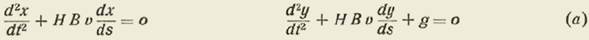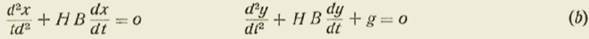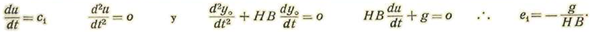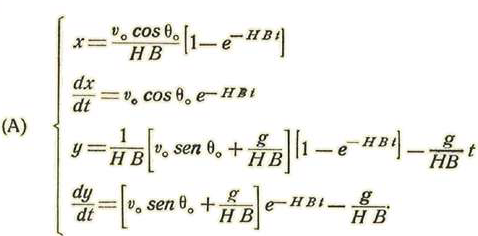NOTA SOBRE LAS GEOMETRIAS PLANAS NO EUCLIDEAS
Después de que el lector se haya informado bien del juicio crítico en referencia y de la manera como se ha confeccionado la Trigonometría plana hiperbólica, se convencerá de que Gauss, Lobattcheffsky y Riemann, y en general los que han estudiado a fondo y detenidamente el asunto, han tenido forzosamente que llegar a las mismas conclusiones a que hemos llegado nosotros respecto del postulado de Euclides. Habiendo tropezado aquellos sabios cou un interesante acertijo, se guardaron de aclararlo para dejar un motivo de entretenimiento a los curiosos, presentando el enigma bajo la forma de verosimilitud de otras Geometrías planas no euclídeas.
El progreso moderno ha sido quizás la causa de que el acertijo no haya sido puesto en claro, pues los quehaceres y entretenimientos impiden al hombre moderno, en esta época de automovilismo y cinematografía, estudiar los asuntos con la debida atención. Por otra parte, se puede afirmar que hoy el mayor número de personas estudiosas, sea por falta de tiempo o sea por desconfianza en la fuerza de su propio entendimiento, prefiere recargar la memoria más bien que cultivar la inteligencia ejercitándola en la investigación de la verdad.
La confusión de conceptos que reina hoy en el mundo sabio respecto de la formación y desarrollo de las ideas cuantitativas, es indudablemente debida a las causas atrás anotadas. Tal confusión de ideas ha sido a su vez causa de que el juguete presentado por Lobattcheffsky haya tomado el carácter de inextricable misterio. En efecto, los geómetras kantianos que, antes de Lobattcheffsky, conferían a los axiomas la categoría de verdades necesarias, admitieron después la existencia lógica de espacios no euclídeos! En cambio, otros sabios que prohijan las ideas psicológicas modernas, discuten no obstante sobre las diferencias que existen entre lo que ellos han llamado espacios visual, táctil y motor y el espacio que llaman geométrico, a fin de poder deducir que este último es convencional y que, por tanto, las Geometrías euclídeas o no euclídeas no encierran verdades sino convenciones más o menos ventajosas unas que otras! Tales sabios psicólogos adulteran profundamente la psicología experimental, según la cual el cerebro, centro nervioso, ha venido transformándose paralela y progresivamente bajo la influencia resultante del conjunto de todos los sentidos y simultáneamente con ellos durante toda la historia de la vida en la labor de adaptación del sér al medio en que actúa. Según esta escuela la idea de espacio proviene del efecto resultante de todas las sensaciones en circunstancias variadísimas, pero consecuentes a la modalidad que se llama coexistencia, y además representables en la imaginación.
No se vaya a creer, por lo que acabamos de decir, que el asunto concierne a la alta Filosofía; muy al contrario, es cuestión sencilla al alcance de todos.
La posibilidad de existencia de toda figura geométrica que la imaginación pueda concebir de una manera clara, es el principio fundamental de la Geometría. Las ideas sobre tales figuras son intuitivas; al hablar en el lenguaje cartesiano se diría que son ideas innatas; según la psicología moderna, deben ser tan antiguas en la historia del desarrollo de la vida, como el mismo centro cuya forma han modelado en la lenta labor de adaptación del individuo al medio.
El lenguaje ordinario de que se ha servido la Geometría pura en la exposición de sus proposiciones, no le permite definir categóricamente los lugares geométricos, como podía hacerlo el simbolismo cuantitativo del análisis; sin embargo, la imaginación al reproducir de manera perfecta los lugares geométricos se halla en capacidad de reconocerles algunas propiedades simples, de las cuales se sirve la Geometría pina para designar las figuras, (ralando de suplir por ese medio la deficiencia anotada. ¿Pero cuántas de aquellas propiedades bastan para caracterizar los diversos lugares?
Al representar en nuestra imaginación la línea recta, por ejemplo, notamos que es la más corta entre dos cualesquiera de sus puntos, pues nos recuerda la forma del hilo en tensión; igualmente reconocemos como consecuencia de aquélla que dos rectas no pueden tener sino un solo minio común, a menos de confundirse en toda su ilimitada extensión, etc., etc.
Así fue como Euclides designó la línea recta por medio de las dos propiedades indicadas; pero bien pronto necesitó de una nueva propiedad para terminar su Geometría; esta nueva propiedad recibió el nombre de Postulado de Euclides.
Como el geómetra griego no necesitó mayor número de propiedades de la línea recta, se puede concluir (¡ue los axiomas de nuclides son necesarios y suficientes para definir cualitativamente la recta. Estos axiomas o postulados son:
1o Entre dos puntos de un plano hay una línea que es la más corta, y es la recta. Consecuencia directa de esta propiedad es la de que dos rectas no pueden tener sino un solo punto común a menos de confundirse; y
2 o En un plano, por un punto fuéra de una recta no puede trazarse sino una sola paralela.
Al decir que las dos propiedades indicadas son a la vez necesarias y suficientes, se quiere significar: a) que sólo la línea recta cumple a la vez las dos condiciones, y b) que, por ejemplo, la primera propiedad no es suficiente para definir cualitativamente la recta por existir otros lugares geométricos que la verifican. Bien entendido que se trata de la manera como se razona en la Geometría pura.
Trazar sobre una faja de papel una raya y llamarla recta con la sola condición de que cumpla la primera propiedad, y considerar al papel como un plano por la condición de que la línea pueda desalojarse sobre él sin cambiar de forma, no son datos suficientes pura que se pueda edificar la Geometría del plano. En efecto, ¿se puede estar seguro de antemano de que no habrá líneas que sin ser rectas cumplan sobre ciertas superficies que no son planas, las propiedades conferidas a las rayas y al papel? Es claro que no. Se podría elaborar la Geometría de ciertas superficies de curvatura constante en la creencia de haber hecho una Geometría plana. Tal es lo acontecido con la Geometría llamada hiperbólica, la cual estudia las propiedades de las figuras formadas por círculos máximos de una esfera imaginaria sobre la cual se mueven dichas figuras. El razonamiento geométrico puro puede, pues, conducir a equivocaciones aun no sospechadas antes de Lobattcheffsky.
Se llama geodésica la línea más corta que une dos puntos de una superficie. Ahora bien: en las superficies de curvatura constante, las geodésicas son las secciones normales. Si, pues, se hace caso omiso del postulado, el raciocinio geométrico no podría conducir sino a propiedades comunes a todas las superficies de curvatura constante, positiva, nula o negativa. Pero si en vez de suprimir el Postulado de Euclides se le sustituye por el de Lobattchefsky, se hallan entonces las propiedades de las figuras de curvatura negativa, etc.
Algunos, sea por haberse dado cuenta de que el Postulado de Euclides no venía a ser sino una condición de incompatibilidad de ecuaciones de primer grado, como lo veremos después, sea por intuición directa, creyeron posible deducir el citado principio como consecuencia de que dos rectas no pueden tener sino un sólo punto común sin confundirse en toda su extensión. Sus tentativas no podían tener éxito, pues emplearon el método usual de la Geometría pura, en el cual no es posible distinguir cuándo las rayas y el papel representan rectas en un plano y cuándo son circunferencias de círculos máximos sobre la esfera real o imaginaria, y el postulado siendo como es propiedad exclusiva de la recta, no podía deducirse como consecuencia lógica de raciocinios aplicables a especies distintas de líneas y de superficies.
Los geómetras, no habiéndose dado cuenta en un principio de la circunstancia que hemos anotado, e insistiendo en la demostración de la citada propiedad euclídea, intentaron llegar a ella por el método del absurdo. Lobattcheffsky sustituyó al Postulado de Euclides el de que por un punto fuéra de una recta y en el plano del punto y de la recta se pueden trazar infinidad de rectas no secantes contenidas dentro de un ángulo desconocido. Pero en lugar de llegar a contradicción vio que una nueva Geometría (la de las superficies de curvatura negativa constante) tan lógica como la del plano deducida por Euclides, se desarrollaba ante la fuerza de sus razonamientos. El geómetra ruso estudió las propiedades de tales figuras en la errónea creencia de que descubría una nueva Geometría plana no euclídea.
La línea recta, siendo una línea de curvatura nula podrá considerarse como el límite de una circunferencia de círculo máximo de esfera real o imaginaria, cuando el módulo del radio de la esfera crece más y más. En realidad las fórmulas de la Trigonometría esférica real y de la Trigonometría esférica imaginaria o hiperbólica, se reducen para mod. R = ∞ a las de la Trigonometría rectilínea.
En la deducción de la Geometría plana hiperbólica, las circunferencias de los círculos máximos de esfera imaginaria se consideraron como líneas rectas sin que nada hiciese recelar de su verdadera forma. Se podría creer que el mismo éxito se hallaría al tratar de establecer la Trigonometría esférica imaginaria como si fuese Trigonometría plana no euclídea; pero tal cosa no es posible, lo cual proviene de que si bien es cierto que la recta puede considerarse como el límite de la circunferencia de un círculo de curvatura positiva o negativa, tal límite no es alcanzado, pues hay una diferencia sustancial entre la recta y las líneas de curvatura constante positiva o negativa, como que la recta no cierra mientras las otras son curvas cerradas. Tal diferencia es de capital importancia desde el punto de vista del análisis, pues el espacio descrito por un punto móvil que se desaloja en determinado sentido no puede servir de variable sino a funciones uniformes de la posición ocupada por aquel punto; mientras que el espacio descrito por un punto que recorre una curva cerrada en determinado sentido puedo servir de variable para expresar funciones periódicas de aquel espacio, las cuales no tienen sino un solo valor para cada posición del punto sobre la curva. Tales funciones serán de período real o imaginario según que la circunferencia sea de radio real o de radio imaginario.
Lobattcheffsky no salió de su error sino cuando se propuso crear la Trigonometría correspondiente a su nueva Geometría.
La teoría de las variables complejas debida a Cauchy permite estudiar las funciones circulares y las hiperbólicas independientemente de toda consideración geométrica, como simples series de potencias enteras y positivas convergentes para todos los valores de las variables. Las funciones circulares senx y cosx siendo funciones periódicas de w cuyo período real es designado por 2 ϖ, pueden determinarse independientemente de toda consideración geométrica por medio de los lazos de Prouet. Las funciones hiperbólicas S (x) y C (x) son también periódicas, pero su período
 o 2ϖi es imaginario1.
o 2ϖi es imaginario1.
Las funciones sen x y cos x son holomorfas y toman valores iguales pero signos contrarios cuando x crece en un múltiple impar de semiperíodos ϖ ; en consecuencia la función tang x que es el cociente del senx por cos x será meromorfa cuyos polos son los ceros de cos x y admitirá por período al semiperíodo ϖ. Igualmente T(x) cociente de S(x) por C(x) admite por período a
Sea (Fig. 1) L'L una recta indefinida, P un punto situado fuéra de ella, PO la perpendicular bajada de P sobre LL’ y O el pie de esa perpendicular. Tomando a O como origen de las distancias contadas sobre la recta L'L y considerando las magnitudes situadas a la derecha de O tales como Om como positivas y las Om' como negativas, un punto móvil que recorra a L'L de izquierda a derecha tendrá a cada instante una distancia z a O la cual variará de una manera continua desde - ∞ hasta + ∞. El punto móvil no pasará sino una sola vez por cada punto m de la recta y no podrá ir de m' a m sino pasando por O, a menos de salirse de la recta.
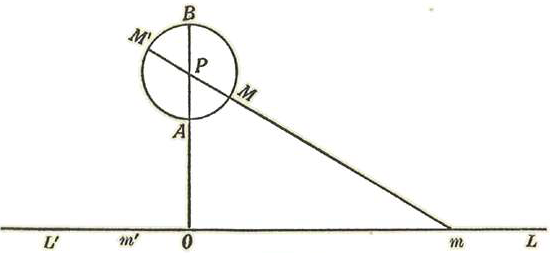
Nota,-Obsérvese la posición relativa de las letras que designan los puntos de esta figura con la de los mismos puntos de la figura segunda (página 570) situados sobre la esfera, pues se ha conservado, de propósito, idéntica su designación.
Figura 1a
Si se une m al punto P se tendrá una nueva recta única, pues por dos puntos no se puede hacer pasar sino una sola recta. Si por P se traza una recta cualquiera en el plano, ésta no podrá cortar a L o L’ en más de un punto y sólo a una distancia real Om = z, la cual podrá hacerse infinita.
Haciendo centro en P y con un radio cualquiera tracemos el círculo À MBM'A el cual quedará cortado en dos partes iguales por la recta MP que formará un diámetro, pues pasa por el centro P.
Las propiedades de rectas y círculos de que acabamos de servirnos son independientes del Postulado de Euclides y no nos detendremos, pues, a demostrarlas, lo cual sería muy sencillo. Tendremos:
arc.MBM' = arc.M'AM = media circunferencia = 1 / 2 C
llamando C la circunferencia entera.
Imaginemos un punto móvil que partiendo de A en el sentido AMBM' recorra la circunferencia. Dicho punto pasará y repasará sucesivamente por los puntos M y M' a. cada nueva vuelta. Los espacios recorridos por el móvil cada vez que pasa por M estarán dados por la fórmula AM + n.C en donde n representa el número de vueltas dadas. Los espacios recorridos por el mismo móvil cada vez que pasa por M’ serán AM + (n + 1 / 2 ) C.
Tomemos por unidad para medir arcos contados sobre la circunferencia AMBM'A un arco tal que la circunferencia entera valga 2ϖ y por tanto ϖ la semicircunferencia. Llamando β0, la medida, en esa unidad, del arco AM, las dos series de arcos que terminan en M y M’ y que determinan una recta única M'PMm serán designadas por los valores siguientes:
(A) En M......β = cc + 2nϖ En M'......β’ = β0 + (2n + 1)ϖ.
Ahora bien: a cada valor real y finito de z corresponde un punto m de la recta, el cual unido al punto P por medio de la recta Pm cortará a la circunferencia en dos puntos opuestos M y M' a los cuales corresponden, respectivamente, las dos series de arcos (A), las cuales dan para la función tang (β) un solo valor, a saber:
tang (β) - tang (β0 + 2nϖ) = tang(β0 + (2n + 1)ϖ) = tangβ'
Sabemos, además, que tanto z como tang β pueden variar desde - ∞ hasta + ∞.
Recíprocamente, dado un valor de tang β, se hallarán dos series (A) de arcos, los cuales determinan una recta única Pm, la cual cortará a L'OL en un punto único m a distancia z = Om. La uniformidad recíproca de las variables z y tang(β) está, pues, rigurosamente establecida, pues ambas cantidades son reales, varían de - ∞ a + ∞ y ambas son funciones periódicas del mismo período de una tercera variable cíclica β; de manera que a cada valor particular de z no corresponde sino un valor particular de tang(β) y recíprocamente.
Podemos, pues, concluir que z y tang(β) están ligadas por una ecuación de la forma
A z. tang (β) + B z + C tang (β) + D = o. (1)
La determinación de los coeficientes es fácil. Para z = o se halla β0 = o y por tanto tang (β) = o. Se tendrá, pues, D = o. Así, la ecuación puede reducirse a
A z. tang (β) + Bz + C tang (β) = o. (1)'
Habiendo tomado las magnitudes Om hacia la derecha como valores positivos para z y los arcos siendo medidos en el sentido atrás indicado, resultará que z y tang(β) tendrán siempre el mismo signo. Por tanto, haciendo z negativa, tendremos también que hacer negativa a tang(β), lo que da:
A z. tang (β) - Bz - C tang (β) = o. (1)"
Sumando (1)' y (1)" se hallará: 2 A z. tang (β) - o De donde resulta que A = o y por tanto, la relación se reduce a: Bz + C tang (β) = o O bien a z = g tang (β) (I)
pues
 deberá ser una magnitud positiva para que z y tang(β) tengan el mismo signo.
deberá ser una magnitud positiva para que z y tang(β) tengan el mismo signo.
Si damos a β cualquiera de las dos series de valores
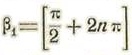 o
o
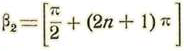 se tendrá : tang β1, = tang β2 = tang ϖ/2 = ∞
se tendrá : tang β1, = tang β2 = tang ϖ/2 = ∞
Y por tanto (I) dará: z = ∞.
Las dos series de arcos no definen sino un mismo diámetro del círculo AMBM'A el cual es perpendicular a PO. En consecuencia no habrá sino una sola recta trazada por P que no corta a L'OL. Esta recta es la perpendicular a PO. Cualquiera otro valor de β dará valor finito para tang β y por tanto, para z. (Postulado de Euclides).
Grande ha debido ser la sorpresa de Lobattcheffsky al hallarse, cuando menos lo esperaba, frente a frente con el postulado de Euclides. ¿Por qué motivo no había hallado antes contradicción alguna en sus raciocinios impecables al suponer falsa la propiedad euclídea de las rectas? La respuesta era clara: no había razonado con rectas situadas en un plano, sino sobre otra clase de líneas y superficies.
¿Cuáles eran esas superficies y esas líneas? En sus raciocinios, Lobattcheffsky había encontrado que la suma de los tres ángulos de un triángulo era menor que dos rectos; precisamente lo contrario de lo que acontece con los triángulos esféricos en donde el exceso esférico es la relación del área del triángulo al cuadrado del radio de la esfera. Si, pues, el radio de la esfera se hiciese imaginario, su cuadrado se haría negativo y el exceso esférico se convertiría en defecto, tal y conforme corresponde al caso estudiado. Lobattcheffsky había, pues, razonado sobre una esfera imaginaria considerada como plano y con círculos máximos de tal esfera considerados como rectas.
Los razonamientos de la Geometría pura son más delicados de lo que se pudiera creer debido al empleo exclusivo del lenguaje ordinario.
Las fórmulas de la Trigonometría correspondiente a la Geometría de Lobattcheffsky son, pues, las de la Trigonometría esférica imaginaria, como vamos a demostrarlo.
Las fórmulas fundamentales de la Trigonometría esférica real son:
Llamemos α β y γ los lados del triángulo esférico referidos a una unidad definida distinta del radio de la esfera y R el radio de ésta en la misma unidad. Las fórmulas se harán
Si en estas fórmulas hacemos
 tendremos:
tendremos:
Sustituyendo estos valores en las formulas anteriores obtendremos las formulas fundamentales de la trigonometría esférica imaginaria, así:
Hagamos
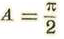 y tendremos, en ese caso particular:
y tendremos, en ese caso particular:
De las últimas dos se deduce:
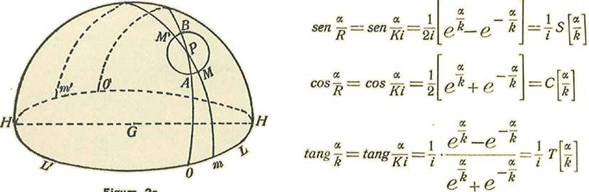
Volviendo sobre la figura 2ª supondremos que las líneas que habíamos considerado como restas sean sino círculos máximos de la esfera imaginaria cuyo radio R tuviese por modulo K.
Hagamos γ=z β=PO y C=θ Tendremos

Como el punto P lo superponemos fijo respecto de L’L se tendrá que β y por tanto
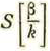 será contante; y llamando A esta constante, se tendrá la formula
será contante; y llamando A esta constante, se tendrá la formula
 (γ)
(γ)
De formula (γ) pueden deducirse las tres fórmulas fundamentales de la trigonometría imaginaria, como lo ha hecho Lobattcheffsky.
La fórmula (γ) puede, por otra parte, establecerse directamente aplicando la fórmula de la relación de dos funciones recíprocamente uniformes cuando se cambia el plano por una esfera imaginaria y las rectas por círculos máximos de tal esfera.
Sea (Fig. 2) la representación simbólica de tal esfera; H'L'OmLHm' un círculo máximo, y k el módulo de la unidad de longitud, de manera que la circunferencia valga 2ϖki; P un punto cualquiera de la superficie, OPO' un círculo máximo perpendicular al anterior.
Sea m un punto de la primera circunferencia, y pongamos mO = z.
Sea m’ el punto diametralmente opuesto; se tendrá:
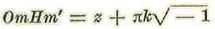 o representando a
o representando a
 por i OmHm' = z + ϖki.
por i OmHm' = z + ϖki.
Supongamos un punto ficticio que describe la circunferencia OmHBO'm'H ; cada vez que pasa por m y por m' el arco descrito tendrá por valor:
En m .... z + 2 ϖnki En m'.... z + (2n + 1) ϖki
Tomando por variable cíclica la relación del arco descrito al módulo k de la unidad elegida, los valores de tal variable φ serán:
Como la tangente hiperbólica admite por período ϖi resultará que
Tracemos la circunferencia AMBM' con polo en P y consideremos un punto móvil que la recorra. Tomemos una variable cíclica representada por la relación del arco descrito por el punto a una unidad tal que la circunferencia valga 2ϖ. El círculo máximo mPm' cortará la circunferencia en cuestión en dos puntos opuestos M y M' los cuales corresponden a los valores de la variable cíclica θ, así:
En M .... 0 = AM + 2ϖn En M' .... θ' = AM + (2ϖ + 1)n.
Como la tangente circular admite por período a resultará que
tang θ = tang (AM + 2 ϖn) = tang (AM + (2 ϖ + 1) n) = tang θ
Cuando el móvil que recorre la circunferencia H'L'OmLH, cada vez que pasa por m si se traza la circunferencia máxima mMPM'm' se tendrá un valor para la tangente hiperbólica de la variable f y también un valor para la tangente circular de la variable θ . Si se da el valor de T(φ) se tendrán dos puntos m y m' correspondientes a una sola circunferencia máxima, la cual corta en dos puntos M y M' a la circunferencia de polo P y por tanto, un solo valor de tang θ. Recíprocamente a un valor de tang θ corresponden dos puntos M y M' opuestos, por los cuales no pasa sino una sola circunferencia máxima mPm'. A los puntos m y m' corresponden dos series de valores de la variable cíclica φ y φ’ los cuales dan un valor único para la tangente hiperbólica T(φ).
Las funciones T(φ) Y tangθ son recíprocamente uniformes, de lo cual se deduce fácilmente la formula (β):
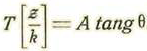
Considerando, pues, las líneas como circunferencias de círculos máximos de esfera imaginaria, se puede establecer la fórmula (β) y por tanto, las fórmulas de la Trigonometría esférica imaginaria.
Cuando se consideran rectas las líneas L'L no es posible establecer con rigor la fórmula (β) sino haciendo caso omiso de los valores imaginarios de la variable, a saber:
Además, ¿cómo se podría justificar la introducción de la constante k ? ¿Qué significaría esa, entonces, misteriosa constante?2.
Si en lugar de considerar imaginario el radio de la esfera lo hubiésemos considerado real, los arcos terminados en m y m' serían:
Como la tangente circular admite por período ϖ resulta que tang φ = tang φ’ y habría perfecta uniformidad recíproca entre ésta y tang θ, de donde se deducirla que
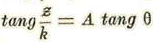 de la cual se deducirían, a su vez, las fórmulas de la Trigonometría esférica real.
de la cual se deducirían, a su vez, las fórmulas de la Trigonometría esférica real.
En resumen: La Geometría cíe Lobattcheffsky es verdadera, sin que por ello dejen de serlo las de Euclides y Riemann; pero mientras la primera se refiere al estudio de las propiedades de las figuras situadas sobre superficies de curvatura negativa y la última al estudio de las figuras situadas sobre esferas reales, la de Euclides se refiere a las figuras planas. No hay, en el fondo, contradicción entre el postulado de Euclides y los de Lobattcheffsky y Riemann. La suma de los ángulos de un triángulo esférico es mayor que dos rectos, sin que dejen de valer dos rectos la suma de los ángulos de un triángulo rectilíneo.
El error consiste en designar con los nombres de Geometrías planas no euclídeas a las Geometrías esféricas y en poner en duda el postulado de Euclides.
***
Llamemos espacio a un continuo ilimitado de tres variables independientes; punto, al conjunto de valores particulares de cada una de las variables (un valor para cada variable); superficie, al conjunto de los puntos cuyas características numéricas satisfacen a una ecuación entre las tres variables; línea, al conjunto de puntos cuyas características numéricas satisfacen a dos ecuaciones entre las tres variables.
Las superficies más sencillas serán las representadas por las ecuaciones más sencillas, esto es, por ecuaciones de primer grado entre las tres variables. Llamemos planos a estas superficies.
Las líneas más sencillas serán las designadas por parejas de las ecuaciones de primer grado entre las tres variables. Llamemos rectas a estas líneas.
Las propiedades de las ecuaciones de primer grado con dos o con tres variables, traducidas al lenguaje convencional que hemos adoptado, nos permiten enunciarlas en la forma siguiente:
Dos rectas que tengan dos puntos comunes se confunden en toda su ilimitada extensión.
Dos planos que tengan tres puntos comunes no situados en linea recta, se confunden en uno solo.
Si por dos puntos de un plano se hace pasar una recta, ésta estará íntegramente situada en el plano.
Una recta y «» punto situado fuera de ella determinan un plano.
Por un punto situado fuéra de un plano no se puede trazar sino un solo plano que sea incompatible (paralelo) al primero. (Postulado referente a los planos).
Por un punto situado fuéra de una recta y en el plano determinado por el sistema de la recta y del punto, no se puede hacer pasar sino una sola recta que sea incompatible (paralela) a la primera. (Postulado de Euclides).
En todo lo que acabamos de decir nos hemos referido al Algebra pura: las variables no son coordenadas, sino simples cantidades numéricas, y, por tanto, no es el caso de señalar petición de principio ni círculo vicioso.
Basto un poco de reflexión para comprender que el postulado de Euclides no es una propiedad geométrica fortuita, sino un caso particular de una propiedad analítica aplicable a la cantidad en general.
En nada se alterarían las consecuencias al considerar un continuo de n variables en lugar de tres, siempre que se llame recta a un sistema de n - 1 ecuaciones de primer grado entre las n variables, y plano a un sistema de n - 2 ecuaciones entre las mismas n variables independientes.
NOTA SOBRE BALISTICA EXTERIOR
ADVERTENCIA DE LA DIRECCION.-Aunque el estudio a continuación no tiene relación alguna con el tema que constituye el fundamento de los apuntes míticos de Garavito, lo insertamos aquí para dar un poco de variedad a la Revista, evitando la pesadez que podría resultar para los lectores de ella, de la insistencia sobre estos tópicos. Así continuaremos en el número próximo con el estudio de Garavito sobre las funciones hiperbólicas, que comprende la nota anterior referente a las Geometrías planas no euclídeas.
I-Presión de los gases.
Sea n el número de moléculas del gas que chocan contra la unidad de superficie, esto es, que atraviesan la unidad de superficie en un solo sentido. Nada nos impide reducir toda la superficie a un punto situado sobre su plano, puesto que todos los puntos de ésta están en condiciones semejantes respecto de las moléculas del gas. Esto supuesto, sobre el punto que representa todos los de una unidad de superficie, vienen a chocar n moléculas del gas en todos los sentidos contenibles en el hemisferio externo del plano.
Sobre una superficie esférica cuyo centro sea el punto 0 pasarán, de afuera para adentro y normalmente a la esfera, n moléculas. Por unidad de superficie, en la unidad de tiempo, el número de moléculas será:

Sobre la zona SS = rdθ de área
du
= 2 ϖr
rd
θ
sen
θ será
η
du= n senθ las cuales, como van a chocar en el centro, tendrán una inclinación θ con la normal
Oz
a la superficie y la componente normal de la velocidad
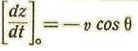 antes del choque.
antes del choque.
Sea Z la resistencia que la superficie opone a la molécula durante el choque; se tendrá:
Después del choque, se tendrá: 2mv cosθ=Z T
La impulsión que las moléculas reciben de parte de la superficie es igual a la acción que estas ejercen sobre aquella, de manera que la impulsión que recibe la superficie de parte de las moléculas contenidas en la zona SS será:
Σ Z T = 2 m v cosθ X η d n = 2 m n v senθ cosθ dθ y de parte de todo el hemisferio
Pero la suma de las impulsiones en la unidad de tiempo es la presión recibida en 0. Esto es en la unidad de superficie. Por tanto
P=m n v (1)
Sea N el número de moléculas contenidas en la unidad de volumen. Nada nos impide llevarlas todas a un punto geométrico y trazar alrededor de este una superficie capaz de encerrar la unidad de volumen. Así, el radio de esa esfera ficticia será tal que verifica la relación

Esto supuesto, el espacio recorrido por las N moléculas, dotadas todas de la velocidad v será la suma de los espacios v (en la unidad de tiempo), esto es Nv. El número de encuentros con la superficie esférica que rodea al punto, será el cociente, por el radio de esta esfera, del espacio total Nv (encuentros todos en un solo sentido de adentro para afuera). Así, como sobre la unidad de superficie es n sobre 4ϖr2 será:
Sustituyendo este valor en (1), se halla
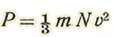
Pero m N es la masa de las moléculas contenidas en la unidad de volumen. Si llamamos w el peso del gas en la unidad de volumen, tendremos
II- Presión de un gas sobre una superficie en movimiento
Buscaremos la velocidad media molecular del gas, relativa de la superficie.
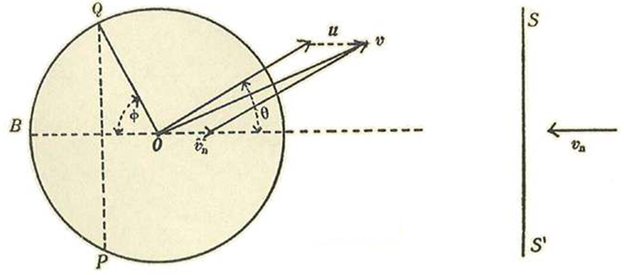
Sean u=velocidad molecular del aire con relación a la tierra, y v cos α = componente de la velocidad normalmente a la superficie = vn.
Sea N el número de moléculas contenidas en la unidad de volumen. Las reduciremos todas a un punto, centro de una esfera de radio r.
Pongamos vn=u cos Φ siendo Φ el ángulo BOQ. Es evidente que las moléculas contenidas o que divergen de centro O al casquete PAQ chocan contra la superficie SS’ mientras que las que divergen dentro del casquete QBP no chocan.
Pongamos
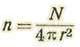 y notando que la velocidad relativa de una molecula, estimada normalmente a la superficie, es V cosw = Vn + u cosθ tendremos, llamando U la velocidad media normal:
y notando que la velocidad relativa de una molecula, estimada normalmente a la superficie, es V cosw = Vn + u cosθ tendremos, llamando U la velocidad media normal:
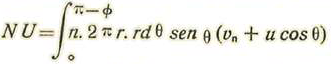 o bien, notando que n 4 ϖ r2 = N
o bien, notando que n 4 ϖ r2 = N
Ahora bien, cuando Vn = 0 se tiene
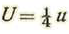
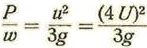
Tendremos pues, para la presión sobre la cara anterior de la superficie:

En la faz posterior las moléculas que chocan contra la superficie son las que divergen según el casquete QBP. Por tanto
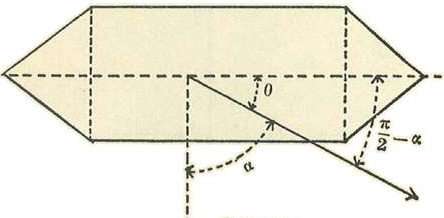
III - Resistencia que experimenta un proyectil cilíndrico-cónico.
Supongamos un proyectil de forma cilíndrica terminada por conos.
A cada elemento ds de la superficie delantera corresponde otro igual cuya normal interna forma con la dirección del movimiento el mismo ángulo que la normal externa del primero.
Las presiones sobre dichos elementos proyectados según la dirección normal al movimiento, se componen en un esfuerzo paralelamente a la dirección del movimiento y sentido opuesto, así:
Intengrando en toda la superficie del proyectil, tendremos la resistencia R1
Llamando α el valor medio de Φ, tendremos:
Llamando A el área opuesta al viento, se tendrá:
Si llamamos s la superficie total del proyectil y A el área de la sección normal a la velocidad, se tendrá evidentemente:
El ángulo
 que hace la longitud del proyectil con la velocidad, es muy pequeño, por tanto
que hace la longitud del proyectil con la velocidad, es muy pequeño, por tanto
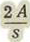 es también muy pequeño, y a mayor razón
es también muy pequeño, y a mayor razón
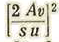 Pues las mayores velocidades de los proyectiles no sobrepasan la velocidad molecular u de las moléculas del aire. Resulta de esto que el paréntesis apenas excede de 1, y los mas grandes cambios en la velocidad
v
del proyectil en su movimiento, apenas modifican ligeramente el valor de este factor, al cual podremos considerar como prácticamente constante.
Pues las mayores velocidades de los proyectiles no sobrepasan la velocidad molecular u de las moléculas del aire. Resulta de esto que el paréntesis apenas excede de 1, y los mas grandes cambios en la velocidad
v
del proyectil en su movimiento, apenas modifican ligeramente el valor de este factor, al cual podremos considerar como prácticamente constante.
Así, llamando
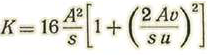 tendremos: R1 = K w u v
tendremos: R1 = K w u v
Llamando B la presión atmosférica, tendremos por la fórmula (4)
siendo θ = 273° +t la temperatura del aire.
Queda, pues, la resistencia que opone el aire a un proyectil en movimiento, expresada en función de la presión barométrica, la temperatura absoluta del aire, la intensidad de la gravedad y la velocidad del proyectil.
Para cada trayectoria g y R pueden considerarse constantes; pero B y θ varían según la estación del año y la altura sobre el mar.
IV-Movimiento del proyectil.
Las ecuaciones de movimiento del proyectil son:
en donde el plano de las xoy es el plano vertical de la trayectoria, el eje ox es horizontal y el oy la vertical hacia arriba.
Las ecuaciones (a) se reducen a la forma lineal siguiente, notando que
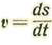
Para fijar las constantes de integración, supondremos que el origen de coordenadas es la boca del arma y que el origen del tiempo es el instante en que el proyectil parte del origen. Llamaremos v 0 la velocidad inicial y B0 el ángulo que hace el eje del arma con el horizonte, esto es, con OX.
Esto supuesto, la integración no presenta ninguna dificultad.
Poniendo X = Aeat+C .'. A + C=O se
 v0 cosθ0= Aa
=
v0 cosθ0= Aa
=
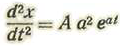 a = -HB de donde
a = -HB de donde
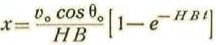
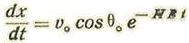
La ecuación en y contiene término independiente. Pondremos y=y 0 +u haciendo u = c1t + C0
Haremos
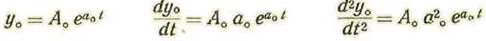 De donde a0= - H B Por tanto
De donde a0= - H B Por tanto
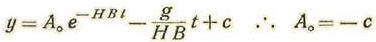 y como
y como

 de donde
de donde
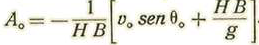 Así
Así
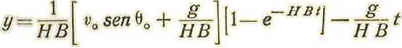
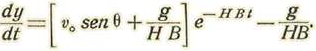
Tendremos, pues
El presente trabajo tiene por objeto hallar la influencia de la presión en el empleo del alza de los cañones, a fin de poder aplicar las tablas de tiro en los países montañosos, como el nuestro en donde la artillería funciona en condiciones muy diferentes de aquellos en los cuales han sido determinadas las constantes de cada cañón.
La resistencia que el aire opone al movimiento de los cuerpos ha sido objeto de gran número de experimentos, pero las fórmulas halladas son todas empíricas, y, por consiguiente, aplicables sólo en las mismas condiciones experimentadas, por lo que no podrían servirnos para el estudio en cuestión. De ahí la necesidad de estudiar el problema partiendo de alguna hipótesis racional.
Elegimos para este efecto aquella sobre la cual se funda la teoría cinética de los gases; pero como dicha hipótesis presume que los moléculas del aire no choquen unas contra otras, o por lo menos que el número de choques sea muy pequeño, lo cual no es probable, por razones que no sería posible expresar aquí, el coeficiente de la resistencia debe ser afectado de un factor desconocido, que la experiencia podría indicar y que lo hemos representado por H. La resistencia presenta un término proporcional a la velocidad y otro al cuadrado de ésta; pero este último, en las condiciones del proyectil, tiene un valor pequeño respecto del primero. Al despreciarlo, la fórmula no quedará evidentemente rigurosa, pero tiene la enorme ventaja de hacer integrables las ecuaciones de movimiento, y, por tanto, de servir, no sólo como una primera aproximación, sobre la cual se pueden fundar experimentos y estudios, sino que la creemos suficiente en la práctica.