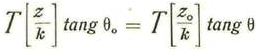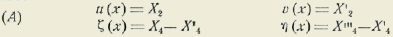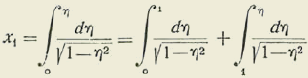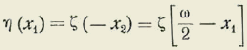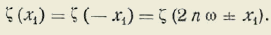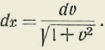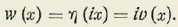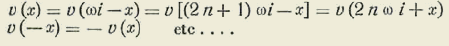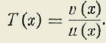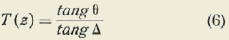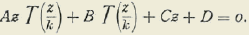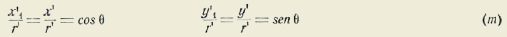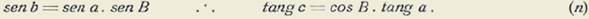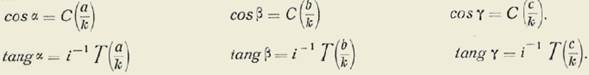Exposición preliminar
Lobattchewsky hacienda caso omiso del postulado de las paralelas, o postulado de Euclides, fundó la trigonometría plana no euclídea sobre la fórmula que dedujo de consideraciones analíticas en las cuales admitió explícitamente los siguientes postulados:
La líneas recta es ilimitada;
No puede ser cortada por otra recta sino a lo más en un punto; y
La forma y dimensiones de las figuras planas son independientes de la posición que ocupan en el plano. Esto último no lo enunció sino lo aplicó en su Geometría en las demostraciones por superposición de figuras.
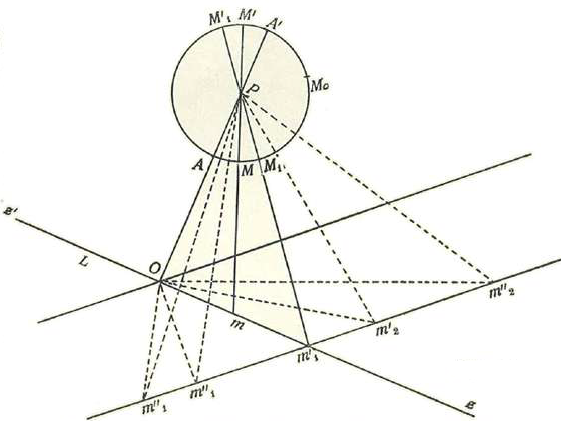
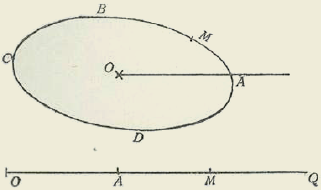
Sea L ua recta indefinida (figura 1a) y P un punto situado fuera de ella (*). Bajemos la perpendicular PO, tracemos la oblicua Pm, llamemos θ el ángulo mP0 entre la perpendicular y la oblicua, y z=m0 al segmento de resta comprendido entre el pie 0 de la perpendicular y el m de la oblicua.
Lobattchewsky llamo k un parámetro constante, pero desconocido. Con estos datos y convenciones estableció la siguiente formula: (1)
 en la cual tang∆ es una constante que tiene por valor
en la cual tang∆ es una constante que tiene por valor
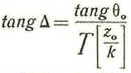 siendo θ0 y z0 dos valores de θ y z correspondientes.
siendo θ0 y z0 dos valores de θ y z correspondientes.
Al ser verdadera la fórmula (I), el ángulo ∆ sería el ángulo máximo que podría hacer la oblicua Pm con la perpendicular, y el ángulo formado por las dos paralelas seria:
ε=ϖ-2∆
El rigor la formula (I) debiera ser considerada como ecuación en k y todo se reduciría a fijar su valor numérico de manera que satisfaga la relación.
Para todos los valores correspondientes de z y θ. Pero no fue este el punto de vista de Lobattchewsky, seguramente por razón de que el parámetro k fue introducido sin previa justificación, y no figura como condición efectiva.
No conocemos el raciocinio original de Lobattchewsky mediante el cual pudo establecer la formula I) pero estamos seguros de que ha debido ser muy hábilmente presentado.
La demostración que se halla publicada en el tomo 2° del “Traité de Geometrie” por Eugène Rouchéet Ch. de Comberousse - 1891 (nota II, pagina 585, 586, 587) debe ser diferente de la original, pues es manifiestamente admisible; lo cual puede explicarse por la brevedad de la exposición. Tal demostración se funda e que las funciones
 y tangθ son respectivamente uniformes, lo cual es falso: puesto que ambas son periódicas, pero sus periodos son distintos, toda vez que la primera admite un periodo imaginario y la segunda periodo real.
y tangθ son respectivamente uniformes, lo cual es falso: puesto que ambas son periódicas, pero sus periodos son distintos, toda vez que la primera admite un periodo imaginario y la segunda periodo real.
Las fórmulas que Lobattchewsky presentó como correspondientes a la Geometría plana no euclídea son las que resultan de la trigonometría esférica cuando se supone imaginario el radio de la esfera. Las funciones trigonométricas de los lados o caras del triedro se vuelven funciones hiperbólicas, pues los arcos se hacen imaginarios. El exceso esférico que es la relación entre el área del triángulo esférico imaginario se hace menor que dos ángulos rectos.
Si se nos admitiese la fórmula evidentemente falsa  (II) en el caso que represente segmentos de la recta L, podríamos concluir, siguiendo paso a paso la exposición de Lobattchewsky, las fórmulas de La Trigonometría esférica como correspondientes a la Trigonometría plana. Ambas fórmulas son igualmente falsas. En lo que respecta a la (II) el error es fácil de ver. A cada valor de tang θ corresponde un valor de
(II) en el caso que represente segmentos de la recta L, podríamos concluir, siguiendo paso a paso la exposición de Lobattchewsky, las fórmulas de La Trigonometría esférica como correspondientes a la Trigonometría plana. Ambas fórmulas son igualmente falsas. En lo que respecta a la (II) el error es fácil de ver. A cada valor de tang θ corresponde un valor de
 Pero a cada valor de
Pero a cada valor de
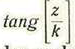 corresponden infinidad de puntos de la recta Oz separados unos de otros por segmentos ϖk a los cuales corresponden otros tantos valores de θ y, por tanto, de tang θ.
corresponden infinidad de puntos de la recta Oz separados unos de otros por segmentos ϖk a los cuales corresponden otros tantos valores de θ y, por tanto, de tang θ.
Este error manifiesto es el mismo que presenta la fórmula (I) de Lobattchewsky, sólo que como los valores de z correspondientes a un valor
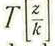 son imaginarios, pasa desapercibido para la mayoría de los lectores poco familiarizados con las fórmulas de la Trigonometría hiperbólica.
son imaginarios, pasa desapercibido para la mayoría de los lectores poco familiarizados con las fórmulas de la Trigonometría hiperbólica.
Después de esta breve exposición nos proponemos demostrar rigurosamente la falsedad de la fórmula (I) que sirve de fundamento a la Trigonometría plana no euclídea.
Es evidente que las fórmulas de las Trigonometrías esféricas, real e imaginaria, se identifican a las de la Trigonometría plana, cuando se hace k = ∞, precisamente, por hacerse planas las dos esferas, puesto que su curvatura se anula. Pero tal cosa no agrega nada a la viabilidad de las fórmulas (I) y (II).
Estudio de las funciones circulares e hiperbólicas independientemente de su interpretación geométrica
1 -Las trascendentes elementales dependen de la exponencial Ҽx En consecuencia sus propiedades son independientes de toda interpretación geométrica.
Los expositores de Análisis acostumbran presentar rápidamente el estudio analítico de las funciones circulares como introducción al de las funciones elípticas con el objeto único de servirse de aquéllas como ejemplo aclaratorio. Las funciones circulares se presuponen conocidas en los estudios anteriores para que haya necesidad de preocuparse especialmente de ellas. De ahí que tales exposiciones no estén exentas de crítica. Se acostumbra representar las variables complejas por medio de funciones circulares de su argumento, y sin cambiar la forma representativa de estas variables se las emplea en el estudio analítico de las funciones circulares, lo cual presenta la apariencia de un círculo vicioso.
La crítica es justa en lo que respecta a la forma expositiva; pero ella no alcanza al fondo de la cuestión, pues la cantidad compleja tiene su manera de ser independientemente del signo, más o menos adecuado, que sirve para simbolizarla. Por ejemplo, las propiedades de los números primos son independientes del sistema de numeración que haya sido adoptado para representarlos.
La Trigonometría plana hiperbólica se funda en la teoría analítica de tales funciones, lo cual fue una luminosa idea de Lobattchewsky.
Creemos útil exponer las propiedades de las funciones circulares independientemente de su interpretación geométrica y de la forma trigonométrica que se suele dar a la variable compleja.
La exposición que hacemos sólo diferirá de la clásica en la notación, pues basta variar ligeramente ésta para que desaparezca toda apariencia de círculo vicioso.
***
2 -En lugar de representar las cantidades imaginarias por el producto del módulo y la exponencial imaginaria, las representaremos por el módulo como valor y el signo, o sea, el sentido. El signo es propiamente el argumento, pero expresado en vueltas completas y fracción de vuelta. El signo vuelve a tomar el mismo significado después de un número completo de vueltas. Conviniendo en representar la vuelta completa por C, por r el módulo, y por θ la desviación respecto del sentido de las cantidades reales, o sea la fracción sobrante de vuelta, se tendrá que las expresiones: r(θ) y r(θ + nC) sirven para representar la misma cantidad imaginaria cuando n representa un número entero.
La unidad real tendrá por representación: 1 (o) O también: 1 (nC).
El producto de dos cantidades complejas r(θ) y r'(θ') será una tercera cantidad R(Φ) que se compone de r(θ) como r'(θ’) se compone de 1(0) según la definición newtoniana de producto. Según esto R será r' veces r (θ). Esto es: rr' (θ) desviada, además, en θ' Y por tanto R (Φ) = rr' (θ +- θ').
Considerémosla raíz cuadrada
 y pongamos: z-a = r(θ + nC).
y pongamos: z-a = r(θ + nC).
Si n es par, se tendrá para valor inicial del radical:

Si
n
es impar, su valor inicial será:

pues la media vuelta
 hace cambiar de sentido a la cantidad. Así, pues, cuando la variable Z da una vuelta alrededor del cero a del radical, su signo cambia de + á -, o también de - á +.
hace cambiar de sentido a la cantidad. Así, pues, cuando la variable Z da una vuelta alrededor del cero a del radical, su signo cambia de + á -, o también de - á +.
3 -Otro punto por considerar se refiere a la integral

alrededor de jos puntos críticos +1 y -1 sobre un círculo infinitesimal de radio e y de centro en el punto crítico respectivo.
Se tiene, integrando en una vuelta alrededor de

Y haciendo Z = 1- ε (θ) se tendrá:

Pues ε=0
Estas consideraciones bastau para poder hacer el estudio analítico de las funciones circulares e hiperbólicas independientemente de toda consideración referente a la Geometría euclideana.
***
4 -Designemos por
X
1
la serie de potencias siguiente:

Tendremos evidentemente:
 en donde los acentos o tildes representan los órdenes de las derivaciones.
en donde los acentos o tildes representan los órdenes de las derivaciones.
Tendremos evidentemente:
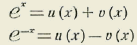 De donde
De donde

Llamando l, i
1
i
2
i
3
las cuatro raíces cuartas de la unidad tendremos:
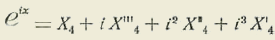 O Bien
O Bien

De estas fórmulas se deduce el valor de x tomando sucesivamente como variables las cantidades u, v, ζ y η
Para efectuar el estudio nos basta considerar la integral

Los puntos de ramificación son + 1 y - 1 y los lazos de Prouct se reducen a:
El otro lazo es
 Al punto
z
corresponden, pues, dos series de valores para x a saber 1a serie x1 + 2nω 2.a serie (2n + 1) - ω- x1
Al punto
z
corresponden, pues, dos series de valores para x a saber 1a serie x1 + 2nω 2.a serie (2n + 1) - ω- x1
***
Valores de x para un valor de ζ
La función ζ es par, y, por tanto, ζ (x 2 ) = ζ (- x 2 ) Por otra parte para x=0 se tiene ζ (0) = 1.
Hagamos ζ
(x
2
) =
η
(-
x
1
) Tendremos:

Por tanto d (x 1 +x 2 )= 0 O bien: x 1 +x 2 constante.
Los ceros de η son x= nω. Los ceros de ζ son

Valores de x para un valor de u.
Se tiene:
 O bien
O bien
 Se tendrá, pues: (x) = ζ (ix) Por tanto: u(o) = ( nωi)=1 ∴
Se tendrá, pues: (x) = ζ (ix) Por tanto: u(o) = ( nωi)=1 ∴
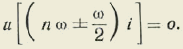
Valores de x para un valor de v
***
6-Definición de t(x) y T(x).
Pongamos:
 Los ceros de x = 0 + nω de η serán t(x) y los ceros de ζ (x) a saber:
Los ceros de x = 0 + nω de η serán t(x) y los ceros de ζ (x) a saber:
 serán polos de t
(x).
Por tanto, cuando x: varía de
serán polos de t
(x).
Por tanto, cuando x: varía de
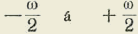 t(x) varía de una manera continua de -∞ Además,
t(x)
tendrá por período ω.
t(x) varía de una manera continua de -∞ Además,
t(x)
tendrá por período ω.
Los ceros de x- O + n ω i de v (x) serán ceros de T (x) Los ceros de u(x) a saber:
 son los polos de T (x). Por tanto T (x) no tiene polos reales sino imaginarios.
son los polos de T (x). Por tanto T (x) no tiene polos reales sino imaginarios.
Además T (x) tendrá por período ωi. En efecto:

Para x= ± ∞ T (± ∞) = ±1
***
7 - Fórmulas fundamentales de las Trigonometrías planas, euclídea y lobattchewskyana ( *).
Sean (véase la figura 1.*) z'Oz una recta L ¡limitada, y un punto P situado fuéra de la recta.
Sean PO y Pm una perpendicular y una oblicua a L.
Haciendo centro en P y con un radio cualquiera PA describamos una circunferencia. Todo diámetro divide la circunferencia en dos partes iguales o semicircunferencias, lo cual se demuestra sin el auxilio del postulado de Euclides, como lo reconoce Lobattchewsky, en lo cual tiene razón. Tomemos un arco AM o por unidad de arco y escogido de manera tal que la circunferencia valga 2 ω siendo ω el valor que hemos hallado atrás. La semicircunferencia valdrá pues ω .
Consideremos un punto móvil que parte de A y describe la circunferencia en el sentido AMM 1 M 0 A'M'M' 1 A. Representemos por θ el arco descrito por el móvil. Cada vez que A vuelve al mismo punto M el arco θ habrá crecido en 2ω. Llamando especialmente θ el menor arco AM se tendrá que siempre que el móvil girando sobre la circunferencia en el sentido positivo o en el negativo, pase por M, el arco descrito tendrá por valor θ + 2ωn siendo n el número de vueltas dadas, esto es, siendo n un número entero positivo o negativo.
Por el punto M y por el punto P tracemos una recta indefinida. Esta recta corta a la circunferencia en dos puntos opuestos y a la recta z'Oz a lo más en un solo punto m. Tomando una unidad cualquiera, pero finita, podremos definir numéricamente el segmento Om por su valor Z, el cual sería positivo a la derecha y negativo a la izquierda.
La variable z es una función de θ susceptible de tomar todos los valores reales desde -∞ hasta + ∞. Es función periódica de θ pues cuando el punto M pasa por M 1 ó M’ 1 la recta MP corta a la recta L en el mismo punto m. Luego a un solo valor de z corresponde infinidad de valores del arco expresados por θ + ω n. Además, para θ = 0 ó θ = ω n, se tiene z = 0.
Consideremos la función analítica
t(x)
reemplazando en ella la variable
x
por el arco θ que describe el punto
M.
Se ve claramente que para
θ = o
ó θ = n ω se tendrá t(θ) = o. Es decir que
z y t(θ) tienen los mismos ceros. Igualmente se ve que ambas cantidades tienen el mismo período y el mismo signo. A cada valor de z, desde -- ∞ hasta + ∞, corresponde una infinidad de valores de θ de la forma θ0+
n
ω; pero a esa infinidad de valores de θ no corresponde sino un valor único de t(θ). Se ve, pues, que t es una función uniforme de
Z
para todos los valores desde -∞ hasta + ∞, sin punto crítico a distancia finita. Se tiene, pues, que
t
es desarrollable en serie en función de Z, por la serie de Maclaurin. Así:
 Serie que será convergente y equivalente para todos los valores de z.
Serie que será convergente y equivalente para todos los valores de z.
Ahora bien, como a cada valor de t corresponden infinidad de valores de θ, a saber: θ = θ1 ± ωn, para n = 1, 2, 3... ., y para todos estos valores no corresponde sino un valor único de z, resulta que para un valor de t no puede corresponder, a lo más, sino un valor único de Z. La serie no podrá contener sino la primera potencia de z, pues, de lo contrario, para cada valor de t corresponderían varios valores de z, lo cual no es posible, pues, una recta que parte de P no puede cortar la 0z en más de un punto. Así, pues, t = f(o) +f’ (o).z. Además, como para z = 0, se tiene θ = nω y t = 0, se deberá tener f(o) = 0. Portanto: t = f’(o). z (1).
La fórmula (1) no lugar a ninguna objeción; es perfectamente correcta y sobre ella se puede establecer la Trigonometría plana y llegar a las mismas fórmulas de la Trigonometría rectilínea euclídea. Volveremos sobre este asunto más adelante.
Fórmula fundamental de la Trigonometría plana no euclídea.
La fórmula en cuestión es, según el Tratado de Geometría, por los señores Rouché y Comberousse (Sexta edición -1891- tomo II, Nota II, página 586), la siguiente:
En la cual se ha puesto:
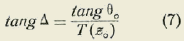 La función designada allí por T(z) no es:
La función designada allí por T(z) no es:
 como debiera ser, sino
como debiera ser, sino
 Y debería haber sido representada por
Y debería haber sido representada por
 y no por T(z). A primera vista se creería que k representa la unidad arbitraria de longitud, la cual debería sor una de las magnitudes constantes de la figura, como por ejemplo PO. Pero no es así: tanto Z como k figuran por sus valores numéricos referidos a una unidad arbitraria. La cantidad k es, pues, una constante especial; pero como la fórmula (6) no resulta de la integración de ninguna ecuación diferencial, dicha constante no es, pues, de integración. Además, siendo lineal la relación que liga a T(z) con tang θ no deberían figurar sino dos constantes, a saber: la constante adicional, que debe ser nula, pues, para θ = 0
z = o y T(z) - 0
, y el coeficiente
y no por T(z). A primera vista se creería que k representa la unidad arbitraria de longitud, la cual debería sor una de las magnitudes constantes de la figura, como por ejemplo PO. Pero no es así: tanto Z como k figuran por sus valores numéricos referidos a una unidad arbitraria. La cantidad k es, pues, una constante especial; pero como la fórmula (6) no resulta de la integración de ninguna ecuación diferencial, dicha constante no es, pues, de integración. Además, siendo lineal la relación que liga a T(z) con tang θ no deberían figurar sino dos constantes, a saber: la constante adicional, que debe ser nula, pues, para θ = 0
z = o y T(z) - 0
, y el coeficiente
 de tangθ
de tangθ
La primera y más grave dificultad con que se tropieza al estudiar la Trigonometría de Lobattchewsky es la justificación del misterioso divisor k. La exposición que se halla en el tratado de Geometría, al cual nos referimos, nada dice a ese respecto. En la citada obra el divisor k aparece como por encantamiento, sin figurar para nada en la demostración; y, sin embargo de esto, se le confiere la más alta importancia, pues su valor es el desideratum de la Geometría euclideana.
Hay aún otra dificultad, la cual consiste en que la magnitud representada por z es real y acíclica y, por tanto, inadecuada para actuar como variable independiente en las funciones hiperbólicas que son funciones periódicas de período imaginario. De esto resulta que no es posible, dado el significado de z, establecer la uniformidad recíproca y perfecta entre tangθ y
 que se requiere para la exactitud de la fórmula (6).
que se requiere para la exactitud de la fórmula (6).
En efecto, a un valor de
 corresponde una infinidad de valores de Z dados por la relación:
corresponde una infinidad de valores de Z dados por la relación:
 O bien z=z1±ϖkni n=1,2,3…
O bien z=z1±ϖkni n=1,2,3…
La infinidad de valores de z resulta necesariamente de que la ecuación en z es de grado infinito. En este caso es necesario considerar a z como variable compleja, y se le podría representar en un plano normal a PO (Véase la figura 1.a), tal como yθz, en donde Oz debería representar el eje de las magnitudes reales, y Oy desviado en un cuarto de vuelta y afectado, por tanto, del signo i, el eje de las magnitudes llamadas imaginarias. Sobre la perpendicular a Oz levantado por el punto m tomaríamos, tanto en el sentido positivo como en el negativo, magnitudes iguales a los múltiplos sucesivos de ϖk; y uniendo estos puntos con P tendríamos infinidad de rectas a las cuales corresponderían otros tantos valores de θ y, por tanto, también para tangθ, pues entre un punto y el siguiente, θ no podría crecer en un semiperíodo ϖ, esto es, en una semivuelta alrededor de P. Se comprende fácilmente que la ecuación (6) no puede corresponder al caso concreto en cuestión, pues la recta Oz tiene significado perfectamente definido como recta real, la que jamás se cierra.
La fórmula (6) requiere para Z el significado de círculo máximo de esfera imaginaria en lo que respecta a los valores imaginarios, de manera que k represente el módulo del radio de dicha esfera. Pero tal interpretación no es posible asignársele a la recta.
En el tratado de Geometría que hemos citado, la fórmula (6) se funda en la uniformidad recíproca entre
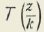 y z y entre z y tangθ. El autor de la demostración conviene en hacer caso omiso de las soluciones imaginarias de z y
y z y entre z y tangθ. El autor de la demostración conviene en hacer caso omiso de las soluciones imaginarias de z y
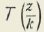 .
.
Dice así tal Tratado: et réciproquement à chaque valear de T(z) repondrá une position unique de m (Om=z), si l'on convient, comme nous l'avons dit, de ne considérer que la valeur principal des logaritmes». (Página 585)
De la uniformidad recíproca entre T (z) y Z y entre Z y tang θ se deduce la misma condición entre T (z) y tangθ.
Para juzgar si los números pueden ser tan complacientes de someterse a lo convenido por el autor de la demostración, se deberán establecer separadamente las dos relaciones, a saber:1.a Entre
 y z y 2.a: entre z y tangθ.
y z y 2.a: entre z y tangθ.
Seguiremos literalmente el fondo de la demostración allí consignada y la aplicaremos sucesivamente a cada una de las dos relaciones indicadas.
Si dos cantidades u y V son recíprocamente uniformes, ellas deben estar ligadas por una relación de la forma: Auv + Bu + Cv + D = 0.
Como para Z = 0,
 se deberá tener D=0. Donde
se deberá tener D=0. Donde
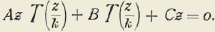
Y como al cambiar el signo de z cambia el de
 se tendrá:
se tendrá:

De donde
 y por tanto, A=0. Finalmente
y por tanto, A=0. Finalmente
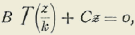 y, en consecuencia
y, en consecuencia
 Haciendo u=tangθ y v=z se hallaría análogamente tang θ=C2z. (β) La eliminación de z conduciría a la fórmula (6); esto es, a:
Haciendo u=tangθ y v=z se hallaría análogamente tang θ=C2z. (β) La eliminación de z conduciría a la fórmula (6); esto es, a:

La relación (β) es correcta; pero el absurdo de la (x) pone de manifiesto la falsedad de la fórmula (6).
La conclusión que se deduce de lo anterior es la de que, aunque el límite de una esfera real o imaginaria es un plano, dicho límite no es alcanzado: esto es, el plano no forma parte del conjunto de esferas reales ni de esferas imaginarias. Más adelante aclararemos esta conclusión.
* * *
8 - Antes de continuar la exposición que nos hemos propuesto hacer, resumiremos los argumentos que han sido presentados en favor de la viabilidad de las Geometrías no euclídeus.
El primero y principal argumento es, indudablemente, el haberse podido crear la Trigonometría plana hiperbólica, de lo cual se deduce la posibilidad de realizar una Geometría analítica no euclídea. A este respecto sabemos ya a qué atenernos.
El segundo argumento consiste en que los geómetras no han podido llegar a contradicción alguna en las deducciones de las Geometrías no euclídeas. Este hecho se comprobó primeramente en el plano; pero se creyó que quizá en el espacio de tres dimensiones se llegaría a tal contradicción. Las investigaciones de Sophus Lie desvanecieron esta esperanza.
He aquí la sustancia de aquellas investigaciones. Supongamos primeramente que se trata solamente de la Geometría de dos dimensiones. Sabemos que una figura plana puede moverse sin cambiar de forma en su plano. Supongamos una figura de n puntos; la posición de todos estos queda definirla por los valores de sus 2n coordenadas referentes a un sistema definido en el plano. La forma y el tamaño requieren solamente 2n-3 ecuaciones entre las 2 n coordenadas. El movimiento de la figura tiene, pues, tres grados de libertad, o, mejor dicho, queda definido por tres parámetros arbitrarios.
Si pasamos al espacio de tres dimensiones, los espacios de dos dimensiones se definen por una ecuación entre las tres coordenadas de los puntos, esto es, por superficies.
Si se investigan las condiciones que deben cumplir tales espacios, o tales superficies, para que una figura compuesta de n puntos, situados inicialmente sobre estos espacios de dos dimensiones, pueda moverse sin cambiar de forma ni de tamaño, se halla que dichas superficies deben ser de curvatura constante, a saber: plano, esfera de radio real y esfera de radio imaginario. Espacios de dos dimensiones que corresponden a las Geometrías euclídea, elíptica e hiperbólica.
Un espacio de tres dimensiones puede considerarse como una superficie representada por una ecuación en un espacio de cuatro dimensiones, o por dos ecuaciones en un espacio de cinco dimensiones, etc.... Si se procede análogamente, para que sea posible la libre movilidad de las figuras de tres dimensiones, se llega a la condición de espacios de curvatura constante y de tres dimensiones. Estos espacios son los correspondientes a los indicados atrás, a saber: espacio parabólico, elíptico o hiperbólico. Tales espacios, con excepción del euclídeo o parabólico, no cumplen la condición indicada sino para una región limitada del espacio entero; esto es, se refieren a la Geometría infinitesimal. Tal cosa no importa: podría suponerse aplicable a todo el espacio. ¿Tendríamos por ello derecho a decir que el espacio real puede ser parabólico, elíptico o hiperbólico? ¿Acaso el espacio real es un sistema de ligamentos como el espacio simbólico que traducen las ecuaciones de condición?
Las investigaciones de Sophus Lie respecto de las Geometrías no euclídeas demuestran ciertamente que tales Geometrías están exentas de contradicción; pero ¿qué se deduce de esto? Veamos un ejemplo: Sea a>b una hipótesis cualquiera; 6<<7 será la consecuencia. Si tomamos ésta como hipótesis, hallamos b<a, y no habría contradicción. ¿Esto demostraría que a es realmente mayor que b? Es claro que no.
De las dos Geometrías planas no euclídeas se deduce que la suma de los ángulos de un triángulo depende del tamaño de aquél; o, en otros términos, que dichas Geometrías no permiten la semejanza de las figuras situadas sobre sus planos. Ahora bien: aunque esta consecuencia está en contradicción con nuestras ideas geométricas sobre el plano euclídeo, no se ha visto por eso contradicción, puesto que se acuerdan muy bien con los postulados de Lobattchewsky o de Riemann, según el caso. En efecto, si el plano no es plano sino tina superficie esférica y la recta no es recta sino un círculo máximo, la suma de los ángulos del triángulo difiere tanto más de dos rectos cuanto mayor es el área del triángulo.
La consecuencia útil que se deduce de los estudios de Sophus Lie es la de que es posible hacer una Geometría esférica de dos dimensiones, tomando por punto de partida el postulado de Riemann; así como también es posible hacer otra Geometría de dos dimensiones fundada sobre el postulado de Lobattchewsky, en donde el plano ha sido sustituido por una esfera imaginaria y la recta por un círculo máximo de tal esfera. En estas geometrías no se ha hecho más que cometer un error de lenguaje, pues se ha llamado recta a una línea que no es recta y plano a una superficie que no es plana. Los nombres, siendo convencionales los raciocinios, quedan correctos y no es posible hallar contradicción.
Pero si los nombres son convenciones del lenguaje, no sucede lo mismo con las ideas. Las figuras geométricas son imágenes impuestas a nuestro entendimiento independientemente de toda definición particular. Las ideas de línea recta, plano, círculo etc., podríamos decir que son innatas al hablar en el lenguaje cartesiano, o atávicas si se admite la psicología positivista; pero do ninguna manera se les puede considerar como convenciones.
Lobattchewsky dio el nombre de recta a un lugar geométrico que debía siempre ser cortado por otra línea de la misma especie en una infinidad de puntos imaginarios separados unos de otros por múltiplos de cierto período; pero que no podían tener sino a lo más un solo punto real de intersección. Ahora bien: tal lugar geométrico no puede ser una recta en el lenguaje propio. ¿Cómo se explicarían las soluciones imaginarias?
Una porción de circunferencia de círculo tiende más y más a la línea recta cuando el radio del círculo crece indefinidamente. Esto se expresa al decir que el arco de círculo tiene por límite la recta; pero se debe también añadir que tal límite no es alcanzado, esto es, que la recta no forma parte del conjunto de círculos por grande que sea el radio de éstos.
9-A fin de evitar toda mala inteligencia hacemos notar, una vez por todas, que no pretendemos demostrar el postulado de Euclides, sino solamente establecer las fórmulas de las Trigonometrías plana y esférica sobre los conceptos usuales de línea recta y de plano.
El postulado de Euclides es una propiedad de las líneas rectas situadas en un plano y para demostrarlo sería necesario poder demostrar lo que es la línea recta y lo que es el plano. Ahora bien, recta y plano son condiciones posibles de la extensión; nociones innatas, o, mejor dicho, de origen hereditario, las que se han formado, perfeccionado y robustecido por la acción de la naturaleza sobre todos los ascendientes, y las que, por tal motivo, no son susceptibles de demostración lógica.
Lo que es posible hacer con el postulado en referencia es presentarlo en forma diferente, o, mejor dicho, hacerlo depender de las nociones de recta y de plano.
Para que se comprenda bien en qué consiste la imposibilidad de demostrar el postulado de Euclides y el papel que han desempeñado a ese respecto las Geometrías no euclídeas, nos serviremos de una comparación.
En la Geometría analítica plana se representan las líneas rectas por ecuaciones de primer grado con dos variables. (Las dos variables siendo las representaciones de las dos dimensiones de este espacio).
No es el caso de discutir aquí la legitimidad de la representación analítica de las rectas, ni de la representación gráfica de las ecuaciones; pero esto no impide el que podamos servirnos, a título de metáfora, de las ideas referentes a las ecuaciones del Algebra para simbolizar las ideas relativas a las líneas en Geometría.
Si convenimos en asimilar las rectas en un plano a las ecuaciones de primer grado con dos variables, las condiciones de incompatibilidad de dos ecuaciones tendrán por traducción, en el lenguaje geométrico, la condición para que dos rectas, situadas en un mismo plano, no tengan punto común.
La condición de incompatibilidad de dos ecuaciones de primer grado con dos variables en Algebra diofantina es la de que la determinante de los coeficientes de las incógnitas sea nula sin que lo sean a la vez las de los numeradores de éstas; y la condición correlativa en Geometría es la del célebre postulado de Euclides.
Ahora bien, si en Algebra suponemos que la condición de incompatibilidad de las dos ecuaciones con dos incógnitas no sea la atrás expresada, se concluirá que las ecuaciones no pueden ser de primer grado.
Igual cosa sucede, punto por punto, en Geometría: pues si se supone que en lugar de una paralela se pueden trazar dos, y que hay una región de incompatibilidad (postulado de Lobattchewsky), se llega a la deducción de que las rectas son círculos máximos de una esfera imaginaria; y si, por el contrario, se supone que no es posible la incompatibilidad (postulado de Riemann), se llega a la deducción de que las rectas son círculos máximos de esfera real. Por tanto, para poder demostrar el postulado de Euclides sería necesario probar que un plano no es una esfera, y que una recta no es un círculo. Ahora bien, esto no es posible.
Lobattchewsky tuvo la rara habilidad de conservar el nombre de recta a la curva especial y de introducir sigilosamente en las fórmulas de su Trigonometría hiperbólica el módulo del radio de la esfera imaginaria a título de constante desconocida. La suma de los tres ángulos de un triángulo de esta clase es menor que dos rectos, y la diferencia es la relación del área del triángulo al cuadrado del radio de la esfera. Tal diferencia queda desconocida como la constante, pero debe ser tanto mayor cuanto mayor es el triángulo. En la Geometría de Riemann acontece lo mismo, sólo que aquí la suma de los ángulos es mayor que dos rectas.
Algunos geómetras confían en que la determinación de las paralajes estelares arrojará algún día luz sobre la curvatura del espacio, y que sea posible entonces saber si dicha curvatura es positiva o negativa.
Otros no creen posible que las observaciones astronómicas estelares puedan decidir respecto de la viabilidad de las geometrías. "Lo que se llama línea recta en Astronomía - dicen- es sencillamente la trayectoria del rayo luminoso. Si, pues, lo que parece imposible, se llegara a descubrir paralajes negativas ( * ) o a demostrar que todas las paralajes son superiores a cierto límite, se podría escoger entre dos conclusiones: podríamos renunciar a la Geometria euclídea o modificar las leyes de la Óptica y admitir que la luz no se propaga rigurosamente en línea recta". Según el parecer de estos geómetras: "El mundo conceptuaría esta última solución como más ventajosa".
Según la opinión de estos últimos matemáticos ninguna de las Geometrías, la euclídea y las no euclídeas, es más verdadera que otra. "Una Geometria no puede ser más verdadera que otra; puede solamente ser más cómoda". ¿Será posible que la determinación de la suma de los tres ángulos de un triángulo rectilíneo esté fuéra de toda experiencia? Este concepto es, como se ve, muy confuso.
Hay aún otro parecer respecto a las geometrías, el cual no podemos menos de indicar: es el de aquellos que aconsejan emplear provisionalmente la Geometría euclídea: "la más sencilla, y, por consiguiente, la más cómoda de aprender", mientras sea fácil de aplicar; pero sustituirla lo más pronto posible por alguno de los sistemas no euclídeos para cuando lo exijan los adelantos industriales, a fin de no retardar el progreso por un solo momento!!
* * *
11 -Las fórmulas de la Trigonometría esférica son tan verdaderas sobre la esfera como las de la Trigonometría plana sobre el plano, y como las de la Trigonometría hiperbólica sobre la esfera imaginaria. En lo que sigue nos ocuparemos de deducir las tres trigonometrías de la fórmula que liga las funciones recíprocamente uniformes. Ninguna de las geometrías es, pues, más verdadera que otra. La suma de los ángulos de un triángulo esférico es mayor que dos rectos sin que la de los triángulos planos deje por ello de ser igual a dos rectos. No hay, pues, contradicción entre el postulado de Euclides y los de Lobattchewsky y Riemann: bien entendido que esto es cuando se da a los lugares geométricos los nombres usuales. De otro modo la incompatibilidad es palmaria.
Consideremos un círculo y tracémosle una tangente. Imaginemos que dos móviles parten del punto de tangencia y que recorren: el uno, la circunferencia con velocidad tal que dé una vuelta en la unidad de tiempo; el otro, la tangente en determinado sentido, y con velocidad igual a la del primero. El punto que recorre la circunferencia pasará por el punto de tangencia a cada unidad de tiempo, por grande que sea el radio del círculo; mientras que el que recorre la tangente no vuelve nunca. Aunque la circunferencia de círculo y la recta sean líneas de curvatura constante existe entre ellas una diferencia profunda; cuestión de nonexídad. Haremos notar el valor de esta diferencia al aplicar correcta y rigurosamente la ecuación que liga dos variables recíprocamente uniformes.
Sistema de coordenadas - Sea (figura 2.a) una curva cerrada y M un punto cualquiera de ésta. Podemos definir la posición de M sobre la curva mediante la consideración del espacio recorrido por un móvil que describe la curva en el sentido positivo ABCD o en el negativo ADCB. El espacio recorrido a partir de una posición inicial A servirá para definir a M sobre la curva. No importa, por lo pronto, la definición que se dé a la longitud de arco.
Notaremos que a cada vuelta C sobre la curva, el móvil pasa por el mismo punto M; luego a una posición de M corresponden infinidad de arcos, a saber:
S = AM±nC
en donde n representa un número entero y C una vuelta completa. Diremos entonces que lu posición de M es función periódica de la variable S. Al contrario, la variable S es función cíclica de la posición M, pues a cada punto M corresponden infinidad de valores de S.
Si, pues, la curva cerrada pudiera prestarse a una interpretación analítica, la relación que ligaría la posición de M con el arco S sería de grado infinito, esto es, no podría ser simplemente un polinomio algebraico sino una serie. Tal es el carácter de las relaciones que ligan las funciones periódicas con las variables cíclicas.
Sea, al contrario, OAQ una recta. Representemos por S el espacio AM. La posición de M sobre la recta quedaría definida únicamente por el valor S=AM, pues un móvil que recorra la recta no pasará sino una sola vez por M. Toda función uniforme de la posición M, cualquiera que sea el sistema elegido, será función uniforme de S.
Los arcos descritos por un punto sobre curvas cerradas son variables cíclicas y pueden tomarse como variables independientes en las funciones que dependen de la posición de un punto sobro la curva; pero sería imposible, en la mayoría de los casos, hallar las funciones periódicas que puedan representarlas.
Un rasgo trazado a mano sobre un papel es, o puede considerarse, como una curva; pero esta curva sería imposible de representar analíticamente, pues está compuesta de trechos curvos de curvaturas distintas, empalmados aproximadamente unos con otros. No podemos atribuir propiedades analíticas a rasgos trazados caprichosamente:
Las figuras geométricas que se imponen a nuestro entendimiento son los rasgos más sencillos de que podemos disponer y solamente de ellos nos podemos servir para formar sistemas de referencia, a fin de representar numéricamente los puntos del espacio.
La recta y el plano son los elementos geométricos más sencillos de que disponemos. Definirlos sería admitir que existiesen otros elementos más simples.
Los segmentos de recta (distancias) son comparables entre sí, esto es, son susceptibles de medida, al elegir uno particular como unidad. Los ángulos formados por dos rectas que se cortan pueden, igualmente, representarse por números. Estos dos elementos numéricos: distancias y ángulos, podemos utilizarlos para expresar numéricamente y, por tanto, analíticamente, la posición de los puntos de un plano con relación a una recta dada y un punto situado sobre ésta.
Tracemos (figura 3.a) la recta x'Ox en un plano. Sea M un punto del plano. Por dos puntos no pasa sino una recta; tracemos, pues, la recta OMu; pero consideremos únicamente la semirrecta Ou. Dicha semirrecta forma con Ox el ángulo xOM. Podemos hacer girar la semirrecta alrededor de O en un número cualquiera de vueltas, y el ángulo que define la posición de ésta tendrá evidentemente infinidad de valores. Llamemos θ0 el más pequeño, C la vuelta entera, y n un número entero: dichos ángulos serán:
θ = θ0±nC.
El punto M podemos representarlo sobre la recta OMu la cual ha sido definida por la variable cíclica θ = θ0± nC. Para representar a M nos basta medir o expresar numéricamente su distancia OM = r. Esta distancia no tiene sino un valor, como lo hemos indicado atrás.
La posición, pues, del punto M sobre el plano quedará definida por dos valores
r=OM y θ = θ0± nC
Estas coordenadas tienen un carácter diferente, no solo en su naturaleza sino en su modo de definir el punto; pues la r no tiene sino un valor, mientras θ tiene infinidad de valores.
Si hacemos r = a = constante, tendremos infinidad de puntos en el plano cuyas coordenadas satisfacen a esa condición, estos puntos se hallan colocados en la circunferencia de un círculo cuyo centro es 0 .
Podemos idear otros medios de representar un punto sobre un plano con el auxilio de variables no cíclicas. Por el punto O levantemos una perpendicular y'Oy à x'Ox y por el punto M bajemos dos perpendiculares MP sobre Ox y MQ sobre Oy. No nos detendremos en la definición de perpendicular; nos basta saber que por un punto de un plano no se puede trazar sino una sola perpendicular sin que por ello entre en juego el postulado euclídeo.
El punto M quedará determinado por los segmentos rectilíneos OP = X 1 OQ=y 1 Ó también por las distancias MQ=X y MP=y; sin que podamos decir nada respecto de las igualdades: X = X 1 é y = y 1 pues tales igualdades implicarían la aceptación del postularlo en referencia.
Tendremos, pues, dos sistemas de valores para definir la posición M en el plano, a saber: X1 é y1
, X é
y.
Estas coordenadas serán funciones de
r y
θ. Y las relaciones:
 serán solamente funciones de θ.
serán solamente funciones de θ.
Estas relaciones no tienen para cada punto sino un solo valor cada una de ellas, mientras que θ tiene infinidad de valores: así resultará que dichas relaciones tendrán que ser funciones periódicas de θ.
Vamos a demostrar que
 son funciones de la forma ζ (θ) y que
son funciones de la forma ζ (θ) y que
 son de la forma η (θ) en donde ζ (θ) y η(θ) son las series estudiadas en los párrafos 4.° y 5.°, en las que la variable
X
ha sido reemplazada por θ.
son de la forma η (θ) en donde ζ (θ) y η(θ) son las series estudiadas en los párrafos 4.° y 5.°, en las que la variable
X
ha sido reemplazada por θ.
Hagamos, para facilitar la expresión, r=constante, y tracemos un circulo con centro en O y que tenga OM por radio.
La unidad de ángulo es arbitraria: elegiremos esta unidad de manera que la vuelta completa valga ω, periodo de las funciones ζ y η así, como también, de las relaciones:
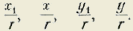
No nos detendremos en las propiedades geométricas de la circunferencia con relación a sus diámetros, ni en las demostraciones de superposición de figuras, porque tales cuestiones no implican el postulado de Euclides.
El ángulo recto valdrá
 la vuelta completa 2ω y la semivuelta ω.
la vuelta completa 2ω y la semivuelta ω.
Sabemos por las propiedades de ζ (θ) que es periódica y de período 2ω. Y, además, tenemos que
ζ (θ)=ζ (-θ) ζ (θ)=-ζ (θ + ω) ζ(o) = l ζ(ω)=-1


Fácilmente se comprueba sobre la figura que se trace, que las relaciones
 satisfacen idénticamente las mismas condiciones.
satisfacen idénticamente las mismas condiciones.
Cuando dos variables p y q funciones de una tercera variable, se manejan de manera que a cada valor particular, real o imaginario, de una de ellas, no corresponda sino un valor real o imaginario otra y, recíprocamente, estas dos cantidades están ligadas por una ecuación de la forma:
Apq + Bp + Cq + D=o
son círculos máximos de esfera real. Por tanto, para poder demostrar el postulado de Euclides sería necesario probar que un plano no es una esfera, y que una recta no es un círculo. Ahora bien, esto no es posible.
Lobattchewsky tuvo la rara habilidad de conservar el nombre de recta a la curva especial y de introducir sigilosamente en las fórmulas de su Trigonometría hiperbólica el módulo del radio de la esfera imaginaria a título de constante desconocida. La suma de los tres ángulos de un triángulo de esta clase es menor que dos rectos, y la diferencia es la relación del área del triángulo al cuadrado del radio de la esfera. Tal diferencia queda desconocida como la constante, pero debe ser tanto mayor cuanto mayor es el triángulo. En la Geometría de Riemann acontece lo mismo, sólo que aquí la suma de los ángulos es mayor que dos rectas.
Algunos geómetras confían en que la determinación de las paralajes estelares arrojará algún día luz sobre la curvatura del espacio, y que sea posible entonces saber si dicha curvatura es positiva o negativa.
Otros no creen posible que las observaciones astronómicas estelares puedan decidir respecto de la viabilidad de las geometrías. "Lo que se llama línea recta en Astronomía -dicen- ex sencillamente la trayectoria del rayo luminoso. Si, pues, lo que parece imposible, se llegara a descubrir paralajes negativas (*) o a demostrar que todas las paralajes son superiores a cierto límite, se podría escoger entre dos conclusiones: podríamos renunciar a la Geometría euclídea o modificar las leyes de la Óptica y admitir que la luz no se propaga rigurosamente en línea recta"'. Según el parecer de estos geómetras: "El mando conceptuarla esta última solución como más ventajosa".
Según la opinión de estos últimos matemáticos ninguna de las Geometrías, la euclídea y las no euclídeas, es más verdadera que otra. "Una Geometría no puede ser más verdadera que otra; puede solamente ser más Cómoda". ¿Será posible que la determinación de la suma de los tres ángulos de un triángulo rectilíneo esté fuera de toda experiencia? Este concepto es, como se ve, muy confuso.
Hay aún otro parecer respecto a las geometrías, el cual no podemos menos de indicar: es el de aquellos que aconsejan emplear provisionalmente la Geometría euclídea: "la más sencilla, y, por consiguiente, la más cómoda de aprender", mientras sea fácil de aplicar; pero sustituirla lo más pronto posible por alguno de los sistemas no en euclídeos para cuando lo exijan los adelantos industriales, a fin de no retardar el progreso por un solo momento!!
11 -Las fórmulas de la Trigonometría esférica son tan verdaderas sobre la esfera como las de la Trigonometría plana sobre el plano, y como las de la Trigonometría hiperbólica sobre la esfera imaginaria. En lo que sigue nos ocuparemos de deducir las tres trigonometrías de la fórmula que liga las funciones recíprocamente uniformes. Ninguna de las geometrías es, pues, más verdadera que otra. La suma de los ángulos de un triángulo esférico es mayor que dos rectos sin que la de los triángulos planos deje por ello de ser igual a dos rectos. No hay, pues, contradicción entre el postulado de Euclides y los de Lobattchewsky y Riemann: bien entendido que esto es cuando se da a los lugares geométricos los nombres usuales. De otro modo la incompatibilidad es palmaria.
Consideremos un círculo y tracémosle una tangente. Imaginemos que dos móviles parten del punto de tangencia y que recorren: el uno, la circunferencia con velocidad tal que dé una vuelta en la unidad de tiempo; el otro, la tangente en determinado sentido, y con velocidad igual a la del primero. El punto que recorre la circunferencia pasará por el punto de tangencia a cada unidad de tiempo, por grande que sea el radio del círculo; mientras que el que recorre la tangente no vuelve nunca. Aunque la circunferencia de círculo y la recta sean líneas de curvatura constante existe entre ellas una diferencia profunda; cuestión de nonexidad. Haremos notar el valor de esta diferencia al aplicar correcta y rigurosamente la ecuación que liga dos variables recíprocamente uniformes.
Sistema de coordenadas - Sea (figura 2.a) una curva cerrada y M un punto cualquiera de ésta. Podemos definir la posición de M sobre la curva mediante la consideración del espacio recorrido por un móvil que describe la curva en el sentido positivo ABCD o en el negativo ADCB. El espacio recorrido a partir de una posición inicial A servirá para definir a M sobre la curva. No importa, por lo pronto, la definición que se dé a la longitud de arco.
Notaremos que a cada vuelta C sobre la curva, el móvil pasa por el mismo punto M; luego a una posición de M corresponden infinidad de arcos, a saber:
S=AM ± nC
en donde n representa un número entero y C una vuelta completa. Diremos entonces que la posición de M es función periódica de la variable S. Al contrario, la variable S es función cíclica de la posición M, pues a cada punto M corresponden infinidad de valores de S.
Si, pues, la curva cerrada pudiera prestarse a una interpretación analítica, la relación que ligaría la posición de M con el arco S sería de grado infinito, esto es, no podría ser simplemente, un polinomio algebraico sino una serie. Tal es el carácter de las relaciones que ligan las funciones periódicas con las variables cíclicas.
Sea, al contrario, OAQ una recta. Representemos por S el espacio AM. La posición de M sobre la recta quedaría definida únicamente por el valor S=AM, pues un móvil que recorra la recta no pasará sino una sola vez por M. Toda función uniforme de la posición M, cualquiera que sea el sistema elegido, será función uniforme de S.
Los arcos descritos por un punto sobre curvas cerradas son variables cíclicas y pueden tomarse como variables independientes en las funciones que dependen de la posición de un punto sobre la curva; pero sería imposible, en la mayoría de los casos, hallar las funciones periódicas que puedan representarlas.
Un rasgo trazado a mano sobre un papel es, o puede considerarse, como una curva; pero esta curva sería imposible de representar analíticamente, pues está compuesta de trechos curvos de curvaturas distintas, empalmado aproximadamente unos con otros. No podemos atribuir propiedades analíticas a rasgos trazados caprichosamente:
Las figuras geométricas que se imponen a nuestro entendimiento son los rasgos más sencillos de que podemos disponer y solamente de ellos nos podemos servir para formar sistemas de referencia, a fin de representar numéricamente los puntos del espacio.
La recta y el plano son los elementos geométricos más sencillos de que disponemos. Definirlos sería admitir que existiesen otros elementos más simples.
Los segmentos de recta (distancias) son comparables entre sí, esto es, son susceptibles de medida, al elegir uno particular como unidad. Los ángulos formados por dos rectas que se cortan pueden, igualmente, representarse por números. Estos dos elementos numéricos: distancias y ángulos, podemos utilizarlos para expresar numéricamente y, por tanto, analíticamente, la posición de los puntos de un plano con relación a una recta dada y un punto situado sobre ésta.
Tracemos (figura 3.a) la recta X'Ox en un plano. Sea M un punto del plano. Por dos puntos no pasa sino una recta; tracemos, pues, la recta OMu; pero consideremos únicamente la semirrecta Ou. Dicha semirrecta forma con Ox el ángulo xOM. Podemos hacer girar la semirrecta alrededor de O en un número cualquiera de vueltas, y el ángulo que define la posición de ésta tendrá evidentemente infinidad de valores. Llamemos θ0 el más pequeño, C la vuelta entera, y n un número entero: dichos ángulos serán: θ= θ0 ± nC
El punto M podemos representarlo sobre la recta OMu la cual ha sido definida por la variable cíclica θ= θ0 ± nC. Para representar a M nos basta medir o expresar numéricamente su distancia OM = r. Esta distancia no tiene sino un valor, como lo hemos indicado atrás.
La posición, pues, del punto M sobre el plano quedará definida por dos valores
r=OM y θ= θ0 ± nC
Estas coordenadas tienen un carácter diferente, no solo en su naturaleza sino en su modo de definir el punto; pues la r no tiene sino un valor, mientras θ tiene infinidad de valores.
Si hacemos r=a = constante, tendremos infinidad de puntos en el plano cuyas coordenadas satisfacen a esa condición. Estos puntos se hallan colocados en la circunferencia de un círculo cuyo centro es O.
Podemos idear otros medios de representar un punto sobre un plano con el auxilio de variables no cíclicas. Por el punto O levantemos una perpendicular y'Oy à x'Ox y por el punto M bajemos dos perpendiculares MP sobre Ox y MQ sobre Oy. No nos detendremos en la definición de perpendicular; nos hasta saber que por un punto de un plano no se puede trazar sino una sola perpendicular sin que por ello entre en juego el postulado euclídeo.
El punto M quedará determinado por los segmentos rectilíneos OP=X1 OQ = y1 O también por las distancias MQ = x y MP =y; sin que podamos decir nada respecto de las igualdades: x = x1 é y=y 1 pues tales igualdades implicarían la aceptación del postulado en referencia.
Tendremos, pues, dos sistemas ríe valores para definir la posición M en el plano, a saber:
X
1
é y1, x é y. Estas coordenadas serán función de r y θ. Y las relaciones
 serán solamente funciones de θ.
serán solamente funciones de θ.
Estas relaciones no tienen para cada punto sino un solo valor cada una de ellas, mientras que θ tiene infinidad de valores: así resultará que dichas relaciones tendrán que ser funciones periódicas de θ.
Vamos a demostrar que
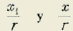 son funciones de la forma ζ (θ) y que
son funciones de la forma ζ (θ) y que
 son de la forma η (θ) en donde ζ (θ) y η (θ) son las series estudiadas en los parágrafos 4.° y 5.", en las que lu variable x ha sido reemplazada por θ.
son de la forma η (θ) en donde ζ (θ) y η (θ) son las series estudiadas en los parágrafos 4.° y 5.", en las que lu variable x ha sido reemplazada por θ.
Hagamos, para facilitar la expresión, r= constante, y tracemos un círculo con centro en O y que tenga OM por radio.
La unidad de ángulo es arbitraria: elegiremos esta unidad de manera que la vuelta completa valga ω, período de las funciones ζ y η así, como también, de las relaciones:

No nos detendremos en las propiedades geométricas de la circunferencia con relación a sus diámetros, ni en las demostraciones de superposición de figuras, porque tales cuestiones no implican el postulado de Euclides.
El ángulo recto valdrá
 vuelta completa 2ω y la semivuelta ω.
vuelta completa 2ω y la semivuelta ω.
Sabemos por las propiedades de ζ (β) que es periódica y de período 2ω. Y, además, tenemos que
ζ (θ)= ζ (-θ) ζ (θ) =- ζ (θ+ω) ζ (0)=i ζ (ω) =-1

Fácilmente se comprueba sobre la figura que se trace, que las relaciones
 satisfacen idénticamente las mismas condiciones.
satisfacen idénticamente las mismas condiciones.
Cuando dos variables p y q, funciones de una tercera variable, se manejan de manera que a cada valor particular, real o imaginario, de una de ellas, no corresponda sino un valor real o imaginario de la otra y, recíprocamente, estas dos cantidades están ligadas por una ecuación de la forma:
Apq + Bp + Cq + D=o (a)
Ahora bien, a cada valor
 no corresponde sino un valor de X1 y, por tanto, un punto P sobre Ox y dos puntos sobre la circunferencia, esto es, dos series de ángulos M0x = x, y el simétrico - x, a las cuales no corresponde sino un solo valor de ζ (θ), a saber: ζ (x) = ζ (-x)
no corresponde sino un valor de X1 y, por tanto, un punto P sobre Ox y dos puntos sobre la circunferencia, esto es, dos series de ángulos M0x = x, y el simétrico - x, a las cuales no corresponde sino un solo valor de ζ (θ), a saber: ζ (x) = ζ (-x)
Recíprocamente a un valor de ζ corresponden dos series de ángulos iguales y de signos contrarios, y, por tanto, dos puntos simétricos respecto del diámetro Ox, y, por tanto, un punto P sobre dicho eje, o bien, un solo valor de X1 y, por tanto, una sola relación

En consecuencia, la ecuación (a) será aplicable a las variables ζ y
 pongamos
pongamos
 y q= ζ (θ). Tendremos sucesivamente: Para θ=0: p = 1 q = 1. Y por tanto: A+B + C + D = 0.
y q= ζ (θ). Tendremos sucesivamente: Para θ=0: p = 1 q = 1. Y por tanto: A+B + C + D = 0.
Para
 P = o q = o. De donde D = o. Para θ=ω p = -1 q = --1. De donde A - B - C + D = O. En consecuencia 2A=-2D=0 B=-C. Y, por tanto, la ecuación (a) se hará: Bp - Cq = θ. O bien
P = o q = o. De donde D = o. Para θ=ω p = -1 q = --1. De donde A - B - C + D = O. En consecuencia 2A=-2D=0 B=-C. Y, por tanto, la ecuación (a) se hará: Bp - Cq = θ. O bien
 Del mismo modo hallaríamos:
Del mismo modo hallaríamos:
 y además:
y además:

Estas relaciones son ciertas aunque r no sea constante, y pueden demostrarse sin el auxilio del círculo, por medio de la ecuación (a).
Como
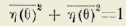 tendremos:
tendremos:
 Cuando sea r=constante, se tendrá x1
2+y1
2=constante x1 + y2 que es la ecuación de la circunferencia del círculo.
Cuando sea r=constante, se tendrá x1
2+y1
2=constante x1 + y2 que es la ecuación de la circunferencia del círculo.
Sobre la circunferencia del círculo se demuestra fácilmente que a ángulos al centro iguales corresponden arcos iguales. Por tanto, si se toma por unidad de arco de círculo aquel que corresponde a la unidad de ángulo, podemos poner
 en vez de θ, siendo σ la unidad de arco.
en vez de θ, siendo σ la unidad de arco.
Tendremos
 Si desarrollamos a
Si desarrollamos a
 tendremos:
tendremos:
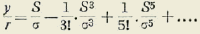 0 bien:
0 bien:

Si hacemos tender S a cero, el arco 2S y la cuerda 2y tenderán a cero, pero su relación tiene un límite, a saber:
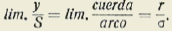
Si se admite que el límite de la relación del arco a la cuerda es la unidad, se tendrá que

0 bien que el arco unidad debe ser el radio para que la circunferencia valga C=2ωr = 2ϖr; ω=ϖ = 3.14155926....
12-Consideremos un casquete esférico sobre una esfera de radio R; sea r el radio del círculo que sirve de base al casquete y r 1 el radio del círculo homotético con relación al centro de la esfera del círculo de radio r, sobre el plano tangente.
Por el polo del casquete y el centro de la esfera tracemos dos planos perpendiculares. Estos planos cortarán al plano tangente y al plano secante según dos rectas perpendiculares entre sí en cada plano, las cuales serán diámetros de círculos de radios r 1 y r. Tomemos en cada uno de estos planos a dichas perpendiculares por ejes coordenados. Consideremos un punto M sobre la circunferencia del círculo menor que sirve de base al casquete, y sea M1 su correspondiente en el plano tangente.
Tracemos por el punto M y por el centro de la esfera tres planos, a saber: uno por el polo del casquete y los otros dos perpendicularmente a los dos planos octogonales trazados antes. Estos planos cortarán a la esfera según círculos máximos, y a los planos tangente y secante del modo siguiente: el primer plano según los radios O1M1 y OM, respectivamente, de los círculos de radios r1 y r; los otros dos según MP, M1P1, MQ, M1Q1.
Para facilitar las exposiciones designaremos los puntos situados sobre el círculo tangente de radio r1 con el índice sub-uno, así como las coordenadas x1 y1; sin índice alguno sobre el plano secante del círculo que sirve de base al casquete, y que tiene por radio r; finalmente, con un acento los puntos y las cantidades referentes a la superficie esférica del casquete. Así el punto 0' polo del casquete, será el mismo punto 01 centro del círculo tangente, y el punto M' del casquete en su base será el mismo punto M. Del mismo modo los puntos ABCD del círculo r serán los puntos A'B'C D' del casquete.
Después de lo expuesto en el parágrafo anterior es inútil que continuemos designando por ζ (θ) y η (θ) las funciones estudiadas en los parágrafos 4.° y 5.°, pues ya está cumplido el objeto de esta notación. Seguiremos de aquí en adelante, designándolas por coseno y seno, respectivamente.
Pondremos (figura 4.a: figuras a, b y c); (Véase la figura en la página siguiente).
(Figura a) 0M=r 0P = x=MQ 0Q = y=MP.
(Figura b) 0’M’ = r 1 0P' = x’ 1 =M'Q' 0’Q’=y’ 1 = M'P’.
(Figura c) 0 1 M 1 = r 1 0 1 P 1 = x 1 -= M 1 Q 1 0Q 1 =y 1 =M i P v
Llamamos θ el ángulo MOx = M'O'A ' = M 1 0 1 x 1 .
Antes de continuar adelante séanos permitido hacer una observación. Consideremos las relaciones siguientes en el casquete esférico:
 y comparemos dichas relaciones con las funciones cos θ y senθ por medio de la ecuación
Apq + Bp + Cq + D
=
0.
y comparemos dichas relaciones con las funciones cos θ y senθ por medio de la ecuación
Apq + Bp + Cq + D
=
0.
Haciendo paso a puso los razonamientos del parágrafo anterior, llamamos como antes:
Ahora bien, estas serían las fórmulas de la Trigonometría plana euclídea aplicadas a los triángulos esféricos.
Preguntaremos: ¿La ecuación (x) se presta a deducir de ella todo lo que se quiera? Si se atiende a la Trigonometría plana hiperbólica establecida por Lobattchewsky y a la Trigonometría esférica parabólica (*) que acabamos de deducir, la respuesta sería afirmativa. Tendrían razón ciertos críticos que han dicho que a las x se les puede hacer decir todo lo imaginable.
Este cargo hecho al análisis matemático es injusto. La fórmula (x) es correcta, pero ha sido mal aplicada en los dos casos indicados. Hicimos notar el error que se cometió en la fórmula fundamental de la Trigonometría plana hiperbólica. En cuanto a las fórmulas
(m)
el error consiste en que las variables
 y COS θ no son recíprocamente uniformes, ni tampoco
y COS θ no son recíprocamente uniformes, ni tampoco
 con
sen θ.
con
sen θ.
En efecto, las magnitudes x' 1 x' 1 y' 1 y' tienen para cada punto M' infinidad de valores, puesto que son arcos de círculo máximo. Así:
Y, finalmente, (r') o ±2ϖNR
En lo que respecta a
sen
θ y
COS
θ estas magnitudes no admiten sino un solo valor para un punto Ai1 del círculo del casquete; en consecuencia, no hay la uniformidad recíproca que se quiere para la aplicación de la fórmula (x), como no la había entre
tang
θ y
T
( ) en el problema de Lobattchewsky.
) en el problema de Lobattchewsky.
***
13-Consideremos el triángulo esférico 0' P' M' (figura b-de la 4.°) y pongamos:
Llamemos, además, B = M' 0' P' al ángulo que habíamos designado por θ. Tendremos, evidentemente:
En el círculo
A BCD
se tiene, según lo visto en el parágrafo 10
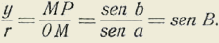
En el círculo
A
1
B
1
C
1
D
1
se tiene:
 Se hallan, pues, las fórmulas:
Se hallan, pues, las fórmulas:
referentes al triángulo esférico rectángulo 0' M' P' Estas ecuaciones Ron suficientes para establecer todas las fórmulas referentes a los triángulos esféricos rectángulos y, por tanto, a todos los triángulos esféricos, pues un triángulo esférico cualquiera puede descomponerse en dos triángulos rectángulos.
* * *
14 - Si suponemos imaginario el radio de la esfera: esto es, si hacemos R =ik
obtrendemos, poniendo
Se hallará, pues:
De igual modo
De estas fórmulas se deducen las de la Trigonometría hiperbólica de Lobattchewsky.
***
Creemos haber dicho lo suficiente para los lectores que poseen criterio propio, a quienes está dedicado este trabajo. Pero haremos, no obstante, algunas reflexiones finales.
Las figuras geométricas se imponen irresistiblemente a los cerebros sanos. La recta infinita no es hipótesis convencional, sino la idea misma de recta; lo propio sucede con el plano. Llamar recta al círculo y plano a la esfera no sería otra cosa que cambiar los nombres de las cosas.
La psicología experimental explica la formación atávica de las ideas geométricas y su completa perfección. Vivimos sobre una esfera y, sin embargo, tenemos la idea perfecta del plano.
El cerebro se transforma sucesivamente al través del tiempo. ¿De qué manera y en qué sentido habrá venido transformando los ideas la práctica de la instrucción artificial?
Las geometrías no euclídeas y la Cinemática de Einstein son datos de altísimo interés a ese respecto. Quizá también se llegue a encontrar la causa por la cual las civilizaciones caducan.
De todos modos, somos deudores a Lobattchewsky de algo de grandísima importancia desde el punto de vista psicológico.
NOTA DE LA DIRECCION.-Con este estudio damos ahora por terminada ¡a labor de Garavito en el campo, más filosófico que matemático, de las especulaciones geométricas encaminadas a desorientar la intuición que. tenemos del espacio euclídeo, aunque entendemos que del sabio Profesor quedan aún algunos papeles dispersos en que se ocupó también del mismo asunto, desde diferentes puntos de vista. Tal vez en alguna época posterior podamos volver sobre tópicos tan interesantes y que no han perdido en forma alguna su oportunidad. Mas antes de hacerlo procuraremos exponer brevemente la historia de las geometrías no euclídeas, extendiéndonos, sobre todo, respecto del alcance que la Ciencia moderna les ha dado, por cuanto juagamos como un deber nuéstro y de esta Academia Colombiana de Ciencias, el no dejar sin comentario ninguno de los trabajos de Garavito, encaminados, como todo lo suyo, a poner orden en el conjunto, un tanto caótico, de la especulación contemporánea. Cuando llegue esta ocasión habremos de prepararnos mediante el estudio de que seamos capaces y con ayuda de la Academia, cuya finalidad de crítica depuradora hemos expuesto en las notas editoriales del presente número, para hacerlo posible en orden a desarrollar estas ideas de Garavito de modo absoluto.