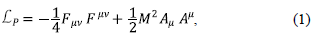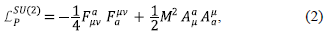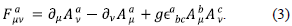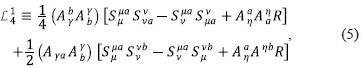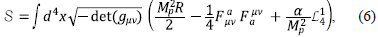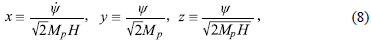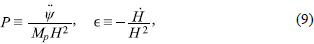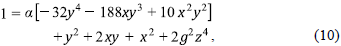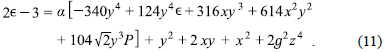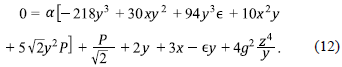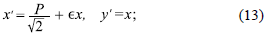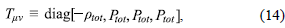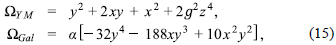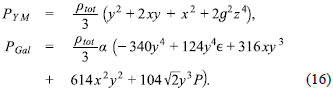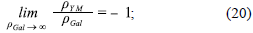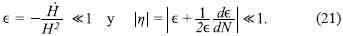Introducción
Los períodos inflacionarios representan eventos notables en la historia del universo por lo que merecen un estudio de su comportamiento a partir de los diferentes modelos cosmológicos disponibles. Esto incluye estudiar la generalización a la acción de Proca. Tal generalización requiere garantizar la ausencia de inestabilidades que impliquen un modelo no realista. Una de las inestabilidades más importantes a evitar es la inestabilidad de Ostrogradski (Ostrogradsky, 1850), la cual implica que el sistema no posee un estado base permitiendo así que la energía tienda a -∞, lo cual es físicamente imposible (Woodard, 2007, 2015). Una condición necesaria mas no suficiente para que este tipo de patologías no se presente en la teoría es asegurar que las ecuaciones de campo no posean derivadas de tercer o mayor orden (Woodard, 2007, 2015); es aquí en donde los campos denominados Galileones juegan un papel importante, pues toda acción compuesta por Galileones generalizados conlleva a ecuaciones de campo de hasta segundo orden (Nicolis, et al., 2009; Deffayet, et al., 2011).
La acción de Proca por sí sola define un período del universo dominado por energía tipo radiación (Quigg, 2013); pero cuando se adiciona el término basado en los Galileones vectoriales no Abelianos,
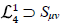 (Allys, et al., 2016b; Rodríguez & Navarro, 2018), la dinámica del sistema es tal que se pueden definir dos fluidos artificiales de tipo radiación. Por una parte está el fluido de Yang- Mills, el cual es un fluido con densidad de energía y presión positiva que, por sí solo, representaría un universo dominado por la radiación (Quigg, 2013; Aitchison & Hey, 2012). Por otra parte está el denominado fluido de los Galileones vectoriales el cual posee tanto presión como densidad de energía negativa, siendo su ecuación de estado
ωGal
≃ 1/3. La separación del Lagrangiano de materia en dos términos asociados a dos fluidos diferentes no es más que un artificio matemático para observar la contribución de cada término en el modelo. Así, se puede observar que, gracias a un comportamiento de auto-ajuste fino, las densidades de energía de Yang-Mills y del Galileón vectorial prácticamente se cancelan dando lugar a un parámetro de estado efectivo ωtotal ≃ -1. (Rodríguez & Navarro, 2018)
(Allys, et al., 2016b; Rodríguez & Navarro, 2018), la dinámica del sistema es tal que se pueden definir dos fluidos artificiales de tipo radiación. Por una parte está el fluido de Yang- Mills, el cual es un fluido con densidad de energía y presión positiva que, por sí solo, representaría un universo dominado por la radiación (Quigg, 2013; Aitchison & Hey, 2012). Por otra parte está el denominado fluido de los Galileones vectoriales el cual posee tanto presión como densidad de energía negativa, siendo su ecuación de estado
ωGal
≃ 1/3. La separación del Lagrangiano de materia en dos términos asociados a dos fluidos diferentes no es más que un artificio matemático para observar la contribución de cada término en el modelo. Así, se puede observar que, gracias a un comportamiento de auto-ajuste fino, las densidades de energía de Yang-Mills y del Galileón vectorial prácticamente se cancelan dando lugar a un parámetro de estado efectivo ωtotal ≃ -1. (Rodríguez & Navarro, 2018)
Una vez obtenido el sistema dinámico autónomo a partir de las ecuaciones de campo, se puede realizar un análisis numérico del comportamiento de las variables adimensionales que allí se definen. Al observar la evolución en el tiempo del sistema dinámico, se aprecia un mecanismo de auto-ajuste fino asociado al módulo del campo "Ψ" y a su primera derivada temporal "Ψ"; este fenómeno actúa como un atractor que, sin importar las condiciones iniciales, conduce a una ecuación de estado de la forma P = -p. Por otra parte, el análisis de los puntos críticos arroja resultados muy interesantes ya que dos de los ocho puntos de equilibrio, los cuales son puntos tipo silla, logran reproducir un período inflacionario primordial lo suficientemente largo para resolver los problemas clásicos de la cosmología estándar, dando lugar posteriormente a un período dominado por la radiación; sin embargo, un cambio en las condiciones iniciales reduciría notablemente la duración del período inflacionario, lo que hace que el modelo pierda efectividad al momento de caracterizar la expansión acelerada primordial.
Teoría de Proca con simetría SU(2) global
La ecuación de Proca representa las ecuaciones de Maxwell del electromagnetismo con un fotón masivo:
siendo Fµv= ∂µAv - ∂µAv, con Aµ siendo el campo vectorial masivo y M siendo su respectiva masa (Quigg, 2013). Para incorporar la simetría SU(2) local a la teoría es necesario añadir los índices de grupo, los cuales se representan con letras latinas, para diferenciarlos de los índices espaciotemporales (índices griegos). En este caso (Quigg, 2013), el Lagrangiano de Proca se representaría de la forma
en donde el tensor Faµv se conoce como el tensor de esfuerzos del campo de gauge, y se define como
Cuando se omite la simetría de gauge no abeliana en la teoría (pero preservando la simetría global), la definición del tensor de esfuerzos es equivalente a la definición (3) sin el último término, el cual es asociado a la simetría SU(2) local, en donde g es la constante de acoplamiento del grupo y Є a bx es el pseudo tensor de Levi-Civita que corresponde a las constantes de estructura del grupo, las cuales se definen de la siguiente manera:
siendo
T¡
los generadores de la transformación. Para comprender la simetría de gauge es conveniente conocer lo que significa SU(N). Las siglas SU provienen de "special unitary group", lo que implica que los generadores de la transformación se representan mediante matrices unitarias, es decir, cumplen la relación
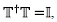 con determinante igual a +1. El número (N) da información de la dimensión del grupo, D = N
2
- 1, en este caso con N = 2, el grupo posee tres dimensiones (Rodríguez, 2015). Un aspecto a resaltar es que el grupo de simetrías SU(2) es isomorfo al grupo SO(3) "grupo de rotaciones en tres dimensiones" (Ryder, 1996), lo cual quiere decir que ambos grupos poseen la misma estructura y por consiguiente exigir simetría SU(2) implica exigir simetría ante rotaciones espaciales en tres dimensiones. Lo anterior resulta de gran utilidad ya que se quiere modelar un universo a gran escala isótropo y homogéneo.
con determinante igual a +1. El número (N) da información de la dimensión del grupo, D = N
2
- 1, en este caso con N = 2, el grupo posee tres dimensiones (Rodríguez, 2015). Un aspecto a resaltar es que el grupo de simetrías SU(2) es isomorfo al grupo SO(3) "grupo de rotaciones en tres dimensiones" (Ryder, 1996), lo cual quiere decir que ambos grupos poseen la misma estructura y por consiguiente exigir simetría SU(2) implica exigir simetría ante rotaciones espaciales en tres dimensiones. Lo anterior resulta de gran utilidad ya que se quiere modelar un universo a gran escala isótropo y homogéneo.
Término S y la tríada cósmica
El término S es un Lagrangiano compuesto por la versión simétrica del tensor de esfuerzos Faµv
,
que surge a partir del análisis de los Galileones vectoriales (Allys, et al., 2016a, 2016b; Beltrán Jiménez & Heisenberg, 2016), y que se emplea para la generalización de la teoría de Proca. Esto se llevó a cabo tomando como base los trabajos realizados por Horndenski en los años 70 (Horndeski, 1974, 1976). La separación de las ecuaciones entre los términos S y aquellos definidos exclusivamente a partir de Fµv permite estudiar las implicaciones físicas de cada uno de estos términos por separado. Ya que el tensor de esfuerzos y su dual de Hodge han sido bien estudiados, se vio conveniente estudiar los Lagrangianos construidos a partir del tensor S. El Lagrangiano a estudiar es entonces de la forma
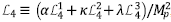 en donde α
, k,
λ, son constantes de acoplamiento,
Mp
es la masa reducida de Planck y
en donde α
, k,
λ, son constantes de acoplamiento,
Mp
es la masa reducida de Planck y
es el término clave de la acción total con la cual se pretende modelar los períodos inflacionarios. Cabe señalar que, en la anterior expresión, R es el escalar de Ricci. Así, es posible construir la acción total considerando también la interacción materia-gravedad; por esta razón se añade la acción de Einstein-Hilbert, la cual permite asociar el tensor de Einstein con el campo vectorial que representa la materia. Como resultado, la acción del modelo a estudiar se define de la siguiente forma:
en donde gµv es la métrica espaciotemporal. Si bien a partir de la variación de la acción se obtienen las ecuaciones de Friedmann y de continuidad, el proceso quedaría incompleto ya que la configuración de Galileones vectoriales da lugar, generalmente, a una elevada anisotropía. La configuración de tríada cósmica (Armendariz-Picon, 2004) asegura la consistencia de las ecuaciones obtenidas con la asunción de un universo isótropo y homogéneo ya que tres vectores de igual norma y ortogonales entre sí no generan ninguna dirección privilegiada. Matemáticamente la tríada cósmica se expresa como
en donde a es el parámetro de expansión, Ψ = Ψ(t) es una función escalar que sólo depende del tiempo y δbµ es la función delta de Kronecker. Una vez impuesta la configuración de tríada cósmica a las ecuaciones de campo, se procede con el análisis analítico y numérico del sistema dinámico autónomo asociado.
Sistema dinámico autónomo
Para adimensionalizar las ecuaciones obtenidas a través de la variación de la acción (6), y simplificarlas de manera óptima, se plantearon las siguientes variables asociadas al campo y su primera derivada:
en donde H es el parámetro de Hubble. También se definieron los parámetros adimensionales
en donde Є se conoce como el parámetro de slow-roll, y la condición Є « 1 indica un período de expansión de tipo rodadura lenta. Con base en las ecuaciones (8) y (9), la componente temporal de las ecuaciones de campo se reescribe como
mientras que las tres componentes espaciales, debido a la configuración de tríada cósmica, son iguales y equivalentes a la expresión
Por otra parte, la variación de la acción respecto al campo A µ a da como resultado
La expresión (12) es consistente con la ecuación de continuidad proveniente de la conservación del tensor momentum - energía ∇µTµv = 0, lo cual brinda confiabilidad y validez al desarrollo llevado a cabo. Por último para completar el conjunto de ecuaciones a resolver, se plantea el sistema dinámico de las variables definidas en la ecuación (8);
en donde x' = dx/dN siendo N = ∫Hdt una escala de tiempo conocida como número de e-folds. La variable adimensional z(t) se deduce mediante el uso de la ligadura (10).
Debido a la consideración de isotropía y homogeneidad, el tensor momentum- energía es el de fluido perfecto y, por lo tanto, adquiere la forma
en un sistema de referencia comóvil y cartesiano. En la anterior expresión ptot y Ptot son la densidad de energía y presión respectivamente. De la adimensionalización de las ecuaciones de campo en las expresiones (10), es evidente que
siendo Ωi = pi/ptot y Ωtot = Ωgal + &ym = 1. Con un análisis similar para la ecuación (11) y teniendo en cuenta que la ecuación de estado para un fluido tipo radiación es Pym = Pym/3, se deduce que
La separación artificial del fluido total (pGal + Pym = Ptot), permite discernir cuál es el aporte al modelo de los dos términos de la acción asociados a los campos vectoriales. Ambos fluidos son de tipo radiación, pero uno es el comúnmente llamado fluido de Yang-Mills con densidad y presión positiva y el otro se denomina el fluido de los "Galileones vectoriales", el cual posee densidad y presión negativa.
Análisis del sistema dinámico
El análisis del sistema dinámico se lleva a cabo en dos etapas. En la primera etapa es necesario hallar los puntos críticos del sistema y observar cómo evoluciona el sistema dinámico en el tiempo sin considerar algún conjunto de condiciones iniciales en específico. En la segunda etapa es necesario hacer una detallada descripción del comportamiento de la solución cuando las condiciones iniciales se imponen cerca de los puntos críticos, ya que el sistema dinámico podría exhibir un comportamiento totalmente diferente en función de las características de los puntos críticos y las condiciones iniciales.
Comportamiento asintótico general y energía oscura
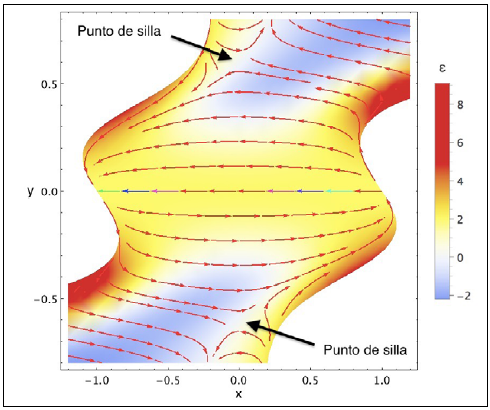
El análisis del espacio de fase (Figura 1) revela el siguiente comportamiento asintótico: si N -- ∞ entonces,
con
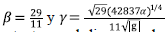 Las tres tendencias descritas anteriormente se ven reflejadas tanto en el diagrama de fase de la figura 1, como en las figuras 2a y 2b, donde también se observa dicho comportamiento asintótico. Al analizar las ecuaciones de evolución (13) para la variable "y" en su límite a tiempo infinito, se obtiene la ecuación diferencial, x' - x/β = 0.
Las tres tendencias descritas anteriormente se ven reflejadas tanto en el diagrama de fase de la figura 1, como en las figuras 2a y 2b, donde también se observa dicho comportamiento asintótico. Al analizar las ecuaciones de evolución (13) para la variable "y" en su límite a tiempo infinito, se obtiene la ecuación diferencial, x' - x/β = 0.
La solución a tal expresión es una exponencial creciente, lo que concuerda con el límite a tiempo infinito de la variable "x". Tal comportamiento hace que la magnitud de la densidad y presión de los dos fluidos artificiales (verfigura 2c) tiendan a infinito. Sin embargo, el sistema en su evolución posee un mecanismo de auto-ajuste fino, en donde ΩGal - ΩYM como se observa en la figura 2d; este hecho evita que la densidad y presión total de energía tiendan a infinito.
Si bien las densidades de energía de ambos fluidos artificiales tienden a ser de igual magnitud y de signos opuestos, el mecanismo de autoajuste fino permite que la densidad total de energía sea finita y diferente de cero. Para demostrarlo, primero se supone que la suma de las dos densidades de energía en mención es
pGal + PYM = Ptot (18)
donde Ptot tiene un valor real finito. Luego se reformula la ecuación de tal forma que
y por último se evalúa en el límite PGal → ∞, dando como resultado la relación entre densidades que se planteó inicialmente,
de esta manera ΩGal → Ωym, y la suma de ambas densidades es un valor finito diferente de cero.
El autoajuste fino posee además una característica importante que le permite describir un período del universo dominado por la energía oscura; si se observa detalladamente el diagrama de fase de la figura 1, se aprecia que a medida que la solución (flechas rojas) tiende al comportamiento asintótico (línea azul correspondiente a y = βx), el parámetro e tiende a cero, lo que implica ω = -1 propio de un universo dominado por la energía oscura. Esto ocurre para un amplio conjunto de condiciones iniciales.
Para reafirmar la información que brinda el diagrama de fase, se puede efectuar un análisis más detallado de la evolución de algunos parámetros. En el conjunto de gráficas que se muestran a continuación, se aprecian las diferentes variables y parámetros en función del tiempo, para un conjunto de condiciones iniciales específico. En la figura 2e se observa que el valor del parámetro de Hubble, H/mP ∞ y2/z2 se aproxima asintóticamente a su valor observado hoy en día, H0 = 9,03h x 10-61, siendo h = 0,678 ± 0,009 (Aghanim, et al., 2018). De otra parte, en la figura 2f se observa el valor del parámetro de estado del fluido de los Galileones vectoriales, el cual tiende a ωGal, → 1/3. Finalmente, en la figura 2g se observa cómo el parámetro de estado total se aproxima asintóticamente a ωtot = -1, representando, por tanto, a un universo en expansión acelerada.
Puntos críticos e inflación primordial
El sistema autónomo obtenido en este modelo, como cualquier otro sistema dinámico, posee puntos de equilibrio en los cuales la solución se comporta de manera diferente a la expuesta en la subsección anterior. Dependiendo de las condiciones iniciales que se impongan y de las propiedades específicas de los puntos de equilibrio, es posible caracterizar un período inflacionario transitorio, propicio para modelar la expansión acelerada primordial.
Al realizar un análisis de los puntos de estabilidad del sistema dinámico (Burton, 1994) descrito en la ecuación (13), se encontraron ocho en total; dos de ellos son descartados rápidamente porque son puntos que poseen al menos una variable adimensional compleja, es decir, un campo y con componente imaginaria. De los seis puntos críticos restantes, cuatro son de la forma, Xc = {xc, yc , zc) = (0, c, 0). Recordando la definición de las variables adimensionales (8), si y = cte y z = 0, entonces H → ∞ lo cual es inconsistente ya que la ecuación de Friedmann asocia directamente el parámetro de Hubble con la densidad de energía total, la cual debe ser finita. Finalmente, dos de los puntos críticos, siendo uno la imagen especular del otro ante una transformación y → -y, cumplen con los requerimientos necesarios para describir un período inflacionario de tipo rodadura lenta (Lyth & Liddle, 2009), lo cual implica cumplir las condiciones «
También se observa la recta y = βx (línea azul), y el valor del parámetro e en las diferentes regiones mediante un código de colores. Nótese que, con excepción de la pequeña región central, la recta y = βx concuerda con ϵ = 0.
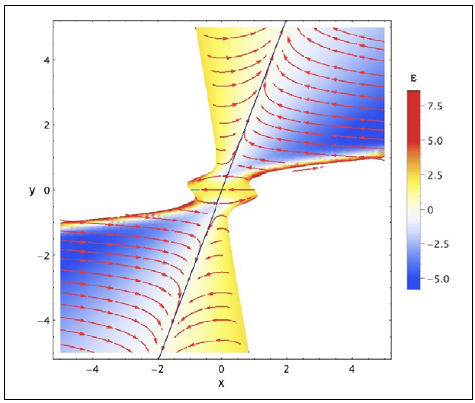
Figura 1 Diagrama de fase para un valor de a = 10-1 en donde se refleja la dinámica de la solución para las variables adimensionales x y y. También se observa la recta y = βx (línea azul), y el valor del parámetro ϵ en las diferentes regiones mediante un código de colores. Nótese que, con excepción de la pequeña región central, la recta y = βx concuerda con ϵ = 0.
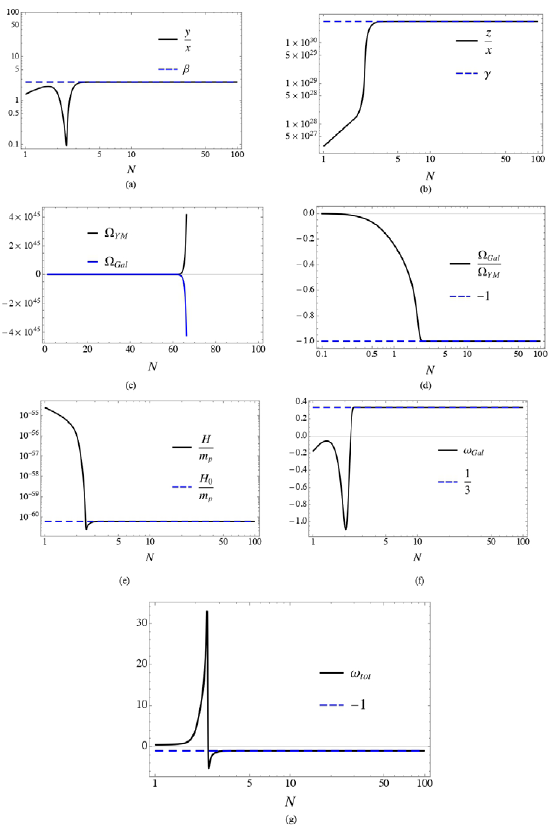
Figura 2 Solución numérica para la obtención de una era del universo dominada por la energía oscura con condiciones iniciales x0 = -1,0099, y0 = 0,01, z0 = 7 x 1024 y los parámetros a = 0,01 y g = -4,37 x 10-61. (a) Gráfica de y/x vs número de e-folds y su valor límite fi (línea discontinua). (b) Esta figura muestra el mismo análisis de la gráfica anterior, pero con la variable z/x y su límite y. (c) Gráfica de la densidad de los dos fluidos artificiales PYM y PGal tendiendo a œ y -œ respectivamente. (d) Esta gráfica comprueba el auto-ajuste fino QGal - -QYM el cual evita que QM - œ. (e) Gráfica del parámetro de Hubble tendiendo a su valor actual H0. (f) Esta gráfica demuestra que el fluido artificial QGal tiende a comportarse como un fluido tipo radiación, mGal = 1/3. (g) Gráfica del parámetro de estado del fluido total mtot indicando un período dominado por la energía oscura.
Sin embargo, es necesario que la inflación tenga una duración de al menos 68 e-folds para resolver los problemas clásicos de la cosmología estándar (Lyth & Liddle, 2009; Peter & Uzan, 2013). Ambos puntos críticos tipo silla, con condiciones iniciales muy precisas, logran el resultado esperado (tabla 1). Lamentablemente para el modelo, la duración de la era inflacionaria es altamente dependiente de las condiciones iniciales ya que un pequeño cambio en ellas hace que la duración del período inflacionario se reduzca drásticamente.
Al realizar un acercamiento al centro de la figura 1, es posible observar con detalle los puntos críticos tipo silla que posee el sistema dinámico (ver figura 3). Como se aprecia, los puntos señalados están asociados con un ϵ → 0; por lo tanto, con las condiciones iniciales apropiadas, la solución se mantendrá cerca al respectivo punto crítico, indicando un período de inflación primordial, para luego alejarse a otra región del diagrama, señalando la culminación de inflación y el inicio de un período del universo dominado por radiación, el cual se ve representado gráficamente por oscilaciones alrededor de la línea y = 0.
Nuevamente, un análisis detallado de los diferentes parámetros y variables del modelo permite complementar la información obtenida a partir del diagrama de fase. Primero, en las figuras 4ay4b se observa un comportamiento de Ψ y Ψ prácticamente constante en un rango superior a 70 e-folds, lo cual es consistente con las curvas de los parámetros de rodadura lenta, ϵ y η, presentadas en la figura 4c. También se aprecia en la figura 4d, un parámetro de Hubble cuya magnitud pertenece al régimen clásico en el cual está soportada la teoría ya que la magnitud de H(N) es mucho menor a la masa de Planck, la cual corresponde al límite entre la gravedad clásica y la gravedad cuántica. Finalmente, las figuras 4ey4f muestran la distribución de la energía total durante inflación, y las figuras 4gy4h confirman una presión negativa que genera expansión acelerada, además de un parámetro ωtot que tiende a 1/3, indicando un período de radiación después de inflación.
Tabla 1 Algunas propiedades fundamentales que los puntos críticos del sistema dinámico deben poseer para poder describir, de manera correcta, un período de expansión acelerada primordial. En ella se observa que dos de los ocho puntos críticos, siendo uno la imagen especular del otro ante una transformación y → -y, cumplen con los tres requisitos, siendo estos puntos críticos los que se señalan en el diagrama de fase de la figura 3.
| Puntos críticos | Coordenadas reales | H finito | Inflación prolongada |
| 1 | x | --- | |
| 2 | x | --- | |
| 3 | ✓ | x | --- |
| 4 | ✓ | x | --- |
| 5 | ✓ | x | --- |
| 6 | ✓ | x | --- |
| 7 | ✓ | ✓ | ✓ |
| 8 | ✓ | ✓ | ✓ |
En esta figura se aprecian mejor los puntos críticos tipo silla que dan lugar a la descripción de un período inflacionario.
Conclusiones
Si bien los campos escalares han sido la principal herramienta para modelar los períodos de expansión acelerada del universo, debido a su capacidad de preservar la homogeneidad e isotropía (Bennett, et al., 2013; Akrami, et al., 2019), se ha demostrado en este artículo que los Galileones vectoriales, específicamente los asociados al término L 4 1 también pueden ser de gran utilidad a la hora de describir un universo en expansión acelerada gracias al concepto de tríada cósmica (Armendariz-Picon, 2004). Una de sus características más importantes es que el período inflacionario obtenido se produce de manera natural sin necesidad de añadir términos que no tienen una explicación física convincente. Esto se debe a que uno de los fundamentos del modelo indica que la acción que describe inflación, al igual que cualquier acción que modela un fenómeno físico, debe estar libre de patologías y, por lo tanto, debe estar contenida en la acción de los Galileones. Tal principio complementado con un término cinético (Sym) y uno geométrico (Seh) dieron lugar a la acción de la teoría, descrita en la ecuación (6).
Al obtener las ecuaciones de campo a partir de la acción, se verificó que el sistema dinámico posee un comportamiento asintótico ideal para modelar el período de la energía oscura, debido a que es un período que actualmente consta de un inicio pero no de un final. Por otra parte, los puntos críticos tipo silla son perfectos para modelar inflación primordial ya que, al poseer un e ≈ 0, encajan con las características de tal época, y al ser inestables posibilitan que la dinámica de la solución describa un período inflacionario finito, cuyo final sea el inicio de una época dominada por la radiación.
A pesar de las virtudes descritas anteriormente, es importante recalcar que el auto-ajuste fino del sistema dinámico claramente no se aplica al caso de los puntos de silla, como se concluye de los diagramas de fase 1 y 3. Por lo tanto, el período de inflación primordial tendrá la duración adecuada para solucionar los problemas clásicos de la cosmología estándar siempre y cuando los valores iniciales para el sistema dinámico sean los adecuados.
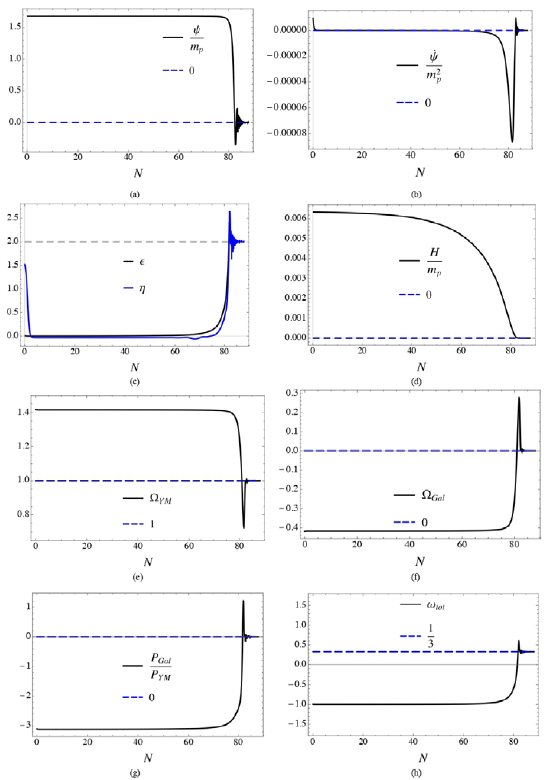
Figura 4 Solución numérica para modelar una época inflacionaria con condiciones iniciales x0 = 0.0011, y0 = 1.189, z0 = 14.911 y los parámetros a = 0.00649 y g = -0.0001. (a) Esta primera figura muestra cómo el módulo del campo vectorial "Ψ" se mantiene casi constante hasta los 80 e-folds, condición necesaria para una inflación de tipo rodadura lenta. (b) Esta figura muestra un comportamiento similar para Ψ y prácticamente con la misma duración de e-folds. (c) Esta figura muestra las funciones 𝜖(N) y η(N), ratificando lo planteado en la ecuación (21). (d) Esta figura muestra el parámetro de Hubble en función de N. (e) Gráfica de la densidad del fluido de Yang-Mills la cual al final de inflación corresponde al total de la densidad de energía, QYM=1. (f) Figura de la densidad del fluido del Galileón vectorial. (g) Relación entre presiones generadas por los dos fluidos artificiales. Se observa que la presión negativa de QGal es dominante durante la inflación a pesar de que la densidad del fluido de Yang-Mills es mayor. (h) Parámetro de estado del fluido total. Se aprecia que al final del período inflacionario ωtot = 1/3, ecuación de estado propia de un período dominado por la radiación.
Cabe aclarar que ésta es una nueva rama de investigación en cuanto a inflación cósmica se refiere; por lo tanto, es necesario seguir analizando el modelo para comprobar su efectividad. Hay que realizar un análisis más profundo al Hamiltoniano del sistema, ya que se debe verificar que realmente no posea ningún tipo de inestabilidades. También es importante examinar qué otros Lagrangianos se pueden incorporar al modelo y robustecerlo, incluso pudiendo lograr que la teoría sea compatible con los más recientes resultados relacionados con la rapidez de las ondas gravitacionales (Abbott, et al., 2017a, 2017b, 2017c).