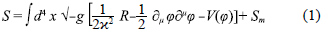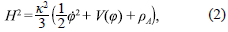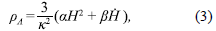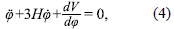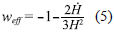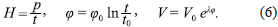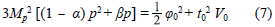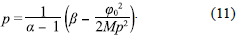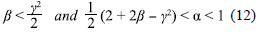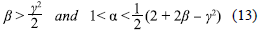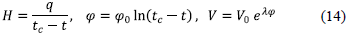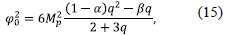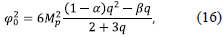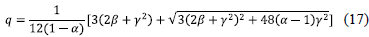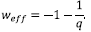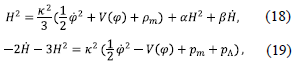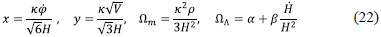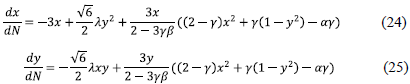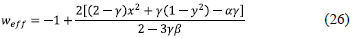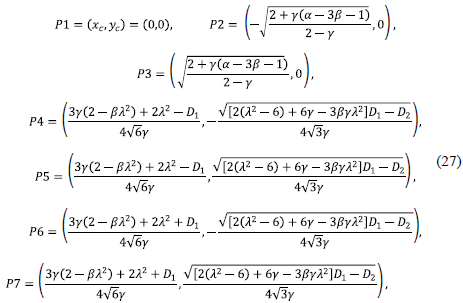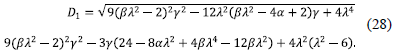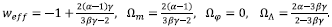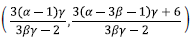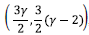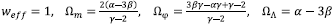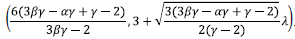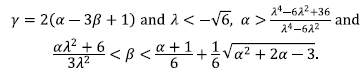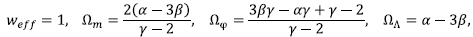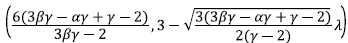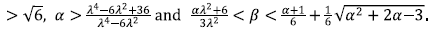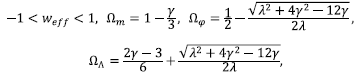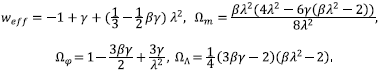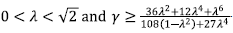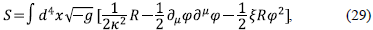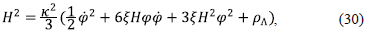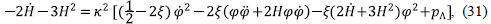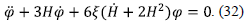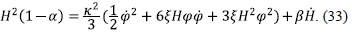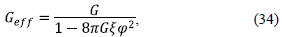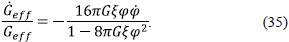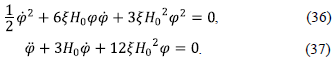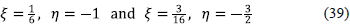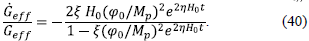Introduction
The current accelerated expansion of the universe (Riess, et al., 1998), (Perlmutter et al., 1998), (Kowalski, et al., 2008), (Hicken, et al., 2009), (Ade, et al., 2016), supposes a great challenge for the contemporary science. The source of this expansion, called dark energy, may consist of cosmological constant, conventionally associated with the energy of the vacuum or alternatively, could came from a dynamical varying scalar field at late times which also account for the missing energy density in the universe. In order to avoid the fine tuning and the coincidence problems, which relate to the inflationary behavior of the early universe and the late time dark energy dominated regime, the dark energy should have dynamical nature. This stimulates the interest in scalar fields that naturally arise in particle physics, including string theory, supergravity and generalized gravity theories such as the scalar tensor theories of gravity. So far a wide variety of scalar field models of dark energy have been proposed, including quintessence (Ratra and Peebles, 1988), k-essence (Armendariz, et al., 2000), tachyon (Padmanabhan and Choudhury, 2002), phantom (Caldwell, 2002), ghost condensate (Arkani-Hamed, et al., 2004) among others. The quintessence is an ordinary scalar field minimally coupled to gravity, with particular potentials that lead to late time accelerated expansion. The equation of state for spatially homogeneous scalar field satisfies the inequality w < -1, and therefore can produce accelerated expansion. According to the current observational data (Riess, et al., 1998), (Perlmutter, et al., 1998), (Kowalski, et al, 2008), (Hicken, et al., 2009), (Ade, et al., 2016), the dark energy equation of state could be in a narrow region below the cosmological constant divide w = -1, i. e. w < -1, indicating that accelerated expansion is going through a phantom phase. Therefore, the quintessence field may not be adequate to describe the state of accelerated expansion of the universe and models which allow the phantom phase seem more suitable.
Among the models of dark energy, especially interesting is the scalar field model non-minimally coupled to curvature, which normally arises in quantum field theory in curved space time (Ford, 19987, Birrell and Davis, 1982) or after compactification of higher dimensional gravity theories and in the context of string theories. These kinds of couplings have been proposed by many authors to address the dark energy problem since these couplings provide in principle a mechanism to evade the coincidence problem, allow phantom crossing in some cases (Perivolaropoulos, 2005). A dynamical system for non-minimally coupled scalar field was studied in (Sami, et al., 2012), and in (Granda and Jimenez, 2017, Granda and Jimenez, 2018), the autonomous system analysis was studied for models with non-minimal Gauss-Bonnet and non-minimal kinetic couplings respectively.
Another interesting approach to explain the nature of the dark energy is based on some facts of quantum gravity known as holographic principle ('t Hooft, 1993), (Susskind, 1994), (Bousso, 1999). This principle establishes a connection between the short distance (ultraviolet) cut-off and the long distance (infrared) cut-off, given by a restriction on the size of the system in such a manner that prevents the formation of black holes with size larger than the size of the system (Cohen, et al., 1999), (Hsu, 2004). Applied to the dark energy issue, if we take the whole universe into account, then the vacuum energy related to this holographic principle is viewed as dark energy, usually called holographic dark energy. Based on this principle, the proposal of holographic dark energy have been developed in (Cohen, et al., 1999), (Hsu, 2004), (Li, 2004). Different IR cut-off scales such as Hubble scale, particle horizon and event horizon have been proposed to establish the holographic dark energy models. The Hubble scale can not give rise to an accelerated universe (Hsu, 2004), while the event horizon can produce an accelerated expansion (Li, 2004), but has problem with causality. A Holographic density model that is free of causality problem can explain the coincidence problem was presented in (Granda and Oliveros, 2008), (Granda and Oliveros, 2008a).
In this work we consider the scalar field in the framework of the holographic principle as proposed in (Granda and Oliveros, 2008), with the holographic density as the background vacuum energy and analyze the possible accelerating regimes that could take place under the effect of a scalar field in the framework the holographic principle. The non-minimal coupling in the framework of holographic principle has been studied in (Ito, 2005) , (Setare and Saridakis, 2008). It should be said that such extension of the scalar field in the frame of holographic principle needs further theoretical foundation related with the microscopic nature of the vacuum energy.
The scalar field in the framework of the holographic principle
Let us consider the simplest model of non-minimally coupled scalar field with potential in the presence of holographic dark energy (vacuum energy). The action for the scalar field with matter in a general background is given by
where x 2 = 8ϖG, S m is the action for the matter fields which in the present case includes the usual baryonic and dark matter. Initially we consider the limit of dark energy dominance and neglect the baryonic and dark matter contribution. We are considering the flat Friedmann-Robertson-Walker (FRW) metric with signature (-,+,+,+). The Friedmann equation including the energy contribution from the holographic principle [40] is
where
and p A is the energy contribution from the holographic principle. The equation of motion for the scalar field is given by
and the effective equation of state resulting from the time evolution of this model is
Quintessence Solutions
To solve the equations (2) and (4), we can propose the following functions
Replacing these expressions in (2) it is found that under the restriction
λφ 0 = -2,
the following relation takes place (here we use ϰ 2= M p 2 )
And from the equation of motion (4) one finds
(3p - 1) φ0 2 - 2t0 2 V0 = 0. (8)
The last two equations give us the initial values and in terms of the parameters
φ0 2 = 2M2 p [(1 - α) p + β], (9)
and
t0 2V0= M2 p (3p - 1) [(1 - α)p + β]. (10)
The scalar field and the potential keep the same functional dependence on time as in the simplest case of the canonical scalar field on FRW background with the advantage, in the present case, that there exist phantom solutions (leading to BR singularities) without resorting to ghost degrees of freedom. Using the initial value φ0 one finds the power p as
In absence of scalar field this equation gives the usual restriction for accelerated expansion [40], β > α - 1, and with the scalar field the Eq. (11) gives more possibilities including negative values of p leading to super acceleration, depending on the relation between φ0 and Mp. Thus, the conditions for accelerated expansion (p > 1) take the form
or
where y = qJMp. Note that these conditions take place whether y is greater than or less than 1.
Big Rip solutions
Let's consider the following solutions
with q > 0, which lead to Big Rip singularity at t = tc. Replacing (14) in the Eqs. (2) and (4) one finds the same restriction, λ = -2/φ0, and the relations
and
and the expression for q in terms of φ0 is given by
where y = φ 0 /Mp. The effective equation of state from (5) takes the value
From (15) and (16) follows that, given q > 0, we don't need to resort to ghost degrees of freedom, since φ2 0 > 0 whenever (1 - α) q - β > 0, which implies that V0 > 0. Thus, the standard canonical scalar field in the vacuum background generated by the holographic principle can describe an accelerated expansion with EoS bellow the phantom divide, i.e.W eff < -1.
The matter contribution and critical points
In this case the cosmological equations take the form
with the scalar potential given by
V = V0еiφ (20)
where p m and p m are the density and pressure of the matter contribution respectively (baryonic and dark matter), pA is the pressure corresponding to the vacuum energy. Both type of energy contributions are modeled by ideal fluids that obey the independent continuity equations
p m + 3H(p m + p m ) = 0, p A + 3H (p A +p A ) = 0 (21)
additionally, we have the equation of motion for the scalar field given by (4) which is not independent of (18) and (19). Here we assume that the equation of state for matter, w m = pm/pm is constant, which allows the integration of the conservation equation, giving pm = Pm0 a-3(1 + W m ). To understand some dynamical properties of the model we will consider the autonomous system and analyze the properties of the critical points. The dynamical variables can be deduced from (18) and will be defined as
which lead to the following restriction from Eq. (18)
x 2 + y2 + Ωm.+ ΩA = 1 (23)
and from Eqs. (4), (19) and (21), it is straightforward to derive the following equations
where N = ln a is the slow-roll variable and y = 1 + Wm. Note that if one sets α = β = 0, then the Eqs. (21)-(25) reduce to the autonomous system for the uncoupled quintessence scalar [33]. The effective equation of state is given by
The following are the fixed points of the dynamical system (23)-(25).
where
By setting a = β = 0 we recover the critical points corresponding to the minimally coupled scalar field. The critical points characterize different cosmological scenarios, depending on the parameters, α β, y, λ. Here we illustrate some cases that involve the effects of the holographic density:
The point PI:
The corresponding eigenvalues are
If we take a = 1, then w eff = -1 and Ωm = 0. Then the energy becomes dominated by the holographic component and the point is a de Sitter solution with eigenvalues (0,-3), which corresponds to marginally stable fixed point. On the other hand, if we take a = 3βy/2, then Weff = y - 1 = w m with the energy density dominated by matter Ωm = 1, and eigenvalues
which corresponds to a saddle point for 0 < y < 2. The case a = β = 0, which corresponds to the standad quintessence scalar, gives the known matter dominated solution
(Ωm = 1) with w
eff
= w
m
[33]. In this last case the eigenvalues become
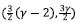 giving a saddle point for 1 < y < 2 . The de Sitter solution in this point is due to the holographic component.
giving a saddle point for 1 < y < 2 . The de Sitter solution in this point is due to the holographic component.
The point P2:
The eigenvalues are
If we take a = 3β, then Ωm = 0 and the solution becomes dominated by the scalar field (Q
φ
= 1) and is stable only under the conditions
λ < -
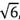 > β,
> β,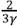 < y<2. Note that w
eff
= 1 for any value of the parameters, including the case of the quintessence scalar field corresponding to a = β = 0 (P2 = (-1,0), giving also Ωm = 0), with the eigenvalues given by (-3(Y -2), 3 +
< y<2. Note that w
eff
= 1 for any value of the parameters, including the case of the quintessence scalar field corresponding to a = β = 0 (P2 = (-1,0), giving also Ωm = 0), with the eigenvalues given by (-3(Y -2), 3 + 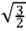 λ), which lead to unstable (λ > -6) or saddle point (λ < -6) for 0 < y < 2. The difference between these two cases is that the inclusion of the holographic component can lead to stable fixed point. There is also a stable solution dominated by matter (Ωm = 1, Ω
φ
+ ΩA = 0) if one sets
λ), which lead to unstable (λ > -6) or saddle point (λ < -6) for 0 < y < 2. The difference between these two cases is that the inclusion of the holographic component can lead to stable fixed point. There is also a stable solution dominated by matter (Ωm = 1, Ω
φ
+ ΩA = 0) if one sets
In this case the scalar field and holographic contribution cancel each other, which is not of interest since one of these density parameters should be negative.
The point P3: his point gives the same results
with eigenvalues
and the stability for the scalar field dominated solution is reached under the conditions,
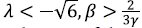 0< y<2. The quintessence case (α = β = 0), giving P3= (1,0)) is unstable for λ <
0< y<2. The quintessence case (α = β = 0), giving P3= (1,0)) is unstable for λ <
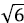 and saddle for λ >
and saddle for λ >
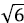 , given that 0 < y < 2. The matter dominated solution that takes place for y = 2 (α- 3β + 1), is stable under the restrictions
, given that 0 < y < 2. The matter dominated solution that takes place for y = 2 (α- 3β + 1), is stable under the restrictions
The point P4: First we note that for the case , and independently of the other parameters (β, y, λ), w
eff
= -1 and Ω
m
= 0, Ω
φ
= 0, ΩA = 1. Due to its complexity to calculate the eigenvalues, we analyzed the case y = 1, and have found that the point is an attractor if
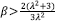 for any λ ≠ 0. This de Sitter attractor is due exclusively to the holographic component. For the quintessence scalar field a = β = 0, the fixed point takes the values
for any λ ≠ 0. This de Sitter attractor is due exclusively to the holographic component. For the quintessence scalar field a = β = 0, the fixed point takes the values
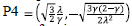 giving the stable scaling solution with w
eff
= w
m
for λ2 > 3y. One case of quintessence solution takes place if one sets α = β = 2/λ2. In this case we find
giving the stable scaling solution with w
eff
= w
m
for λ2 > 3y. One case of quintessence solution takes place if one sets α = β = 2/λ2. In this case we find
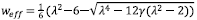 with
with
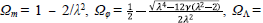
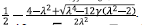 This point is an attractor with 0 < Ωm, Ω
φ
, ΩA < 1 and -1 < w
eff
< 0 if
This point is an attractor with 0 < Ωm, Ω
φ
, ΩA < 1 and -1 < w
eff
< 0 if
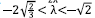 and 0 < y < λ2/3. Another stable quintessence solution is obtained by taking a = y/3 and β = 2/λ2, giving
and 0 < y < λ2/3. Another stable quintessence solution is obtained by taking a = y/3 and β = 2/λ2, giving
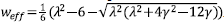 . This point is an attractor with
. This point is an attractor with
where all the density parameters are in the interval 0 < Ωm, Ω
9
, Ω
A
< 1 whenever
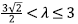 and
and
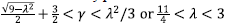 and
and
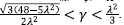
The point P5 as in the case of the point P4 contains a de Sitter attractor (w eff = -1) dominated by the holographic component (Ωa = 1) for a = 1, and the stability results from the restriction y = 1 and β > 2/3 (λ2 + 3) for any λ ≠ 0. This critical point contains also the quintessence solutions described for the point P4 with the same stability properties.
The point P6: For the scalar quintessence field, taking a = β = 0, this critical point takes the values
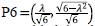 and becomes stable node dominated by the scalar field with w
eff
= -1 + λ2 /3, provided that λ <
and becomes stable node dominated by the scalar field with w
eff
= -1 + λ2 /3, provided that λ <
 and y > λ2 /3. By setting α = 1 in this point we find
and y > λ2 /3. By setting α = 1 in this point we find
This point satisfies all the conditions for an attractor solution with accelerated expansion, but the analytical expression for the conditions on the parameters are very large and we limit ourselves here to the two numerical examples: taking λ =
 , β = 0.9, y = 1.05, it is found w
eff
= -0.785, Ωm = 0.18, Ω
φ
= 0.11 and Ωa = 0.71. Taking λ = 3
, β = 0.9, y = 1.05, it is found w
eff
= -0.785, Ωm = 0.18, Ω
φ
= 0.11 and Ωa = 0.71. Taking λ = 3 , β = 0.7, y = 1.065, one finds w
eff
= -0.999, Ω
m
= 0.0007, Ω
φ
= 0.00008 and ΩA = 0.999. The above expressions for the main physical parameters simplify if one sets β = 2/λ
2
. In this case we obtain
, β = 0.7, y = 1.065, one finds w
eff
= -0.999, Ω
m
= 0.0007, Ω
φ
= 0.00008 and ΩA = 0.999. The above expressions for the main physical parameters simplify if one sets β = 2/λ
2
. In this case we obtain
w eff = -1 + λ2/3, Ω m = 0, Ω φ = 1, ΩA = 0
This scalar field dominated critical point is an attractor if
By taking a = 1 and
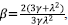 this point gives a de Sitter saddle point dominated by the holographic component (ΩA = 1, Ω
m
= 0, Ω
φ
= 0) with eigenvalues (-3,0).
this point gives a de Sitter saddle point dominated by the holographic component (ΩA = 1, Ω
m
= 0, Ω
φ
= 0) with eigenvalues (-3,0).
The point P7 presents the same properties as the point P6, leading to stable de Sitter and quintessence attractors.
Non-minimal coupling in the framework of the holographic principle
Here we assume the generalization of the holographic principle in the presence of non-minimally coupled scalar field. Let us start with the following action for a dark energy dominated universe
Variation with respect to the metric, and assuming that the scalar field <p has only time dependence, gives the following modified Friedman Eqs. in the flat FRW background [44, 45].
which corresponds to the (00) component of the variation with respect to the metric, and for the (11) component it is obtained
where H is the Hubble parameter, and Pa, Pa are the energy density and pressure of the holographic dark energy. The equation of motion of the scalar field is the modified Klein-Gordon equation
Replacing the holographic density (3) in (3), leads to the following Friedmann equation
Although the above equations may include the potential, in this case we show that the effect of accelerated expansion can be obtained without the need to introduce a potential. Due to the non-minimal coupling from (30), the effective gravitational coupling can be expressed as
where G is the constant Newtonian coupling. The relative time variation of the gravitational coupling, obtained from (34) is given by
An appropriate solution of the equations (32) and (33) should give the relative variation of the gravitational coupling consistent with current observational bounds.
The equation (33) simplifies under the restriction a = 1, and has an exact solution for the scalar field for H = H0 = const., corresponding to de Sitter expansion with w eff = -1.
Setting a = 1 and H = H0 the equations (32) and (33) become
If one assumes the scalar field of the form
then, the Eqs. (36) and (37) have two solutions corresponding to
Of special interest is the solution with ξ = 1/6 corresponding to the conformal coupling of the scalar field. This de Sitter solution is not possible in absence of the holographic energy density. So, the non-minimally coupled scalar field in the framework of the holographic energy density can produce the same effect as the cosmological constant, leading to a de Sitter expansion when the coupling constant takes the conformal value ξ = 1/6 and the scalar field evolves as φ = φ0eηHot.
For the solution (38), and using Eq. (35) we find the current value of
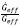 as
as
Here we used
8ϖG=
M-2
p
(M
p
is the Planck mass) and H0 is the current value of the Hubble parameter. For the case of the conformal coupling (ξ= 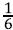 , η =-1), if we take φ0
/M
p
≃10-3 and t ~ H
0
-1
, then the relative variation of
, η =-1), if we take φ0
/M
p
≃10-3 and t ~ H
0
-1
, then the relative variation of
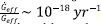 the gravitational coupling is of the order of , clearly satisfying the observational bounds.
the gravitational coupling is of the order of , clearly satisfying the observational bounds.
Discussion
In the present work we considered the usual canonical minimally coupled scalar field with an additional source, given by the vacuum energy, modeled by the holographic density (Granda and Oliveros, 2008). It was found that, under exponential potential, in the vacuum background generated by the holographic principle, the model admits the same solutions of the minimally coupled scalar field for the power-law expansion, with the advantage that in the present case additionally appear phantom solutions (leading to future Big Rip singularities) without resorting to ghost degrees of freedom. In presence of matter with constant equation of state wm, the model presents a rich variety of critical points that give de Sitter attractors, stable quintessence solutions and saddle points. Thus for instance, the point P1 contains a de Sitter solution dominated by the holographic component, with marginal stability due to the eigenvalues (0,-3). This point also contains matter dominated solution with w eff = wm which is a saddle point as in the case of absence of the holographic component. The point P4 contains a de Sitter attractor dominated by the holographic component, and also contains stable quintessence (-1 < w eff < 0) solutions where all the energy components contribute.
The point P6 contains attractor solutions with accelerated expansion where the different components can give contributions to the energy density, and also contains a scalar field dominated solution which is a stable node with accelerated expansion. The de Sitter solution for this critical point is dominated by the holographic component and is a marginally stable fixed point with eigenvalues (-3, 0). These results show that the phase space of the autonomous system is richer than in the case of minimally coupled scalar field, giving rise to more accelerated expansion scenarios.
In the case of non-minimally coupled scalar field, the holographic dark energy as given by (3), leads to interesting late time cosmological scenario: the model behaves as the cosmological constant, giving an exact de Sitter solution with dynamically evolving scalar field and without potential in the conformal coupling ξ= 1/6) regime.
It is worth doing a further analysis of the dynamical system for the scalar field with non-minimal coupling, in the framework of the holographic principle, to study its critical points and check if there are critical points with phantom behavior since, according to current observations, the equation of state of the dark energy could be below the cosmological constant divide. It would be also of interest to analyze the dynamical system of the scalar field, model (1)-(3), with a potential different from exponential, for instance with power-law potential.