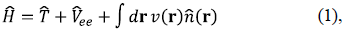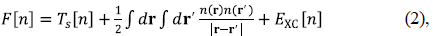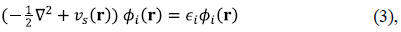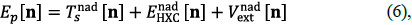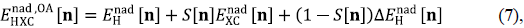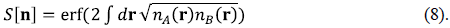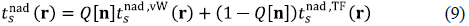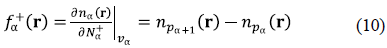English (pdf)
Article in xml format
Article references
Automatic translation
Send this article by e-mail
Cited by SciELO 
Cited by Google 
Similars in
SciELO 
Similars in Google 
Permalink
Introduction
"What is the shape of atoms in molecules?" is a question without an answer. Atoms in molecules do not have a real, independent existence. When we say that a water molecule has two hydrogen atoms and one oxygen atom, what we mean is that an appropriate supply of energy can split the molecule into these three atoms. Each of these atoms, when isolated, is spherical, but the ground-state electronic density of the water molecule is not simply the sum of three spheres. However, it is approximately equal to the sum of three spheres (Figure 1) and can be written exactly as the sum of three distorted spheres. Thus, the question of the title may be vague, but it is not meaningless. All molecular information (i.e., what makes a molecule different from the simple sum of its isolated constituents) is coded into a set of atomic density distortions.
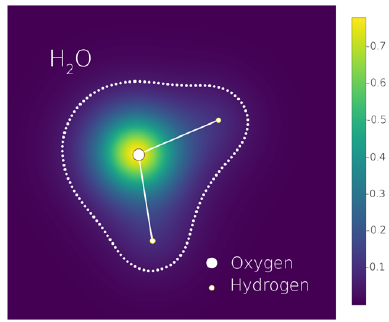
Figure 1 Ground state density of a water molecule on the plane of the three atoms. Calculated using Psi4 (Smith, et aL, 2018) (Parrish, et al, 2017) with CCSD(T)/UGBS. The dotted line indicates a density iso-contour.
There is no unique way of defining these atomic density distortions. In fact, there are infinitely many ways in which one can decompose a given molecular density n (r) into the sum of atomic-like functions n α (r) (here we use the subscript a to label atoms). For example, Bader's partitioning (Bader, 1990) based on the topology of the electron density is a popular choice with merits and limitations that have been amply discussed (Nalewajski, et al., 2000). In spite of the many possible definitions of atomic densities, there is a unique set of densities {nα (r)} that sum up to n (r) while minimizing the sum of the atomic energies. It is this special set of densities to which we turn our attention in this article.
The density functional theory (DFT) (Hohenberg & Kohn, 1964; Kohn & Sham, 1965) establishes that any electronic property P of a molecule is a functional of its ground-state electronic density P = P[n]. The uniqueness of the set {nα (r)} for a given density allows one to understand molecular properties, in principle, as functionals P = P[{na (r)}] of that set. Decades of research in DFT have taught us how the total density n (r) can be used as the main variable in molecular calculations, as explained briefly in Section II. Our group is investigating how the atomic densities, as opposed to the total molecular density, may be used as the main variables, which we discuss in Section III. This change of perspective has advantages and disadvantages. The most obvious advantage is a significant lowering of the computational cost of the calculations because instead of having to solve the N-electron Schrödinger equation (a second-order differential equation on 3N coupled variables), only a small number of independent equations has to be solved, each for less than N electrons. A second advantage will be explained and illustrated in Section IV: By focusing on atomic densities rather than on total molecular densities, one can fix pervasive errors of density functional approximations and significantly improve the accuracy of certain calculations. A third advantage will be discussed in Section V: The chemical reactivity between two atoms or molecular fragments that approach each other is best described in a theory that employs atomic (or fragment) densities as the main variables. On the downside, many of the theorems and techniques that have been explored over the last six decades to describe molecular systems are not directly applicable to the new set of variables, so entirely new methods and approximations need to be developed. A growing community of researchers working under the umbrella of embedding methods (Jacob & Neugebauer, 2014; Lee, et al., 2019; Sun & Chan, 2015; Nafziger & Wasserman, 2015; Niffenegger, et al, 2019) are pursuing this direction. We highlight here some of the recent developments.
The molecular density as the main variable
In the world of quantum chemistry, one is normally concerned with electronic hamiltonians given within the Born-Oppeheimer approximation by:
where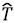 
is the kinetic energy operator for N electrons, 
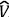ee the electron-electron repulsion operator, v(r) the attractive potential generated by the nuclei, and 
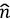(r) the density operator. The expectation value of the latter in the N-electron ground state v|/ is the density n(r) = ⟨Ψ| (r) | Ψ⟩, but an accurate, explicit representation of Ψ is unachievable for all but the smallest systems. Ground-breaking work by Kohn, et al. (Hohenberg & Kohn, 1964; Kohn & Sham, 1965) showed that it is possible to construct a theory that completely circumvents the calculation of Ψ so that any property, such as the ground-state energy E = ⟨Ψ|
|Ψ⟩ can be calculated as a functional of the density. The functional E[n] is normally split into the contribution from the nuclear potential ∫ drn (r) v(r), and a universal functional F[n] independent of v(r). In Kohn-Sham-DFT (KS-DFT), the most common formulation of DFT, the functional F[n], is decomposed as:
where T s [n] is the kinetic energy for an auxiliary system of non-interacting electrons with density n(r), the second term is the Hartree energy, and E XC [n] is the exchange-correlation (XC) energy functional, the only quantity that needs to be approximated in practical calculations. We sometimes combine the Hartree and the XC-contributions into one functional, E HXC [n], whose derivative with respect to the density is a potential, v HXC (r) = δE HXC [n]/δn(r). What one solves in practice are the KS equations:
with vs(r)= v(r) + v HXC (r) leading to ∑i|Φi(r)|2 = n(r) where the sum goes over the occupied orbitals Φi(r). An ample literature exists documenting the successes and failures of different approximations to E XC [n]. We point the reader to recent reviews (Pribram-Jones, et al., 2015; Wasserman, et al., 2017; Yang, 2012) and stress that some of the most pervasive failures of approximate KS-DFT appear when stretching chemical bonds (Dutoi, et al., 2016; Makmal, et al., 2011; Komsa & Staroverov, et al., 2016). The large errors observed in these cases encompass both fractional-charge (or delocalization) and fractional-spin (or static correlation) errors (Cohen, et al., 2008a; Cohen, et al., 2008b; Mori-Sánchez, et al., 2008), which are ultimately due to the inability of the approximate XC-functionals to reduce the molecular density to the correct atomic densities (or spin-densities) when bonds are stretched. We illustrate both types of errors below for the local density approximation (LDA), the simplest and earliest approximation for E XC [n] on which the modern ladder of approximations is built (Perdew, et al., 2001).
Fractional-charge error
Consider stretching H + 2 The true ground-state density has left-right symmetry, with 72 electron on the left atom and 1/2 electron on the right atom. The physical state at infinite separation must break this symmetry and produce a neutral hydrogen atom on one side and a bare proton on the other. Both solutions (broken-symmetry and symmetric) should, therefore, have the same energy at infinite separation, but this feature is not achieved by the LDA or other approximations built upon it. The LDA energy of an H atom with half an electron is much lower than what it should be (half the energy of infinitely stretched H + 2), which leads to the incorrect binding shown in dashed pink in figure 2.
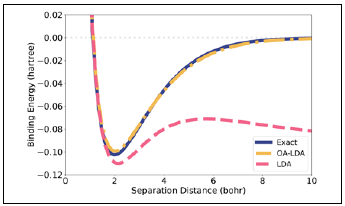
Figure 2 Electronic binding energy of H 2 . Exact (solid, blue), KS-LDA (dashed, pink), and OA-LDA(dash-dotted, yellow) from (Nafziger, 2015), as explained in Sec.IV.
Fractional-spin error
Now consider stretching neutral H2. The issues of the previous paragraph are no longer a problem because each atom has exactly one electron at infinite separation. However, an analogous problem arises for fractional spins. The true-ground state of H2 is spin unpolarized and must remain so at very large separations in the absence of environmental perturbations. Yet, an isolated H atom is spin-polarized so the energy of two spin-polarized H atoms should be identical to that of two spin-unpolarized H atoms (each having half-spin up, half-spin down). This condition is again violated by the LDA leading to the significant overestimation of the binding as shown in dashed pink in figure 3.
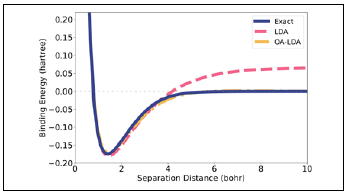
Figure 3 Electronic binding energy of H 2 . Exact (solid, blue), KS-LDA (dashed, pink), and OA-LDA (dash-dotted, yellow) from (Nafziger&Wasserman, 2015), as explained in Sec.IV
These errors, illustrated here for the two simplest open-shell and closed-shell molecules, are ubiquitous in quantum chemistry. Every time a bond is stretched, as in transition states along chemical reactions, a combination of these errors can creep into and contaminate the DFT calculations. Cancellation between the two errors can occur sometimes (note they have opposite signs) and lead to accidentally accurate results for complex systems, but predicting such cancellations is generally extremely difficult and not something DFT users want to or should rely on. Results from approximate KS-DFT calculations are thus often suspect. A theory that uses atomic densities as the main variables, as opposed to the total molecular density, has the potential to fix such errors. Furthermore, it has the potential to provide information about individual atomic density distortions along with a chemical insight into the reactivity of individual fragments.
Atomic densities as the main variables
As mentioned in the Introduction, there is a unique set of atomic densities {n α (r)} that minimizes E f =∑α E α [nα] while satisfying the density constraint:
The atomic energies E α [n α ] in the above definition of E f are not true ground-state energies but rather given by E α [n α ]= F [n α ] + ∫ d r v α (r) n α (r), where v α (r) is the α-atomic potential. The constraint of Equation (4) prevents nα(r) from being the ground-state density of the corresponding v α (r). However, each of the n α (r) can be shown to be the ensemble ground-state density of vα(r) + v p (r), where v p (r) is a unique a-independent potential. More specifically, the partition potential theorem (PPT) (Cohen & Wasserman, 2006) establishes the following: If a molecular potential v(r) is decomposed into atomic potentials {v α (r)}, i.e. v(r) = ∑ α v α (r), then, for a set of fragment occupations {n α } there is a unique local potential v p (r) such that, when added to the individual v α (r)'s, leads to ensemble ground-state densities {n α } summing up to the correct total density n(r).
Simple Illustration of the PPT
Figure 4 provides the simplest illustration of this theorem. Consider first one electron moving in the ID-potential v 1 (x) (dotted grey line in the middle panel). Its ground-state density, when isolated, is n1 (0) (x) (dotted orange line in the upper panel). Similarly, one electron in v 1 (x) has density n 2 (0) (x). Now consider two non-interacting electrons in the double-well potential v(x) = v 1 (x) + v 2 (x) (dashed yellow line in the middle panel). The density of this system, n(x), is not equal to n(0)(x) = n1 (0)(x) + n2 (0)(x), but it is close to it: n(x) ≈ n(0)(x), especially if v1(x) overlaps weakly with v2(x). The PPT establishes that there is only one potential vp(x) (purple line in the middle panel) such that, when added separately to v 1 (x) (blue line in the lower panel) and v 2 (x), leads to ground-state densities n 1 (x) (blue line in the upper panel) and n2(x) that differ from n 1 (0) (x) and n2 (0)(x) in just the right way, so that n1(x) + n2(x) = n(x). The theorem applies to any number of interacting electrons in 3D and to any number of fragments (Cohen & Wasserman, 2006).
The algorithm to calculate v p (r)
Several algorithms have been developed to solve the constrained optimization problem involved in calculating vp(r) (i.e., minimizing E f [n α ] under the constraint of Equation (4)). The algorithm described here is perhaps conceptually the simplest:
Choose an approximation for E XC [n], solve the KS equations in Equation (3) for the isolated atoms, and find their self-consistent densities (na (0)(r)} and corresponding KS-potentials {v 0 s,α(r)}.
Build an approximate molecular density as n(0) (r) ≈ ∑a n a (0) (r).
Invert the KS equations to find the effective KS-potential vs (0)(r) corresponding to n(0) (r). For the exact density, this potential would be identical to v (r) + v HXC (r), but for the approximate density it is not. The difference between the two, therefore, can be used as a correction to generate an improved atomic KS potential
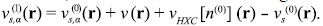
Solve the KS equations for the atoms again with the improved atomic KS potential and repeat until self-consistency is achieved. If convergence is achieved after iterating k times, then the atomic KS potentials vs,α ®(r) are given by vα(r) + vp(r) + v HXC [nα (k-1)\(r). The partition potential emerges as an α-independent piece to be added to the a-nuclear potential.
Just as for the model system of figure 4, the main feature of vp(r) in real diatomic molecules is an attractive well in between the nuclei. The presence of this well distorts the density of each isolated atom by pulling it toward the bonding region. There are generally also positive plateaus in vp(r) due to kinetic effects (Nafziger & Wasserman, 2014) (contributions from the functional derivatives of T s [nα]) and a singularity at the nuclei whose strength is proportional to the value of the density of one atom at the location of the other (Nafziger & Wasserman, 2014), modifying the isolated-atom density of the nuclei according to Kato's cusp condition. This is our partial response to the question without an answer: "The shape of atoms in molecules is determined by vp(r)."
Although we exemplify the use of Partition-DFT with systems composed of two atoms, it must be noted that the framework is not limited to atomic densities. Any meaningful fragmentation can be applied, such as individual molecules in dimers or functional groups. This selective fragmentation not only has conceptual benefits but also computational because it allows regions to be treated with different levels of theory so that the most reactive regions are calculated using higher-level methods, as is the common practice in WFT-in-DFT embedding (Lee, et al., 2019). This is consistent with the goal of the theory to lower the computational cost while still accurately describing the relevant properties of a larger system.
Fixing errors of approximate XC-functionals
Now define the partition energy E p as the difference between the total energy E and the sum of atomic energies E f Using a bold n(r) to denote the set of atomic densities, n(r) = {nα (r)},
with the KS energy-decomposition of Equation (2), the partition energy is given by:
where the "nad" superscript is used to indicate nonadditive quantities, i.e., the difference between the total and the sum of the fragments. Thus, Ts nad[n] = T s [n] - ∑ α T s [n α ], E nad HXC [n]= EHxc [n] _ ∑α EHXC [nα], and the last term stands for the non-additive external (nuclear) energy given by v nad ext [n]= ∫ drn(r)v(r) - ∑α ∫ drn α (r)v a (r). We have again combined the non-additive exchange-correlation and Hartree terms of Equation (2) into E nad HXC .For a given approximation to E XC [n], the algorithm described in the previous section exactly reproduces the results of the corresponding KS calculation including all of its errors. It can be seen (Elliot, et al., 2010) that the partition potential is the functional derivative of the partition energy with respect to any of the atomic densities at the minimum. Since v nad ext [n] is known exactly, the key to improving over Kohn-Sham is to propose adequate approximations for the other two components of Equation (6), T s nad [n] and E nad HXC [n]. We discuss each of these separately.
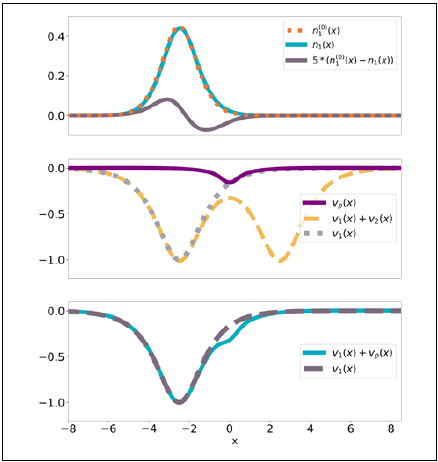
Figure 4 Graphic example of simplest PPT case for 2 non-interacting electrons in 1D potentials of the form v1.2(x) = cosh-2 (x ± a), with a = 2.5. Upper panel: The gray line magnifies the atomic-density distortion n 1 (x) - n 1 (x) 0 by a factor of 5 to highlight what occurs upon formation of the chemical bond: The density of the isolated atom is pulled towards the bonding region. Middle panel: Left atomic potential v1(x) (dotted), total 'molecular potential' (dashed), and partition potential (solid, purple). Bottom panel: Comparison of the isolated atomic potential v1(x) and the effective potential v 1 (x) + v p (x) for which the polarized density n 1 (x) is a ground-state density.
Approximating Enad HXC[n]
The origin of common errors of approximate XC functionals is well understood especially for homonuclear diatomic molecules (Cohen, et al., 2008b) (see discussion above for H2 and H2 +). For these and other molecules composed of two fragments, A and B, we have shown how a simple overlap approximation (OA) to E nad HXC [n] can fix both errors simultaneously (Nafziger & Wasserman, 2015), a result that no approximate XC functional can achieve with comparable accuracy within KS-DFT. The OA is defined by:
where S[ n ] is a measure of the overlap between the two atomic densities:
The term ∆E nad H [n] in Eq.(7) is a correction to the non-additive Hartree contribution, so that both fractional-charge and fractional-spin errors are suppressed as the molecule is stretched (Nafziger & Wasserman, 2015). The results shown in yellow in figure 2 and labeled "OA-LDA" go a step further (Nafziger, 2015) and replace E nad HXC [n] in Equation (7) by the non-additive exact-exchange functional canceling completely the self-interaction error and leading to the exact E p [n] in this case. The only deviation from the exact binding here is due to the effect that the slightly incorrect LDA fragment densities have on Ep[n]. We stress that the correct energy is obtained here as the molecule is stretched without symmetry breaking: The ground state of H2 + retains left-right symmetry and the ground-state of H2 + remains a spin-singlet throughout the entire range of separations. This is a proof-of-principle demonstration that it is possible to use a simple functional of the density for the atoms (not for the molecule) while approximating E nad HXC [n] to fix the underlying errors due to fragmentation. The route is complementary to the efforts of many others to develop sophisticated XC-functionals of the total density (Hedge, 2017; Mardirossian & Head-Gordon, 2017; Sun, et al., 2015; Yu, et al., 2016; Zhang, 2018).
Approximating E nad s[n]
Even with a robust and accurate functional for E nad HXC [n] (based perhaps on future generalizations of the OA), an explicit approximation for T s nad [n] is needed if one wants to reach the goal of linear-scaling calculations. Step 3 of the algorithm described in Section III relies on iterative inversions that make the method computationally impractical (at least, not more efficient than regular KS-DFT). The most obvious way to avoid such inversions is by resorting to orbital-free DFT (OF-DFT) (Chen, et al., 2016) and approximate T s nad [n] as an explicit functional of the set of atomic densities. Kinetic-energy functionals are famously difficult to approximate and state-of-the-art functionals are still far from reaching chemical accuracy, but we are looking for approximations to the non-additive part of T s [n], which is altogether a different challenge. The non-interacting kinetic energies for the atoms are still calculated exactly via orbitals and we wish to approximate the much smaller T s nad [n]. Recent work shows that this approach is promising. For example, writing T s nad [n] = ∫ drn(r)ts nad (r), an expression for the non-additive kinetic energy density t s nad (r) of the type
has been shown (Jiang, et al., 2018) to provide an excellent approximation to the exact T s nad in covalent o-bonds. In Equation (9), T s nad,vw (r) is the von Weizsäcker kinetic-energy density (Weizsäcker, 1935), which is exact for one-orbital systems, T nad,TF s (r) is the Thomas-Fermi kinetic-energy density (Fermi, 1927; Thomas, 1927), exact for uniform-density systems, and Q[n] is a switching functional whose role is analogous to that of S[n] in Equation (7), as described in detail in Jiang, et al, 2018. It determines the spatial regions where a one-orbital description should dominate.
Embedding methods provide the most promising route to truly calculate ab-initio electronic structures of large, complex, molecular systems (Yao, et al., 2019; Lee, et al., 2019; Mi&Pavanello, 2020). Although Partition-DFT has been applied so far only to model systems (Elliot, et al, 2010), diatomic molecules (Nafziger & Wasserman, 2014) and small hydrogen-bonded clusters (Gómez, et al., 2017; Gómez, et al., 2019), an ongoing implementation into the Psi4 package (Chávez, et al., 2020) will allow more for more widespread application. An accurate and explicit functional of the fragment densities for T nad s [n] will make Partition-DFT amenable to linear scaling implementations and, thus, applicable to systems of ever-larger complexity.
Towards a quantum theory of chemical reactivity
We glossed over one key feature of the PPT of Section III. The minimization of E f [n] is performed under the constraint that the nα(r) add to n(r) without individual normalization constraints for the atomic densities. The na(r) can integrate to fractional numbers of electrons N a as long as the total density integrates to the correct number of electrons, i.e., ∑α N α = N. A sensible interpretation of fractional number densities is provided by an ensemble description where the fractional number arises as an ensemble average over integer-number components. One result of the extension of DFT for fractional electron numbers (Perdew, et al., 1982) is that for N α between the integers p α and pα+1, the minimizing density (for the exact E XC ) is given by nα(r) = (1- ω α ) n pα (r) + ω α n pα+1 (r), where 0 ≤ ω α ≤ 1. The minimization of E f [n] is to be performed over the set of the {m α } leading to possibly fractional-number densities. One immediate advantage of such fractional densities is that chemical reactivity indices involving derivatives of various properties with respect to the electron number become sharply defined for the atoms (Geerlings, et al., 2003; Geerlings, et al., 2014). For example, Fukui functions are given directly by
as normally defined (Parr & Yang, 1984), but here the bordering-integer densities include the polarizing effect of the partition potential which accounts for the detailed environment of the atom in the molecule. Similarly, the {ω α } are those that lead to electronegativity equalization (Cohen & Wasserman, 2006; Parr, et al., 1978).
Perspective
The approximations of Equations (7) and (9) need to be extended to be applicable to realistic, complex chemical systems. The roads to robust approximations of general applicability and to efficient and accurate linear-scaling algorithms will be long and winding. Therefore, one might wonder whether these roads are worth taking in the first place, especially given that: (a) As computers get more powerful and machine-learning conquers the quantum-chemistry landscape, KS-DFT calculations with sophisticated approximations to E XC will become applicable to an ever-expanding frontier of chemical complexity; (b) several other fragment-based (Gordon, et al., 2012) and embedding methods (Jacob & Neugebauer, 2014; Lee, et al., 2019; Sun & Chan, 2016) are enabling multi-million atom and multi-scale calculations where individual fragment densities are of little use, and (c) quantum computing, when finally here, will allow for the direct calculation of many-electron wave functions rendering DFT-based methods obsolete.
Our current take on these three valid concerns is the following: (a) Further improvements of approximate XC functionals will continue via two directions: A non-empirical approach in which more exact constraints will be incorporated, especially perhaps in the framework of Generalized-Kohn-Sham (Kummel & Kronik, 2008; Seidl, et al., 1996), and an empirical approach exploiting large data sets of chemical information through machine-learning tools (Seino, et al., 2018; Snyder, et al., 2012). All of these positive developments can be readily incorporated into the framework described in Section III. Furthermore, as mentioned toward the end of Section III, the fragments do not need to be atoms but could be monomers, functional groups, protein backbones, etc., and calculations will greatly benefit from improved approximations to EXC; (b) there is plenty of room in quantum chemistry for more than one type of embedding method. When minimizing the total energy is the only goal, our approach is admittedly not essential. When, however, besides minimizing the energy one is interested in examining the individual fragment density distortions or understanding the reactivity of one fragment in a specific chemical environment, then our approach offers a unique, useful perspective; (c) yes, someday quantum computers will be ready to solve the many-electron Schrödinger equation for large molecules. However, one will always want to understand the results, which involves determining how individual atoms or fragments in the molecule are distorted due to the interactions with neighboring atoms or fragments. The tools described here allow us to accomplish precisely this, regardless of the type of computers employed.
