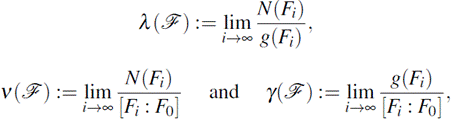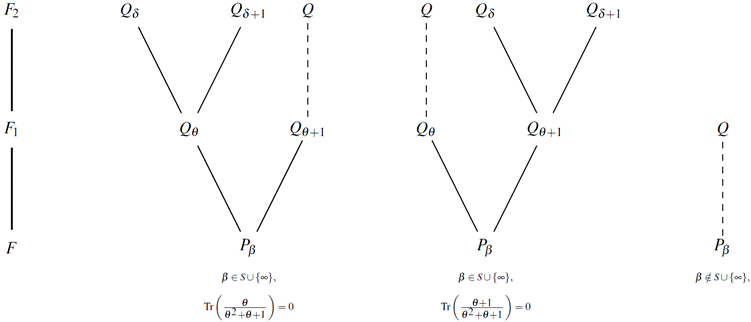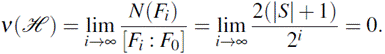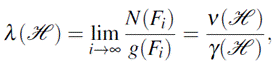Introduction

Let 𝔽 _q be a finite field with q = p ⁿ elements, where p is a prime and n ≥ 1 an integer. Let 𝔽/𝔽 _q be an algebraic function field whose constant field is 𝔽 _q . (^{Weil, 1948}) proved that the number N = N(F) of rational places of F/𝔽 _q is bounded by

where g = g(F) denotes the genus of F. (^{Ihara, 1981}) observed that the Weil bound can be improved if g is large with respect to q. In order it study how many rational places a function field F/𝔽 _q of large genus can have, he introduced the function

where

In the same paper he used reduction of Shimura curves to prove that Aq≥q-1 for q = p ^2m . He also gave the upper bound A(q) ≤ 1/2 + 1 8q+1 which is better that the upper bound for A(q) obtained from the Weil bound. This result was improved by (^{Drinfel’d & Vladut, 1983}) showing the inequality

which is still the best known upper bound. Using class field theory, (^{Serre, 1983}) showed that A(q) > 0 for any q. The exact value of A(q) is however unknown when q is not a square. (^{Tsfasman, et al., 1982}) showed the existence of linear codes with parameters improving the so-called Gilbert-Varshamov bound using a sequence of modular curves over 𝔽 _p2 that reaches the Drinfel’d-Vladut bound and a construction of linear codes due to Goppa. After that, the interest in the study of the quantity A(q) increased. However, the techniques involved are far from being elementary and the curves (function fields) used are not explicit, which is crucial for potential applications in coding theory.

(^{Garcia & Stichtenoth, 1995}) introduced the concept of recursive towers of function fields over finite fields, i.e., towers defined by bivariate equations f (x, y)= 0. However, not any f (x, y) defines a tower, so a convenient choice of f (x, y) must be made. The limit of a recursive tower of function fields over 𝔽 _q is a real non-negative real number. One can see that it is a lower bound for A(q). (See section 2 for details).

While the main purpose in this theory is to construct recursive towers with positive limit to obtain non-trivial lower bounds for A(q), this search can be reduced by showing when a recursive tower has limit equal to zero. According to (^{Garcia & Stichtenoth, 2000}), a recursive tower has limit equal to zero if it is skew in the sense that the degree of the equation defining the tower is not the same in each variable. Since a tower with infinite genus has limit equal to zero, (^{Chara & Toledano, 2015}) gave conditions to prove the infiniteness of the genus and noticed that many known examples of non-skew recursive towers with infinite genus are particular cases of these conditions. However, there is not an easy way to determine the limit of a recursive tower non-skew of finite genus.

Among the class of recursive towers there is an important one, namely the class of Artin-Schreier type towers which are recursively defined by equations of the form

for some suitable rational function f (x) ∈ 𝔽 _q (x), where p = char (𝔽 _q ) and 0 ≠ b ∈ 𝔽 _q . (^{Beelen et al., 2004}) gave necessary conditions on the form of f (x) in order to have a tower with positive limit. Unfortunately, those conditions are not sufficient, so if one chooses one of these f (x) ∈ 𝔽 _q (x) still one has to prove that the equation (1) defines a tower and also to determine the limit of the tower, which is a non-trivial task. For instance, (^{Ling et al., 2005}) showed that the equation (1) defines a tower over 𝔽 _q , where

0 ≠ c ∈ 𝔽 _q and c ≠ b. Moreover, adding the condition bc(b-c) ^2p−2 = 1 they proved that it has finite genus, but so far it has not been possible the determination of the limit of this class of towers.

In (^{Chara et al., 2018}) was proven that sequence 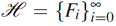of function fields defined by the Artin-Schreier equation

is a tower with finite genus over 𝔽 2 s for any positive integer s and it is asymptotically good when s is even. In particular, this tower reaches the Drinfeld-Vladut bound when s = 2. The main motivation to study this tower over 𝔽 2 𝑠 for any s odd is that recursive towers over fields with two and three elements with positive limit are not known. The aim of this note is to show that the number of rational places of each function field F _i of the tower H over 𝔽 2 𝑠 , when s is a positive integer odd, is constant. As a consequence the tower H over 𝔽 2 𝑠 for any s odd has limit equal to zero.

1 Notations and Preliminaries

An algebraic function field F over 𝔽 _q is a finite algebraic extension F of the rational function field 𝔽 _q (x), where x is a transcendental element over 𝔽 _q .

Let F be a function field over 𝔽 _q . The symbol ℙ(F) stands for the set of all places of F and g(F) for the genus.

Let F^′ be a finite extension of F and let Q ∈ ℙ(F^′). We will write Q|P when the place Q of F^’ lies over the place P of F, i.e., P = Q ∩ F.

A tower F of function fields over a finite field 𝔽 _q is a sequence 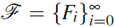of function fields over F _i /𝔽 _q satisfying the following conditions:

1. F _i ⊊ F _i+1 for all i ≥ 0.

2. The extension F _i+1 /F _i is finite and separable, for all i ≥ 1.

3. The field 𝔽 _q is algebraically closed in F _i , for all i ≥ 0.

4. The genus g(F _i ) → ∞ as i → ∞.

A tower of function field 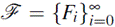over 𝔽 _q if called a recursive tower if there exist a sequence of transcendental elements xi∞i=0 over 𝔽 _q and a bivariate polynomial f (x, y) ∈ 𝔽 _q [x, y] such that F₀ = 𝔽 _q (x₀) and

where f (x _i , x _i+1 )= 0 for all i ≥ 0. In this case we say that the tower F is defined by the equation

The limit λ (F), the splitting rate ν(F) and the genus of a tower 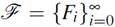over 𝔽 _q are defined as

respectively, where N(F _i ) denote the number of 𝔽 _q -rational points of F _i .

Proposition 1.1. (^{Stichtenoth, 2009}, chap 7)Let 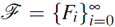be a tower over 𝔽 _q . Then

i. 0 ≤ λ (F ) ≤ A(q).

ii. 0 ≤ ν(F ) < ∞.

iii. 0 < γ(F ) ≤ ∞.

A tower F over 𝔽 _q is called asymptotically good if λ (F) > 0, asymptotically optimal if λ (F) = A(q) and asymptotically bad if λ (F)= 0.

As an immediate consequence of the Proposition 1.1 and of the definitions above, one can see that a tower F over 𝔽 _q is asymptotically good if and only if ν(F) > 0 and λ (F) < ∞.

In the following theorem we summarize the mean properties of the tower 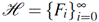defined by the equation (2).

Theorem 1.2. (^{Chara et al., 2018}) Consider the tower H over 𝔽 2 𝑠 , where s is a positive integer.

i. [F _i : F₀]= 2 ⁱ .

ii. H has finite genus.

2 The splitting rate of the tower H

Throughout this section k = 𝔽 2 𝑠 will be a finite field with 2 ^s elements where s is an odd integer and Tr denotes the trace map from 𝔽 2 𝑠 to 𝔽₂.

We begin with the following technical lemma.

Lemma 2.1. Let θ, β ∈ k such that θ2 + θ = ββ2+β+1. Then

Proof. Suppose that

then

On the other hand, by hypothesis

then

Finally, since Tr(1) = 1 and Tr(α) = Tr(α²) for all α ∈ k, we have

contradicting (3).

Lemma 2.2. Let F be a function field over k such that k is its full field of constants and let x ∈ F\k. Consider the Artin-Schreier extensions F₁ = F(y) and F₂ = F₁(z) defined by the equations

and the set

Then

i. A rational place P of F such that x(P)= ∞ or x(P)= β for some β ∈ S splits completely in F₁ into two rational places Q _θ and Q _θ+1 such that y(Q _θ )= θ and y(Q _θ+1 )= θ + 1, for some θ ∈ k.

ii. For each pair of rational places Q _θ and Q _θ+1 of F₁ one and only one of them splits completely in F₂ into two rational places Q _δ and Q _δ+1 such that z(Q _δ )= δ and z(Q _δ+1 )= δ + 1, for some δ ∈ k.

iii. The number of rational places N(F _i ) of F _i , i = 1, 2, is

Proof. Let P be a rational place of F. Then x(P)= β for some β ∈ k or x(P)= ∞. We write P := P _β or P := P_∞. Since the extension F₁/F is defined by the polynomial

And β2+β+1≠0 because k = F2s with s odd, we have that the reduction modulo P of φ is the polynomial

in the first case, and

in the second one. On the other hand, we know that φ _β is irreducible over k if and only if

and φ _β splits completely over k if and only if

Note that β ∉ S if and only if β satisfies (4). Hence, by Kummer’s Theorem (^{Stichtenoth, 2009}, T heorem 3.3.7), there is only one place of degree 2 of F₁ lying over P _β when β ∉ S (see figure 1). Now, for β ∈ S ⋃ {∞} the polynomial φ _β splits into two different linear factors over k. Clearly if θ ∈ k is a root of φ _β then we have that φ _β (T)= (T + θ )(T + (θ + 1)). Again by Kummer’s Theorem, there are exactly two rational places Q _θ , Q _θ+1 of F₁ = F(y) lying over P _β such that y(Q _θ )= θ and y(Q _θ+1 )= θ + 1. This proves (i), and since a rational place of F₁ lying over a rational place of F, we also have

Now, consider two rational places Q _θ and Q _θ+1 of F₁, for some θ ∈ k. For the proof of i)

for some β ∈ S. It is clear that the extension F₂/F₁ is defined by the polynomial

and the reduction of 𝜑 modulo Q _θ and modulo Q _θ+1 is the polynomial

respectively. By Lemma 2.1, we can assume w.l.o.g. that

This implies that φθ is irreducible over k and φθ+1 splits completely over k. Hence, by Kummer’s Theorem there is only one place of degree two of F₂ lying over Q _θ and the place Q _θ+1 splits completely in F₂ into two rational places of the form Q _δ and Q _δ+1 such that z(Q _δ )= δ and z(Q _δ+1 )= δ + 1, where δ ∈ k is a root of φθ+1. (See figure 1). It remains to prove that

As each rational place R of F₂ lies over a rational place of F₁, then R lies over a place of the form Q _θ or Q _θ+1 for some θ ∈ k. By ii), one and only one of this places splits completely in F₂. On the other hand, we have seen in the proof of i) that N(F2)= 2(|S| + 1). Thus, we obtain

Now we are in a position to state and prove one of our main results.

Theorem 2.3. Consider the tower 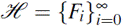over k. The number of rational places N(F _i ) of F _i is

for all i ≥ 1, where S is defined as in Lemma 2.2.

Proof. Let P_α be the only zero of x₀ + α in F₀ = k(x₀) and P_∞ be the only pole of x₀ in F₀. We show by induction that a place P_α, with α ∈ S ⋃ {∞}, has exactly two rational places in F _i for all I ≥ 1. It is true for i = 1 by Lemma 2.2, and we assume now that the assertion holds for some i. Let R₁ and R₂ the two rational places in F _i lying over P_α. We have proved in Lemma 2.2 that both places R₁ and R₂ lying over a rational place P _β of F _i−1 for some β S, and one and only one place between R₁ and R₂ has two rational places in F _i+1 . Hence, there exist two rational places in F _i+1 lying over P_α. Finally, we conclude that

for all i ≥ 1.

As an immediate consequence of the above result we have:

Theorem 2.4. The splitting rate of the tower H over k is zero.

Proof. From Theorem 2.3 we have that

Corollary 2.5. The tower H over k is asymptotically bad.

Proof. Since

we conclude λ (H )= 0.

3 Conclusions

In this note we have completed the classification of the asymptotic behavior of the tower H over a finite field with 2 ^s in terms of the parity of s. This work was started by (^{Chara et al., 2018}). As stated by (^{Beelen et al., 2006}) there are only four recursive towers of Artin-Schreier type over a field with two elements including the tower H . As a future work, one can study the remaining three in order to determine if is possible a classification such as the one given above.