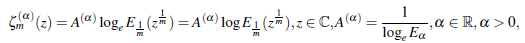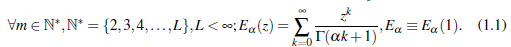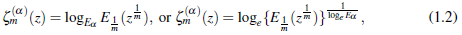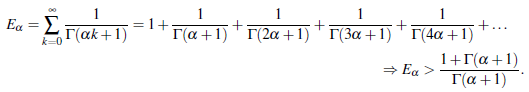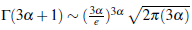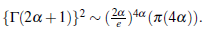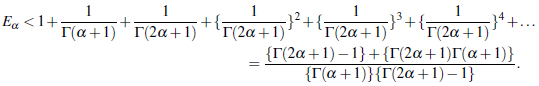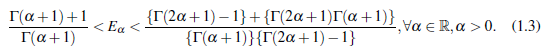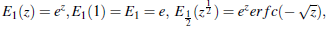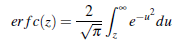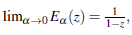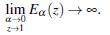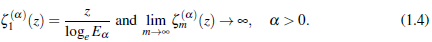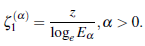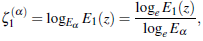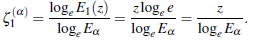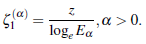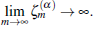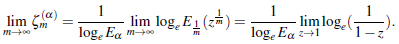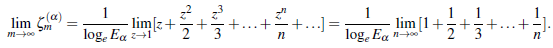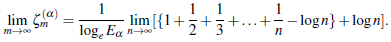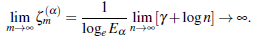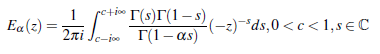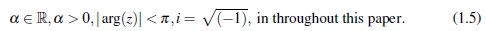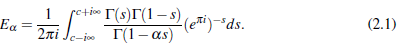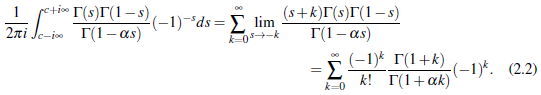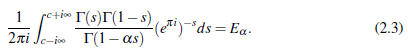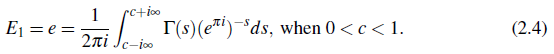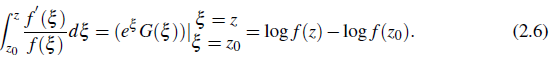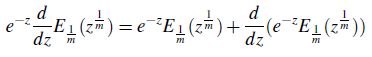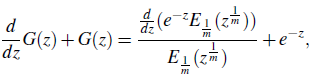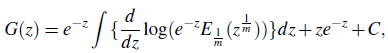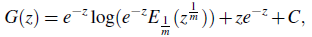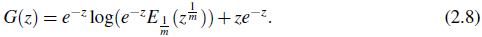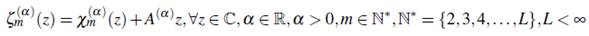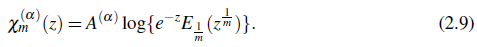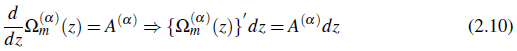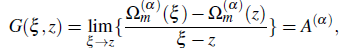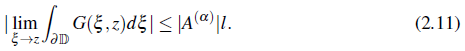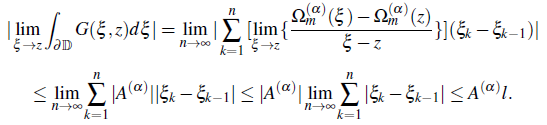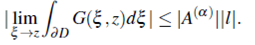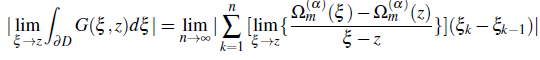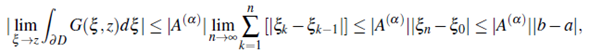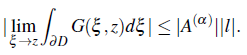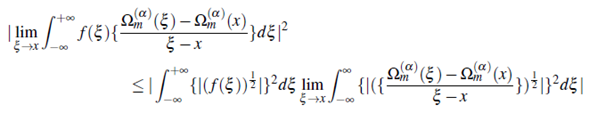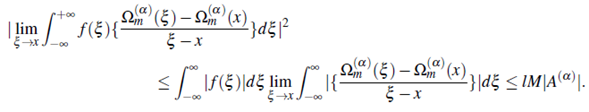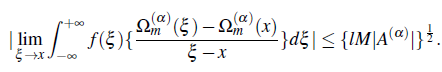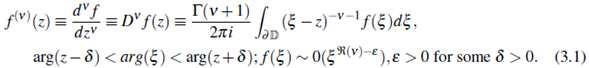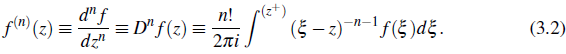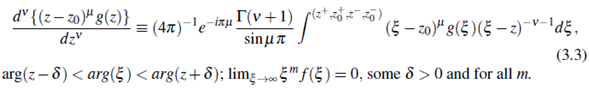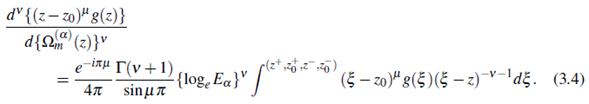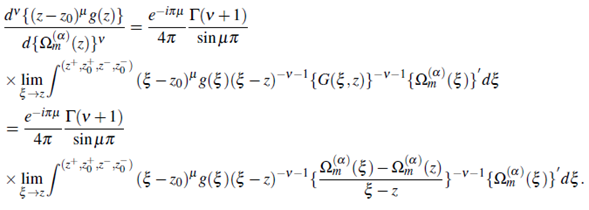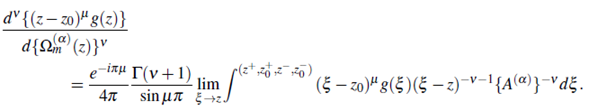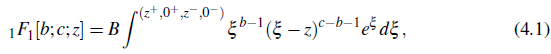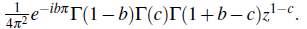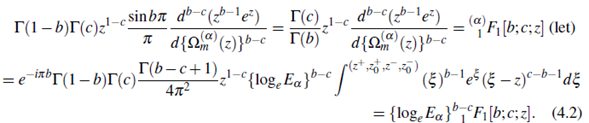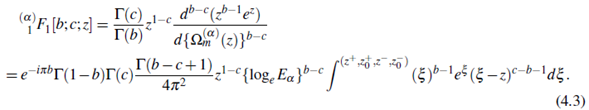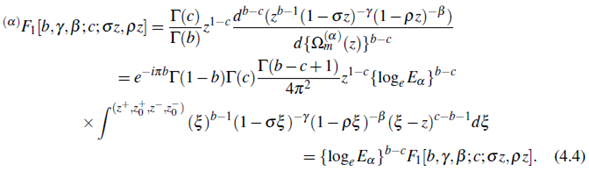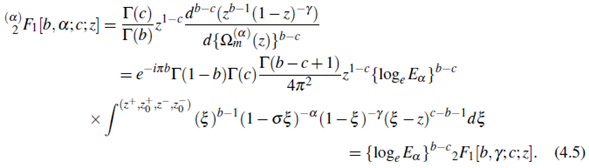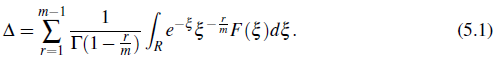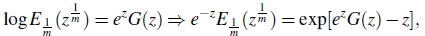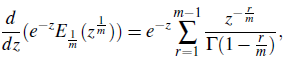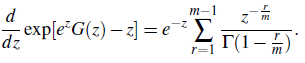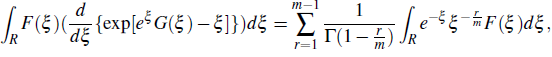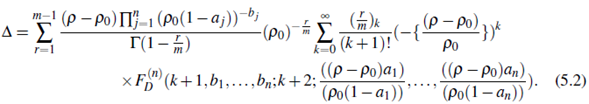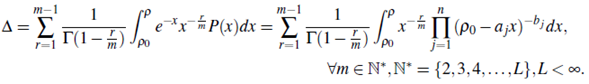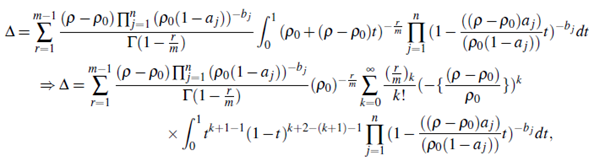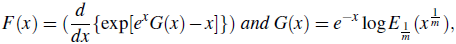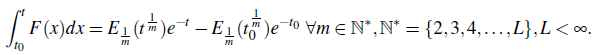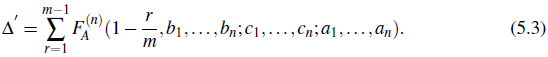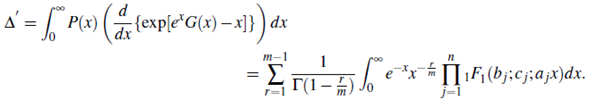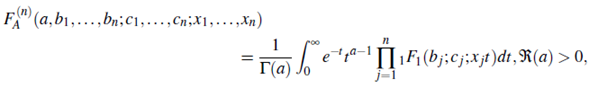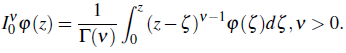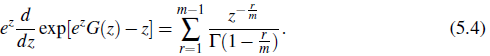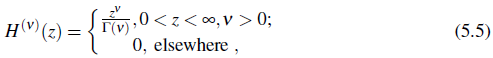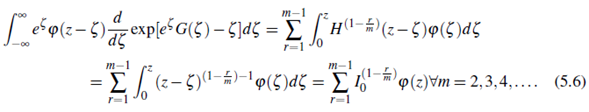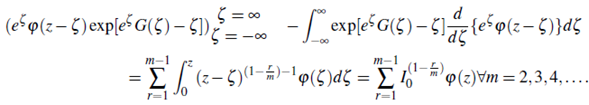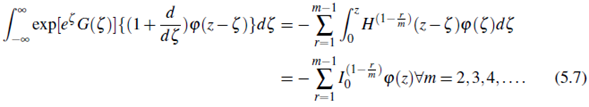1 Introduction
The study of classical Mittag-Leffler functions ((Gerenflo, Loutchko, & Luchko, 2002),(Gorenflo, Luchko, & Mainardi, 1999), (Mittag-Leffler, 1903),(Wiman 1905)) has tremendous applications in solving many of scientific problems involving fractional derivates and integrals (for example (Mathai & Haubold,2018), (Oldham & Spanier, 2006) and (Pathan & Kumar, 2019)). In this presentacion, we consider a transformation formula involving the logarithm of Mittag-Leffler function in the form:
By simple logarithmic rulings, the function (1.1) is written in the form
where all conditions given in (1.1) are followed.
Further, we find the inequality of E a greater than as
Also we have,
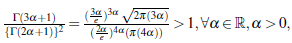 so that Γ(3α+1) > (Γ(2α+1))2
so that Γ(3α+1) > (Γ(2α+1))2
Similarly, we find that
Γ(4α +1) > (Γ (2 α + 1))3, Γ (5 α +1) > (Γ (2 α + 1))4,...,
(these results are verified by MATLAB for ∀α Є R, α > 0).
Thus, we obtain the inequality of E a less than by the series as
Therefore, the value of E a bounds between the numbers
Particularly, when a = 1, the inequality (1.3) becomes well known inequality 2 < e < 3.
Some other special cases of Mittag - Leffler function Ez(z) (see (Gorenflo et al., 2002), (Gorenflo et al., 199d) and (Peng & Li, 2010) and the earlier papers cited therein ) are
where,
Therefore by the relations of Mittag - Leffler functions given in (1.3), the function
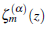 defined in (1.1) and (1.2), gives us the values
defined in (1.1) and (1.2), gives us the values
I) To prove that
Proof. For α > 0, consider the formula
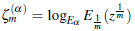 given in (1.2), and use the logarithmic formula
given in (1.2), and use the logarithmic formula
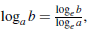 we write
we write
finally, on using the relations E1 (z) = e z , loge e = 1, we find
Therefore, we have
II) Again, to prove that
Proof Use the relations
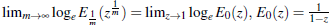 in theEqn. (1.2) and by above logarithmic formula given in I), we find that
in theEqn. (1.2) and by above logarithmic formula given in I), we find that
Thus there exists following relations
Therefore, we may write
Now, here use the relation of Euler - Maacheroni constant y, (H. M. Srivastava & Manocha, 1984, p. 20) given by
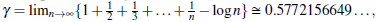 we write
we write
In order to discuss some more properties of Mittag - Leffler function Eα, we prefer to use the Mellin-Barnes integral formula given by (Mathai & Heubold, 2008, p. 88) and
And
Also, we determine the analyticity of logarithmic Mittag -Leffler function
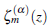 and introduce the theory and concept of derivative of complex order defined by Campos (Campos, 1984) as the derivative of complex order _ of complex function f (z) with respect to the complex variable z. Next, we apply fractional calculus theory and obtain extended Pochhammer’s type integral representations and Rodrigues formulae (Oldham & Spanier, 2006, pp. 186 -192) of some known special functions through their complex order derivatives. In a compartment method, to obtain the area of spread of infectious disease, it is supposed that the area spread depends on various parameters with weight functions. A quite different approach using a property of the logarithmic Mittag - Leffler function, we obtain the spread area of infectious diseases for different weight functions and parameters in terms of Lauricella’s multiple hypergeometric functions (H. M. Srivastava & Manocha, 1984, p. 60). It is noted that various distinguished roles of the Mittag-Leffler function and its properties are described in the researches ((Kilbas, Srivastava, & Trujillo, 2006) - (Kiryakova & Luchko, 2010), (Rogosin, 2015) - (B. L. Srivastava, Pathan, & Kumar, 2020)) and its generalizations in fractional analysis and fractional modeling are analysed in the work of researchers ((Caponetto, Dongola,&L. Fortuna, 2010), (Diethelm, 2010), (Dzherbashian, 1966), (Gorenflo, Kilbas, Mainardi, & Rogosin, 2014), (Gorenflo, Mainardi, & Srivastava, 1998), (Hilfer, 2000), (Osler, 1972) and (Podlubny, 1999)).
and introduce the theory and concept of derivative of complex order defined by Campos (Campos, 1984) as the derivative of complex order _ of complex function f (z) with respect to the complex variable z. Next, we apply fractional calculus theory and obtain extended Pochhammer’s type integral representations and Rodrigues formulae (Oldham & Spanier, 2006, pp. 186 -192) of some known special functions through their complex order derivatives. In a compartment method, to obtain the area of spread of infectious disease, it is supposed that the area spread depends on various parameters with weight functions. A quite different approach using a property of the logarithmic Mittag - Leffler function, we obtain the spread area of infectious diseases for different weight functions and parameters in terms of Lauricella’s multiple hypergeometric functions (H. M. Srivastava & Manocha, 1984, p. 60). It is noted that various distinguished roles of the Mittag-Leffler function and its properties are described in the researches ((Kilbas, Srivastava, & Trujillo, 2006) - (Kiryakova & Luchko, 2010), (Rogosin, 2015) - (B. L. Srivastava, Pathan, & Kumar, 2020)) and its generalizations in fractional analysis and fractional modeling are analysed in the work of researchers ((Caponetto, Dongola,&L. Fortuna, 2010), (Diethelm, 2010), (Dzherbashian, 1966), (Gorenflo, Kilbas, Mainardi, & Rogosin, 2014), (Gorenflo, Mainardi, & Srivastava, 1998), (Hilfer, 2000), (Osler, 1972) and (Podlubny, 1999)).
2 Analyticity of logarithmic Mittag-Leffler function ζ m (α)(z)
To determine foe malyticity of logarithmic Mittag -Leffler function ζ m (α)(z), we present following lemmas and theorems
Lemma 2.1. If s Є C and α Є R, α > 0, then for 0 < c < 1, the Mellin - Barnes type integral of Eα is given by
Proof The contour integral m (2.1) separates all potes s = -k.k.= 0,1,2,... to the left and all poles s = n +1 , n = 0,1,2,... to the right. Hence, by calculus of residue
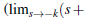
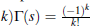 and the sum of the residue, at the points s= 0, -1, 2, ... fo the contour integral in (2. 1), we write
and the sum of the residue, at the points s= 0, -1, 2, ... fo the contour integral in (2. 1), we write
Now, using the definition of E α (z) given in (1.1) with z = 1, (2.2) becomes
Hence, the result (2.1) is found. This result is obviously identical to the formula (1.5) (when, z = 1)
Set α = 1 m the formula (2.1) to get the Mellim - Barnes type integral for E1 e = as
Lemma 2.2. If f (z) is holomorphic on a simply connected domain ⅅ ⊂ ℂ and 0 ∉ f (ⅅ) then there exists another function(z) holomorphic on ⅅ and f (ⅅ) = ℂ∖{0} is not simply connected .
Proof. By the relation g(z)=log f (z), we may write f (z)=exp[g(z)]=exp[g(z)+2nΠi] ∀n= 0,1,2, . . . Since there is no complex number [g(z)+ 2nΠi] ∈ ℂ ∀n = 0,1,2, . . . so that f (z) becomes zero, hence 0 ∉ f (ℂ) ∀ z ∈ ⅅ = ℂ. Again, ⅅ is simply connected, then, there exists
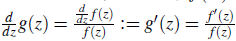 Thus we have
Thus we have
Now in (2.5), for example set f (z) = e z , then by the relation g(z) = log f (z), the left hand side of (2.5) becomes z, and that of right hand side is z - z0 and thus ultimately, the result is C0ntradlctl0n. Hence g(z) could not be defined for a continuous single-valued branch of log f (z). Therefore in this case f (ⅅ) = ℂ \{0} is not simply C0nneCted. □
Lemma 2.3. If f (z) is an entire function ∀z ∈ ℂ, in the complex plane, then there exists another function G(z) = e -z log f (z) analyticyz ∀z ∈ ℂ in that complex plane.
Proof By the relation G(z) = e -z log f (z), we have log f (z) = e z G(z) s0 that by Lemma 2.2, we get
Now for trie complex: anylysis involved, we refeo Conway (Conway, 1973). It eollows immediately that the proof. of the Lemma 2.33 is triviel. To verify the equality, we set /(z) =s ef th lbotls sides oft this result and the Lemma is followed.
For another example, set f (z)=
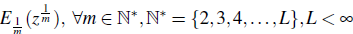 , in Lemma 2.3, then we have an analytic function
, in Lemma 2.3, then we have an analytic function
Now on differentiating both the sides of (2.7), we have
which is a linear differential equation
whence, upon integration, we obtain an integral function
C is arbitrary constant, or its equivalent form
C is arbitrary constant.
But, by (2.7) G(0) = 0 and limz→0 log
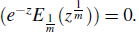 . Thus C = 0 and we find that
. Thus C = 0 and we find that
Now multiply both sides of (2.8) by A (α) and then use(1.1) and (1.2) to get a valuable relation
where
Again then, letting
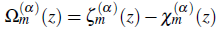 in (2.9),we have
in (2.9),we have
and
where the equation
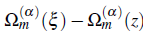 = 0 has a single root ξ = z in a complex ξ - plane in a region ⅅ. □
= 0 has a single root ξ = z in a complex ξ - plane in a region ⅅ. □
Theorem 2.1. If
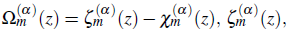 , and X
m(α)
(z) are given in (1.1) and (2.9), respectively, ∀z ∈ ⅅ- ∂ⅅ ⊂ ℂ, α∈ ℝ α>0, m ℕ* ℕ*= {2,3,4…, L} < ∞, and there is a continuous function G(ξ,z)= lim
ξ→z
, and X
m(α)
(z) are given in (1.1) and (2.9), respectively, ∀z ∈ ⅅ- ∂ⅅ ⊂ ℂ, α∈ ℝ α>0, m ℕ* ℕ*= {2,3,4…, L} < ∞, and there is a continuous function G(ξ,z)= lim
ξ→z
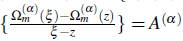 the equation
the equation
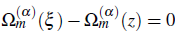 in a region ⅅ ofα complex ξ -plane , has single root ξ = z, and on a regular arc ∂ⅅ of length l, where ν
k
is a point on the regular arc ∂ⅅ lying between the points ξk-1
and ξk
and v
k
= ξ (Τ
k
) = x(Tk ) + iy(Tk) ∀
tk-1
≤ T
k
≤ tk ; k = 1,2,..., also
in a region ⅅ ofα complex ξ -plane , has single root ξ = z, and on a regular arc ∂ⅅ of length l, where ν
k
is a point on the regular arc ∂ⅅ lying between the points ξk-1
and ξk
and v
k
= ξ (Τ
k
) = x(Tk ) + iy(Tk) ∀
tk-1
≤ T
k
≤ tk ; k = 1,2,..., also
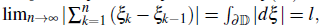 then there exists an dbsoliite value
then there exists an dbsoliite value
Proof. Since in the Theorem 2.1, ∀z ∈ ⅅ- ∂ⅅ ⊂ ℂ α ∈ ℝ α >0, m ∈ ℕ*, ℕ*= {2,3,4…,} L<∞ the equation
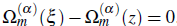 , in a region ⅅ of a complex ξ
-
plane , has single root ξ = z on a regular arc ∂ ⅅ of length l, where v
k
is a point on the regular arc ∂ⅅ lying between the points ξ
k-1
and ξ
k
and v
k
= ξ (T
k
)= x(T
k
) + iy(Tk) ∀
tk-1
≤
T
k
≤
t
k
;k = 1,2,…, so let the points α = ξ0
< ξ
1
<…< ξ
n
= b lie on the arc of length l in the interval (a,b) ⊂ (-∞,∞ ). Then by (2.10) and by Campos theory for compleX derivatives (Campos, 1984), the left hand side of the integral of the equation (2.11) is written as
, in a region ⅅ of a complex ξ
-
plane , has single root ξ = z on a regular arc ∂ ⅅ of length l, where v
k
is a point on the regular arc ∂ⅅ lying between the points ξ
k-1
and ξ
k
and v
k
= ξ (T
k
)= x(T
k
) + iy(Tk) ∀
tk-1
≤
T
k
≤
t
k
;k = 1,2,…, so let the points α = ξ0
< ξ
1
<…< ξ
n
= b lie on the arc of length l in the interval (a,b) ⊂ (-∞,∞ ). Then by (2.10) and by Campos theory for compleX derivatives (Campos, 1984), the left hand side of the integral of the equation (2.11) is written as
Hence, the theorem is followed.
Full proof of the inequality
Consider
By Eqns. (2.9) and (2.10), Such that
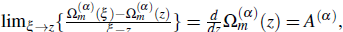 then we find
then we find
And then, we get
Theorem 2.2. Iff: ℝ
→
ℝ de/med fry the formula T ( f )
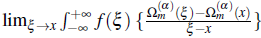 ,dξ then,for
,dξ then,for
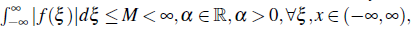 there exists anestimate
there exists anestimate
Proof. Statmg with the inequality given in and the inequality of the integral (2.11), and using the techniques for Cauchy Schwarz ine quality in (Steele, 2004, p.108), the left hand(2.12) is written as
On applying the Theorem 2.1, we have
In this way, we obtain the estimate
Hence, inequality of the Theorem 2.2 is established.
3 Campos theory and extended derivative of complex function f (z) with respect to a complex function Ω.m(α) (z)
In this section, we introduce the theory and concept of derivative of complex order defined by Campos (Campos, 1984, Eqn. (1), p. 113) as the derivative of complex order v of complex function /(z) with respect to z, the complex variable, in the form
Here in formula (3.1), v is any complex number other than a negative integer, implying that the Gamma function Γ(v + 1) is analytic, as its poles; v + 1 = 0, - 1, - 2,... ; have been excluded. The function f (z) is a complex function of a complex variable z, analytic in the (open) interior ⅅ - ∂ⅅ of the (closed) region of mtegration ⅅ, which may or may not include the point-at-infinity; the borradary ∂ⅅ is a simple and regular (or rectifiable) curve, and on it the function f (ξ) satisfies one of the progressrvdy less stringent conditions that it is analytic and it is unifomily Contuous f (z) → f (ξ) as z i0 ⅅ - ∂ⅅ tends to ξ on ⅅ; it is bounded on ∂ⅅ, with at most a finite number of discontinuities.
The Cauchy kernel (ξ −z)−v−1 is single valued if v is an integer, and the principal branch of this many-valued function is taken if v is not an integer. The contour of integration ∂ⅅ is described in the positive (counterclockwise) direction around z, and does not cross any branch-cuts in the ξ-plane; if any of the branch-cuts is infinite, the contour ∂ⅅ must be open, and can only touch the cut at the point at infinity; if there are no branch-cuts, or all are finite, the contour ∂ⅅ is closed and finite (i.e. a loop), and may or may not touch a branchpoint, as necessary to ensure that the integrand returns to the initial value after describing the loop; the integral should be independent of the contour (provided it is deformed without crossing branch-cuts or touching any new branch-points and z remains in its interior), and uniformly convergent with regard to z.
In a case, when we set v = +n, ∀n∈ ℤ +, in (3.1), it becomes the Cauchy (1825) integral theorem, given by Campos (Campos, 19884, Eqn. (2), p. 114)
(See also, (Conway, 1973), (Oldham & Spanier, 2006) and (Pathan & Kumar, 2019)).
In another case, when a function f (z) with a branch - point at z = z0 and with complex exponent μ, not an integer, that is f (z) = (z−z0)μ g(z), g(z)is analytic, then the derivative of complex order v of complex function f (z) of complex variable z, is defined by an Pochhammer’s type integral as (see Campos (Campos, 1984, Eqn. (13), p. 118))
Theorem3.1. IfG(ξ,z) =
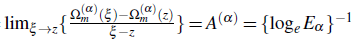 and the equation
and the equation
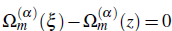 has single root ξ = z in ⅅ, Ω(α)m (z) is given (2.10), and the function f : ⅅ → ℂ, defined by f (z) = (z- z0)μ g(z) ∀z,zo ∈ ℂ, g(z) is analytic in complex ξ -plane, then ∀v,μ ∈ ℂ there exists a extended Pochhammer’s type contour integral formula for complex _ order derivative with respect to the function Ω(α)m (z) as
has single root ξ = z in ⅅ, Ω(α)m (z) is given (2.10), and the function f : ⅅ → ℂ, defined by f (z) = (z- z0)μ g(z) ∀z,zo ∈ ℂ, g(z) is analytic in complex ξ -plane, then ∀v,μ ∈ ℂ there exists a extended Pochhammer’s type contour integral formula for complex _ order derivative with respect to the function Ω(α)m (z) as
Proof. By the rulings of (3.1) and (3.3), we define
Then, in it apply the results due to (2.10), the Theorem 2.1 and (1.1).Thus, we get the result
By making use of this result, we easily obtain (3.4). This completes the proof of the Theorem.
Remark 3.1. To verify above result (3.4), put α = 1 in formula (3.4) and use the property of Eα in (1.3) for logee Eα as l logee Eα |α = 1 =1, then A(α) =1 and Ω(α)m (z)=z and hence, this formula becomes equivalent to the formula (3.3), (see Campos (Campos, 1984)).
4 An application to obtain the extended Pochhammer's type integral representations and Rodrigues formulae of hypergeometric functions
In this section, we apply our result (3.4) of the Theorem 3.1 and obtain the extended Pochhamrne°'s type integral representations and Rodrigues formulae of vaious known hy-p°rgeometric fonctions.
To achieve our goal, we present an integral representation of Kummer's function 1 F1[.] by Erdelyi (ErdImagelyi, Magnus, Oberhettinger, & Tricomi, 1953, Vol. 1, p. 271) due to Campos (Campos, 1984, Eqn. (37) with (36b)) as the Pochhammer type contour integral given by
Now in (3.4), put μ = b -1,v = b- c,z0 = 0,g(n) = ez, the nomplex b - 1 is not an integer, and thus multiply both of the sides by the function Γ(1 - b) Γ (c)z1-c 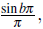 and use the results (2.10) and (1.1), and compare with (4.1) to get
and use the results (2.10) and (1.1), and compare with (4.1) to get
Therefore, the extended Pochhammer type contour integral representation of Kummer's type hypergeometric function
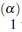 F1 [b;c;z] is of the form
F1 [b;c;z] is of the form
Remark 4.1. Setting α = I in the result (4.3), we find the results of Compos (Campos, 1984, Eqn. (37) with (36b)).
Again in (3.4), set μ = b - 1, v = b - c,zo = 0,g(z) = (1 - σz)-Y(1 - ρz)-β, the complex b - 1 is not an integer, │σz│< 1, │ρz│ < 1 and then multiply both the sides by the function Γ(1 - b)Γ(c)z1-c
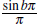 . Now use the results of (4.2) together with the formula (Srivastava and Manocha (H. M. Srivastava & Manocha, 19841, p.290)) to obtain the Pochhammer contour integral of App ell's function F1 [.,.] of two variables, given by
. Now use the results of (4.2) together with the formula (Srivastava and Manocha (H. M. Srivastava & Manocha, 19841, p.290)) to obtain the Pochhammer contour integral of App ell's function F1 [.,.] of two variables, given by
Further, put σ = 1, ρ = 0 in Eqn. (4.4), to find the Pochhammer's type contour integral formula for the Gaussian hypergeometric function 2 F1 [.], given by
Remark 4.2. Setting α = 1 in the result (4.5), we find the results of Compose (Campos, 1984, Eqn. (32) with (31b)).
5 An application in the case of spread of infectious disease in terms of multiple hypergeometric functions
In this section, we consider another property of the logarithmic Mittag - Leffler function to obtain the area of spread of infectious disease for different parameters and weight functions. The results are evaluated in terms of Lauricella's multiple hypergeometric functions.
Theorem 5.1. IfG(z) =
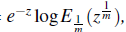 (given in Lemma 2.3) and
(given in Lemma 2.3) and
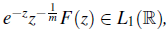
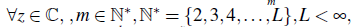 there exists a function F : ℝ → ℝ, defined
there exists a function F : ℝ → ℝ, defined
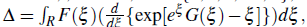 and then
and then
Proof. Since G(z) =
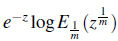 , we may write
, we may write
so that on using the formula (see Mathai and Haubold (Mathai & Haubold, 2008, p. 84)),
we may further write as
Thus we have
which gives the result (5.1).
Theorem 5.2. Let the infectious disease is spreading by the rulings F (x) =
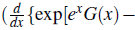
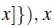 > 0, where, G(x) =
> 0, where, G(x) =
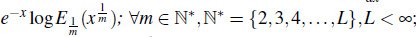 e
-x
logE1 with the weight function P(x) =
e
-x
logE1 with the weight function P(x) =
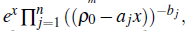 , and the parameters ρ
0
> 0, bj ∈ ℝ, 0 < aj < 1∀ j = 1, 2,3,...,n; then, for ρ > ρ
0
, the spreading area A of the disease in the domain (p0, p ) G R, is obtained by the formula ∆ =
, and the parameters ρ
0
> 0, bj ∈ ℝ, 0 < aj < 1∀ j = 1, 2,3,...,n; then, for ρ > ρ
0
, the spreading area A of the disease in the domain (p0, p ) G R, is obtained by the formula ∆ =
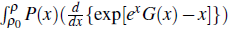 dx and found by
dx and found by
Here, the F (n) D (.)being a Lauricella's multiple hypaergeometric function defined in (H. M. Srivastava & Manocha, 1984, Eqn.(4),p. 60).
Proof. Starting from (5.1), we have
Now suppose 0 <ρ0<ρ, x-ρ 0 = (ρ0-ρ0)t ∀0 < ρ 0 ≤ x ≤ ρ,t ≥0+ then
which on applying the technique of Chandel, Agrawal and Kumar (Chandel, Agrawal, & Kumar, 1993), and the formula of the Exton (Exton, 1976, Eqn. (2.3.6), p. 49) yields the result (5.2). □
Remark 5.1. In the Theorem 5.2,we have used the ruling,
which emphasize the following useful integral
Theorem 5.3. Let the infectious disease is spreading by the rulings F(x) =
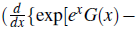
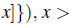 0,where, G(x) =
0,where, G(x) =
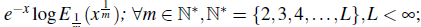 ; with the weight function P(x)=
; with the weight function P(x)=
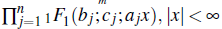 and the parameters bj ∈ ℝ, aj > 0, cj ≠ 0,
-
1, -2,..., ∀j = 1,2,3,...,n, and │a
1
+... + a
n
│< 1. Then the spreading area ∆ of the disease in the domain (0,∞) ⊂ ℝ, is obtained by the formula ∆' =
and the parameters bj ∈ ℝ, aj > 0, cj ≠ 0,
-
1, -2,..., ∀j = 1,2,3,...,n, and │a
1
+... + a
n
│< 1. Then the spreading area ∆ of the disease in the domain (0,∞) ⊂ ℝ, is obtained by the formula ∆' =
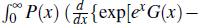 -
-
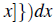 and found by
and found by
Proof. In the similar manner of Theorem 5.2, we have
Then apply the Euler integral formula of Exton (Exton, 1976, Eqn. (2.4.2), p. 49)
to get the formula (5.4).The F (n) (.) being a Lauricella's multiple hypaergeometric function defined in (H. M. Srivastava & Manocha, 1984, Eqn. (1), p. 60).
Relations of logarithmic Mittag Leffler function into Riemann-Liouville fractional integral
From the Theorem 5.1, consider that
G(z) = e
-z
log E
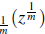 m = 2,3,4,..., and that the Riemann - Liouville fractional integral, given by (Diethelm, 2010, p.13)
m = 2,3,4,..., and that the Riemann - Liouville fractional integral, given by (Diethelm, 2010, p.13)
Therefore by proof of the Theorem 5.1, we have
Now, define that
and any function Φ (z) such that limz →±∞ Φ(z)= 0.
Then for z > 0, make an appeal to the Theorem 5.1 and along with formulae (5.4) and (5.5), we obtain the relation of logarithmic function with the Riemann - Liouville fractional integral as
In another way, we write
Therefore, we get
Conclusions
The ideas and techniques employed for the Mittag-Leffler function can be used for numerical calculation of other functions of the hypergeometric type (see for example ((Gorenflo et al., 2002) and (Peng & Li, 2010)). In particular, the same method with some small modifications can be applied for the Wright function playing a very important role in the theory of partial differential equations of fractional order (see for example, (Gorenflo et al., 1999)).To this end, simple examples of Mittag - Leffler function are well known. Some of the more complicated examples on logarithmic Mittag - Leffler function do not seem to be well known. In our investigation, we defined the logarithmic Mittag - Leffler function with prescribed conditions and discussed some of its analytic properties. In order to illustrate the application of the general properties, we have demonstrated the usefulness of the concept, in connection with the theory of special functions, their extended Pochhammer's type integral representations, Rodrigues formulae and fractional calculus. In certain conditions, it becomes very useful in obtaining complex order derivative to develop the uses of special functions, their Rodrigues formulae and fractional calculus. The results obtained in our paper are involving Kummer hypergeometric function, Gaussian hypergeometric function and Appell's function. By manipulation of their parameters, we may find Bessel's function, Laguerre function, Legendre function, Hermite function, Tchebycheff function and Gegenbauer function of complex order on the lines of the work found in the literature of Campos (Campos, 1984).