Introduction
The use of information and communication technology (ICT), as for instance computational mathematical software, helps in the visualization and dynamical representations of abstract ideas and establishment of connections with algebra (Wright, 2005;Hohenwarter, Hohenwarter, Kreis, & Lavicza, 2008;Lavicza, 2010;Kreis, 2004). Among the technological resources used for teaching and learning mathematics are dynamic geometric environments (DGE), computer algebra system (CAS), and object programming software. In the case of the GeoGebra software, we have an immediately interaction between geometrical 2D and 3D view, Algebra views and CAS views. For these reasons, GeoGebra seem to us a resource with great potentialities that we can use for teaching and learning mathematics, in any level of education. As a 21st-century software conception, GeoGebra is one of the several new-generation mathematics learning technologies that are reshaping the represen tational infrastructure of mathematics education, providing the world community with an easy and freely software to interact with powerful mathematical processes and tools (Bu, Spector, & Haciomeroglu, 2011). In fact, several mathematicians point the role of visu alization in the genesis of many of mathematical concepts and ideas, supporting and type of teach and learning in opposition a bourbaker point of view. Tristan Nendhan says that the bourbaker point of view led to the "divorce from one's sensory experience of the world, despite the fact that the very phenomena one is studying were often discovered by appealing to geometric (and perhaps physical) intuition" (Needham, 1998, p. vii).
In spite of the use of technology in teaching mathematics at the university level, the knowl edge about its efficiency as a teaching resource is insignificant (Lavicza, 2010). Here we are interesting in studying the effectiveness of GeoGebra in the teaching and learning of some properties of complex functions.
Literature Review
Here, our focus of attention is the exploration of the power of visualization for teaching and learning complex function analysis using, in a first moment, the framework about visualiza tion proposed by (Gutierrez, 1996) and based in the action-process-object-schema (APOS) view of an individual's mental construction of a concept (Asiala et al., 1997).
Studies concerning teaching and learning complex numbers are very scarce (Danenhower, 2006; Harel, 2013; Nemirovsky & Soto-Johnson, 2013; Panaoura, Elia, Gagatsis, & Giatilis, 2006; Soto-Johnson & Troup, 2014; Nordlander & Nordlander, 2012). These studies are essentially related with the sense and concept of the complex numbers and some of their algebraic properties. The results of these studies show that participants struggle to reason geometrically about complex numbers. Briefly, Panaoura et al. (2006) found that high school students had difficulty in the transition between algebraic and geomet ric reasoning. Within the framework of DNR - based on the three foundational principles of duality, necessity, and repeated-reasoning - (Harel, 2013) conducted three teaching ex periments with prospective and in-service mathematics teachers as well as tested a DNR-based unit on complex numbers He highlighted three ways of thinking: structural reasoning (theory building and non-computational); deductive reasoning (definitional reasoning and reasoning in terms of quantifiers, connectives, and conditional statements); and reflective reasoning (retrospective reflection and forward reflection) (2013, p. 55). Harel also noted that the pre-service teachers of the experiments have serious difficulties to attach a geo metric meaning to the addition and multiplication of complex numbers. Nemirovsky and Soto-Johnson (2013) observed that the use of the classroom floor as a model of the com plex plane and making use of stick-on dots and strings, pre-service teachers discovered that multiplying by i corresponds to a 90° rotation around the origin.
Soto-Johnson and Troup (2014) found that undergraduates were integrating both algebraic and geometric reasoning while drawing a representative diagram of the algebraic opera tions. In this work the effect of gestures by the teacher's interactions with their students was also an object of study. Danenhower (2006) has in consideration the university students' understanding of their representations of complex numbers and the shift among these rep resentations, using join Sfard's (1991) and APOS (Dubinsky, 1991) theoretical framework: algebraic extension representation; Cartesian vector representation; polar representation; and symbolic representation. He found that, while students were competent in polar and Cartesian forms, they were somehow "less proficient in translating from one to the other, and nearly half did not have good judgment about when to shift to another form" (Danenhower, 2006, p. 151), and whereas "almost all the interviewed students had a process understanding of the polar form; none had a clear object understanding" (Danenhower, 2006, p. 150).
Considering the integration of technology in the teaching process, some authors suggest that technology can cause harm by promoting over-generalizations (Clements & Battista, 1992; Olive, 2000) or an over-reliance on technology (Salomon, 1990). Other studies reveal that technology can help students and teachers in improving and clarifying mathematical ideas (Arcavi & Hadas, 2000; Barrera-Mora & Reyes-Rodríguez, 2013; Hollebrands, 2007; Jones, 2000; Olive, 2000; Tabaghi & Sinclair, 2013; Heid & Blume, 2008; Vitale, Black, & Swart, 2014). DGEs such as GeoGebra have been shown to help the development of mathematical concepts related to real-valued differentiation (Hohenwarter et al., 2008). (Olive, 2000) and (Hollebrands, 2007) state that Geometer's SketchPad, another DGE, makes abstract ideas appear more concrete, which could help students ground reasoning and model the reality. (Salomon, 1990) suggested that DGEs may help students by providing multiple representations of mathematical objects.
(Nemirovsky & Soto-Johnson, 2013) conducted a study, using microethnographic analysis techniques, involving the exploration of the function f (z) = e az , using Geometer's Sketch pad, by two pre-service teachers. From Sfard's theoretical framework (Sfard, 1991, 1994), their results suggest that perceptuomotor activities involving technology may serve as an in strument in facilitating reification of abstract mathematical objects such as complex-valued functions.
Next, we analyze some results of the research, considering the mathematical content to be studied, which requires: the use of multiple representations of the same mathematical object, the characteristics of our experiment target group, and the students visualization capabilities.
In the study that we have carried out, the visualization had a crucial role; the students visual ization of GeoGebra applets, built by them, allowed that specific properties of the complex functions were acquired by the students. Indeed, the visualization includes processes of con structing and transforming both visual and mental images and graphical sketches that may led to mathematical reasoning (Presmeg, 1997). These sketches are central for mathemat ical communication and comprehension of certain rules/properties/concepts (Roth, 2003, p. 3). As Arcavi states:
" visualization is described as the process and the product of creation, interpretation, use of and reflection upon images, diagrams, in our minds, on paper or with technological tools, with the purpose of depicting and communicating information, thinking about and develop ing previously unknown ideas and advancing understandings (Arcavi, 2003, p. 217)."
Also, the role of visualization in teaching and learning mathematics, namely in higher ed ucation, has been studied by several authors (Mascarello & Winkelmann, 1986). For instance, (Meng, Jiang, Shi, & Liang, 2014) have used MatLab in the context of simu lation problems. ming Zhang and Wang (2013) mention the use of computational tools, they refer "mathematical software", to compute integrals of complex functions in a collabo rative context. It worth mention that the above-mentioned authors, focused in mathematical computations and visualization. It should be noted that in the described research GeoGebra is not used.
We found the use of GeoGebra, in a research work with a control student group, as a collab orative and cooperative learning tool focused in topics of real analysis (Takaci, Stankov, & Milanovic, 2015), and there are also works making use of GeoGebra for the illustra tion of some geometric properties of complex functions using two 2D views of GeoGebra
The technology used in this experiment allows the learner to perform several relevant ex plorations for the study of complex functions analysis, reducing mindless calculations and promoting situations of questioning, conjecturing, explanation and verbalisation, which are fundamental for the development of mathematical reasoning - inductive, deductive and even abductive (A. M. D.Breda & Dos Santos, 2016).
In fact, the authors of this paper have created specific GeoGebra tools for the colouring domain technique in the complex plane. This technique was initially developed by Farris in 1997(Farris, 1997) and latter on was broadly used for visualising properties of complex functions (Poelke & Polthier, 2009; Wegert & Semmler, 2010; Wegert, 2012). Briefly, in GeoGebra we have construct, among others, tools to get the stereographic projection of spherical points making use of GeoGebra dynamic color proprieties (Liste, 2014) to create coloring domains (A.Breda et al., 2013; A. M. D. Breda & Dos Santos, 2015).
In relation to the teaching and learning of mathematics our study took in consideration the role of mediation in the learning processes. The concept of mediation, central in Vygotsky's theory of learning (Vygotsky, 1978), considers that the use of devices, socially and cultur ally constructed, with effects on the conceptions and the individual learning are dependent on the contexts of interaction (Cole & Wertsch, 1996). In our study we made use of the human interaction and the technological and educational mediation devices. By human interaction we mean all the actions among students and students and teachers. The techno logical device of mediation used was the environment provided by GeoGebra, supporting the exploratory nature of the educational tasks proposed. Finally, the educational mediation is given by the communication established in the class, in particular, the communication of results expressed through written productions.
The APOS (Action-Process-Objects-Schema) theory for the learning of mathematics, namely in the contents of algebra and functions related to complex analysis, will be part of our theo retical framework. (Dubinsky, 1991; Dubinsky, Czarnocha, Prabhu, & Vidakovic, 1999; Dubinsky & Mcdonald, 2002; Dubinsky & Wilson, 2013). It is the gap between the expe rience and the individual mental structure that drive his/her cognitive development and the acquisition/construction of new knowledge. The new object of knowledge is assimilated by the students through the structures already constituted, the being of the new object per ceived in a certain way. The new object made produces internal conflicts, which are or not overcome by the accommodation of cognitive structures. When the internal conflict end-up the new object is perceived in another way. New knowledge is being built.
An action in APOS theory context is a repeatable physical or mental manipulation that transforms objects (Dubinsky, 1984). Actions are procedures or transformations that are performed on objects, usually in a very step-by-step manner. In the tasks proposed, namely in the analysis of the domain and the co-domain of the complex functions, the actions can be repeated several times until the student interiorize the behaviour of the function in anal ysis. GeoGebra assists the transformation of a physical action (by dragging) into mental action when a student is able to make instant identification of some property, with or with out the graphical resource of the function. Indeed, here in the action process dragging "offers a feedback to the discovering phase, and in this way it provides support to the role of proofs as real "explanations" of conjectures or properties." (Arzarello, Olivero, Paola, & Robutti, 2002, p. 66) Also, in the change of the function algebraic expression we have actions supported by the multiple views present in GeoGebra.
Through interiorization, a sequence of actions can be reflected upon, envisioned and ana lyzed trough mental procedures. When an individual interiorize a sequence of actions we say that they have constructed a process.
Here, when the students apply a set of actions in the analysis of several functions behavior, we consider that they have constructed a process. In this sense the use of GeoGebra ap plications and tools for complex functions is of great help in getting, from the graphical representation of a complex function, several outputs. The written description of properties inferred by distinct representations, given by GeoGebra, are evidence that a process has oc curred. These evidences are visible in the collected videos of the dyads and in the written responses of the students. Note that a process can be transformed in an object when it is perceived as an entity upon which actions and processes can be made, however there are objects that never can’t be a process (Dubinsky, 1984).
When an individual is able to reflect upon a process as a whole and even apply other actions to that process, we say that the individual has encapsulated that process into an object. In our study, we expect to obtain data whose analysis reveals that the students encapsulated some processes in their heuristics.
Finally, actions, processes, and objects are associated to schemas. The construction of these schemas by the students will be an object of analysis looking at their written answers.
According to Ponte (2005), there are two main factors determining learning: the activity students develop and the reflection they carry out on the activity. The task is the starting point for a mathematical activity, which may or not occur (Ponte, 2005). The tasks can be differentiated by their degree of structure and the degree of difficulty. In terms of the degree of structure, we distinguish between closed and open tasks. In closed tasks it is clearly stated what is given and what is requested, being left to the executer the way to a get solution; in open tasks, there is a considerable degree of uncertainty, leaving the executer the freedom to play an important role in chose the data to work with and what can be discover under the choosing assumptions (Ponte, 2005). With regard to the degree of difficulty, tasks may represent a reduced challenge or a high challenge. Thus, among the open tasks, we have explorations and investigations running through in an increasing degree of challenge. In our study, given the time limitation and our interest in focusing on the influence of the use of GeoGebra in the insights and in the argumentative process used by the students, we have chosen some specific problems.
In the research we have conducted the researcher interact with the student and research object, the learning procedures, and where they do occur, having in mind that the experiment is being done in a context of social interaction in the presence of diverse languages. Thus, considering the objectives of this study, we place ourselves in an interpretative paradigm, within a qualitative approach (Bogdan & Biklen, 1997; Guba, Guba, & Lincoln, 1994).
The study, here reported has several characteristics of qualitative research, according to the perspective of (Bogdan & Biklen, 1997). Namely, researchers are the main agents for collecting and interpreting data. These data have a highly descriptive and detailed na ture, allowing them to analyze actions and facts in detail. Choosing to carry out a teach ing experiment research methodology the identification and the analysis of the process of the phenomenon under study are the main focus of this research. The learning outcomes are also subject to scrutiny, not being our main concern. It should be pointed out that (Bogdan & Biklen, 1997) understand the role of the qualitative researchers as being a non-interventional role, looking for the least effect of possible contamination with their immer sion in the medium that intends to investigate. However, given the research design chosen for the study, the researchers were intentionally interventional, but this was also scrutinized and following all the corresponding ethical rules.
The option by the interpretive paradigm results from the need to explore, interpret and understand the facts from the point of view of the participants in the study, taking into account the particularities of the environment where the study took place.
The teaching experiment as a research methodology emerged in the United States in the 1970s. "It has a nature of intervention, since it intends to investigate the possibilities for educational improvement bringing up new forms of learning in order and studding them." (Cobb, Confrey, DiSessa, Lehrer, & Schauble, 2003). The design of the teaching experi ment involves the elaboration of a sequence of tasks to be proposed to the students, which is used as a teaching hypothesis subject to re-evaluations and readjustments (Cobb et al., 2003).
The learning sequence consisted of eight tasks involving: the action of complex functions over subsets of their domain; the use of colored domain to obtain properties of complex functions, making the interpretation of its colored graphs; and the study of Mobius trans formations. All tasks forced the use of GeoGebra tools that students would have to adapt to the situations proposed to be analyzed. The tasks were chained in a logical sequence, with progressive levels of difficulty, some of them being held in classes, others to be executed as homework and send the resolutions/doubts by email to the researchers.
The tasks were given in printed on paper, accompanied by the necessary GeoGebra files. They should write their answers in printed tasks and save their GeoGebra applications. Another instrument of analysis is the students' attitudes to GeoGebra inventory (IAAFG) (Dos Santos & Peres, 2012), the students answered the IAAFG at the beginning and at the end of the experiment.
Materials, participants and methods
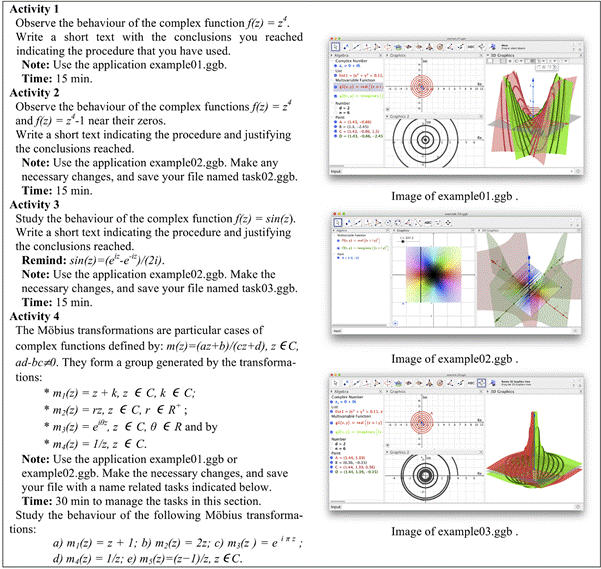
We have conceived tasks appealing to the use the GeoGebra tools to visualize the domain, the co-domain, the action of a complex function, f, of a subset of its domain and also the 3D visualizations of the graphs components function of f. We have also make use of the coloring domain technique (A. M. D.Breda & Dos Santos, 2016). In the task conception the mediation processes were also taking in consideration, focusing in the interaction among students, teachers and technology. A sequence of tasks that obey to an increasing level of difficulties was thought. The nine conceived tasks were grouped in four activities as follows, see figure 1.
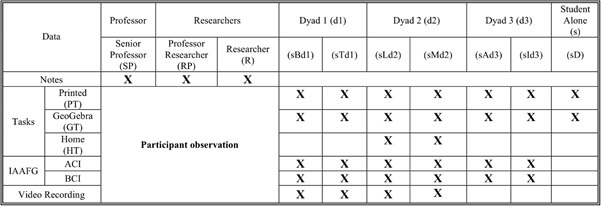
In this study the participants are: the students attending the complex analysis course; the senior professor responsible for the course, which we will designate from now on by a class professor; two researchers, one has assumed the role of tutor of the class (which we will be designate, from now on, by research professor) and the other researcher focused on the observation of the student's interactions, cautioning computational and video recording mechanisms necessary for the realization of the experiment.
Each one of the seven students, who participate in the experiment, were enrolled in a com plex analysis course, a curricular unity of a mathematics undergraduate course (3rd year) at a Portuguese university. Three of the seven students were females. The students' ages were between nineteen and twenty. All the participants accepted to be part of the experiment, being guaranteed, their anonymity and privacy.
Special attention to ethical dilemmas were taken in consideration. The students' partici pation in this research did not interfere with the class professor's decisions regarding the students' formal evaluation process.
The teaching experiment took place during a lecture; the students by themselves have cho sen to work in dyads and only one student work alone. The classroom was equipped with computers that would allow them work individually.
During the teaching experiment several data were collected in different supports allowing its analysis and triangulation. The matrix of the collected data can be visualized in figure 2. The data included work carried out autonomously at home and during the lecture about mentioned. However only two students from the same dyad (d2) sent their homework.
Discussion and results
The lecture begun and was led by the research teacher, who presented the tasks, giving brief indications of the procedures to be used in GeoGebra using the complex function f (z) = z 2 , z ∈ C as example in the first task. In the other tasks, the students worked in an autonomous way, answering the questions in the printed tasks. During the autonomous work of the students the researchers were available to answer to any question posed by them, as well as to observe the actions, reactions and the work of the students performance.
One of the strategies used, by the students, to analyze properties of complex functions was the exploration/visualization of the behavior of the action of complex function on specific subsets of its domain. Within this purpose, GeoGebra tools were developed, namely, tools creating specific types of grids. Using two GeoGebra views students were observing at the same time the movement of a point in the domain of the function, f, and the correspondence movement of its images under the action of f.
Being GeoGebra a software that allows the user interaction with geometric and algebraic properties simultaneously, the possibility of moving points on particular subsets of the do main and the assessment to instantaneous images of the image set of these points, allowed the arise of conjectures. The use of the 3D capabilities of GeoGebra applied to the compo nents of the complex function (A.Breda et al., 2013), has deepen their knowledge about some properties of functions of complex variable.
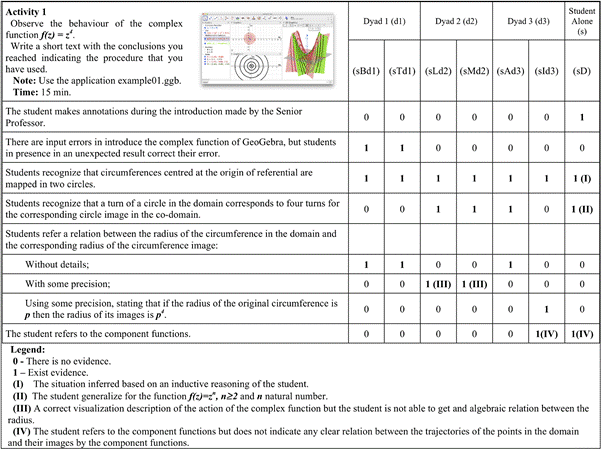
In the Activity 1, the written responses were analyzed and categorized as shown in figure 3. All the students involved were able: to input the complex functions in GeoGebra; view the domain; the co-domain; and the graph of the correspondents component functions.
In the analysis of their answers it was observed that they clearly visualize that circular orbits of the domain, centred at the origin, are transformed into circular orbits in the co-domain. In regard to the variation of the "periodicity" of the circular path, it was observed that only four of the seven students make records consistent with the property observed. Only the student who worked with the class professor made a generalization to the family of functions, f (z) = z n , n ≥ 2 and n natural number (fig. 6).
In relation to Activity 2, where the focus is on coloring domain technique and its interpre tation, all the dyads observe that around the value of 0 + 0i the black color remains black when that action f (z) = z 4 is activate. The dyads also observed the repetition, four times, of the colorings pattern around the image of 0 + 0i.
Considering the study of the map f (z)= z 4 - 1 activity, all students identify the existence of four zeros by the presence of four black zones in the image. They also identified the repetition of the standard colored pattern, four times, around the four black areas, see figure 4.
Despite the identifications, above mentioned, it should be noted that one dyad, two of the seven students, did not provide any justification for these facts. Only a dyad felt the need to write the algebraic representation of one of the four zeros. In relation to the repetition of the colored pattern, five students relate this repetition to the fourth power of z, and only one dyad gave of a more elaborate explanation stating some angular relations related with the colors involved.
It should also be noted that two of the dyads refer explicitly to the color pattern as standard or associated with the identity function. It is interesting to note that these statements only arise after the exploration of the colored domain of a function with more than one zero.
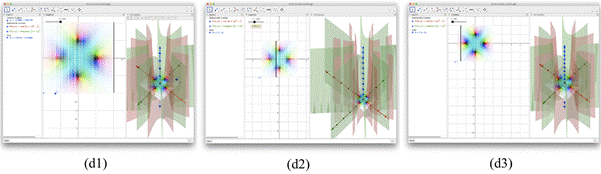
Regarding the behavior of the dyads, based on the visualization of the videos of two dyads, whose work was recorded, many differences were noticed. There is a direct relationship among the observed interaction of the dyads with the software, the discussion generated between them, and the quality of the answers given in writing texts.
The analysis of the videos also show perceptuomotor activity, by the two dyads, when they interact with the images generated in the GeoGebra applications. Similar results to the ones reported by (Nemirovsky & Soto-Johnson, 2013), were also detected. Students have used many gestures, producing several interactions between the elements of the dyad, which give rise to a writing activity.
In this analysis we have not taken in consideration the student who worked alone, since he was interfacing all the time with the class professor, who as a qualified mediator could have conditioned both the type and the quality of the answers given by this student.
Considering the proposed autonomous work only two female students has sent their work. These students elaborated answers indicating an adequate use of the software and also their expected answers regarding the mathematical topics under analysis. It should be noted that the written work sent by these students were quite different though these students belong to the same dyad.
From the observations of the collected video data, we realize that dragging points, changing the expression of the functions, and the use of GeoGebra tools and commands were profi ciently performed. This is quite surprising since, for all of them, this is the first time they were using GeoGebra.
The actions developed by the student’s triggered different interactions in the dyads, among them we mention: the use of gestures after dragging and viewing in the screen its effect, the discussion between the elements of the dyad, and the writing annotations and the driven conclusions, recorded in the tasks worksheets.
The analysis of the written productions, having in account the data collected in video; show that students were able to identify properties as a result of the process of handling the soft ware. Besides the identification of the properties, students also described the actions they have performed to get them, using a rudimental mathematical writing. It should be noted that students tend to be very descriptive in their explanations.
The heuristics present in the students' answers led to conjectures. However their justifica tions are, in general, not clear. The essential points are mentioned but there is no formal justification. The fact that was not explicitly requested a proof could be the reason behind the non-existence of a formal justification.
However, generalization processes appear in the students' responses due to the adequate visualization of the graphs of the complex functions. For example, the student's gener alization of the coloured domain pattern associated with the codomain complex function f (z) = z n , n ≥ 2, see figure 6.
When analyzing the IAAFG applied to the seven students, before and after the experiment, significant differences were found in the responses given after the experiment, when the results were analyzed by gender. The responses given by the female gender show the will ingness to continue using GeoGebra, recognizing the role of using the software in the study of the topic, these those not occur with the male gender student. These differences are significative, since the written answers given by female students are much more complete than the answers given by the male gender. In addition, it was the female students who had invested in homework assignments.
From the detailed study of the case of dyad d2, who were the students most invested in the experiment, it was verified that the results obtained by them are very positive. This evaluation was also reported by them, see figure 7.
It is worthwhile to mention that: 1) no student had ever use GeoGebra; 2) it was the first time that they have used technology for the understanding of complex analysis topics. The collected date allows us to conclude that: 1) the student learning trajectories are consistent with the proposal activities (based on the students produced texts); 2) the tasks executions are performed without great excitation (based on the video recorder); 3) the elements of one of dyads interact constantly with each other and with the software reflected in the different records and texts production; 4) the analysis of the data reinforces the adjustment of the APOS theory as framework for these experiment; 5) like other studies, the use of gestures was a form of communication of mathematical ideas between the elements of the dyads.
Concluding Remarks
The study revealed the potential of GeoGebra software in the understanding of the behavior and properties of complex functions, as result of the data content analysis. GeoGebra re veal to be a powerful mean in the development of visual capabilities, in the development of inductive reasoning (conjectures), as a technological mediator in the teaching and learning processes, as shown by the video and audio recording data. The design of new tasks, tak ing into account the dynamic and interactive capabilities of GeoGebra and pre-established topics in complex analysis will be an added value to the teaching and learning of this cur ricular unity, as indicated in the answers worksheets and in the class professor perception. We would like to emphasize the role of GeoGebra as a mediator mean of several types of interaction among students and teachers.
The experience should be repeated and deepened to overcome some of the impasses related to the researchers' role of mediation. What we can say right now is that mediation between software and students is really effective.
We recognize the limitations of the present study given the small number of students in volved and the short duration of the experience, although we consider that our methodolog ical option was the most appropriated and should be the methodology to be used in future studies.